A New Way for Cartesian Coordinate Transformation and Its Precision Evaluation

Abstract

High-precision coordinate transformation is vital for high-quality data fusion involving different coordinate systems. The transformation precision is mainly evaluated by the transformation parameters’ estimation precision, the root mean square error (RMSE) of the conversion of common points, or the RMSE of the conversion of check points. However, there are a number of issues associated with the rotation parameters’ precision estimated by the existing transformation methods. First, the estimated precision is related to the rotation matrix, so it is not suitable for scenarios where different rotation matrices are used. Second, the RMSE of the conversion of check points may not be consistent with the RMSE of the conversion of common points, so that the RMSE of the conversion of common points should not be used as a transformation precision index. In addition, some engineering applications do not have check points, and many applications need to know which range of points can meet our requirements. To deal with these limitations, this paper proposes a new way to calculate the translation parameters and evaluate the transformation precision. A lot of experimental data was used to verify the effectiveness and applicability of the proposed transformation model.

1. Introduction

Coordinate transformation is widely used in data fusion involving different coordinate systems, such as the data conversion between an independent coordinate system and national coordinate system, the conversion of point clouds between different kinds of Lidar devices, the image conversion between different photogrammetric coordinate systems, and so on [1,2,3]. To perform coordinate transformation, a rigid body transformation model is first constructed using a number of common points with two sets of coordinates in two different coordinate systems, then the transformation parameters are determined, and finally the coordinates of all non-common points under the desired coordinate system are calculated [4,5,6,7].

Coordinate transformation has been widely studied in the literature, with a focus on modeling and parameter estimation. Several different transformation models exist, including the small-rotation-angle transformation model (e.g., bursa model, Molodensky model, and Wuce model) [8,9], and arbitrary-rotation-angle transformation model (e.g., Euler angle model, unit-quaternions model, and Rodrigue matrix model) [9,10,11,12]. At the same time, a range of methods for estimating model parameters have been proposed, including the 7-parameter linear adjustment method [9,11,13,14], 8-parameter linear adjustment method [9,13], 13-parameters linear adjustment method [1], nonlinear estimation method and its improved method [2,15], Procrusters-based direct solutions [16], analytical close-form solutions [6], ill-condition model solution [17,18], and total least squares method based on the errors-in-variables model [13,19,20].

At present, how to determine the coordinate transformation precision of different transformation schemes when “the root mean square error (RMSE) of the common points in different schemes is equal”, “no check points can be used to calculate the RMSE of the check points in different schemes” (where we usually use the RMSE of the common points or the RMSE of the check points to evaluate the precision of different transformation schemes), or “the root mean square error (RMSE) of the common points or check points are not suitable for evaluating the points of different objects ” [21] (where we have proved that the coordinate transformation error for any point in space is related to its position and the translation parameters’ estimation precision [22]) has not been studied. Furthermore, there has been no research on how to reduce the influence of the rotation matrix itself on the estimation precision of rotation parameters (where the estimation precision of rotation parameters is proportional to the rotation angle of the rotation matrix). It is therefore difficult to determine the error caused by transformation and which transformation is the best regarding the minimum error, and thus it is unknown whether the transformation results meet the requirements of engineering practice. In this paper, we propose a new method for evaluating the coordinate transformation precision of different transformation schemes based on the analysis of the existing coordinate transformation models. The proposed method is evaluated extensively with simulation experiments and engineering example and the results demonstrate that the method proposed performs well.

2. Methods

In this part, we present the current transformation model and its parameters estimation, and some common evaluation indices of the transformation precision. Then, we give the new transformation model and its implementation procedure.

2.1. Related Works

2.1.1. Rigid Body Transformation

The rigid body transformation in the Cartesian coordinate system is expressed by Equation (1), in which the coordinates of points in coordinate system-(i + 1) are transformed into those in coordinate system-i using one scale parameter ($k$), three translation parameters ($t_x$, $t_y$, $t_z$), and three Euler angle parameters (${\omega }_x$, ${\omega }_y$, ${\omega }_z$) [10,23] or three Rodrigue parameters ($a$, $b$, $c$) [4,10,11,22]:

$$p_j^i=\left[\begin{array}{c}{x}_j^i\\ y_j^i\\ z_j^i\end{array}\right]=k{R}_{i+1}\left[\begin{array}{c}{x}_j^{i+1}\\ y_j^{i+1}\\ z_j^{i+1}\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]=k{R}_{i+1}{p}_j^{i+1}+T_{i+1},$$

(1)

where $p_j^i=(x_j^i,y_j^i,z_j^i)$ and $p_j^{i+1}=(x_j^{i+1},y_j^{i+1},z_j^{i+1})$ represent the positions of the common point $p_j$ in coordinate system-i and coordinate system-(i + 1), respectively; $k$ is usually equal to 1; $T_{i+1}={\left[\begin{array}{ccc}{t}_x& t_y& t_z\end{array}\right]}^T$ is the $3\times 1$ translation vector; $R_{i+1}$ is the standard $3\times 3$ rotation matrix, satisfying $R_{i+1}^T=R_{i+1}^{-1}$ and $\left|R_{i+1}\right|=1$, which is given by

$$R_{i+1}=\{\begin{array}{l}\left[\begin{array}{ccc}\cos {\omega }_y\cos {\omega }_z& \cos {\omega }_x\sin {\omega }_z+\sin {\omega }_x\sin {\omega }_y\cos {\omega }_z& \sin {\omega }_x\sin {\omega }_z-\cos {\omega }_x\sin {\omega }_y\cos {\omega }_z\\ -\cos {\omega }_y\sin {\omega }_z& \cos {\omega }_x\cos {\omega }_z-\sin {\omega }_x\sin {\omega }_y\sin {\omega }_z& \sin {\omega }_x\cos {\omega }_z+\cos {\omega }_x\sin {\omega }_y\sin {\omega }_z\\ \sin {\omega }_y& -\sin {\omega }_x\cos {\omega }_y& \cos {\omega }_x\cos {\omega }_y\end{array}\right]\\ or\\ \frac{1}{1+a^2+b^2+c^2}\left[\begin{array}{ccc}1+a^2-b^2-c^2& 2(ab+c)& 2(ac-b)\\ 2(ab-c)& 1-a^2+b^2-c^2& 2(bc+a)\\ 2(ac+b)& 2(bc-a)& 1-a^2-b^2+c^2\end{array}\right]\end{array},$$

(2)

$${[\begin{array}{ccc}a& b& c\end{array}]}^T=\tan \frac{\delta }{2}\cdot \stackrel{\rightharpoonup }{n},$$

(3)

where $\overrightarrow{n}={\left[\begin{array}{ccc}{n}_x& n_y& n_z\end{array}\right]}^T$ is the unit rotation axis of $R_{i+1}$, satisfying $n_x^2+n_y^2+n_z^2=1$; and $\delta$ is the corresponding rotation angle of $R_{i+1}$ given by:

$$\angle R_{i+1}=\arccos (\frac{tr(R_{i+1})-1}{2}),$$

(4)

where tr (.) is the trace of the matrix.

2.1.2. Parameter Estimation of the Current Transformation Model

Assume the approximate values of the rotation matrix R_i+1 are $R_{i+1,0}$ ($R_{i+1}\approx R_{i+1,0}$, $R_{i+1,0}$ is also a standard $3\times 3$ rotation matrix); the rotation parameters of $R_{i+1}$ are ${\omega }_x$, ${\omega }_y$, ${\omega }_z$, $a$, $b$, $c$; the approximate values of the rotation parameters are ${\omega }_{x0}$, ${\omega }_{y0}$, ${\omega }_{z0}$, $a_0$, $b_0$, $c_0$; and the approximate values of the translation parameters and scale parameter are $t_{x0}$, $t_{y0}$, $t_{z0}$, $k_0$. Based on the orthogonal Procrustes method in Appendix A and Equation (6), we can obtain the values of ${\omega }_{x0}$, ${\omega }_{y0}$, ${\omega }_{z0}$, $a_0$, $b_0$, $c_0$, $t_{x0}$, $t_{y0}$, $t_{z0}$, $k_0$, and $R_{i+1,0}$. With all the common points ${\left\{p_j^i,p_j^{i+1}\right\}}_{j=1,\cdots ,n}$, we can construct the error equation of the transformation model in the following equation:

$$V=Bx-l,$$

(5)

where $V$ is a $3n\times 1$ residual matrix, $B$ is a $3n\times 7$ coefficient matrix (in this paper, we assume that the coefficient matrix $B$ is no error), $x$ is a $7\times 1$ error vector of the translation parameters’ approximations, and $l$ is a $3n\times 1$ matrix (see Equations (A9)–(A16) in Appendix B for detailed derivation, or Equations (A24)–(A31) in Appendix C for detailed derivation).

Assume $P$ is the weight matrix of $l$. By using the principle of least squares adjustment [8] and minimizing $V^{T}PV$, we can obtain the estimation value $\widehat{x}$ of $x$, the estimation value $\hat{X}$ of the transformation parameters, and the estimation value ${\widehat{R}}_{i+1}$ of $R_{i+1}$ as:

$$\widehat{x}={(B^{T}PB)}^{-1}{B}^{T}Pl,$$

(6)

$$\hat{X}=X_0+\hat{x},$$

(7)

$${\widehat{R}}_{i+1}=\{\begin{array}{l}\left[\begin{array}{ccc}\cos {\widehat{\omega }}_y\cos {\widehat{\omega }}_z& \cos {\widehat{\omega }}_x\sin {\widehat{\omega }}_z+\sin {\widehat{\omega }}_x\sin {\widehat{\omega }}_y\cos {\widehat{\omega }}_z& \sin {\widehat{\omega }}_x\sin {\widehat{\omega }}_z-\cos {\widehat{\omega }}_x\sin {\widehat{\omega }}_y\cos {\widehat{\omega }}_z\\ -\cos {\widehat{\omega }}_y\sin {\widehat{\omega }}_z& \cos {\widehat{\omega }}_x\cos {\widehat{\omega }}_z-\sin {\widehat{\omega }}_x\sin {\widehat{\omega }}_y\sin {\widehat{\omega }}_z& \sin {\widehat{\omega }}_x\cos {\widehat{\omega }}_z+\cos {\widehat{\omega }}_x\sin {\widehat{\omega }}_y\sin {\widehat{\omega }}_z\\ \sin {\widehat{\omega }}_y& -\sin {\widehat{\omega }}_x\cos {\widehat{\omega }}_y& \cos {\widehat{\omega }}_x\cos {\widehat{\omega }}_y\end{array}\right]\\ or\\ \frac{1}{1+{\widehat{a}}^2+{\widehat{b}}^2+{\widehat{c}}^2}\left[\begin{array}{ccc}1+{\widehat{a}}^2-{\widehat{b}}^2-{\widehat{c}}^2& 2(\widehat{c}+\widehat{a}\widehat{b})& 2(\widehat{a}\widehat{c}-\widehat{b})\\ 2(\widehat{a}\widehat{b}-\widehat{c})& 1-{\widehat{a}}^2+{\widehat{b}}^2-{\widehat{c}}^2& 2(\widehat{a}+\widehat{b}\widehat{c})\\ 2(\widehat{b}+\widehat{a}\widehat{c})& 2(\widehat{b}\widehat{c}-\widehat{a})& 1-{\widehat{a}}^2-{\widehat{b}}^2+{\widehat{c}}^2\end{array}\right]\end{array},$$

(8)

where:

$$\begin{array}{l}\{\begin{array}{l}\widehat{X}={\left[\begin{array}{ccccccc}{\widehat{t}}_x& {\widehat{t}}_y& {\widehat{t}}_z& {\widehat{\omega }}_x& {\widehat{\omega }}_y& {\widehat{\omega }}_z& \widehat{k}\end{array}\right]}^T\\ \widehat{x}={\left[\begin{array}{ccccccc}d{\widehat{t}}_x& d{\widehat{t}}_y& d{\widehat{t}}_z& d{\widehat{\omega }}_x& d{\widehat{\omega }}_y& d{\widehat{\omega }}_z& d\widehat{k}\end{array}\right]}^T\end{array}\\ or\\ \{\begin{array}{l}\widehat{X}={\left[\begin{array}{ccccccc}{\widehat{t}}_x& {\widehat{t}}_y& {\widehat{t}}_z& \widehat{a}& \widehat{b}& \widehat{c}& \widehat{k}\end{array}\right]}^T\\ \widehat{x}={\left[\begin{array}{ccccccc}d{\widehat{t}}_x& d{\widehat{t}}_y& d{\widehat{t}}_z& d\widehat{a}& d\widehat{b}& d\widehat{c}& d\widehat{k}\end{array}\right]}^T\end{array}\end{array}.$$

(9)

2.1.3. Evaluation Indices of Transformation Precision

If ${\sigma }_0$ is the unit weight variance (usually determined in the initial processing before transformation), from error propagation [24] and Equation (6), the variance-covariance $D_{\widehat{X}}$ of the estimated transformation parameters $\widehat{X}$ can be expressed as:

$$D_{\widehat{X}}={\sigma }_0^2{Q}_{\widehat{X}}={\sigma }_0^2{Q}_{\widehat{x}}={\sigma }_0^2{(B^{T}PB)}^{-1},$$

(10)

where $D_{\widehat{X}}$, $Q_{\widehat{X}}$, $Q_{\widehat{x}}$ are $7\times 7$ matrices; and $Q_{\widehat{X}}$, $Q_{\widehat{x}}$ are the cofactor matrices of $\widehat{X}$ and $\widehat{x}$, respectively.

From Equation (10), the evaluation index of transformation precision can be expressed as:

$$\{\begin{array}{l}{\sigma }_T=\sqrt{D_{\widehat{X}}(1,1)+D_{\widehat{X}}(2,2)+D_{\widehat{X}}(3,3)}\\ {\sigma }_R=\sqrt{D_{\widehat{X}}(4,4)+D_{\widehat{X}}(5,5)+D_{\widehat{X}}(6,6)}\\ {\sigma }_k=\sqrt{D_{\widehat{X}}(7,7)}\end{array},$$

(11)

$$\{\begin{array}{l}RMS{E}_{same}=\sqrt{\frac{1}{n}{\displaystyle \sum _{j_1=1}^n{\Delta }_{j_1}^2}}\\ RMS{E}_{check}=\sqrt{\frac{1}{m}{\displaystyle \sum _{j_2=1}^m{\Delta }_{j_2}^2}}\end{array},$$

(12)

where ${\sigma }_T$, ${\sigma }_R$, and ${\sigma }_k$ are the evaluation indices of translation parameters’ estimation precision, rotation parameters’ estimation precision, and scale parameter’ estimation precision, respectively; $RMS{E}_{same}$ and $RMS{E}_{check}$ are the root mean square error of the common points and the check points, respectively; $D_{\widehat{X}}(1,1)$, $D_{\widehat{X}}(2,2)$, $D_{\widehat{X}}(3,3)$, $D_{\widehat{X}}(4,4)$, $D_{\widehat{X}}(5,5)$, $D_{\widehat{X}}(6,6)$, $D_{\widehat{X}}(7,7)$ are the diagonal elements of the matrix $D_{\widehat{X}}$; $n$ and $m$ are the total number of the common points and check points, respectively; and ${\Delta }_{j_1}$ and ${\Delta }_{j_2}$ are the transformation error of the common points and the check points, respectively, and:

$${\Delta }_{j_1}=p_{j_1}^i-\widehat{k}{\widehat{R}}_{i+1}{p}_{j_1}^{i+1}-{\widehat{T}}_{i+1}, {\Delta }_{j_2}=p_{j_2}^i-\widehat{k}{\widehat{R}}_{i+1}{p}_{j_2}^{i+1}-{\widehat{T}}_{i+1}, {\widehat{T}}_{i+1}=\left[\begin{array}{c}{\widehat{t}}_x\\ {\widehat{t}}_y\\ {\widehat{t}}_z\end{array}\right].$$

(13)

2.2. New Transformation Model

Let $R_{i+1,s}=R_{i+1}{R}_{i+1,0}^T$, $p_{j,s}^{i+1}=R_{i+1,0}{p}_j^{i+1}$. According to Equation (1), we can construct our new transformation model (where the rotation angle of the rotation matrix is close to zero):

$$p_j^i=k{R}_{i+1}{R}_{i+1,0}^T{R}_{i+1,0}{p}_j^{i+1}+T_{i+1}=k{R}_{i+1,s}{p}_{j,s}^{i+1}+T_{i+1},$$

(14)

where $R_{i+1,s}\approx R_{i+1,0}{R}_{i+1,0}^T=\left[\begin{array}{ccc}1& & \\ & 1& \\ & & 1\end{array}\right]=E_{3\times 3}, \angle R_{i+1,s}=\arccos (\frac{tr(R_{i+1,s})-1}{2})\approx 0$.

Given the rotation parameters of $R_{i+1,s}$ as ${\omega }_{xs}$, ${\omega }_{ys}$, ${\omega }_{zs}$, $a_s$, $b_s$, and $c_s$, and the approximate values of the rotation parameters as ${\omega }_{xs0}$, ${\omega }_{ys0}$, ${\omega }_{zs0}$, $a_{s0}$, $b_{s0}$, and $c_{s0}$, we can set $R_{i+1,s,0}=E_{3\times 3}$, ${\omega }_{xs0}=0$, ${\omega }_{ys0}=0$, ${\omega }_{zs0}=0$, $a_{s0}=0$, $b_{s0}=0$, and c_s0 = 0.

With all the common points ${\{p_j^i,p_j^{i+1}\}}_{j=1,\dots ,n}$, we can construct the error equation of the new transformation model in Equation (15):

$$V_s=B_s{x}_s-l,$$

(15)

where $V_s$ is a $3n\times 1$ residual matrix, $B_s$ is a $3n\times 7$ coefficient matrix, $x_s$ is the errors of the approximations $X_{s0}={\left[\begin{array}{ccccccc}{t}_{x0}& t_{y0}& t_{z0}& 0& 0& 0& k_0\end{array}\right]}^T$, $t_{x0}$, $t_{y0}$, $t_{z0}$, $k_0$, and $l$ are the same as Section 2, and:

$$x_s=\{\begin{array}{l}{\left[\begin{array}{ccccccc}d{t}_x& d{t}_y& d{t}_z& d{\omega }_{xs}& d{\omega }_{ys}& d{\omega }_{zs}& dk\end{array}\right]}^T\\ or\\ {\left[\begin{array}{ccccccc}d{t}_x& d{t}_y& d{t}_z& d{a}_s& d{b}_s& d{c}_s& dk\end{array}\right]}^T\end{array},$$

(16)

$$V_s=\left[\begin{array}{c}{v}_{s1}\\ ⋮\\ v_{sn}\end{array}\right], v_{sj}=B_{sj}{x}_s-l_j, j=1,\cdots ,n,$$

(17)

$$\begin{array}{l}{B}_s=\left[\begin{array}{c}{B}_{s1}\\ ⋮\\ B_{sn}\end{array}\right]\\ \end{array}, B_{sj}=\{\begin{array}{l}\left[\begin{array}{ccccc}{E}_{3\times 3}& \frac{\partial R_{i+1,s}}{\partial {\omega }_{xs}}{p}_{j,s}^{i+1}& \frac{\partial R_{i+1,s}}{\partial {\omega }_{ys}}{p}_{j,s}^{i+1}& \frac{\partial R_{i+1,s}}{\partial {\omega }_{zs}}{p}_{j,s}^{i+1}& p_{j,s}^{i+1}\end{array}\right]\\ or\\ \left[\begin{array}{ccccc}{E}_{3\times 3}& \frac{\partial R_{i+1,s}}{\partial a_s}{p}_{j,s}^{i+1}& \frac{\partial R_{i+1,s}}{\partial b_s}{p}_{j,s}^{i+1}& \frac{\partial R_{i+1,s}}{\partial c_s}{p}_{j,s}^{i+1}& p_{j,s}^{i+1}\end{array}\right]\end{array},$$

(18)

$$\{\begin{array}{l}\frac{\partial R_{i+1,s}}{\partial {\omega }_{xs}}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& -1& 0\end{array}\right],\frac{\partial R_{i+1,s}}{\partial {\omega }_{ys}}=\left[\begin{array}{ccc}0& 0& -1\\ 0& 0& 0\\ 1& 0& 0\end{array}\right],\frac{\partial R_{i+1,s}}{\partial {\omega }_{zs}}=\left[\begin{array}{ccc}0& 1& 0\\ -1& 0& 0\\ 0& 0& 0\end{array}\right]\\ or\\ \frac{\partial R_{i+1,s}}{\partial a_s}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 2\\ 0& -2& 0\end{array}\right],\frac{\partial R_{i+1,s}}{\partial b_s}=\left[\begin{array}{ccc}0& 0& -2\\ 0& 0& 0\\ 2& 0& 0\end{array}\right],\frac{\partial R_{i+1,s}}{\partial c_s}=\left[\begin{array}{ccc}0& 2& 0\\ -2& 0& 0\\ 0& 0& 0\end{array}\right]\end{array},$$

(19)

where $\frac{\partial R_{i+1,s}}{\partial {\omega }_{xs}}$, $\frac{\partial R_{i+1,s}}{\partial {\omega }_{ys}}$, $\frac{\partial R_{i+1,s}}{\partial {\omega }_{zs}}$, and $\frac{\partial R_{i+1,s}}{\partial a_s}$, $\frac{\partial R_{i+1,s}}{\partial b_s}$, $\frac{\partial R_{i+1,s}}{\partial c_s}$ are the partial derivation of matrix $R_{i+1,s}$ at ${\omega }_{xs0}=0$, ${\omega }_{ys0}=0$, ${\omega }_{zs0}=0$ (see Equations (A14)–(A16) in Appendix B for detailed derivation), and $a_{s0}=0$, $b_{s0}=0$, $c_{s0}=0$ (see Equations (A29)–(A31) in Appendix C for detailed derivation). Using the principle of least squares adjustment [8] and minimizing $V_s^{T}P{V}_s$, we can respectively obtain the estimation value ${\widehat{x}}_s$, ${\widehat{X}}_s$, ${\widehat{R}}_{i+1,s}$ and ${\widehat{R}}_{i+1}$ of $x_s$, $X_s$, $R_{i+1,s}$, and $R_{i+1}$ as:

$${\widehat{x}}_s={(B_s^{T}P{B}_s)}^{-1}{B}_s^{T}Pl,$$

(20)

$${\widehat{X}}_s=X_{s0}+{\widehat{x}}_s,$$

(21)

$${\widehat{R}}_{i+1}=\{\begin{array}{l}\left[\begin{array}{ccc}\cos {\widehat{\omega }}_{ys}\cos {\widehat{\omega }}_{zs}& \cos {\widehat{\omega }}_{xs}\sin {\widehat{\omega }}_{zs}+\sin {\widehat{\omega }}_{xs}\sin {\widehat{\omega }}_{ys}\cos {\widehat{\omega }}_{zs}& \sin {\widehat{\omega }}_{xs}\sin {\widehat{\omega }}_{zs}-\cos {\widehat{\omega }}_{xs}\sin {\widehat{\omega }}_{ys}\cos {\widehat{\omega }}_{zs}\\ -\cos {\widehat{\omega }}_{ys}\sin {\widehat{\omega }}_{zs}& \cos {\widehat{\omega }}_{xs}\cos {\widehat{\omega }}_{zs}-\sin {\widehat{\omega }}_{xs}\sin {\widehat{\omega }}_{ys}\sin {\widehat{\omega }}_{zs}& \sin {\widehat{\omega }}_{xs}\cos {\widehat{\omega }}_{zs}+\cos {\widehat{\omega }}_{xs}\sin {\widehat{\omega }}_{ys}\sin {\widehat{\omega }}_{zs}\\ \sin {\widehat{\omega }}_{ys}& -\sin {\widehat{\omega }}_{xs}\cos {\widehat{\omega }}_{ys}& \cos {\widehat{\omega }}_{xs}\cos {\widehat{\omega }}_{ys}\end{array}\right]\\ or\\ \frac{1}{1+{\widehat{a}}_s^2+{\widehat{b}}_s^2+{\widehat{c}}_s^2}\left[\begin{array}{ccc}1+{\widehat{a}}_s^2-{\widehat{b}}_s^2-{\widehat{c}}_s^2& 2({\widehat{c}}_s+{\widehat{a}}_s{\widehat{b}}_s)& 2({\widehat{a}}_s{\widehat{c}}_s-{\widehat{b}}_s)\\ 2({\widehat{a}}_s{\widehat{b}}_s-{\widehat{c}}_s)& 1-{\widehat{a}}_s^2+{\widehat{b}}_s^2-{\widehat{c}}_s^2& 2({\widehat{a}}_s+{\widehat{b}}_s{\widehat{c}}_s)\\ 2({\widehat{b}}_s+{\widehat{a}}_s{\widehat{c}}_s)& 2({\widehat{b}}_s{\widehat{c}}_s-{\widehat{a}}_s)& 1-{\widehat{a}}_s^2-{\widehat{b}}_s^2+{\widehat{c}}_s^2\end{array}\right]\end{array},$$

(22)

$${\widehat{R}}_{i+1}={\widehat{R}}_{i+1,s}{R}_{i+1,0},$$

(23)

where:

$$\begin{array}{l}\{\begin{array}{l}{\widehat{X}}_s={\left[\begin{array}{ccccccc}{\widehat{t}}_x& {\widehat{t}}_y& {\widehat{t}}_z& {\widehat{\omega }}_{xs}& {\widehat{\omega }}_{ys}& {\widehat{\omega }}_{zs}& \widehat{k}\end{array}\right]}^T\\ {\widehat{x}}_s={\left[\begin{array}{ccccccc}d{\widehat{t}}_x& d{\widehat{t}}_y& d{\widehat{t}}_z& d{\widehat{\omega }}_{xs}& d{\widehat{\omega }}_{ys}& d{\widehat{\omega }}_{zs}& d\widehat{k}\end{array}\right]}^T\end{array}\\ or\\ \{\begin{array}{l}{\widehat{X}}_s={\left[\begin{array}{ccccccc}{\widehat{t}}_x& {\widehat{t}}_y& {\widehat{t}}_z& {\widehat{a}}_s& {\widehat{b}}_s& {\widehat{c}}_s& \widehat{k}\end{array}\right]}^T\\ {\widehat{x}}_s={\left[\begin{array}{ccccccc}d{\widehat{t}}_x& d{\widehat{t}}_y& d{\widehat{t}}_z& d{\widehat{a}}_s& d{\widehat{b}}_s& d{\widehat{c}}_s& d\widehat{k}\end{array}\right]}^T\end{array}\end{array}.$$

(24)

2.3. Implementation Procedure of the New Transformation Model

We may compute the estimated transformation parameters ${\hat{X}}_s$ and the corresponding transformation precision evaluation indices with the following steps:

Step 1: Input the weight matrix $P$, the coordinates of the common points $p_{j_1}^i$ and $p_{j_1}^{i+1}$, and the check points $p_{j_2}^i$ and $p_{j_2}^{i+1}$ in coordinate system-i and coordinate system-(i + 1). ${\widehat{X}}_s$ The number of the common points and check points is $n$ and $m$, and the estimation threshold values of the translation parameters, the rotation parameters, and the scale parameters $Th{r}_T$, $Th{r}_R$, and $Th{r}_k$, respectively;

Step 2: Calculate the rotation matrix $R_{i+1,0}$ and the transformation parameters: $k_0$, ${\omega }_{x0}$, ${\omega }_{y0}$, ${\omega }_{z0}$, $a_0$, $b_0$, $c_0$, $t_{x0}$, $t_{y0}$, $t_{z0}$ according to Equations (A1)–(A7) in Appendix A;

Step 3: Let $X_{s0}={\left[\begin{array}{ccccccc}{t}_{x0}& t_{y0}& t_{z0}& 0& 0& 0& k_0\end{array}\right]}^T$;

Step 4: Let $p_{j_1,s}^{i+1}=R_{i+1,0}{p}_{j_1}^{i+1}$,$j_1=1,\cdots ,n$, and $p_{j_2,s}^{i+1}=R_{i+1,0}{p}_{j_2}^{i+1}$, and $j_2=1,\cdots ,m$;

Step 5: Constitute the coefficient matrix $B_s$ by Equation (18);

Step 6: Constitute the matrix $l$ by Equation (A11) or Equation (A26);

Step 7: Calculate the estimated transformation parameter vector ${\widehat{x}}_s$ by Equation (20);

Step 8: Calculate the estimated rotation matrix ${\widehat{R}}_{i+1,s}$ by Equation (22);

Step 9: If ${\widehat{x}}_s$ is less than the given threshold, which is $\max \text{{}\mathrm{abs}\text{{}{\widehat{x}}_s(1:3)\text{}}\}\le T{h}_T$, $\max \text{{}\mathrm{abs}\text{{}{\widehat{x}}_s(4:6)\text{}}\}\le T{h}_R$, and $\max \text{{}\mathrm{abs}\text{{}{\widehat{x}}_s(7)\text{}}\}\le T{h}_k$ (here $\max \text{{}\cdot \text{}}$ is the maximum value, $\mathrm{abs}\text{{}\cdot \text{}}$ is the absolute value), continue; if not, $R_{i+1,0}={\widehat{R}}_{i+1,s}{R}_{i+1,0}$, $X_{s0}(1:3)=X_{s0}(1:3)+{\widehat{x}}_s(1:3)$, $X_{s0}(7)=X_{s0}(7)+{\widehat{x}}_s(7)$, back to Step 4;

Step 10: Calculate the variance and covariance of the estimated transformation parameters ${\sigma }_{R_s}$,${\sigma }_T$, and ${\sigma }_k$:

$$\{\begin{array}{l}{\sigma }_T=\sqrt{D_{{\widehat{X}}_s}(1,1)+D_{{\widehat{X}}_s}(2,2)+D_{{\widehat{X}}_s}(3,3)}\\ {\sigma }_{R_s}=\sqrt{D_{{\widehat{X}}_s}(4,4)+D_{{\widehat{X}}_s}(5,5)+D_{{\widehat{X}}_s}(6,6)}\\ {\sigma }_k=\sqrt{D_{{\widehat{X}}_s}(7,7)}\end{array}, D_{{\widehat{X}}_s}={\sigma }_0^2{(B_s^{T}P{B}_s)}^{-1};$$

(25)

Step 11: Calculate the RMSE of the common points and the check points $RMS{E}_{same}$ and $RMS{E}_{check}$ by Equation (12).

3. Experiments and Discussion

In this part, we set a series of simulation experiments and a practical engineering experiment to demonstrate the usability and efficiency of our proposed model. We first introduce the constraints for the simulation experiments and the simulation method. Then, we give a practical engineering experimental approach. Finally, we analyze the two current transformation models and the two new transformation models with the results of the experiments.

3.1. Constraint Conditions

Without affecting the conclusion of the simulation experiments, we make some assumptions: (1) The errors of the coordinates of common points and check points in coordinate system-(i + 1) are not considered in this paper; (2) unit weight variance ${\sigma }_0=5 \mathrm{mm}$, since the size of ${\sigma }_0$ dose not affect the relative relationship between different values of different evaluation indices, and many laser scanner acquisition error = 5 mm@50 m [10]; (3) the threshold value $Th{r}_k$ of the translation parameters is ${10}^{-4}$ (equivalent to 0.1 mm), the threshold value $Th{r}_k$ of the rotation parameters is ${10}^{-9}$ (equivalent to less than 0.001″), and the threshold value $Th{r}_k$ of the scale parameters is ${10}^{-8}$ (equivalent to less than $0.1 \mathrm{mm}/100 \mathrm{km}$) [14]; (4) the check points are the same in Experiment I and Experiment II; and (4) the unit weight is used in all of the experiments in this paper.

3.2. Simulation Experiments

We generate the rotation matrices with different rotation angles and different fixed rotation axes, and 1000 sets of coordinates of common points and check points in coordinate system-i are randomly simulated by the common points and check points in experiment I (see Table 1, different rotation axes $\alpha$, different rotation angles $\delta$, same common points, same check points). Then, we calculate the mean value of five transformation precision indices ${\sigma }_R$, ${\sigma }_T$, ${\sigma }_k$, $RMS{E}_{same}$, and $RMS{E}_{check}$ of the Euler angle method (EA-Method, see Appendix B), Rodrigue method (R-Method, see Appendix C), new Euler angle method (NEA-Method, see Section 2.3), and new Rodrigue method (NR-Method, see Section 2.3) using the procedure shown in Appendix D. Similarly, we generate the rotation matrices with different rotation angles, different fixed common points distributions, and a fixed rotation axis, and randomly simulate 1000 sets of coordinates of common points and check points in coordinate system-I by the coordinates of common points and check points in experiment II (see Table 1, fixed rotation axes $\alpha$, different rotation angles $\delta$, different common points, same check points). We calculate the mean value of ${\sigma }_R$, ${\sigma }_T$, ${\sigma }_k$, $RMS{E}_{same}$, and $RMS{E}_{check}$ of EA-Method, R-Method, NEA-Method, and NR-Method using the procedure shown in Appendix D. The specific experimental procedure is summarized as follows:

Table 1. The true coordinates of common points and check points *.

Name	Common Points	Check Points
Experiment I $\alpha \in \left\{0,\frac{\pi }{6},\dots ,\frac{5\pi }{6}\right\}$ $\delta \in \left[-\pi ,\pi \right]$	$p_{01}^{i+1}=4p_1^{i+1}$$, p_{02}^{i+1}=4p_2^{i+1}$$, p_{03}^{i+1}=4p_3^{i+1}$	$p_1^{i+1}={\left[\begin{array}{ccc}0& \frac{-5}{\sqrt{3}}& 0\end{array}\right]}^T$, $p_2^{i+1}={\left[\begin{array}{ccc}-2.5& \frac{-2.5}{\sqrt{3}}& 0\end{array}\right]}^T$, $p_3^{i+1}={\left[\begin{array}{ccc}2.5& \frac{-2.5}{\sqrt{3}}& 0\end{array}\right]}^T$, $p_4^{i+1}=12p_1^{i+1}$$, p_5^{i+1}=12p_2^{i+1}$, $p_6^{i+1}=12p_3^{i+1}$$, p_7^{i+1}=40p_1^{i+1}$, $p_8^{i+1}=40p_2^{i+1}$$, p_9^{i+1}=40p_3^{i+1}$
Experiment II $\alpha =\frac{\pi }{2}$ $\delta \in \left[-\pi ,\pi \right]$	$\mathrm{Distribution}1 p_{11}^{i+1}=2p_1^{i+1}$$, p_{12}^{i+1}=2p_2^{i+1}$$, p_{13}^{i+1}=2p_3^{i+1}$
	$\mathrm{Distribution} 2 p_{21}^{i+1}=6p_1^{i+1}$$, p_{22}^{i+1}=6p_2^{i+1}$$, p_{23}^{i+1}=6p_3^{i+1}$
	$\mathrm{Distribution} 3 p_{31}^{i+1}=10p_1^{i+1}$$, p_{32}^{i+1}=10p_2^{i+1}$$, p_{33}^{i+1}=10p_3^{i+1}$
	$\mathrm{Distribution} 4 p_{41}^{i+1}=14p_1^{i+1}$$, p_{42}^{i+1}=14p_2^{i+1}$$, p_{43}^{i+1}=14p_3^{i+1}$
	$\mathrm{Distribution} 5 p_{51}^{i+1}=18p_1^{i+1}$$, p_{52}^{i+1}=18p_2^{i+1}$$, p_{53}^{i+1}=18p_3^{i+1}$
	$\mathrm{Distribution} 6 p_{61}^{i+1}=22p_1^{i+1}$$, p_{62}^{i+1}=22p_2^{i+1}$$, p_{63}^{i+1}=22p_3^{i+1}$

* (a) α is the angle between the rotation axis $\stackrel{\rightharpoonup }{n}$ and the plane XOY of coordinates-i + 1 and represents a fixed rotation axis; (b) δ is the angle of the simulated rotation matrix R_i−1; (c) experiment I and experiment II have the same check points; (d) the unit of the coordinates is meter.

Step 1: Assume the total number of the common points $n=3$; the total number of the check points $m=9$; and the angle between the rotation axis $\overrightarrow{n}$ and the plane $XOY$ of Coordinate system-(i + 1) is $\alpha$ (corresponding to different rotation axes);

Step 2: Input the weight matrix $P$ and the coordinates of common points and check points in Experiment I;

Step 3: Let $\alpha =0,\frac{\pi }{6},\frac{2\pi }{6},\frac{3\pi }{6},\frac{4\pi }{6},\frac{5\pi }{6}$. The EA-Method and the R-Method are separately used to calculate the mean value of ${\sigma }_R$, ${\sigma }_T$, ${\sigma }_k$, $RMS{E}_{same}$, and $RMS{E}_{check}$ for different fixed rotation axes and different rotation angles using the procedure shown in Appendix D (see Figure 1);

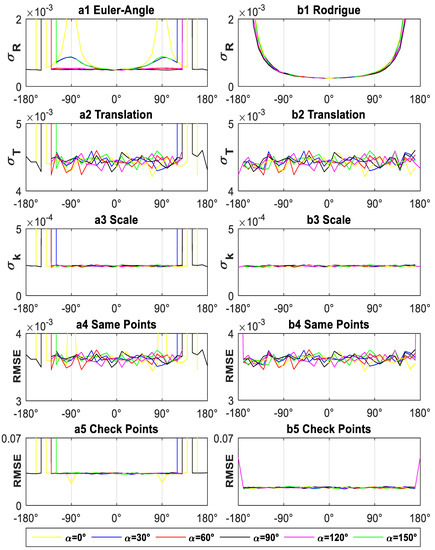
Figure 1. Transformation precision of the current transformation model for experiment I (each x axis value represents a different rotation angle, each y axis value represents a different precision for a different precision index (a1)-(rad), (b1)-(a.u.), (m), (a.u.), RMSE(m)), each color represents a different rotation axis for different, (a1–a5) shows the results of the EA-Method, subgraph (b1–b5) shows the results of the R-Method).

Step 4: Let $\alpha =0,\frac{\pi }{6},\frac{2\pi }{6},\frac{3\pi }{6},\frac{4\pi }{6},\frac{5\pi }{6}$. The NEA-Method and the NR-Method are separately used to calculate the mean value of ${\sigma }_R$, ${\sigma }_T$, ${\sigma }_k$, $RMS{E}_{same}$, and $RMS{E}_{check}$ for different fixed rotation axes and different rotation angles using the procedure shown in Appendix D (see Figure 2);

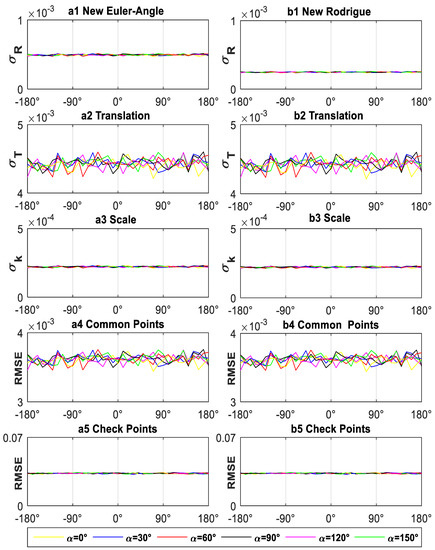
Figure 2. Transformation precision of the new transformation model for experiment I (each x axis value represents a different rotation angle, each y axis value represents a different precision for a different precision index (a1)-(rad), (b1)-(a.u.), (a.u.), (m), RMSE(m)), each color represents a different rotation axis for different, (a1–a5) shows the results of the proposed NEA-Method, (b1–b5) shows the results of the proposed NR-Method).

Step 5: Input $P$ and the coordinates of common points and check points in Experiment II;

Step 6: Let $\alpha =\frac{\pi }{2}$. The EA-Method and the R-Method are separately used to calculate the mean value of ${\sigma }_R$, ${\sigma }_T$, ${\sigma }_k$, $RMS{E}_{same}$, and $RMS{E}_{check}$ for different common points distributions using the procedure shown in Appendix D (see Figure 3);

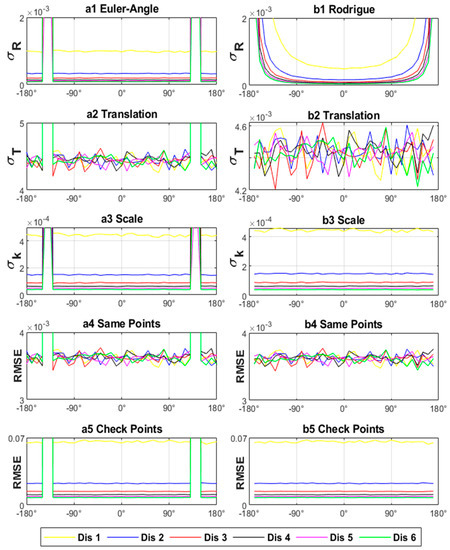
Figure 3. Transformation precision of the current transformation model for experiment II (each x axis value represents a different rotation angle, each y axis value represents a different precision for a different precision index (a1)-${\sigma }_R$(rad), (b1)-${\sigma }_R$(a.u.), ${\sigma }_T$(m), ${\sigma }_k$(a.u.), RMSE(m)), each color represents a different common points’ distribution, (a1–a5) shows the results of the EA-Method, (b1–b5) shows the results of the R-Method).

Step 7: Let $\alpha =\frac{\pi }{2}$. The NEA-Method and the NR-Method are separately used to calculate the mean value of ${\sigma }_R$, ${\sigma }_T$, ${\sigma }_k$, $RMS{E}_{same}$, and $RMS{E}_{check}$ for different common points distributions using the procedure shown in Appendix D (Figure 4).

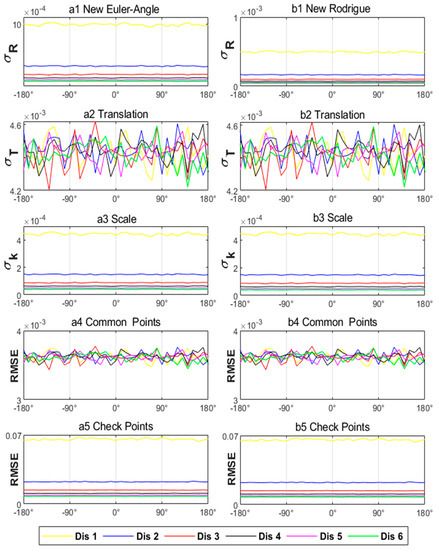
Figure 4. Transformation precision of the new transformation model for experiment II (each x axis value represents a different rotation angle, each y axis value represents a different precision for a different precision index (a1)-${\sigma }_R$(rad), (b1)-${\sigma }_R$(a.u.), ${\sigma }_T$(m), ${\sigma }_k$(a.u.), RMSE(m)), each color represents a different common points’ distribution, (a1–a5) shows the results of the proposed NEA-Method, (b1–b5) shows the results of the proposed NR-Method).

3.3. Practical Engineering Case

To further verify the applicability of the proposed method described in Section 2.3 we selected a dataset from a practical engineering application in Guangzhou’s new airport terminal [1,15], which consists of the true coordinates and measured coordinates of 15 nodes and 2 hinge center points in a component of the grid structure, as shown in Table 2. The origin in the true coordinates and the measured coordinates are the center of the end hinge of the component and any hypothetical point, respectively. In total, 5 cases are considered in this study, each of which selects 5 out of 17 points as common points: Case A selects {1, 11, 12, 13, 23}; Case B selects {1, 8, 9, 10, 23}; Case C selects {1, 14, 15, 16, 23}; Case D selects {1, 5, 6, 7, 23}; and Case E selects {1, 17, 18, 19, 23}. We then calculate ${\sigma }_R$, $RMS{E}_{same}$, and $RMS{E}_{check}$ by the EA-Method, R-Method, NEA-Method, and NR-Method, respectively. The detailed experimental procedure is summarized as follows:

Table 2. Actual and measured coordinates [1,15].

Point Number	True Coordinates (mm)			Measured Coordinates (mm)
	$x^i$	$y^i$	$z^i$	$x^{i+1}$	$y^{i+1}$	$z^{i+1}$
1	0.0	0.0	0.0	108,521.0	96,611.0	101,222.0
5	289.0	0.0	3327.0	108,819.0	99,931.0	101,213.0
6	−114.0	216.5	3327.0	108,379.0	99,937.0	101,438.0
7	−114.0	−216.5	3327.0	108,378.0	99,939.0	100,996.0
8	444.0	0.0	5327.0	108,965.0	101,930.0	101,206.0
9	−222.0	333.0	5327.0	108,302.0	101,930.0	101,538.0
10	−222.0	−333.0	5327.0	108,302.0	101,931.0	100,879.0
11	600.0	0.0	7327.0	109,126.0	103,938.0	101,202.0
12	−300.0	450.0	7327.0	108,225.0	103,926.0	101,639.0
13	−300.0	−450.0	7327.0	108,224.0	103,925.0	100,762.0
14	444.0	0.0	9327.0	108,955.0	105,927.0	101,212.0
15	−222.0	333.0	9327.0	108,290.0	105,916.0	101,540.0
16	−222.0	−333.0	9327.0	108,291.0	105,914.0	100,880.0
17	289.0	0.0	11,327.0	108,785.0	107,926.0	101,223.0
18	−114.0	216.5	11,327.0	108,354.0	107,914.0	101,440.0
19	−114.0	−216.5	11,327.0	108,355.0	107,908.0	100,997.0
23	0.0	0.0	14,625.0	108,473.0	111,215.0	101,228.0

Step 1: Let the number of common points and check points be $n=5$ and $m=17$, respectively;

Step 2: Input $P$, the coordinate of 17 position points in Table 2;

Step 3: Let the coordinate of common points be Case A, Case B, Case C, Case D, and Case E, respectively; the EA-Method and the NEA-Method are separately used to calculate the ${\sigma }_R$, $RMS{E}_{same}$, and $RMS{E}_{check}$ using the procedure shown in Appendix B and the procedure in Section 2.3 (see Figure 5);

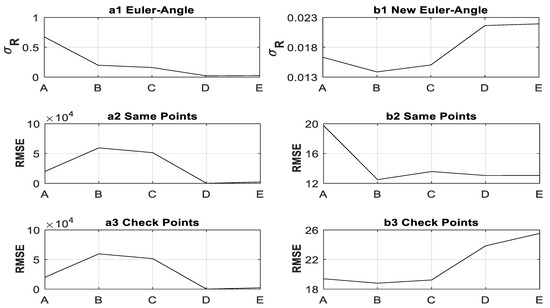
Figure 5. Transformation precision comparison of the EA-Method and NEA-Method for practical engineering application (each x axis value represents a different case selection of the common points, each y axis value represents a different precision for a different precision index (${\sigma }_R$(rad), RMSE (mm)), (a1–a3) shows the results of the EA-Method, (b1–b3) shows the results of the NEA-Method).

Step 4: Let the coordinate of common points be Case A, Case B, Case C, Case D, and Case E, respectively; the R-Method and the NR-Method are separately used to calculate the ${\sigma }_R$, $RMS{E}_{same}$, and $RMS{E}_{check}$ using the procedure shown in Appendix C and the procedure in Section 2.3 (see Figure 6).

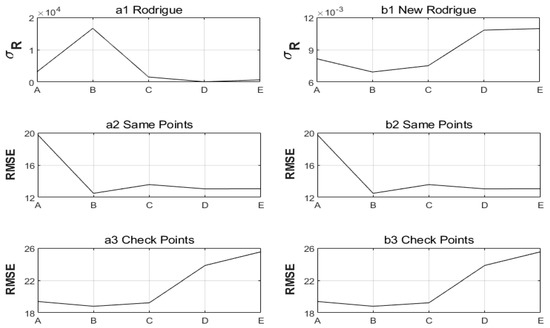
Figure 6. Transformation precision comparison of the R-Method and NR-Method for practical engineering application (each x axis value represents a different case selects of the common points, each y axis value represents a different precision for a different precision index (${\sigma }_R$(a.u.), RMSE (mm)) ((a1–a3) shows the results of the R-Method, (b1–b3) shows the results of the NR-Method).

3.4. Discussion

From Figure 1 and Figure 3, it may be concluded that: (1) EA-Method becomes singular when the rotation angle is around 90° and 140°, and R-Method is singular when the rotation angle is close to 180°. Thus, the current EA-Method and R-Method are not suitable for estimating the transformation parameters in some circumstances. (2) RMSE of the common points and check points is independent of the rotation angle and rotation axis, but the rotation parameters’ precision ${\sigma }_R$ estimated by R-Method is related to the rotation axis and proportional to the absolute value of the rotation angle. Therefore, in the case where the rotation matrices are different, the small value of the rotation parameters’ estimation precision cannot represent that the corresponding transformation precision is better than the larger value of the rotation parameters’ estimation precision, and the rotation parameters’ precision estimated by R-Method is not suitable for evaluating the RMSE of the check points. (3) RMSE of the different common points in Experiment II can be considered the same, and the translation parameters’ precision ${\sigma }_T$ can also be considered the same, but the corresponding RMSE of the check points is not equal when different common points are used. Thus, the RMSE of the common points and the translation parameters’ precision all cannot be used to evaluate the RMSE of the check points.

From Figure 2 and Figure 4, it may be concluded that: (1) NEA-Method can resolve the singularity problem of EA-Method under some rotation angles, and NR-Method can also resolve the singularity problem of R-Method under the near 180° rotation angle; (2) the rotation parameters’ precision ${\sigma }_R$ estimated by NEA-Method and that by NR-Method is independent of the rotation angle and the rotation axis, so the evaluation indices of ${\sigma }_R$ estimated by NEA-Method and NR-Method are unique to different coordinate transformations; and (3) the rotation parameters’ precision ${\sigma }_R$ estimated by NEA-Method and that by NR-Method is proportional to the RMSE of the check points. Thus, the evaluation indices of ${\sigma }_R$ estimated by NEA-Method and NR-Method can be used to evaluate the RMSE of the check points.

From Figure 5 and Figure 6, several observations can be made as follows:(1) EA-Method still has singularity for A, B, and C distributions, where the RMSE of the common points and check points are more than 10,000 mm, so EA-Method is not suitable for this experiment; (2) the RMSE of the check points for NE-Method, R-Method, and NR-Method in the same case are equal, and its RMSE values for case A, B, C, D, and E are 19.4, 18.8, 19.2, 23.9, and 25.5 mm, respectively (the size is comparable to the calculated value in the literature [1,15], the results are correct), respectively, where the size relationship is E > D > A > C > B (see subgraph Figure 5b3 and Figure 6a3,b3); that is, “the size relationship of the check points’ RMSE is inconsistent with that of the common points’ RMSE”, so the RMSE of the check points cannot be used to evaluate the RMSE of the common points; (3) the RMSE values of the common points for NE-Method, R-Method, and NR-Method in the same case are also equal, but its RMSE values for case A, B, C, D, and E are 19.8, 12.5, 13.6, 13.05, and 13.06 mm, respectively, where the size relationship is A > C > E > D > B (see subgraph Figure 5b2 and Figure 6a2,b2); that is, “the size relationship of the common points’ RMSE is inconsistent with that of the check points’ RMSE”, so the RMSE of the common points cannot be used to evaluate the RMSE of the check points; (4) for NEA-Method and NR-Method, the size relationship of ${\sigma }_R$ in case A, B, C, D, E is E > D > A > C > B (see subgraph Figure 5b1), and for R-Method, the size relationship is B > A > C > E > D (see subgraph Figure 6a1; that is, “the size relationship of ${\sigma }_R$ calculated by R-Method is inconsistent with that of the check points’ RMSE, and the size relationship of ${\sigma }_R$ calculated by NEA-Method and NR-Method is consistent with that of the check points’ RMSE”, so the rotation parameters’ precision calculated by NEA-Method and NR-Method is suitable for evaluating the size relationship of the different check points’ RMSE but that by R-Method is not.

4. Conclusions

Motivated by the observation that the current coordinate transformation models’ have some limitations, this paper proposed a new method for coordinate transformation to deal with these limitations. The new transformation method was constructed by using the orthogonality of rotation matrix, the theorem of “any vector multiplied by the identity matrix does not change”, and the approximation of the rotation matrix (which is calculated by the orthogonal Procrustes method). The corresponding estimation formulas of th new transformation method were derived from the linearization theorem, the partial derivation theorem of matrix, and the principle of least squares adjustment.

We designed two simulation experiments and a practical engineering case to verify the effectiveness and applicability of the new transformation method. The results demonstrated that (1) the new transformation model is suitable for the Cartesian coordinate transformation under any rotation angle; (2) the rotation parameters’ precision calculated by the new method can be used to evaluate the transformation precision; (3) the new transformation method can be used to resolve the evaluation problem in the absence of check points.

However, it should be noted that “we do not consider the effects of linearization errors or coefficient matrix errors”; “our method only evaluates the accuracy of conversion parameters while the accuracy of any point in space is related to the accuracy of parameter conversion, the coordinates of any point, and the measurement accuracy of coordinates of any point and when calculating the accuracy of any point in space, it is necessary to refer to the related formula in [22]”; and “the relationship between the accuracy of conversion parameters and the accuracy of the final converted results requires further analytical investigation”.