An Adaptive Surrogate-Assisted Endmember Extraction Framework Based on Intelligent Optimization Algorithms for Hyperspectral Remote Sensing Images

Abstract

As the foremost step of spectral unmixing, endmember extraction has been one of the most challenging techniques in the spectral unmixing processing due to the mixing of pixels and the complexity of hyperspectral remote sensing images. The existing geometrial-based endmember extraction algorithms have achieved the ideal results, but most of these algorithms perform poorly when they do not meet the assumption of simplex structure. Recently, many intelligent optimization algorithms have been employed to solve the problem of endmember extraction. Although they achieved the better performance than the geometrial-based algorithms in different complex scenarios, they also suffer from the time-consuming problem. In order to alleviate the above problems, balance the two key indicators of accuracy and running time, an adaptive surrogate-assisted endmember extraction (ASAEE) framework based on intelligent optimization algorithms is proposed for hyperspectral remote sensing images in this paper. In the proposed framework, the surrogate-assisted model is established to reduce the expensive time cost of the intelligent algorithms by fitting the fully constrained evaluation value with the low-cost estimated value. In more detail, three commonly used intelligent algorithms, namely genetic algorithm, particle swarm optimization algorithm and differential evolution algorithm, are specifically designed into the ASAEE framework to verify the effectiveness and robustness. In addition, an adaptive weight surrogate-assisted model selection strategy is proposed, which can automatically adjust the weights of different surrogate models according to the characteristics of different intelligent algorithms. Experimental results on three data sets (including two simulated data sets and one real data set) show the effectiveness and the excellent performance of the proposed ASAEE framework.

1. Introduction

Hyperspectral remote sensing image, with hundreds of continuous spectra containing rich ground object information in each pixel [1], has been used in various fields, such as terrain change detection [2], geological exploration [3] and agricultural monitoring [4]. However, limited to the low spatial resolution of the hyperspectral remote sensor, mixed pixels are inevitably appear in the hyperspectral image. The mixed pixels contain at least one ground object material, such as water, soil, and trees, etc., which interferes with the accurate analysis of the hyperspectral image to a certain extent [5,6]. Spectral unmixing, as an efficient technique to solve the problem of mixed pixels, aims to decompose the mixed pixels into a set of pure substances (also known as endmembers) and estimate the proportion of the corresponding endmembers (also called abundances) [7]. In general, endmember extraction and abundance estimation are the two main tasks of spectral unmixing. There are many mixture models in spectral unmixing, such as linear mixture model (LMM), bilinear mixture model and nonlinear mixture models [8]. However, other models have higher complexity than LMM, most endmember extraction researches are based on the LMM. In the LMM [9], it assumes that each observable pixel can be expressed as a linear combination of pure endmembers. Therefore, for a hyperspectral image consisting of $\mathit{m}$ endmembers, each pixel in the LMM can be written as

$${\mathit{y}}_{\mathit{i}}=\mathit{E}\mathbf{\alpha }+{\mathit{n}}_{\mathit{i}}$$

(1)

where ${\mathit{y}}_{\mathit{i}}={[{\mathit{y}}_1,{\mathit{y}}_2,...,{\mathit{y}}_{\mathit{L}}]}^{\mathit{T}}$ is the $\mathit{i}$-th mixed pixel in the hyperspectral image; $\mathit{E}=[{\mathit{e}}_1,{\mathit{e}}_2,...,{\mathit{e}}_{\mathit{m}}]$ represents the set of endmembers that reconstructs the hyperspectral image $\mathit{Y}$, in which each endmember in $\mathit{e}$ contains $\mathit{L}$ spectral bands; $\mathbf{\alpha }={[{\alpha }_1,{\alpha }_2,...,{\alpha }_{\mathit{m}}]}^{\mathit{T}}$ denotes the abundance vector of the corresponding endmember set $\mathit{e}$; ${\mathit{n}}_{\mathit{i}}={[{\mathit{n}}_1,{\mathit{n}}_2,...,{\mathit{n}}_{\mathit{L}}]}^{\mathit{T}}$ is the noise term for the $\mathit{i}$-th mixed pixel. For a hyperspectral image with $\mathit{N}$ observed pixels, (1) can be written as the matrix form

$$\mathit{Y}=\mathit{E}\mathit{A}+\mathit{N}$$

(2)

where $\mathit{Y}=[{\mathit{y}}_1,{\mathit{y}}_2,...,{\mathit{y}}_{\mathit{N}}]$ is the hyperspectral image matrix, $\mathit{A}=[{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,...,{\mathit{\alpha }}_{\mathit{N}}]$ and $\mathit{N}=[{\mathit{n}}_1,{\mathit{n}}_2,...,{\mathit{n}}_{\mathit{N}}]$ represent the abundance matrix and the noise matrix, respectively. Due to physical limitations and constraints, the abundance needs to satisfy two constraints, namely the abundance sum-to-one constraint (ASC, ${\sum }_{\mathit{j}=1}^{\mathit{m}}{\alpha }_{\mathit{j}}=1$) and the abundance nonnegative constraint (ANC, ${\alpha }_{\mathit{j}}\ge 0,\mathit{j}=1,2,...,\mathit{m}$) [10].

Geometrically, it is assumed that there are pure endmembers in the hyperspectral image, and all pixels can be contained in a simplex whose vertices correspond to the endmember set constituting the image [11]. Therefore, in recent decades, many geometrial-based endmember extraction methods have been proposed to obtain the vertices of the simplex, among which the classical algorithms include the pixel purity index (PPI) [12], N-FINDR [13] and the vertex component analysis (VCA) [14], etc. PPI extracts the endmember set by projecting spectral vectors into random vectors and employed the minimum noise fraction for reducing the dimension. N-FINDR selects the simplex with the largest volume, and their vertices are used as the terminal endmembers. VCA obtains the endmembers by continuously projecting the extreme values until reaching the prescribed number of endmembers. Low computational complexity and high accuracy of extraction results are the advantages of these algorithms, but there are also some unavoidable shortcomings. For example, when the data do not meet the simple structure, the extraction accuracy of geometrial-based method will be significantly reduced, and it is also vulnerable to noise and outliers [15,16].

In order to alleviate the above problems, some intelligent optimization algorithms have been applied in endmember extraction in recent years. In the literature, the intelligent-based endmember extraction algorithms can be roughly divided into three main categories, which are the based on the genetic algorithms (GA) [17,18,19,20], the particle swarm optimization (PSO) algorithms [21,22,23,24,25,26,27] and the differential evolution (DE) algorithms [28,29]. Zhang et al. [21] employed the discrete particle swarm optimization (DPSO) to minimize the root mean square error (RMSE) between the reconstructed image and the original image to obtain the appropriate endmember set by encoding each particle as the potential position of the active endmember in the hyperspectral image. In [19], the combination of genetic algorithm and the orthogonal projection, called genetic orthogonal projection (GOP), was proposed to solve the problem of endmember extraction. To overcome the problem of poor performance and low efficiency, Zhong et al. [28] proposed an adaptive differential evolution (ADEE) algorithm, which explore the endmember set with the adaptive crossover and mutation strategies to avoid manual setting of parameters. Liu et al. [23] explored a novel quantum-behaved particle swarm optimization (QPSO) with the row-column coding to overcome the dimension disaster of the standard PSO algorithm, and a cooperative approach is designed to expand the whole particle swarm search space. In [26], an improved QPSO (IQPSO) was designed to enhance the precision of extracted endmembers. Although the above intelligent-based endmember extraction algorithms are more effective and robust than the traditional algorithms, they suffer from a serious problem of time-consuming. It is difficult to satisfy the rapidity of endmember extraction in practical applications. In addition, if the time-consuming is reduced by decreasing the number of algorithm cycles, the intelligent-based algorithms are easy to fall into the local optimum.

As mentioned earlier, the abundance is subject to the ASC and the ANC, and four abundance estimation strategies including the fully constrained least squares (FCLS), the sum-to-one constrained least squares (SCLS), the nonnegative constrained least squares (NCLS) and the unconstrained least squares (UCLS) can be employed to solve this problem. However, mathematically, it takes much less time to solve the abundance inversion problem with the other three methods than FCLS. Therefore, some intelligent-based endmember extraction algorithms [25,30] directly employed the UCLS for the abundance inversion in order to reduce the computational cost. Nevertheless, the extraction accuracy of the SCLS, NCLS and UCLS is not convincing compared with the FCLS. Therefore, it is urgent to reduce the computational cost for the intelligent-based endmember extraction algorithms. The surrogate-assisted evolutionary algorithms (SAEAs), have been widely adopted as one of the most effective methods to solve the expensive optimization problems [31,32,33]. As the name suggests, it aims to establish a surrogate model to approximate the expensive objective evaluation function to significantly reduce the computational cost. At present, many efficient surrogate models such as polynomial regression (PR) [34], support vector machines (SVM) [35,36,37], radial basis function networks (RBF) [38,39] and Gaussian processes (GP) [40,41] have been studied and developed. Taking this cue, it is a natural idea to estimate the expensive evaluation value of FCLS from the cheap estimates with the SAEAs. In summary, an efficient adaptive surrogate-assisted intelligent algorithms (ASAEE) framework for endmember extraction is proposed in this paper to overcome the costly time problem. The major contributions of this paper are threefold:

(1)

This paper solves the endmember extraction problem with the proposed ASAEE framework. The overall convergence characteristics and the time-consuming issue can be significantly improved by the proposed framework.

(2)

Three algorithms of ASAEE-GA, ASAEE-PSO and ASAEE-DE based on the ASAEE framework are specifically designed. The experimental results of these three algorithms have been greatly improved compared with the corresponding state-of-the-art intelligent-based endmember extraction algorithms.

(3)

An adaptive weight surrogate-assisted model selection algorithm is designed, which is able to automatically adjust the weights of different surrogate-assisted models according to the characteristics of different intelligent optimization algorithms.

(4)

We also transfer the ASAEE framework to other intelligent-based endmember extraction algorithms, which greatly reduces the expensive time cost while maintaining the accuracy.

The remainder of this paper is structured as follows. Section 2 briefly reviews the research related to the employing of intelligent algorithms to solve the endmember extraction problem. In Section 3, the proposed ASAEE framework and its combination with three intelligent optimization algorithms, namely ASAEE-GA, ASAEE-PSO, and ASAEE-DE are described in detail. Section 4 reports the experimental results of the proposed method compared with several state-of-the-art endmember extraction algorithms. Conclusions are drawn in Section 5.

2. Related Work

In this section, we first review the intelligent-based optimization algorithms for endmember extraction. Relevant researches on the surrogate-assisted models are also briefly introduced.

2.1. Intelligent-Based Endmember Extraction Algorithms

The intelligent-based endmember extraction methods can effectively compensate for the shortcomings of geometrial-based methods in terms of reduced accuracy when the simplex condition is not satisfied. Furthermore, they can obtain the better accuracy for endmembers with undesirable distribution in the search space, which means that the intelligent-based algorithms have higher robustness and less dependence on data. Most of the intelligent-based methods transform the endmember extraction task of hyperspectral images into a combinatorial optimization problem and solve it by intelligent optimization algorithms, such as GA, PSO and DE.

The optimization objective function is important for the final results of endmember extraction. Most of the endmember extraction methods focus on the RMSE value, and the result will have a smaller RMSE when it is closer to the ground truth. Zhang et al. [21] proposed the DPSO which represents the combination of endmembers in hyperspectral image with binary encoding for particle positions and velocities, and searches for the optimal result in the discrete feasible space with the classical discrete particle swarm optimization. In subsequent studies, QPSO [23] is designed with the quantum-behaved strategy to strengthen the robustness and the convergence rate and in the multi-dimensional search space. IQPSO [26] improved the QPSO in the global search capability and the high-dimensional difficulty. In [19], Rezaei et al. employed a GA to determinate the exact number and position of each endmember obtained by the projecting the data in an orthogonal subspace. In [28], Zhong et al. designed an adaptive differential evolution strategy to the classical DE algorithm, which solves the drawback that traditional differential evolution method requires multiple runs to find the appropriate parameters for different practical problems.

The other commonly used optimization objective is to maximize the volume. As the volume of the convex simplex with the endmembers as the vertices, the larger volume is obtained when the result is closer to the real endmember set, which is defined as follows

$$\mathit{Volume}\left(\mathit{E}\right)=\frac{\left|det\left[\begin{array}{cccc}1& 1& ...& 1\\ e_1& e_2& ...& e_m\end{array}\right]\right|}{(m-1)!}$$

(3)

where m is the number of endmembers. A novel mutation operator accelerated quantum-behaved particle swarm optimization (MOAQPSO) [24] proposed by Xu et al. is one of the methods based on maximization of volume. Different from the DPSO, there is no velocity vector in MOAQPSO, which explores the best combination of endmembers by the position of the particles and employs the mutation rate to avoid falling into local optimum.

Some researches also employed other intelligent-based optimization algorithms for endmember extraction, such as the ant colony optimization algorithms [15,42], the bee colony optimization algorithms [43], and the discrete firefly algorithms [44], etc. In addition, refs. [18,22,25,26,27,29] have turned to multiobjective optimization algorithms to optimize two indicators simultaneously, namely minimizing the RMSE and maximizing the volume.

2.2. Brief Introduction of the Surrogate-Assisted Models

The purpose of establishing the surrogate-assisted models is to reduce the expensive evaluation cost of the intelligent optimization algorithms by employing a small amount of expensive real evaluation to construct and update the surrogate-assisted model, which is also known as data-driven optimization. Most of regression or classification techniques, such as PR, RBF, SVM, GP, etc., can be employed as the surrogate-assisted models.

The data-driven surrogate-assisted evolutionary optimization is mainly divided into two major research directions, namely offline and online data-driven optimization. The modeling of the surrogate-assisted model can only rely on offline data in the offline data-driven evolutionary optimization process. While the online data-driven evolutionary optimization is to select the appropriate data in the evolutionary search process to improve the fitting quality of the surrogate-assisted model. Therefore, in the online surrogate management methods, many model management strategies such as population-based, individual-based and generation-based are widely studied. The population-based model management employed multiple populations for evaluation, and each population is evaluated with different fidelity. As its name suggests, the individual-based model management aims to construct and update the surrogate model according to the specific individuals, pre-selection method, clustering based method, uncertainty based method, random strategy and best strategy are often employed in the selection of individuals. The generation-based model management, a relatively simple example, is to use some data to construct the surrogate-assisted model before optimization, and be updated in the number of iterations with the appropriate data to improve the surrogate-assisted model.

In the field of remote sensing, the surrogate-assisted models have also been explored in many research directions in accelerating the convergence and improving the efficiency, such as endmember selection [20], hyperspectral image classification [45] and hyperspectral nonlinear substitution [46], etc.

3. Proposed Method

In this section, we first describe the motivation for designing the surrogate-assisted model with the intelligent optimization algorithms to solve the endmember extraction problem. Then initialization mechanism and the objective optimization function will be introduced. Subsequently, the ASAEE framework will be described in detail, including the construction and updating of the surrogate model. Finally, the ASAEE framework with the evolution strategies of GA, PSO and DE are proposed.

3.1. Motivation

After determining the optimal endmember set with the intelligent-based optimization algorithms, the extracted endmembers must meet two constraints, i.e., all abundances cannot be negative, and the sum of all abundances is one. In general, the FCLS can be employed to accurately estimate the abundance of inversion. However, mathematically, due to the time spent by FCLS is very expensive, some researches have turned to the NCLS, UCLS and other low-time-cost abundance inversion methods instead. However, it will lead to inaccurate situations where the abundance from the inverse is negative or the sum is not one. Therefore, it is very promising to employ the surrogate model to replace the true FCLS abundance inversion value and reduce the expensive time cost of the intelligent-based endmember extraction algorithms.

3.2. Initialization and Objective Optimization Function

Considering that the evolution strategies of different intelligent algorithms have their own advantages and disadvantages, it is very important for the ASAEE framework to design a unified coding and initialization which is suitable for most intelligent algorithms. The encoding of individual or particle is shown in Figure 1. Specifically, the length of the encoded vector is $\mathit{N}$, and the elements in the vector are all binary encoded. Among them, the element of 0 means that the corresponding pixel in the hyperspectral image is not a candidate endmember. On the contrary, if the element is 1, it means that the pixel is the endmember to be extracted. In summary, the number of elements in the vector is equal to the pixels in the hyperspectral image, and the sparsity of the vector (i.e., the number of 1 elements) is equal to the number of endmembers to be extracted.

In this paper, we mainly focus on the single objective optimization. For the evaluation of individual or particle, as an important measurement index for endmember extraction, RMSE is regarded as the optimization objective, which can be expressed as

$${\mathit{f}}_{\mathit{ASAEE}}=\mathit{RMSE}(\mathit{Y},\widehat{\mathit{Y}})=\frac{1}{\mathit{N}}\sum _{\mathit{i}=1}^{\mathit{N}}\sqrt{\frac{1}{\mathit{L}}{\parallel {\mathit{y}}_{\mathit{i}}-{\widehat{\mathit{y}}}_{\mathit{i}}\parallel }_2^2}$$

(4)

where ${\mathit{y}}_{\mathit{i}}$ and ${\widehat{\mathit{y}}}_{\mathit{i}}$ are the pixels in the original image $\mathit{Y}$ and the reconstructed image $\widehat{\mathit{Y}}$, respectively. $\mathit{N}$ and $\mathit{L}$ represent the number of pixels and the number of spectral bands, respectively.

3.3. ASAEE Framework

The pseudo code of the overall framework is shown in Algorithm 1. The entire ASAEE framework can be divided into three parts, namely the construction of the surrogate-assisted model, evolution strategies and the updating of the surrogate-assisted model. The first step is to generate the initial population and construct the adaptive surrogate-assisted model. Because different surrogate-assisted models have their own characteristics, it is difficult to determine only one surrogate-assisted model to optimize for a specific optimization problem. Therefore, a stable and efficient surrogate-assisted model with adaptive weights is designed to be constructed, which can be expressed as

$${\mathit{S}}_{\mathit{aw}}=\sum _{\mathit{t}=1}^{\mathit{s}}{\mathit{w}}_{\mathit{t}}{\mathit{S}}_{\mathit{t}}$$

(5)

where ${\mathit{S}}_{\mathit{t}}$ is the $\mathit{t}$-th of all $\mathit{s}$ surrogate-assisted models. Four classical surrogate-assisted models including the PR, SVM, RBF and GP are employed in this paper. ${\mathit{w}}_{\mathit{t}}$ is the weight corresponding to the $\mathit{t}$-th surrogate-assisted model, which is defined as

$${\mathit{w}}_{\mathit{t}}=\frac{{\sum }_{\mathit{q}=1}^{\mathit{s}}{\mathit{r}}_{\mathit{q}}-{\mathit{r}}_{\mathit{t}}}{2{\sum }_{\mathit{q}=1}^{\mathit{s}}{\mathit{r}}_{\mathit{q}}}$$

(6)

where ${\mathit{r}}_{\mathit{t}}$ is defined as: ${\sum }_{\mathit{i}=1}^{\mathit{R}}\sqrt{\frac{1}{\mathit{R}}{\parallel {\mathit{f}}_{\mathit{i}}-{\widehat{\mathit{f}}}_{\mathit{i}}\parallel }^2}$, $\mathit{R}$ is the number of samples used to construct or update the surrogate model, ${\mathit{f}}_{\mathit{i}}$ and ${\widehat{\mathit{f}}}_{\mathit{i}}$ are the value evaluated by FCLS and the surrogate-assisted model, respectively.

Algorithm 1 The ASAEE Framework

Input:Y: the original hyperspectral image, Maxgen: the max generation number, K: the population size. Output:$\widehat{\mathit{E}}$: the endmember set for reconstructing the remixed image. 1: Generate the initial population ${\mathit{P}}_0$. 2: %Construct the surrogate-assisted model 3: ${\mathit{D}}_0\leftarrow$Randomly select $\mathit{K}/10$ individuals and Evaluate them with FCLS. 4: Construct the surrogate-assisted model by: ${\mathit{S}}_{\mathit{aw}}={\sum }_{\mathit{t}=1}^{\mathit{s}}{\mathit{w}}_{\mathit{t}}{\mathit{S}}_{\mathit{t}}$. 5: Evaluate each ${\mathit{p}}_{\mathit{i}}$ in ${\mathit{P}}_0$ with the surrogate model ${\mathit{S}}_{\mathit{aw}}$. 6: $\mathit{gen}\leftarrow$ 1. 7: whilegen < Maxgen do 8:     Evolve the ${\mathit{P}}_{\mathit{gen}}$ with an intelligent optimization algorithm. 9:     Evaluate each ${\mathit{p}}_{\mathit{i}}$ in ${\mathit{P}}_{\mathit{gen}}$ with the surrogate-assisted model ${\mathit{S}}_{\mathit{aw}}$. 10:    %Update the surrogate-assisted model 11:    ${\mathit{P}}_{\mathit{gen}}^{{}^{\prime }}\leftarrow$ the reinitialized population with $\mathit{K}/10$ individuals. 12:    $({\mathit{x}}_{\mathit{gen}}^{*},{\mathit{y}}_{\mathit{gen}}^{*})\leftarrow$ Obtain the individual with the best fitness in ${\mathit{P}}_{\mathit{gen}}$. 13:    $({\mathit{x}}_{\mathit{gen}}^{\mathit{u}},{\mathit{y}}_{\mathit{gen}}^{\mathit{u}})\leftarrow$ Obtain the individual with the most uncertain in ${\mathit{P}}_{\mathit{gen}}$. 14:    $({\mathit{x}}_{\mathit{gen}}^{\mathit{r}},{\mathit{y}}_{\mathit{gen}}^{\mathit{r}})\leftarrow$ Obtain the individual by randomly selecting in ${\mathit{P}}_{\mathit{gen}}^{{}^{\prime }}$. 15:    Calculate the fitness of $({\mathit{x}}_{\mathit{gen}}^{*},{\mathit{y}}_{\mathit{gen}}^{*})$, $({\mathit{x}}_{\mathit{gen}}^{\mathit{u}},{\mathit{y}}_{\mathit{gen}}^{\mathit{u}})$ and $({\mathit{x}}_{\mathit{gen}}^{\mathit{r}},{\mathit{y}}_{\mathit{gen}}^{\mathit{r}})$ with FCLS. 16:    ${\mathit{D}}_{\mathit{gen}}\leftarrow {\mathit{D}}_{\mathit{gen}}\cup ({\mathit{x}}_{\mathit{gen}}^{*},{\mathit{y}}_{\mathit{gen}}^{*})\cup ({\mathit{x}}_{\mathit{gen}}^{\mathit{u}},{\mathit{y}}_{\mathit{gen}}^{\mathit{u}})\cup ({\mathit{x}}_{\mathit{gen}}^{\mathit{r}},{\mathit{y}}_{\mathit{gen}}^{\mathit{r}})$. 17:    Update the surrogate-assisted model ${\mathit{S}}_{\mathit{aw}}$ with ${\mathit{D}}_{\mathit{gen}}$. 18:    $\mathit{gen}$ = $\mathit{gen}$ + 1. 19: end while

The construction of the surrogate-assisted model with adaptive weights is shown in Figure 2. It is difficult to determine which surrogate-assisted model is more suitable for expensive evaluation problems. Therefore, it makes more sense to assign the corresponding weights according to the errors of different surrogate-assisted models.

After constructing the surrogate-assisted model, since the samples selected at the beginning are not enough for the predicted value of the surrogate-assisted model to simulate the whole real abundance inversion value, we design the online data-driven model management strategy to update the surrogate-assisted model. In each generation of evolution, the optimal fitness sample $({\mathit{x}}_{\mathit{gen}}^{*},{\mathit{y}}_{\mathit{gen}}^{*})$, the most uncertain sample $({\mathit{x}}_{\mathit{gen}}^{\mathit{u}},{\mathit{y}}_{\mathit{gen}}^{\mathit{u}})$ and a random sample $({\mathit{x}}_{\mathit{gen}}^{\mathit{r}},{\mathit{y}}_{\mathit{gen}}^{\mathit{r}})$ are selected to update the surrogate-assisted model to ensure accurate and efficient approximation of the expensive evaluation function. It should be noted that the $({\mathit{x}}_{\mathit{gen}}^{*},{\mathit{y}}_{\mathit{gen}}^{*})$ is obtained by selecting the individual with the best fitness value evaluated by the surrogate-assisted model for all the individuals in ${\mathit{P}}_{\mathit{gen}}$. The $({\mathit{x}}_{\mathit{gen}}^{\mathit{u}},{\mathit{y}}_{\mathit{gen}}^{\mathit{u}})$ is obtained by calculating the maximum neighborhood distance of all individuals evaluation values in ${\mathit{P}}_{\mathit{gen}}$. The $({\mathit{x}}_{\mathit{gen}}^{\mathit{r}},{\mathit{y}}_{\mathit{gen}}^{\mathit{r}})$ is randomly selected from an initial population ${\mathit{P}}_{\mathit{gen}}^{{}^{\prime }}$ with $\mathit{K}/10$ individuals. With the above designs, the overall computational complexity of the ASAEE framework is almost reduced by $\mathit{Kgen}{\mathcal{O}}_{\mathit{FCLS}}$ times compared with the traditional intelligent-based algorithms.

3.4. Evolution Strategies

In this section, in order to verify the generality and robustness of our proposed ASAEE framework, three intelligent algorithms, including the GA, PSO and DE, are employed to design with the ASAEE framework for evolution.

3.4.1. ASAEE-GA

For the ASAEE-GA, population ${\mathit{P}}_{\mathit{gen}}$ will first form the parent population ${\mathit{P}}_{\mathit{gen}}^{{}^{\prime }}$ with the tournament selection, which is used to generate the offspring population ${\mathit{C}}_{\mathit{gen}}$. Then each two individuals $p_{\mathit{a}}$ and $p_{\mathit{b}}$ are selected from ${\mathit{P}}_{\mathit{gen}}^{{}^{\prime }}$ for the crossover and mutation, and their corresponding offspring are generated as: ${\mathit{c}}_{\mathit{i}}=\mathit{Mutation}\left(\mathit{Crossover}({\mathit{p}}_{\mathit{a}},{\mathit{p}}_{\mathit{b}})\right)$, where the $\mathit{Crossover}\left(\right)$ and $\mathit{Mutation}\left(\right)$ are the multi-point crossover operator and the uniform mutation operator, respectively. The crossover operation randomly selects multiple points on the parent chromosome, and then exchanges part of genes in ${\mathit{p}}_{\mathit{a}}$ and ${\mathit{p}}_{\mathit{b}}$ to obtain two new individuals. In addition, uniform mutation randomly generates a number within the interval $[{\mathit{U}}_{\mathit{max}},{\mathit{U}}_{\mathit{min}}]$ to replace the original variable at the mutated genes. ${\mathit{U}}_{\mathit{max}}$ and ${\mathit{U}}_{\mathit{min}}$ are respectively the upper and lower bounds of the decision variable. The offspring population ${\mathit{C}}_{\mathit{gen}}$ is generated through repeating this step until there is no unselected individual in the population ${\mathit{P}}_{\mathit{gen}}^{{}^{\prime }}$. Then $\mathit{K}$ individuals with the best fitness are selected from ${\mathit{P}}_{\mathit{gen}}\cup {\mathit{C}}_{\mathit{gen}}$ to form the next parent population ${\mathit{P}}_{\mathit{gen}+1}$. As the current generation reaches the maximum number of generations $\mathit{Maxgen}$, the individual with the best fitness is selected as the reconstructed endmember set $\widehat{\mathit{E}}$.

3.4.2. ASAEE-PSO

In the ASAEE-PSO, the concept of basic PSO is applied to quantum space, and the wave functions is used to describe the motion states of the particles, which enables the motion of particles in feasible solution space to exhibit global randomness. Instead of the traditional PSO that uses position and velocity to represent the particle state, quantum-behaved PSO (QPSO) evolves only with the particle positions, which also has the advantage of fewer parameters. For the evolution of the ASAEE-PSO, suppose that the $\mathit{j}$-th decision variable of the $\mathit{i}$-th particle at generation $\mathit{gen}$ is expressed as ${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}$. In addition, ${\mathit{x}}_{\mathit{ibest}}^{\mathit{gen}}$ and ${\mathit{x}}_{\mathit{gbest}}^{\mathit{gen}}$ represent the self-optimum position of the $\mathit{i}$-th particle and the global optimal position of all particles, respectively. The self-optimum position and the global optimal position can be obtained according to the objective function (4), and their update rules are shown as follows

$$\begin{array}{cc}\hfill {\mathit{x}}_{\mathit{ibest}}^{\mathit{gen}+1}& =\left\{\begin{array}{c}{\mathit{x}}_{\mathit{i}}^{\mathit{gen}+1},\mathit{if}{\mathit{f}}_{\mathit{ASAEE}}\left({\mathit{x}}_{\mathit{i}}^{\mathit{gen}+1}\right)<{\mathit{f}}_{\mathit{ASAEE}}\left({\mathit{x}}_{\mathit{ibest}}^{\mathit{gen}}\right)\\ {\mathit{x}}_{\mathit{ibest}}^{\mathit{gen}},\mathit{if}{\mathit{f}}_{\mathit{ASAEE}}\left({\mathit{x}}_{\mathit{i}}^{\mathit{gen}+1}\right)\ge {\mathit{f}}_{\mathit{ASAEE}}\left({\mathit{x}}_{\mathit{ibest}}^{\mathit{gen}}\right)\end{array}\right.\hfill \\ \hfill {\mathit{x}}_{\mathit{gbest}}^{\mathit{gen}+1}& =\mathit{argmin}\{{\mathit{f}}_{\mathit{ASAEE}}\left({\mathit{x}}_{\mathit{ibest}}^{\mathit{gen}+1}\right\},\mathit{i}=1,2,...,\mathit{K}.\hfill \end{array}$$

(7)

In a quantum system, particles are attracted by quantum delta potential wells centered on local attractor points. The update of the ${\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{gen}+1}$ is obtained by solving the probabilistic model of the particle position and then transforming it from the quantum state to the classical state by Monte Carlo Simulation method, which is expressed as follows

$$\begin{array}{cc}\hfill {\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{gen}+1}& ={\mathit{o}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}\pm \ast \beta \ast \left|{\mathit{best}}_{\mathit{j}}^{\mathit{gen}}-{\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}\right|\ast \mathit{ln}\left[\frac{1}{{\mathit{u}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}}\right]\hfill \\ \hfill {\mathit{u}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}& =\mathit{rand}(0,1),\mathit{i}=1,2,...,\mathit{K},\mathit{j}=1,2,...,\mathit{m}\hfill \\ \hfill {\mathit{best}}_{\mathit{j}}^{\mathit{gen}}& =\frac{1}{\mathit{K}}\sum _{\mathit{i}=1}^{\mathit{K}}{\mathit{x}}_{\mathit{ibest},\mathit{j}}^{\mathit{gen}},\mathit{j}=1,2,...,\mathit{m},\hfill \end{array}$$

(8)

where $\beta$ is the contraction-expansion coefficient, which controls the convergence speed of the algorithm and its value will change linearly with $\mathit{gen}$ from 1.0 to 0.5 according to [47]. ${\mathit{best}}_{\mathit{j}}$ is the average position of the $\mathit{j}$-th decision variable in the self-optimum particles of all individuals, and ${\mathit{u}}_{\mathit{i},\mathit{j}}$ is a random number in the interval [0, 1]. In addition, ${\mathit{o}}_{\mathit{i},\mathit{j}}$ is the position of the local attractor, which can be expressed as

$$\begin{array}{cc}\hfill {\mathit{o}}_{\mathit{i},\mathit{j}}& ={\phi }_{\mathit{i},\mathit{j}}\ast {\mathit{x}}_{\mathit{ibest},\mathit{j}}+(1-{\phi }_{\mathit{i},\mathit{j}})\ast {\mathit{x}}_{\mathit{gbest},\mathit{j}}\hfill \\ \hfill {\phi }_{\mathit{i},\mathit{j}}& =\mathit{rand}(0,1),\mathit{i}=1,2,...,\mathit{K},\mathit{j}=1,2,...,\mathit{m},\hfill \end{array}$$

(9)

where ${\phi }_{\mathit{i},\mathit{j}}$ is also a random number in the interval [0, 1]. After the number of generations reaches the termination condition, the particle of ${\mathit{x}}_{\mathit{gbest}}^{\mathit{gen}}$ is taken as the optimal endmember set.

3.4.3. ASAEE-DE

Different from ASAEE-GA, the mutation in ASAEE-DE adds the difference of the selection vectors to the basis vector to realize the change of the decision variable. The mutation operator adopts the “DE/rand/1” strategy, which can be expressed as follows

$$\begin{array}{c}\hfill {\mathit{v}}_{\mathit{i}}^{\mathit{gen}}={\mathit{x}}_{{\mathit{r}}_1}^{\mathit{gen}}+\mathit{F}({\mathit{x}}_{{\mathit{r}}_2}^{\mathit{gen}}-{\mathit{x}}_{{\mathit{r}}_3}^{\mathit{gen}}),\end{array}$$

(10)

where ${\mathit{v}}_{\mathit{i}}$ is the i-th vector generated by the individuals (${\mathit{x}}_{{\mathit{r}}_1},{\mathit{x}}_{{\mathit{r}}_2},{\mathit{x}}_{{\mathit{r}}_3}$) through the mutation operator. $\mathit{F}$ is the mutation scaling factor, and ${\mathit{r}}_1,{\mathit{r}}_2$ and ${\mathit{r}}_3$ are three mutex integers randomly selected from the range [1, K]. In addition, the binomial crossover is employed after the mutation operation to generate offspring $\mathit{c}$, which is shown as follows

$${\mathit{c}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}=\left\{\begin{array}{c}{\mathit{v}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}\mathit{if}\mathit{j}={\mathit{j}}_{\mathit{rand}}\mathit{or}{\mathit{rand}}_{\mathit{i}},\mathit{j}\le \mathit{Cr}\hfill \\ {\mathit{x}}_{\mathit{i},\mathit{j}}^{\mathit{gen}}\mathit{otherwise},\hfill \end{array}\right.$$

(11)

where ${\mathit{j}}_{\mathit{rand}}$ is an integer randomly selected from the range [1, m] and ${\mathit{rand}}_{\mathit{i}},\mathit{j}$ is a random number within the interval [0, 1]. The crossover rate Cr and the mutation scaling factor F will be adaptively updated according to [28]. A ($\mu$ + $\lambda$) strategy [48,49] is applied in the selection stage, which combines $\mu$ parents and $\lambda$ generated offsprings to obtain a population with ($\mu$ + $\lambda$) individuals, and the best $\mu$ individuals are selected to enter the next generation. In ASAEE-DE, the number of parents $\mu$ and the number of offspring $\lambda$ are the same as the size of the population K. Finally, the individual with the best fitness in the max generation $\mathit{Maxgen}$ is regarded as the final endmember set.

4. Experimental Results

In order to verify the effectiveness of the proposed ASAEE framework, a series of experiments are designed and performed on three benchmark data sets, including two simulated data sets and one real data set. In the following, these three data sets are briefly introduced first. Then the ablation experiments are analyzed to prove the rationality of the ASAEE framework design. Then the ablation experiments are analyzed to prove the rationality of the ASAEE framework. The proposed method is compared with other endmember extraction algorithms on different data sets. In addition, three algorithms of the proposed framework are compared with the state-of-the-art peer competitors. Finally, the generality of the proposed framework is reflected in the transfer to some classical intelligent-based endmember extraction algorithms.

4.1. Data Sets Description

In these experiments, three widely used endmember extraction benchmark data sets are employed to examine the performance of the proposed ASAEE framework. The first data set (DS1) and the second data set (DS2) are two simulated hyperspectral image from the USGS spectral library [50], which are displayed separately in Figure 3a,b. Five endmembers including the Alunite, Buddingtonite, Calcite, Kaolinite and Muscovite synthesize the DS1 with 80 × 100 pixels. On the basis of these five endmembers, five more endmembers (Illite, Jarosite, Nontronite, Halloysite, and Pyrophyllite) constitute a total of ten endmembers to simulate DS2 with 160 × 160 pixels. The spectra of DS1 and DS2 are shown in Figure 3c,d, respectively. The third data set (DS3) is a widely used real hyperspectral image [19] (the AVIRIS Cuprite image) with 400 × 350 pixels, including 50 spectral bands, which is shown in Figure 4.

In addition, two important indicators are employed to measure the performance of the algorithms, which are the RMSE and the running time. The RMSE is an index to measure the difference between the reconstructed image and the original image, and the running time is an important manifestation of the efficiency of the algorithms. Moreover, for the simulated data sets, experiments will be performed on three different levels of signal-to-noise ratio (SNR), namely, 20, 30 and 40 dB. The endmembers in the simulated data sets are known in advance, so the number of endmembers in DS1 and DS2 is set to 5 and 10, respectively. In the real data set, since the number of endmembers cannot be obatined as the priori knowledge, the number of endmembers is set to 5, 10, 15, 20 respectively as recommended in reference [21,28]. In all the intelligent-based algorithms, the number of individuals or particles is set to 20 and the number of iterations is set to 200. Besides, all the experimental results take the average of 10 independent experiments as the final presentation. All the experiments are implemented on the Matlab 2021 platform using Intel i5-10400 [email protected].

4.2. Experiments on the Proposed ASAEE Framework

In this section, two ablation experiments are performed to prove the rationality and validity of constructing the adaptive surrogate-assisted model. First, we would investigate whether the construction of surrogate-assisted model will affect the endmember extraction performance. Second, we would also explore the performance between the proposed adaptive surrogate-assisted model and other single surrogate-assisted models.

The experimental results on two simulated data sets of with and without surrogate-assisted model are shown in Figure 5. In the results, EE-GA, EE-PSO, and EE-DE represent three classic intelligent-based endmember extraction algorithms, and the FCLS are all employed for their individual evaluations. On the contrary, ASAEE-GA, ASAEE-PSO and ASAEE-PSO are combined with the proposed ASAEE framework. It can be observed from the experimental results that the endmember extraction algorithms based on the ASAEE framework can significantly reduce the expensive time cost compared with ordinary intelligent-based endmember extraction algorithms. In addition, the comparison results on the real data set with and without the ASAEE framework are illustrated in Figure 6. The above experimental results clearly shows that the proposed ASAEE framework improves the expensive cost of previous intelligent-based endmember extracion algorithms on all the benchmarks. To be specific, the ASAEE framework reduces the time in simulated data sets and the real data set by almost thirty times and two thousand times respectively compared with the original algorithms, which coincides with the analysis of the algorithm complexity in Section 3.3.

Besides, Figure 7 illustrates the experimental results of different surrogate-assisted models and the proposed adaptive surrogate-assisted model. In other word, four representative surrogate models constructed with PR, SVM, RBF and GP are compared with the proposed model. It can be concluded that the performance of different surrogate models has great differences for each hyperspectral data sets, but the proposed adaptive surrogate model strategy can assign different weights to each surrogate model for obtaining a compromise between these surrogate models, which is capable of better approaching the real evaluation results. In summary, the design of adaptive surrogate-assisted model can not only reduce the expensive time cost for the intelligent algorithms, but also allocate the appropriate weights to select the most suitable surrogate models according to their corresponding fitting.

4.3. Comparison of the Proposed ASAEE with Other Methods

In this section, three algorithms based on the ASAEE framework are compared with other endmember extraction algorithms. The comparison algorithms employed in this paper include PPI [51], N-FINDR [13], VCA [14], GOP [19], DPSO [21], ADEE [28], QPSO [23] and IQPSO [26]. Specifically, the PPI, N-FINDR and VCA are three classical geometrial-based approaches, and the GOP, DPSO, ADEE, QPSO and IQPSO represent the endmember extraction algorithms based on GA, PSO and DE in the intelligent algorithms. For the sake of fairness, the parameter settings of these intelligent-based algorithms are consistent with their respective papers. In addition, in the experimental results presented in the table, the best data is shown in bold, and the second best data is shown in bold and underlined.

Table 1. Comparison of the proposed ASAEE framework with other algorithms on DS1.

Attributes	SNR	20		30		40
	Methods	RMSE	Time (s)	RMSE	Time (s)	RMSE	Time (s)
	PPI	0.6062	3.100	0.6069	3.365	0.6055	3.599
Geometrial-based	N-FINDR	0.0823	1.436	0.0263	1.522	0.0183	1.626
	VCA	0.0735	0.910	0.0232	0.936	0.0173	0.980
	GOP	0.0784	1558.228	0.0224	1835.942	0.0109	2212.031
	DPSO	0.0811	1429.519	0.0196	1701.182	0.0115	2064.372
Intelligent-based	ADEE	0.0809	1291.413	0.0171	1534.217	0.0098	1727.190
	QPSO	0.0739	1357.904	0.0157	1660.213	0.0091	1882.512
	IQPSO	0.0717	1332.013	0.0138	1653.510	0.0072	1861.607
	ASAEE-GA	0.0731	66.706	0.0171	70.272	0.0095	74.264
ASAEE-based	ASAEE-PSO	0.0722	59.958	0.0143	62.391	0.0080	66.220
	ASAEE-DE	0.0697	43.331	0.0114	45.447	0.0061	47.059

,

Table 2. Comparison of the proposed ASAEE framework with other algorithms on DS2.

Attributes	SNR	20		30		40
	Methods	RMSE	Time (s)	RMSE	Time (s)	RMSE	Time (s)
	PPI	0.5132	4.522	0.5063	4.642	0.5051	4.723
Geometrial-based	N-FINDR	0.0805	1.995	0.0336	2.061	0.0218	2.102
	VCA	0.0711	1.236	0.0306	1.309	0.0189	1.381
	GOP	0.0780	2050.407	0.0295	2273.227	0.0113	2587.485
	DPSO	0.0802	1813.623	0.0305	2099.171	0.0136	2392.728
Intelligent-based	ADEE	0.0759	1472.874	0.0273	1651.492	0.0101	1884.253
	QPSO	0.0724	1668.131	0.0262	1891.692	0.0098	2105.269
	IQPSO	0.0679	1613.092	0.0240	1810.125	0.0082	2080.572
	ASAEE-GA	0.0702	74.408	0.0273	78.559	0.0094	83.952
ASAEE-based	ASAEE-PSO	0.0684	67.945	0.0265	71.623	0.0089	75.798
	ASAEE-DE	0.0658	54.151	0.0208	58.847	0.0075	62.801

and

Table 3. Comparison of the proposed ASAEE framework with other algorithms on DS3.

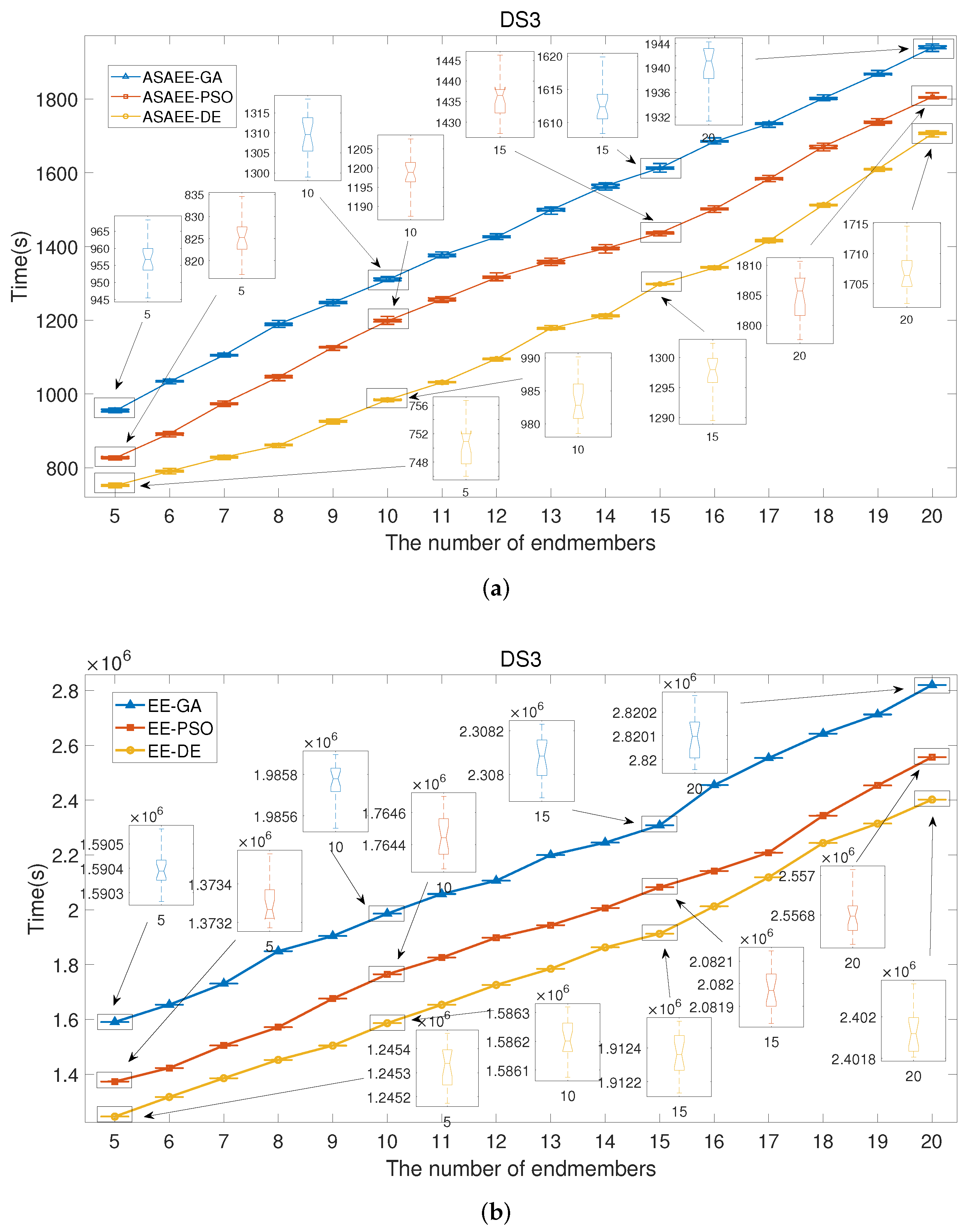
Attributes	Endmember	5		10		15		20
	Methods	RMSE	Time (s)	RMSE	Time (s)	RMSE	Time (s)	RMSE	Time (s)
	PPI	20.7768	30.774	18.3991	42.293	16.8536	57.495	14.3208	65.473
Geometrial-based	N-FINDR	5.8611	26.633	4.0298	34.205	3.8376	48.465	3.2275	59.217
	VCA	5.5463	25.495	3.8370	32.197	3.5101	43.151	2.9383	57.542
	GOP	5.2643	1.590 × 10${}^6$	3.8251	1.985 × 10${}^6$	3.5212	2.308 × 10${}^6$	2.9180	2.820 × 10${}^6$
	DPSO	4.5321	1.373 × 10${}^6$	3.3797	1.764 × 10${}^6$	3.0944	2.081 × 10${}^6$	2.7488	2.556 × 10${}^6$
Intelligent-based	ADEE	4.2970	1.24 × 10${}^6$	3.3102	1.586 × 10${}^6$	3.0206	1.912 × 10${}^6$	2.6831	2.401 × 10${}^6$
	QPSO	4.1542	1.270 × 10${}^6$	3.1326	1.600 × 10${}^6$	2.9437	2.005 × 10${}^6$	2.6704	2.493 × 10${}^6$
	IQPSO	4.0720	1.258 × 10${}^6$	3.0327	1.581 × 10${}^6$	2.7794	1.990 × 10${}^6$	2.5925	2.451 × 10${}^6$
	ASAEE-GA	4.3364	954.296	3.4417	1309.780	3.1561	1613.094	2.7436	1940.092
ASAEE-based	ASAEE-PSO	4.0862	826.323	3.1058	1198.461	2.8456	1436.977	2.6024	1805.624
	ASAEE-DE	3.7321	751.325	2.8469	984.226	2.5564	1318.374	2.2613	1705.950

present the indicators’ values obtained by three ASAEE-based algorithms and the comparison algorithms in identifying the real endmembers on two simulated data sets under different SNR and four endmember situations in the real data set, respectively. In general, in the simulated data sets, the performance of all algorithms are improved as the SNR increases, and the time spent are also increase except for the geometrial-based algorithms. In terms of the indicator of time, although the traditional geometrial-based algorithms have achieved the excellent results, their performance in accurate extraction are not ideal reflected by the RMSE indicator. On the contrary, the intelligent-based algorithms are generally better than the traditional methods in terms of endmember extraction accuracy, but the time of these algorithms is also very expensive. However, the endmember extraction algorithms with the ASAEE framework has achieved a good compromise between these two indicators. Specifically, the ASAEE-DE has the best endmember extraction performance in two simulated data sets, while ASAEE-GA has the excellent performance in the real data sets. In terms of time index, ASAEE-DE takes the shortest time due to the simplicity of its evolutionary steps, followed by ASAEE-PSO and ASAEE-GA takes the longest.

From Table 1, Table 2 and Table 3, we can find that the indicators’ values obtained by ASAEE framework are smaller than those obtained by other comparison algorithms except for one time value compared with geometrial-based algorithms. For the results of real data set, Figure 8 illustrates the comparison of abundance inversion results of some endmembers obtained by the ASAEE framework. Overall, the results are in line with our expectations, the original intention of the ASAEE design is to reduce the expensive time cost while ensuring that the extraction accuracy is not severely affected for the intelligent-based endmember extraction algorithms.

4.4. Transfer to Other Intelligent-Based Endmember Extraction Algorithms

In this section, we will prove the applicability of the ASAEE framework by transferring it to five intelligent-based comparison methods. As can be seen from Figure 9, the results are the time comparison before and after the transfer of ASAEE framework. It can be concluded that it is very significant with the evaluation from the surrogate-assisted model to the intelligent-based algorithms in endmember extraction. Theoretically, as long as it is an intelligent-based algorithm involving individual or particle evaluation, the ASAEE framework can be transferred and greatly shorten the entire evaluation time.

5. Conclusions

This paper has proposed an adaptive surrogate-assisted intelligent optimization algorithms framework to deal with the endmember extraction for hyperspectral remote sensing image. Specially, the surrogate-assisted model is established in the abundance inversion stage of the intelligent algorithms, an adaptive weight strategy are designed to automatically assign the weights according to the fitting degree of various surrogate models, so as to reduce the evaluation time and accelerate the convergence of the algorithms under the condition of ensuring certain accuracy. Three intelligent algorithms, ASAEE-GA, ASAEE-PSO, and ASAEE-DE, combined with the design of an adaptive surrogate-assisted model, are proposed to efficiently solve the endmember extraction problem.

In the future work, we will focus on solving more complex endmember extraction scenarios and improve the robustness and practicability of the ASAEE framework. In addition, other intelligent-based algorithms, such as the ant colony algorithms and bee colony algorithms, will also be explored to incorporate into the ASAEE framework. The MOEA-based intelligent endmember extraction algorithms will also be studied.