Treatment of Tide Gauge Time Series and Marine GNSS Measurements for Vertical Land Motion with Relevance to the Implementation of the Baltic Sea Chart Datum 2000
Abstract
:1. Introduction
2. Treatment of Tide Gauge Time Series for Vertical Land Motion
2.1. Baltic Sea Chart Datum 2000
2.2. Tide Gauge Time Series in Relation to the Baltic Sea Chart Datum 2000
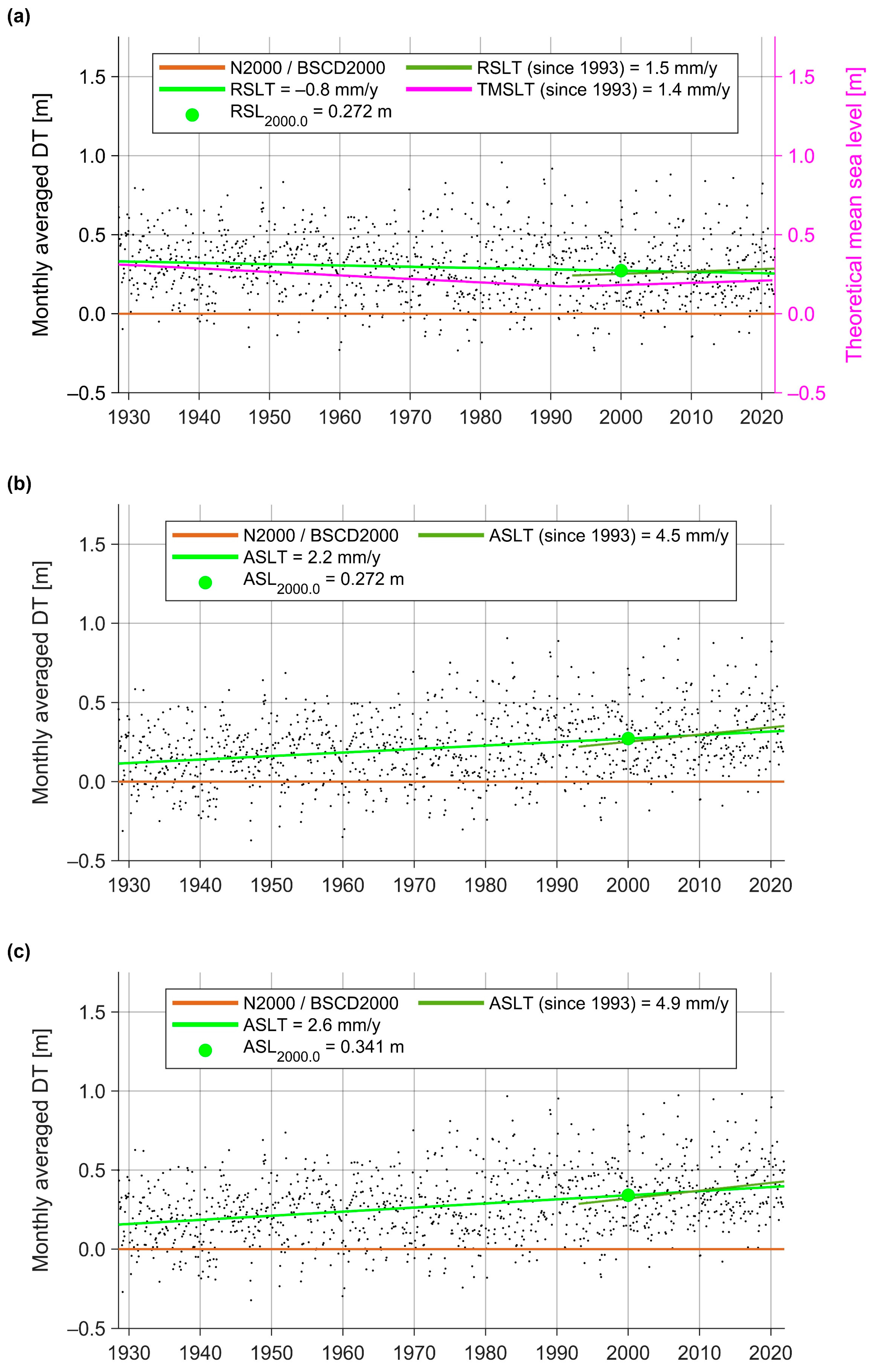
2.3. Numerical Examples
Theoretical Mean Sea Level for Finnish Tide Gauge Data
3. Treatment of Marine GNSS Measurements for Vertical Land Motion
3.1. A Numerical Example
3.1.1. Derivation of Offshore Dynamic Topography
3.1.2. Determination of Residuals
3.1.3. Correction for Vertical Land Motion
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spada, G.; Galassi, G. New estimates of secular sea level rise from tide gauge data and GIA modelling. Geophys. J. Int. 2012, 191, 1067–1094. [Google Scholar] [CrossRef] [Green Version]
- Breili, K.; Simpson, M.J.R.; Nilsen, J.E.Ø. Observed sea-level changes along the Norwegian coast. J. Mar. Sci. Eng. 2017, 5, 29. [Google Scholar] [CrossRef] [Green Version]
- Jahanmard, V.; Delpeche-Ellmann, N.; Ellmann, A. Realistic dynamic topography through coupling geoid and hydrodynamic models of the Baltic Sea. Cont. Shelf Res. 2021, 222, 104421. [Google Scholar] [CrossRef]
- Watson, C.S.; Legresy, B.; King, M.A. On the uncertainty associated with validating the global mean sea level climate record. Adv. Space Res. 2021, 68, 487–495. [Google Scholar] [CrossRef]
- Klos, A.; Kusche, J.; Fenoglio-Marc, L.; Bos, M.S.; Bogusz, J. Introducing a vertical land motion model for improving estimates of sea level rates derived from tide gauge records affected by earthquakes. GPS Solut. 2019, 23, 102. [Google Scholar] [CrossRef] [Green Version]
- Denys, P.H.; Beavan, R.J.; Hannah, J.; Pearson, C.F.; Palmer, N.; Denham, M.; Hreinsdottir, S. Sea level rise in New Zealand: The effect of vertical land motion on century-long tide gauge records in a tectonically active region. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018055. [Google Scholar] [CrossRef]
- Raucoules, D.; Le Cozannet, G.; Wöppelmann, G.; de Michele, M.; Gravelle, M.; Daag, A.; Marcos, M. High nonlinear urban ground motion in Manila (Philippines) from 1993 to 2010 observed by DInSAR: Implications for sea-level measurement. Remote Sens. Environ. 2013, 139, 386–397. [Google Scholar] [CrossRef] [Green Version]
- Fokker, P.A.; van Leijen, F.J.; Orlic, B.; van der Marel, H.; Hanssen, R.F. Subsidence in the Dutch Wadden Sea. Neth. J. Geosci. 2018, 97, 129–181. [Google Scholar] [CrossRef] [Green Version]
- Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef] [Green Version]
- Santamaría-Gómez, A.; Gravelle, M.; Dangendorf, S.; Marcos, M.; Spada, G.; Wöppelmann, G. Uncertainty of the 20th century sea-level rise due to vertical land motion errors. Earth Planet. Sci. Lett. 2017, 473, 24–32. [Google Scholar] [CrossRef]
- Hammond, W.C.; Blewitt, G.; Kreemer, C.; Nerem, R.S. GPS imaging of global vertical land motion for studies of sea level rise. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022355. [Google Scholar] [CrossRef]
- Shirzaei, M.; Bürgmann, R. Global climate change and local land subsidence exacerbate inundation risk to the San Francisco Bay area. Sci. Adv. 2018, 4, eaap9234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grgić, M.; Bender, J.; Bašić, T. Estimating vertical land motion from remote sensing and in-situ observations in the Dubrovnik area (Croatia): A multi-method case study. Remote Sens. 2020, 12, 3543. [Google Scholar] [CrossRef]
- Pfeffer, J.; Allemand, P. The key role of vertical land motions in coastal sea level variations: A global synthesis of multisatellite altimetry, tide gauge data and GPS measurements. Earth Planet. Sci. Lett. 2016, 439, 39–47. [Google Scholar] [CrossRef]
- Steffen, H.; Wu, P. Glacial isostatic adjustment in Fennoscandia—A review of data and modelling. J. Geodyn. 2011, 52, 169–204. [Google Scholar] [CrossRef]
- Simpson, M.J.R.; Ravndal, O.R.; Sande, H.; Nilsen, J.E.Ø.; Kierulf, H.P.; Vestøl, O.; Steffen, H. Projected 21st century sea-level changes, observed sea level extremes, and sea level allowances for Norway. J. Mar. Sci. Eng. 2017, 5, 36. [Google Scholar] [CrossRef] [Green Version]
- Idžanović, M.; Gerlach, C.; Breili, K.; Andersen, O.B. An attempt to observe vertical land motion along the Norwegian coast by CryoSat-2 and tide gauges. Remote Sens. 2019, 11, 744. [Google Scholar] [CrossRef] [Green Version]
- De Biasio, F.; Baldin, G.; Vignudelli, S. Revisiting vertical land motion and sea level trends in the northeastern Adriatic Sea using satellite altimetry and tide gauge data. J. Mar. Sci. Eng. 2020, 8, 949. [Google Scholar] [CrossRef]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring sea level in the coastal zone with satellite altimetry and tide gauges. Surv. Geophys. 2017, 38, 33–57. [Google Scholar] [CrossRef] [Green Version]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Fu, L.-L.; Picot, N.; Raynal, M.; Roinard, H. Satellite altimetry measurements of sea level in the coastal zone. Surv. Geophys. 2019, 40, 1319–1349. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef] [Green Version]
- Vestøl, O.; Ågren, J.; Steffen, H.; Kierulf, H.; Tarasov, L. NKG2016LU: A new land uplift model for Fennoscandia and the Baltic region. J. Geod. 2019, 93, 1759–1779. [Google Scholar] [CrossRef] [Green Version]
- Siegismund, F.; Köhl, A.; Rummel, R.; Stammer, D. Temporal variations of the marine geoid. J. Geophys. Res. Oceans 2020, 125, e2020JC016433. [Google Scholar] [CrossRef]
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Validation of marine geoid models by utilizing hydrodynamic model and shipborne GNSS profiles. Mar. Geod. 2020, 43, 134–162. [Google Scholar] [CrossRef]
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Applications of airborne laser scanning for determining marine geoid and surface waves properties. Eur. J. Remote Sens. 2021, 54, 557–567. [Google Scholar] [CrossRef]
- Ludwigsen, C.A.; Khan, S.A.; Andersen, O.B.; Marzeion, B. Vertical land motion from present-day deglaciation in the wider Arctic. Geophys. Res. Lett. 2020, 47, e2020GL088144. [Google Scholar] [CrossRef]
- Simon, K.M.; Riva, R.E.M.; Vermeersen, L.L.A. Constraint of glacial isostatic adjustment in the North Sea with geological relative sea level and GNSS vertical land motion data. Geophys. J. Int. 2021, 227, 1168–1180. [Google Scholar] [CrossRef]
- Hünicke, B.; Zorita, E. Statistical analysis of the acceleration of Baltic mean sea-level rise, 1900–2012. Front. Mar. Sci. 2016, 3, 125. [Google Scholar] [CrossRef] [Green Version]
- Gräwe, U.; Klingbeil, K.; Kelln, J.; Dangendorf, S. Decomposing mean sea level rise in a semi-enclosed basin, the Baltic Sea. J. Clim. 2019, 32, 3089–3108. [Google Scholar] [CrossRef]
- Madsen, K.S.; Høyer, J.L.; Suursaar, Ü.; She, J.; Knudsen, P. Sea level trends and variability of the Baltic Sea from 2D statistical reconstruction and altimetry. Front. Earth Sci. 2019, 7, 243. [Google Scholar] [CrossRef]
- Agha Karimi, A.; Bagherbandi, M.; Horemuz, M. Multidecadal sea level variability in the Baltic Sea and its impact on acceleration estimations. Front. Mar. Sci. 2021, 8, 702512. [Google Scholar] [CrossRef]
- Passaro, M.; Müller, F.L.; Oelsmann, J.; Rautiainen, L.; Dettmering, D.; Hart-Davis, M.G.; Abulaitijiang, A.; Andersen, O.B.; Høyer, J.L.; Madsen, K.S.; et al. Absolute Baltic Sea level trends in the satellite altimetry era: A revisit. Front. Mar. Sci. 2021, 8, 647607. [Google Scholar] [CrossRef]
- Suursaar, Ü.; Kall, T. Decomposition of relative sea level variations at tide gauges using results from four Estonian precise levelings and uplift models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1966–1974. [Google Scholar] [CrossRef]
- Schwabe, J.; Ågren, J.; Liebsch, G.; Westfeld, P.; Hammarklint, T.; Mononen, J.; Andersen, O.B. The Baltic Sea Chart Datum 2000 (BSCD2000)—Implementation of a common reference level in the Baltic Sea. Int. Hydrogr. Rev. 2020, 23, 63–83. [Google Scholar]
- Kollo, K.; Ellmann, A. Geodetic reconciliation of tide gauge network in Estonia. Geophysica 2019, 54, 27–38. [Google Scholar]
- Woodworth, P.L.; Hughes, C.W.; Bingham, R.J.; Gruber, T. Towards worldwide height system unification using ocean information. J. Geod. Sci. 2013, 2, 302–318. [Google Scholar] [CrossRef] [Green Version]
- Lan, W.-H.; Kuo, C.-Y.; Kao, H.-C.; Lin, L.-C.; Shum, C.K.; Tseng, K.-H.; Chang, J.-C. Impact of geophysical and datum corrections on absolute sea-level trends from tide gauges around Taiwan, 1993–2015. Water 2017, 9, 480. [Google Scholar] [CrossRef]
- Amjadiparvar, B.; Rangelova, E.; Sideris, M.G. The GBVP approach for vertical datum unification: Recent results in North America. J. Geod. 2016, 90, 45–63. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Filmer, M.S. The north-south tilt in the Australian Height Datum is explained by the ocean’s mean dynamic topography. J. Geophys. Res. Oceans 2012, 117, C08035. [Google Scholar] [CrossRef] [Green Version]
- Amjadiparvar, B.; Rangelova, E.V.; Sideris, M.G.; Véronneau, M. North American height datums and their offsets: The effect of GOCE omission errors and systematic levelling effects. J. Appl. Geod. 2013, 7, 39–50. [Google Scholar] [CrossRef]
- Saaranen, V.; Lehmuskoski, P.; Rouhiainen, P.; Takalo, M.; Mäkinen, J.; Poutanen, M. The new Finnish height reference N2000. In Geodetic Reference Frames; Drewes, H., Ed.; International Association of Geodesy Symposia Book Series (IAG SYMPOSIA); Springer: Berlin/Heidelberg, Germany, 2009; Volume 134, pp. 297–302. [Google Scholar] [CrossRef]
- Svensson, R.; Ågren, J.; Olsson, P.-A.; Eriksson, P.-O.; Lilje, M. The new Swedish height system RH 2000 and geoid model SWEN 05LR. In Proceedings of the XXIII International FIG Congress: Shaping the Change, Munich, Germany, 8–13 October 2006. [Google Scholar]
- Ågren, J.; Svensson, R. Postglacial Land Uplift Model and System Definition for the New Swedish Height System RH 2000; Lantmäteriet: Gävle, Sweden, 2007. [Google Scholar]
- Vestøl, O. Determination of postglacial land uplift in Fennoscandia from leveling, tide-gauges and continuous GPS stations using least squares collocation. J. Geod. 2006, 80, 248–258. [Google Scholar] [CrossRef]
- Kempe, C.; Jivall, L.; Lidberg, M.; Lilje, M. On the management of reference frames in Sweden. In Proceedings of the FIG Working Week 2016: Recovery from Disaster, Christchurch, New Zealand, 2–6 May 2016. [Google Scholar]
- EVRS Height Datum Relations. Available online: https://evrs.bkg.bund.de/Subsites/EVRS/EN/Projects/HeightDatumRel/height-datum-rel.html (accessed on 1 November 2021).
- EVRF2019. Available online: https://evrs.bkg.bund.de/Subsites/EVRS/EN/EVRF2019/evrf2019.html (accessed on 3 November 2021).
- Ågren, J.; Strykowski, G.; Bilker-Koivula, M.; Omang, O.; Märdla, S.; Forsberg, R.; Ellmann, A.; Oja, T.; Liepins, I.; Parseliunas, E.; et al. The NKG2015 gravimetric geoid model for the Nordic-Baltic region. In Proceedings of the International Symposium on Gravity, Geoid and Height Systems 2016, Thessaloniki, Greece, 19–23 September 2016. [Google Scholar] [CrossRef]
- Ågren, J.; Liebsch, G.; Mononen, J. Specification of the Baltic Sea Chart Datum 2000 (BSCD2000). Available online: http://www.bshc.pro/media/documents/CDWG/CDWG+Specification+of+the+Baltic+Sea+Chart+Datum+2000.pdf (accessed on 7 December 2021).
- Schwabe, J.; Strykowski, G.; Ågren, J.; Ellmann, A.; Varbla, S.; Forsberg, R.; Teitsson, H. Status of the “FAMOS Finalization”/BSCD2000 Geoid. Available online: http://www.bshc.pro/media/documents/CDWG/CDWG13+FAMOS+Finalization+2021-09-07.pdf (accessed on 20 January 2022).
- Varbla, S.; Ellmann, A.; Märdla, S.; Gruno, A. Assessment of marine geoid models by ship-borne GNSS profiles. Geod. Cartogr. 2017, 43, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Nordman, M.; Kuokkanen, J.; Bilker-Koivula, M.; Koivula, H.; Häkli, P.; Lahtinen, S. Geoid validation on the Baltic Sea using ship-borne GNSS data. Mar. Geod. 2018, 41, 457–476. [Google Scholar] [CrossRef]
- Lu, B.; Barthelmes, F.; Li, M.; Förste, C.; Ince, E.S.; Petrovic, S.; Flechtner, F.; Schwabe, J.; Luo, Z.; Zhong, B.; et al. Shipborne gravimetry in the Baltic Sea: Data processing strategies, crucial findings and preliminary geoid determination tests. J. Geod. 2019, 93, 1059–1071. [Google Scholar] [CrossRef]
- Ince, E.S.; Förste, C.; Barthelmes, F.; Pflug, H.; Li, M.; Kaminskis, J.; Neumayer, K.-H.; Michalak, G. Gravity measurements along commercial ferry lines in the Baltic Sea and their use for geodetic purposes. Mar. Geod. 2020, 43, 573–602. [Google Scholar] [CrossRef]
- Saari, T.; Bilker-Koivula, M.; Koivula, H.; Nordman, M.; Häkli, P.; Lahtinen, S. Validating geoid models with marine GNSS measurements, sea surface models, and additional gravity observations in the Gulf of Finland. Mar. Geod. 2021, 44, 196–214. [Google Scholar] [CrossRef]
- Poutanen, M.; Vermeer, M.; Mäkinen, J. The permanent tide in GPS positioning. J. Geod. 1996, 70, 499–504. [Google Scholar] [CrossRef]
- Ihde, J.; Mäkinen, J.; Sacher, M. Conventions for the Definition and Realization of a European Vertical Reference System (EVRS); Version 5.2; Federal Agency for Cartography and Geodesy (BKG): Frankfurt, Germany, 2019.
- Ihde, J.; Augath, W. European Vertical Reference System (EVRS). In Proceedings of the EUREF Symposium 2000, Tromsø, Norway, 22–24 June 2000. [Google Scholar]
- Gruber, T.; Ågren, J.; Angermann, D.; Ellmann, A.; Engfeldt, A.; Gisinger, C.; Jaworski, L.; Marila, S.; Nastula, J.; Nilfouroushan, F.; et al. Geodetic SAR for height system unification and sea level research–observation concept and preliminary results in the Baltic Sea. Remote Sens. 2020, 12, 3747. [Google Scholar] [CrossRef]
- SMHI Oceanographic Observations. Available online: https://www.smhi.se/data/oceanografi/ladda-ner-oceanografiska-observationer/#param=sealevelrh2000,stations=all (accessed on 4 November 2021).
- FMI Observations. Available online: https://en.ilmatieteenlaitos.fi/download-observations#!/ (accessed on 4 November 2021).
- Permanent Service for Mean Sea Level, Pietarsaari. Available online: https://www.psmsl.org/data/obtaining/stations/194.php (accessed on 24 November 2021).
- Permanent Service for Mean Sea Level, Hamina. Available online: https://www.psmsl.org/data/obtaining/stations/315.php (accessed on 24 November 2021).
- Medvedev, I.; Kulikov, E. Low-frequency Baltic Sea level spectrum. Front. Earth Sci. 2019, 7, 284. [Google Scholar] [CrossRef]
- Visser, H.; Dangendorf, S.; Petersen, A.C. A review of trend models applied to sea level data with reference to the “acceleration-deceleration debate”. J. Geophys. Res. Oceans 2015, 120, 3873–3895. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea rise: A redetermination. Surv. Geophys. 1997, 18, 279–292. [Google Scholar] [CrossRef]
- Theoretical Mean Water and Geodetical Height Systems in Finland. Available online: https://en.ilmatieteenlaitos.fi/theoretical-mean-sea-level (accessed on 4 November 2021).
- Metsar, J.; Kollo, K.; Ellmann, A. Modernization of the Estonian national GNSS reference station network. Geod. Cartogr. 2018, 44, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Metsar, J.; Kollo, K.; Ellmann, A.; Rüdja, A.; Pihlak, P. Multi-epoch GNSS campaigns of the national geodetic network in Estonia. Geophysica 2019, 54, 51–60. [Google Scholar]
- Koivula, H.; Laaksonen, A.; Lahtinen, S.; Kuokkanen, J.; Marila, S. Finnish permanent GNSS network, FinnRef. In Proceedings of the FIG Working Week 2017: Surveying the World of Tomorrow—From Digitalisation to Augmented Reality, Helsinki, Finland, 29 May–2 June 2017. [Google Scholar]
- Koivula, H. Finnish Permanent GNSS Network FinnRef. Ph.D. Thesis, Aalto University, Espoo, Finland, 2019. [Google Scholar]
- Lilje, M.; Wiklund, P.; Hedling, G. The use of GNSS in Sweden and the national CORS network SWEPOS. In Proceedings of the FIG Congress 2014: Engaging the Challenges—Enhancing the Relevance, Kuala Lumpur, Malaysia, 16–21 June 2014. [Google Scholar]
- EUREF Permanent GNSS Network. Available online: https://www.epncb.oma.be/_organisation/about.php (accessed on 4 November 2021).
- Kall, T.; Oja, T.; Kruusla, K.; Liibusk, A. New 3D velocity model of Estonia from GNSS measurements. Est. J. Earth Sci. 2021, 70, 107–125. [Google Scholar] [CrossRef]
- Kierulf, H.P.; Steffen, H.; Barletta, V.R.; Lidberg, M.; Johansson, J.; Kristiansen, O.; Tarasov, L. A GNSS velocity field for geophysical applications in Fennoscandia. J. Geodyn. 2021, 146, 101845. [Google Scholar] [CrossRef]
- Lahtinen, S.; Jivall, L.; Häkli, P.; Nordman, M. Updated GNSS velocity solution in the Nordic and Baltic countries with a semi-automatic offset detection method. GPS Solut. 2022, 26, 9. [Google Scholar] [CrossRef]
- Lavrov, D.; Even-Tzur, G.; Reinking, J. Expansion and improvement of the Israeli geoid model by shipborne GNSS measurements. J. Surv. Eng. 2017, 143, 04016022. [Google Scholar] [CrossRef]
- Roggenbuck, O.; Reinking, J. Sea surface heights retrieval from ship-based measurements assisted by GNSS signal reflections. Mar. Geod. 2019, 42, 1–24. [Google Scholar] [CrossRef]
- Slobbe, D.C.; Verlaan, M.; Klees, R.; Gerritsen, H. Obtaining instantaneous water levels relative to a geoid with a 2D storm surge model. Cont. Shelf Res. 2013, 52, 172–189. [Google Scholar] [CrossRef]
- Rulent, J.; Calafat, F.M.; Banks, C.J.; Bricheno, L.M.; Gommenginger, C.; Green, J.A.M.; Haigh, I.D.; Lewis, H.; Martin, A.C.H. Comparing water level estimation in coastal and shelf seas from satellite altimetry and numerical models. Front. Mar. Sci. 2020, 7, 549467. [Google Scholar] [CrossRef]
- Lagemaa, P.; Elken, J.; Kõuts, T. Operational sea level forecasting in Estonia. Est. J. Eng. 2011, 17, 301–331. [Google Scholar] [CrossRef] [Green Version]
- Hordoir, R.; Axell, L.; Höglund, A.; Dieterich, C.; Fransner, F.; Gröger, M.; Liu, Y.; Pemberton, P.; Schimanke, S.; Andersson, H.; et al. Nemo-Nordic 1.0: A NEMO-based ocean model for the Baltic and North seas–research and operational applications. Geosci. Model Dev. 2019, 12, 363–386. [Google Scholar] [CrossRef] [Green Version]
- Kärnä, T.; Ljungemyr, P.; Falahat, S.; Ringgaard, I.; Axell, L.; Korabel, V.; Murawski, J.; Maljutenko, I.; Lindenthal, A.; Jandt-Scheelke, S.; et al. Nemo-Nordic 2.0: Operational marine forecast model for the Baltic Sea. Geosci. Model Dev. 2021, 14, 5731–5749. [Google Scholar] [CrossRef]
- Ellmann, A.; Märdla, S.; Oja, T. The 5 mm geoid model for Estonia computed by the least squares modified Stokes’s formula. Surv. Rev. 2020, 52, 352–372. [Google Scholar] [CrossRef]
- Barrass, C.B. Ship Design and Performance for Masters and Mates; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Roggenbuck, O.; Reinking, J.; Härting, A. Oceanwide precise determination of sea surface height from in-situ measurements on cargo ships. Mar. Geod. 2014, 37, 77–96. [Google Scholar] [CrossRef]
- Mostafavi, M.; Delpeche-Ellmann, N.; Ellmann, A. Accurate sea surface heights from Sentinel-3A and Jason-3 retrackers by incorporating high-resolution marine geoid and hydrodynamic models. J. Geod. Sci. 2021, 11, 58–74. [Google Scholar] [CrossRef]
- Varbla, S.; Ellmann, A.; Delpeche-Ellmann, N. Utilizing airborne laser scanning and geoid model for near-coast improvements in sea surface height and marine dynamics. J. Coast. Res. 2020, 95, 1339–1343. [Google Scholar] [CrossRef]
- Ardalan, A.A.; Jazireeyan, I.; Abdi, N.; Rezvani, M.-H. Evaluation of SARAL/AltiKa performance using GNSS/IMU equipped buoy in Sajafi, Imam Hassan and Kangan Ports. Adv. Space Res. 2018, 61, 1537–1545. [Google Scholar] [CrossRef]
- Chupin, C.; Ballu, V.; Testut, L.; Tranchant, Y.-T.; Calzas, M.; Poirier, E.; Coulombier, T.; Laurain, O.; Bonnefond, P.; Team FOAM Project. Mapping sea surface height using new concepts of kinematic GNSS instruments. Remote Sens. 2020, 12, 2656. [Google Scholar] [CrossRef]
- Zhou, B.; Watson, C.; Legresy, B.; King, M.A.; Beardsley, J.; Deane, A. GNSS/INS-equipped buoys for altimetry validation: Lessons learnt and new directions from the Bass Strait validation facility. Remote Sens. 2020, 12, 3001. [Google Scholar] [CrossRef]






| Country | Height System | Number of TG Stations | Managing Authority | |
|---|---|---|---|---|
| Estonia | EH2000 | 2000.0 | 15 | Estonian Environment Agency (EEA) |
| Finland | N2000 | 2000.0 | 14 | Finnish Meteorological Institute (FMI) |
| Sweden | RH 2000 | 2000.0 | 54 | Swedish Meteorological and Hydrological Institute (SMHI) |
| Country | GNSS-CORS Network | Number of GNSS Stations | Managing Authority | |
|---|---|---|---|---|
| Estonia | ESTPOS | 1997.56 | 29 | Estonian Land Board (ELB) |
| Finland | FinnRef | 1997.0 | 47 | National Land Survey of Finland (NLS) |
| Sweden | SWEPOS | 1999.5 | 68 + 406 2 | Lantmäteriet |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varbla, S.; Ågren, J.; Ellmann, A.; Poutanen, M. Treatment of Tide Gauge Time Series and Marine GNSS Measurements for Vertical Land Motion with Relevance to the Implementation of the Baltic Sea Chart Datum 2000. Remote Sens. 2022, 14, 920. https://doi.org/10.3390/rs14040920
Varbla S, Ågren J, Ellmann A, Poutanen M. Treatment of Tide Gauge Time Series and Marine GNSS Measurements for Vertical Land Motion with Relevance to the Implementation of the Baltic Sea Chart Datum 2000. Remote Sensing. 2022; 14(4):920. https://doi.org/10.3390/rs14040920
Chicago/Turabian StyleVarbla, Sander, Jonas Ågren, Artu Ellmann, and Markku Poutanen. 2022. "Treatment of Tide Gauge Time Series and Marine GNSS Measurements for Vertical Land Motion with Relevance to the Implementation of the Baltic Sea Chart Datum 2000" Remote Sensing 14, no. 4: 920. https://doi.org/10.3390/rs14040920
APA StyleVarbla, S., Ågren, J., Ellmann, A., & Poutanen, M. (2022). Treatment of Tide Gauge Time Series and Marine GNSS Measurements for Vertical Land Motion with Relevance to the Implementation of the Baltic Sea Chart Datum 2000. Remote Sensing, 14(4), 920. https://doi.org/10.3390/rs14040920






