A Study of Possible Correlations between Seismo-Ionospheric Anomalies of GNSS Total Electron Content and Earthquake Energy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Earthquake Data
2.2. GIM TEC
2.3. TEC Anomalies
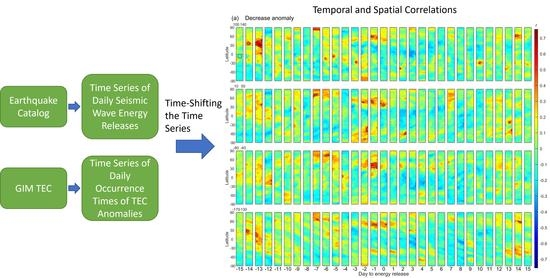
2.4. Removing Storm Effects and Other Experimental Designs
3. Results
3.1. 110–130°E
3.2. Region A
3.3. Region B
3.4. Region C
3.5. Geographical Dependence
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yen, H.Y.; Chen, C.H.; Yeh, Y.H.; Liu, J.Y.; Lin, C.R.; Tsai, Y.B. Geomagnetic Fluctuations during the 1999 Chi-Chi Earthquake in Taiwan. Earth Planets Space 2004, 56, 39–45. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.H.; Liu, J.Y.; Yen, H.Y.; Zeng, X.; Yeh, Y.H. Changes of Geomagnetic Total Field and Occurrences of Earthquakes in Taiwan. Terr. Atmos. Ocean. Sci. 2004, 15, 361–370. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.H.; Liu, J.Y.; Lin, P.Y.; Yen, H.Y.; Hattori, K.; Liang, W.T.; Chen, Y.I.; Yeh, Y.H.; Zeng, X. Pre-Seismic Geomagnetic Anomaly and Earthquake Location. Tectonophysics 2010, 489, 240–247. [Google Scholar] [CrossRef]
- Chen, C.H.; Wang, C.H.; Wen, S.; Yeh, T.K.; Lin, C.H.; Liu, J.Y.; Yen, H.Y.; Lin, C.; Rau, R.J.; Lin, T.W. Anomalous Frequency Characteristics of Groundwater Level before Major Earthquakes in Taiwan. Hydrol. Earth Syst. Sci. 2013, 17, 1693–1703. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.H.; Wen, S.; Yeh, T.K.; Wang, C.H.; Yen, H.Y.; Liu, J.Y.; Hobara, Y.; Han, P. Observation of Surface Displacements from GPS Analyses before and after the Jiashian Earthquake (M = 6.4) in Taiwan. J. Asian Earth Sci. 2013, 62, 662–671. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Pulinets, S.A.; Tsai, Y.B.; Chuo, Y.J. Seismo-Ionospheric Signatures Prior to M ≥ 6.0 Taiwan Earthquakes. Geophys. Res. Lett. 2000, 27, 3113–3116. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Chuo, Y.J.; Tsai, H.F. Variations of Ionospheric Total Electron Content during the Chi-Chi Earthquake. Geophys. Res. Lett. 2001, 28, 1383–1386. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.Y.; Chen, Y.I.; Chen, C.H.; Liu, C.Y.; Nishihashi, M.; Li, J.Z.; Xia, Y.Q.; Oyama, K.I.; Hattori, K.; Lin, C.C.H. Seismoionospheric GPS Total Electron Content Anomalies Observed before the 12 May 2008 Mw 7.9 Wenchuan Earthquake. J. Geophys. Res. Space Phys. 2009, 114, A04320. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Chen, C.H.; Hattori, K. Temporal and Spatial Precursors in the Ionospheric Global Positioning System (GPS) Total Electron Content Observed before the 26 December 2004 M 9.3 Sumatra-Andaman Earthquake. J. Geophys. Res. Space Phys. 2010, 115, A09312. [Google Scholar] [CrossRef]
- Liu, J.Y.; Le, H.; Chen, Y.I.; Chen, C.H.; Liu, L.; Wan, W.; Su, Y.Z.; Sun, Y.Y.; Lin, C.H.; Chen, M.Q. Observations and Simulations of Seismoionospheric GPS Total Electron Content Anomalies before the 12 January 2010 M 7 Haiti Earthquake. J. Geophys. Res. Space Phys. 2011, 116, A04302. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.Y.; Chen, Y.I.; Huang, C.C.; Parrot, M.; Shen, X.H.; Pulinets, S.A.; Yang, Q.S.; Ho, Y.Y. A Spatial Analysis on Seismo-Ionospheric Anomalies Observed by DEMETER during the 2008 M 8.0 Wenchuan Earthquake. J. Asian Earth Sci. 2015, 114, 414–419. [Google Scholar] [CrossRef]
- Yan, R.; Shen, X.; Huang, J.; Wang, Q.; Chu, W.; Liu, D.; Yang, Y.; Lu, H.; Xu, S. Examples of Unusual Ionospheric Observations by the CSES Prior to Earthquakes. Earth Planet. Phys. 2018, 2, 515–526. [Google Scholar] [CrossRef]
- Chen, Y.I.; Huang, C.S.; Liu, J.Y. Statistical Evidences of Seismo-Ionospheric Precursors Applying Receiver Operating Characteristic (ROC) Curve on the GPS Total Electron Content in China. J. Asian Earth Sci. 2015, 114, 393–402. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, Y.I.; Chuo, Y.J.; Chen, C.S. A Statistical Investigation of Preearthquake Ionospheric Anomaly. J. Geophys. Res. 2006, 111, A05304. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.Y.; Chen, C.H.; Chen, Y.I.; Yang, W.H.; Oyama, K.I.; Kuo, K.W. A Statistical Study of Ionospheric Earthquake Precursors Monitored by Using Equatorial Ionization Anomaly of GPS TEC in Taiwan during 2001–2007. J. Asian Earth Sci. 2010, 39, 76–80. [Google Scholar] [CrossRef]
- Pulinets, S.; Davidenko, D. Ionospheric Precursors of Earthquakes and Global Electric Circuit. Adv. Space Res. 2014, 53, 709–723. [Google Scholar] [CrossRef]
- Oyama, K.I.; Chen, C.H.; Bankov, L.; Minakshi, D.; Ryu, K.; Liu, J.Y.; Liu, H. Precursor Effect of 11 March 2011 off the Coast of Tohoku Earthquake on High and Low Latitude Ionospheres and Its Possible Disturbing Mechanism. Adv. Space Res. 2019, 63, 2623–2637. [Google Scholar] [CrossRef]
- Kelley, M.C.; Swartz, W.E.; Heki, K. Apparent Ionospheric Total Electron Content Variations Prior to Major Earthquakes Due to Electric Fields Created by Tectonic Stresses. J. Geophys. Res. Space Phys. 2017, 122, 6689–6695. [Google Scholar] [CrossRef]
- Kim, V.P.; Hegai, V.V.; Liu, J.Y.; Ryu, K.; Chung, J.K. Time-Varying Seismogenic Coulomb Electric Fields as a Probable Source for Pre-Earthquake Variation in the Ionospheric F2-Layer. J. Astron. Space Sci. 2017, 34, 251–256. [Google Scholar] [CrossRef]
- Masci, F.; Thomas, J.N.; Secan, J.A. On a Reported Effect in Ionospheric TEC around the Time of the 6 April 2009 L’Aquila Earthquake. Nat. Hazards Earth Syst. Sci. 2017, 17, 1461–1468. [Google Scholar] [CrossRef] [Green Version]
- Nenovski, P.I.; Pezzopane, M.; Ciraolo, L.; Vellante, M.; Villante, U.; de Lauretis, M. Local Changes in the Total Electron Content Immediately before the 2009 Abruzzo Earthquake. Adv. Space Res. 2015, 55, 243–258. [Google Scholar] [CrossRef] [Green Version]
- Dautermann, T.; Calais, E.; Haase, J.; Garrison, J. Investigation of Ionospheric Electron Content Variations before Earthquakes in Southern California, 2003–2004. J. Geophys. Res. 2007, 112, B02106. [Google Scholar] [CrossRef]
- Thomas, J.N.; Huard, J.; Masci, F. A Statistical Study of Global Ionospheric Map Total Electron Content Changes Prior to Occurrences of M ≥ 6.0 Earthquakes during 2000–2014. J. Geophys. Res. Space Phys. 2017, 122, 2151–2161. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Earthquake Magnitude, Intensity, Energy, and Acceleration. Bull. Seismol. Soc. Am. 1956, 46, 105–145. [Google Scholar] [CrossRef]
- CODE Final Product Series for the IGS; Astronomical Institute, University of Bern: Bern, Switzerland, 2020. [CrossRef]
- Liu, J.Y.; Yang, W.H.; Lin, C.H.; Chen, Y.I.; Lee, I.T. A Statistical Study on the Characteristics of Ionospheric Storms in the Equatorial Ionization Anomaly Region: GPS-TEC Observed over Taiwan. J. Geophys. Res. Space Phys. 2013, 118, 3856–3865. [Google Scholar] [CrossRef]
- Zhu, F.; Su, F.; Lin, J. Statistical Analysis of TEC Anomalies Prior to M 6.0 + Earthquakes During 2003–2014. Pure Appl. Geophys. 2018, 175, 3441–3450. [Google Scholar] [CrossRef]
- Illowsky, B.; Dean, S. Testing the Significance of the Correlation Coefficient. In Introductory Statistics; OpenStax: Houston, TX, USA, 2013; Available online: https://opentextbc.ca/introstatopenstax/chapter/testing-the-significance-of-the-correlation-coefficient/ (accessed on 30 November 2021).
















| EQK Number | Total EQK Number | Total Energy Release (erg) | % of Global EQK Number | % of Global Energy Release | ||||
|---|---|---|---|---|---|---|---|---|
| M < 5 | 5 ≤ M < 6 | 6 ≤ M < 7 | 7 ≤ M < 8 | |||||
| All | 7307 | 711 | 58 | 4 | 8080 | 4.40 × 1023 | 6.54% | 3.43% |
| A | 2652 | 244 | 26 | 1 | 2923 | 1.37 × 1023 | 2.37% | 1.07% |
| B | 3392 | 343 | 21 | 3 | 3759 | 2.66 × 1023 | 3.04% | 2.07% |
| C | 1000 | 93 | 10 | 0 | 1103 | 3.26 × 10 22 | 0.89% | 0.25% |
| Region | With Outliers | Without Outliers | ||||
|---|---|---|---|---|---|---|
| Sample Size | rα=0.01 | Max. Daily Energy Release in M | Sample Size | rα=0.01 | Max. Daily Energy Release in M | |
| A | 34–44 | 0.384–0.436 | 6.906–7.000 | 29–37 | 0.418–0.471 | 6.480–6.512 |
| B | 41–52 | 0.354–0.398 | 7.300–7.505 | 35–45 | 0.380–0.430 | 6.201–6.201 |
| C | 14–20 | 0.561–0.661 | 6.429–6.701 | 10–16 | 0.623–0.765 | 6.154–6.200 |
| Min. p | D | Lat. | Long. | r | |||
|---|---|---|---|---|---|---|---|
| 110–130 °E (all samples) | Decrease anomaly | 2.025 × 10−7 | −13 | 35 | 135 | 0.169 * | |
| Increase anomaly | 8.448 × 10−7 | 8 | 15 | −90 | 0.158 * | ||
| Region A | All samples | Decrease anomaly | 1.382 × 10−6 | −13 | 30 | 135 | 0.156 * |
| Increase anomaly | 7.497 × 10−6 | −15 | −87.5 | 30 | 0.144 * | ||
| E ≥ M5.5 | Decrease anomaly | 8.411 × 10−9 | −13 | 32.5 | 125 | 0.750 * | |
| Increase anomaly | 8.951 × 10−6 | 9 | −12.5 | 70 | 0.650 * | ||
| E ≥ M5.5 and outliers removed | Decrease anomaly | 4.617 × 10−8 | 3 | −45 | 165 | 0.764 * | |
| Increase anomaly | 1.741 × 10−5 | −12 | 55 | 40 | 0.633 * | ||
| Region B | All samples | Decrease anomaly | 1.753 × 10−5 | −5 | −70 | 95 | 0.138 * |
| Increase anomaly | 1.136 × 10−6 | 9 | 15 | −70 | 0.156 * | ||
| E ≥ M5.5 | Decrease anomaly | 2.295 × 10−7 | −6 | −40 | 110 | 0.689 * | |
| Increase anomaly | 9.674 × 10−7 | 8 | 62.5 | −100 | 0.637 * | ||
| E ≥ M5.5 and outliers removed | Decrease anomaly | 1.641 × 10−6 | 1 | −77.5 | 50 | 0.669 * | |
| Increase anomaly | 4.097 × 10−5 | 10 | 7.5 | −160 | 0.553 | ||
| Region C | All samples | Decrease anomaly | 6.410 × 10−9 | 15 | −35 | 140 | 0.187 * |
| Increase anomaly | 1.171 × 10−6 | 2 | −5 | 90 | 0.156 * | ||
| E ≥ M5.5 | Decrease anomaly | 1.454 × 10−8 | −11 | −35 | 65 | 0.947 * | |
| Increase anomaly | 1.624 × 10−7 | −3 | 50 | −80 | 0.902 * | ||
| E ≥ M5.5 and outliers removed | Decrease anomaly | 3.089 × 10−7 | −9 | −50 | −165 | 0.940 | |
| Increase anomaly | 2.102 × 10−8 | −4 | 85 | −65 | 0.944 | ||
| Min. p | D | Lat. | Long. | r | |||
|---|---|---|---|---|---|---|---|
| Region A | Using Dst index | Decrease anomaly | 2.929 × 10−5 | 4 | −47.5 | 95 | 0.726 |
| Increase anomaly | 7.909 × 10−6 | −12 | 55 | 40 | 0.750 | ||
| Using Kp and F107 | Decrease anomaly | 3.391 × 10−7 | −2 | −20 | 135 | 0.847 * | |
| Increase anomaly | 7.988 × 10−7 | −11 | 40 | −45 | 0.879 * | ||
| Region B | Using Dst index | Decrease anomaly | 2.716 × 10−5 | 8 | 52.5 | −15 | 0.677 |
| Increase anomaly | 1.607 × 10−6 | 10 | 27.5 | 55 | 0.698 * | ||
| Using Kp and F107 | Decrease anomaly | 1.589 × 10−5 | 2 | −47.5 | −20 | 0.692 | |
| Increase anomaly | 3.129 × 10−8 | 13 | 5 | 25 | 0.763 * | ||
| Region C | Using Dst index | Decrease anomaly | 1.088 × 10−7 | −11 | −35 | 10 | 0.959 |
| Increase anomaly | 1.525 × 10−6 | −4 | 47.5 | −75 | 0.934 | ||
| Using Kp and F107 | Decrease anomaly | 4.741 × 10−8 | −12 | −50 | −170 | 0.965 | |
| Increase anomaly | 1.236 × 10−7 | −1 | 17.5 | 105 | 0.968 | ||
| Min. p | D | Lat. | Long. | r | |||
|---|---|---|---|---|---|---|---|
| Region A | Using Dst index | Decrease anomaly | 1.598 × 10−7 | −13 | 32.5 | 125 | 0.783 |
| Increase anomaly | 6.166 × 10−5 | −7 | −32.5 | 95 | 0.704 * | ||
| Using Kp and F107 | Decrease anomaly | 4.036 × 10−6 | −8 | −17.5 | 65 | 0.756 * | |
| Increase anomaly | 7.127 × 10−7 | 7 | 0 | 95 | 0.823 * | ||
| Region B | Using Dst index | Decrease anomaly | 1.792 × 10−7 | −4 | −50 | −130 | 0.756 * |
| Increase anomaly | 2.243 × 10−7 | 8 | −10 | 155 | 0.744 * | ||
| Using Kp and F107 | Decrease anomaly | 1.842 × 10−7 | −4 | 60 | 35 | 0.706 | |
| Increase anomaly | 7.943 × 10−14 | 13 | 7.5 | −135 | 0.875 * | ||
| Region C | Using Dst index | Decrease anomaly | 4.196 × 10−10 | 15 | −35 | 125 | 0.980 * |
| Increase anomaly | 1.525 × 10−6 | −4 | 47.5 | −75 | 0.934 | ||
| Using Kp and F107 | Decrease anomaly | 3.849 × 10−9 | −11 | −30 | 60 | 0.984 | |
| Increase anomaly | 7.780 × 10−9 | 0 | 7.5 | −145 | 0.988 * | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.-C.; Sha, J. A Study of Possible Correlations between Seismo-Ionospheric Anomalies of GNSS Total Electron Content and Earthquake Energy. Remote Sens. 2022, 14, 1155. https://doi.org/10.3390/rs14051155
Su Y-C, Sha J. A Study of Possible Correlations between Seismo-Ionospheric Anomalies of GNSS Total Electron Content and Earthquake Energy. Remote Sensing. 2022; 14(5):1155. https://doi.org/10.3390/rs14051155
Chicago/Turabian StyleSu, Yung-Chih, and Jinming Sha. 2022. "A Study of Possible Correlations between Seismo-Ionospheric Anomalies of GNSS Total Electron Content and Earthquake Energy" Remote Sensing 14, no. 5: 1155. https://doi.org/10.3390/rs14051155
APA StyleSu, Y.-C., & Sha, J. (2022). A Study of Possible Correlations between Seismo-Ionospheric Anomalies of GNSS Total Electron Content and Earthquake Energy. Remote Sensing, 14(5), 1155. https://doi.org/10.3390/rs14051155