A Simple Statistical Intra-Seasonal Prediction Model for Sea Surface Variables Utilizing Satellite Remote Sensing
Abstract
:1. Introduction
2. Observations and Prediction Model
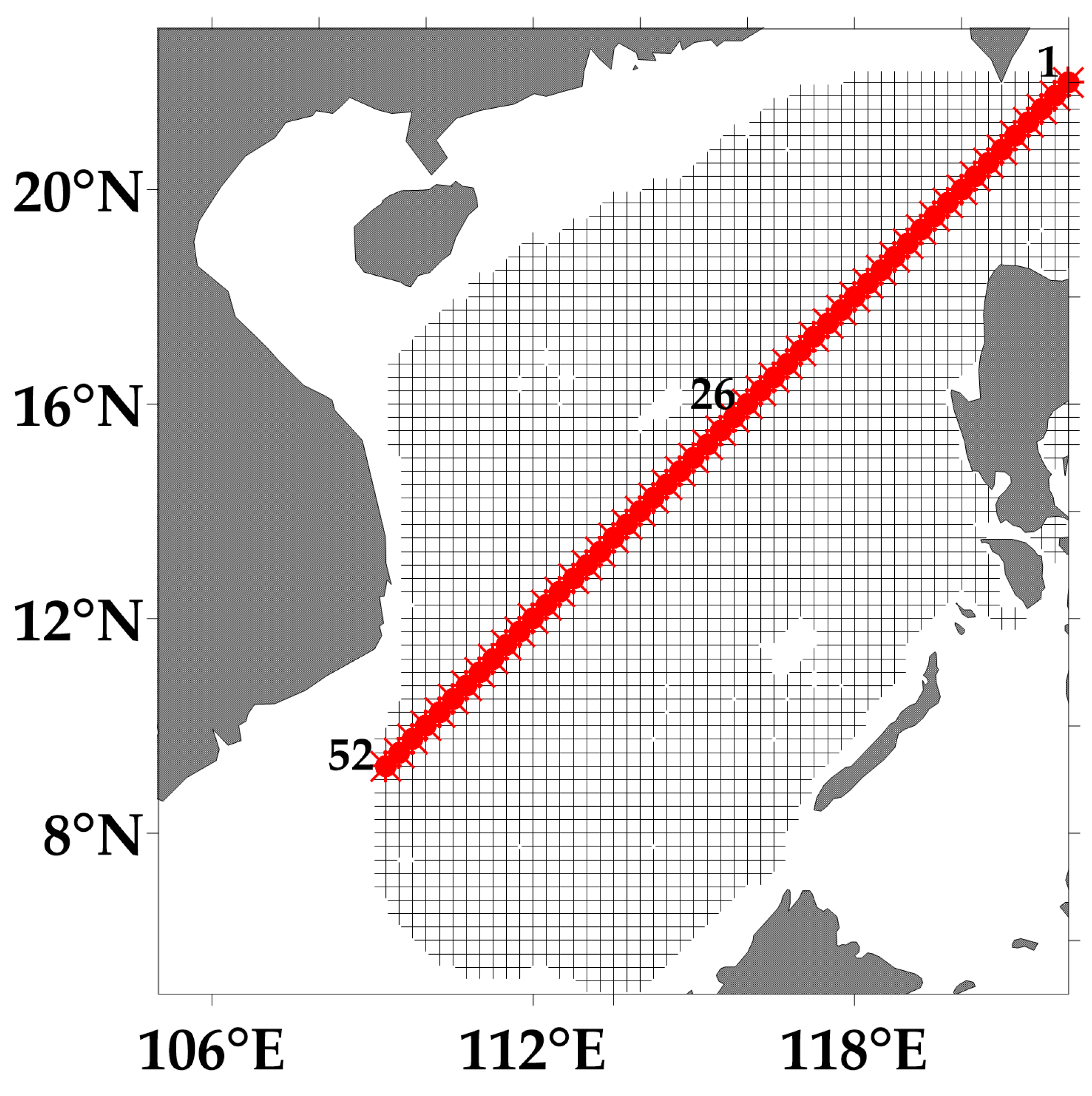
2.1. Data Collection
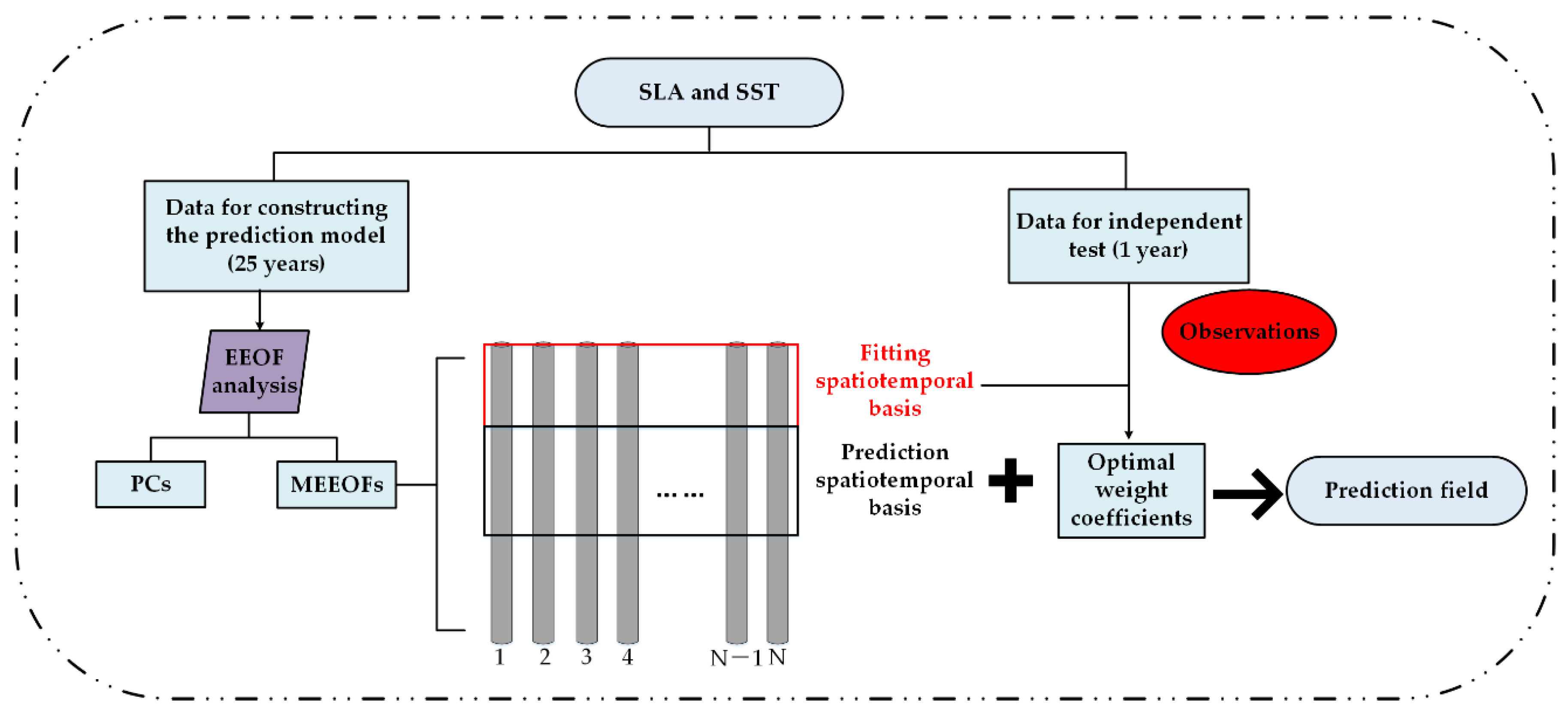
2.2. Description of the Proposed Prediction Model
2.3. Extended Empirical Orthogonal Function Analysis of Multivariate Observations
2.4. Multivariate Prediction
3. Experimental Results
3.1. Performance Evaluation Criteria
3.2. Code Performance
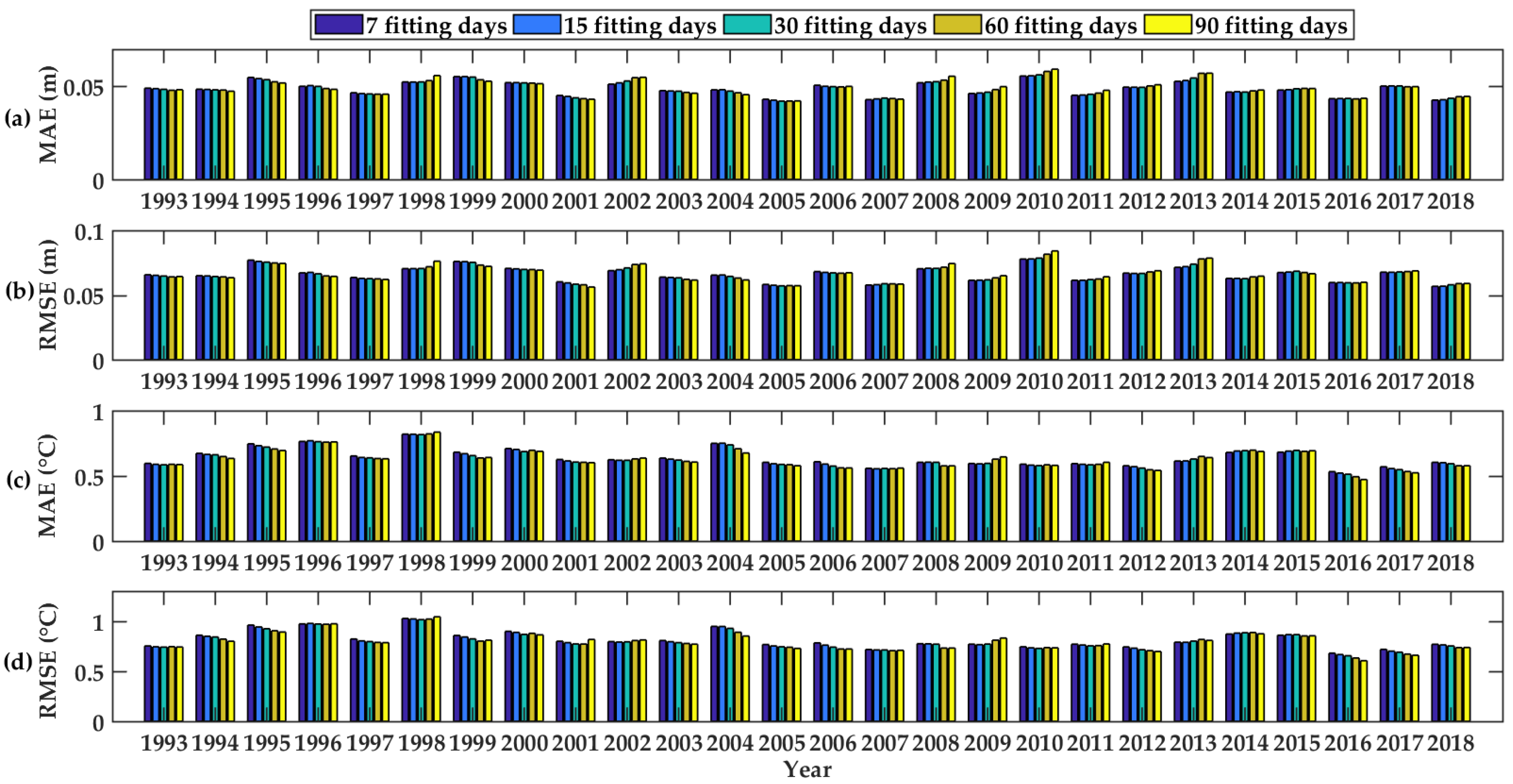
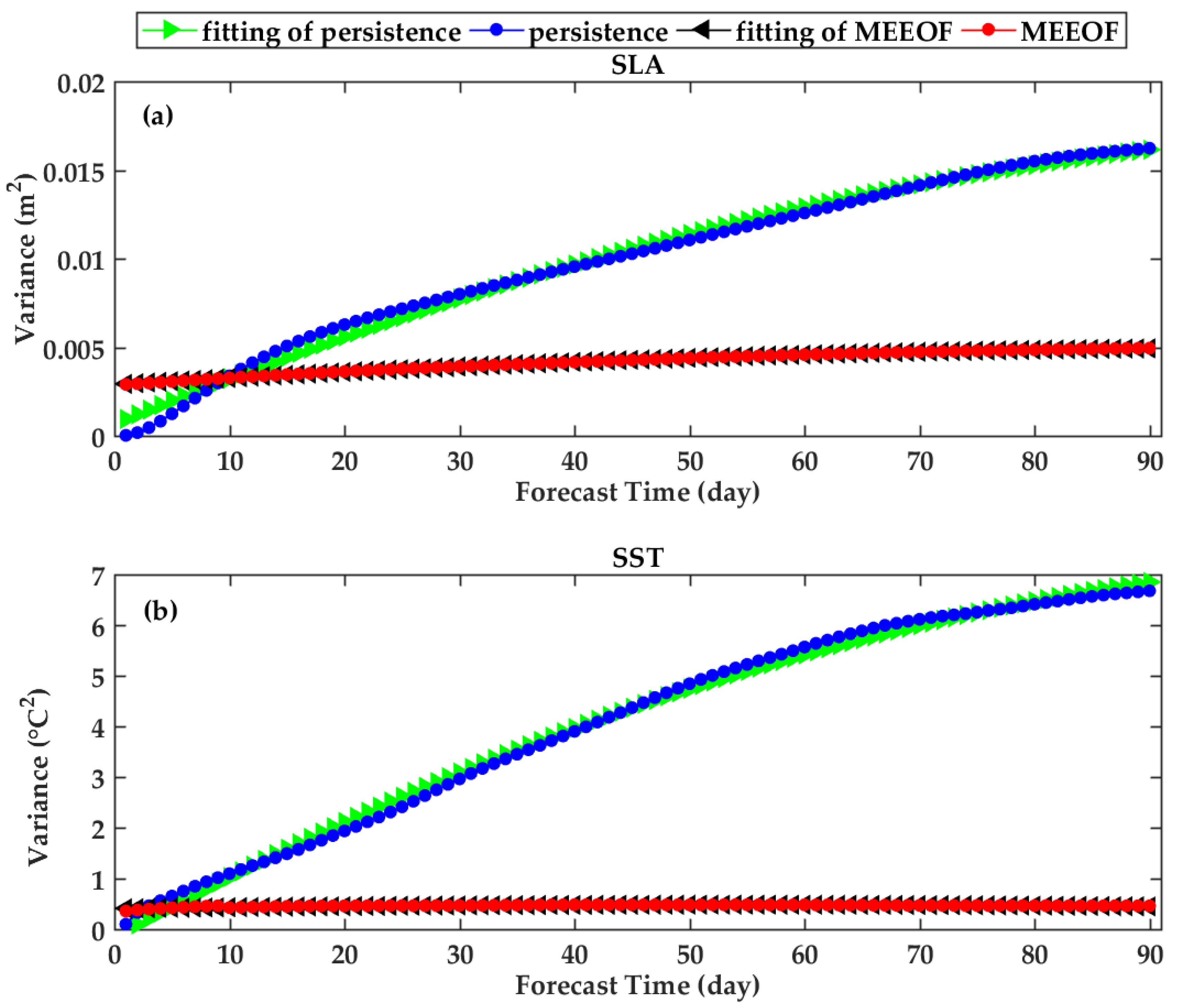
3.3. Fitting Performance and Parameters Determination
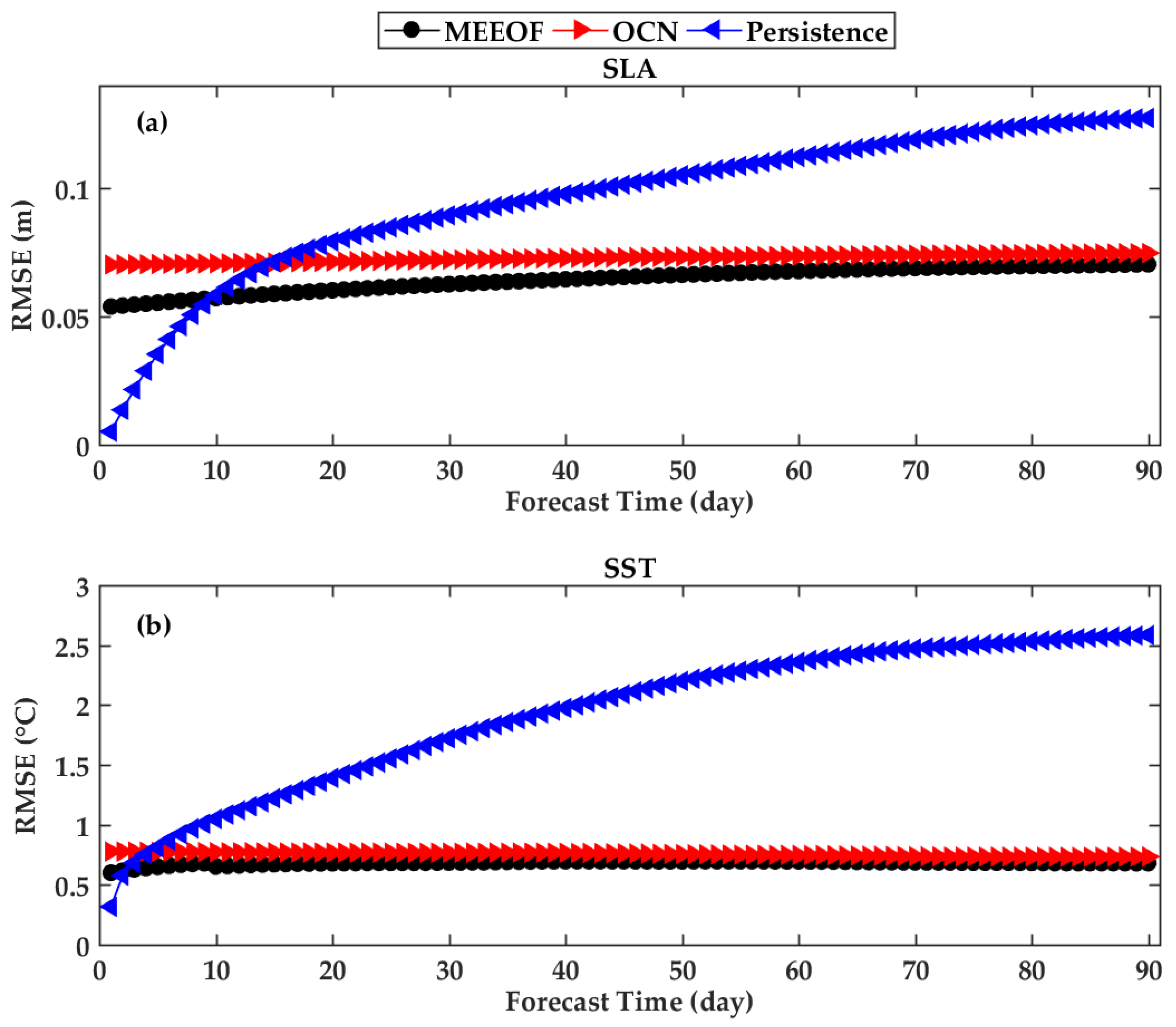
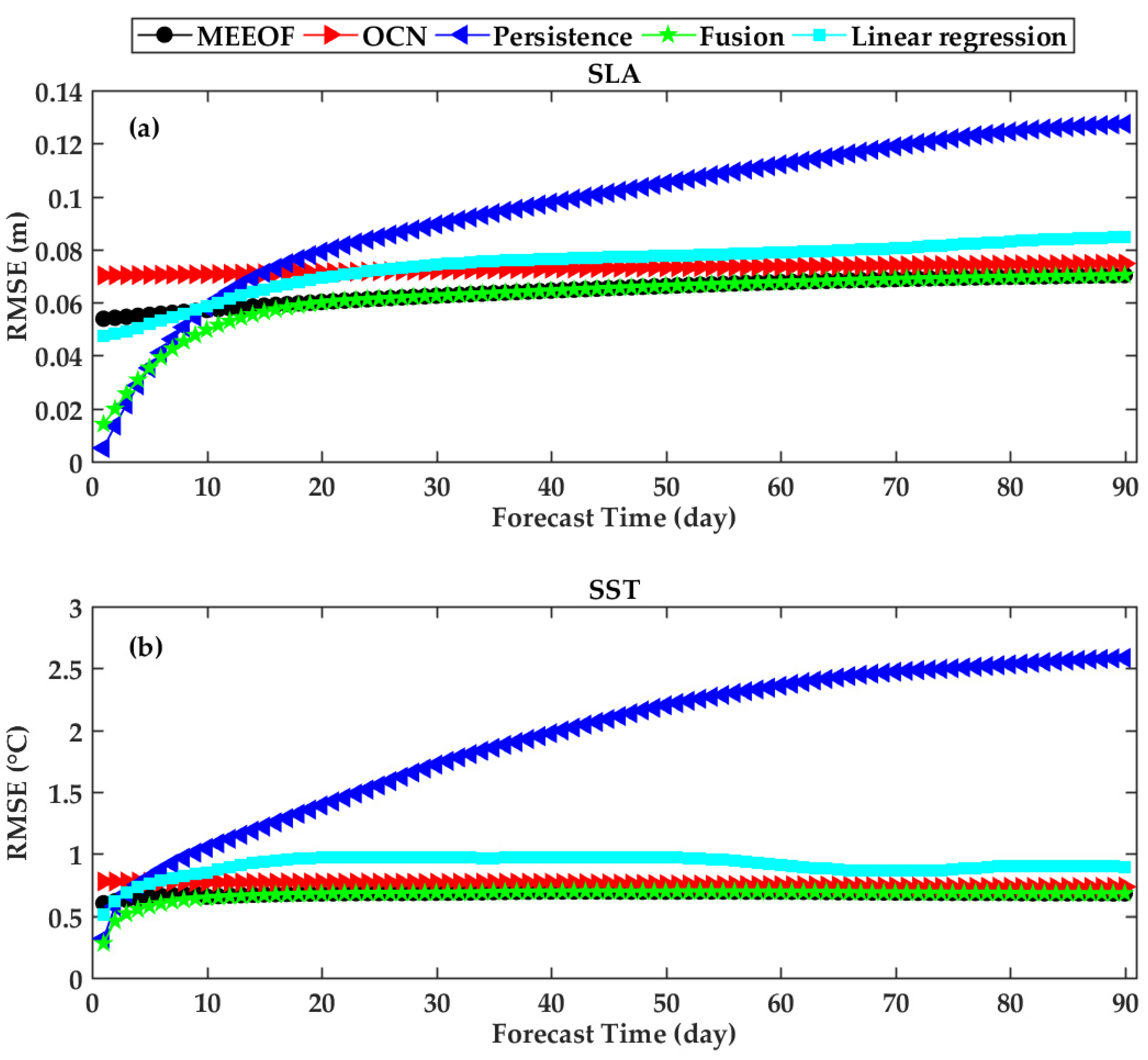
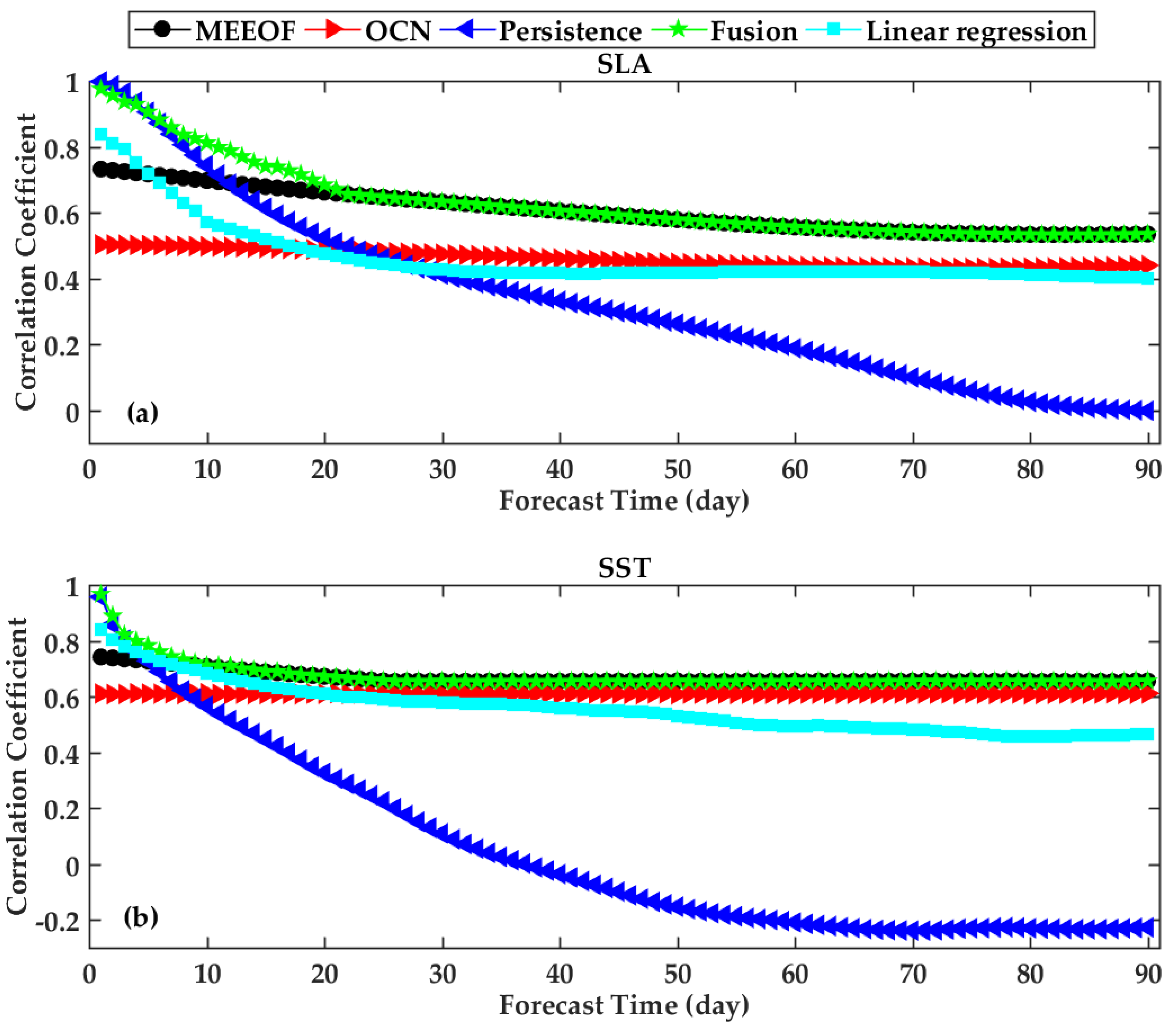
3.4. RMSE and CC Evaluation of Forecast Performance
4. Fusion Model
4.1. Description of the Fusion Model
4.2. Forecast Performance of the Fusion Model
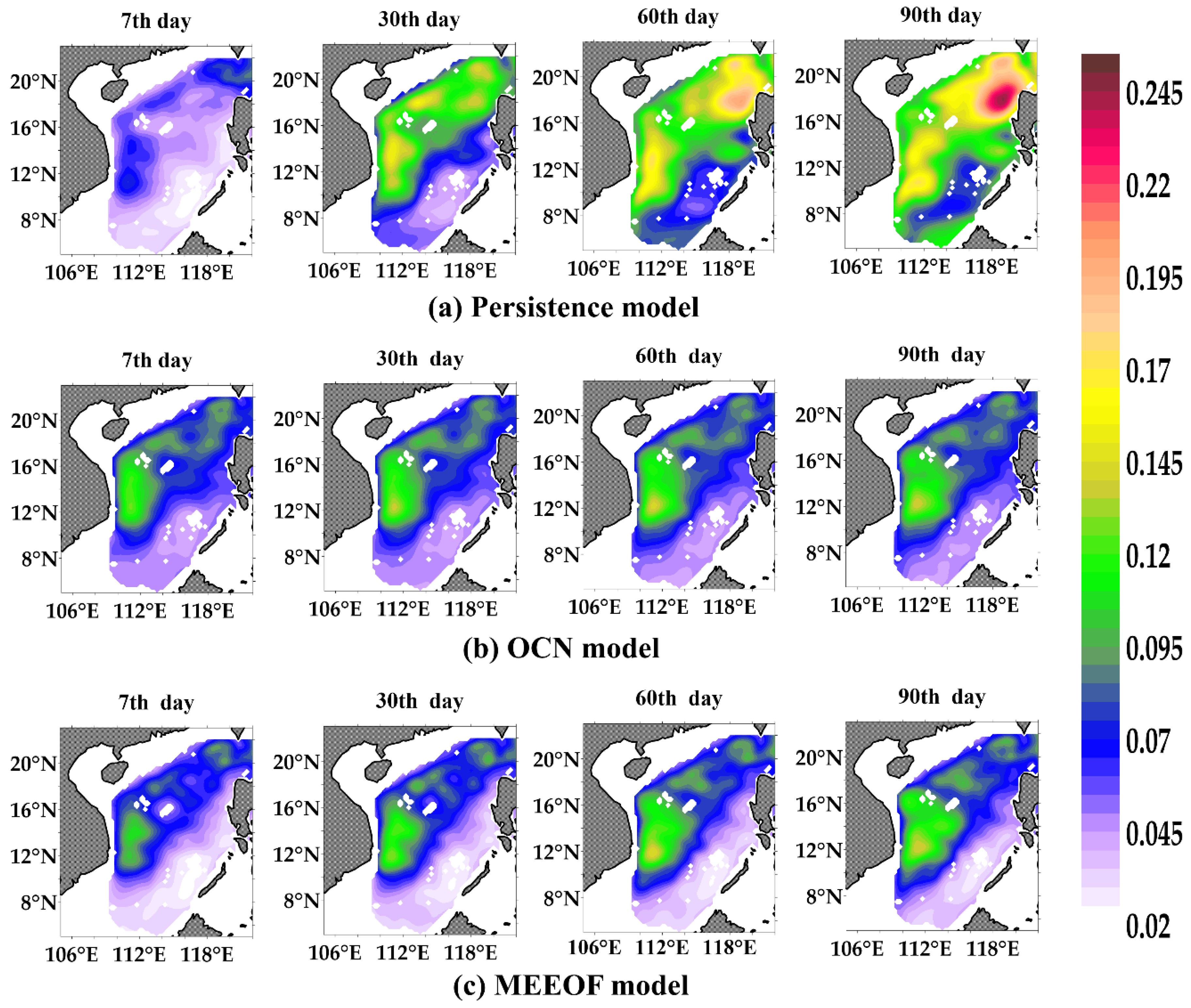
4.3. Forecast Example
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
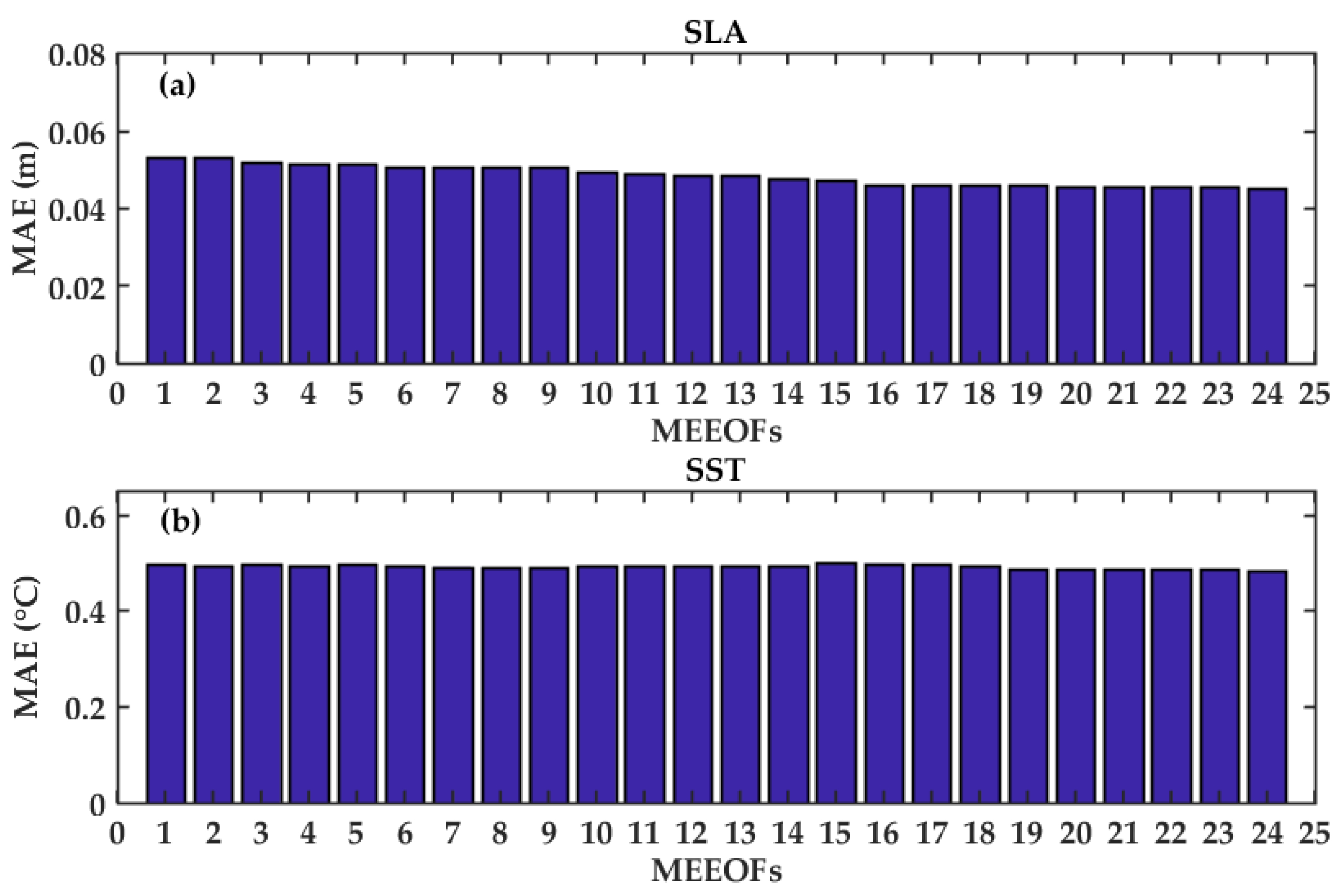
Appendix A. Choice of MEEOFs
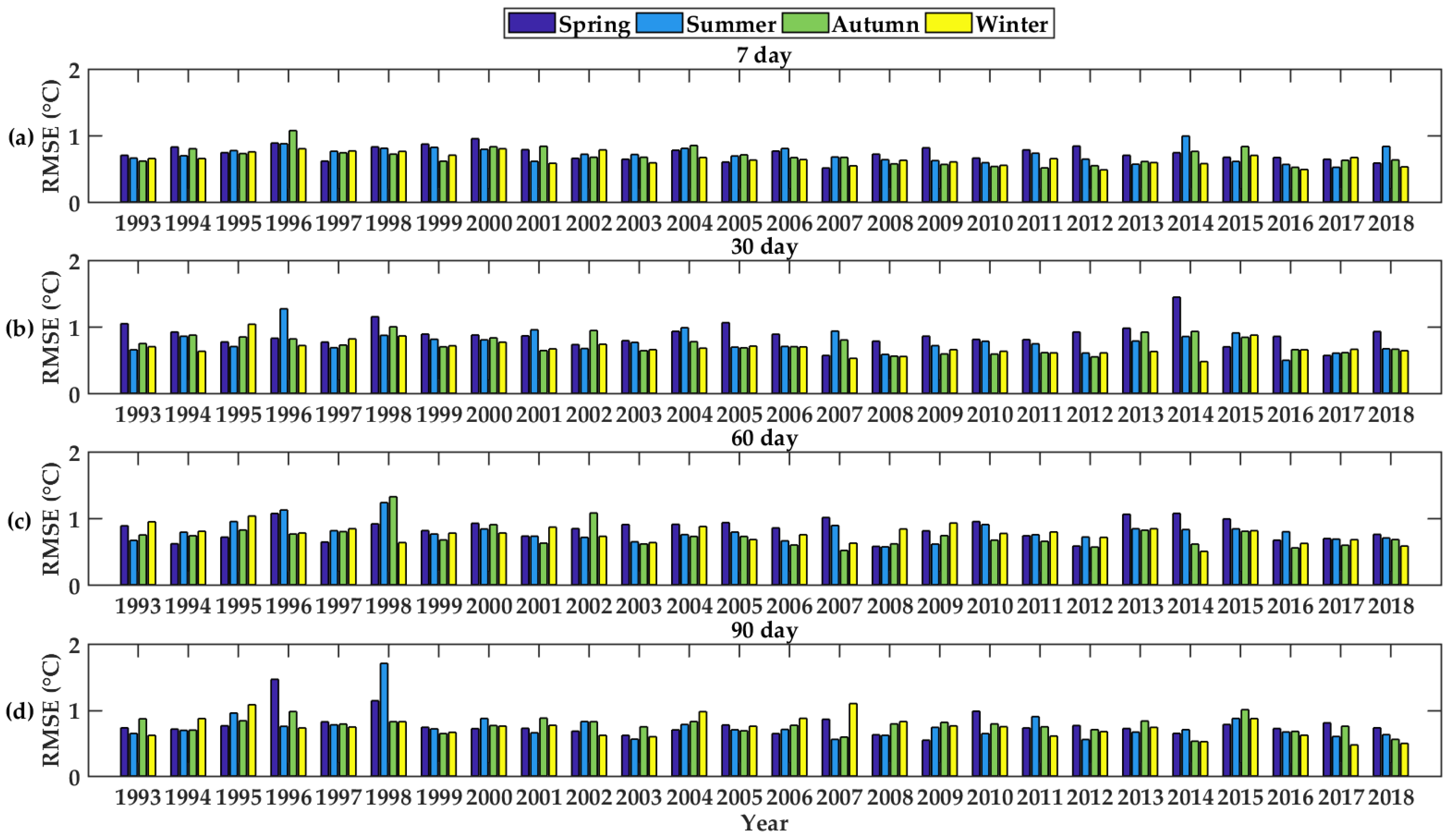
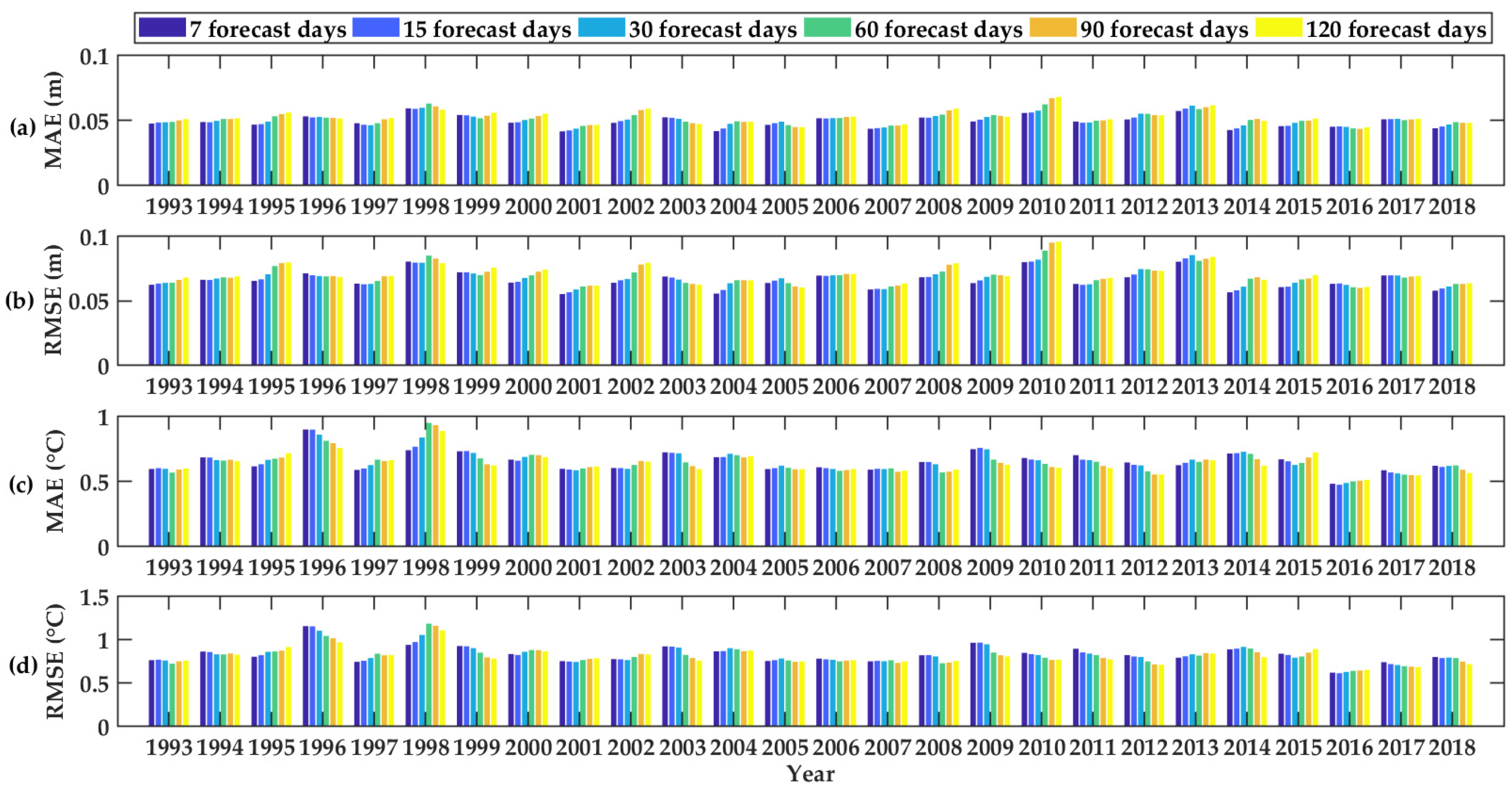
Appendix B. Seasonal Performance

References
- Schiller, A.; Brassington, G.B. Operational Oceanography in the 21st Century; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Francis, P.A.; Vinayachandran, P.N.; Shenoi, S.S.C. The Indian Ocean Forecast System. Curr. Sci. 2013, 104, 1354–1368. [Google Scholar]
- Wang, G. Mesoscale eddies in the South China Sea observed with altimeter data. Geophys. Res. Lett. 2003, 30, 2121. [Google Scholar] [CrossRef] [Green Version]
- Pei, Y.; Zhang, R.-H.; Zhang, X.; Jiang, L.; Wei, Y. Variability of sea surface height in the South China Sea and its relationship to Pacific oscillations. Acta Oceanol. Sin. 2015, 34, 80–92. [Google Scholar] [CrossRef]
- Jianyu, H.; Kawamura, H.; Huasheng, H.; Kobash, F.; Dongxiao, W. 3~6 Months Variation of Sea Surface Height in the South China Sea and Its Adjacent Ocean. J. Oceanogr. 2001, 57, 69–78. [Google Scholar]
- Xiu, P.; Chai, F.; Shi, L.; Xue, H.; Chao, Y. A census of eddy activities in the South China Sea during 1993–2007. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Patil, K.; Deo, M.C.; Ravichandran, M. Prediction of Sea Surface Temperature by Combining Numerical and Neural Techniques. J. Atmos. Ocean. Technol. 2016, 33, 1715–1726. [Google Scholar] [CrossRef]
- Barron, C.N.; Birol Kara, A.; Hurlburt, H.E.; Rowley, C.; Smedstad, L.F. Sea Surface Height Predictions from the Global Navy Coastal Ocean Model during 1998–2001. J. Atmos. Ocean. Technol. 2004, 21, 1876–1893. [Google Scholar] [CrossRef] [Green Version]
- Rowley, C.; Banon, C.; Smedstad, L.; Rhodes, R. Real-time ocean data assimilation and prediction with global NCOM. In Proceedings of the OCEANS ‘02 MTS/IEEE, Biloxi, MI, USA, 29–31 October 2002; pp. 775–780. [Google Scholar]
- Chassignet, E.; Hurlburt, H.; Metzger, E.J.; Smedstad, O.; Cummings, J.; Halliwell, G.; Bleck, R.; Baraille, R.; Wallcraft, A.; Lozano, C.; et al. US GODAE: Global Ocean Prediction with the HYbrid Coordinate Ocean Model (HYCOM). Oceanography 2009, 22, 64–75. [Google Scholar] [CrossRef]
- Powell, B.S.; Moore, A.M.; Arango, H.G.; Di Lorenzo, E.; Milliff, R.F.; Leben, R.R. Near real-time ocean circulation assimilation and prediction in the Intra-Americas Sea with ROMS. Dyn. Atmos. Ocean. 2009, 48, 46–68. [Google Scholar] [CrossRef]
- Noori, R.; Abbasi, M.R.; Adamowski, J.F.; Dehghani, M. A simple mathematical model to predict sea surface temperature over the northwest Indian Ocean. Estuar. Coast. Shelf Sci. 2017, 197, 236–243. [Google Scholar] [CrossRef] [Green Version]
- Cummings, J.A. Operational multivariate ocean data assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3583–3604. [Google Scholar] [CrossRef] [Green Version]
- Carman, J.C.; Eleuterio, D.P.; Gallaudet, T.C.; Geernaert, G.L.; Harr, P.A.; Kaye, J.A.; McCarren, D.H.; McLean, C.N.; Sandgathe, S.A.; Toepfer, F.; et al. The National Earth System Prediction Capability: Coordinating the Giant. Bull. Am. Meteorol. Soc. 2017, 98, 239–252. [Google Scholar] [CrossRef] [Green Version]
- Drévillon, M.; Bourdallé-Badie, R.; Derval, C.; Lellouche, J.M.; Rémy, E.; Tranchant, B.; Benkiran, M.; Greiner, E.; Guinehut, S.; Verbrugge, N.; et al. The GODAE/Mercator-Ocean global ocean forecasting system: Results, applications and prospects. J. Oper. Oceanogr. 2014, 1, 51–57. [Google Scholar] [CrossRef]
- Miyazawa, Y. Ensemble forecast of the Kuroshio meandering. J. Geophys. Res. 2005, 110, C10026. [Google Scholar] [CrossRef] [Green Version]
- Jifan, C. Predictability Of The Atmosphere. Adv. Atmos. Sci. 1988, 6, 335–346. [Google Scholar] [CrossRef]
- Patil, K.; Deo, M.C. Basin-Scale Prediction of Sea Surface Temperature with Artificial Neural Networks. J. Atmos. Ocean. Technol. 2018, 35, 1441–1455. [Google Scholar] [CrossRef]
- Kug, J.; Kang, I.; Lee, J.; Jhun, J. A statistical approach to Indian Ocean sea surface temperature prediction using a dynamical ENSO prediction. Geophys. Res. Lett. 2004, 31, 112–124. [Google Scholar] [CrossRef]
- Tang, B.; Hsieh, W.W.; Monahan, A.H.; Tangang, F.T. Skill Comparisons between Neural Networks and Canonical Correlation Analysis in Predicting the Equatorial Pacific Sea Surface Temperatures. J. Clim. 2000, 13, 287–293. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Leetmaa, A. Forecasts of tropical Pacific SST and sea level using a Markov model. Geophys. Res. Lett. 2000, 27, 2701–2704. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Guan, L.; Qu, L. Prediction of Sea Surface Temperature in the South China Sea by Artificial Neural Networks. IEEE Geosci. Remote Sens. Lett. 2019, 17, 558–562. [Google Scholar] [CrossRef]
- Wei, L.; Guan, L.; Qu, L.; Guo, D. Prediction of Sea Surface Temperature in the China Seas Based on Long Short-Term Memory Neural Networks. Remote Sens. 2020, 12, 2697. [Google Scholar] [CrossRef]
- Imani, M.; You, R.-J.; Kuo, C.-Y. Analysis and prediction of Caspian Sea level pattern anomalies observed by satellite altimetry using autoregressive integrated moving average models. Arab. J. Geosci. 2013, 7, 3339–3348. [Google Scholar] [CrossRef]
- Patil, K.; Deo, M.C. Prediction of daily sea surface temperature using efficient neural networks. Ocean Dyn. 2017, 67, 357–368. [Google Scholar] [CrossRef]
- Shaw, P.-T. The seasonal variation of the intrusion of the Philippine sea water into the South China Sea. J. Geophys. Res. Ocean. 1991, 96, 821–827. [Google Scholar] [CrossRef]
- Hu, W.; Wu, R.; Liu, Y. Relation of the South China Sea Precipitation Variability to Tropical Indo-Pacific SST Anomalies during Spring-to-Summer Transition. J. Clim. 2014, 27, 5451–5467. [Google Scholar] [CrossRef]
- NOAA. Optimum Interpolation Sea Surface Temperature (OISST). Available online: https://www.ncdc.noaa.gov/oisst (accessed on 17 July 2021).
- Chu, P.C.; Ivanov, L.M.; Korzhova, T.P.; Margolina, T.M.; Melnichenko, O.V. Analysis of Sparse and Noisy Ocean Current Data Using Flow Decomposition. Part I: Theory. J. Atmos. Ocean. Technol. 2003, 20, 478–491. [Google Scholar] [CrossRef]
- Yuan, D.; Han, W.; Hu, D. Surface Kuroshio path in the Luzon Strait area derived from satellite remote sensing data. J. Geophys. Res. 2006, 111, 1–16. [Google Scholar] [CrossRef] [Green Version]
- North, G.R. Empirical Orthogonal Functions and Normal Modes. J. Atmos. Sci. 1983, 41, 879–887. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Empirical orthogonal functions and statistical weather prediction. Dept. Meteorol. Mass. Inst. Technol. Stat. Forecast. Proj. Rep 1956, 1, 1–49. [Google Scholar] [CrossRef]
- Chavez, F.; Messié, M. Global Modes of Sea Surface Temperature Variability in Relation to Regional Climate Indices. J. Clim. 2011, 24, 4314–4331. [Google Scholar] [CrossRef]
- Deser, C.; Alexander, M.A.; Xie, S.P.; Phillips, A.S. Sea surface temperature variability: Patterns and mechanisms. Ann. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Feng, G.; Zheng, Z.; Zhang, D.; Jia, Z. Evolution of tropical interannual sea surface temperature variability and its connection with boreal summer atmospheric circulations. Int. J. Climatol. 2019, 40, 2702–2716. [Google Scholar] [CrossRef]
- Lau, K.H.; Lau, N.C. Observed structure and propagation characteristics of tropical summertime synoptic scale disturbances. Mon. Weather Rev. 1990, 118, 1888–1913. [Google Scholar] [CrossRef]
- Weare, B.C.; Nasstrom, J.S. Examples of extended empirical orthogonal function analyses. Mon. Weather Rev. 1982, 110, 481–485. [Google Scholar] [CrossRef]
- Mares, C.; Mares, I. Improvement of Long-Range Forecasting by EEOF Extrapolation Using an AR-MEM Model. Weather Forecast. 2003, 18, 311–324. [Google Scholar] [CrossRef]
- Fox, D.N.; Teague, W.J.; Barron, C.N. The Modular Ocean Data Assimilation System. J. Atmos. Ocean. Technol. 2000, 19, 240–252. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Xue, H.; Wang, H. A simple predictive model for the eddy propagation trajectory in the northern South China Sea. Ocean Sci. 2019, 15, 401–412. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Barnston, A.G. Long-Lead Seasonal Temperature Prediction Using Optimal Climate Normals. J. Clim. 1996, 9, 809–817. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]




| The Number of Subsamples | m | n | Running Time(s) |
|---|---|---|---|
| 20-year | 1,679,730 | 20 | 331.860 |
| 21-year | 1,679,730 | 21 | 358.150 |
| 22-year | 1,679,730 | 22 | 382.580 |
| 23-year | 1,679,730 | 23 | 411.270 |
| 24-year | 1,679,730 | 24 | 445.730 |
| 25-year | 1,679,730 | 25 | 483.330 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, Q.; Zhao, Y.; Li, W.; Han, G.; Hou, G.; Li, C.; Liu, S.; Gong, Y.; Liu, H.; Qu, P. A Simple Statistical Intra-Seasonal Prediction Model for Sea Surface Variables Utilizing Satellite Remote Sensing. Remote Sens. 2022, 14, 1162. https://doi.org/10.3390/rs14051162
Shao Q, Zhao Y, Li W, Han G, Hou G, Li C, Liu S, Gong Y, Liu H, Qu P. A Simple Statistical Intra-Seasonal Prediction Model for Sea Surface Variables Utilizing Satellite Remote Sensing. Remote Sensing. 2022; 14(5):1162. https://doi.org/10.3390/rs14051162
Chicago/Turabian StyleShao, Qi, Yanling Zhao, Wei Li, Guijun Han, Guangchao Hou, Chaoliang Li, Siyuan Liu, Yantian Gong, Hanyu Liu, and Ping Qu. 2022. "A Simple Statistical Intra-Seasonal Prediction Model for Sea Surface Variables Utilizing Satellite Remote Sensing" Remote Sensing 14, no. 5: 1162. https://doi.org/10.3390/rs14051162
APA StyleShao, Q., Zhao, Y., Li, W., Han, G., Hou, G., Li, C., Liu, S., Gong, Y., Liu, H., & Qu, P. (2022). A Simple Statistical Intra-Seasonal Prediction Model for Sea Surface Variables Utilizing Satellite Remote Sensing. Remote Sensing, 14(5), 1162. https://doi.org/10.3390/rs14051162






