Research on Shore-Based River Flow Velocity Inversion Model Using GNSS-R Raw Data
Abstract
:1. Introduction
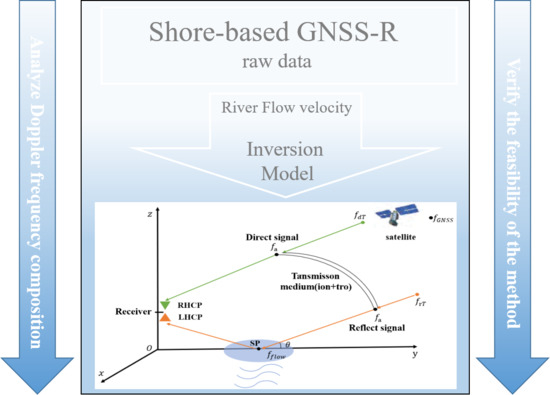
2. River Flow Velocity Inversion Model
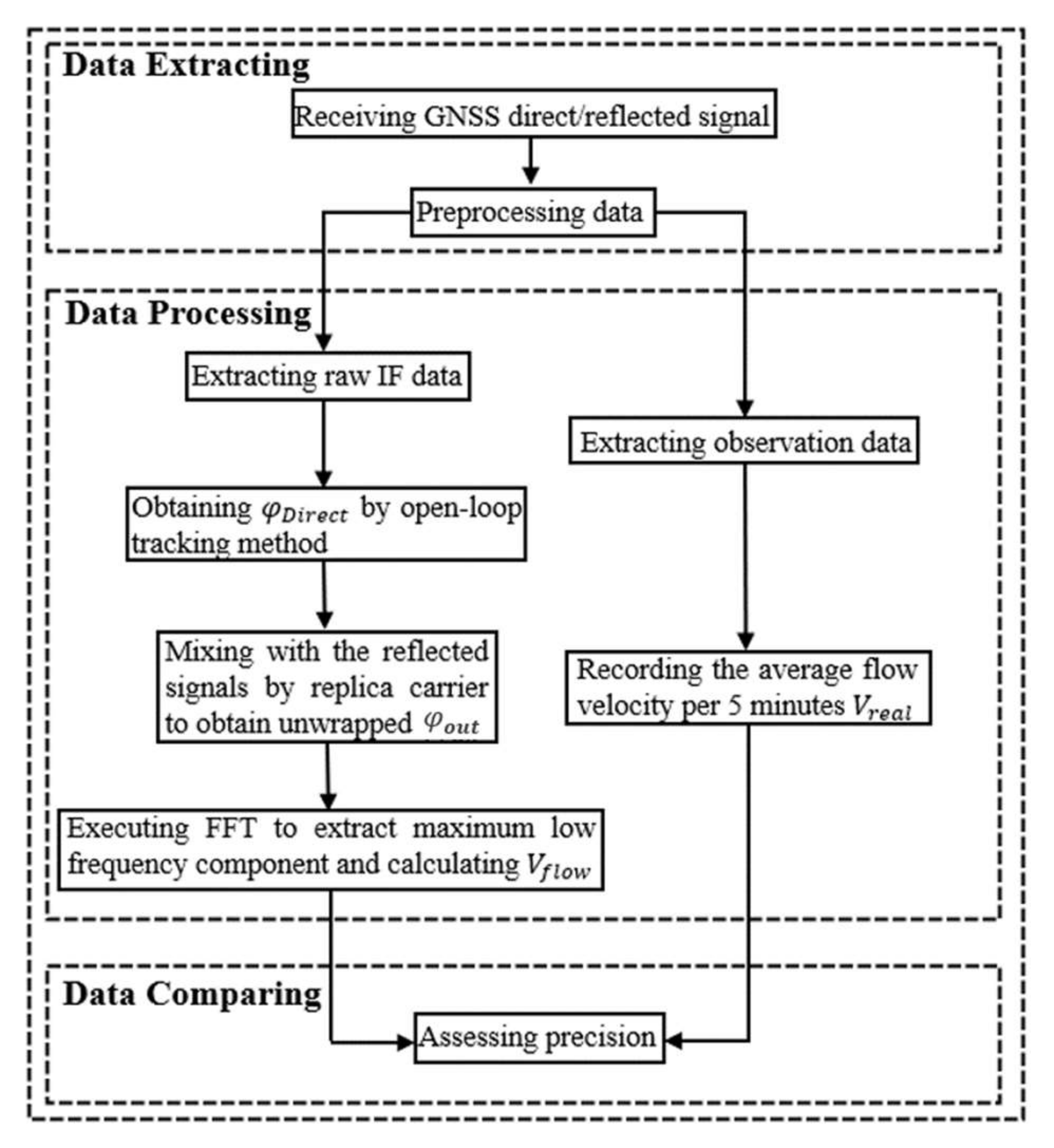
2.1. GNSS-R Reiver Velocity Inversion Process
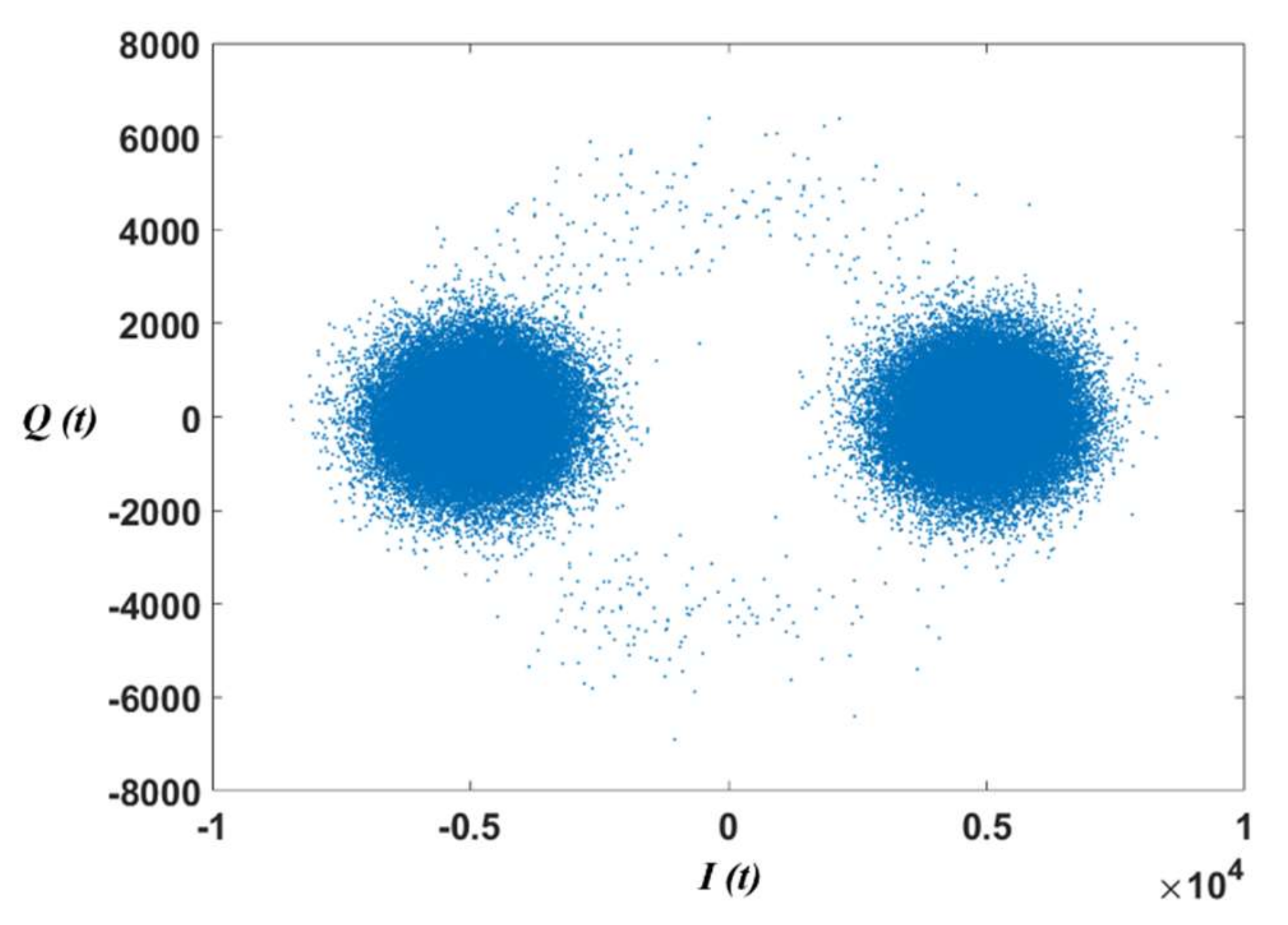
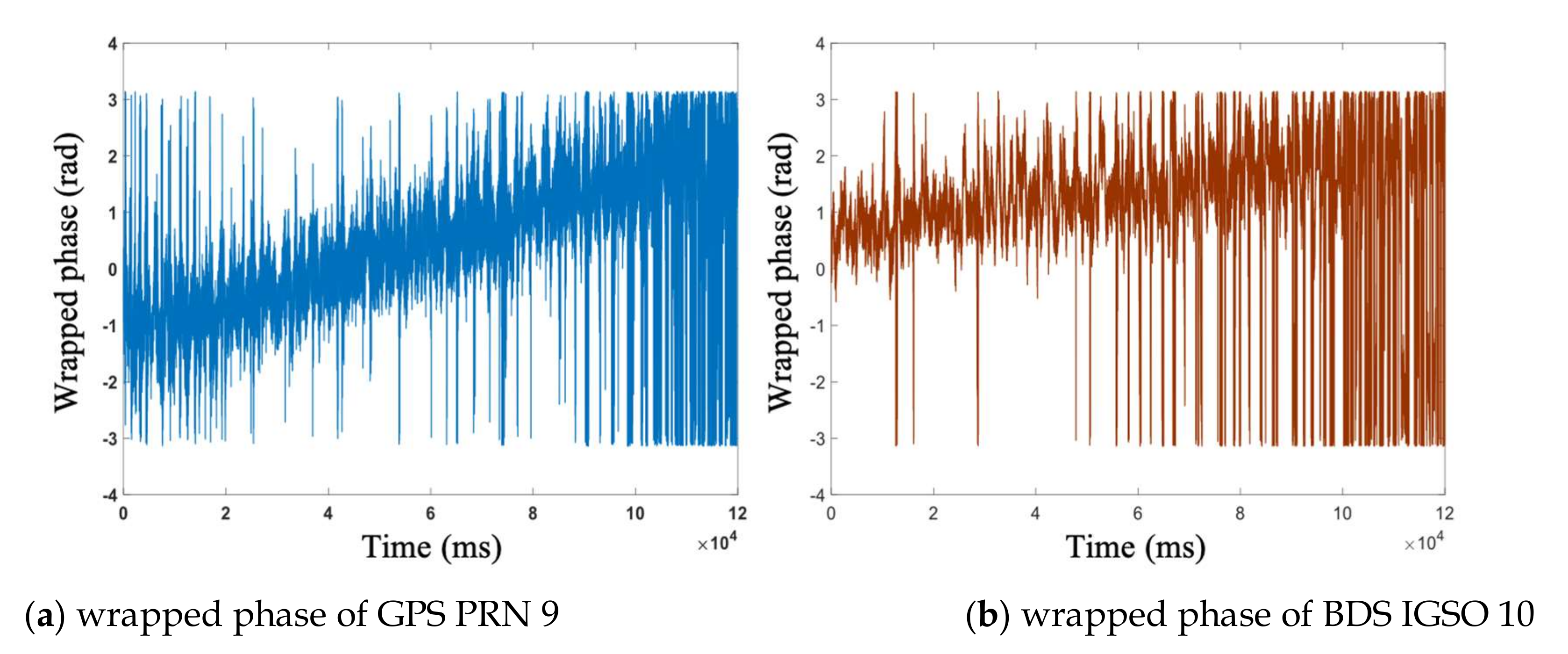
2.2. Signal Open-Loop Tracking Method
2.3. Inversion Method
3. Shore-Based Velocity Inversion Experiment
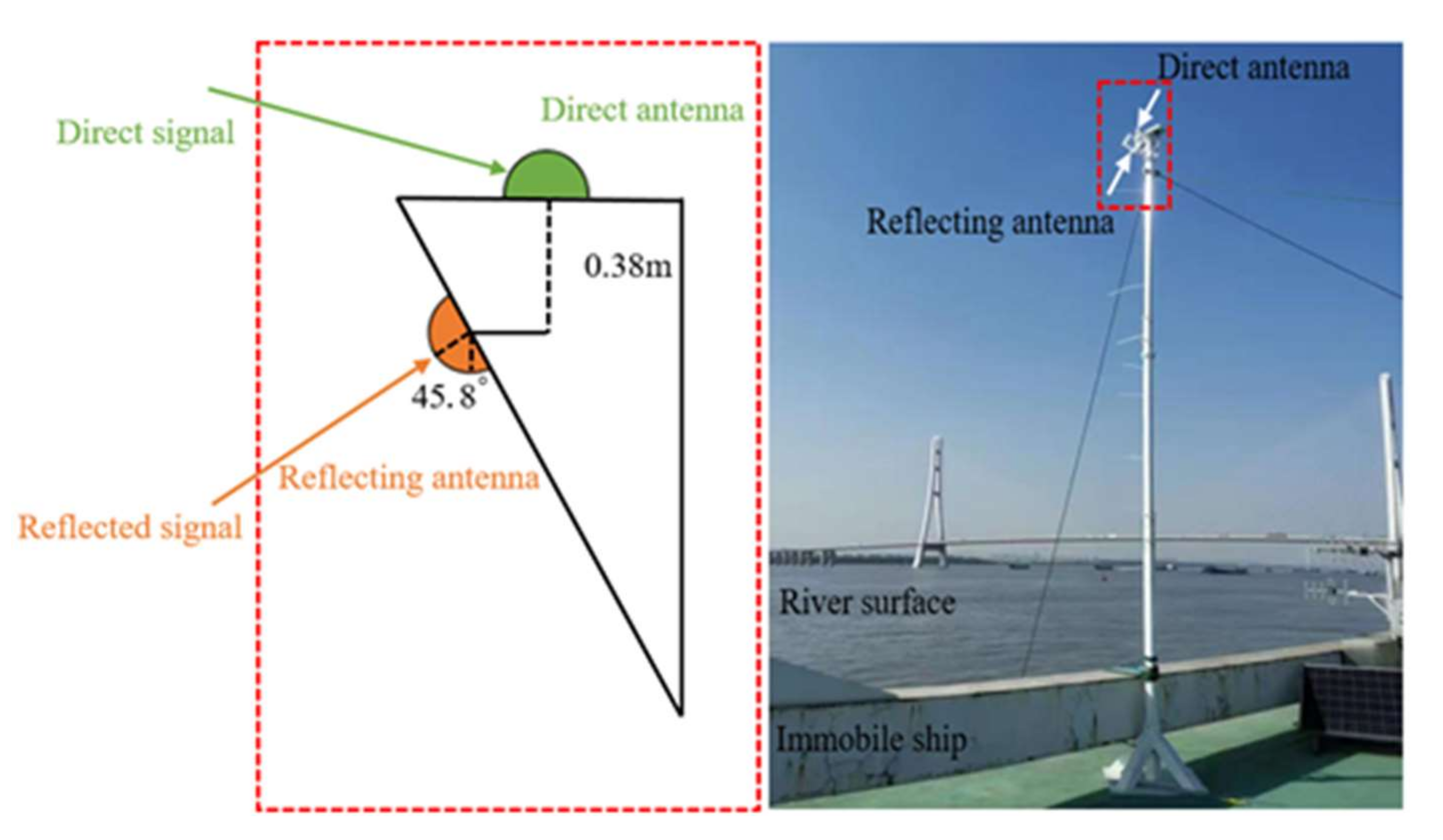
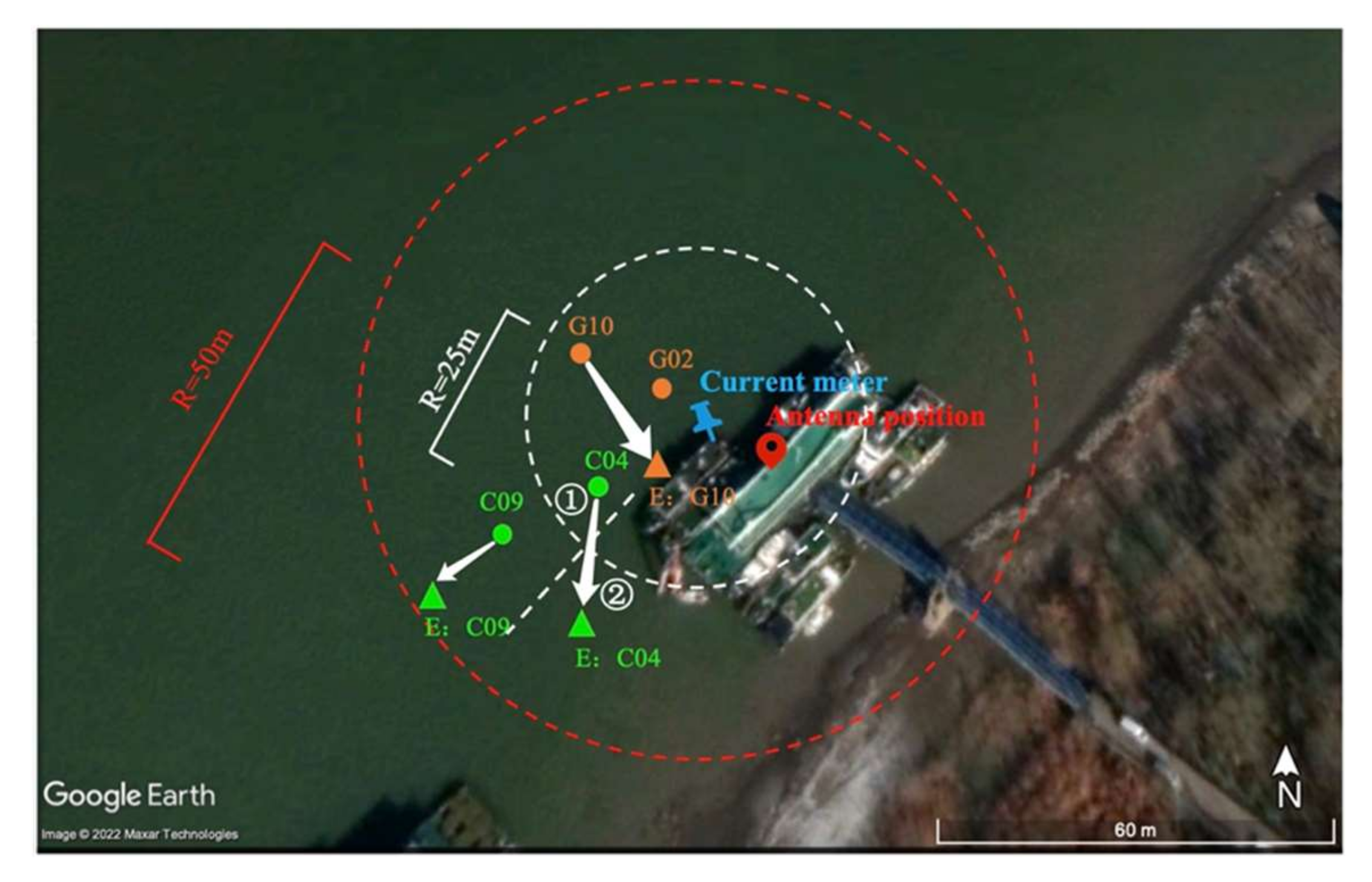
3.1. The Experimental Set-Up
3.2. Experimental Configuration
4. River Flow Velocity Inversion Result and Analysis
4.1. River Flow Velocity Inversion Results
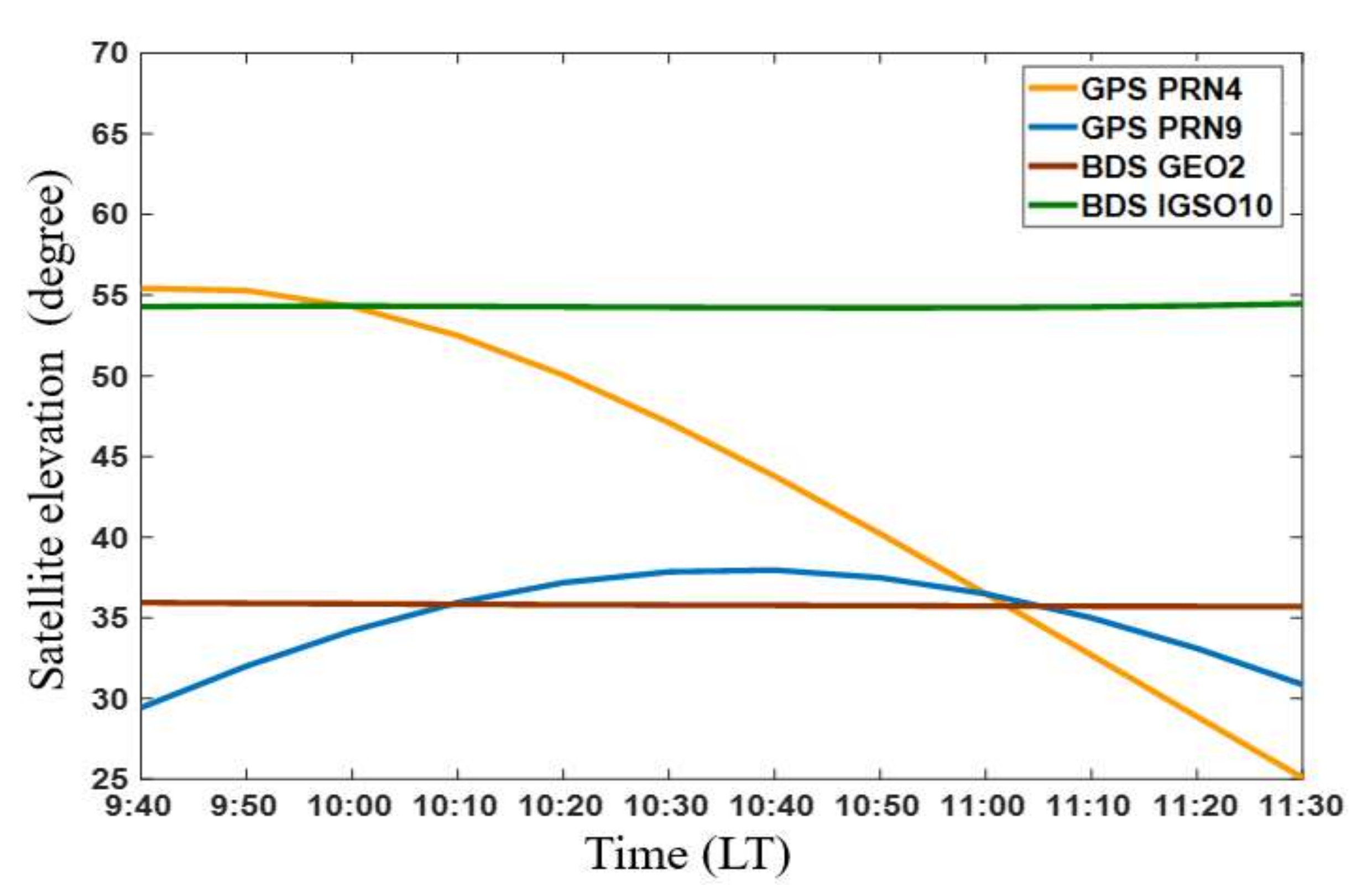
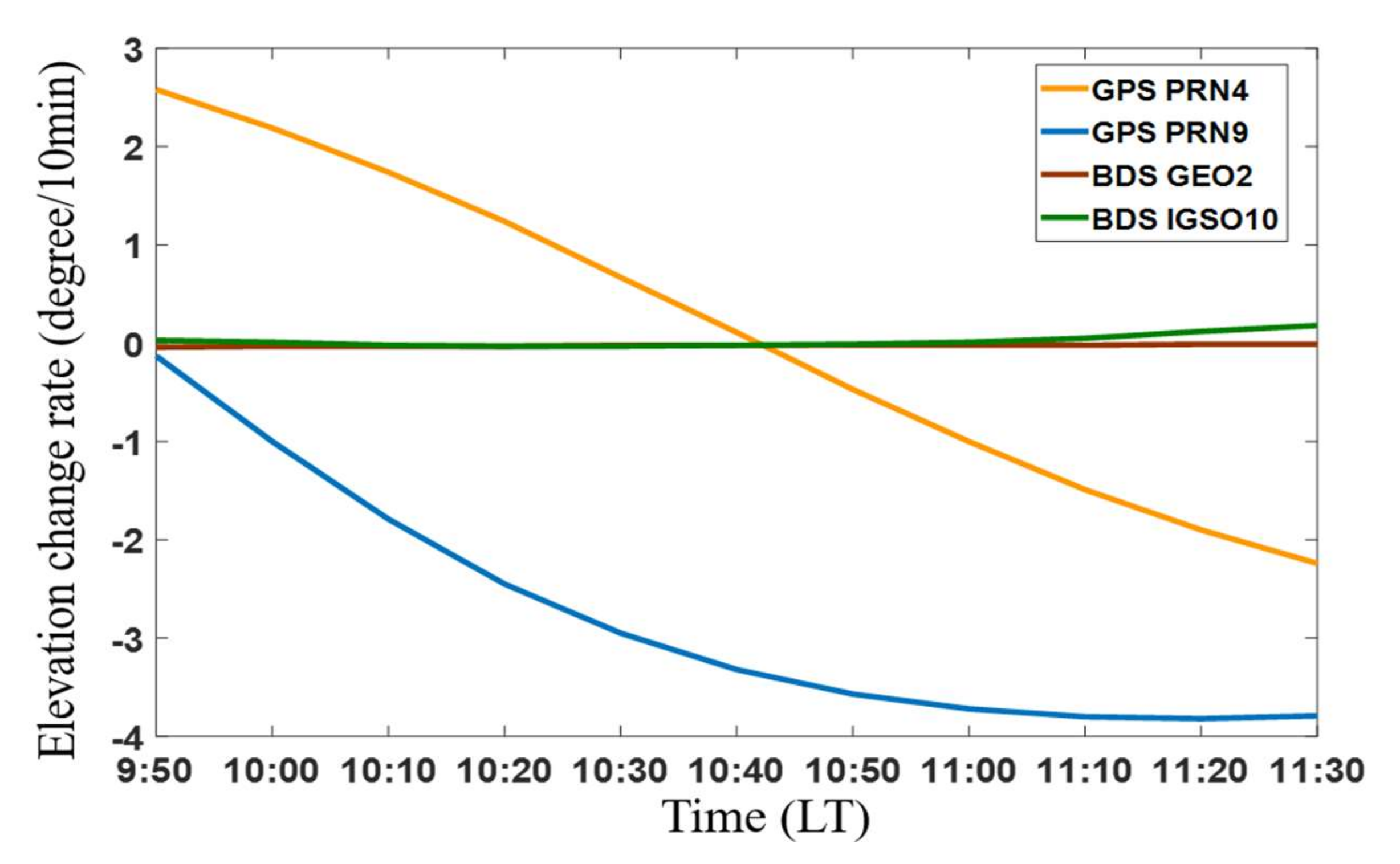
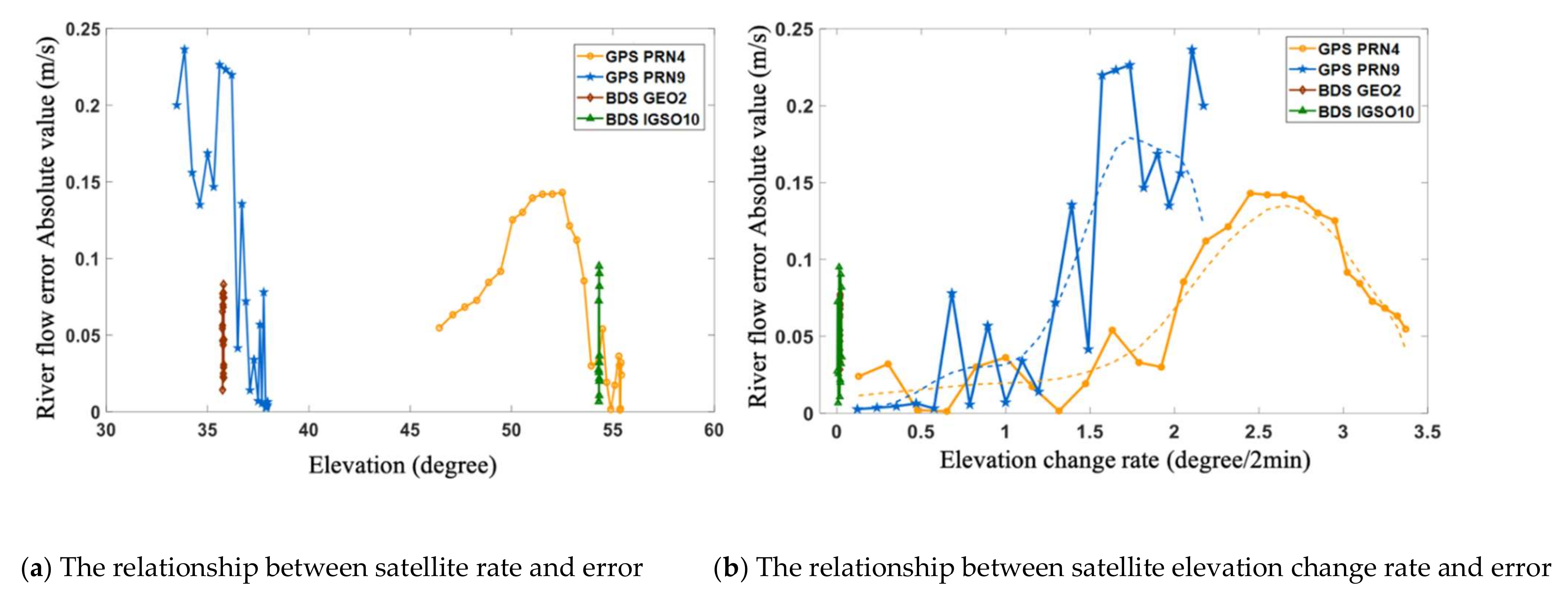
4.2. Influence of Elevation Change Rate
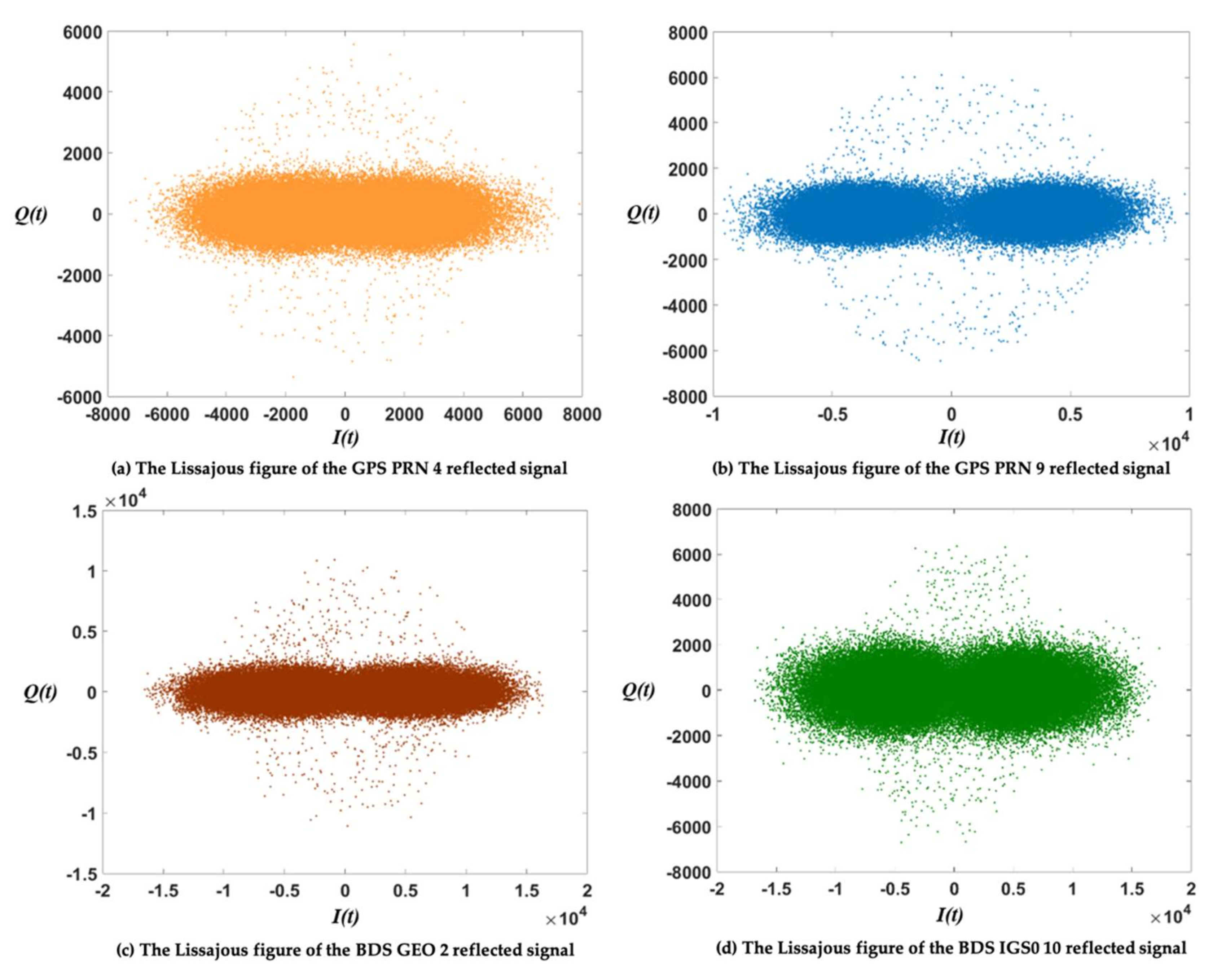
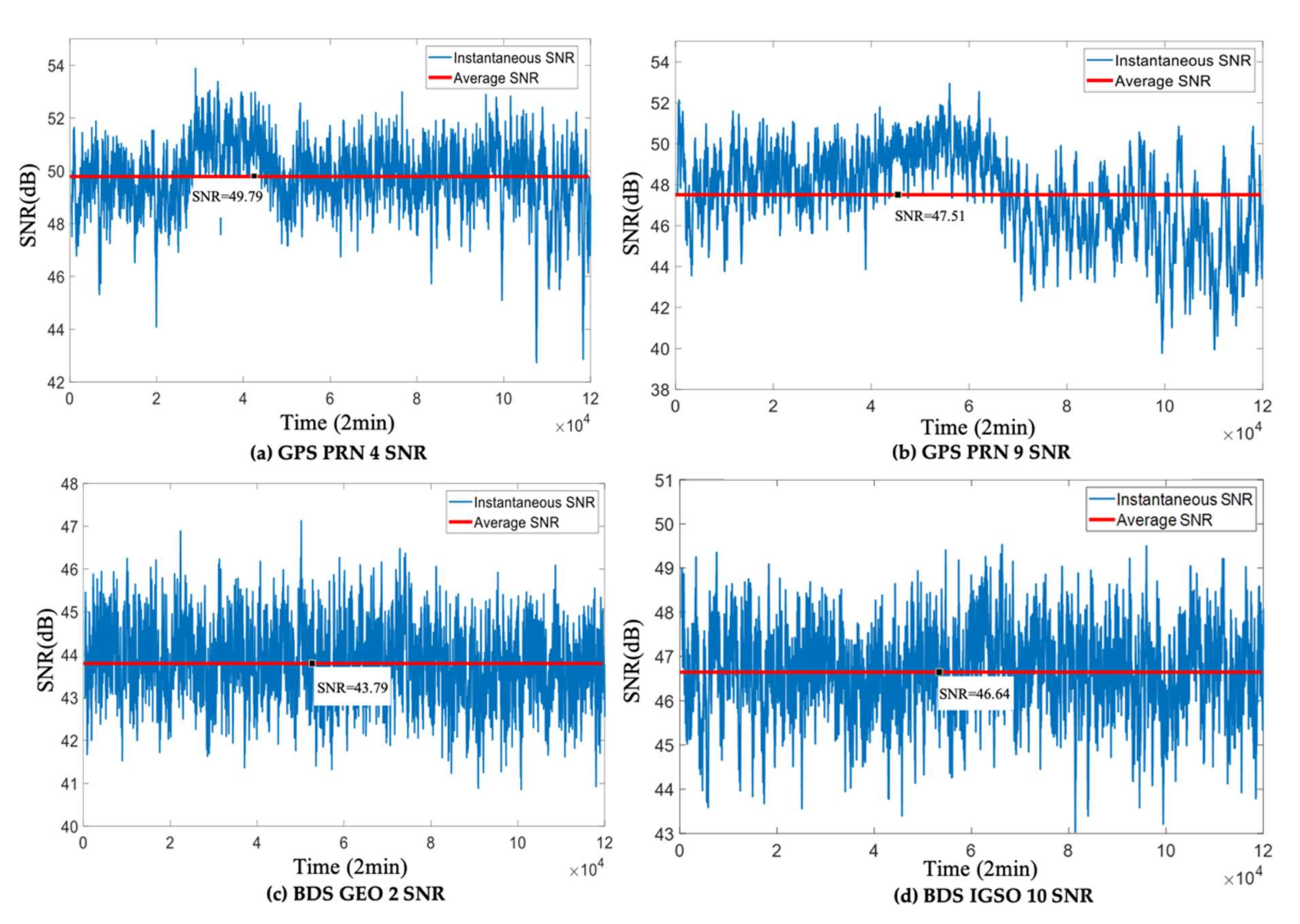
4.3. Influence of Reflected Signal Strength
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sauquet, E.; Shanafield, M.; Hammond, J.C.; Sefton, C.; Datry, T. Classification and trends in intermittent river flow regimes in Australia, northwestern Europe and USA: A global perspective. J. Hydrol. 2021, 597, 126–170. [Google Scholar] [CrossRef]
- Sanjou, M.; Shigeta, A.; Kato, K.; Aizawa, W. Portable unmanned surface vehicle that automatically measures flow velocity and direction in rivers. Flow Measurement and Instrumentation. Flow Meas Instrum. 2021, 6, 2411–2502. [Google Scholar] [CrossRef]
- Wang, H.; Zang, J.; Wang, X. Research and Application of the Flow Calculation Model Based on the Average Velocity Distribution of the Vertical Line of the Cross Section. Hydrology 2019, 49, 50–54. [Google Scholar]
- Zhang, Y.; Xie, X.; Meng, W. Bohai Sea Ice Detection Based on Beidou GEO Satellite Reflected Signal. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 257–263. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, D.; Meng, W. Research on sea level inversion of GPS Reflection Signal based on Techdemosat-1 satellite. J. Beijing Univ. Aeronaut. Astronaut. 2019, 10, 1941–1948. [Google Scholar] [CrossRef]
- Zhang, Y.; Hang, S.; Han, Y. Sea Ice Thickness Detection Using Coastal BeiDou Reflection Setup in Bohai Bay. IEEE Geosci. Remote. Sens. Lett. 2020, 99, 1–5. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Akos, D.M.; Zavorotny, V.U. Airborne GNSS-R Wind Retrievals Using Delay–Doppler Maps. IEEE Trans. Geosci. Remote Sens. 2013, 51, 626–641. [Google Scholar] [CrossRef]
- Valencia, E.; Zavorotny, V.U.; Akos, D.M. Using DDM Asymmetry Metrics for Wind Direction Retrieval From GPS Ocean-Scattered Signals in Airborne Experiments. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3924–3936. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Yan, Q.; Huamg, W. Spaceborne GNSS-R Sea Ice Detection Using Delay-Doppler Maps: First Results From the U.K. TechDemoSat-1 Mission. IEEE J.-STARS. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Alonso-Arroyo, A.; Zavorotny, V.U.; Camps, A. Sea Ice Detection Using U.K. TDS-1 GNSS-R Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4989–5001. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Tao, T.; Zou, J. Spaceborne GNSS reflectometry for retrieving sea ice concentration using TDS-1 data. IEEE Trans. Geosci. Remote Sens. 2020, 18, 612–616. [Google Scholar] [CrossRef]
- Gerlein-Safdi, C.; Ruf, C.S. A CYGNSS-based algorithm for the detection of inland waterbodies. Geophys. Res. Lett. 2019, 46, 12065–12072. [Google Scholar] [CrossRef]
- Ghasemigoudarzi, P.; Huang, W.; Silva, O.D. A machine learning method for inland water detection using CYGNSS data. IEEE Geosci. Remote. Sens. Lett. 2020, 19, 8001105. [Google Scholar] [CrossRef]
- Valencia, E.; Camps, A.; Rodriguez-Alvarez, N. Using GNSS-R Imaging of the Ocean Surface for Oil Slick Detection. IEEE J.-STARS 2013, 6, 217–223. [Google Scholar] [CrossRef]
- Li, C.; Huang, W.; Gleason, S. Dual Antenna Space-Based GNSS-R Ocean Surface Mapping: Oil Slick and Tropical Cyclone Sensing. IEEE J.-STARS 2015, 8, 425–435. [Google Scholar] [CrossRef]
- Ca Parrini, M.; Egido, A.; Soulat, F. Oceanpal: Monitoring sea state with a GNSS-R coastal instrument. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 23–28. [Google Scholar]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G. The Accidental Tide Gauge: A GPS Reflection Case Study From Kachemak Bay. IEEE Trans. Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef] [Green Version]
- Treuhaft, N.; Lowe, S.T.; Zuffada, C. 2-cm GPS altimetry over Crater Lake. Geophys. Res. Lett. 2001, 28, 4343–4346. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Lowe, S.T. An Assessment of the Precision and Accuracy of Altimetry Retrievals for a Monterey Bay GNSS-R Experiment. IEEE J.-STARS 2017, 9, 4660–4668. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, B. Phase Altimetry Using Reflected Signals From BeiDou GEO Satellites. IEEE Trans. Geosci. Remote Sens. 2016, 13, 1–5. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martín-Neira, M. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4992–5004. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Park, H.; Camps, A. GNSS-R Derived Centimetric Sea Topography: An Airborne Experiment Demonstration. IEEE IGARSS 2013, 6, 1468–1478. [Google Scholar] [CrossRef]
- Fabra, F.; Cardellach, E.; Ribo, S. Is Accurate Synoptic Altimetry Achievable by Means of Interferometric GNSS-R? Remote Sens. 2019, 11, 505–520. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Benson, C.; Rizos, C. Single-Pass Sub-Meter Space-Based GNSS-R Ice Altimetry: Results From TDS-1. IEEE J.-STARS 2017, 11, 3782–3788. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F. Lake Level and Surface Topography Measured with Spaceborne GNSS in eflectometry from CYGNSS Mission: Example for the Lake Qinghai. Geophys. Res. Lett. 2018, 45, 313–332. [Google Scholar] [CrossRef]
- Zuffada, C.; Haines, B.; Hajj, G. Assessing the Altimetric Measurement from CYGNSS Data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; Volume 7. [Google Scholar]
- Semmling, A.M.; Schmidt, T.; Wickert, J.; Schön, S.S.; Fabra, F.; Cardellach, E.; Rius, A. On the retrieval of the specular reflection in GNSS carrier observations for ocean altimetry. Radio Sci. 2012, 47, RS6007. [Google Scholar] [CrossRef]
- Bai, W.; Xia, J.; Wei. W. A first comprehensive evaluation of China’s GNSS-R airborne campaign: Part II-river remote sensing. Sci. Bull. 2015, 17, 1527–1534. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y. Principle and Implementation Technology of Beidou/GPS Dual-Mode Software Receiver, 3rd ed.; Publishing House of Electronics Industry: Beijing, China, 2016; pp. 163, 204–206, 212. [Google Scholar]
- Lu, Y. GPS Global Positioning Receiver: Principle and Software Implementation, 1st ed.; Publishing House of Electronics Industry: Beijing, China, 2009; pp. 76–78. [Google Scholar]
- Yang, D. Zhang, Q. GNSS Reflected Signal Processing Basis and Practice: GNSS Reflected Signal Processing Basis and Practice, 1st ed.; Publishing House of Electronics Industry: Beijing, China, 2012; pp. 76–77, 90–91. [Google Scholar]
- Beyerle, G.; Schmidt, T.; Wickert, J. Observations and simulations of receiver-induced refractivity biases in GPS radio occultation. J. Geophys. Res. 1970, 111, D12. [Google Scholar] [CrossRef] [Green Version]
- Geng, Q.; Huang, Z.; Li, Q. Doppler shift estimation and compensation of low and medium orbit satellite signals. Systems Eng. Electron. 2009, 31, 256–260. [Google Scholar] [CrossRef]
- Wang, J.W. Signal-to-Noise Ratio (SNR). Encycl. Neurosci. 2008, 47, 4833–4840. [Google Scholar] [CrossRef]







| Attributes | Value |
|---|---|
| Antenna latitude | 31°57′43″ N |
| Antenna longitude | 118°38′27″ E |
| Antenna azimuth angle | 304° (northwest) |
| Tilt angle of reflecting antenna | 45.8° |
| Height of antenna | 5.45 m |
| Vertical height difference of direct/reflective antenna | 0.38 m |
| Satellites System | PRN | Close Points Rate (Close Points/Total Points) | MAE(m/s) | RMSE(m/s) | R |
|---|---|---|---|---|---|
| GPS L1 | PRN 4 (1st period) | 100% | 0.028 | 0.036 | 0.855 |
| GPS L1 | PRN 4 (2nd period) | 13% | 0.080 | 0.090 | 0.401 |
| GPS L1 | PRN 9 | 0% | 0.103 | 0.14 | 0.378 |
| BDS B1I | GEO 2 | 100% | 0.048 | 0.063 | 0.806 |
| BDS B1I | IGSO 10 | 100% | 0.061 | 0.073 | 0.763 |
| Satellite System | PRN | R |
|---|---|---|
| GPS L1 | PRN 4 | 0.652 |
| GPS L1 | PRN 9 | 0.876 |
| GPS L1 | ALL | 0.727 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yan, Z.; Yang, S.; Meng, W.; Gu, S.; Qin, J.; Han, Y.; Hong, Z. Research on Shore-Based River Flow Velocity Inversion Model Using GNSS-R Raw Data. Remote Sens. 2022, 14, 1170. https://doi.org/10.3390/rs14051170
Zhang Y, Yan Z, Yang S, Meng W, Gu S, Qin J, Han Y, Hong Z. Research on Shore-Based River Flow Velocity Inversion Model Using GNSS-R Raw Data. Remote Sensing. 2022; 14(5):1170. https://doi.org/10.3390/rs14051170
Chicago/Turabian StyleZhang, Yun, Ziyu Yan, Shuhu Yang, Wanting Meng, Siqi Gu, Jin Qin, Yanling Han, and Zhonghua Hong. 2022. "Research on Shore-Based River Flow Velocity Inversion Model Using GNSS-R Raw Data" Remote Sensing 14, no. 5: 1170. https://doi.org/10.3390/rs14051170
APA StyleZhang, Y., Yan, Z., Yang, S., Meng, W., Gu, S., Qin, J., Han, Y., & Hong, Z. (2022). Research on Shore-Based River Flow Velocity Inversion Model Using GNSS-R Raw Data. Remote Sensing, 14(5), 1170. https://doi.org/10.3390/rs14051170