Deep-Learning-Based Multispectral Image Reconstruction from Single Natural Color RGB Image—Enhancing UAV-Based Phenotyping
Abstract
:1. Introduction
2. Materials and Methods
2.1. tcRGB and ncRGB Image Acquisition from Hyperspectral Images
2.2. UAV Image Acquisition of MSI and ncRGB Images from Maize and Rice Fields
2.3. Model Selection, Training, Validation and Testing
2.4. Ground Truthing of Reconstructed MSIs Using NDVI, and Comparison with RGB-Derived TGI
3. Results
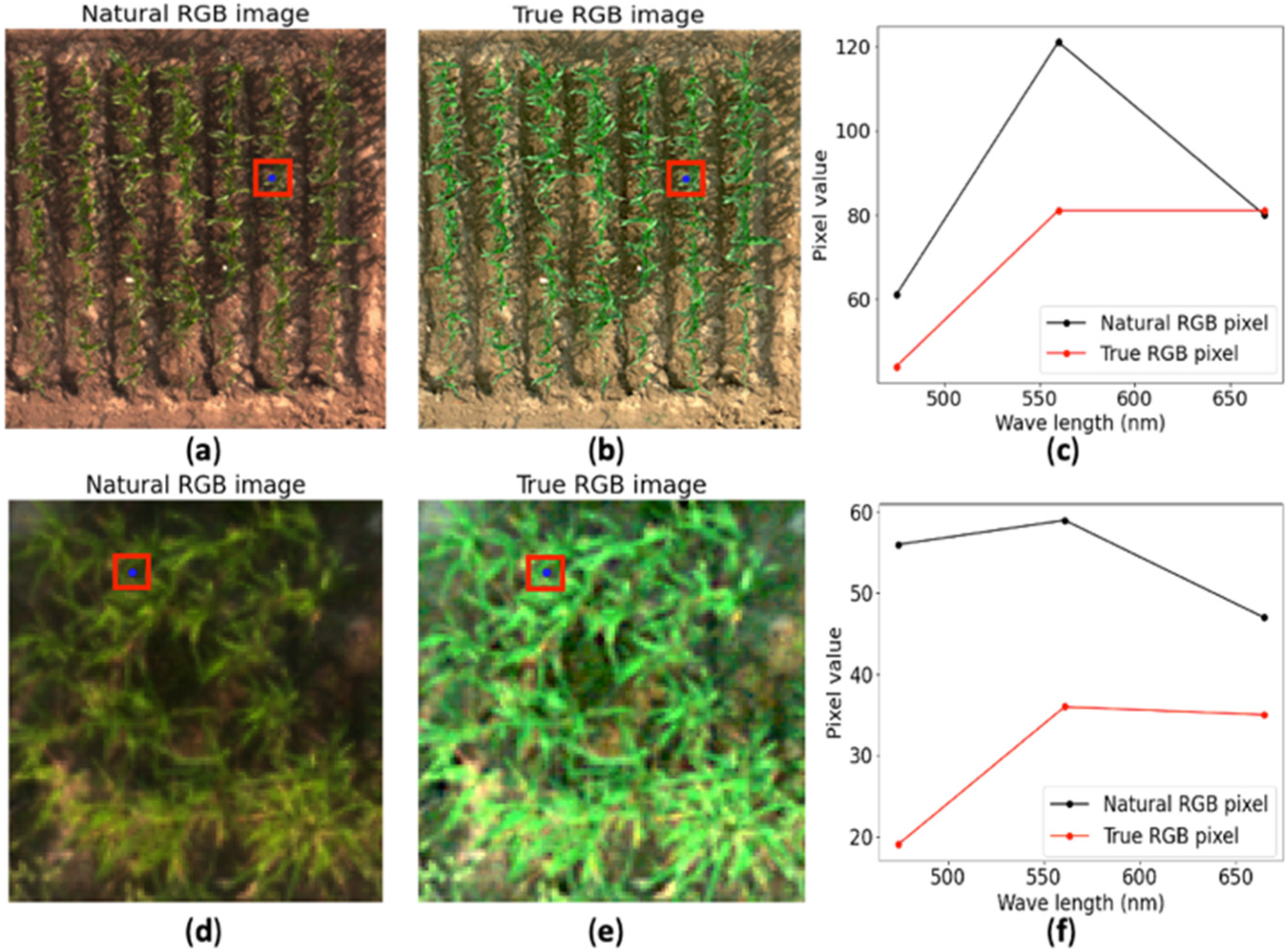
3.1. Natural Color Image Rendering
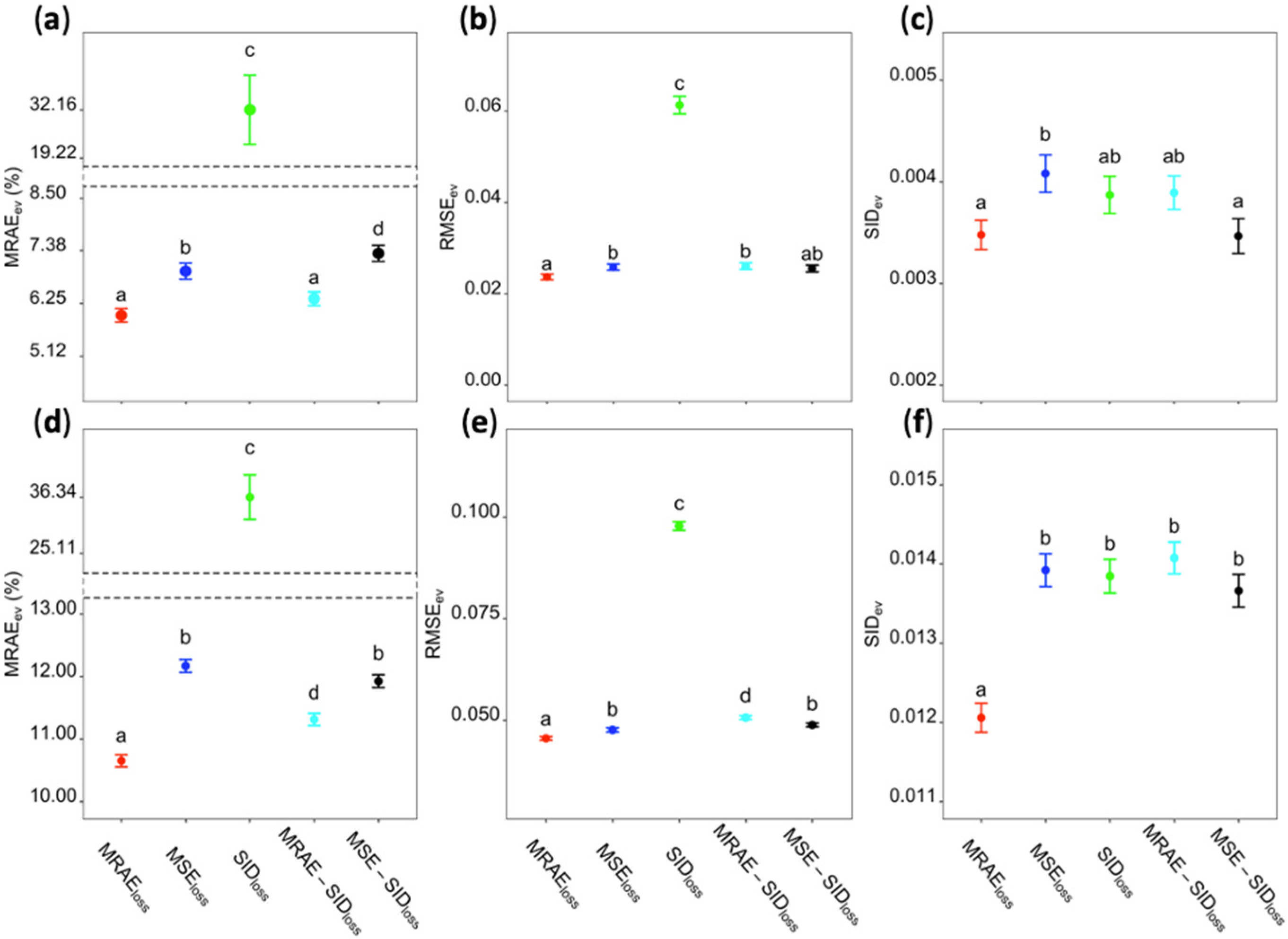
3.2. Model Convergence with Different Loss Functions
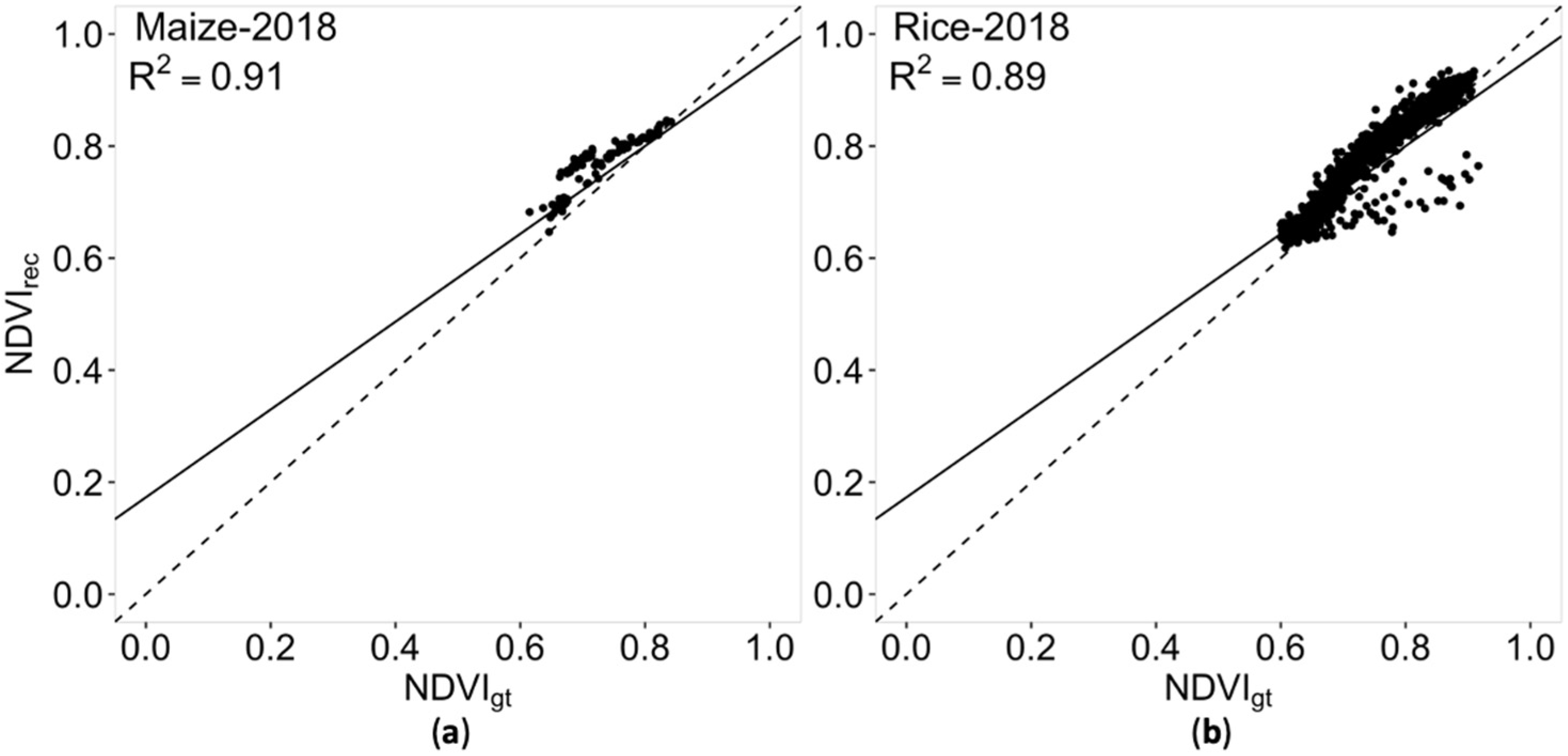
3.3. Universality of Models Trained with Different Loss Functions
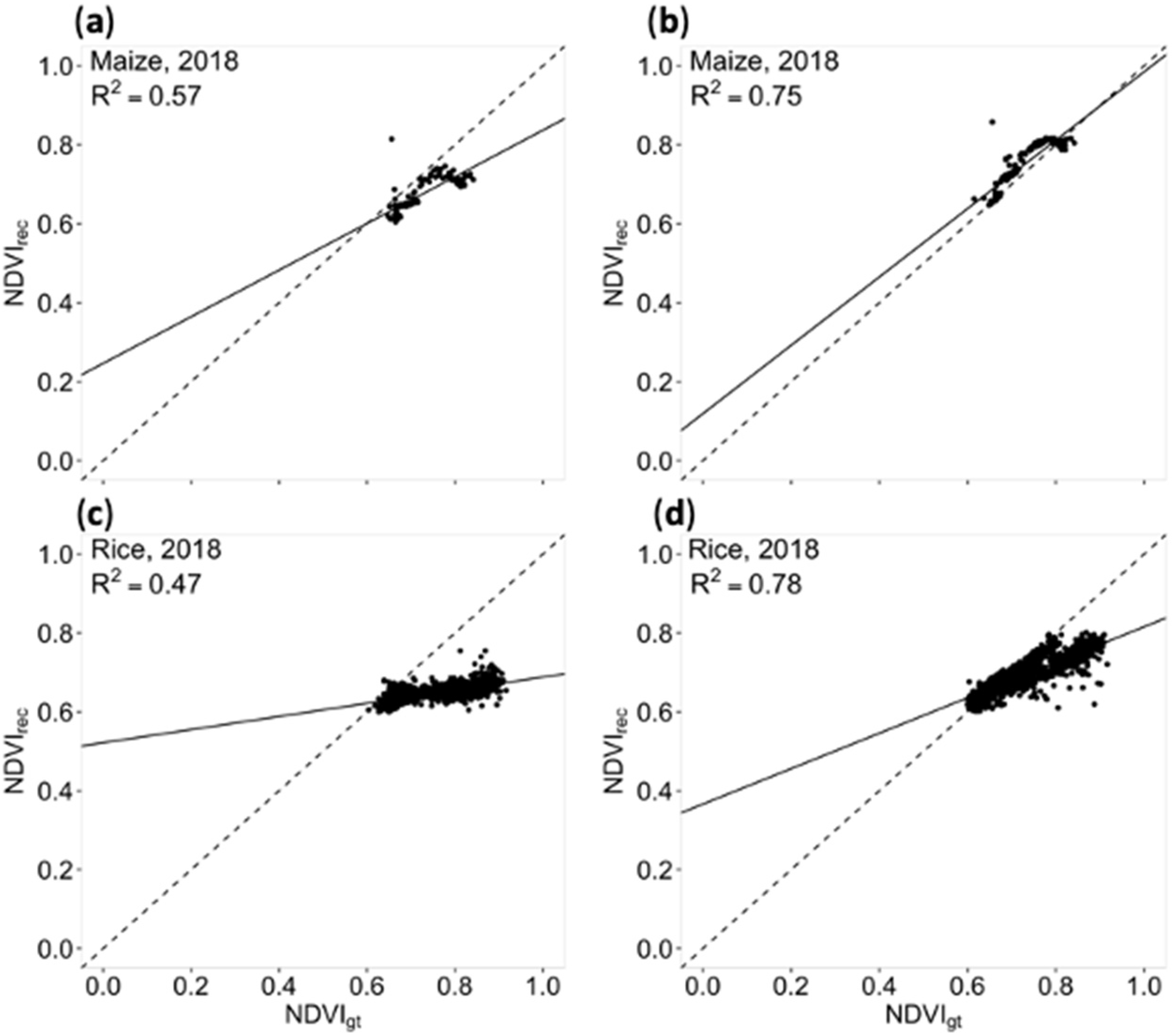
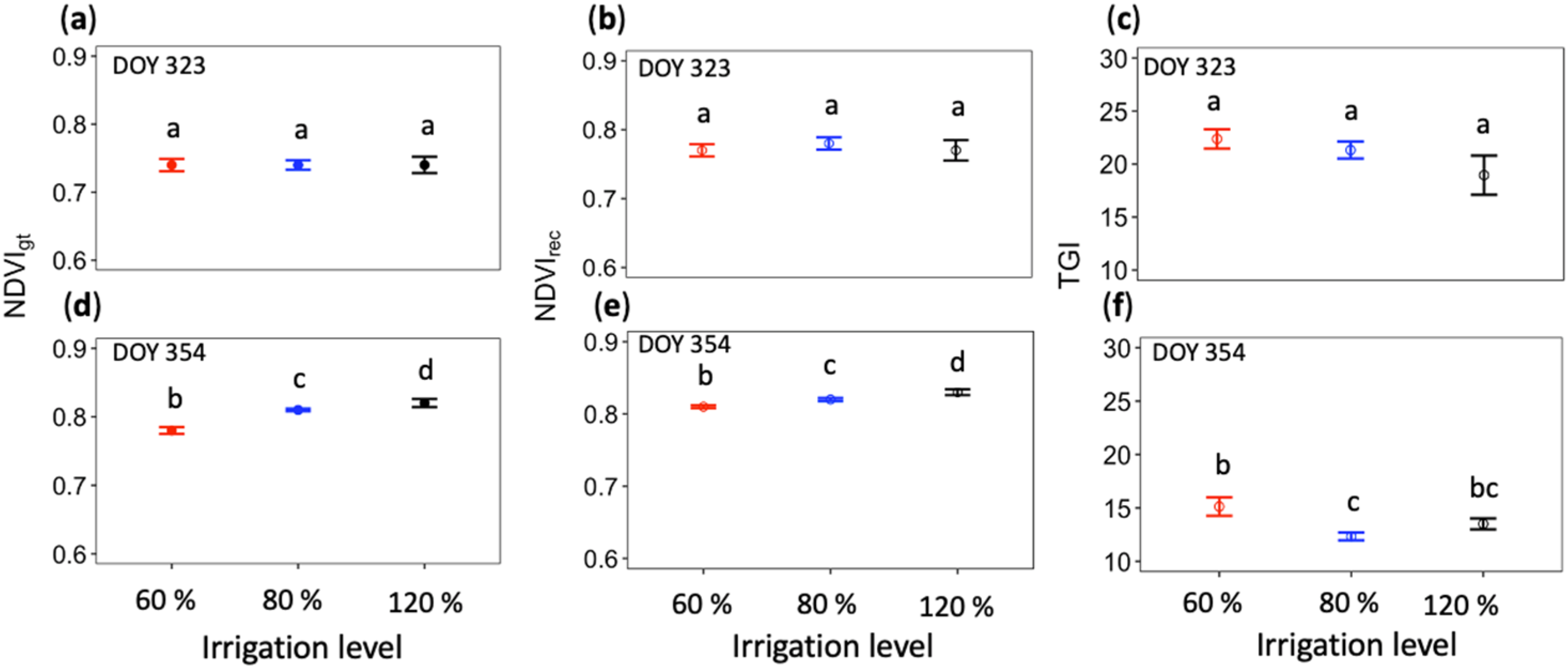
3.4. Effectiveness of MSIs Reconstructed from ncRGB-Cam-Con Images through NDVI and TGI Comparisons
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Han, W.; Niu, X.; Li, G. Maize crop coefficient estimated from UAV-measured multispectral vegetation indices. Sensors 2019, 19, 5250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DeJonge, K.C.; Mefford, B.S.; Chávez, J.L. Assessing corn water stress using spectral reflectance. Int. J. Remote Sens. 2016, 37, 2294–2312. [Google Scholar] [CrossRef]
- Somasegaran, P.; Bohlool, B. Ben Single-strain versus multistrain inoculation: Effect of soil mineral N availability on rhizobial strain effectiveness and competition for nodulation on chick-pea, soybean, and dry bean. Appl. Environ. Microbiol. 1990, 56, 3298–3303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cucho-Padin, G.; Loayza, H.; Palacios, S.; Balcazar, M.; Carbajal, M.; Quiroz, R. Development of low-cost remote sensing tools and methods for supporting smallholder agriculture. Appl. Geomat. 2020, 12, 247–263. [Google Scholar] [CrossRef] [Green Version]
- Lowe, B.; Kulkarni, A. Multispectral image analysis using random forest. Int. J. Soft Comput. Sci. 2015, 6, 1–14. [Google Scholar] [CrossRef]
- Arad, B.; Timofte, R.; Ben-Shahar, O.; Lin, Y.-T.; Finlayson, G.D. Ntire 2020 challenge on spectral reconstruction from an rgb image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 446–447. [Google Scholar]
- Tian, M.; Ban, S.; Yuan, T.; Ji, Y.; Ma, C.; Li, L. Assessing rice lodging using UAV visible and multispectral image. Int. J. Remote Sens. 2021, 42, 8840–8857. [Google Scholar] [CrossRef]
- Navarro, P.J.; Miller, L.; Gila-Navarro, A.; Díaz-Galián, M.V.; Aguila, D.J.; Egea-Cortines, M. 3DeepM: An Ad Hoc Architecture Based on Deep Learning Methods for Multispectral Image Classification. Remote Sens. 2021, 13, 729. [Google Scholar] [CrossRef]
- Cai, Y.; Huang, H.; Wang, K.; Zhang, C.; Fan, L.; Guo, F. Selecting Optimal Combination of Data Channels for Semantic Segmentation in City Information Modelling (CIM). Remote Sens. 2021, 13, 1367. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Witharana, C.; Liljedahl, A.K.; Jones, B.M.; Daanen, R.; Epstein, H.E.; Kent, K.; Griffin, C.G.; Agnew, A. Understanding the effects of optimal combination of spectral bands on deep learning model predictions: A case study based on permafrost Tundra landform mapping using high resolution multispectral satellite imagery. J. Imaging 2020, 6, 97. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, T.; Zheng, Y.; Zhang, D.; Huang, H. Joint camera spectral response selection and hyperspectral image recovery. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 256–272. [Google Scholar] [CrossRef]
- Arad, B.; Ben-Shahar, O. Sparse recovery of hyperspectral signal from natural RGB images. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 19–34. [Google Scholar]
- Shi, Z.; Chen, C.; Xiong, Z.; Liu, D.; Wu, F. HSCNN+: Advanced cnn-based hyperspectral recovery from rgb images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 939–947. [Google Scholar]
- Sovdat, B.; Kadunc, M.; Batič, M.; Milčinski, G. Natural color representation of Sentinel-2 data. Remote Sens. Environ. 2019, 225, 392–402. [Google Scholar] [CrossRef]
- Su, J.; Liu, C.; Coombes, M.; Hu, X.; Wang, C.; Xu, X.; Li, Q.; Guo, L.; Chen, W.-H. Wheat yellow rust monitoring by learning from multispectral UAV aerial imagery. Comput. Electron. Agric. 2018, 155, 157–166. [Google Scholar] [CrossRef]
- Prathap, G.; Afanasyev, I. Deep learning approach for building detection in satellite multispectral imagery. In Proceedings of the 2018 International Conference on Intelligent Systems (IS), Funchal, Portugal, 25–27 September 2018; pp. 461–465. [Google Scholar]
- Malla, S.; Tuladhar, A.; Quadri, G.J.; Rosen, P. Multi-Spectral Satellite Image Analysis for Feature Identification and Change Detection VAST Challenge 2017: Honorable Mention for Good Facilitation of Single Image Analysis. In Proceedings of the 2017 IEEE Conference on Visual Analytics Science and Technology (VAST), Phoenix, AZ, USA, 3–6 October 2017; pp. 205–206. [Google Scholar]
- Mahdianpari, M.; Salehi, B.; Rezaee, M.; Mohammadimanesh, F.; Zhang, Y. Very deep convolutional neural networks for complex land cover mapping using multispectral remote sensing imagery. Remote Sens. 2018, 10, 1119. [Google Scholar] [CrossRef] [Green Version]
- Neagoe, I.; Faur, D.; Vaduva, C.; Datcu, M. Exploratory visual analysis of multispectral EO images based on DNN. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2079–2082. [Google Scholar]
- Woerd, H.J.; Wernand, M.R. True color classification of natural waters with medium-spectral resolution satellites: SeaWiFS, MODIS, MERIS and OLCI. Sensors 2015, 15, 25663–25680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.-T.; Finlayson, G.D. Physically Plausible Spectral Reconstruction. Sensors 2020, 20, 6399. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Z.; Shi, Z.; Li, H.; Wang, L.; Liu, D.; Wu, F. HSCNN: Cnn-based hyperspectral image recovery from spectrally undersampled projections. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 518–525. [Google Scholar]
- Fu, Y.; Lei, Y.; Wang, T.; Curran, W.J.; Liu, T.; Yang, X. Deep learning in medical image registration: A review. Phys. Med. Biol. 2020, 65, 20TR01. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fairman, H.S.; Brill, M.H.; Hemmendinger, H. How the CIE 1931 color-matching functions were derived from Wright-Guild data. Color Res. Appl. 1997, 22, 11–23. [Google Scholar] [CrossRef]
- Mandanici, E.; Bitelli, G. Preliminary comparison of sentinel-2 and landsat 8 imagery for a combined use. Remote Sens. 2016, 8, 1014. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Franses, P.H. A note on the mean absolute scaled error. Int. J. Forecast. 2016, 32, 20–22. [Google Scholar] [CrossRef] [Green Version]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. In Summaries of the Third Annual JPL Airborne Geosceince Workshop; AVIRIS Workshop: Pasadena, CA, USA, 1992; pp. 147–149. [Google Scholar]
- Windrim, L.; Ramakrishnan, R.; Melkumyan, A.; Murphy, R.J.; Chlingaryan, A. Unsupervised feature-learning for hyperspectral data with autoencoders. Remote Sens. 2019, 11, 864. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Chang, C.-I.; Ren, H.; Chang, C.-C.; Jensen, J.O.; D’Amico, F.M. New hyperspectral discrimination measure for spectral characterization. Opt. Eng. 2004, 43, 1777–1786. [Google Scholar]
- Naresh Kumar, M.; Seshasai, M.V.R.; Vara Prasad, K.S.; Kamala, V.; Ramana, K.V.; Dwivedi, R.S.; Roy, P.S. A new hybrid spectral similarity measure for discrimination among Vigna species. Int. J. Remote Sens. 2011, 32, 4041–4053. [Google Scholar] [CrossRef] [Green Version]
- Nidamanuri, R.R.; Zbell, B. Normalized Spectral Similarity Score (NS3) as an Efficient Spectral Library Searching Method for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 4, 226–240. [Google Scholar] [CrossRef]
- Staenz, K.; Schwarz, J.; Vernaccini, L.; Vachon, F.; Nadeau, C. Classification of hyperspectral agricultural data with spectral matching techniques. In Proceedings of the International Symposium on Spectral Sensing Research (ISSSR’99), Las Vegas, NV, USA, 31 October–4 November 1999; Bruzewicz, A.J., Ed.; US Army Corps of Engineers: Hanover, NH, USA, 1999. [Google Scholar]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspdectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Kumar, A.; Desai, S.V.; Balasubramanian, V.N.; Rajalakshmi, P.; Guo, W.; Naik, B.B.; Balram, M.; Desai, U.B. Efficient Maize Tassel-Detection Method using UAV based Remote Sensing. Remote Sens. Appl. Soc. Environ. 2021, 23, 100549. [Google Scholar] [CrossRef]
- Morales, N.; Kaczmar, N.S.; Santantonio, N.; Gore, M.A.; Mueller, L.A.; Robbins, K.R. ImageBreed: Open-access plant breeding web–database for image-based phenotyping. Plant Phenome J. 2020, 3, e20004. [Google Scholar] [CrossRef]
- Lastilla, L.; Belloni, V.; Ravanelli, R.; Crespi, M. DSM Generation from Single and Cross-Sensor Multi-View Satellite Images Using the New Agisoft Metashape: The Case Studies of Trento and Matera (Italy). Remote Sens. 2021, 13, 593. [Google Scholar] [CrossRef]
- Zhao, J.; Kechasov, D.; Rewald, B.; Bodner, G.; Verheul, M.; Clarke, N.; Clarke, J.L. Deep Learning in Hyperspectral Image Reconstruction from Single RGB images—A Case Study on Tomato Quality Parameters. Remote Sens. 2020, 12, 3258. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, L.; Xie, Z.; Chen, Z. Building extraction in very high resolution remote sensing imagery using deep learning and guided filters. Remote Sens. 2018, 10, 144. [Google Scholar] [CrossRef] [Green Version]
- Hua, Y.; Mou, L.; Zhu, X.X. Relation network for multilabel aerial image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4558–4572. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zhang, X.; Peng, C.; Xue, X.; Sun, J. Exfuse: Enhancing feature fusion for semantic segmentation. In Proceedings of the European conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 269–284. [Google Scholar]
- Liu, Y.; Cheng, M.-M.; Fan, D.-P.; Zhang, L.; Bian, J.-W.; Tao, D. Semantic edge detection with diverse deep supervision. Int. J. Comput. Vis. 2022, 130, 179–198. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1026–1034. [Google Scholar]
- Koundinya, S.; Sharma, H.; Sharma, M.; Upadhyay, A.; Manekar, R.; Mukhopadhyay, R.; Karmakar, A.; Chaudhury, S. 2d-3d cnn based architectures for spectral reconstruction from rgb images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 844–851. [Google Scholar]
- Yan, Y.; Zhang, L.; Li, J.; Wei, W.; Zhang, Y. Accurate Spectral Super-Resolution from Single RGB Image Using Multi-scale CNN. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Guangzhou, China, 23–26 November 2018; pp. 206–217. [Google Scholar]
- Ceccarelli, M.; di Bisceglie, M.; Galdi, C.; Giangregorio, G.; Ullo, S.L. Image registration using non-linear diffusion. In Proceedings of the IGARSS 2008–2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 5, p. V-220. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- De Ocampo, A.L.P.; Bandala, A.A.; Dadios, E.P. Estimation of Triangular Greenness Index for Unknown PeakWavelength Sensitivity of CMOS-acquired Crop Images. In Proceedings of the 2019 IEEE 11th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment, and Management (HNICEM), Laoag, Philippines, 29 November–1 December 2019; pp. 1–5. [Google Scholar]
- Millard, S.P.; Kowarik, A.; Kowarik, M.A. Package ‘EnvStats’. Package for Environmental Statistics. Version 2. 2018, pp. 31–32. Available online: https://cran.r-project.org/web/packages/EnvStats/EnvStats.pdf (accessed on 20 December 2021).
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011.
- Tarek Stiebel, D.M. Brightness Invariant Deep Spectral Super-Resolution. Sensors 2020, 20, 5789. [Google Scholar] [CrossRef] [PubMed]
- Arad, B.; Ben-Shahar, O. Filter selection for hyperspectral estimation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3153–3161. [Google Scholar]
- Scepanovic, S.; Joglekar, S.; Law, S.; Quercia, D. Jane Jacobs in the Sky: Predicting Urban Vitality with Open Satellite Data. Proc. ACM Hum. Comput. Interact. 2021, 5, 1–25. [Google Scholar] [CrossRef]
- Wei, W.; Nie, J.; Li, Y.; Zhang, L.; Zhang, Y. Deep Recursive Network for Hyperspectral Image Super-Resolution. IEEE Trans. Comput. Imaging 2020, 6, 1233–1244. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, X.; Lu, X. Hyperspectral image super-resolution with self-supervised spectral-spatial residual network. Remote Sens. 2021, 13, 1260. [Google Scholar] [CrossRef]
- Mamaghani, B.; Salvaggio, C. Multispectral sensor calibration and characterization for sUAS remote sensing. Sensors 2019, 19, 4453. [Google Scholar] [CrossRef] [Green Version]
- Finlayson, G.D.; Hordley, S.D.; Drew, M.S. Removing shadows from images. In Proceedings of the European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; pp. 823–836. [Google Scholar]
- Winkens, C.; Adams, V.; Paulus, D. Automatic shadow detection using hyperspectral data for terrain classification. Electron. Imaging 2019, 2019, 31. [Google Scholar] [CrossRef]
- Nansen, C.; Singh, K.; Mian, A.; Allison, B.J.; Simmons, C.W. Using hyperspectral imaging to characterize consistency of coffee brands and their respective roasting classes. J. Food Eng. 2016, 190, 34–39. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Cerra, D.; Müller, R. Shadow Detection and Restoration for Hyperspectral Images Based on Nonlinear Spectral Unmixing. Remote Sens. 2020, 12, 3985. [Google Scholar] [CrossRef]
- Qu, L.; Tian, J.; He, S.; Tang, Y.; Lau, R.W.H. Deshadownet: A multi-context embedding deep network for shadow removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4067–4075. [Google Scholar]
- Le, H.; Samaras, D. Shadow removal via shadow image decomposition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 8578–8587. [Google Scholar]
- Chang, C.-I. Spectral information divergence for hyperspectral image analysis. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium (IGARSS 1999), Hamburg, Germany, 28 June–2 July 1999; pp. 509–511. [Google Scholar]
- Colwell, J.E. Vegetation canopy reflectance. Remote Sens. Environ. 1974, 3, 175–183. [Google Scholar] [CrossRef]
- Haichao, L.; Shengyong, H.; Qi, Z. Fast seamless mosaic algorithm for multiple remote sensing images. Infrared Laser Eng. 2011, 40, 1381–1386. [Google Scholar]
- Rau, J.; Chen, N.-Y.; Chen, L.-C. True orthophoto generation of built-up areas using multi-view images. Photogramm. Eng. Remote Sens. 2002, 68, 581–588. [Google Scholar]
- Jiang, J.; Liu, D.; Gu, J.; Süsstrunk, S. What is the space of spectral sensitivity functions for digital color cameras? In Proceedings of the 2013 IEEE Workshop on Applications of Computer Vision (WACV), Clearwater Beach, FL, USA, 15–17 January 2013; pp. 168–179. [Google Scholar]
- Hunt, E.R.; Daughtry, C.S.T.; Eitel, J.U.H.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef] [Green Version]
- Fuentes-Peailillo, F.; Ortega-Farias, S.; Rivera, aM.; Bardeen, M.; Moreno, M. Comparison of vegetation indices acquired from RGB and Multispectral sensors placed on UAV. In Proceedings of the 2018 IEEE International Conference on Automation/XXIII Congress of the Chilean Association of Automatic Control (ICA-ACCA), Concepcion, Chile, 17–19 October 2018; pp. 1–6. [Google Scholar]
- Liu, H.; Bruning, B.; Garnett, T.; Berger, B. Hyperspectral imaging and 3D technologies for plant phenotyping: From satellite to close-range sensing. Comput. Electron. Agric. 2020, 175, 105621. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, B.; Song, Y. Urban land-use mapping using a deep convolutional neural network with high spatial resolution multispectral remote sensing imagery. Remote Sens. Environ. 2018, 214, 73–86. [Google Scholar] [CrossRef]
- He, S.; Peng, B.; Dong, J.; Du, Y. Mask-ShadowNet: Toward Shadow Removal via Masked Adaptive Instance Normalization. IEEE Signal Process. Lett. 2021, 28, 957–961. [Google Scholar] [CrossRef]
- Han, H.; Han, C.; Lan, T.; Huang, L.; Hu, C.; Xue, X. Automatic shadow detection for multispectral satellite remote sensing images in invariant color spaces. Appl. Sci. 2020, 10, 6467. [Google Scholar] [CrossRef]


| Model-TN | ||||||
|---|---|---|---|---|---|---|
| Loss Function | Evaluation Metric | |||||
| MRAEev | RMSEev | SIDev | Total | Epochs | Time (s) | |
| MRAEloss | 0.0432 | 0.0127 | 0.00266 | 0.0586 | 7965 | 3510 |
| MSEloss | 0.0566 | 0.0152 | 0.00457 | 0.0764 | 3724 | 248 |
| SIDloss | 0.4670 | 0.0878 | 0.00394 | 0.5590 | 4534 | 512 |
| MRAE-SIDloss | 0.0428 | 0.0128 | 0.00261 | 0.0582 | 8660 | 3723 |
| MSE-SIDloss | 0.0476 | 0.0130 | 0.00302 | 0.0636 | 3729 | 250 |
| Model-NM | ||||||
|---|---|---|---|---|---|---|
| Loss Function | Evaluation Metric | |||||
| MRAEev | RMSEev | SIDev | Total | Epochs | Time (s) | |
| MRAEloss | 0.0353 | 0.0188 | 0.00606 | 0.0602 | 2777 | 22,969 |
| MSEloss | 0.0534 | 0.0209 | 0.0119 | 0.0862 | 2269 | 20,952 |
| SIDloss | 1.1180 | 0.1070 | 0.00564 | 1.2310 | 2995 | 35,298 |
| MRAE-SIDloss | 0.0344 | 0.0173 | 0.00541 | 0.0571 | 4642 | 40,634 |
| MSE-SIDloss | 0.2250 | 0.0266 | 0.00614 | 0.2580 | 4950 | 40,461 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Kumar, A.; Banoth, B.N.; Marathi, B.; Rajalakshmi, P.; Rewald, B.; Ninomiya, S.; Guo, W. Deep-Learning-Based Multispectral Image Reconstruction from Single Natural Color RGB Image—Enhancing UAV-Based Phenotyping. Remote Sens. 2022, 14, 1272. https://doi.org/10.3390/rs14051272
Zhao J, Kumar A, Banoth BN, Marathi B, Rajalakshmi P, Rewald B, Ninomiya S, Guo W. Deep-Learning-Based Multispectral Image Reconstruction from Single Natural Color RGB Image—Enhancing UAV-Based Phenotyping. Remote Sensing. 2022; 14(5):1272. https://doi.org/10.3390/rs14051272
Chicago/Turabian StyleZhao, Jiangsan, Ajay Kumar, Balaji Naik Banoth, Balram Marathi, Pachamuthu Rajalakshmi, Boris Rewald, Seishi Ninomiya, and Wei Guo. 2022. "Deep-Learning-Based Multispectral Image Reconstruction from Single Natural Color RGB Image—Enhancing UAV-Based Phenotyping" Remote Sensing 14, no. 5: 1272. https://doi.org/10.3390/rs14051272
APA StyleZhao, J., Kumar, A., Banoth, B. N., Marathi, B., Rajalakshmi, P., Rewald, B., Ninomiya, S., & Guo, W. (2022). Deep-Learning-Based Multispectral Image Reconstruction from Single Natural Color RGB Image—Enhancing UAV-Based Phenotyping. Remote Sensing, 14(5), 1272. https://doi.org/10.3390/rs14051272








