How Much Attenuation Extinguishes mm-Wave Vertically Pointing Radar Return Signals?
Abstract
:1. Introduction
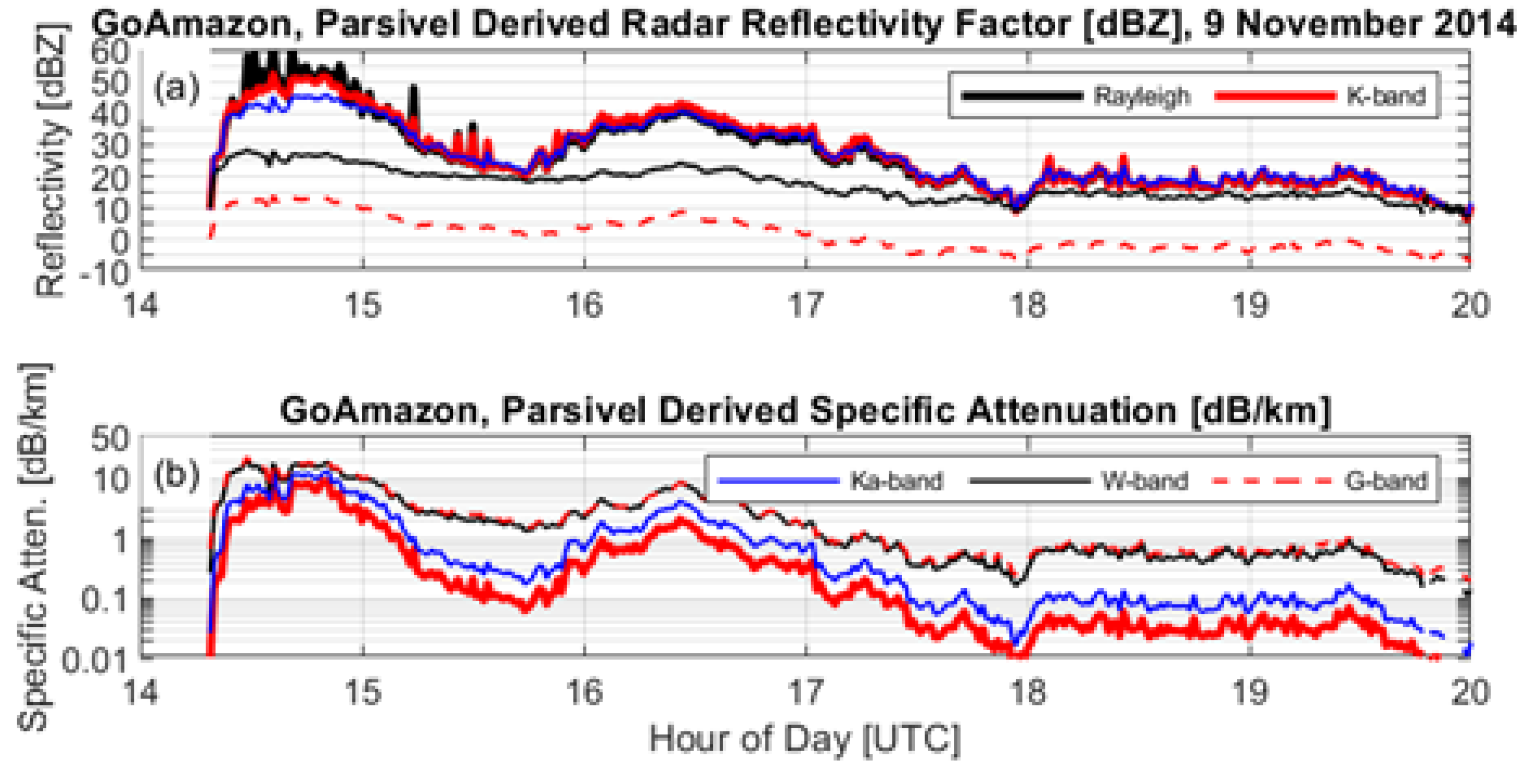
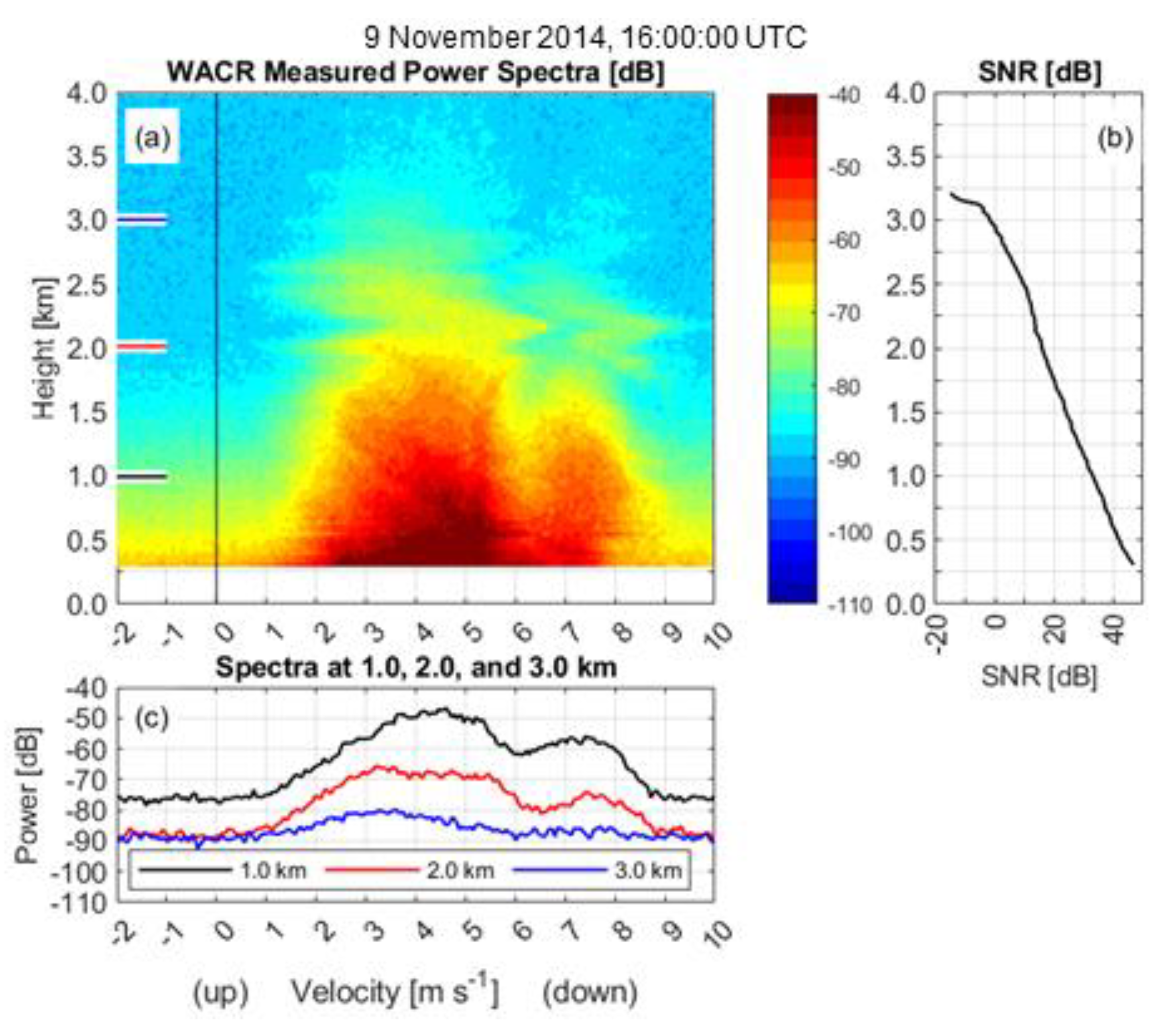
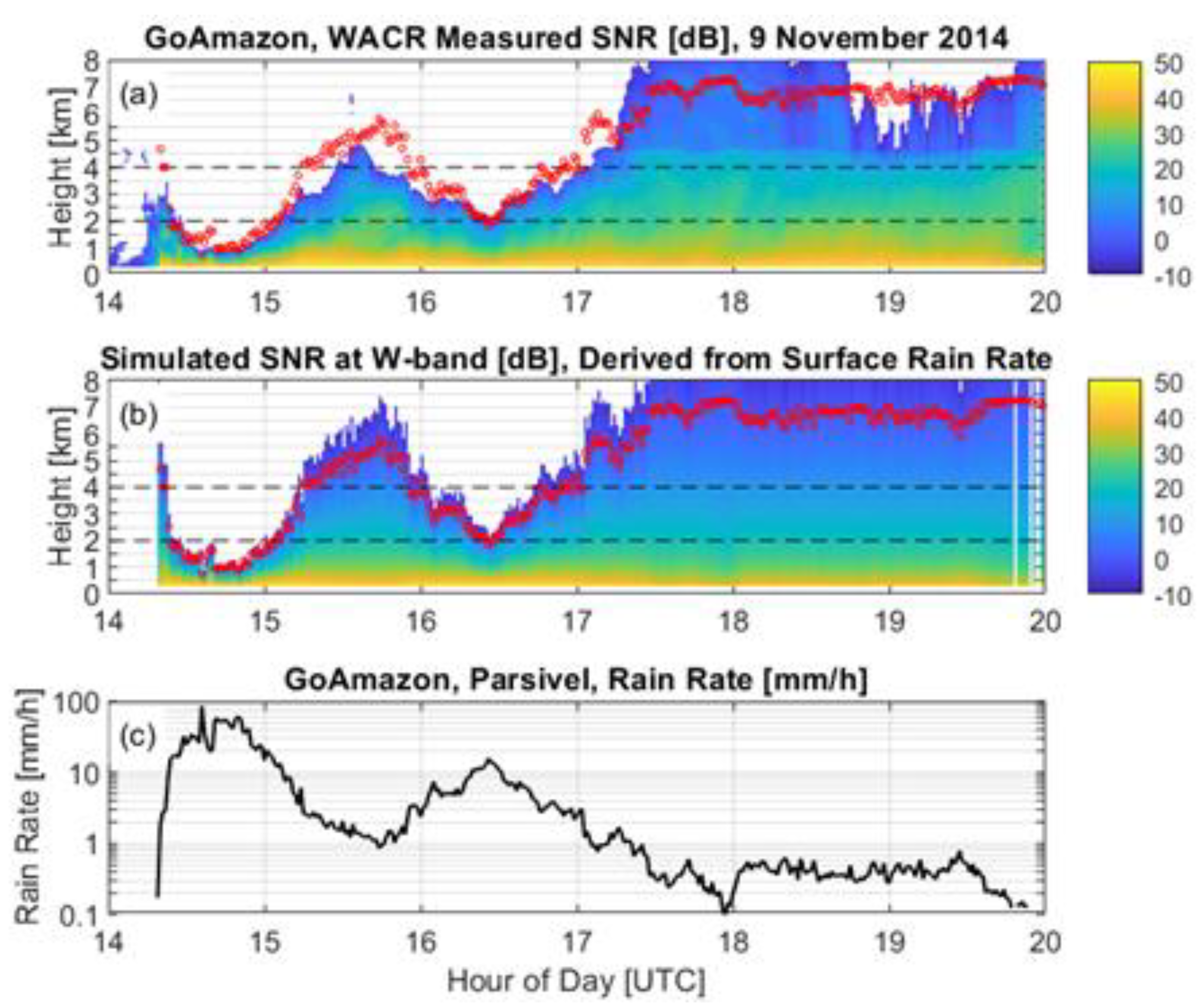
2. Observations
3. Methods
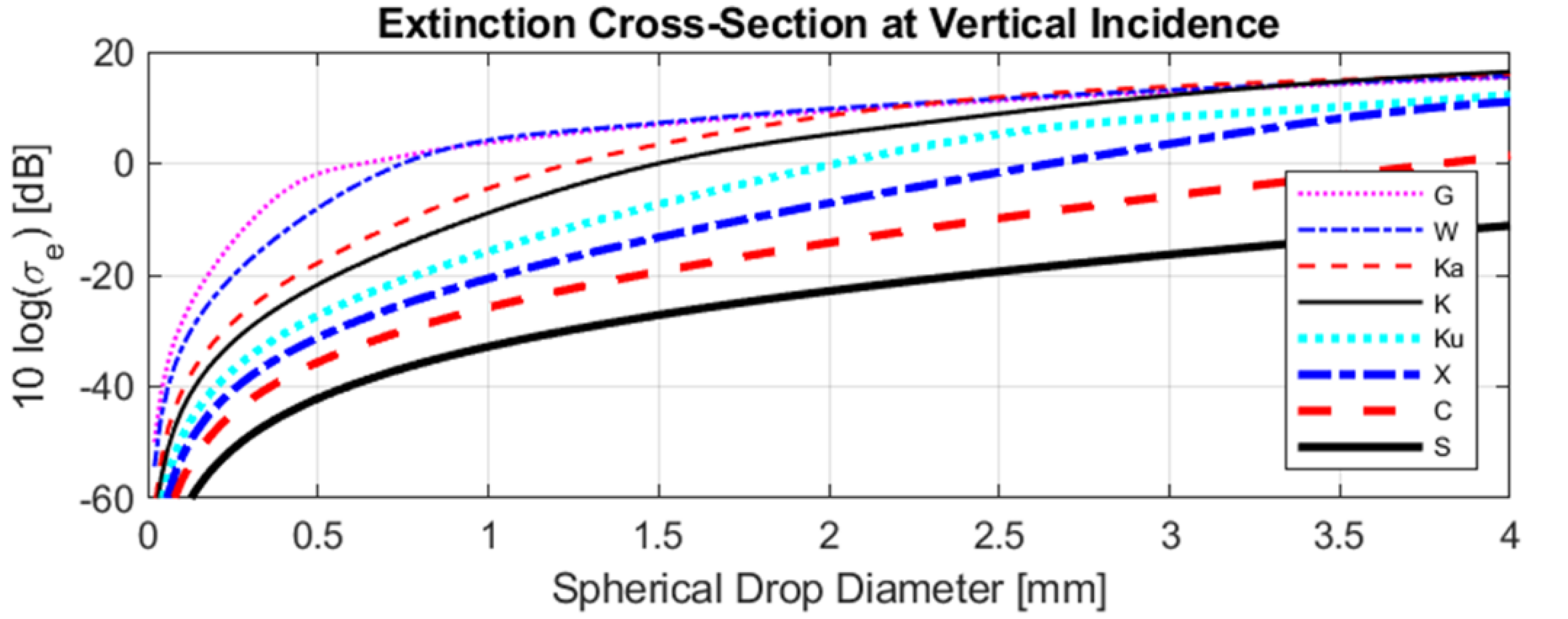
3.1. Raindrop Backscattering and Extinction Cross-Sections
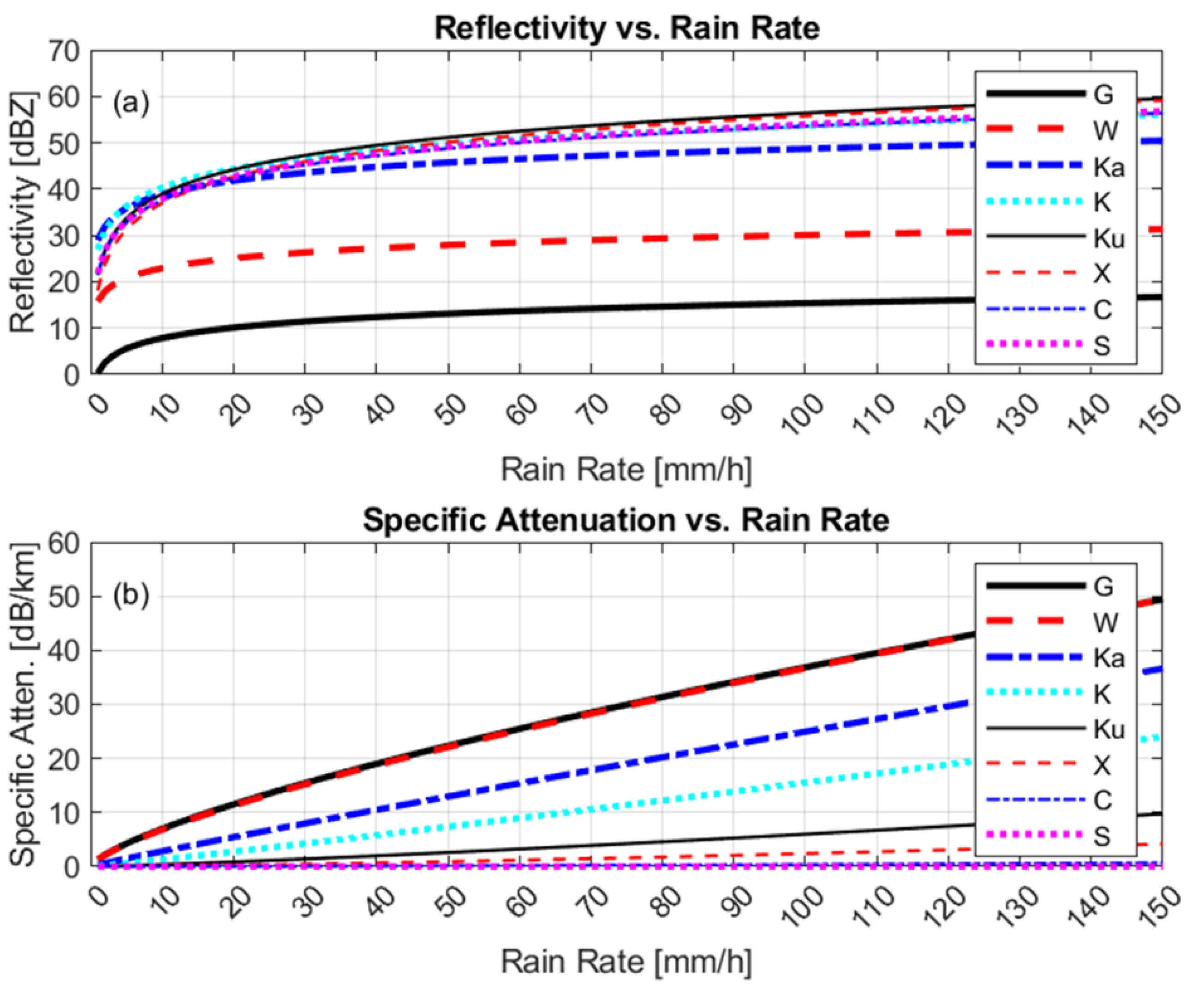
3.2. Power-Law Relationships for VPR Simulations
3.3. Specific Attenuation Due to Atmospheric Gases
4. Results
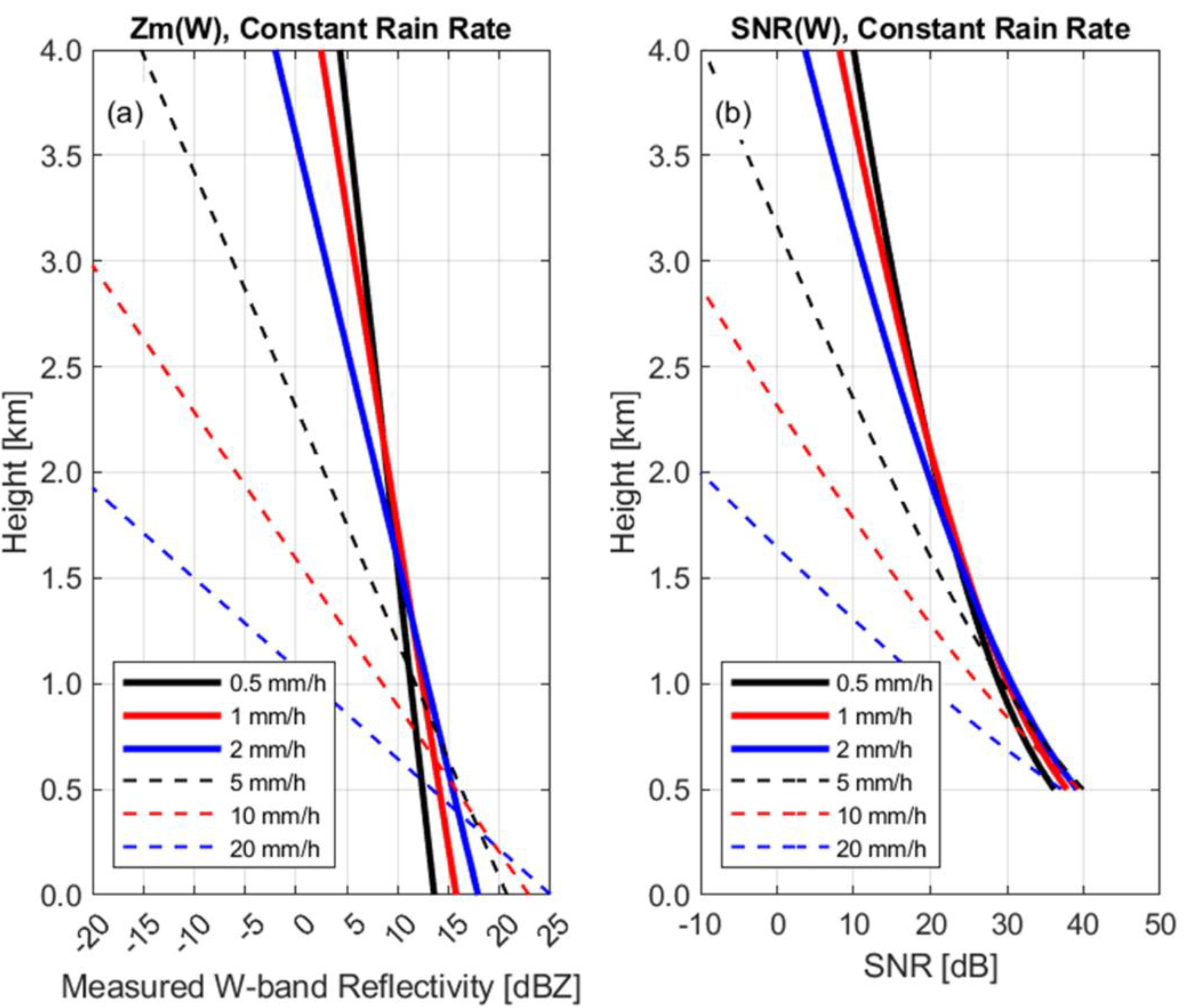
4.1. Estimated Attenuated Radar Reflectivity Factor Profiles
4.2. Estimated Radar Signal-to-Noise Ratio Profiles
4.3. Maximum Range Based on Radar Receiver Dynamic Range
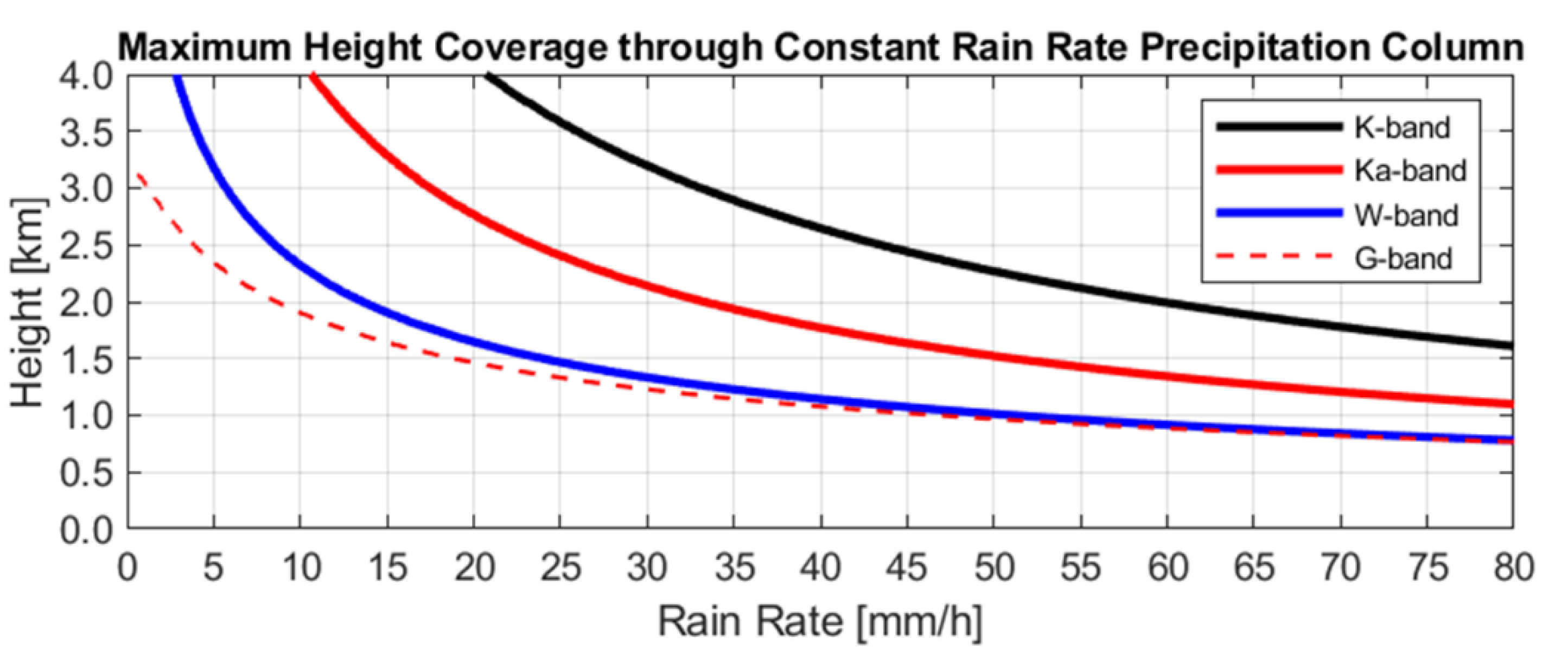
4.4. Simulated Maximum Range into Constant Rain Rate Shafts at Multiple Radar Bands
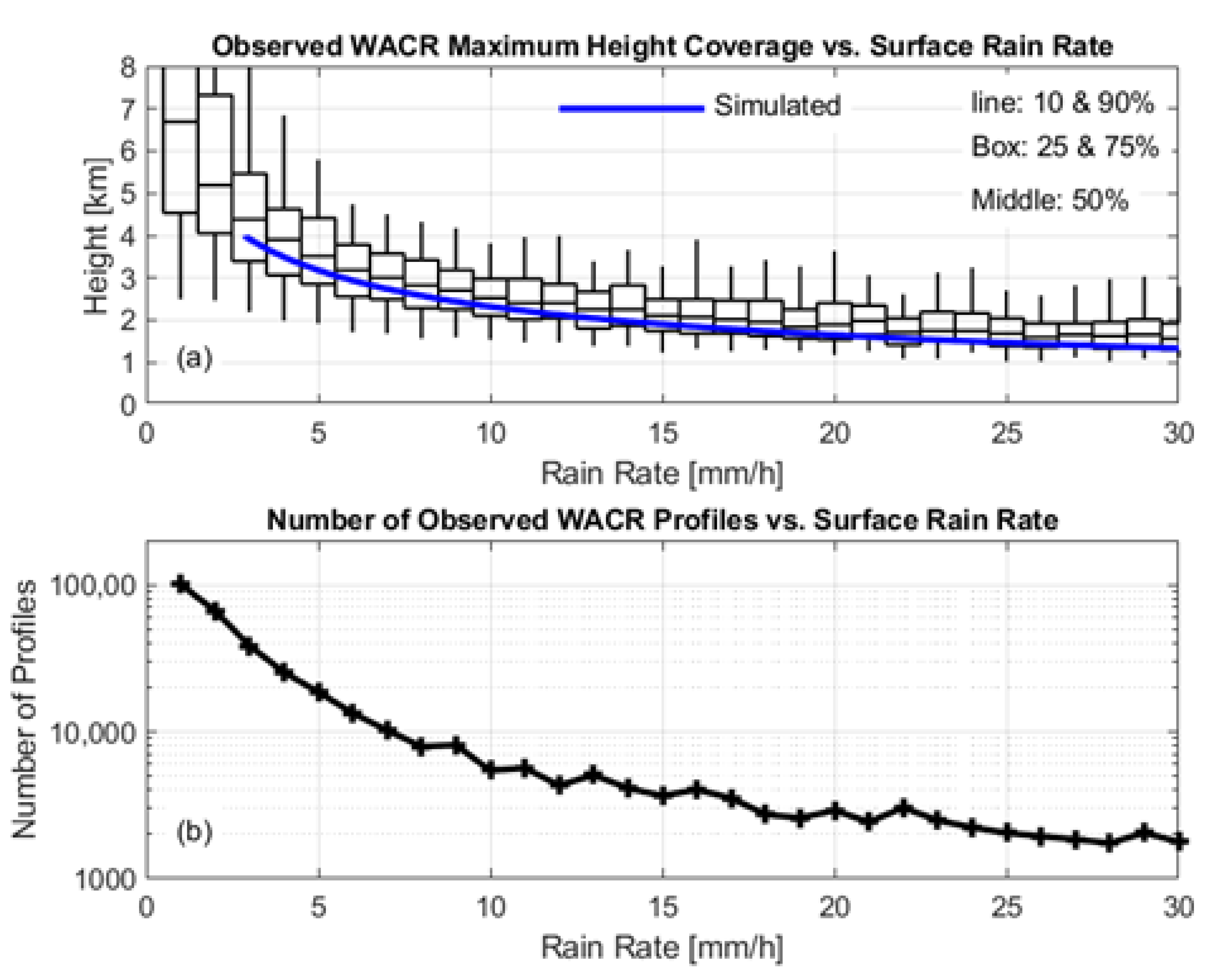
4.5. Observed Maximum WACR Range versus Observed Surface Rain Rate
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ecklund, W.L.; Gage, K.S.; Williams, C.R. Tropical precipitation studies using a 915-MHz wind profiler. Radio Sci. 1995, 30, 1055–1064. [Google Scholar] [CrossRef]
- Ecklund, W.L.; Williams, C.R.; Johnston, P.E.; Gage, K.S. A 3-GHz Profiler for Precipitating Cloud Studies. J. Atmos. Ocean. Technol. 1999, 16, 309–322. [Google Scholar] [CrossRef]
- Kollias, P.; Clothiaux, E.E.; Miller, M.A.; Albrecht, B.A.; Stephens, G.L.; Ackerman, T.P. Millimeter-wavelength radars: New frontier in atmospheric cloud and precipitation research. Bull. Amer. Meteor. Soc. 2007, 88, 1608–1624. [Google Scholar] [CrossRef] [Green Version]
- Kollias, P.; Bharadwaj, N.; Clothiaux, E.E.; Lamer, K.; Oue, M.; Hardin, J.; Isom, B.; Lindenmaier, I.; Matthews, A.; Luke, E.P.; et al. The ARM radar network: At the leading edge of cloud and precipitation observations. Bull. Amer. Meteor. Soc. 2020, 101, E588–E660. [Google Scholar] [CrossRef] [Green Version]
- Görsdorf, U.; Lehmann, V.; Bauer-Pfundstein, M.; Peters, G.; Vavriv, D.; Vinogradov, V.; Volkov, V. A 35-GHz polarimetric doppler radar for long-term observations of cloud parameters-description of system and data processing. J. Atmos. Ocean. Technol. 2015, 32, 675–690. [Google Scholar] [CrossRef]
- Battaglia, A.; Kollias, P. Evaluation of differential absorption radars in the 183 GHz band for profiling water vapour in ice clouds. Atmos. Meas. Tech. 2019, 12, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Battaglia, A.; Courtier, B.; Huggard, P.; Mroz, K. First observations of multi-frequency radar Doppler spectra including a G-band (200 GHz) radar. In Proceedings of the American Geophysical Union Annual Fall Meeting, New Orleans, LA, USA, 13–17 December 2021. [Google Scholar]
- Lhermitte, R.M. Cloud and Precipitation Remote Sensing at 94 GHz. IEEE Trans. Geosci. Remote Sens. 1988, 26, 207–216. [Google Scholar] [CrossRef]
- Lhermitte, R.M. Observation of rain at vertical incidence with a 94 GHz Doppler radar: An insight on Mie scattering. Geophys. Res. Lett. 1988, 15, 1125–1128. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Babb, D.M.; Verlinde, J. Processing Millimeter Wave Profiler Radar Spectra. J. Atmos. Ocean. Technol. 2001, 18, 1577–1583. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Luke, E.P.; Kollias, P. Automated retrievals of precipitation parameters using non-Rayleigh scattering at 95 GHz. J. Atmos. Ocean. Technol. 2010, 27, 1490–1503. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Luke, E.P.; Kollias, P. Characterization of vertical velocity and drop size distribution parameters in widespread precipitation at ARM facilities. J. Appl. Meteor. Climatol. 2012, 51, 380–391. [Google Scholar] [CrossRef] [Green Version]
- Kollias, P.; Lhermitte, R.; Albrecht, B.A. Vertical air motion and raindrop size distributions in convective systems using a 94 GHz radar. Geophys. Res. Lett. 1999, 26, 3109–3112. [Google Scholar] [CrossRef]
- Williams, C.R. Vertical air motion retrieved from dual-frequency profiler observations. J. Atmos. Ocean. Technol. 2012, 29, 1471–1480. [Google Scholar] [CrossRef]
- Tridon, F.; Battaglia, A. Dual-frequency radar doppler spectral retrieval of rain drop size distributions and entangled dynamics variables. J. Geophys. Res. 2015, 120, 5585–5601. [Google Scholar] [CrossRef] [Green Version]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar; Cambridge University Press: Cambridge, UK, 2001; p. 636. [Google Scholar]
- Williams, C.R.; Beauchamp, R.M.; Chandrasekar, V. Vertical Air Motions and Raindrop Size Distributions Estimated Using Mean Doppler Velocity Difference from 3-and 35-GHz Vertically Pointing Radars. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6048–6060. [Google Scholar] [CrossRef]
- Kneifel, S.; Moisseev, D. Long-term statistics of riming in nonconvective clouds derived from ground-based doppler cloud radar observations. J. Atmos. Sci. 2020, 77, 3495–3508. [Google Scholar] [CrossRef]
- Martin, S.T.; Artaxo, P.; Machado, L.; Manzi, A.O.; Souza, R.A.F.; Schumacher, C.; Wang, J.; Biscaro, T.; Brito, J.; Calheiros, A.; et al. The Green Ocean Amazon experiment (GOAmazon 2014/5) observes pollution affecting gases, aerosols, clouds, and rainfall over the rain forest. Bull. Amer. Meteor. Soc. 2017, 98, 981–997. [Google Scholar]
- Coulter, R.; Muradyan, P.; Martin, T. Atmospheric Radiation Measurement (ARM) User Facility, Radar Wind Profiler (1290RWPPRECIPSPEC). 2014-11-09, ARM Mobile Facility (MAO) Manacapuru, Amazonas, Brazil; AMF1 (M1). 2014. Available online: http://dx.doi.org/10.5439/1502660 (accessed on 12 May 2016).
- Bharadwaj, N.; Lindenmaier, I.; Johnson, K.; Nelson, D.; Matthews, A. Atmospheric Radiation Measurement (ARM) User Facility, W-Band (95 GHz) ARM Cloud Radar (WACRSPECCMASKCOPOL). 2014-09-25 to 2015-12-01, ARM Mobile Facility (MAO) Manacapuru, Amazonas, Brazil; AMF1 (M1). 2014. Available online: http://dx.doi.org/10.5439/1025318 (accessed on 14 May 2016).
- Mather, J.; Voyles, J. The ARM climate research facility: A review of structure and capabilities. Bull. Amer. Meteorol. Soc. 2013, 94, 377–392. [Google Scholar] [CrossRef]
- Wang, D.; Bartholomew, M.; Shi, Y. Atmospheric Radiation Measurement (ARM) User Facility, Laser Disdrometer (LD). 2014-09-25 to 2015-12-01, ARM Mobile Facility (MAO) Manacapuru, Amazonas, Brazil, Supplemental Site (S10). 2014. Available online: http://dx.doi.org/10.5439/1779709 (accessed on 20 February 2018).
- Gunn, R.; Kinzer, G.D. The terminal velocity of fall for water drops in stagnant air. J. Meteorol. 1949, 6, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Leinonen, J. High-level interface to T-matrix scattering calculations: Architecture, capabilities and limitations. Optics Express 2014, 22, 1655–1660. [Google Scholar] [CrossRef]
- Leinonen, J. Python Code for T-Matrix Scattering Calculations. Available online: https://github.com/jleinonen/pytmatrix/ (accessed on 1 October 2021).
- Thurai, M.; Huang, G.J.; Bringi, V.N.; Randeu, W.L.; Schönhuber, M. Drop shapes, model comparisons, and calculations of polarimetric radar parameters in rain. J. Atmos. Ocean. Technol. 2007, 24, 1019–1032. [Google Scholar] [CrossRef]
- Pujol, O.; Georgis, J.F.; Féral, L.; Sauvageot, H. Degradation of radar reflectivity by cloud attenuation at microwave frequency. J. Atmos. Ocean. Technol. 2007, 24, 640–657. [Google Scholar] [CrossRef]
- Li, L.; Sekelsky, S.M.; Reising, S.C.; Swift, C.T.; Durden, S.L.; Sadowy, G.A.; Dinardo, S.J.; Li, F.K.; Huffman, A.; Stephens, G.; et al. Retrieval of Atmospheric Attenuation Using Combined Ground-Based and Airborne 95-GHz Cloud Radar Measurements. J. Atmos. Ocean. Technol. 2001, 18, 1345–1353. [Google Scholar] [CrossRef] [Green Version]
- ITU-R. Recommendation ITU-R P.835-6 (12/2017) Reference Standard Atmospheres. International Telecommunication Union, 2017. Available online: https://www.itu.int/rec/R-REC-P.835 (accessed on 8 January 2022).
- ITU-R. Recommendation ITU-R P.676-12 (08/2019) Attenuation by Atmospheric Gases and Related Effects. International Telecommunication Union, 2019. Available online: https://www.itu.int/rec/R-REC-P.676 (accessed on 8 January 2022).
- Küchler, N.; Kneifel, S.; Löhnert, U.; Kollias, P.; Czekala, H.; Rose, T. A W-band radar-radiometer system for accurate and continuous monitoring of clouds and precipitation. J. Atmos. Ocean. Technol. 2017, 34, 2375–2392. [Google Scholar] [CrossRef]
- Hartten, L.M.; Johnston, P.E.; Castro, V.M.R.; Pérez, P.S.E. Postdeployment calibration of a tropical UHF profiling radar via surface-and satellite-based methods. J. Atmos. Ocean. Technol. 2019, 36, 1729–1751. [Google Scholar] [CrossRef]



| Parameter | RWP | WACR |
|---|---|---|
| Operating Frequency | 1.2 GHz | 95 GHz |
| Operating Wavelength | 250 mm | 3.2 mm |
| Distance between Range Gates | 225 m | 30 m |
| Range to First Range Gate | 510 m | 300 m |
| Range to Last Range Gate | 17 km | 18 km |
| Dwell Time | 2 s | 2 s |
| Time between Samples | 12 s | 2 s |
| Band | Wavelength [mm] | m (0 °C) | (0 °C) | m (20 °C) | (20 °C) |
|---|---|---|---|---|---|
| S (2.7 GHz) | 111.0 | 9.092 + 1.266i | 0.934 | 8.875 + 0.675i | 0.928 |
| C (5.6 GHz) | 53.6 | 8.340 + 2.226i | 0.933 | 8.615 + 1.315i | 0.928 |
| X (9 GHz) | 33.3 | 7.364 + 2.805i | 0.930 | 8.176 + 1.910i | 0.927 |
| Ku (13.6 GHz) | 22.1 | 6.329 + 2.977i | 0.925 | 7.502 + 2.392i | 0.924 |
| K (24 GHz) | 12.5 | 4.876 + 2.803i | 0.908 | 6.201 + 2.807i | 0.918 |
| Ka (35.6 GHz) | 8.4 | 4.033 + 2.438i | 0.879 | 5.192 + 2.779i | 0.908 |
| W (94 GHz) | 3.1 | 2.819 + 1.387i | 0.688 | 3.372 + 1.935i | 0.815 |
| G (200 GHz) | 1.5 | 2.448 + 0.749i | 0.482 | 2.668 + 1.174i | 0.622 |
| Band | Wavelength [mm] | ||||
|---|---|---|---|---|---|
| S (2.7 GHz) | 111.0 | 150 | 1.610 | 2.28 × 10−04 | 1.038 |
| C (5.6 GHz) | 53.6 | 144 | 1.599 | 7.88 × 10−04 | 1.349 |
| X (9 GHz) | 33.3 | 64.5 | 1.884 | 4.18 × 10−03 | 1.380 |
| Ku (13.6 GHz) | 22.1 | 139 | 1.749 | 2.35 × 10−02 | 1.203 |
| K (24 GHz) | 12.5 | 489 | 1.340 | 0.110 | 1.075 |
| Ka (35.6 GHz) | 8.4 | 781 | 0.988 | 0.320 | 0.946 |
| W (94 GHz) | 3.1 | 37.5 | 0.716 | 1.26 | 0.732 |
| G (200 GHz) | 1.5 | 1.06 | 0.756 | 1.32 | 0.723 |
| S- | C- | X- | Ku- | K- | Ka- | W- | G- |
|---|---|---|---|---|---|---|---|
| 0.008 | 0.009 | 0.01 | 0.03 | 0.15 | 0.1 | 0.4 | 3 |
| Path Length | X-Band | Ku-Band | K-Band | Ka-Band | W-Band | G-Band |
|---|---|---|---|---|---|---|
| 4.0 km | 116 | 55 | 21 | 11 | 3 | -1. |
| 3.5 km | 138 | 67 | 26 | 14 | 4 | -1. |
| 3.0 km | 166 | 84 | 33 | 18 | 6 | 1 |
| 2.5 km | >200 | 107 | 44 | 24 | 9 | 4 |
| 2.0 km | >200 | 142 | 60 | 33 | 14 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, C.R. How Much Attenuation Extinguishes mm-Wave Vertically Pointing Radar Return Signals? Remote Sens. 2022, 14, 1305. https://doi.org/10.3390/rs14061305
Williams CR. How Much Attenuation Extinguishes mm-Wave Vertically Pointing Radar Return Signals? Remote Sensing. 2022; 14(6):1305. https://doi.org/10.3390/rs14061305
Chicago/Turabian StyleWilliams, Christopher R. 2022. "How Much Attenuation Extinguishes mm-Wave Vertically Pointing Radar Return Signals?" Remote Sensing 14, no. 6: 1305. https://doi.org/10.3390/rs14061305
APA StyleWilliams, C. R. (2022). How Much Attenuation Extinguishes mm-Wave Vertically Pointing Radar Return Signals? Remote Sensing, 14(6), 1305. https://doi.org/10.3390/rs14061305






