Lidar and Radar Signal Simulation: Stability Assessment of the Aerosol–Cloud Interaction Index
Abstract
:1. Introduction
2. Methodology
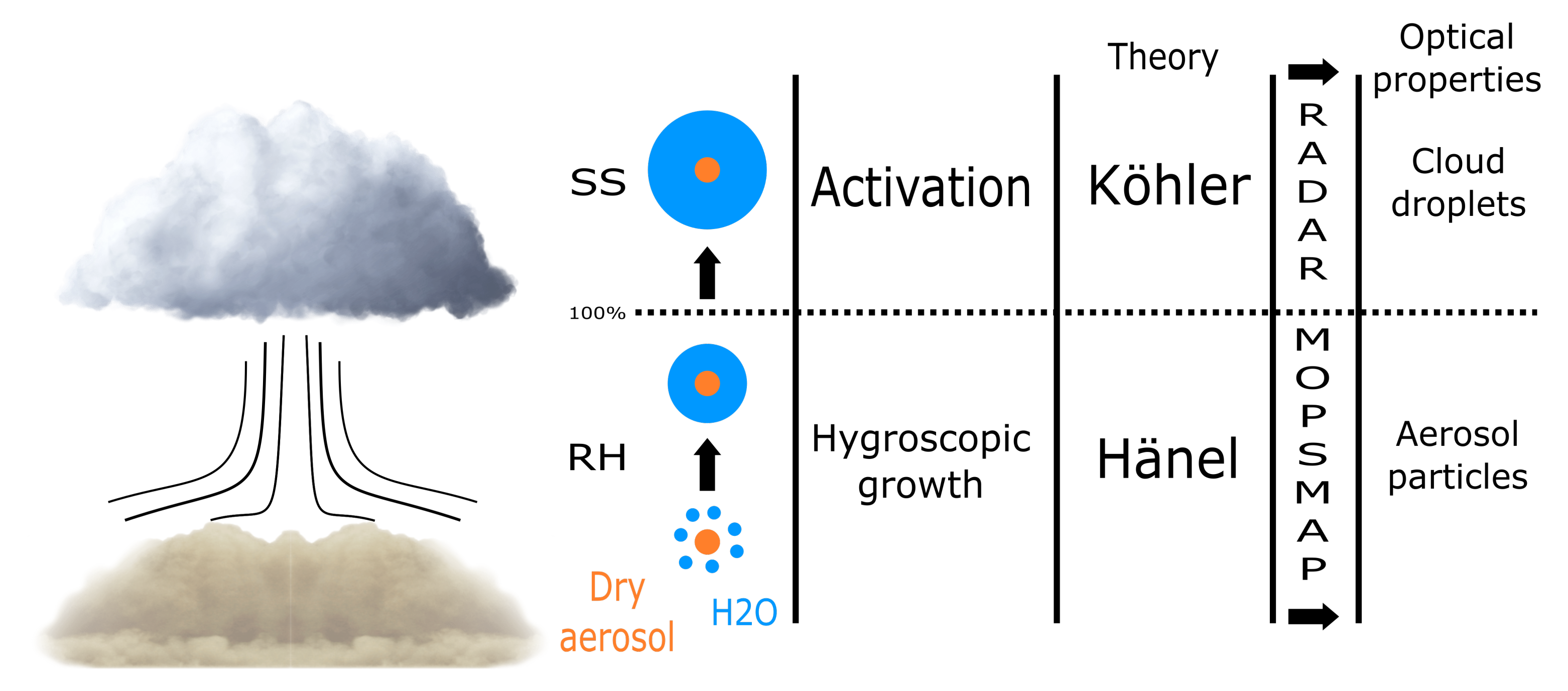
2.1. Lidar and Radar Signal Simulator (LARSS)
- The PSD and DSD are described by a log-normal size distribution.
- The aerosol number concentration is constant with height, presenting the same PSD except for hygroscopic growth.
- The minimum to start the droplet formation is established by the PSD bin with the largest radius.
- The LWP is constant, as it is a requirement for retrieving the ACI indexes.
- The updraft velocity is constant with height.
- The droplets are only allowed to grow through condensation, making the maximum radius of a droplet at m (the limit where coalescence growth starts to present a considerable contribution).
2.2. ACI Indices Estimation by LARSS
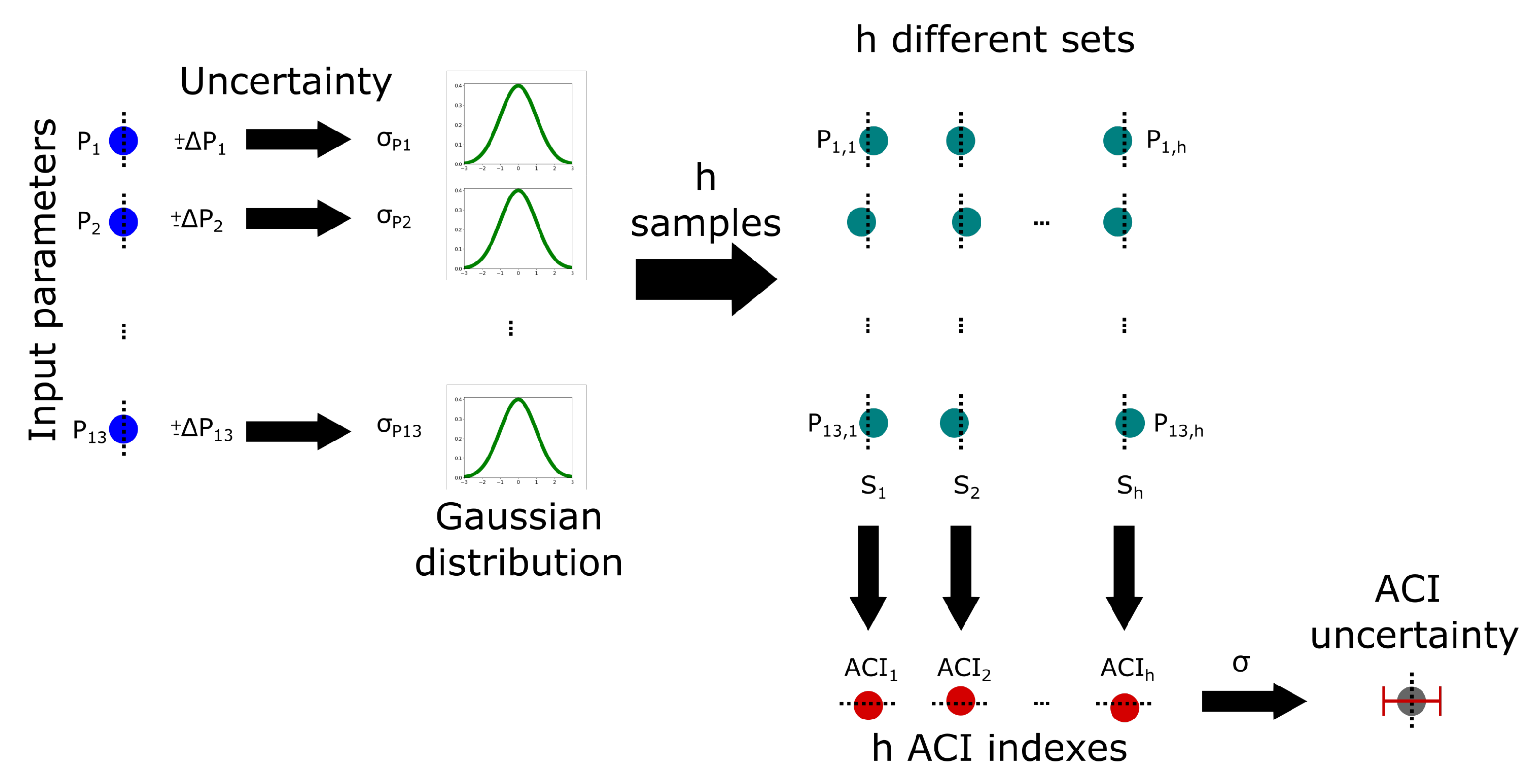
2.2.1. ACI Uncertainty Based on Monte Carlo Technique
- 1.
- Table 1 shows the 13 initial parameters required to initialize one simulation with LARSS (, ,…, ). This set of parameters is noted as S.
- 2.
- The uncertainty associated to each parameter is represented by its relative error .
- 3.
- A Gaussian distribution is associated to the uncertainty of each parameter where its standard, , is derived from .
- 4.
- From each Gaussian distribution, h random values are selected (e.g., , , …, ).
- 5.
- Random values are grouped in h sets (e.g., , , …, ). For example, the set is given by , , …, .
- 6.
- h ACI indexes are retrieved with the generated sets.
- 7.
- The ACI index uncertainty is the standard deviation of the h ACI indexes.
3. LARSS Evaluation and ACI Assessment for Simulated Data
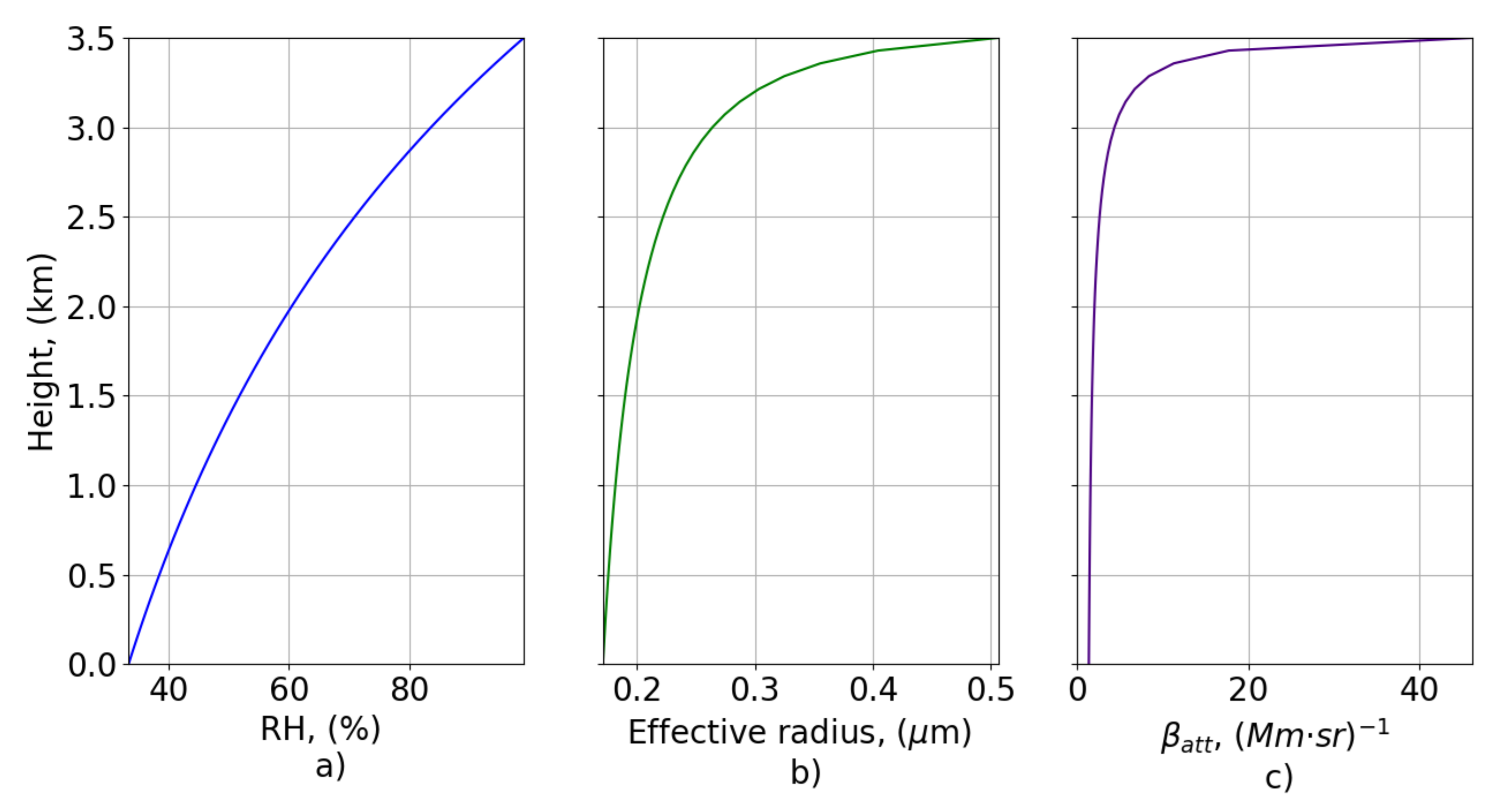
3.1. LARSS Evaluation against Experimental Data
3.2. Analysis of the ACI Indices for Different Aerosol Types
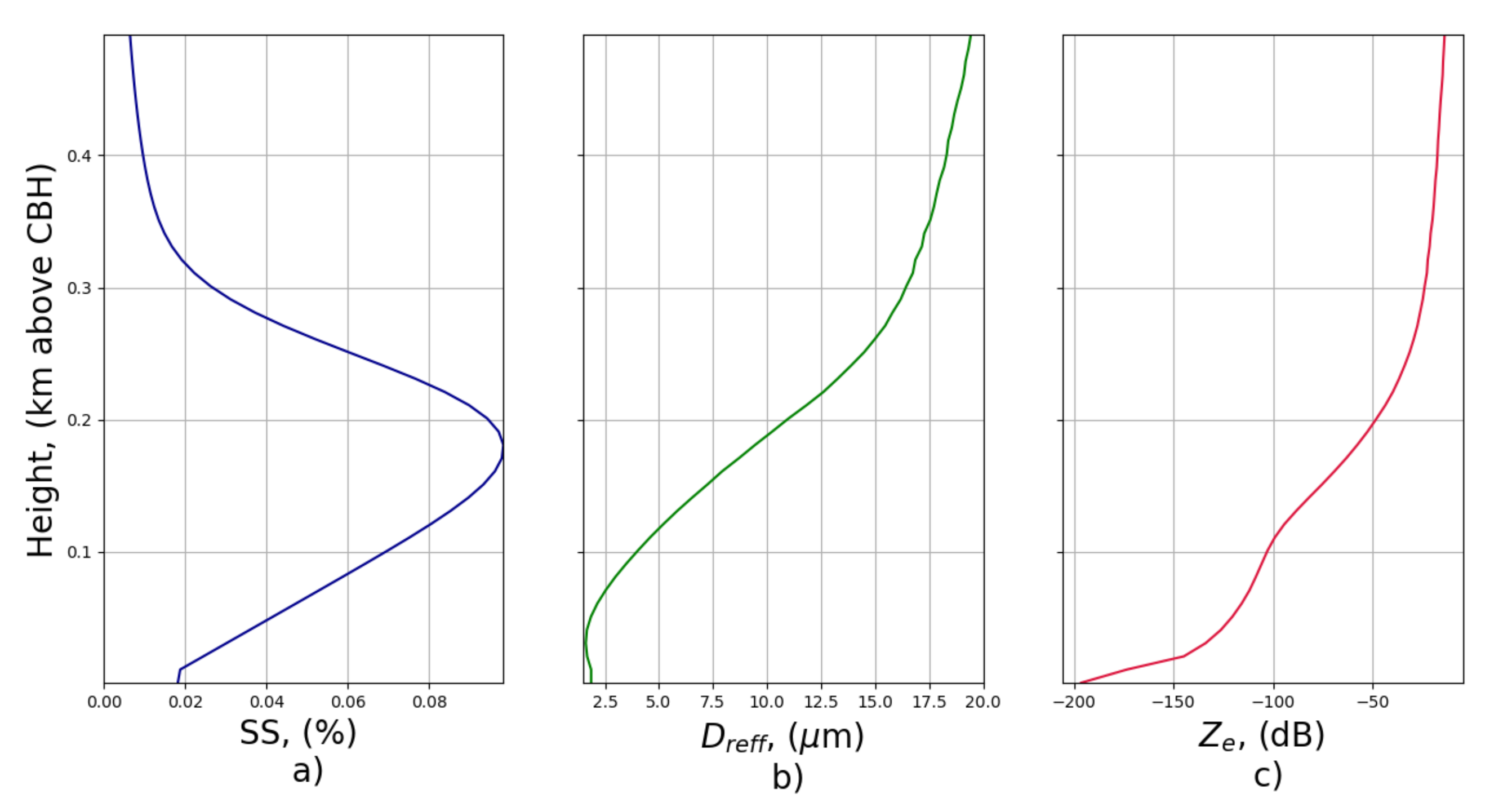
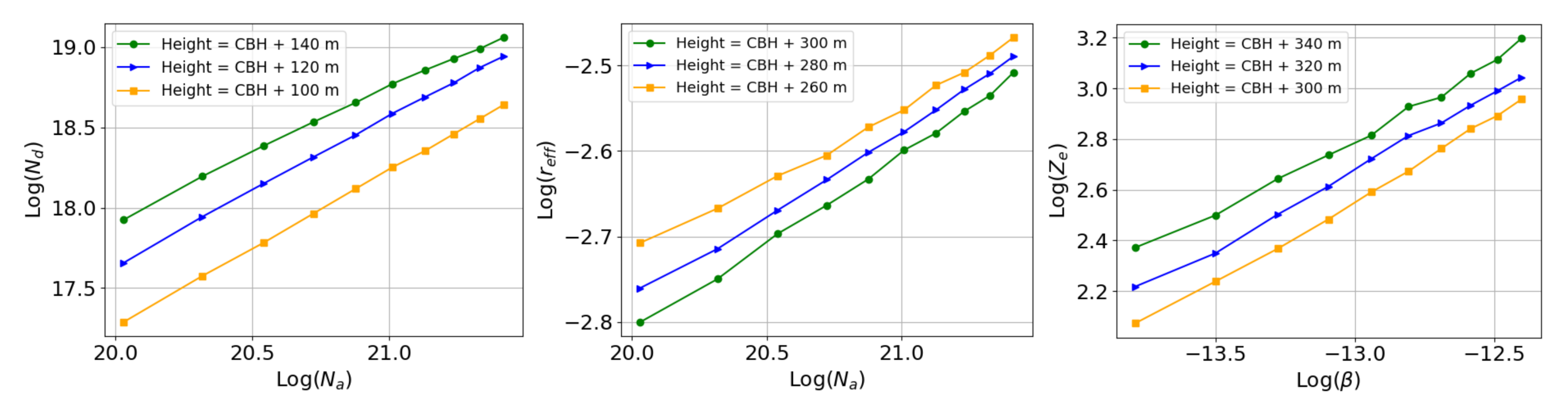
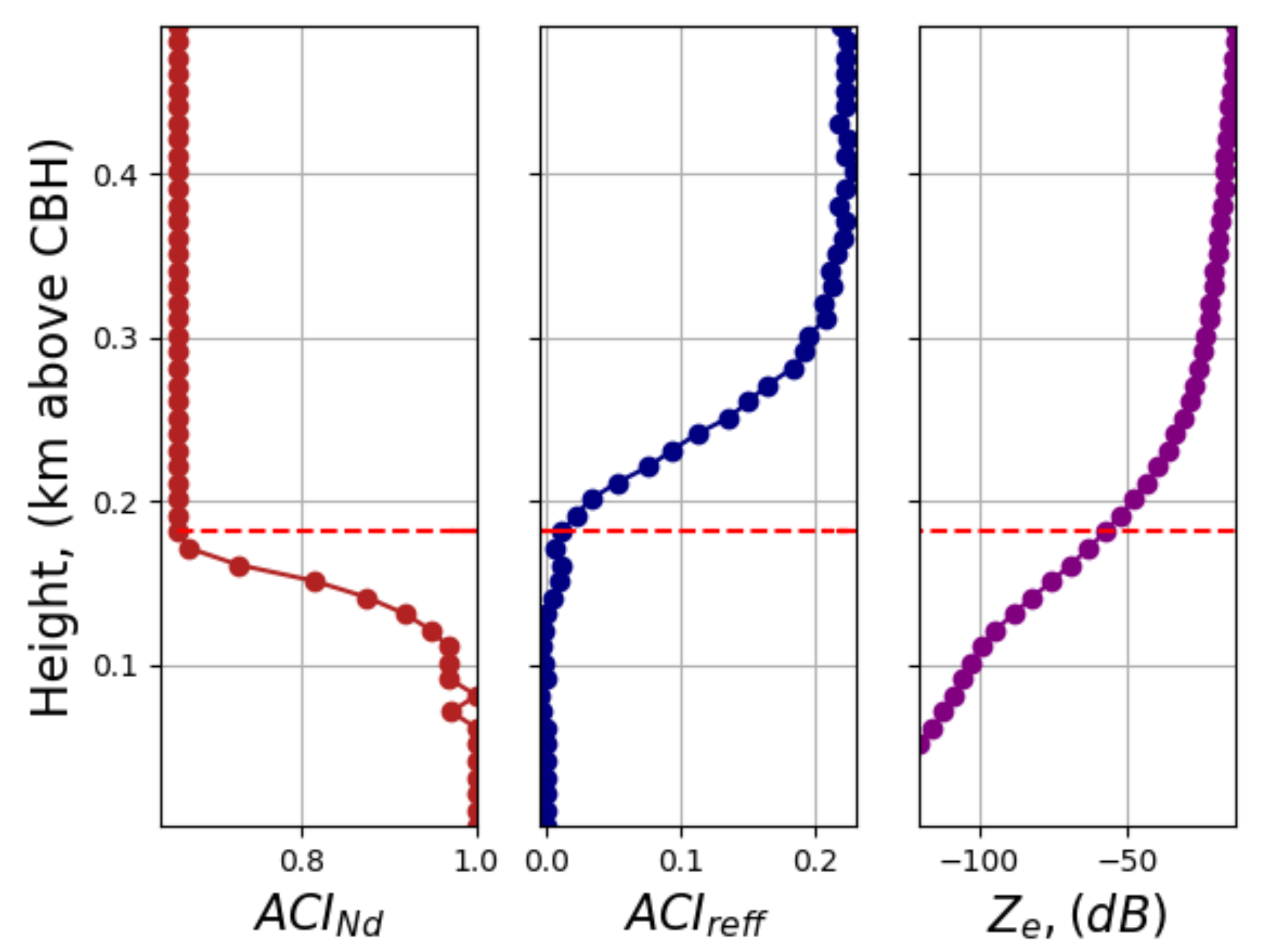
4. Results: ACI Index Sensitivity to Atmospheric Conditions
5. Proposal of ACI Index Based on Remote-Sensing Measurements (ACIRs)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description | Units |
| - | ||
| Aerosol cloud interaction | - | |
| Aerosol cloud interaction index based on the backscatter coefficient | - | |
| Aerosol cloud interaction based on the aerosol optical depth | - | |
| Activation fraction | - | |
| Aerosol optical depth | - | |
| C | Initial supersaturation | - |
| Cloud condensation nuclei | ||
| Specific heat capacity of most air at constant pressure | ||
| Droplet diameter | ||
| Droplet effective radius | ||
| Droplet modal radius | ||
| DSD | Droplet number size distribution | - |
| g | Mean gravitational acceleration | |
| water vapor mixing ratio (mass of water per 1 kg of air) | - | |
| Liquid water mixing ratio (mass of liquid water per 1 kg of dry air) | - | |
| - | ||
| Refractive index of water | - | |
| Droplet number concentration with a diameter d | ||
| Aerosol number concentration | ||
| Droplet number concentration | ||
| PSD | Particle number size distribution | - |
| R | Specific gas constant of most gases | |
| Correlation coeficient | - | |
| RH | Relative humidity | % |
| Dry aerosol-particle modal radius | ||
| Wet aerosol-particle modal radius | ||
| Specific gas constant of water vapor | ||
| Supersaturation | - | |
| Maximum supersaturation | - | |
| T | Temperature | K |
| Reference temperature | K | |
| w | Updraft velocity | |
| z | Height above ground level | m |
| Radar reflectivity | ||
| Extinction coefficient | ||
| Backscatter coefficient | ||
| Attenuated backscatter coefficient | ||
| aerosol proxy | − | |
| ACI | Variability between the ACI index with and without fluctuations | % |
| Fluctuation of the dry aerosol-particle modal radius | % | |
| Fluctuation of the wet aerosol-particle modal radius | % | |
| Fluctuation of the updraft velocity | % | |
| Hygroscopicity parameter | - | |
| Radar wavelength | ||
| Standard deviation | - | |
| Droplet effective cross-section |
Appendix A. Additional LARSS Simulations
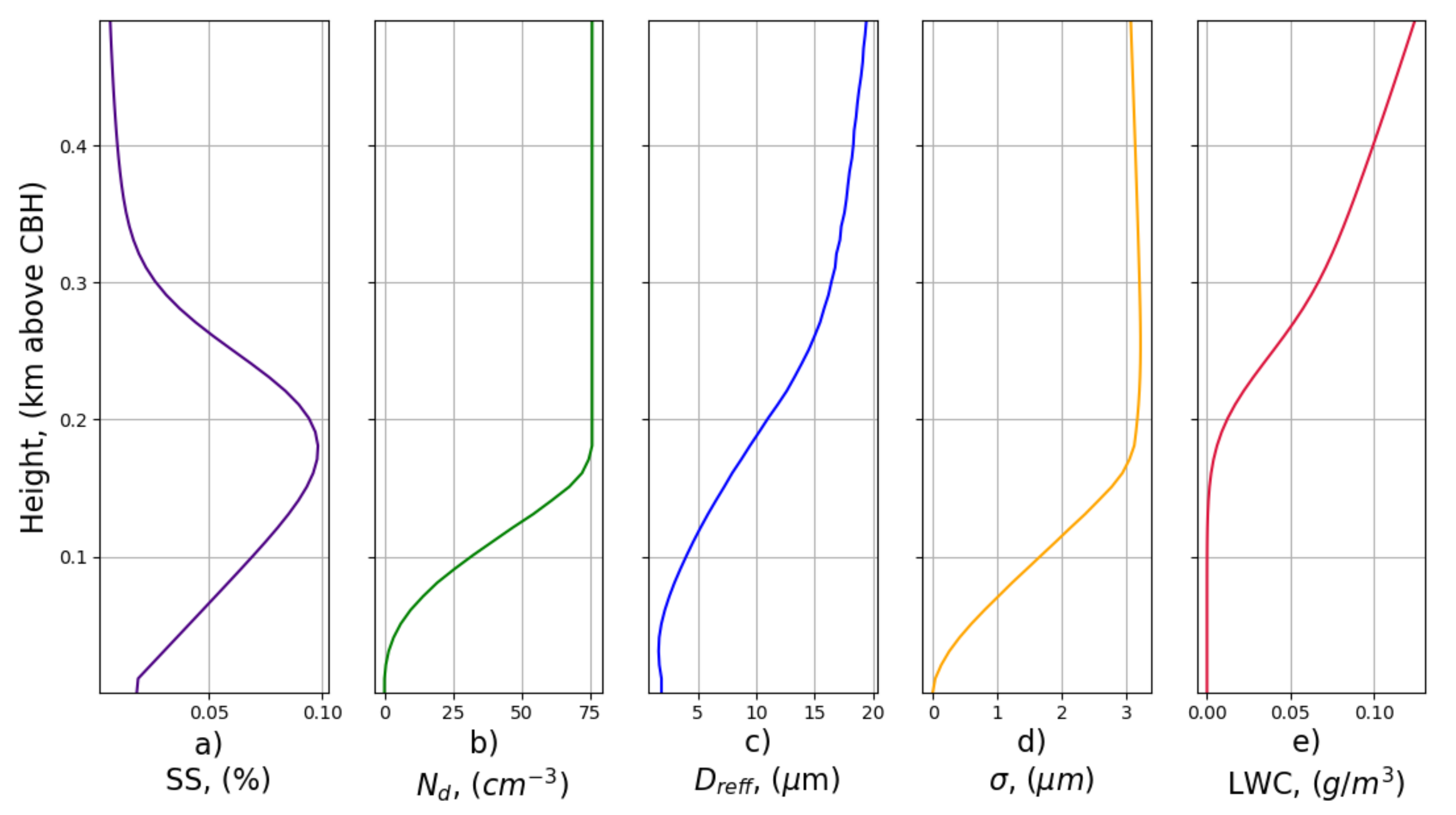
Appendix A.1. Simulation of the Twomey Effect by LARSS
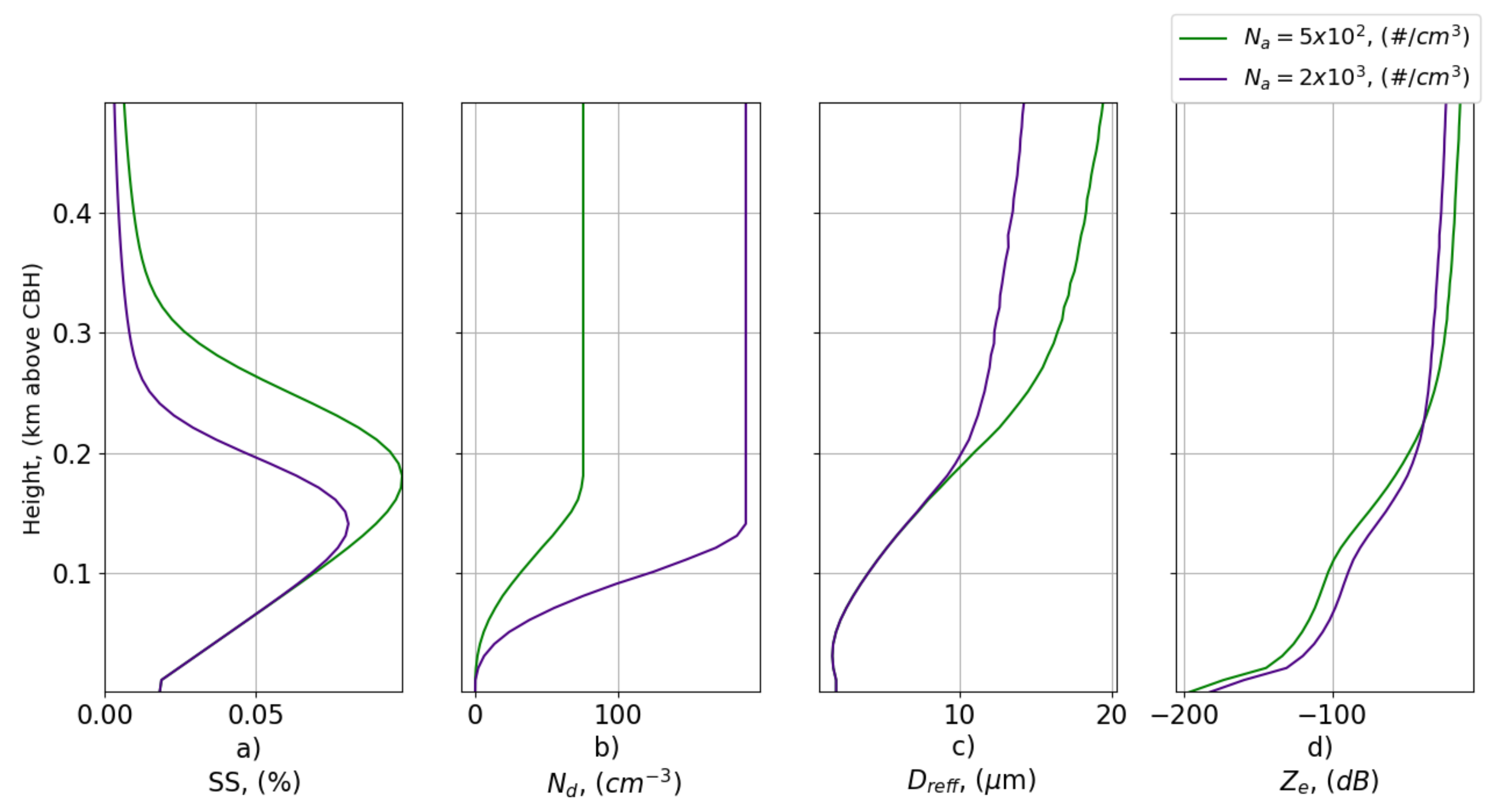
Appendix A.2. Variations in ACI Related to the Presence of a Second (Coarse) Mode in the PSD
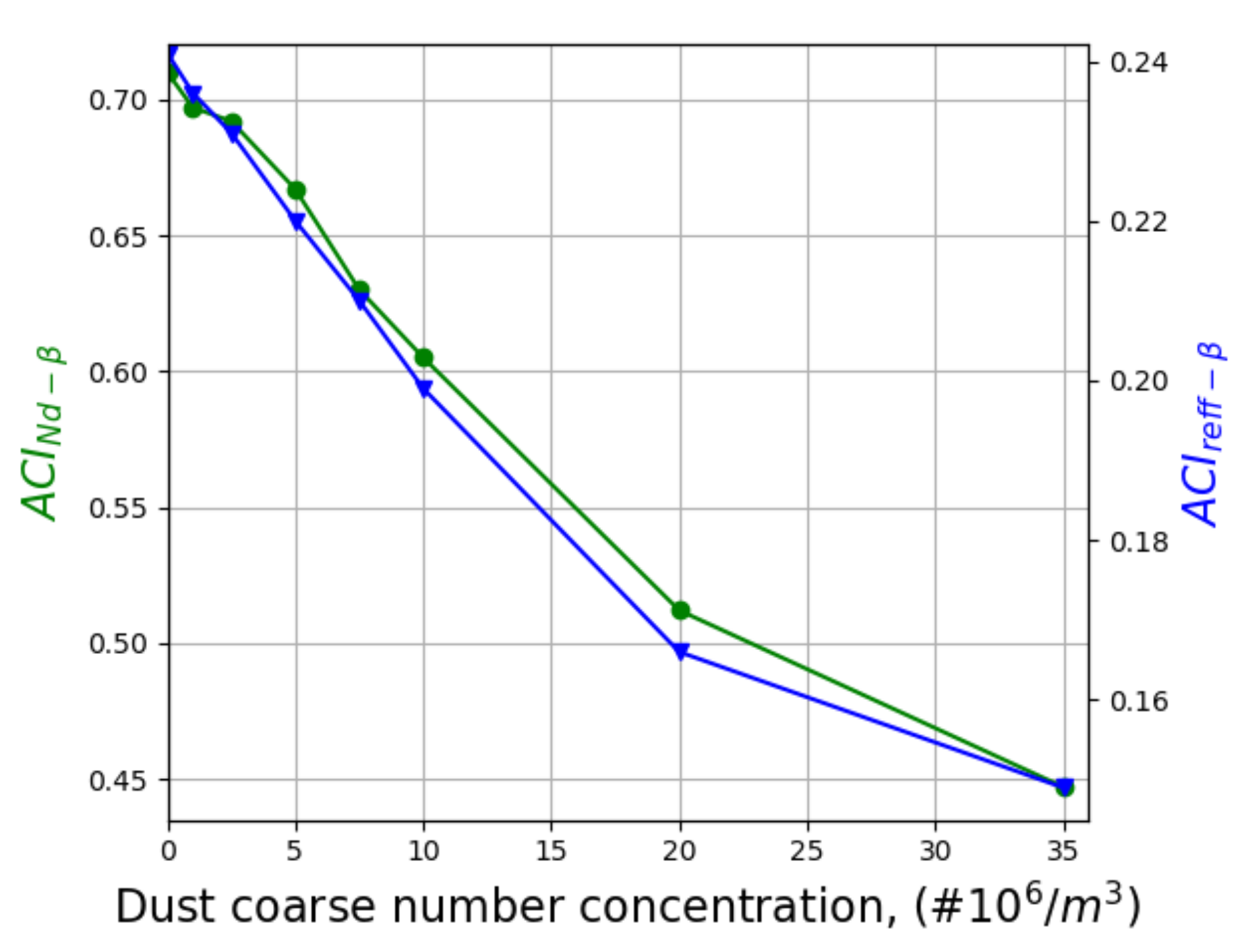
Appendix A.3. Range-Dependence of Cloud Microphysics
Appendix B. Additional Figures
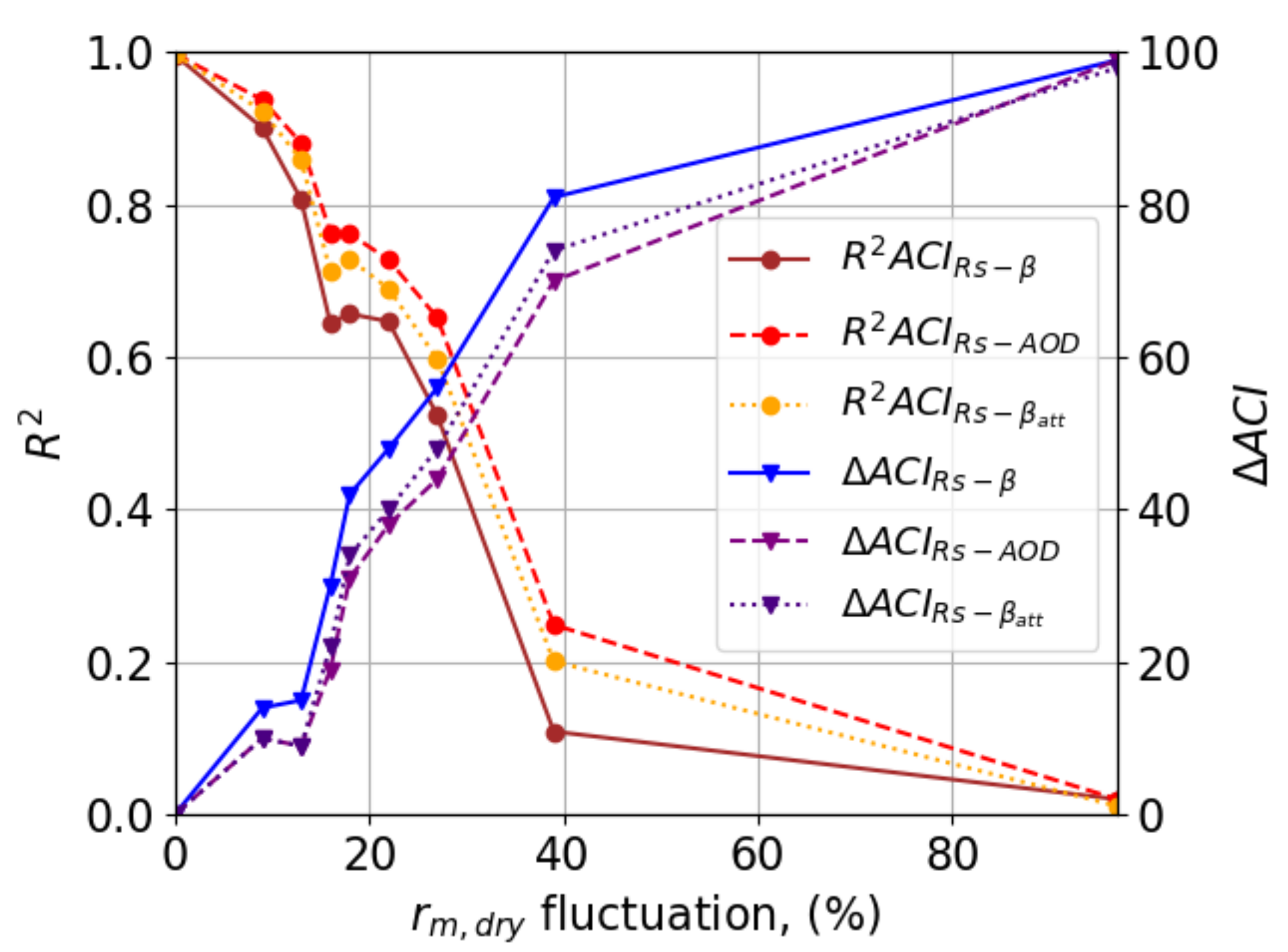
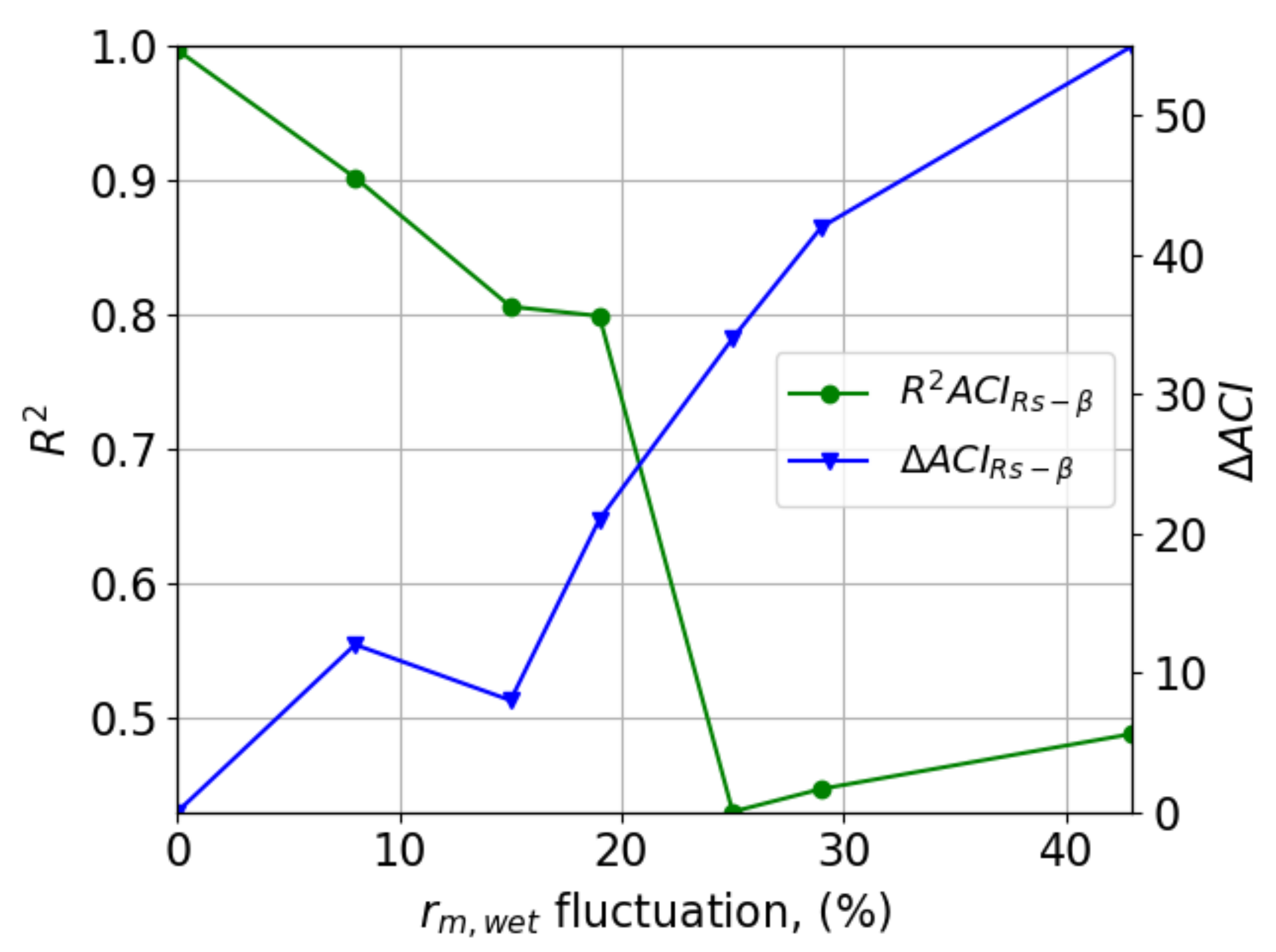
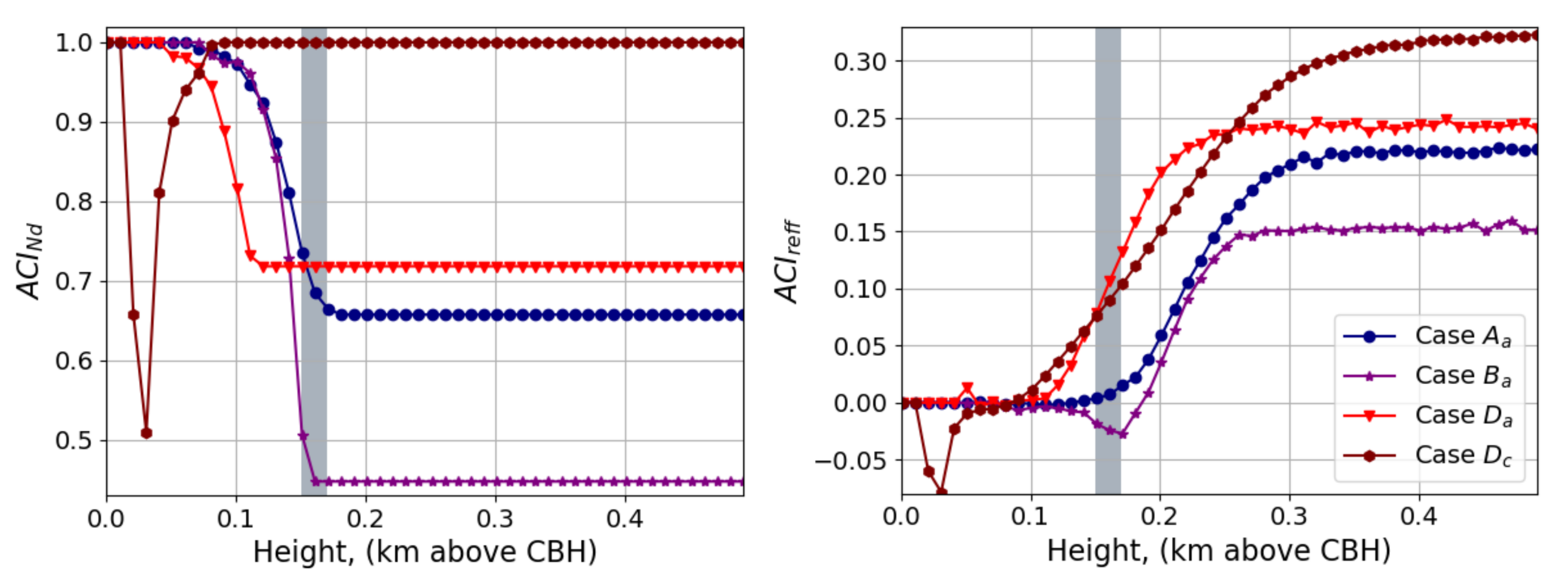
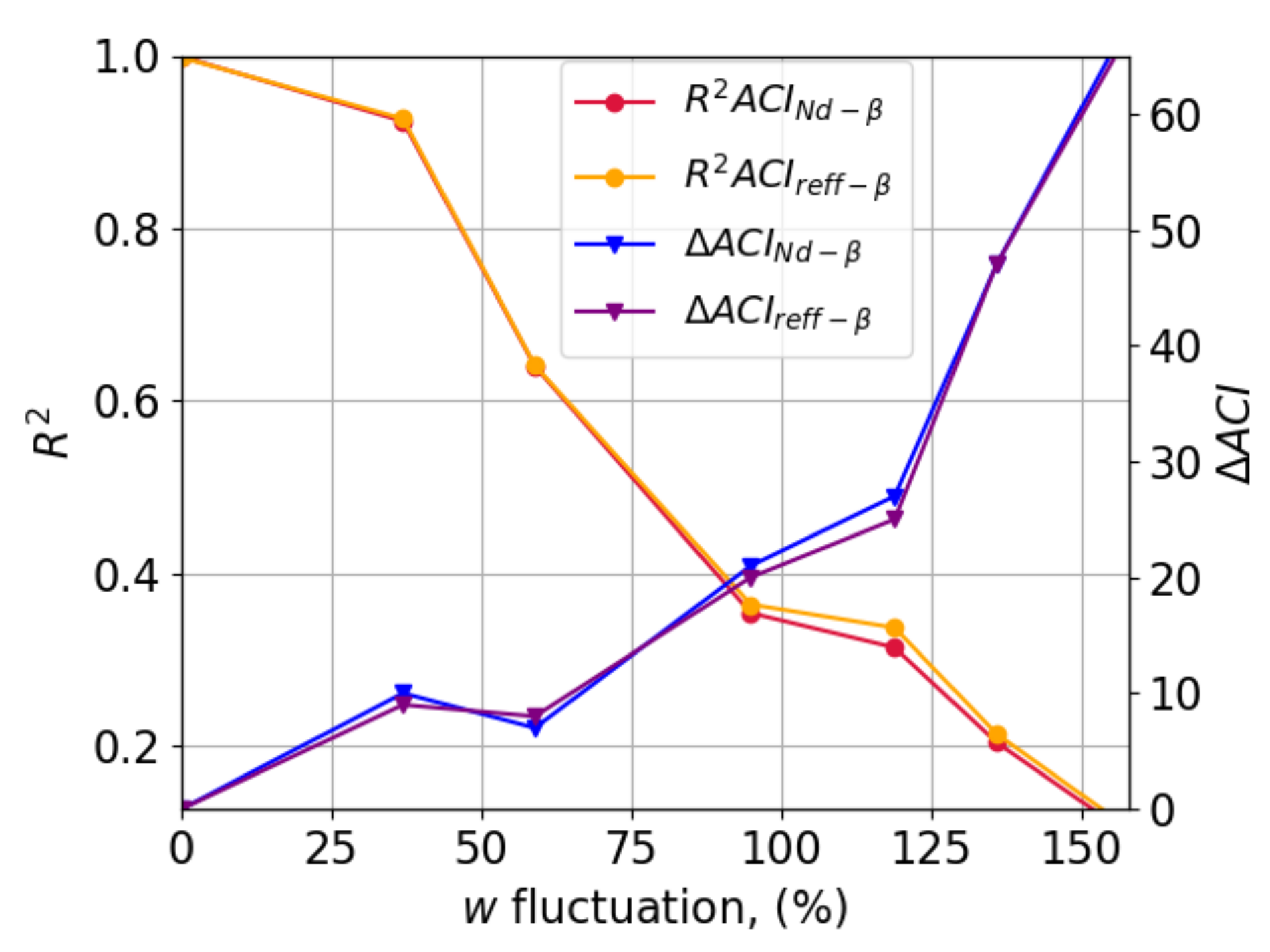
Appendix B.1. ACIRs Sensitivity to rm,dry, rm,wet and w

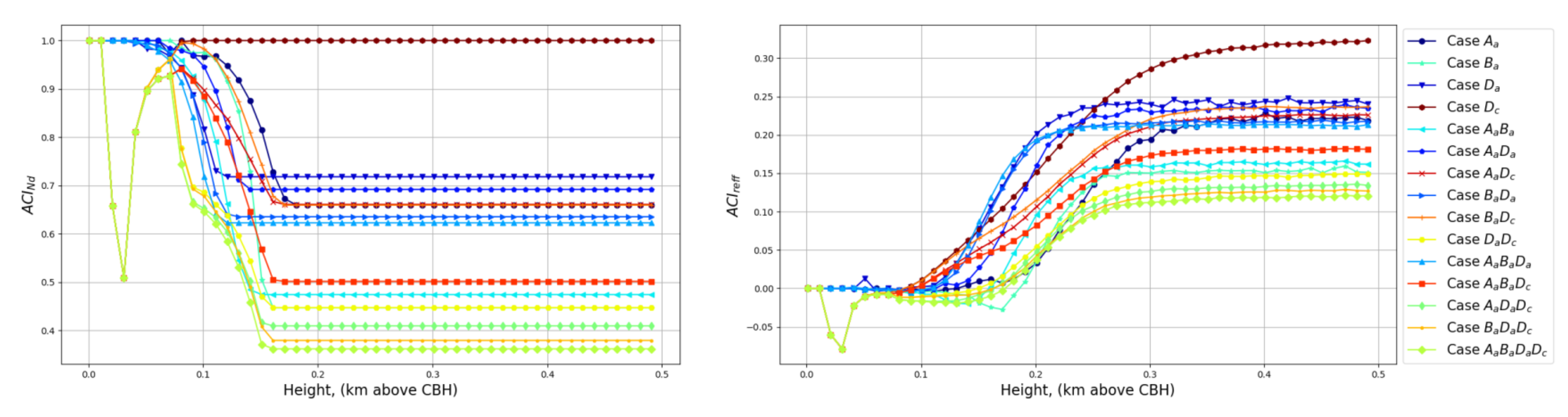
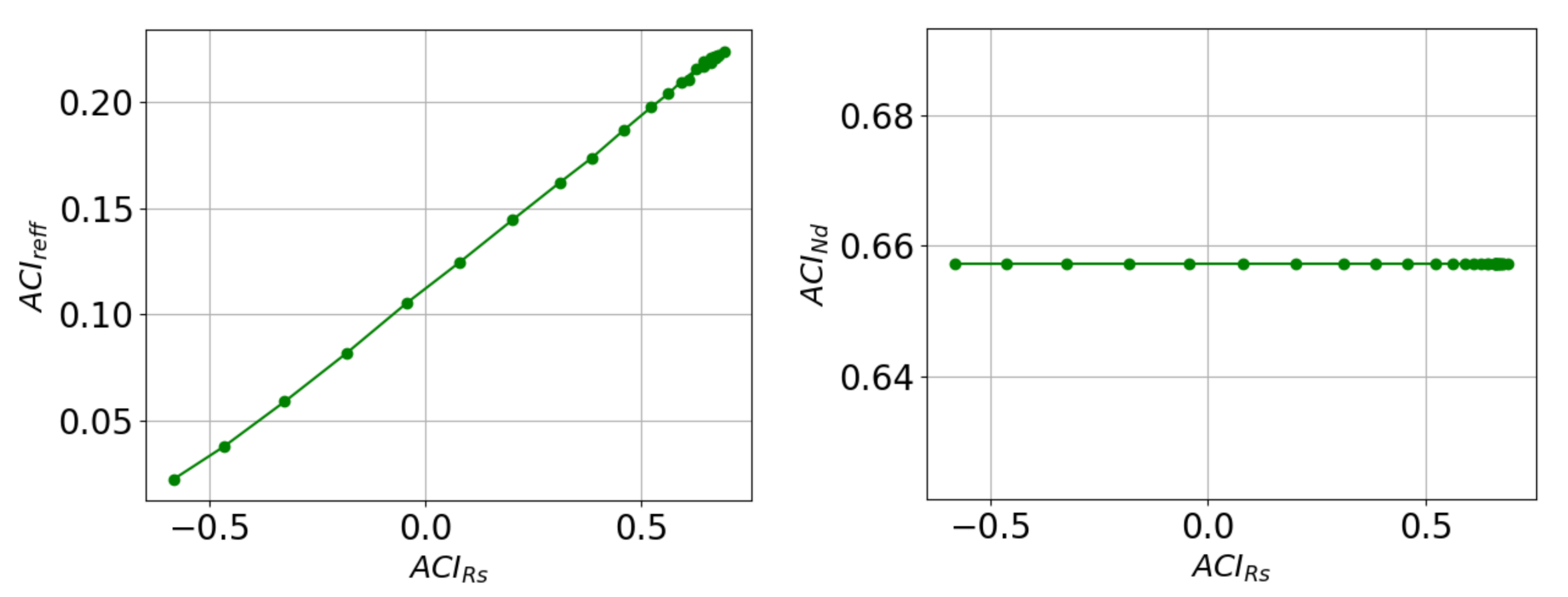
Appendix B.2. ACINd and ACIreff for All the Cases Used in LARSS
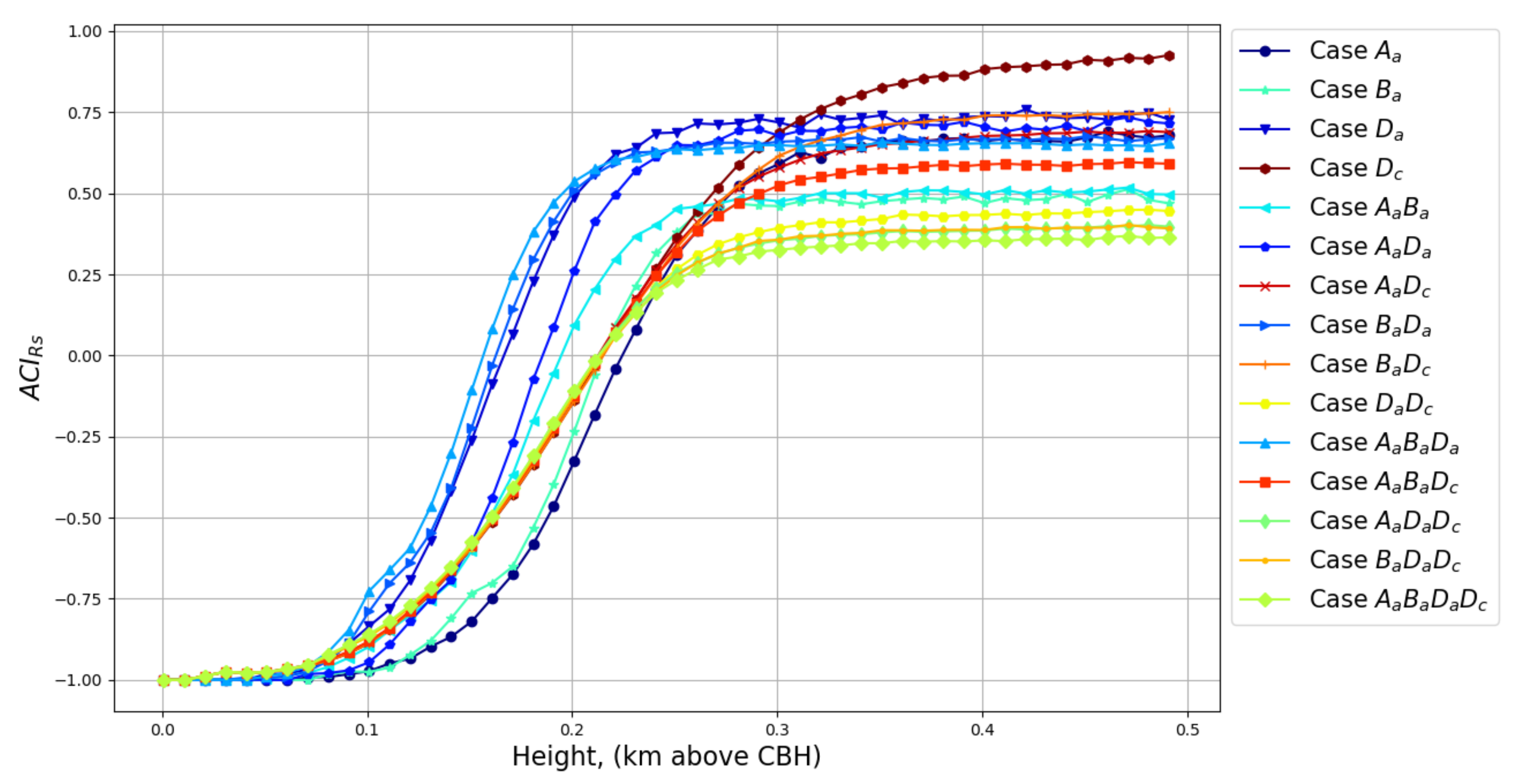
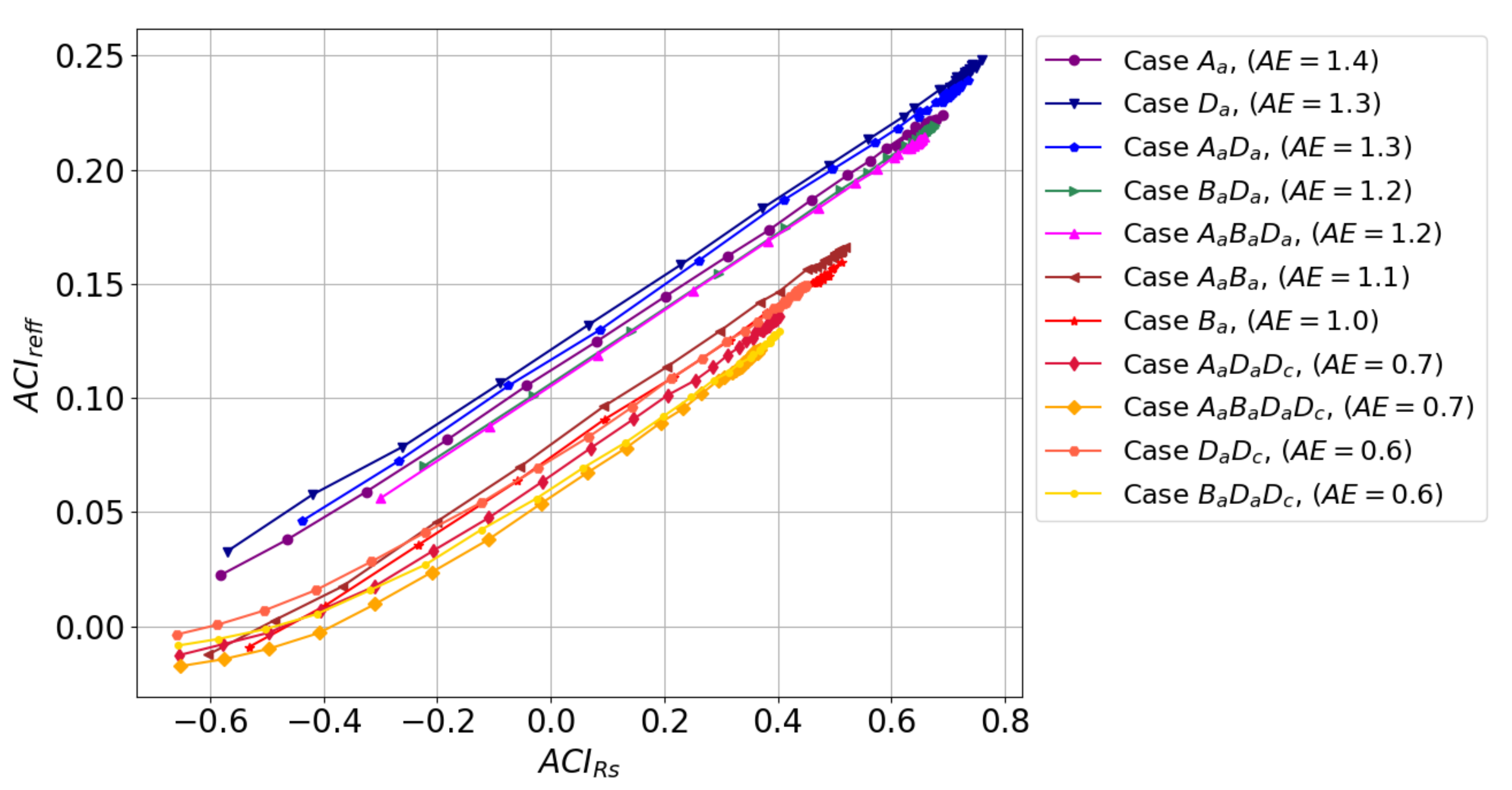
Appendix B.3. ACIRs for All the Cases Used in LARSS
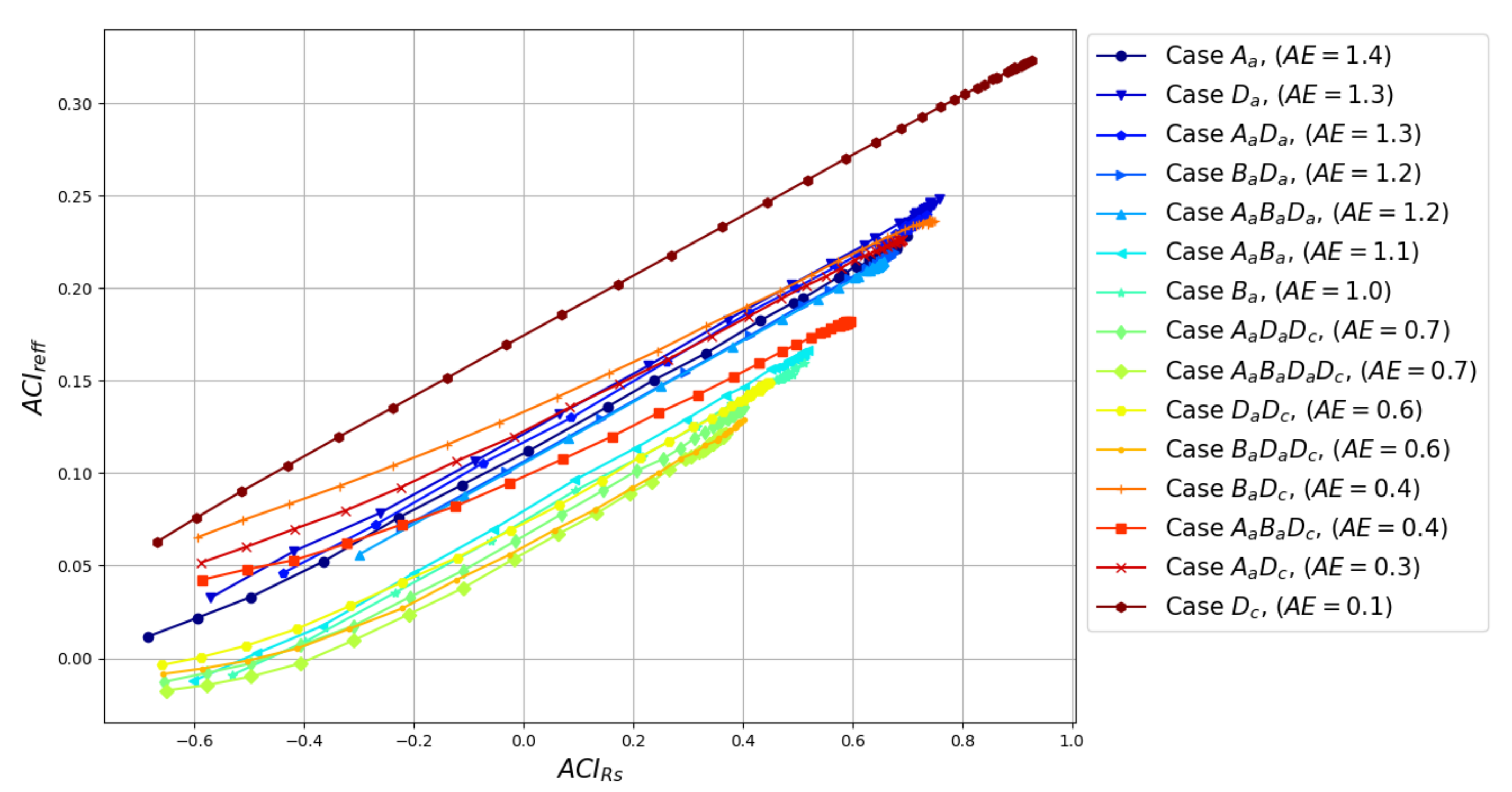
Appendix B.4. ACIRs to ACIreff Relation for All the Cases Used in LARSS
References
- Solomon, S.; Qin, D.; Manning, M.; Alley, R.B.; Berntsen, T.; Bindoff, N.L.; Chen, Z.; Chidthaisong, A.; Gregory, J.M.; Hegerl, G.C.; et al. Technical Summary; Cambridge University Press: Cambridge, UK, 2007; Volume 151. [Google Scholar]
- Ciscar, J.C.; Soria, A.; Goodess, C.M.; Christensen, O.B.; Iglesias, A.; Garrote, L.; Moneo, M.; Quiroga, S.; Feyen, L.; Dankers, R.; et al. Climate Change Impacts in Europe. Final Report of the PESETA Research Project; Technical Report; Joint Research Centre (Seville Site): Seville, Spain, 2009. [Google Scholar]
- López-Romero, J.M.; Montávez, J.P.; Jerez, S.; Lorente-Plazas, R.; Palacios-Peña, L.; Jiménez-Guerrero, P. Precipitation response to aerosol–radiation and aerosol–cloud interactions in regional climate simulations over Europe. Atmos. Chem. Phys. 2021, 21, 415–430. [Google Scholar] [CrossRef]
- Li, Z.; Rosenfeld, D.; Fan, J. Aerosols and their impact on radiation, clouds, precipitation, and severe weather events. In Oxford Research Encyclopedia of Environmental Science; USDOE: Richland, WA, USA, 2017. [Google Scholar]
- Li, Z. Influence of absorbing aerosols on the inference of solar surface radiation budget and cloud absorption. J. Clim. 1998, 11, 5–17. [Google Scholar] [CrossRef] [Green Version]
- Feingold, G.; Jiang, H.; Harrington, J.Y. On smoke suppression of clouds in Amazonia. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Cheng, Y.; Wang, S.; Wei, C.; Pöhlker, M.; Pöhlker, C.; Artaxo, P.; Shrivastava, M.; Andreae, M.O.; Pöschl, U.; et al. Impact of biomass burning aerosols on radiation, clouds, and precipitation over the Amazon during the dry season: Dependence of aerosol–cloud and aerosol-radiation interactions on aerosol loading. Atmos. Chem. Phys 2020, 20, 13283–13301. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, cloud microphysics, and fractional cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Lohmann, U.; Raga, G.B.; O’Dowd, C.D.; Kulmala, M.; Fuzzi, S.; Reissell, A.; Andreae, M.O. Flood or drought: How do aerosols affect precipitation? Science 2008, 321, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of IPCC the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; 1535p. [Google Scholar]
- Twomey, S. The influence of pollution on the shortwave albedo of clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef] [Green Version]
- Feingold, G.; Remer, L.; Ramaprasad, J.; Kaufman, Y. Analysis of smoke impact on clouds in Brazilian biomass burning regions: An extension of Twomey’s approach. J. Geophys. Res. Atmos. 2001, 106, 22907–22922. [Google Scholar] [CrossRef]
- Lihavainen, H.; Kerminen, V.M.; Remer, L. Aerosol–cloud interaction determined by both in situ and satellite data over a northern high-latitude site. Atmos. Chem. Phys. 2010, 10, 10987–10995. [Google Scholar] [CrossRef] [Green Version]
- Jia, H.; Ma, X.; Liu, Y. Exploring aerosol–cloud interaction using VOCALS-REx aircraft measurements. Atmos. Chem. Phys. 2019, 19, 7955–7971. [Google Scholar] [CrossRef] [Green Version]
- Padmakumari, B.; Maheskumar, R.; Harikishan, G.; Morwal, S.; Prabha, T.; Kulkarni, J. In situ measurements of aerosol vertical and spatial distributions over continental India during the major drought year 2009. Atmos. Environ. 2013, 80, 107–121. [Google Scholar] [CrossRef]
- Zhao, C.; Qiu, Y.; Dong, X.; Wang, Z.; Peng, Y.; Li, B.; Wu, Z.; Wang, Y. Negative aerosol–cloud re relationship from aircraft observations over Hebei, China. Earth Space Sci. 2018, 5, 19–29. [Google Scholar] [CrossRef] [Green Version]
- Kant, S.; Panda, J.; Rao, P.; Sarangi, C.; Ghude, S.D. Study of aerosol–cloud-precipitation-meteorology interaction during a distinct weather event over the Indian region using WRF-Chem. Atmos. Res. 2021, 247, 105144. [Google Scholar] [CrossRef]
- Radenz, M.; Bühl, J.; Seifert, P.; Baars, H.; Engelmann, R.; Barja González, B.; Mamouri, R.E.; Zamorano, F.; Ansmann, A. Hemispheric contrasts in ice formation in stratiform mixed-phase clouds: Disentangling the role of aerosol and dynamics with ground-based remote sensing. Atmos. Chem. Phys. Discuss. 2021, 21, 17969–17994. [Google Scholar] [CrossRef]
- Zheng, X.; Xi, B.; Dong, X.; Wu, P. Environmental Effects on Aerosol–cloud Interaction in non-precipitating MBL Clouds over the Eastern North Atlantic. Atmos. Chem. Phys. Discuss. 2021, 22, 335–354. [Google Scholar] [CrossRef]
- Sarna, K.; Russchenberg, H.W. Ground-based remote sensing scheme for monitoring aerosol–cloud interactions. Atmos. Meas. Tech. (Online) 2016, 9, 1039–1050. [Google Scholar] [CrossRef]
- Mamouri, R.E.; Ansmann, A. Potential of polarization lidar to provide profiles of CCN-and INP-relevant aerosol parameters. Atmos. Chem. Phys. 2016, 16, 5905–5931. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, C.; Ansmann, A.; Engelmann, R.; Donovan, D.; Malinka, A.; Seifert, P.; Wiesen, R.; Radenz, M.; Yin, Z.; Bühl, J.; et al. The dual-field-of-view polarization lidar technique: A new concept in monitoring aerosol effects in liquid-water clouds–case studies. Atmos. Chem. Phys. 2020, 20, 15265–15284. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Sherwood, S.; Wood, R.; Donner, L. Climate effects of aerosol–cloud interactions. Science 2014, 343, 379–380. [Google Scholar] [CrossRef]
- Hänel, G. The properties of atmospheric aerosol particles as functions of the relative humidity at thermodynamic equilibrium with the surrounding moist air. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1976; Volume 19, pp. 73–188. [Google Scholar]
- Zieger, P.; Fierz-Schmidhauser, R.; Weingartner, E.; Baltensperger, U. Effects of relative humidity on aerosol light scattering: Results from different European sites. Atmos. Chem. Phys. 2013, 13, 10609. [Google Scholar] [CrossRef] [Green Version]
- Köhler, H. The nucleus in and the growth of hygroscopic droplets. Trans. Faraday Soc. 1936, 32, 1152–1161. [Google Scholar] [CrossRef]
- Petters, M.; Kreidenweis, S. A single parameter representation of hygroscopic growth and cloud condensation nucleus activity. Atmos. Chem. Phys. 2007, 7, 1961–1971. [Google Scholar] [CrossRef] [Green Version]
- Pinsky, M.; Mazin, I.; Korolev, A.; Khain, A. Supersaturation and diffusional droplet growth in liquid clouds: Polydisperse spectra. J. Geophys. Res. Atmos. 2014, 119, 12872–12887. [Google Scholar] [CrossRef]
- Gasteiger, J.; Wiegner, M. MOPSMAP v1. 0: A versatile tool for the modeling of aerosol optical properties. Geosci. Model Dev. 2018, 11, 2739–2762. [Google Scholar] [CrossRef] [Green Version]
- Pruppacher, H.R.; Klett, J.D. Microphysics of clouds and precipitation. Nature 1980, 284, 88. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Mészáros, A. On the concentration and size distribution of atmospheric sulfate particles under rural conditions. Atmos. Environ. (1967) 1978, 12, 2425–2428. [Google Scholar] [CrossRef]
- Hande, L.B.; Engler, C.; Hoose, C.; Tegen, I. Parameterizing cloud condensation nuclei concentrations during HOPE. Atmos. Chem. Phys. 2016, 16, 12059–12079. [Google Scholar] [CrossRef] [Green Version]
- Curtis, D.B.; Aycibin, M.; Young, M.A.; Grassian, V.H.; Kleiber, P.D. Simultaneous measurement of light-scattering properties and particle size distribution for aerosols: Application to ammonium sulfate and quartz aerosol particles. Atmos. Environ. 2007, 41, 4748–4758. [Google Scholar] [CrossRef]
- Tu, K.; Kanapilly, G. Generation and characterization of submicron ammonium sulfate and ammonium hydrogen sulfate aerosols. Atmos. Environ. (1967) 1978, 12, 1623–1629. [Google Scholar] [CrossRef]
- Pappalardo, G.; Amodeo, A.; Pandolfi, M.; Wandinger, U.; Ansmann, A.; Bösenberg, J.; Matthias, V.; Amiridis, V.; De Tomasi, F.; Frioud, M.; et al. Aerosol lidar intercomparison in the framework of the EARLINET project. 3. Raman lidar algorithm for aerosol extinction, backscatter, and lidar ratio. Appl. Opt. 2004, 43, 5370–5385. [Google Scholar] [CrossRef]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Guerrero, J.L. Técnica Lidar para la Caracterización Atmosférica Mediante Dispersión Elástica y Ramán. Ph.D. Thesis, Centro Andaluz del Medio Ambiente, Universidad de Granada, Granada, Spain, 2009. [Google Scholar]
- Rejano, F.; Titos, G.; Casquero-Vera, J.A.; Lyamani, H.; Andrews, E.; Sheridan, P.; Cazorla, A.; Castillo, S.; Alados-Arboledas, L.; Olmo, F.J. Activation properties of aerosol particles as cloud condensation nuclei at urban and high-altitude remote sites in southern Europe. Sci. Total Environ. 2021, 762, 143100. [Google Scholar] [CrossRef] [PubMed]
- Ervens, B.; Cubison, M.; Andrews, E.; Feingold, G.; Ogren, J.A.; Jimenez, J.L.; DeCarlo, P.; Nenes, A. Prediction of cloud condensation nucleus number concentration using measurements of aerosol size distributions and composition and light scattering enhancement due to humidity. J. Geophys. Res. Atmos. 2007, 112, D10S32. [Google Scholar] [CrossRef] [Green Version]
- Almeida, G.; Brito, J.; Morales, C.; Andrade, M.; Artaxo, P. Measured and modelled cloud condensation nuclei (CCN) concentration in S ao Paulo, Brazil: The importance of aerosol size-resolved chemical composition on CCN concentration prediction. Atmos. Chem. Phys. 2014, 14, 7559–7572. [Google Scholar] [CrossRef] [Green Version]
- Sauvageot, H.; Omar, J. Radar reflectivity of cumulus clouds. J. Atmos. Ocean. Technol. 1987, 4, 264–272. [Google Scholar] [CrossRef] [Green Version]
- Yau, M.K.; Rogers, R.R. A Short Course in Cloud Physics; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Psichoudaki, M.; Nenes, A.; Florou, K.; Kaltsonoudis, C.; Pandis, S.N. Hygroscopic properties of atmospheric particles emitted during wintertime biomass burning episodes in Athens. Atmos. Environ. 2018, 178, 66–72. [Google Scholar] [CrossRef]
- Zhai, J.; Lu, X.; Li, L.; Zhang, Q.; Zhang, C.; Chen, H.; Yang, X.; Chen, J. Size-resolved chemical composition, effective density, and optical properties of biomass burning particles. Atmos. Chem. Phys. 2017, 17, 7481. [Google Scholar] [CrossRef] [Green Version]
- Dentener, F.; Kinne, S.; Bond, T.; Boucher, O.; Cofala, J.; Generoso, S.; Ginoux, P.; Gong, S.; Hoelzemann, J.; Ito, A.; et al. Emissions of primary aerosol and precursor gases in the years 2000 and 1750, prescribed data-sets for AeroCom. Atmos. Chem. Phys. 2006, 6, 4321–4344. [Google Scholar] [CrossRef] [Green Version]
- Remer, L.; Kaufman, Y.; Holben, B.; Thompson, A.; McNamara, D. Biomass burning aerosol size distribution and modeled optical properties. J. Geophys. Res. Atmos. 1998, 103, 31879–31891. [Google Scholar] [CrossRef] [Green Version]
- Keil, A.; Haywood, J.M. Solar radiative forcing by biomass burning aerosol particles during SAFARI 2000: A case study based on measured aerosol and cloud properties. J. Geophys. Res. Atmos. 2003, 108, 8467. [Google Scholar] [CrossRef]
- Denjean, C.; Cassola, F.; Mazzino, A.; Triquet, S.; Chevaillier, S.; Grand, N.; Bourrianne, T.; Momboisse, G.; Sellegri, K.; Schwarzenboeck, A.; et al. Size distribution and optical properties of mineral dust aerosols transported in the western Mediterranean. Atmos. Chem. Phys. 2016, 16, 1081–1104. [Google Scholar] [CrossRef] [Green Version]
- D’Almeida, G.A.; Koepke, P.; Shettle, E.P. Atmospheric Aerosols: Global Climatology and Radiative Characteristics; A Deepak Pub: Hampton, VA, USA, 1991. [Google Scholar]
- Yuan, T.; Li, Z.; Zhang, R.; Fan, J. Increase of cloud droplet size with aerosol optical depth: An observation and modeling study. J. Geophys. Res. Atmos. 2008, 113, D04201. [Google Scholar] [CrossRef]
- Dusek, U.; Frank, G.; Hildebrandt, L.; Curtius, J.; Schneider, J.; Walter, S.; Chand, D.; Drewnick, F.; Hings, S.; Jung, D.; et al. Size matters more than chemistry for cloud-nucleating ability of aerosol particles. Science 2006, 312, 1375–1378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carslaw, K.; Lee, L.; Reddington, C.; Pringle, K.; Rap, A.; Forster, P.; Mann, G.; Spracklen, D.; Woodhouse, M.; Regayre, L.; et al. Large contribution of natural aerosols to uncertainty in indirect forcing. Nature 2013, 503, 67–71. [Google Scholar] [CrossRef] [PubMed]
- Regayre, L.; Pringle, K.; Booth, B.; Lee, L.; Mann, G.; Browse, J.; Woodhouse, M.; Rap, A.; Reddington, C.; Carslaw, K. Uncertainty in the magnitude of aerosol–cloud radiative forcing over recent decades. Geophys. Res. Lett. 2014, 41, 9040–9049. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Climate change 2007: The physical science basis. Agenda 2007, 6, 333. [Google Scholar]
- Feingold, G.; Eberhard, W.L.; Veron, D.E.; Previdi, M. First measurements of the Twomey indirect effect using ground-based remote sensors. Geophys. Res. Lett. 2003, 30, 1287. [Google Scholar] [CrossRef] [Green Version]
- Raghavan, S. Radar Meteorology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 27. [Google Scholar]
- Mei, F.; Setyan, A.; Zhang, Q.; Wang, J. CCN activity of organic aerosols observed downwind of urban emissions during CARES. Atmos. Chem. Phys. 2013, 13, 12–155. [Google Scholar] [CrossRef] [Green Version]

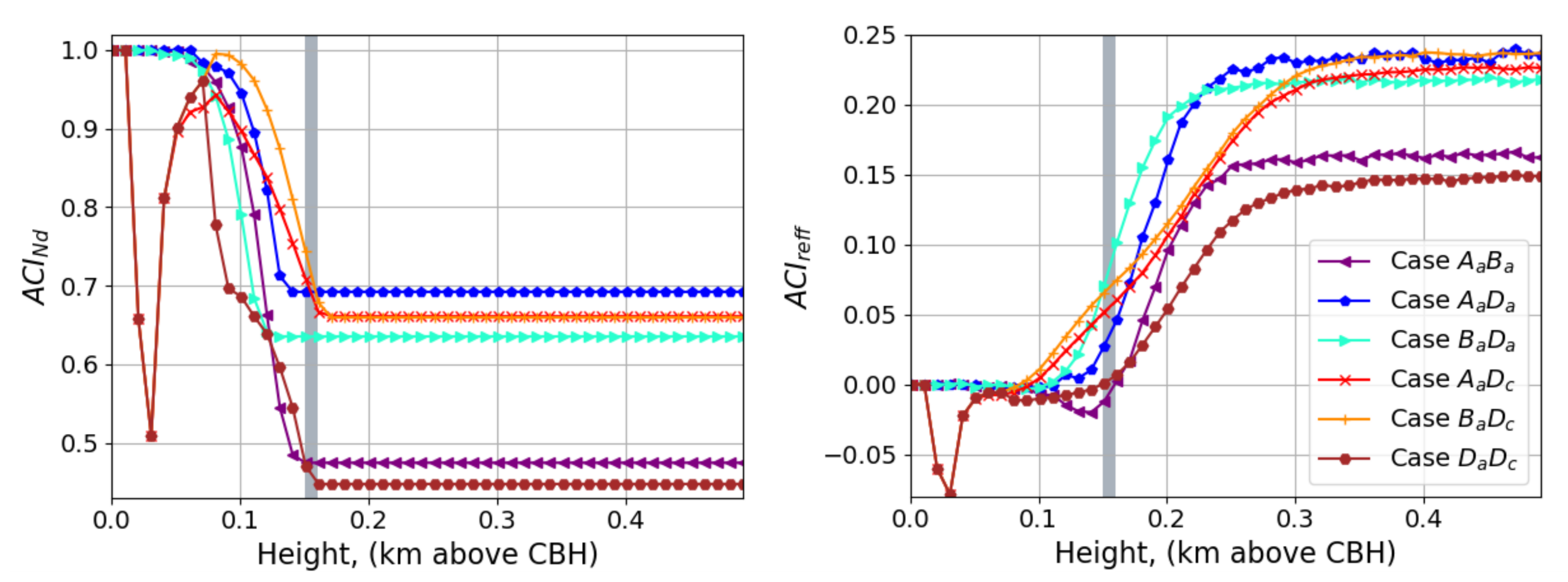
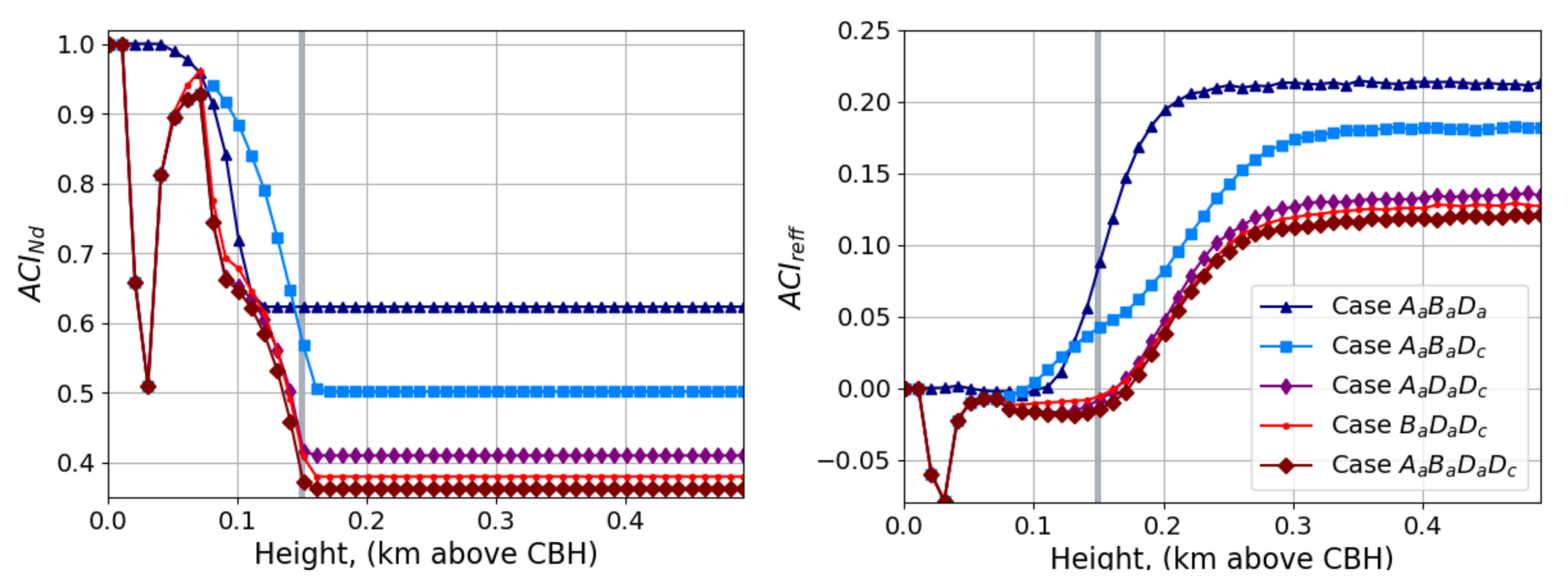
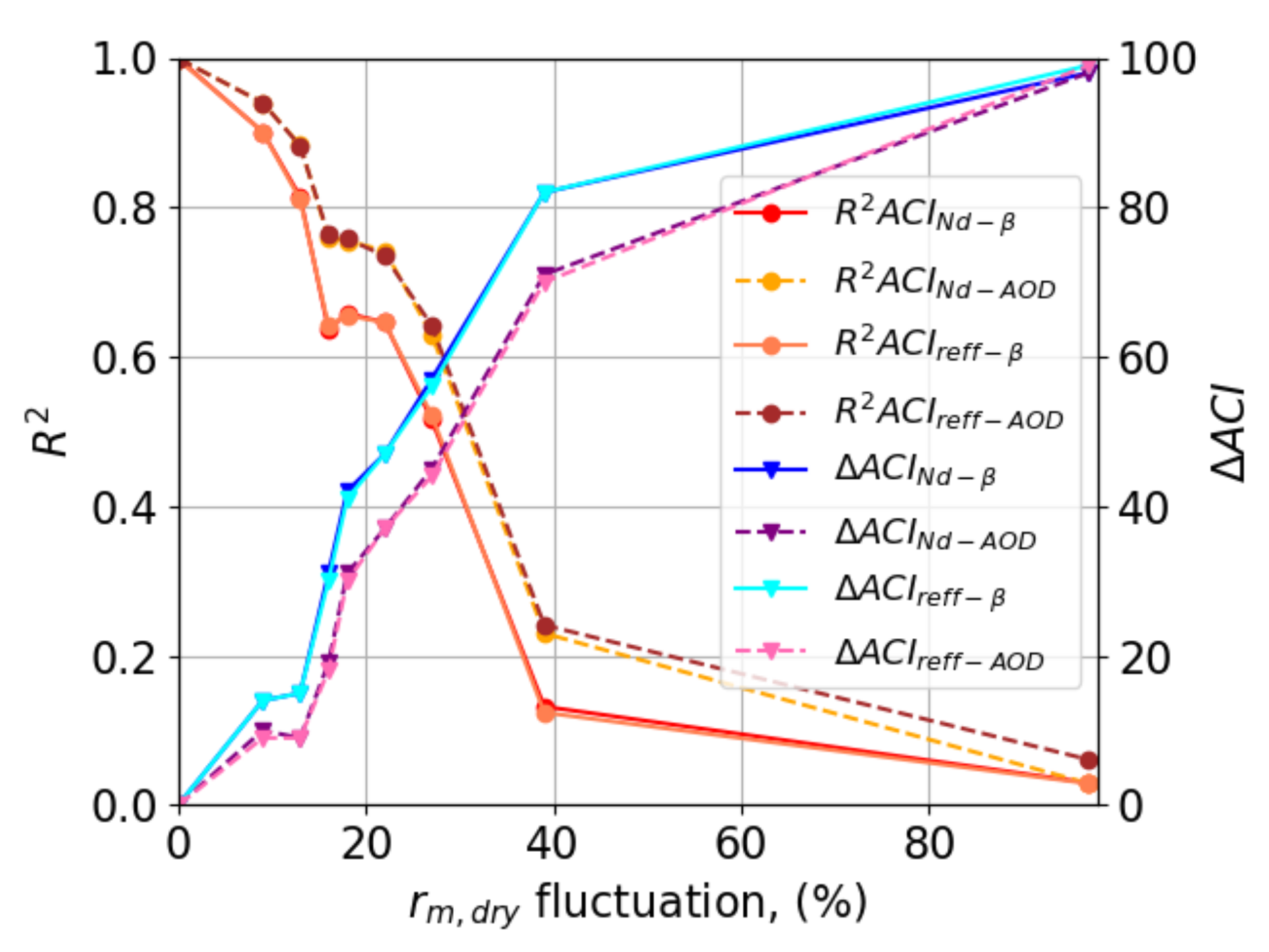
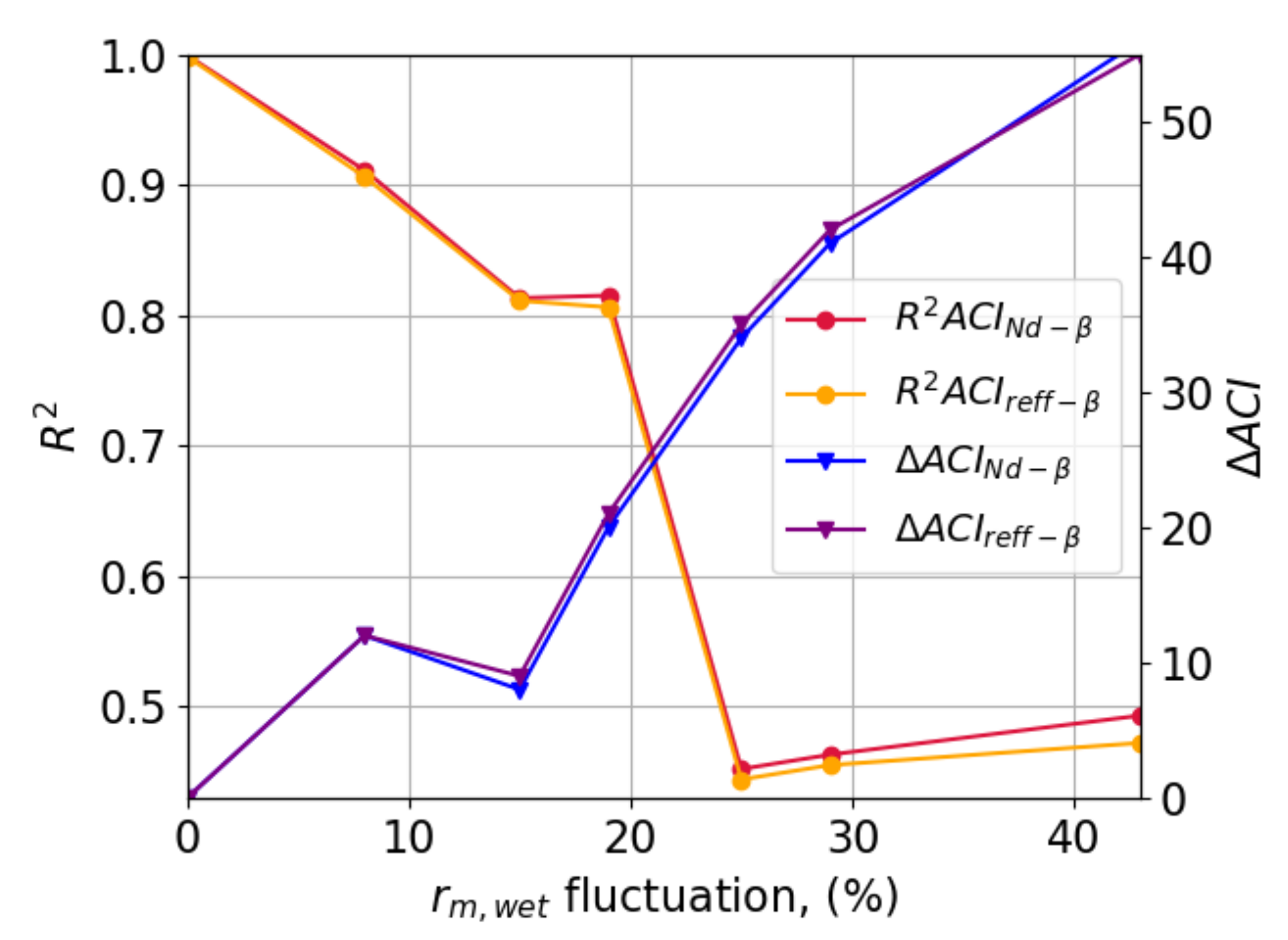

| Atmospheric properties | Specie | Ammonium sulfate | Atmospheric conditions |
Temperature (K) | 298 |
| Number concentration () | |||||
| Minimun radius () | Pressure () | 101 | |||
| Modal radius () | Updraft () | 2 | |||
| Maximun radius () | Water-vapor ratio | 8 | |||
| PSD standard deviation | Instrumental parameters | Lidar wavelength () | 355 | ||
| Hygroscopicity parameter | |||||
| Density () | Radar wavelength () | ||||
| Refractive index |
| Height (m) | 100 | 120 | 140 |
|---|---|---|---|
| 0.97 ± 0.04 | 0.92 ± 0.04 | 0.81 ± 0.04 | |
| Height (m) | 260 | 280 | 300 |
| 0.17 ± 0.01 | 0.20 ± 0.01 | 0.21 ± 0.01 | |
| Height (m) | 300 | 320 | 340 |
| 0.59 ± 0.03 | 0.61 ± 0.03 | 0.64 ± 0.03 |
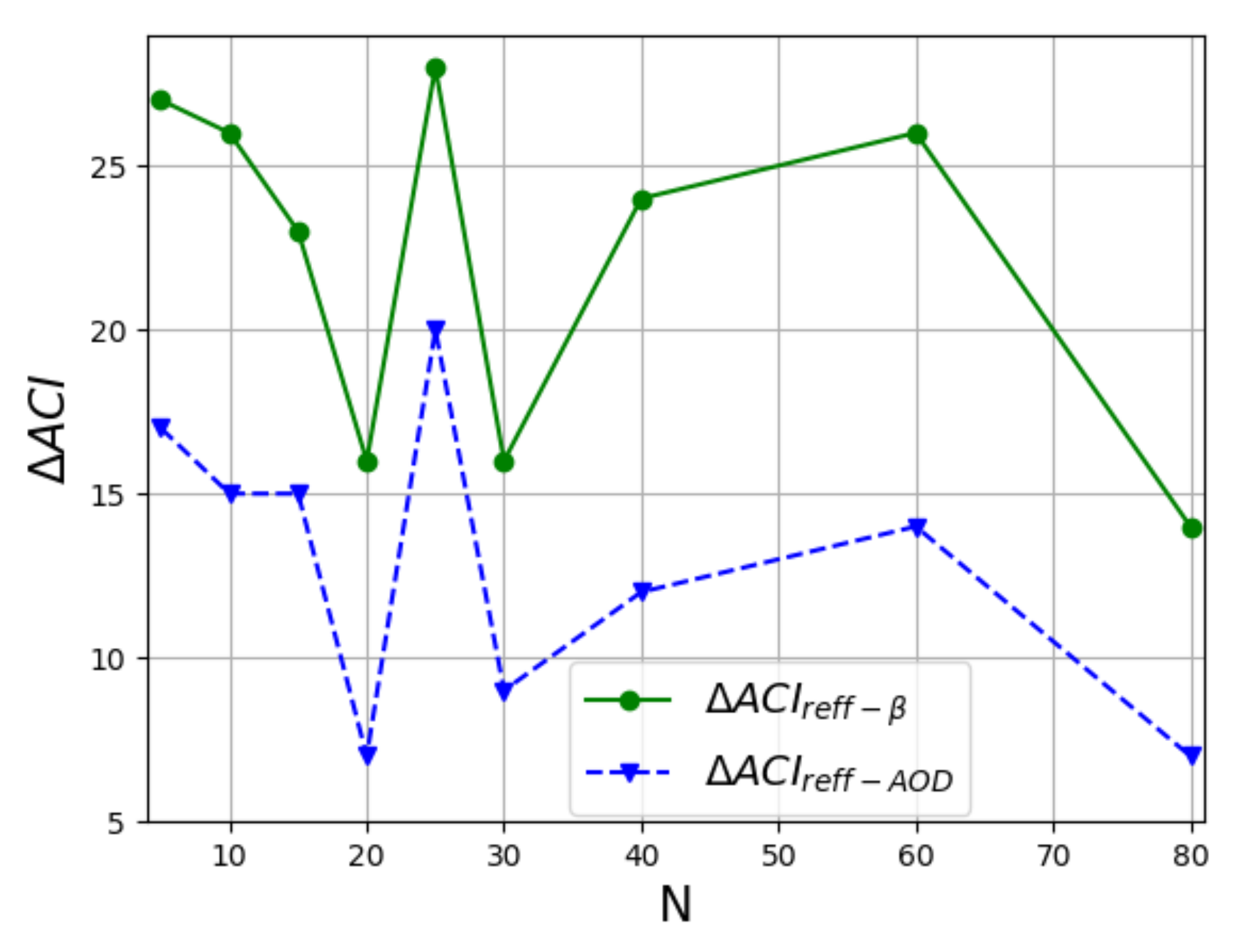
| Uncertainty | |||
|---|---|---|---|
| h | |||
| 10 | |||
| 20 | |||
| 30 | |||
| 40 | |||
| Atmospheric aerosol properties | Measurement location | UGR | SNS |
| Number concentration () | 130 | 27 | |
| Minimun radius () | 0.012 | 0.012 | |
| Modal radius () | 0.045 | 0.062 | |
| Maximun radius () | 0.514 | 0.514 | |
| Hygroscopicity parameter | 0.186 | 0.198 | |
| Density () | 1.76 | 2.08 | |
| Refractive index | 1.51 +0.005i | 1.51 +0.005i | |
| Cloud properties | Supersaturation (%) | 0.2 | 0.25 |
| Activation-related properties | CCN concentration () | 10.06 | 4.13 |
| Activation fraction | 0.077 | 0.152 |
| Case | Aerosol Type | Aerosol Mode |
|---|---|---|
| Ammonium sulfate | Accumulation | |
| Biomass burning | Accumulation | |
| Dust | Accumulation | |
| Dust | Coarse |
|
Atmospheric properties | Specie | Ammonium sulfate [] | Burning Biomass [] | Dust Accumulation [] | Dust Coarse [] | Atmospheric conditions | Temperature (K) | 298 |
|---|---|---|---|---|---|---|---|---|
| Number concentration () | 5.00 | 18.90 | 7.00 | 0.35 | ||||
| Minimun radius () | 0.01 | 0.05 | 0.05 | 0.50 | Pressure () | 101 | ||
| Modal radius () | 0.10 | 0.14 | 0.20 | 1.30 | Updraft () | 2 | ||
| Maximun radius () | 0.5 | 0.5 | 0.5 | 6.0 | Water-vapor ratio () | 8 | ||
| Standard deviation | 1.6 | 1.3 | 1.59 | 2.00 | Instrumental parameters | Lidar wavelength () | 355 | |
| Hygroscopicity parameter | 0.51 | 0.22 | 0.14 | 0.14 | ||||
| Density () | 1.77 | 1.15 | 2.60 | 2.60 | Radar wavelength () | |||
| Refractive index | 1.448 + | 1.520 + | 1.530 + | 1.530 + |
| ACI Index Variability | |||||
|---|---|---|---|---|---|
| ACI Based on | <10% | <20% | <30% | ||
| Parameter fluctuation (%) | Refractive index | 1 | 3 | 5 | |
| AOD | 15 | 24 | 35 | ||
| PSD standard deviation at surface | 4 | 6 | 10 | ||
| AOD | 6 | 10 | 16 | ||
| Dry modal radius at surface | 7 | 13 | 16 | ||
| AOD | 13 | 16 | 18 | ||
| Wet modal radius at CBH | 15 | 17 | 20 | ||
| AOD | |||||
| Dry maximum radius at surface | 46 | 57 | 63 | ||
| AOD | 63 | 65 | 67 | ||
| Hygroscopicity parameter at CBH | 56 | 87 | 94 | ||
| AOD | |||||
| Updraft | 59 | 95 | 119 | ||
| AOD | |||||
| Wet maximum radius at CBH | 74 | 144 | 178 | ||
| AOD | |||||
| Hygroscopicity parameter at surface | 82 | 135 | 216 | ||
| AOD | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fajardo-Zambrano, C.M.; Bravo-Aranda, J.A.; Granados-Muñoz, M.J.; Montilla-Rosero, E.; Casquero-Vera, J.A.; Rejano, F.; Castillo, S.; Alados-Arboledas, L. Lidar and Radar Signal Simulation: Stability Assessment of the Aerosol–Cloud Interaction Index. Remote Sens. 2022, 14, 1333. https://doi.org/10.3390/rs14061333
Fajardo-Zambrano CM, Bravo-Aranda JA, Granados-Muñoz MJ, Montilla-Rosero E, Casquero-Vera JA, Rejano F, Castillo S, Alados-Arboledas L. Lidar and Radar Signal Simulation: Stability Assessment of the Aerosol–Cloud Interaction Index. Remote Sensing. 2022; 14(6):1333. https://doi.org/10.3390/rs14061333
Chicago/Turabian StyleFajardo-Zambrano, Carlos Mario, Juan Antonio Bravo-Aranda, María José Granados-Muñoz, Elena Montilla-Rosero, Juan Andrés Casquero-Vera, Fernando Rejano, Sonia Castillo, and Lucas Alados-Arboledas. 2022. "Lidar and Radar Signal Simulation: Stability Assessment of the Aerosol–Cloud Interaction Index" Remote Sensing 14, no. 6: 1333. https://doi.org/10.3390/rs14061333
APA StyleFajardo-Zambrano, C. M., Bravo-Aranda, J. A., Granados-Muñoz, M. J., Montilla-Rosero, E., Casquero-Vera, J. A., Rejano, F., Castillo, S., & Alados-Arboledas, L. (2022). Lidar and Radar Signal Simulation: Stability Assessment of the Aerosol–Cloud Interaction Index. Remote Sensing, 14(6), 1333. https://doi.org/10.3390/rs14061333












