Accuracy Assessment, Comparative Performance, and Enhancement of Public Domain Digital Elevation Models (ASTER 30 m, SRTM 30 m, CARTOSAT 30 m, SRTM 90 m, MERIT 90 m, and TanDEM-X 90 m) Using DGPS

Abstract

Publicly available Digital Elevation Models (DEM) derived from various space-based platforms (Satellite/Space Shuttle Endeavour) have had a tremendous impact on the quantification of landscape characteristics, and the related processes and products. The accuracy of elevation data from six major public domain satellite-derived Digital Elevation Models (a 30 m grid size—ASTER GDEM version 3 (Ast30), SRTM version 3 (Srt30), CartoDEM version V3R1 (Crt30)—and 90 m grid size—SRTM version 4.1 (Srt90), MERIT (MRT90), and TanDEM-X (TDX90)), as well as the improvement in accuracy achieved by applying a correction (linear fit) using Differential Global Positioning System (DGPS) estimates at Ground Control Points (GCPs) is examined in detail. The study area is a hard rock terrain that overall is flat-like with undulating and uneven surfaces (IIT (ISM) Campus and its environs) where the statistical analysis (corrected and uncorrected DEMs), correlation statistics and statistical tests (for elevation and slope), the impact of resampling methods, and the optimum number of GCPs for reduction of error in order to use it in further applications have been presented in detail. As the application of DGPS data at GCPs helps in the substantial reduction of bias by the removal of systematic error, it is recommended that DEMs may be corrected using DGPS before being used in any scientific studies.

1. Introduction

Accurate and precise estimates of elevation are crucial to various regional and local scale scientific projects [1,2]. As space-based technology progresses, various satellite-based location estimates using remote sensing techniques (optical, microwave and lidar technologies) are delivering continuous maps and data of estimated positions (X, Y, and Z) in the form of digital elevation models (DEMs) [2]. DEMs from space, especially those available freely in the public domain, are a valuable and dependable data source for many scientific endeavors, such as hydrological mapping [3,4,5], extraction of hydrological parameters [6], flood flow mapping [7,8], flood flow modelling, production of orthoimageries [9], topographic characterization [10], ecological modelling [11], and fault kinematics and facet geomorphology [12]. The DEM is critical for tracking the movement and spread of dust plumes [13]. It provides an important data source for determining the geomorphological features and derivation of an alluvial fines map (AFM) for dust source identification [14,15]. The assessments of watershed regions, slopes, discharge, stream power, erosion rate, etc., can be carried out using the publicly available Shuttle Radar Topography Mission (SRTM) DEM [1,16,17].

On the ground, the determination of spatial positioning in three dimensions at any location on the Earth’s surface—that is, latitudes (Y-coordinates), longitudes (X-coordinates), and elevation (Z-coordinates)—is aided by DGPS and MobileGPS. MobileGPS, hereinafter, refers to GPS or aided GPS (AGPS) on mobile or cell phones. DGPS technology, which is often used with a base and rover arrangement, is one of the most exact and precise kinds of equipment for calculating the spatial positioning at any location with up to millimeter (mm) level accuracy, as opposed to centimeter–meter (cm-m) level accuracy in the case of mobileGPS. MobileGPS, on the other hand, is far less expensive, ubiquitous, and simple to use. DGPS remains the favored instrument in many scientific and civil investigations where accuracy and precision of the estimates of positioning, particularly elevation, is critical. For instance, local networks of GPS data with mm level accuracy are useful in studying strain patterns [18]. As a result, a comparison of the performance, accuracy, and usefulness of DGPS and MobileGPS for ground truth (ground control points, GCPs) against satellite-based DEMs is necessary.

The Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model (GDEM), SRTM DEM, Cartosat-1 Digital Elevation Model (CartoDEM), Multi-Error-Removed Improved-Terrain DEM (MERIT DEM), and TanDEM-X 90 m DEM are public domain digital elevation models. Due to their free availability and wide range of applicability, these DEMs are of great concern to many researchers from time to time (

Table 1. Summary of previous studies carried out by researchers worldwide regarding accuracy assessment of elevation obtained from widely used DEMs.

Sl.	Author	Study Area	No. of GCPs. Land Cover Type	DEM Used and Corresponding RMSE/Bias/Other Statistics
1.	[22]	Lower Tapi Basin, India, 3837 km2	GCPs = 117. Topography comprising narrow valley, hilly terrain, gently sloping ground, agricultural fields and coastal regions	RMSE values of DEM elevation for: – SRTM30: 2.88 m – ASTER GDEM2: 5.46 m – CartoDEM.V3.1: 3.52 m – AW3D30 (ALOS30): 2.45 m.
2.	[29]	Nile, delta Region, 23,235 km2	GCPs = 200. Delta region	RMSE values of DEM elevation for: – AW3D30: 2.19 m – ASTER v2: 5.13 m – EARTHEnv-DEM90: 2.20 m – GLOBE: 7.26 m – GMTED2010: 2.32 m – GTOPO30: 7.32 m – SRTM 1: 2.62 m – SRTM 3: 2.35 m
3.	[20]	Najran City, Saudi Arabia, 900 km2	GCPs = 50 (with outlier) 49 for ASTER and 48 for SRTM30 after removing outlier. Mountainous area with high elevation differences	RMSE values with and without outlier: – ASTE GDEM2: 7.45 m (outliers included) – ASTE GDEM2: 5.07 m (no outlier) – SRTM30: 7.92 m (outliers included) – SRTM30: 5.94 m (no outliers)
4.	[31]	MANITB, M.P., India	GCPs = 830. Uneven topography with small hills	RMSE values of DEM elevation without applying any interpolation for: – Cartosat-1 (30 m): 3.49 m – ASTER DEM (30 m): 6.03 m – SRTM (90): 3.72 m After applying interpolation, bilinear method is giving the best result with RMSE for DEM elevation for: – Cartosat-1 DEM: 3.36 m – ASTER: 6.12 m, SRTM: 2.73 m
5.	[47]	Comparison of Samsung smartphones	Samsung Galaxy series Y, S3 Mini, S4, S5, S6 and S7	Two newest generations smartphones, S6 and S7 obtained lower vertical accuracies than their predecessors with RMSE for: – Samsung S6 = 11.11 m and – Samsung S7 = 6.04 m
6.	[23]	Western Shiwalik, Himalaya, India	GCPs = 11. Topography dominated by hills, valleys, steep slopes and rivers	RMSE values of DEM elevation for: – ASTER GDEM version2: 6.08 m – SRTM: 9.2 m – Cartosat-1 DEM: 3.64 m
7.	[26]	Andean Patagonia, Argentina, 540 km2	GCPs = 78 Rugged Topography	RMSE values of DEM elevation for: – ASTER GDEM: 9.4 ± 2.3 m (CI at 95%) – SRTM 90: 8.3 ± 2.9 m (CI at 95%) – CI (confidence interval) at 95% taken from [48]
8.	[28]	Shiwalik Himalaya, India	GCPs = 11. Rugged terrain with steep slopes, ridges, undulations with flat topography in southern part	RMSE values for Cartosat-1 DEM: 3.14–7.24 m, varying with grid spacing from 10–150 m
9.	[19]	Chandra and Bhaga Basin, Himalayan Region, India	GCPs = 2835 (Chandra). GCPs = 2160 (Bhaga). Basin	Bias of elevation data for: – Chandra Basin: 12.7 m – Bhaga Basin: 13 m Standard deviation of elevation for: – Chandra Basin: 10.8 m (before correction) – 6 m (after correction) – Bhaga Basin: 9 m (before correction) – 7.05 m (after correction) Bias correction to CartoDEM elevation data has improved the vertical accuracy. Here ICESat/GLAS elevation data taken as reference data.
10.	[38]	SNAMP and CZO, USA	GCPs = − Coastal Vegetated Mountainous Areas	Correction applied to SRTM DEM RMSE values fof DEM elevation, prior to and after correction, for SRTM DEM are: – RMSE: 7.01 m–10.431 m (uncorrected) – RMSE: 2.889 m–7.822 m (Corrected)
11.	[36]	Himalayan Region, India	GCPs = 6. Rugged and hilly topography	RMSE values for Cartosat-1 DEM: – Planimetric RMSE = 2.5 m – Vertical RMSE = 2.95 m
12.	[24]	Shahjahanpur district, UP, India	GCPs = 20 Plains of Ganga interrupted by valleys and numerous streams	Horizontal accuracy of ASTER GDEM1and SRTM90 DEM with respect to Cartosat-1 is evaluated. RMSE for horizontal accuracy are: – SRTMv4: 2.17 m – ASTER GDEM1: 2.817 m
13.	[49]	Jagathsinghpur, Orissa (flat); Dharmsala, Himachal Pradesh (hilly); Alwar, Rajasthan (mixed)	GCPs = 15 (Jagathsinghpur), 8 (Dharmsala), 59 (ICP over Alwar). Flat, hilly and mixed type	RMSE for CatoDEM30 elevation data at – Jagathsinghpur = 3.4 m (flat) – Dharmsala = 4.72 m (hilly) – Alwar = 4.7 m (mixed topography) RMSE for CatoDEM90: – Jagathsinghpur = 3.44 m (flat) – Dharmsala = 4.79 m (hilly) – Alwar = 5.5 m (mixed topography)
14.	[50]	Thessaloniki, North Greece	ICESat reference Points = 10,792. Varying topography: flat to mountainous.	Standard deviation of absolute elevation error for: – SRTMv1: 6.4 m – SRTMv2: 6.4 m – SRTMv3: 7.3 m – SRTMv4: 6.4 m
15.	[51]	MRB: Muthirapuzha River Basin (271.75 km2). PRB: Pambar River Basin (288.53 km2)	GCPs = 28. Topography is dominated by hills and plateau	RMSE values for various DEMs
						Relief (m/km2)
				DEMs	Area	<200	200–400	>400
				TOPO	MRB	11.07	9.54	8.11
					PRB	6.15	10.34	10.36
				ASTER	MRB	21.83	31.75	42.08
					PRB	9.16	19.26	33.12
				SRTM	MRB	10.46	22.51	29.55
					PRB	10.86	15.88	27.68
				GMTED	MRB	36.54	50.99	86.75
					PRB	33.78	40.49	62.09
16.	[52]	Roja Village, UP, India,4575 km2	GCPs = 20 Upland plains of Ganga valley, predominated by valleys, streams, and water sources	RMSE values for DEM elevation, taking elevation values of CARTOSAT-1 DEM as reference, for: – ASTER GDEM v1: 137.65 m – SRTM90m: 186.65 m
17.	[21]	Peru	GCPs = 139 Flat, Arid Coast, Semi-dry Andes, Amazon rainforest	RMSE values of DEM elevation for: – ASTER GDEM2(30 m): 6.907 m – SRTMv3(30 m): 5.113 m – AW3D30: 6.246 m – TanDEM-X: 1.666 m
18.	[10]	Rio Colorado, Bolivia	GCPs = 1290 Basin type located at ocean-continent convergent margin	RMSE values of DEM elevation for: – ASTER GDEM1: 3.03 m – SRTMv3: 6.02 m – TDX-12m: 0.47 m – ALOS 12.5 m: 4.58 m
19.	[27]	Iraq	GCPs = 12 Mountainous	RMSE values for: – ALOS PALSAR 12.5 m: 7.3 m – SRTM 30 m: 7.6 m – TanDEM-X 90 m: 6.5 m
20.	[25]	Hispaniola, USA, 75,000 km2	GCPs = 2287 Topography dominated by Mountains and valleys, coastal areas	RMSE values of DEM elevation for: – ASTER GDEM2: 8.44 m – SRTMv3: 3.82 – ALOS 30 m: 2.08 – TanDEM-X: 1.74
21.	[30]	Baoji city, China, 2500 km2	GCPs = - Combination of flat, hilly and mountainous areas	RMSE values of DEM elevation for: – ASTER GDEM2: 11.57 m – SRTMv3: 6.90 m – ZY3DEM: 15.34 m – (AW3D30 taken as reference DEM for calculation)

). The bias and error characteristics have been studied around the globe to find the best performing DEMs. Moreover, ways to enhance the accuracy of DEMs, use of an optimum number of GCPs, choice of DEM, and resampling methods require further attention. The bias and errors that may persist in these digital elevation data sets may be due to bad surveying conditions on the ground, sensor instabilities, several processing steps, adopted methodology, and limitations of the techniques [19]. The quantification of errors in DEM is important for projects, and the localized evaluation of DEM’s quality and accuracy is critical to verifying its appropriateness for any specific area.

Vertical Accuracy of DEMs

The vertical accuracy assessment of space-borne elevation data sets has been one of the major concerns for worldwide researchers [20,21,22,23,24,25]. Some of the recent studies show a multilevel assessment of DEM, e.g., geolocation, elevation and morphological, horizontal and vertical accuracy assessment, and optimization accuracies of different digital elevation models [24,26,27,28] for environmental applications to analyze the hazardous impact of subsidence and sea level rise [29], the effect of vertical accuracy of DEM on lineament extraction [30], and comparative analysis of interpolation methods and relative vertical accuracy assessment [31].

Digital elevation data sets were utilized in certain studies [32,33,34] without being corrected for imperfections. These inaccuracies could lead to erroneous topographic parameter estimates. On the other hand, attempts have been made in some studies to increase accuracy by making appropriate corrections [19,35,36,37,38]. A correction based on a linear correlation between GNSS and DEM-derived elevation data for all areas and all DEM has been suggested [21]. Though the SRTM DEM yielded slightly better results than the ASTER GDEM, both DEMs are suitable for the compilation of topographic parameters in glacier inventories [39]. Over the glacier, the ASTER GDEM compared to SRTM also shows large standard deviations [39]. The absolute vertical accuracy of SRTM and ASTER elevation data in Najran City, Saudi Arabia was found to be ±5.94 m and ±5.07 m, respectively [20]. The elevation data from CARTOSAT DEM (or CartoDEM) data show RMSE of 4.38 and 3.69 m, respectively, over the moderately undulating (Dehradun) and hilly (Shimla) areas [40].

The accuracy of a DEM is greatly influenced by DEM resampling techniques such as nearest neighbour, bilinear, and bicubic. Previous findings [41] show that resampling techniques have a significant impact on urban inundation modelling at a local scale, especially when spatial variability is high. On the other hand, they are insignificant and insensitive to the extraction of topographic information, hydrological components, elevation, and slope gradient, but significant to lateral flow [42,43]. The RMSE values of interpolation techniques such as Inverse Distance Weighted (IDW), Kriging, ANUDEM, Nearest Neighbour, and Spline approaches were evaluated with reference to terrain variation. Kriging method provided better estimates of elevation compared to IDW, as it can adapt to variations in the terrain [44,45].

The prior assessment of different resampling techniques is crucial to the utility of the DEM in any field. The selection of an appropriate resampling technique may improve the DEM’s accuracy, and this study is a step in that direction. Several studies have been carried out to investigate the impact of spatial resolution (resampling) on hydrological and inundation modelling [46], but the impact of resampling methods on the vertical accuracy of DEM has received the least attention and testing. A comparison is required to examine the relative efficacy of different resampling algorithms on the vertical accuracy of DEM. It’s worth noting that the performance characteristics and detailed assessment for three newly released DEMs (ASTER GDEM (v3), MERIT, and TanDEM-X) are not well documented in the literature, particularly at the local scale.

The current research represents a step forward in examining the following: (1) comparative performance of ground-based equipment: DGPS and android-based MobileGPS; (2) vertical accuracy assessment of public domain DEMs: ASTER GDEM v3, SRTM v3, SRTM v4.1, CartoDEM v3R1, MERIT, and TanDEM-X DEM over the IIT(ISM) campus and the surrounding area; (3) enhancement of vertical accuracy of DEMs, corrected using linear fit, and removal of systematic error; (4) comparison of corrected and uncorrected DEMs through statistical analysis and tests; (5) comparison of three commonly used interpolation methods; nearest neighbour (nn), bilinear (bl) and bicubic (bc) in DEM resampling; and (6) to find the optimum number of GCPs with minimum error.

2. Study Area, Data and Methodology

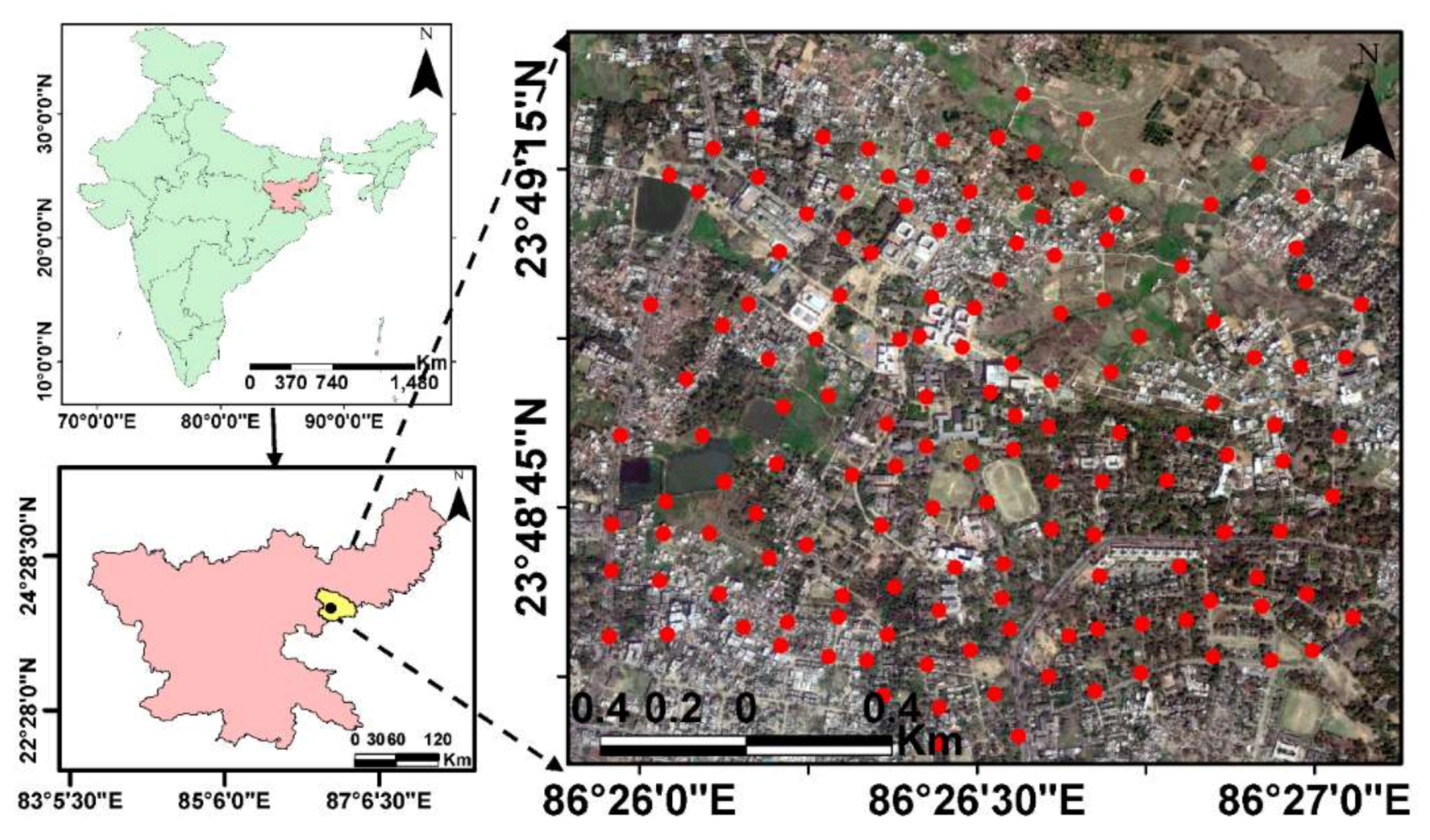
2.1. Study Area

The study area comprises a part of Dhanbad city, the coal capital of India, which is situated in the state of Jharkhand (Figure 1). It mainly includes the campus of the Institute (IIT (ISM) Dhanbad—Indian Institute of Technology (Indian School of Mines) Dhanbad) and its environs. It is geographically situated between 23°48′00″–23°49′30″N, and 86°25′56″–86°27′6″E (

Table 2. Details of space borne elevation (DEM) data sets.

DEM Details	ASTER (30 m)	CARTOSAT-1 (30 m)	SRTM (30 m)	SRTM (90 m)	MERIT DEM (90 m)	TanDEM-X (90 m)
Release Year	2019	2005	2015	2008	2017	2018
Product Format	GEOTIFF	GEOTIFF	GEOTIFF	GEOTIFF	GEOTIFF	GEOTIFF
Co-ordinate System	GCS_WGS_1984	GCS_WGS_1984	GCS_WGS_1984	GCS_WGS_1984	GCS_WGS_1984	GCS_WGS_1984
Sensor	ASTER	Pan (2.5 m)	SIR-C X-SAR	SIR-C X-SAR	SIR-C X-SAR	SAR-X Band
Satellite	Terra	Cartosat-1	Space Shuttle Endeavour	Space Shuttle Endeavour	Space Shuttle Endeavour	TerraSAR-X and TanDEM-X
Resolution	30 m	30 m	30 m	90 m	90 m	90 m
Projection	Geographic (Lat., Long.)	Geographic (Lat., Long.)	Geographic (Lat., Long.)	Geographic (Lat., Long.)	Geographic (Lat., Long.)	Geographic (Lat., Long.)
Datum	WGS_1984 (H) EGM96 (V)	WGS_1984 (H) WGS_1984 (V)	WGS_1984 (H) EGM96 (V)	WGS_1984 (H) EGM96 (V)	WGS_1984 (H) EGM96 (V)	WGS_1984 (H) WGS_1984 (V)
Version	V3	V3 R1	V3	V4.1	V1	V1
Data Sources	https://earthexplorer.usgs.gov/	http://bhuvan.nrsc.gov.in	https://earthexplorer.usgs.gov/	http://srtm.csi.cgiar.org/	http://hydro.iis.u-tokyo.ac.jp/~yamadai/MERIT_DEM/	https://download.geoservice.dlr.de/TDM90/
Last Accessed	16 November 2021	27 January 2019	27 January 2019	27 January 2019	16 November 2021	16 November 2021

). The topography of the research area is a hard rock terrain that overall is flat-like with undulating and uneven surfaces for the most part, with an average elevation of 188.29 m (range 174.05–201.53 m, standard deviation 5.83 m) as obtained from DGPS data (

Table 3. The descriptive statistics and measures of differences between values obtained from the two ground-based devices (DGPS and MobileGPS) based on their positional estimates at the GCPs.

		Elevation (Z)	Easting (E)	Northing (N)
Avg. (in m)	DGPS	244.41	-	-
	MobileGPS	243.09	-	-
Max. (in m)	DGPS	257.63	-	-
	MobileGPS	275.12	-	-
Min. (in m)	DGPS	230.22	-	-
	MobileGPS	221.11	-	-
SD (in m)	DGPS	5.85	-	-
	MobileGPS	9.54	-	-
RSD (in %)	DGPS	2.39	-	-
	MobileGPS	3.92	-	-
SE (in m)	DGPS	0.49	-	-
	MobileGPS	0.79	-	-
RMSE (in m)	MobileGPS–DGPS	8.93	10.10	5.02
RMSE(in %)	MobileGPS–DGPS	3.68	-	-
MBE (in m)	MobileGPS–DGPS	−1.32	0.49	1.43
MBE (in %)	MobileGPS–DGPS	−0.52	-	-
MAE (in m)	MobileGPS -DGPS	6.21	4.59	3.56

).

2.2. Data

2.2.1. Satellite/Space Shuttle Derived Digital Elevation Model (DEM) Data

In the current investigation, six satellite/space shuttle derived elevation data sets were used (Table 2). These most commonly used DEM datasets are ASTER GDEM version 3 (Ast30), SRTM version 3 (Srt30), CartoDEM version v3R1 (Crt30)) with a 30 m spatial resolution, and SRTM version 4.1 (Srt90), MERIT (MRT90) and TanDEM-X DEM (TDX90) with a 90 m spatial resolution. The basic information about these DEMs and sources in the public domain is given in Table 2.

ASTER DEM

The ASTER (Advanced Space borne Thermal Emission and Reflection Radiometer) is an advanced system of multispectral imaging (https://asterweb.jpl.nasa.gov/, last accessed on 16 November 2021). The Ministry of Economy, Trade, and Industry (METI) of Japan and the National Aeronautics and Space Administration (NASA) of the United States jointly released three versions of ASTER GDEM: GDEM 1 in June 2009, the upgraded version GDEM 2 in October 2011, and the latest and most upgraded version GDEM 3 in August 2019 [53]. The ASTER imaging system has three subsystems: VNIR (visible and near infrared), SWIR (shortwave infrared), and TIR (thermal infrared), with only VNIR having bands 3N and 3B (Band 3-Nadir Looking and Band 3-Backward Looking) that provide stereo capability [51] and a base-to-height ratio of 0.6 [23]. The initial version, ASTER GDEM 1, was constructed from a stereo-pair of images assembled by the ASTER sensor on board the Terra satellite and covered Earth’s land surfaces between 83° North and 83° South with a spatial resolution of 30 m, encompassing 99 percent of the planet’s land area [54].

The ASTER GDEM v2 is an upgraded version of the ASTER GDEM, with 260,000 additional stereo-pairs of images provided to improve coverage, thereby yielding higher spatial resolution, improved water masking, and fewer artefacts. The ASTER GDEM 2 uses the same GeoTIFF format, gridding, and tile structure as the ASTER GDEM 1. ASTERGDEM data has a horizontal accuracy of ±15 m, and a better vertical accuracy of ±15–25 m, depending on the region’s environmental situation [51]. On average, the absolute vertical accuracy of the GDEM2 was found to be within 0–20 m [55]. Further, data co-registration between the SRTM DEM and ICESat/GLAS data showed an increase in the accuracy of SRTM3 DEM ([56]). The ASTER GDEM v3 is the latest upgraded version that requires further detailed assessment in terms of accuracy assessment, particularly in localized projects.

SRTM DEM

The Shuttle Radar Topography Mission (SRTM) was a collaborative international mission of the NGA (National Geospatial-Intelligence Agency) and NASA (National Aeronautics and Space Administration) [57]. The details of the Shuttle Radar Topography Mission are documented in [1]. The mission collected data over 11 days, from 11 February to 22 February 2000, using an improved imaging radar system [58,59]. The purpose was to map elevation data on a worldwide scale, encompassing the 60°N to 56°S latitude range [1]. The elevation data for SRTM is acquired from C-SIR (C-Band Space-borne Imaging Radar) and X-SAR (X-Band Synthetic Aperture Radar) sensors at a wavelength of 5.6 cm and a frequency of 5.3 GHz [58,60,61]. The SRTM Version 3 with a 30 m grid size dataset was released in January 2015 by NASA’s Land Processes Distributed Active Archive Center (LP DAAC) to include coverage over Asia and Australia. This version is a void-filled product using ASTER GDEM2, USGS GMTED (Global Multi-resolution Terrain Elevation Data), and NED (National Elevation Dataset) [62].

The SRTM elevation data is available at 30 m grid sizes for North America and 90 m grid sizes for the rest of the world [1,58]. Summarily, the absolute and relative height errors, representing 90% error in meters, were reported to be below 10 m for Australia, Africa, Eurasia, Islands, and North and South America [1], which was well within the design and scope of the mission. Two types of elevation data products are available: non-void-filled and void-filled. At a 90% confidence level, the horizontal and vertical accuracy for the first version are expected to be 20 m and 16 m, respectively [63]. The void-filled version is superior to the non-void-filled version [50].

Cartosat DEM

The CartoDEM is a public domain DEM generated from Cartosat-1 stereo-pairs with a spatial resolution of 30 m. The CartoDEM over the Indian region is distributed by the Indian Space Research Organization (ISRO) and is freely downloadable from the National Remote Sensing Centre (NRSC) Bhuvan website (bhuvan.nrsc.gov.in, accessed on 27 January 2019). Cartosat-1, also known as IRS-P5, is an Indian satellite launched by ISRO on 5 May 2005 [23,64]. It possesses a pair of panchromatic cameras, namely Fore and Aft with forward and rear looking capabilities, tilted at +260 and −50, respectively, that capture along-track stereo images globally at 2.5 m spatial resolution on the horizontal plane and a 27 km ground swath with a 0.63 base-to-height ratio [19,22,65]. The CartoDEM is created by Augmented Stereo Strip Triangulation (ASST), which includes very precise ground control points, interactive cloud masking, and automatic dense conjugate pair generation using aspect-based correlation to determine the best match point [66]). The planimetric and vertical accuracies of the DEM derived from the Cartosat-1 stereo-pairs were validated and found to be 15 and 8 m, respectively [49].

MERIT DEM

The MERIT DEM is a public domain global DEM created by existing DEMs (SRTM3 v2.1 and AW3D-30m v1) with additional datasets from all over the world and released in 2017 [67]. Multiple error components and major vertical elevation errors (absolute bias, speckle noise, stripe noise, and tree height bias) were removed from previous spaceborne DEMs to create the MERIT DEM. It depicts terrain heights with a 3 s resolution (90 m at the equator) and covers land areas between 90N and 60S [68]. It is freely available for download. The global land area mapped with 2 m or more elevation accuracy increased from 39% to 58% after errors were removed from the original DEM, but the local validation of this new DEM in the Fens region of eastern England suggested the requirement for more ground truth data in order to assess or improve the accuracy at a local scale [68].

TanDEM-X DEM

The TanDEM-X DEM, with 0.4 arc second posting (12 m) and covering 150 million square kilometers of all landmasses of Earth from pole to pole [69,70,71,72], was released in September 2016 by DLR (German Aerospace Center) and is the main product of the TanDEM mission. By averaging the elevation values derived from the 0.4 arc second product, two other TanDEM-X products with reduced resolutions of 30 m and 90 m (at equator) were released in 2016 and 2018, respectively [73,74]. The absolute vertical accuracy of 10 m (90% linear error, LE90) and relative height accuracy of 2 m have been reported by mission specification for slopes <20%, or 4 m for slopes >40% [75]. The vertical accuracy of the 12 m TanDEM-X DEM product has been assessed using ICESat points [70], GPS ground truth values, and LiDAR observed values [76]—or a height error map (HEM) [77] for reference. However, to date, very few studies [78] have been conducted to assess the vertical accuracy of the TanDEM-X 90 m DEM and, particularly, its comparison with other freely available global DEMs [74,79,80].

2.2.2. Ground Observation-Based Data

A ground survey has been conducted over the IIT(ISM) campus and surrounding area using ground-based equipment: DGPS and android-based mobile GPS (MobileGPS). The DGPS make was a Leica CS14/GS15 DGPS system. For the DGPS survey, one unit was employed as a fixed station on a tripod (base mode) and the other as a moving unit mounted on a pole (rover mode) in DGPS, and they were connected by a radio link for real-time correction. The measurements using the rover unit were made in static mode with a radio link to the base unit. With UTM projection and WGS1984 datum, the rover unit of DGPS was utilized to accurately measure the three-dimensional coordinates at 145 locations (GCPs). At the same time and location, the Android phone’s GPS (MobileGPS) was utilised to record observations for later comparison. The model of the Android phone used in this study was the “Samsung Galaxy on 7” with a SiRFstar III GPS chip.

DGPS and Mobile GPS measurements and relative accuracies:

A DGPS system employs a technique called relative positioning. The DGPS system uses two or more GPS receivers to track the same (at least four or more) satellites at the same time to correct for errors, thereby improving the positioning [81]. A base receiver that remains stationary over a known place (base station) and one rover receiver (for campaign stations) were used in the current study. The rover receiver moves between the unknown points (campaign stations) for at least one minute at each location. This strategy is appropriate since the survey included a high number of unknown points in close proximity (i.e., within 1–2 km) of a known point (base station). The receiver stations can correct their pseudo-ranges by the same amount as the difference between the detected satellite pseudo-ranges and the actual (internally computed) pseudo-ranges in this configuration. Locally, ground-based transmitters typically send the digital correction signal over short distances of 1–3 km (from base station to rover). It is critical that at least four satellites are monitored. Stop-and-go surveying is expected to provide superior positional accuracy (centimeter-level accuracy) since inaccuracies are averaged out when the receiver stops at unknown locations [81].

Mobile or cell phones, thanks to advancements in mobile phone technology, are now ubiquitous and versatile devices that, because they are equipped with GNSS (global navigation satellite systems) receivers, may serve as navigators and provide reliable position estimates. Recently, studies have been carried out towards the comparative performance of older and newer versions, with indoor and outdoor accuracy variations in urban and rural environments [47,82,83]. Research shows that the Android phones without the ability to use GLONASS signals have relatively lower accuracy (27.7 m) than the Android phones with the ability to use GLONASS signals (6.1 m) [83], implying that better positional accuracy was achieved in the latest smartphones with advanced GPS technology. On the other hand, one of the studies conducted for the respective performances of six Samsung Galaxy series smartphones—Galaxy Y, S3 Mini, S4, S5, S6, and S7—does not substantiate the incremental improvement in accuracy with the launch of newer models [47]. As a result of technological developments, MobileGPS may offer greater location accuracy (especially elevation), which warrants more investigation. Despite years of innovation and expansion in GPS constellation operations, achieving high positioning accuracy in comparison to the competition (DGPS) remains a significant challenge for smartphone manufacturers (static and kinematic modes). Given that the technical and performance characteristics of inbuilt GPS/AGPS for Android phones are not readily available, the results of a comparative evaluation of DGPS and MobileGPS are of major importance to the cell phone users’ community.

2.3. Methodology

The methodology, techniques, and processing steps in the comparative analysis employed in this study are summarized in the flowchart (Figure 2). The study was performed using six sets of space-based elevation data sets: ASTER GDEM version 3, SRTM version 3, and Cartosat-1 version 3—each with 30 m spatial resolution—as well as SRTM version 4.1, MERIT, and TanDEM-X global DEM—each with 90 m spatial resolution. These space-borne elevation data sets were downloaded from different data sources (Table 2). The ground observation data at 145 ground control points (GCPs) were acquired by an Android phone (Samsung Galaxy on 7) and a Leica CS14/GS15 DGPS system in static mode and is referred to as MobileGPS and DGPS, respectively.

For comparative analysis, it is essential to bring all datasets (DEMs, DGPS, and MobileGPS) to the same projection and datum (EPSG 4326 with WGS84 ellipsoid, and vertical datum (height) adjusted as EGM96 for comparison of elevation). Therefore, the GCPs were imported as point vectors and reprojected using EPSG code 4326 in the ArcGIS environment to unify with the coordinate system of the DEMs utilized in this study. Further, it is noteworthy here that all DEMs had the same vertical datum (EGM96), except CartoDEM and TanDEM-X (Table 2). To achieve this, the vertical datum of CartoDEM and TanDEM-X were transformed to EGM96 using the GDAL utilities (version 2.4) via a command line interface [84,85]. In the station–rover configuration of DGPS used in this study (as described in Section 2.2.2), the original measurement of elevation was with respect to the WGS84 ellipsoid [86]. Therefore, the DGPS and MobileGPS elevation estimates (height) were transformed to EGM96 using the commonly used “Geoid Height Calculator” tool of UNAVCO [87].

After transforming the vertical datum to EGM96 for comparison, the elevation estimates at GCPs for all six sets of DEMs were sampled by employing three resampling methods one by one: nearest neighbour (nn), bilinear (bl), and bicubic (bc) in the QGIS environment. In order to find the degree of correlation, the linear-fit regression analysis was performed over all sets of the extracted elevation estimates using Minitab software and Microsoft Excel. Based on the linear-fit, a correction was applied to the original/extracted data sets. For all uncorrected and corrected data sets, statistical calculations and analysis were performed by assuming DGPS-based elevation data as reference/true values. The conclusions were reached based on the findings of the statistical measures and their graphical representation. The abbreviations used in this study are summarized in Table S1.

2.3.1. Statistics

The descriptive statistics of individual ground-based survey datasets (DGPS, MobileGPS), comparison of DEMs before and after the correction, and their comparison with DGPS values (before and after correction of DEMs) have been carried out using the following statistical measures (

Table 4. The descriptive statistics and measures of differences between values obtained from the space-based DEMs (ASTER, CARTOSAT, SRTM, MERIT, and TanDEM-X) and one of the ground-based devices (DGPS) based on their positional estimates of “elevation (Z)” at the GCPs locations. The “u” refers to the use of “uncorrected DEM elevation data”. The “c” refers to the use of “corrected DEM elevation data” based on the DGPS data and the model (Table 5) applied for correction of DEMs in this study. Further, the DEM resampling over the GCPs was carried out using the three interpolation methods (nearest neighbour (nn), bilinear (bl), and bicubic (bc)) for comparison.

		Mean (Z) (in m)		SD (in m)		SE (in m)		RMSE (in m)		RMSE%		MBE (in m)		MBE%		MAE (in m)		RSD %
		u	c	u	c	u	c	u	c	u	c	u	c	u	c	u	c	u	c
Ast30	nn	250.37	244.46	8.41	7.04	0.70	0.58	7.65	3.91	3.12	1.60	5.96	0.05	2.43	0.02	6.35	3.11	3.37	2.89
	bl	250.29	244.51	8.25	6.88	0.68	0.57	7.39	3.61	3.01	1.48	5.89	0.10	2.40	0.04	6.18	2.86	3.30	2.82
	bc	250.28	244.42	8.32	6.95	0.69	0.58	7.47	3.75	3.04	1.53	5.87	0.01	2.39	0.01	6.21	2.97	3.33	2.85
Crt30	nn	249.78	244.40	6.20	6.60	0.51	0.55	6.10	3.04	2.51	1.26	5.37	0.00	2.20	0.00	5.37	2.22	2.49	2.71
	bl	249.69	244.40	6.04	6.39	0.50	0.53	5.83	2.58	2.40	1.07	5.29	−0.01	2.17	0.00	5.29	1.97	2.43	2.62
	bc	249.65	244.42	6.10	6.46	0.51	0.54	5.85	2.72	2.41	1.13	5.25	0.01	2.15	0.01	5.25	2.06	2.45	2.65
Srt30	nn	249.21	244.43	6.49	6.23	0.54	0.52	5.31	2.14	2.17	0.88	4.81	0.02	1.97	0.01	4.84	1.71	2.61	2.56
	bl	249.23	244.41	6.39	6.20	0.53	0.51	5.27	2.04	2.16	0.84	4.83	0.01	1.97	0.00	4.85	1.64	2.57	2.54
	bc	249.24	244.45	6.43	6.18	0.53	0.51	5.29	2.07	2.17	0.86	4.83	0.05	1.98	0.02	4.86	1.65	2.59	2.53
Srt90	nn	249.23	244.34	6.40	6.24	0.53	0.52	5.31	2.16	2.17	0.89	4.82	−0.06	1.97	−0.03	4.84	1.79	2.58	2.56
	bl	249.23	244.51	6.19	6.16	0.51	0.51	5.19	1.91	2.13	0.79	4.82	0.10	1.97	0.04	4.82	1.59	2.49	2.53
	bc	249.27	244.37	6.31	6.16	0.52	0.51	5.26	1.94	2.15	0.80	4.87	−0.04	1.99	−0.02	4.87	1.62	2.54	2.53
MRT90	nn	248.40	244.40	6.19	6.24	0.51	0.52	4.54	2.18	1.86	0.90	3.99	−0.01	1.63	0.00	4.03	1.81	2.50	2.56
	bl	248.40	244.40	6.01	6.17	0.50	0.51	4.43	1.97	1.82	0.82	3.99	0.00	1.64	0.00	3.99	1.67	2.43	2.54
	bc	248.44	244.40	6.12	6.18	0.51	0.51	4.49	1.99	1.84	0.82	4.03	0.00	1.65	0.00	4.04	1.68	2.47	2.54
TDX90	nn	248.03	244.39	6.58	6.28	0.55	0.52	4.35	2.28	1.78	0.94	3.62	−0.01	1.48	−0.01	3.71	1.85	2.66	2.58
	bl	248.06	244.43	6.34	6.17	0.53	0.51	4.17	1.95	1.71	0.81	3.65	0.02	1.49	0.01	3.66	1.64	2.56	2.53
	bc	248.09	244.41	6.49	6.19	0.54	0.51	4.27	2.03	1.75	0.84	3.69	0.00	1.51	0.00	3.70	1.70	2.62	2.54
Avg. of nn, bl & bc	Ast30	250.31	244.46	8.33	6.96	0.69	0.58	7.51	3.75	3.06	1.54	5.91	0.05	2.41	0.02	6.25	2.98	3.33	2.85
	Crt30	249.71	244.41	6.11	6.48	0.51	0.54	5.93	2.78	2.44	1.15	5.30	0.00	2.17	0.00	5.30	2.08	2.46	2.66
	Srt30	249.23	244.43	6.44	6.20	0.53	0.51	5.29	2.08	2.17	0.86	4.82	0.02	1.97	0.01	4.85	1.67	2.59	2.54
	Srt90	249.24	244.41	6.30	6.19	0.52	0.51	5.25	2.01	2.15	0.83	4.84	0.00	1.98	0.00	4.84	1.67	2.54	2.54
	MRT90	248.41	244.40	6.11	6.20	0.51	0.51	4.49	2.05	1.84	0.85	4.01	0.00	1.64	0.00	4.02	1.72	2.47	2.55
	TDX90	248.06	244.41	6.47	6.21	0.54	0.52	4.26	2.09	1.74	0.86	3.65	0.00	1.49	0.00	3.69	1.73	2.62	2.55

). A statistical analysis has been carried out assuming that the DGPS readings at given locations (N = 145) are considered as estimates for GCPs. Thus, the DGPS values are considered the true estimates of elevation. The measures of central tendency (mean), measures of dispersion (SD, RSD), measures of error (SE), commonly used measures of systematic error (MBE), and measures of magnitude of error (MAE, RMSE) have been calculated using the standard formulae given below [88,89,90].

Mean ($\overline{\mathit{x}}$): The average of the samples is defined as Mean ($\overline{\mathit{x}}$). The formula is:

$$\overline{\mathit{x}}=\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{x}}_i$$

(1)

Standard Deviation (SD): One of the measures of dispersion that is SD is defined as:

$$\mathbf{SD}=\sqrt{\frac{\sum {\left({\mathit{x}}_{\mathit{i}}-\overline{\mathit{x}}\right)}^2}{\mathit{n}-1}}$$

(2)

Standard Error (SE): One of the measures of error that is SE is calculated using formula:

$$\mathrm{SE}=\frac{\mathrm{SD}}{\sqrt{\mathit{n}}}$$

(3)

Relative Standard Deviation (RSD): A special form of the standard deviation is calculated using formula:

$$\mathrm{RSD}=\frac{\mathrm{SD}}{\overline{\mathit{x}}}\times 100$$

(4)

Mean Bias Error (MBE): Bias $(x_i-x_t)$ is defined as the estimate of the systematic error. The positive values indicate overestimation and negative values indicate underestimation with respect to true values (${\mathit{x}}_{\mathit{t}}$). The MBE (in m) was calculated using formula:

$$\mathrm{MBE} (\mathrm{in} m)=\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}\left({\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{t}}\right)$$

(5)

The MBE (in %) for the purpose of direct comparison between the corrected and uncorrected DEM was calculated using formula:

$$\mathrm{MBE} (\mathrm{in} \%)=\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}\frac{\left({\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{t}}\right)}{{\mathit{x}}_{\mathit{t}}}\times 100$$

(6)

Mean Absolute Error (MAE): MAE is the average of the absolute values of the errors $\left(x_i-x_t\right)$, thereby indicating the average magnitude of the errors. MAE was calculated using formula:

$$\mathrm{MAE} (\mathrm{in} m)=\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}\left|\left({\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{t}}\right)\right|$$

(7)

Root-Mean-Square Error (RMSE): RMSE is a commonly used measure of the difference between values predicted by a model or an estimator (DEMs) and the values observed (DGPS) over the GCPs. RMSE is an indicator of the magnitude of the error as the difference between the model (DEMs) and corresponding observed values (DGPS) is squared and then averaged over the samples to determine the size of the error. Given that the errors are squared before being averaged, the RMSE gives higher weight to large errors as compared to the MBE. As a result, the RMSE is most beneficial when large errors are involved. The RMSE is always positive and a value of 0 would indicate that the two data sets (DEM and DGPS) are perfectly matched. RMSE (in m) is calculated using formula:

$$\mathrm{RMSE} (\mathrm{in} m)=\sqrt{\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\left({\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{t}}\right)}^2}$$

(8)

The RMSE (in %) for the purpose of direct comparison between the corrected and uncorrected DEM was calculated using formula:

$$\mathrm{RMSE} (\mathrm{in} \%)=\sqrt{\frac{1}{\mathit{n}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\left(\frac{{\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{t}}}{{\mathit{x}}_{\mathit{t}}}\right)}^2}\times 100$$

(9)

Here, the mean elevation (Z) is represented by $\overline{\mathit{x}}$ and $x_i$ is the elevation value extracted at the specific (ith) GCP. The DEM values extracted over the GCPs using three resampling methods (nn, bl, bc $x_i{x}_t$ represents the reference elevation value observed by DGPS at the same locations. The n is the total number of GCPs where DGPS (and MobileGPS) observations have been taken during the field campaign using a dual-frequency dual DGPS setup (as base and rover).

2.3.2. Statistical Analysis, Correlation Statistics, Tests and Optimum Number of GCPs

Statistical analysis, correlation statistics, and performance analysis (uncorrected vs. corrected) were performed using data from suitable pairs of space-based DEMS (ASTER, SRTM, and CARTOSAT) and DGPS over GCPs. Further, the DEM resampling over the GCPs was carried out using the three most commonly used interpolation methods (nearest neighbour (nn), bilinear (bl), and bicubic (bc)) for comparison.

The elevation values from DGPS and DEMs (corrected/uncorrected) were paired for the statistical tests. Further, the elevation and slope values were obtained from the corrected and uncorrected DEMs (ASTER, SRTM, and CARTOSAT). A paired t-test and an F-test were carried out for the slope values, which were similar to the elevation values, to highlight the significant differences before and after the correction of DEMs.

The study also explored the number of GCPs required to achieve a desired level of accuracy through the sensitivity of statistical measures (RMSE, MBE, SE, RSD) with the increasing number of samples. The results and discussion section summarize the statistical and correlative analysis, statistical tests, and optimum number of GCPs.

2.3.3. Correction of DEMs Using DGPS Data

The DGPS values obtained at GCPs were used as reference data for statistical calculations. The GCPs were imported and reprojected using EPSG code 4326 (vertical datum as EGM96, as described in the methodology section). The elevation values were extracted at all GCPs, opting for three resampling methods one by one for each DEM. The interpolation techniques chosen for DEM raster resampling were nn, bl, and bc. A linear regression was performed for each set of extracted elevation data against the reference dataset (DGPS values). The mathematical relationship, based on a linear regression, was established between each pair of space-borne elevation data and DGPS values at GCPs (

Table 5. Linear fit based equations, used for correction, exhibiting relation between space-borne elevations (resampled using different interpolation methods) with DGPS. The nn, bl, and bc refer to the interpolation methods (nearest neighbour, bilinear, and bicubic, respectively) used in the extraction of elevation values from space-borne DEMs over the GCPs. (Ast30 = ASTER GDEM V3, Crt30 = CartoDEM v3.R1, Srt30 = SRTM.v3, Srt90 = SRTM.v4.1, MRT90 = MERIT DEM, TDX90 = TanDEM-X 90 m).

Aster30
Ast30.nn.overDGPS = −41.76 + (1.195 × DGPS)
Ast30.bl.overDGPS = −42.87 + (1.199 × DGPS)
Ast30.bc.overDGPS = −42.05 + (1.196 × DGPS)
CRT30
Crt30.nn.overDGPS = 20.21 + (0.9393 × DGPS)
Crt30.bl.overDGPS = 18.81 + (0.9447 × DGPS)
Crt30.bc.overDGPS = 18.85 + (0.9443 × DGPS)
SRTM30
Srt30.nn.overDGPS = −5.482 + (1.042 × DGPS)
Srt30.bl.overDGPS = −2.999 + (1.032 × DGPS)
Srt30.bc.overDGPS = −3.4949 + (1.036 × DGPS)
SRTM90
Srt90.nn.overDGPS = −1.469 + (1.026 × DGPS)
Srt90.bl.overDGPS = 3.495 + (1.005 × DGPS)
Srt90.bc.overDGPS = −0.96 + (1.024 × DGPS)
MRT90
MRT90.nn.overDGPS = 6.296 + (0.9906 × DGPS)
MRT90.bl.overDGPS = 10.35 + (0.974 × DGPS)
MRT90.bc.overDGPS = 6.285 + (0.9908 × DGPS)
TDX90
TDX90.nn.overDGPS = −8.096 + (1.048 × DGPS)
TDX90.bl.overDGPS = −3.212 + (1.028 × DGPS)
TDX90.bc.overDGPS = −8.044 + (1.048 × DGPS)

).

Thereafter, the linear-regression-based correction was applied to each extracted elevation dataset (DEMs) using the mathematical equation below:

Corrected value = (uncorrected value − Intercept)/slope

(10)

After applying correction, corrected elevation data were obtained for each set of corresponding uncorrected elevation data. Correlation statistics such as co-efficient of determination (r2), standard error of elevation estimate (se(y)), slope (m), standard error of slope (se(m)), intercept (C), and standard error of intercept (se (C)) were calculated for all uncorrected and corrected elevation data sets using the LINEST function in Microsoft Excel. The summary of percent changes observed in the statistical values for various space-based DEMs (ASTER, SRTM, CARTOSAT) after necessary correction using the DGPS elevation data at the GCPs locations is shown in

Table 6. The summary of percent changes observed in the statistical values for various space-based DEMs (ASTER, CARTOSAT, SRTM, MERIT, and TanDEM-X) after necessary correction using DGPS elevation data at the GCPs locations. The percent change was calculated using “u” and “c” values given in the previous table (Table 4). The average values (average of nearest neighbour (nn), bilinear (bl), and bicubic (bc)) were used for the calculation of the percent change (% change).

	Ast30	Crt30	Srt30	Srt90	MRT90	TDX90
	% Change [(c − u)/u] × 100	% Change [(c − u)/u] × 100	% Change [(c − u)/u] × 100	% Change [(c − u)/u] × 100	% Change [(c − u)/u] × 100	% Change [(c − u)/u] × 100
mean (Z)	−2.34%	−2.12%	−1.92%	−1.94%	−1.61%	−1.47%
SD	−16.43%	6.07%	−3.72%	−1.80%	1.51%	−3.97%
SE	−16.43%	6.07%	−3.72%	−1.80%	1.51%	−3.97%
RMSE	−50.01%	−53.07%	−60.62%	−61.82%	−54.37%	−51.02%
MBE	−99.07%	−99.98%	−99.48%	−99.98%	−100.12%	−99.92%
MAE	−52.30%	−60.72%	−65.64%	−65.58%	−57.18%	−53.12%

. The bias (DEM-DGPS) from using uncorrected and corrected datasets was obtained (

Table 7. Bias (DEM—DGPS) for space-based elevation data (for both uncorrected (u) and corrected (c) elevation) sampled over GCPs. The ground-based DGPS data were used for the calculation of bias. The elevation values were derived from DEMs using the three interpolation methods (DEM resampling), that is, nearest neighbour (nn), bilinear (bl), and bicubic (bc).

		Bias (DEM-DGPS) for Uncorrected “u” Data			Bias (DEM-DGPS) for Corrected “c” Data			Avg. (of nn,bl,bc) “u” Data	Avg. (of nn,bl,bc) “c” Data
		nn	bl	bc	nn	bl	bc
Ast30	Avg.	5.96	5.89	5.87	0.05	0.10	0.01	5.91	0.05
	Min.	−5.98	−5.09	−5.93	−10.36	−9.49	−10.27	−5.67	−10.04
	Max.	17.45	16.68	17.50	10.76	9.21	9.56	17.21	9.84
Crt30	Avg.	5.37	5.29	5.25	0.00	−0.01	0.01	5.30	0.00
	Min.	−0.12	0.81	0.76	−5.80	−4.71	−4.70	0.48	−5.07
	Max.	20.15	16.13	17.20	15.44	11.21	12.40	17.83	13.02
Srt30	Avg.	4.81	4.83	4.83	0.02	0.01	0.05	4.82	0.02
	Min.	−1.12	−0.86	−1.05	−5.49	−5.24	−5.25	−1.01	−5.33
	Max.	11.45	10.30	10.41	6.59	5.21	5.55	10.72	5.79
Srt90	Avg.	4.82	4.82	4.87	−0.06	0.10	−0.04	4.84	0.00
	Min.	−0.91	0.65	0.15	−5.43	−4.04	−4.45	−0.04	−4.64
	Max.	9.58	8.76	9.43	4.73	4.04	4.35	9.26	4.37
MRT90	Avg.	3.99	3.99	4.03	−0.01	0.00	0.00	4.01	0.00
	Min.	−1.19	−0.03	−0.55	−5.32	−4.36	−4.70	−0.59	−4.79
	Max.	9.14	8.28	8.25	5.14	4.30	4.22	8.56	4.55
TDX90	Avg.	3.62	3.65	3.69	−0.01	0.02	0.00	3.65	0.00
	Min.	−2.93	−0.20	−0.57	−6.04	−3.75	−4.10	−1.24	−4.63
	Max.	10.07	9.00	9.03	6.41	5.39	5.37	9.37	5.72

) for further analysis.

3. Results and Discussion

3.1. Descriptive Statistics and Comparison of Ground-Based Equipment (DGPS and MobileGPS)

• The boxplots exhibit the changes observed in the elevation range and bias before and after correction of DEMs using DGPS values (Figure 3).
• The descriptive statistics of DGPS and MobileGPS (Table 3) show that MobileGPS has a higher SD, RSD (%), and SE as compared to DGPS for the elevation (Z) measured at GCPs. The MBE (in m) shows that the mean bias error shown by MobileGPS with respect to DGPS is in the range of meters. For instance, the underestimation of elevation by MobileGPS is −1.32 m compared to DGPS.
• The correlation statistics show poor correlation between elevation estimates obtained from DGPS and MobileGPS (r² = 17.45%) (Table S2).
• The differences in values of positional attributes (ΔX, ΔY, ΔZ, shown in the lower panel) observed at GCPs by DGPS and MobileGPS are shown in Figure 3.
• The mean bias error (MBE) for the positioning attributes (MobileGPS–DGPS) observed at GCPs was found to be relatively poor (0.49 m, 1.43 m, and −1.32 m for easting (E), northing (N), and elevation (Z), respectively) (Table 3).
• The root mean square error (RMSE) for the positioning attributes (MobileGPS–DGPS) observed at GCPs was found to be relatively poor (10.10 m, 5.02 m, and 8.93 m for easting (E), northing (N), and elevation (Z), respectively) (Table 3).
• The mean absolute error (MAE) for the positioning attributes (MobileGPS–DGPS) observed at GCPs was found to be relatively poor (4.59 m (ΔX), 3.56 m (ΔY), and 6.21 m (ΔZ) for easting (E), northing (N), and elevation (Z), respectively) (Table 3).
• These observations (based on Table 3 and Table 4) suggest that MobileGPS equipment can be used as a relatively cheaper option for positioning purposes if the desired RMSE is within the range of approximately 5 m (for Northing), 10 m (for Easting), and 9 m (for Elevation).
• Therefore, DGPS estimates at GCPs have been used as a reference dataset for further comparison with space-based DEMs as MobileGPS gives relatively poor estimates of elevation, as mentioned above.

3.2. Comparison of DEMs with Respect to DGPS Estimates

The descriptive statistics and commonly used statistical measures of differences between values obtained from the space-based DEMs (ASTER, SRTM, CARTOSAT) and one of the ground-based devices (DGPS), based on their positional estimates of “elevation (Z)” at the GCPs locations, are shown in Figure 4 and Table 4. The important findings are:

3.2.1. Mean Elevation (Mean (Z))

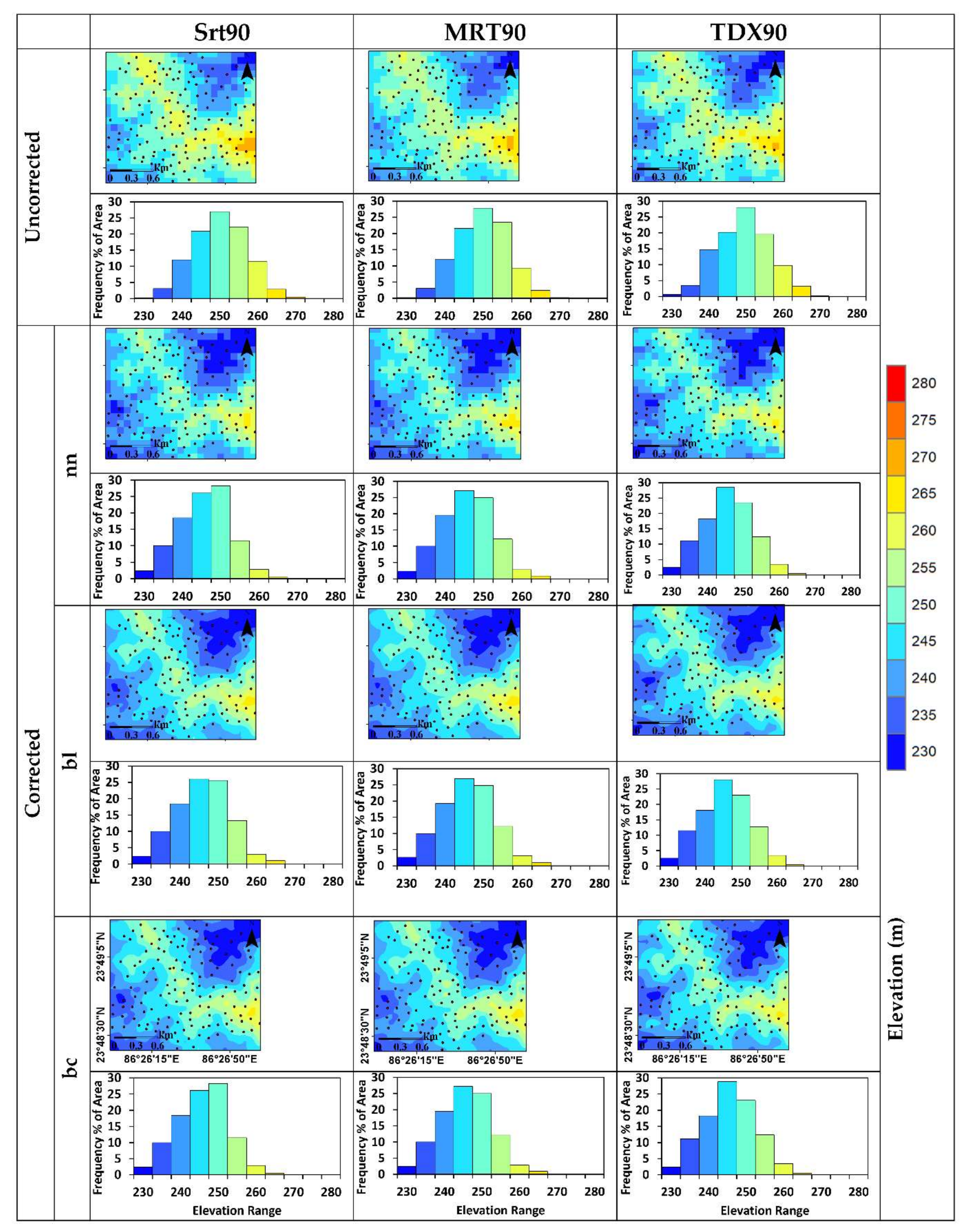
• The average elevation was found to be varying between 248.03–250.37 m in the uncorrected (original) elevation datasets.
• After applying correction using the DGPS values as described in the methodology section, the average elevation of all the datasets was found to be consistent (ranging between 244.34–244.51 m) and is also comparable to the reference DGPS value of 244.41 m (Figure 4, Table 4).
• The percent change in the mean elevation is found to be approximately −1.47 to −2.34% after correction for space-based DEMs (Table 6). The measures of error (RMSE, MBE, and MAE) show a substantial reduction after applying correction (Table 6).
• After correction, all DEMs (ASTER, CARTOSAT, SRTM, MERIT, and TanDEM-X) show consistency in the elevation values, with only negligible differences due to the interpolation methods (nn, bl, and bc).
• As the elevation values obtained from the corrected DEMs are found to be consistent with respect to the reference dataset (DGPS), it is recommended that DEMs need to be corrected using DGPS estimates over GCPs before being used in any scientific studies.

Statistical tests: Uncorrected Vs Corrected DEMs

• The pairs of elevation values from the corrected and uncorrected DEMs were also tested for any significant difference using a paired t-test at 99% CL & α = 0.01 (Table S3). The elevation estimates from DEMs, before and after correction (uncorrected vs. corrected), were found to be significantly different for all cases (nn, bl, and bc).
• It is notable that the two-tail F-test for finding the differences in the variances of elevation values (at 99% CL & α = 0.01) using uncorrected (u) and corrected (c) DEM rasters were found to be insignificant (Table S4). This implies that the variances of these two datasets (uncorrected and corrected DEMs) are similar.
• These statistical tests emphasize the usefulness of the correction of DEMs using DGPS values.

Statistical tests: DGPS vs. corrected/uncorrected DEMs

• The two-tail paired t-test for the hypothesized mean difference of the elevation (Z) values (at 99% CL & α = 0.01) was carried out taking pairs of elevation values observed by DGPS and sampled over (corrected/uncorrected) DEM rasters to test whether the difference in the mean of elevation before and after the correction was significant or not with respect to DGPS (

  Table 8. Results of two-tail paired t-test for mean of elevation (Z) values (at 99% CL & α = 0.01) carried out taking pairs of elevation values observed by “DGPS” and sampled over “uncorrected (u)” DEM rasters, where values were extracted by three interpolation methods: nearest neighbour (nn), bilinear (bl), and bicubic (bc) at GCPs.

  DEM (u) Vs DGPS	Pair Name (Elevation)	$\overline{\mathbf{X}}$	S2	N	df	t Stat	p-Value	t Critical	H1: μd ≠ 0
  Ast30	u.Ast30.nn	250.37	70.80	145	144	14.89	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Ast30.bl	250.29	68.02	145	144	15.78	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Ast30.bc	250.28	69.16	145	144	15.23	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  Crt30	u.Crt30.nn	249.78	38.41	145	144	22.38	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Crt30.bl	249.69	36.49	145	144	25.84	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Crt30.bc	249.65	37.16	145	144	24.30	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  Srt30	u.Srt30.nn	249.21	42.16	145	144	25.71	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Srt30.bl	249.23	40.88	145	144	27.46	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Srt30.bc	249.24	41.40	145	144	26.72	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  Srt90	u.Srt90.nn	249.23	40.94	145	144	26.03	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Srt90.bl	249.23	38.28	145	144	30.17	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.Srt90.bc	249.27	39.84	145	144	29.28	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  MRT90	u.MRT90.nn	248.40	38.26	145	144	22.16	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.MRT90.bl	248.40	36.17	145	144	24.85	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.MRT90.bc	248.44	37.48	145	144	24.56	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  TDX90	u.TDX90.nn	248.03	43.33	145	144	18.04	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.TDX90.bl	248.06	40.21	145	144	21.78	<0.001	2.61	T
  	DGPS	244.41	34.21	145
  	u.TDX90.bc	248.09	42.12	145	144	20.65	<0.001	2.61	T
  	DGPS	244.41	34.21	145

  Null Hypothesis: H₀: μ_d = 0; Alternative Hypothesis: H₁: μ_d ≠ 0. Where, μ_d = hypothesized mean difference, Ast30 = ASTER GDEM V3, Crt30 = CartoDEM v3.R1, Srt30 = SRTM.v3, Srt90 = SRTM.v4.1, MRT90 = MERIT DEM, TDX90 = TanDEM-X 90 m, $\overline{\mathrm{X}}$ = mean, S² = variance, N = No. of observations, df = degree of freedom, t Stat = t-statistic, t Critical = critical value of two-tail paired t-Test, p-value = probability distribution for two-tail paired t-Test, CL = Confidence Level, α = level of significance, T = True, F = False.

  and

  Table 9. Results of two-tail paired t-test for mean of elevation (Z) (at 99% CL & α = 0.01) carried out taking pairs of elevation values observed by “DGPS” and sampled over “corrected (c)” DEM rasters, where values were extracted by three interpolation methods: nearest neighbour (nn), bilinear (bl), and bicubic (bc) at GCPs.

  DEM (c) Vs DGPS	Pair Name (Elevation)	$\overline{\mathbf{X}}$	S2	N	df	t Stat	p-Value	t Critical	H1: μd ≠ 0
  Ast30	c.Ast30.nn	244.46	49.58	145	144	0.155	0.877	2.61	F
  	DGPS	244.41	34.21	145
  	c.Ast30.bl	244.51	47.32	145	144	0.332	0.741	2.61	F
  	DGPS	244.41	34.21	145
  	c.Ast30.bc	244.42	48.35	145	144	0.045	0.964	2.61	F
  	DGPS	244.41	34.21	145
  Crt30	c.Crt30.nn	244.40	43.53	145	144	−0.006	0.995	2.61	F
  	DGPS	244.41	34.21	145
  	c.Crt30.bl	244.40	40.89	145	144	−0.038	0.970	2.61	F
  	DGPS	244.41	34.21	145
  	c.Crt30.bc	244.42	41.68	145	144	0.055	0.957	2.61	F
  	DGPS	244.41	34.21	145
  Srt30	c.Srt30.nn	244.43	38.83	145	144	0.132	0.895	2.61	F
  	DGPS	244.41	34.21	145
  	c.Srt30.bl	244.41	38.38	145	144	0.034	0.973	2.61	F
  	DGPS	244.41	34.21	145
  	c.Srt30.bc	244.45	38.13	145	144	0.262	0.794	2.61	F
  	DGPS	244.41	34.21	145
  Srt90	c.Srt90.nn	244.34	38.89	145	144	−0.347	0.729	2.61	F
  	DGPS	244.41	34.21	145
  	c.Srt90.bl	244.51	37.90	145	144	0.659	0.511	2.61	F
  	DGPS	244.41	34.21	145
  	c.Srt90.bc	244.37	38.00	145	144	−0.240	0.811	2.61	F
  	DGPS	244.41	34.21	145
  MRT90	c.MRT90.nn	244.40	38.99	145	144	−0.044	0.965	2.61	F
  	DGPS	244.41	34.21	145
  	c.MRT90.bl	244.40	38.12	145	144	−0.019	0.985	2.61	F
  	DGPS	244.41	34.21	145
  	c.MRT90.bc	244.40	38.18	145	144	−0.020	0.984	2.61	F
  	DGPS	244.41	34.21	145
  TDX90	c.TDX90.nn	244.39	39.45	145	144	−0.077	0.939	2.61	F
  	DGPS	244.41	34.21	145
  	c.TDX90.bl	244.43	38.05	145	144	0.136	0.892	2.61	F
  	DGPS	244.41	34.21	145
  	c.TDX90.bc	244.41	38.35	145	144	0.006	0.995	2.61	F
  	DGPS	244.41	34.21	145

  Null Hypothesis: H0: μd = 0; Alternative Hypothesis: H₁: μd ≠ 0. Where, μd = hypothesized mean difference, Ast30 = ASTER GDEM V3, Crt30 = CartoDEM v3.R1, Srt30 = SRTM.v3, Srt90 = SRTM.v4.1, MRT90 = MERIT DEM, TDX90 = TanDEM-X 90m, $\overline{\mathrm{X}}$ = mean, S2 = variance, N = No. of observations, df = degree of freedom, t Stat = t-statistic, t Critical = critical value of two-tail paired t-Test, p-value = probability distribution for two tail paired t-Test, CL = Confidence Level, α = level of significance, T = True, F = False.

  ). The elevation estimates from DGPS and DEMs were found to be significantly different before applying correction (Table 8), whereas they turned out to be insignificant after correction.
• Similarly, two-tail F-test for the variances of the elevation values (at 99% CL & α = 0.01) were carried out between DGPS and DEMs (uncorrected or corrected) (Tables S5 and S6). The differences in the variances of these two pairs were found to be insignificant, that is, the variances of these two datasets (DGPS and DEMs (uncorrected or corrected)) were similar.

3.2.2. Measure of Dispersion (Standard deviation (SD), Relative Standard Deviation (RSD) and Measure of Eror (Standard Error (SE))

• In general, the statistical measures (SD, RSD, and SE) show similar values before and after correction for all DEMs. The values of SD, RSD, and SE for all DEMs range between 6–8.41 m, 2.43–3.37% and 0.50–0.70 m, respectively (Figure 4, Table 4).
• The SD/RSD/SE values for the bilinear method show lower values compared to other interpolation methods for all DEMs, and also for uncorrected and corrected datasets.
• After correction, the percent change in SD for DEMs is observed to be variable. The percent change in SD for the Ast30, Crt30, Srt30, Srt90, MRT90, and TDX90 datasets is −16.43%, −6.07%, −3.72%, −1.80%, 1.51% and −3.97%, respectively (Table 6). A similar percent change was observed for SE (Table 6). Ast30 shows a considerably higher percentage change in SD/SE, after correction, compared to other DEMs.

3.2.3. Measures of Systematic Error (MBE) and Magnitude of Errors (RMSE and MAE)

• The measures of error were found to vary for different DEMs and interpolation methods. The RMSE for uncorrected datasets was found to be between 4.17 and 7.65 m, while MBE and MAE were found to be falling within the range of 3.62–5.96 m and 3.66–6.35 m, respectively.
• After correction, there was a substantial reduction in bias (MBE), which was also reflected in the RMSE and MAE values (Figure 4, Table 4). The reduced range of RMSE and MAE was 1.91–3.91 m and 1.59–3.11 m, respectively. The MBE was reduced to nearly zero after the correction. The amount of error reduction is visible in the form of a percent decline in the RMSE, MBE, and MAE values (Table 6). The percent decline in RMSE due to correction is observed to be nearly 50–62%, whereas this reduction is about 99–100% for MBE and about 50–65% reduction in MAE. Such a reduction in RMSE achieved using linear fit correction of DEMs is less than the 91% to 93% reduction in RMSE achieved using the back-propagation neural network (BPNN) technique [91].
• For the SRTM DEM, previous research found a vertical accuracy (RMSE) of 5 m [21] utilizing GPS-derived ground truth and 14.9 m (RMSE) [92] using LiDAR data as true values. Our results agree well with the previous studies and show an even lower RMSE value (~2 m, Table 4) for the corrected datasets.
• Our results for MRT90 show an average RMSE value, including all three resampling methods (nn, bl, and bc), which show ranges of 4.49–5.54 m before correction and 1.99–2.18 m after correction (Table 4). The average RMSE, before (4.49 m) and after correction (2.05 m), falls well within the expected accuracy of 12 m reported by product specification [68], and even shows a much lower average RMSE than previous findings [79,80].
• The average RMSE value of the nn, bl, and bc techniques obtained for TDX90 in this investigation is: before (4.26 m) and after (2.09 m) correction. This falls well within the expected accuracy range of 10 m [70] and shows a considerably lower value of RMSE for the corrected DEM, as reported by other researchers [74,80]. The MAE (3.69 m before and 1.73 m after correction) and MBE (3.65 m before and nearly zero after correction) as observed for TDX90 reflect the quality of the product, even showing lower values than those obtained for the Indian region [79]. The lower values of MAE and MBE in this case may be attributed to relatively planar topography compared to the moderate and rugged topography from the previous findings.
• The average RMSE value observed for CartoDEM in both cases (before correction, 5.93 m, and after correction, 2.78 m (Table 4)) meets the product specification RMSE value of 8 m [64,66]. The RMSE value after correction shows a lower value compared to previous studies [40,93]. However, it is slightly higher than 1.96 m, as reported by another study for a plain area [79].
• Among the 30 m elevation datasets, Srt30 shows a relatively lower value of RMSE, MBE, and MAE, both before and after correction, and performs better than the other two DEMs (Ast30 and Crt30)—followed by Crt30 (Table 4).
• On the other hand, among the 90 m elevation datasets, TDX90 shows better performance before correction, as indicated by its lower RMSE, MBE, and MAE values, while after correction, all the datasets (Srt90, MRT90 and TDX90) are exhibiting similar performance with consistent RMSE, MBE, and MAE values with negligible differences (Table 4).
• Overall, the Ast30 dataset shows a relatively poor performance in both cases—before and after correction. This can be seen in the relatively higher values of RMSE/MBE/MAE (Table 4). Similar results have been obtained by many researchers for the older version of Aster GDEM [51,73,80,94,95]. The results obtained for the latest version of ASTER GDEM (ASTER GDEM version 3) in this study agree well with recent investigations for this latest version [96].
• Despite the coarser resolution, TDX90, before correction, exhibits considerably lower RMSE/MBE/MAE values compared to the rest of the DEMs (ASTER GDEM, CartoDEM, SRTM, and MERIT DEM) utilized in this study.
• Though the differences arising from the interpolation methods can be considered to be negligible for all DEMs, the RMSE values are relatively lower for the bilinear method—both before and after correction (Table 4).
• The impact of the correction of DEMs using DGPS values is visible in the form of the substantial reduction of error (RMSE/MBE/MAE).
• The better performance of TDX90 can be attributed to data collection and processing techniques. The elevation data were derived by single pass SAR (Synthetic Aperture Radar) interferometry using pairs of SAR images, which were acquired during the four-year period of between December 2010 and January 2015 [71] by the twin satellites in bistatic mode (TerraSAR-X and TanDEM-X). The landmasses with complex topography were covered at least twice, which involved the repositioning of orbits in order to avoid the shadowing effect in rugged/mountainous terrain [71,97,98].
• As both Ast30 and Crt30 have been generated through optical stereoscopy, the better accuracy obtained for Crt30 over Ast30 can be attributed to CartoDEM’s generation technique and the finer spatial resolution of the input data. CartoDEM is created using high-resolution (2.5 m) optical stereoscopic imaging, which can capture topographic differences at a finer scale. The ASST (Augmented Stereo Strip Triangulation) technique was used to create the CartoDEM, which included very precise ground control points, interactive cloud masking, and automatic dense conjugate pair generation using aspect-based correlations to determine the best match point [66]. In stereo-pairs, aspect-based correlation is particularly effective and efficient [99].

3.2.4. Bias (DEM-DGPS)

The ground-based DGPS data was used for the calculation of bias. The elevation range and bias (DEM—DGPS) for space-based elevation data (for both uncorrected (u) and corrected (c) elevation) sampled over GCPs are shown in Figure 3 and Table 7.

• The bias before correction, which is observed for different DEMs, is found to show variation that ranged between 3–6 m. The lowest average bias among 30m datasets is observed for Srt30 (4.82 m). On the other hand, TDX90 (3.65 m) shows the lowest bias among the 90 m datasets (Figure 3, Table 7)). After correction, all DEMs show nearly zero bias, which can also be observed in the percent reduction in MBE after correction (Table 6).
• In the Bias vs. Slope chart (Figure S1), the uncorrected datasets show the systematic nature of bias while the corrected datasets show a random distribution of bias. The removal of systematic bias using DGPS values can help in the reduction of associated errors. Therefore, after the correction of DEMs, a substantial improvement in bias is visible compared to uncorrected DEMs. This underlines the importance of applying correction to DEMs using DGPS estimates. The improvement is also visible in the spatial distribution of bias in elevation (between corrected and uncorrected DEMs) in the form of a map and corresponding histogram (Figures S2 and S3).

3.3. Slope

The slope values (in degree) were calculated at GCPs for space-borne elevation datasets. The average and range of the slope values, before and after correction and the effect of the interpolation algorithms, is summarized in

Table 10. Slope values (in degree) calculated at GCPs for space-borne elevation data sets. The nn, bl, and bc refer to the interpolation methods (nearest neighbour, bilinear, and bicubic, respectively) used in the extraction of elevation values from space-borne DEMs over the GCPs.

Group		Uncorrected Raster	Corrected Raster
Methods			nn	bl	bc
Ast30	Avg.	5.25	4.40	4.39	4.40
	Min.	0.36	0.30	0.30	0.30
	Max.	13.63	11.47	11.44	11.46
Crt30	Avg.	3.28	3.49	3.47	3.47
	Min.	0.36	0.38	0.38	0.38
	Max.	9.19	9.78	9.72	9.73
Srt30	Avg.	2.72	2.62	2.64	2.62
	Min.	0.51	0.48	0.49	0.48
	Max.	6.53	6.27	6.33	6.27
Srt90	Avg.	1.75	1.70	1.74	1.70
	Min.	0.00	0.00	0.00	0.00
	Max.	4.44	4.33	4.42	4.34
MRT90	Avg.	1.63	1.64	1.67	1.64
	Min.	0.17	0.17	0.17	0.17
	Max.	4.24	4.28	4.35	4.28
TDX90	Avg.	1.87	1.79	1.82	1.79
	Min.	0.48	0.46	0.46	0.46
	Max.	4.57	4.36	4.44	4.36

.

• The elevation datasets with a coarser resolution (Srt90, MRT90, and TDX90) were found to show lower average slope values compared to datasets with relatively finer resolution (Ast30, Crt30, and Srt30) (Table 10), which is expected for a coarser resolution dataset (at 90 m vs. 30 m DEMs).
• For all DEMs, the slope values (average, minimum, and maximum) show a marginal drop in values before and after the correction (Table 10). The smoothening over a larger area had led to lower slope values in Srt90 compared to Srt30. Therefore, for ground flow modelling, which is directly dependent on slope values across different directions, Srt30 is preferable over Srt90. Thus, it can be concluded that for surface ground flow modeling, finer resolution datasets are preferable over coarser ones.
• From the paired t-test for the means of the slope values (at 99% CL & α = 0.01) for all DEMs, it is observed that the change in slope values (before and after correction) is significantly different (Table S7), which is similar to that observed for the elevation data as well (Table S3). Further, a two-tail F-test for the variances of the slope values (at 99% CL & α = 0.01, Tables S8 and S9) was carried out by taking pairs of slope values over uncorrected (u) and corrected (c) DEMs. The slope rasters show that the variances are not significantly different, which is similar to that observed for the elevation data as well (Table S4).

3.4. Correlation between DEMs and DGPS

• The correlation statistics, which were derived using the Microsoft Excel LINEST function, between the estimates of elevation from space-borne DEMs (corrected/uncorrected) and the ground-based equipment (DGPS) at GCPs locations are summarized in Figure S4 and

  Table 11. Statistical measures of correlation established between the corrected/uncorrected elevation estimates derived from DEM and DGPS.

  		r2 (%)		se (y)		m		se (m)		C		se (C)
  		u	c	u	c	u	c	u	c	u	c	u	c
  Ast30	nn	69.02	69.02	4.70	3.93	1.20	1.00	0.07	0.06	−41.76	0.00	16.37	13.70
  	bl	72.35	72.35	4.35	3.63	1.20	1.00	0.06	0.05	−42.87	0.00	15.16	12.64
  	bc	70.76	70.76	4.51	3.77	1.20	1.00	0.06	0.05	−42.05	0.00	15.72	13.14
  Crt30	nn	78.57	78.57	2.88	3.07	0.94	1.00	0.04	0.04	20.21	0.00	10.03	10.68
  	bl	83.66	83.66	2.45	2.59	0.94	1.00	0.03	0.04	18.81	0.00	8.54	9.04
  	bc	82.08	82.08	2.59	2.74	0.94	1.00	0.04	0.04	18.85	0.00	9.02	9.55
  Srt30	nn	88.12	88.12	2.25	2.16	1.04	1.00	0.03	0.03	−5.48	0.00	7.82	7.51
  	bl	89.12	89.12	2.12	2.05	1.03	1.00	0.03	0.03	−3.00	0.00	7.37	7.14
  	bc	88.66	88.66	2.17	2.09	1.04	0.99	0.03	0.03	−3.95	0.00	7.57	7.27
  Srt90	nn	87.90	87.90	2.23	2.18	1.03	1.00	0.03	0.03	−1.47	0.00	7.78	7.58
  	bl	90.32	90.32	1.93	1.92	1.01	1.00	0.03	0.03	3.49	0.00	6.73	6.69
  	bc	90.00	90.00	2.00	1.96	1.02	1.00	0.03	0.03	−0.96	0.00	6.98	6.81
  MRT90	nn	87.72	87.72	2.18	2.20	0.99	1.00	0.03	0.03	6.30	0.00	7.58	7.65
  	bl	89.72	89.72	1.94	1.99	0.97	1.00	0.03	0.03	10.35	0.00	6.74	6.92
  	bc	89.58	89.58	1.98	2.00	0.99	1.00	0.03	0.03	6.29	0.00	6.91	6.97
  TDX90	nn	86.70	86.70	2.41	2.30	1.05	1.00	0.03	0.03	−8.10	0.00	8.39	8.01
  	bl	89.91	89.91	2.02	1.97	1.03	1.00	0.03	0.03	−3.21	0.00	7.04	6.85
  	bc	89.20	89.20	2.14	2.04	1.05	1.00	0.03	0.03	−8.04	0.00	7.46	7.11

  . The corresponding scatterplots are shown in Figure S5 (for 30 m corrected and uncorrected DEMs) and Figure S6 (for 90 m corrected and uncorrected DEMs).
• There are no observed changes in the coefficient of determination (r²) before and after DEM correction. After correction, the slope (m) values are found to be one, with a nearly zero constant (C) (Table 11).
• Among the corrected datasets, the standard error of elevation estimates (se(y)) for Ast30, Srt30, Srt90, MRT90, and TDX90 are showing a range of values between 1.92 to 3.93 m. In general, the bilinear method shows the same for the lowest values.

3.5. Optimum Number of GCPs

Using random selection of the number of samples (at GCPs), the variation and sensitivity of statistical measures (RMSE, MBE, SE, RSD) with the increasing number of samples have been explored to find the optimum number of GCPs (Figure 5, Figure 6 and Figure 7 and Figure S7). For this purpose, RMSE, MBE, SE, and RSD were computed, and the results were plotted against an increasing number of samples that were selected randomly. The important findings are:

• In general, the variation in the calculated values of RMSE, MBE, SE, or RSD, with an increasing number of GCPs (randomly selected), exhibits a relatively sharper drop in the values up to approximately 40–60 GCPs and, thereafter, remains nearly invariable (for 60–145 no. of GCPs) for the corrected DEMs (Figure 5, Figure 6 and Figure 7 and Figure S7).
• Overall, there is a sharp reduction in RMSE and MBE for the corrected space-borne elevation datasets (Figure 5 and Figure 6, Table 4).
• Summarily, there is a minor change in SE and RSD (%) for the corrected space-borne elevation datasets (Figure 7 and Figure S4, Table 4).
• As the changes in the values of RMSE, MBE, SE, and RSD are nearly invariable after 60 GCPs, it is noticeable that the optimum level of these errors are achievable with around 40–60 samples (minimum GCPs) for similar study areas.
• The bilinear method shows relatively low RMSE values compared to the nn and bc methods. In general, as observed for MBE, SE, and RSD, the differences between the interpolation methods (nn, bl, and bc) are negligible (Figure 5, Figure 6 and Figure 7 and Figure S7).

The spatial map and corresponding histograms (Figure 8 and Figure 9) depict the “elevation ranges” for the uncorrected and corrected DEMs.

4. Summary and Conclusions

• DGPS (dual-frequency with base-rover setup) provides much more robust estimates compared to single frequency MobileGPS in static mode. Thus, DGPS estimates at GCPs are recommended for use as a reference dataset for correction of DEMs.
• MobileGPS equipment may be considered as a relatively economically cheaper option for positioning purposes if the desired RMSE is within the range of approximately 5 m (for Northing), 10 m (for Easting), and 9 m (for Elevation).
• As the elevation values obtained from corrected DEMs are found to be consistent with respect to the reference dataset (DGPS) with a substantial reduction in error (RMSE, MBE, MAE), it is recommended that DEMs may be corrected using DGPS estimates over GCPs before use in any scientific studies.
• Correction to space-borne elevation datasets helps in reducing the bias by removing systematic error. The corrected DEMs show much lower values of RMSE, MBE, SE compared to the uncorrected DEMs.
• The significance test of changes brought by correction, as seen in the results of the statistical tests on the elevation and slope, corroborates the importance of correction of DEMs. For instance, the difference between the elevation values obtained from corrected DEMs and DGPS was found to be consistently insignificant (at 99% CL) for all cases (all DEMs and all interpolation methods). This implies that the DEMs and DGPS values are comparable after correction.
• The SRTM elevation data (Srt30) is one of the most preferred DEMs if correction is applied. However, without any correction, TanDEM-X (90 m) among the 90 m datasets and Srt30 or CartoDEM (30 m) among the 30 m datasets may be preferable over the Indian region due to the lower SE, RMSE, MBE, and MAE compared to other datasets.
• Srt30 is preferable as it has much finer spatial resolution (grid size) compared to Srt90, MRT90, and TDX90. The corrected Srt90, MRT90, and TDX90 (average of nn, bl, bc) show comparable RMSE (2.01 m, 2.05 m, and 2.09 m, respectively) and MBE is nearly zero when compared to that of Srt30 (RMSE of 2.08 m and MBE of 0.02 m). The slope values obtained from Srt30 are more realistic for ground flow modelling at a finer resolution compared to Srt90/MRT90/TDX90, where smoothening over a larger area may affect the ground flow model results.
• ASTER DEM (Ast30) shows relatively poor performance compared to SRTM, MERIT, TanDEM-X, and CartoDEM (Srt30, Srt90, MRT90, TDX90, and Crt30).
• Though the differences arising due to the interpolation methods can be considered to be negligible for all DEMs, the bilinear method (after correction) can be preferred as RMSE values are relatively lower compared to other methods. As the difference due to these methods is marginal in most cases, the choice of interpolation may depend upon the project objectives.
• For all DEMs, the slope values (average, minimum, and maximum) show only a marginal change in values before and after the correction of DEMs, implying that the slope values were largely unaffected while correcting for the elevation values (through the removal of systematic error).
• From the sensitivity of statistical measures (RMSE, MBE, SE, RSD) with the increasing number of GCPs, it was observed that the optimum number of GCPs required to achieve nearly stable values of (RMSE, MBE, SE, RSD) is around 40-60 in most cases when compared to 145 GCPs. Therefore, the minimum number of GCPs is recommended to be around 60 for study areas showing similar variability and range in the topography (a hard rock terrain that overall is flat-like with undulating and uneven surfaces).