Estimating Species-Specific Stem Size Distributions of Uneven-Aged Mixed Deciduous Forests Using ALS Data and Neural Networks
Abstract
:1. Introduction
- To develop a straightforward method for estimating species-specific SSDs using ALS and FMI data for mixed uneven-aged deciduous forests.
- To use a hybrid approach in which predictions were made at the segment level (i.e., tree crowns were slightly over-segmented, a tree crown could correspond to one or several segments), but thereafter aggregated at stand level.
- To use the potential and versatility of NNs to simultaneously predict the three components required to compute species-specific SSDs: species, circumference class, and number of stems.
2. Materials and Methods
2.1. Study Area
2.2. Forest Management Inventory Plots
2.3. Independent Plots
2.4. ALS Data
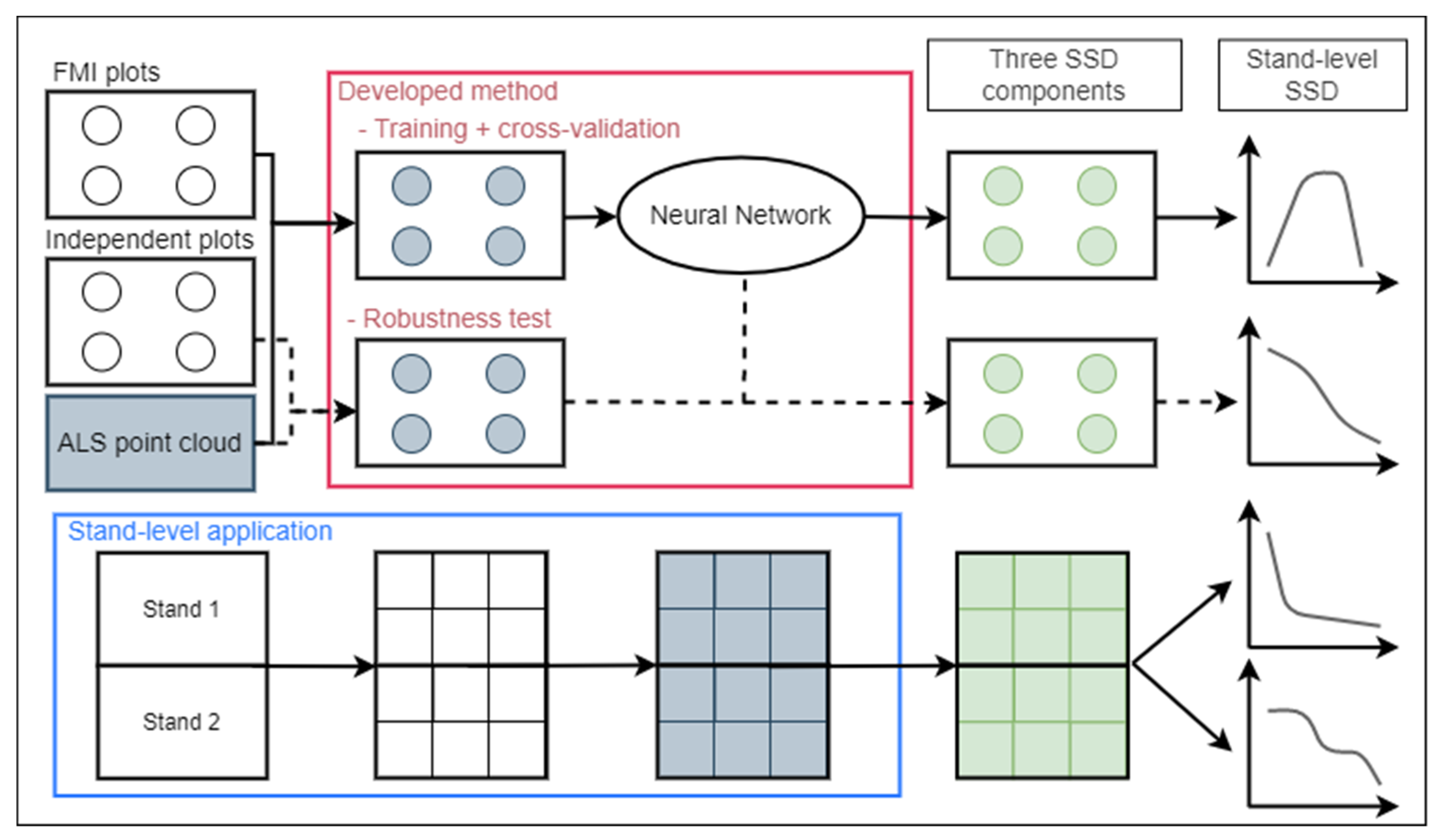
2.5. Overall Approach and Method Overview
2.6. Field Data Pre-Processing
2.7. FMI Crown Digitalization
2.8. Tree Detectability Status Assessment
2.9. Canopy Segmentation and Segment Selection
2.10. Calculation of Metrics
2.11. Neural Network Implementation
2.12. Neural Network Accuracy
2.13. Robustness Test
3. Results
3.1. Neural Network Accuracy
3.2. Robustness Test Using the Independent Dataset
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Geometric Metrics | Description |
|---|---|
| area_m2 | Segment area (m2) |
| Height metrics | Description |
| acc | Average height increase from 2014–2018 (m/year) |
| sd_CHM | Standard deviation of CHM pixels (m) |
| cv_CHM | Coefficient of variation of CHM pixels |
| sd_h | Standard deviation (m) of point heights |
| cv_h | Coefficient of variation of point heights |
| kurt_h | Kurtosis of point heights |
| skew_h | Skewness of point heights |
| cv_lad | Coefficient of variation of the leaf area density |
| entr_h | Entropy of point heights |
| ah_ratio | Ratio of segment area to 98th percentile of CHM pixels |
| ri | Rumple index of point heights |
| mn_slope_h | Average slope calculated between the highest point and all other points |
| sd_slope_h | Standard deviation of slope calculated between the highest point and all other points |
| mn_slope_h_fr | Average slope calculated between the highest first return point and all other first return points |
| sd_slope_h_fr | Standard deviation of slope calculated between the highest first return point and all other first return points |
| Intensity metrics | Description |
| max_i_c1 | Maximum of point intensity for the C1 channel |
| mean_i_c1 | Mean of point intensity for the C1 channel |
| sd_i_c1 | Standard deviation of point intensity for the C1 channel |
| kurt_i_c1 | Kurtosis of point intensity for the C1 channel |
| skew_i_c1 | Skewness of point intensity for the C1 channel |
| cv_i_c1 | Coefficient of variation of point intensity for the C1 channel |
| entr_i_c1 | Entropy of point intensity for the C1 channel |
| max_i_fr_c1 | Mean of point intensity for the C1 channel; first returns only |
| mean_i_fr_c1 | Mean of point intensity for the C1 channel; first returns only |
| sd_i_fr_c1 | Standard deviation of point intensity for the C1 channel; first returns only |
| cv_i_fr_c1 | Coefficient of variation of point intensity for the C1 channel; first returns only |
| kurt_i_fr_c1 | Kurtosis of point intensity for the C1 channel; first returns only |
| skew_i_fr_c1 | Skewness of point intensity for the C1 channel; first returns only |
| entr_i_fr_c1 | Entropy of point intensity for the C1 channel; first returns only |
| max_i_c2 | Maximum of point intensity for the C2 channel |
| mean_i_c2 | Mean of point intensity for the C2 channel |
| sd_i_c2 | Standard deviation of point intensity for the C2 channel |
| kurt_i_c2 | Kurtosis of point intensity for the C2 channel |
| skew_i_c2 | Skewness of point intensity for the C2 channel |
| cv_i_c2 | Coefficient of variation of point intensity for the C2 channel |
| entr_i_c2 | Entropy of point intensity for the C2 channel |
| max_i_fr_c2 | Mean of point intensity for the C2 channel; first returns only |
| mean_i_fr_c2 | Mean of point intensity for the C2 channel; first returns only |
| sd_i_fr_c2 | Standard deviation of point intensity for the C2 channel; first returns only |
| cv_i_fr_c2 | Coefficient of variation of point intensity for the C2 channel; first returns only |
| kurt_i_fr_c2 | Kurtosis of point intensity for the C2 channel; first returns only |
| skew_i_fr_c2 | Skewness of point intensity for the C2 channel; first returns only |
| entr_i_fr_c2 | Entropy of point intensity for the C2 channel; first returns only |
| Vegetation index | Description |
| ndgi_mm_f | Green normalized difference vegetation index (mean_i_C1 − mean_i_C2)/(mean_i_C1 + mean_i_C2) |
| r_topo_bathy | Channel ratio mean_I_C1/mean_I_C2 |
References
- FAO. Global Forest Ressources Assessment 2020—Key Findings; FAO: Rome, Italy, 2020. [Google Scholar]
- O’Hara, K.L.; Gersonde, R.F. Stocking control concepts in uneven-aged silviculture. Forestry 2004, 77, 131–143. [Google Scholar] [CrossRef]
- Boncina, A.; Diaci, J.; Cencic, L. Comparison of the two main types of selection forests in Slovenia: Distribution, site conditions, stand structure, regeneration and management. Forestry 2002, 75, 365–373. [Google Scholar] [CrossRef] [Green Version]
- Duchateau, E.; Schneider, R.; Tremblay, S.; Dupont-Leduc, L. Density and diameter distributions of saplings in naturally regenerated and planted coniferous stands in Québec after various approaches of commercial thinning. Ann. For. Sci. 2020, 77, 38. [Google Scholar] [CrossRef]
- Rubin, B.D.; Manion, P.D.; Faber-Langendoen, D. Diameter distributions and structural sustainability in forests. For. Ecol. Manag. 2006, 222, 427–438. [Google Scholar] [CrossRef]
- Cameron, A.; Prentice, L. Determining the sustainable irregular condition: An analysis of an irregular mixed-species selection stand in Scotland based on recurrent inventories at 6-year intervals over 24 years. Forestry 2016, 89, 208–214. [Google Scholar] [CrossRef] [Green Version]
- Næsset, E. Area-Based inventory in norway—From innovation to an operational reality. In Forestry Applications of Airborne Laser Scanning; Springer: Berlin/Heidelberg, Germany, 2014; pp. 215–240. [Google Scholar] [CrossRef]
- Kangas, A.; Astrup, R.; Breidenbch, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Naesset, E.; et al. Remote sensing and forest inventories in Nordic countries—Roadmap for the future. Scand. J. For. Res. 2018, 33, 397–412. [Google Scholar] [CrossRef] [Green Version]
- Maltamo, M.; Packalen, P.; Kangas, A. From comprehensive field inventories to remotely sensed wall-to-wall stand attribute data—A brief history of management inventories in the nordic countries. Can. J. For. Res. 2020, 51, 257–266. [Google Scholar] [CrossRef]
- Rondeux, J. La Mesure des Arbres et des Peuplements Forestiers, 3rd ed.; Les Presses Agronomiques de Gembloux: Gembloux, Belgium, 2021. [Google Scholar]
- Lei, X.D.; Tang, M.P.; Lu, Y.C.; Hong, L.X.; Tian, D.L. Forest inventory in China: Status and challenges. Int. For. Rev. 2009, 11, 52–63. [Google Scholar] [CrossRef]
- Rahlf, J.; Hauglin, M.; Astrup, R.; Breidenbach, J. Timber volume estimation based on airborne laser scanning—Comparing the use of national forest inventory and forest management inventory data. Ann. For. Sci. 2021, 78, 49. [Google Scholar] [CrossRef]
- Hoover, C.M.; Bush, R.; Palmer, M.; Treasure, E. Using forest inventory and analysis data to support national forest management: Regional case studies. J. For. 2020, 118, 313–323. [Google Scholar] [CrossRef]
- Vega, C.; Renaud, J.-P.; Sagar, A.; Bouriaud, O. A new small area estimation algorithm to balance between statistical precision and scale. Int. J. Appl. Earth Obs. Geoinf. 2021, 97, 102303. [Google Scholar] [CrossRef]
- Scott, C.T.; Gove, J.H. Forest inventory. Encycl. Environ. 2002, 2, 814–820. [Google Scholar]
- Packalén, P.; Maltamo, M. Estimation of species-specific diameter distributions using airborne laser scanning and aerial photographs. Can. J. For. Res. 2008, 38, 1750–1760. [Google Scholar] [CrossRef]
- Maltamo, M.; Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Packalén, P. Non-parametric prediction of diameter distributions using airborne laser scanner data. Scand. J. For. Res. 2009, 24, 541–553. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J. Estimating species-specific diameter distributions and saw log recoveries of boreal forests from airborne laser scanning data and aerial photographs: A distribution-based approach. Silva Fenn. 2008, 42, 625–641. [Google Scholar] [CrossRef] [Green Version]
- Peuhkurinen, J.; Tokola, T.; Plevak, K.; Sirparanta, S.; Kedrov, A.; Pyankov, S. Predicting tree diameter distributions from airborne laser scanning, SPOT 5 satellite, and field sample data in the Perm Region, Russia. Forests 2018, 9, 639. [Google Scholar] [CrossRef] [Green Version]
- Strunk, J.L.; Gould, P.J.; Packalen, P.; Poudel, K.P.; Andersen, H.E.; Temesgen, H. An examination of diameter density prediction with k-NN and airborne lidar. Forests 2017, 8, 444. [Google Scholar] [CrossRef] [Green Version]
- Räty, J.; Packalen, P.; Maltamo, M. Comparing nearest neighbor configurations in the prediction of species-specific diameter distributions. Ann. For. Sci. 2018, 75, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Mauro, F.; Frank, B.; Monleon, V.J.; Temesgen, H.; Ford, K.R. Prediction of diameter distributions and tree-lists in southwestern oregon using lidar and stand-level auxiliary information. Can. J. For. Res. 2019, 49, 775–787. [Google Scholar] [CrossRef]
- Maltamo, M.; Mehtätalo, L.; Valbuena, R.; Vauhkonen, J.; Packalen, P. Airborne laser scanning for tree diameter distribution modelling: A comparison of different modelling alternatives in a tropical single-species plantation. Forestry 2017, 91, 121–131. [Google Scholar] [CrossRef]
- Arias-Rodil, M.; Diéguez-Aranda, U.; Álvarez-González, J.G.; Pérez-Cruzado, C.; Castedo-Dorado, F.; González-Ferreiro, E. Modeling diameter distributions in radiata pine plantations in Spain with existing countrywide LiDAR data. Ann. For. Sci. 2018, 75, 36. [Google Scholar] [CrossRef] [Green Version]
- Cosenza, D.N.; Soares, P.; Guerra-Hernandez, J.; Pereira, L.; Gonzalez-Ferreiro, E.; Castedo-Dorado, F.; Tomé, M. Comparing Johnson’s SB and weibull functions to model the diameter distribution of forest plantations through ALS data. Remote Sens. 2019, 11, 2792. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Cao, L.; Mulverhill, C.; Liu, H.; Pang, Y.; Li, Z. Prediction of diameter distributions with multimodal models using LiDAR data in subtropical planted forests. Forests 2019, 10, 125. [Google Scholar] [CrossRef] [Green Version]
- Gobakken, T.; Næsset, E. Estimation of diameter and basal area distributions in coniferous forest by means of airborne laser scanner data. Scand. J. For. Res. 2004, 19, 529–542. [Google Scholar] [CrossRef]
- Gorgoso, J.J.; Alvarez Gonzalez, J.G.; Rojo, A.; Grandas-Arias, J.A. Modelling diameter distributions of Betula alba L. stands in northwest Spain with the two-parameter Weibull function. Investig. Agrar. Sist. Recur. For. 2007, 16, 113–123. [Google Scholar] [CrossRef] [Green Version]
- Maltamo, M.; Suvanto, A.; Packalén, P. Comparison of basal area and stem frequency diameter distribution modelling using airborne laser scanner data and calibration estimation. For. Ecol. Manag. 2007, 247, 26–34. [Google Scholar] [CrossRef]
- Breidenbach, J.; Gläser, C.; Schmidt, M. Estimation of diameter distributions by means of airborne laser scanner data. Can. J. For. Res. 2008, 38, 1611–1620. [Google Scholar] [CrossRef]
- Thomas, V.; Oliver, R.D.; Lim, K.; Woods, M. LiDAR and Weibull modeling of diameter and basal area. For. Chron. 2008, 84, 866–875. [Google Scholar] [CrossRef] [Green Version]
- Mulverhill, C.; Coops, N.C.; White, J.C.; Tompalski, P.; Marshall, P.L.; Bailey, T. Enhancing the estimation of stem-size distributions for unimodal and bimodal stands in a boreal mixedwood forest with airborne laser scanning data. Forests 2018, 9, 95. [Google Scholar] [CrossRef] [Green Version]
- Paris, C.; Bruzzone, L. A growth-model-driven technique for tree stem diameter estimation by using airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2018, 57, 76–92. [Google Scholar] [CrossRef]
- Malek, S.; Miglietta, F.; Gobakken, T.; Næsset, E.; Gianelle, D.; Dalponte, M. Prediction of stem diameter and biomass at individual tree crown level with advanced machine learning techniques. iForest-Biogeosciences For. 2019, 12, 323–329. [Google Scholar] [CrossRef] [Green Version]
- Räty, J.; Packalen, P.; Kotivuori, E.; Maltamo, M. Fusing diameter distributions predicted by an area-based approach and individual-tree detection in coniferous-dominated forests. Can. J. For. Res. 2020, 50, 113–125. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Mehtätalo, L. Matching remotely sensed and field-measured tree size distributions. Can. J. For. Res. 2015, 45, 353–363. [Google Scholar] [CrossRef]
- Xu, Q.; Hou, Z.; Maltamo, M.; Tokola, T. Calibration of area based diameter distribution with individual tree based diameter estimates using airborne laser scanning. ISPRS J. Photogramm. Remote Sens. 2014, 93, 65–75. [Google Scholar] [CrossRef]
- Kansanen, K.; Vauhkonen, J.; Lähivaara, T.; Seppänen, A.; Maltamo, M.; Mehtätalo, L. Estimating forest stand density and structure using Bayesian individual tree detection, stochastic geometry, and distribution matching. ISPRS J. Photogramm. Remote Sens. 2019, 152, 66–78. [Google Scholar] [CrossRef]
- Spriggs, R.A.; Coomes, D.A.; Jones, T.A.; Caspersen, J.P.; Vanderwel, M.C. An alternative approach to using LiDAR remote sensing data to predict stem diameter distributions across a temperate forest landscape. Remote Sens. 2017, 9, 944. [Google Scholar] [CrossRef] [Green Version]
- Magnussen, S.; Renaud, J.P. Multidimensional scaling of first-return airborne laser echoes for prediction and model-assisted estimation of a distribution of tree stem diameters. Ann. For. Sci. 2016, 73, 1089–1098. [Google Scholar] [CrossRef] [Green Version]
- Shang, C.; Treitz, P.; Caspersen, J.; Jones, T. Estimating stem diameter distributions in a management context for a tolerant hardwood forest using ALS height and intensity data. Can. J. Remote Sens. 2017, 43, 79–94. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.S.; Longo, M.; Clark, D.B. Tropical tree size–frequency distributions from airborne lidar. Ecol. Appl. 2020, 30, 2154. [Google Scholar] [CrossRef]
- Budei, B.C.; St-Onge, B.; Hopkinson, C.; Audet, F.A. Identifying the genus or species of individual trees using a three-wavelength airborne lidar system. Remote Sens. Environ. 2018, 204, 632–647. [Google Scholar] [CrossRef]
- Dalponte, M.; Ene, L.T.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting selected forest stand characteristics with multispectral ALS data. Remote Sens. 2018, 10, 586. [Google Scholar] [CrossRef] [Green Version]
- Hastings, J.H.; Ollinger, S.V.; Ouimette, A.P.; Sanders-DeMott, R.; Palace, M.W.; Ducey, M.J.; Sullivan, F.B.; Basler, D.; Orwig, D.A. Tree species traits determine the success of LiDAR-based crown mapping in a mixed temperate forest. Remote Sens. 2020, 12, 309. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Hyyppä, J.; Litkey, P.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Single-sensor solution to tree species classification using multispectral airborne laser scanning. Remote Sens. 2017, 9, 108. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.H.; Zhang, Y.Z.; Xu, M.M. A multi-threshold segmentation for tree-level parameter extraction in a deciduous forest using small-footprint airborne LiDAR data. Remote Sens. 2019, 11, 2109. [Google Scholar] [CrossRef] [Green Version]
- Korpela, I.; Tuomola, T.; Välimäki, E. Mapping forest plots: An efficient method combining photogrammetry and field triangulation. Silva Fenn. 2007, 41, 457–469. [Google Scholar] [CrossRef] [Green Version]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Grossi, E.; Buscema, M. Introduction to artificial neural networks. Eur. J. Gastroenterol. Hepatol. 2007, 19, 1046–1054. [Google Scholar] [CrossRef]
- Alderweireld, M.; Burnay, F.; Pitchugin, M.; Lecomte, H. Inventaire Forestier Wallon-Résultats 1994–2012; SPW: Jambes, Belgium, 2015. [Google Scholar]
- Claessens, H.; Perin, J.; Latte, N.; Lecomte, H.; Brostaux, Y. Une chênaie n’est pas l’autre: Analyse des contextes sylvicoles du chêne en forêt wallonne. Forêt Wallonne 2010, 108, 3–18. [Google Scholar]
- PDAL Contributors. PDAL Point Data Abstraction Library. Available online: https://pdal.io/ (accessed on 8 February 2022).
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating pit-free canopy height models from airborne lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. Lidr: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Korpela, I.; Ole Ørka, H.; Maltamo, M.; Tokola, T.; Hyyppä, J. Tree species classification using airborne LiDAR—Effects of stand and tree parameters, downsizing of training set, intensity normalization, and sensor type. Silva Fenn. 2010, 44, 319–339. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing, R Core Team: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 8 February 2022).
- Pebesma, E. Simple features for R: Standardized support for spatial vector data. R J. 2018, 10, 439–446. [Google Scholar] [CrossRef] [Green Version]
- Hijmans, R. Raster: Geographic Data Analysis and Modelling, R Package Version 3.3–13. Available online: https://rspatial.org/raster (accessed on 8 February 2022).
- Perin, J.; Pitchugin, M.; Hébert, J.; Brostaux, Y.; Lejeune, P.; Ligot, G. SIMREG, a tree-level distance-independent model to simulate forest dynamics and management from national forest inventory (NFI) data. Ecol. Model. 2021, 440, 109382. [Google Scholar] [CrossRef]
- Michez, A.; Huylenbroeck, L.; Bolyn, C.; Latte, N.; Bauwens, S.; Lejeune, P. Can regional aerial images from orthophoto surveys produce high quality photogrammetric Canopy Height Model ? A single tree approach in Western Europe. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102190. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. A robust approach for tree segmentation in deciduous forests using small-footprint airborne LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 532–541. [Google Scholar] [CrossRef] [Green Version]
- Grizonnet, M.; Michel, J.; Poughon, V.; Inglada, J.; Savinaud, M.; Cresson, R. Orfeo ToolBox: Open source processing of remote sensing images. Open Geospat. Data Softw. Stand. 2017, 2, 15. [Google Scholar] [CrossRef] [Green Version]
- Packalen, P.; Strunk, J.L.; Pitkänen, J.A.; Temesgen, H.; Maltamo, M. Edge-tree correction for predicting forest inventory attributes using area-based approach with airborne laser scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1274–1280. [Google Scholar] [CrossRef]
- Allaire, J.J.; Chollet, F. Keras: RInterface to Keras. R Package Version 2.3.0.0. 2020. Available online: https://CRAN.R-project.org/package=keras (accessed on 8 February 2022).
- Agresti, A. Categorical Data Analysis, 2nd ed.; Wiley: Gainesville, FL, USA, 2002; Volume 35, pp. 583–584. [Google Scholar] [CrossRef]
- Garavaglia, S.; Sharma, A.; Hill, M. A smart guide to dummy variables: Four applications and macro. In Proceedings of the northeast SAS Users Group Conference, Nashville, TN, USA, 22–25 March 1998; Volume 43. [Google Scholar]
- Potdar, K.; Pardawala, T.S.; Pai, C.D. A comparative study of categorical variable encoding techniques for neural network classifiers. Int. J. Comput. Appl. 2017, 175, 7–9. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, S.; Athaiya, A. Activation functions in neural networks. Int. J. Eng. Appl. Sci. Technol. 2020, 4, 310–316. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Droupout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Yoshida, Y.; Okada, M. Data-dependence of plateau phenomenon in learning with neural network—Statistical mechanical analysis. In Advances in Neural Information Processing Systems; NeurIPS: Vancouver, BC, Canada, 2019; pp. 1722–1730. [Google Scholar]
- Reynolds, M.R.; Burk, T.E.; Huang, W.-C. Goodness-of-fit tests and model selection procedures for diameter distribution models. For. Sci. 1988, 34, 373–399. [Google Scholar]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of individual longleaf pine (Pinus palustris mill.) tree attributes from field and LiDAR data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Axelsson, A.; Lindberg, E.; Olsson, H. Exploring multispectral ALS data for tree species classification. Remote Sens. 2018, 10, 183. [Google Scholar] [CrossRef] [Green Version]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Forest understory trees can be segmented accurately within sufficiently dense airborne laser scanning point clouds. Sci. Rep. 2017, 7, 6770. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the 2016 4th International Conference 3D Vision, 3DV 2016, Stanford, CA, USA, 25–28 October 2016; pp. 601–610. [Google Scholar]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real time Object Recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Vertical stratification of forest canopy for segmentation of under-story trees within small-footprint airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 385–392. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Leão, F.M.; Nascimento, R.G.M.; Emmert, F.; Santos, G.G.A.; Caldeira, N.A.M.; Miranda, I.S. How many trees are necessary to fit an accurate volume model for the Amazon forest? A site-dependent analysis. For. Ecol. Manag. 2021, 480, 118652. [Google Scholar]
- Rana, P.; Vauhkonen, J.; Junttila, V.; Hou, Z.; Gautam, B.; Cawkwell, F.; Tokola, T. Large tree diameter distribution modelling using sparse airborne laser scanning data in a subtropical forest in Nepal. ISPRS J. Photogramm. Remote Sens. 2017, 134, 86–95. [Google Scholar] [CrossRef]
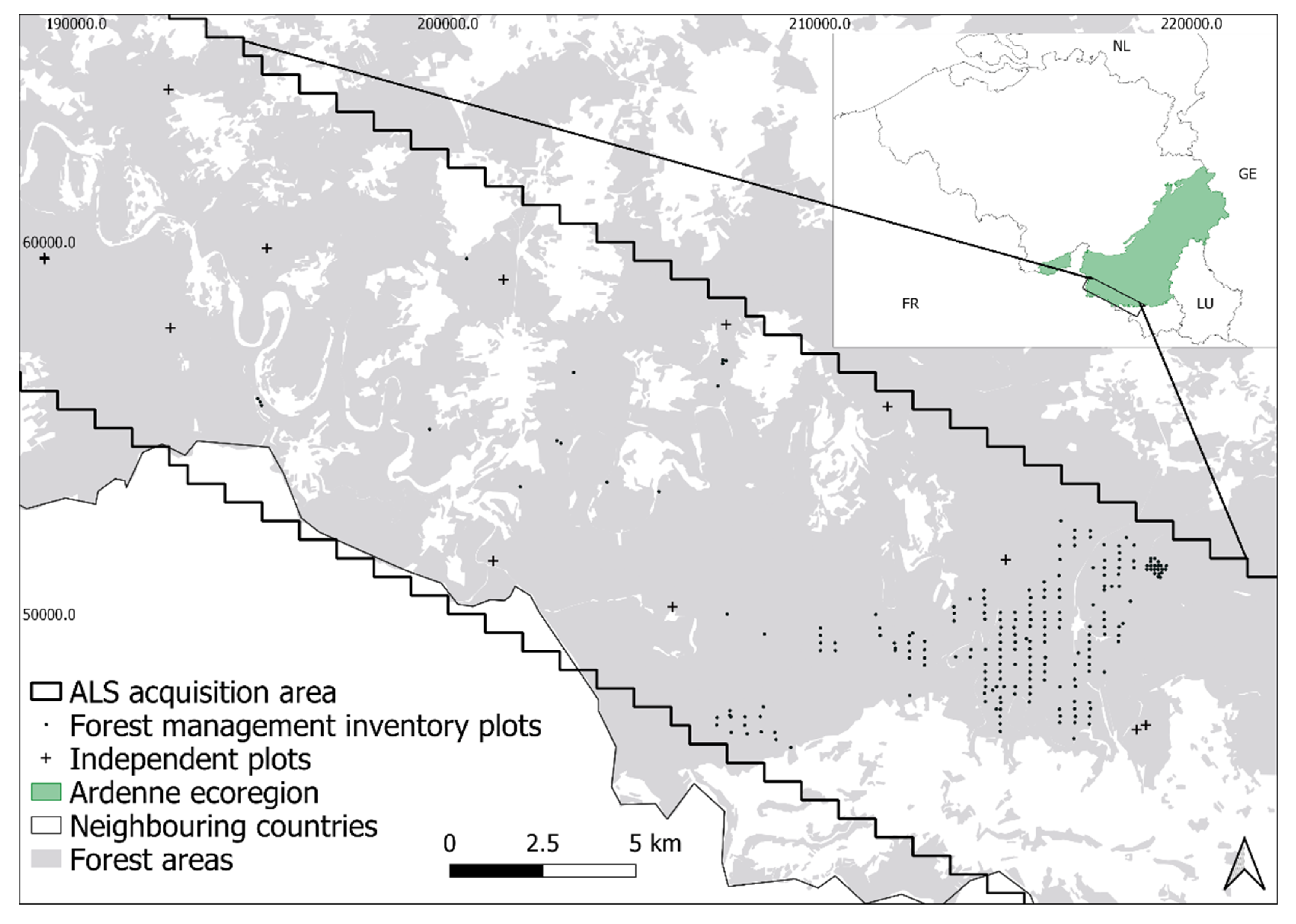








| Attribute | Mean | Std. Dev. | Min. | Max. |
|---|---|---|---|---|
| Number of stems per hectare (stems/ha) | 238.26 | 162.25 | 9.82 | 837.62 |
| Basal area per hectare (m2/ha) | 22.57 | 8.05 | 3.17 | 51.38 |
| Root mean quadratic circumference (cm) | 123.85 | 41.33 | 49.75 | 261.39 |
| Proportion of dominant species | 0.93 | 0.16 | 0.03 | 1.00 |
| Canopy height (m) | 26.94 | 3.81 | 11.94 | 36.79 |
| Attribute | Mean | Std. Dev. | Min. | Max. |
|---|---|---|---|---|
| Number of stems per hectare (stems/ha) | 224.37 | 89.13 | 76.22 | 415.38 |
| Basal area per hectare (m2/ha) | 21.95 | 3.68 | 13.28 | 26.70 |
| Root mean quadratic circumference (cm) | 115.94 | 27.52 | 82.28 | 186.67 |
| Proportion of dominant species | 0.95 | 0.10 | 0.64 | 1.00 |
| Canopy height (m) | 26.98 | 1.84 | 23.97 | 30.51 |
| Sensor Property | ||
|---|---|---|
| Number of returns recorded per pulse | Up to 4 | |
| Pulse frequency (kHz) | 200 | |
| Scanning frequency (scans/s) | 70 | |
| Footprint diameter (m) | 0.28 | |
| Scan angle | ±16° | |
| Channel | Wavelength (nm) | Mean point density (pts/m2) |
| C1: Infra-red | 1064 | 56 |
| C2: Green | 532 | 48 |
| Output Variable | Block Number | Variable Type | Activation Function | Loss Function | Accuracy Index |
|---|---|---|---|---|---|
| Species class | 1 | Categorical nominal (converted into four binary variables) | Softmax | Categorical cross-entropy | Categorical accuracy |
| Circumference class | 2 | Categorical ordinal (converted into twelve binary variables) | Sigmoid | Binary cross-entropy | Binary accuracy |
| Number of stems | 3 | Numerical continuous | Linear (none) | Mean squared error | R2 |
| Prediction | Producer Accuracy | |||||
|---|---|---|---|---|---|---|
| Oak | Beech | Other | Spruce | |||
| Training | Oak | 1116 | 108 | 33 | 1 | 0.89 |
| Beech | 175 | 2305 | 7 | 12 | 0.92 | |
| Other | 15 | 4 | 254 | 0 | 0.93 | |
| Spruce | 0 | 2 | 0 | 373 | 0.99 | |
| User accuracy | 0.85 | 0.95 | 0.86 | 0.97 | Overall accuracy 0.92 | |
| Prediction | Producer Accuracy | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 70 | 90 | 110 | 130 | 150 | 170 | 190 | 210 | 230 | 250 | 270 | |||
| Training | 50 | 47 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.84 |
| 70 | 5 | 79 | 36 | 2 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0.63 | |
| 90 | 0 | 17 | 127 | 51 | 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.63 | |
| 110 | 0 | 4 | 44 | 123 | 78 | 7 | 9 | 0 | 0 | 0 | 0 | 0 | 0.46 | |
| 130 | 0 | 7 | 15 | 52 | 133 | 87 | 53 | 17 | 2 | 0 | 0 | 0 | 0.36 | |
| 150 | 0 | 0 | 3 | 13 | 57 | 132 | 133 | 114 | 28 | 2 | 1 | 0 | 0.27 | |
| 170 | 0 | 0 | 1 | 7 | 24 | 56 | 272 | 271 | 127 | 30 | 0 | 0 | 0.35 | |
| 190 | 0 | 2 | 0 | 5 | 9 | 30 | 189 | 297 | 158 | 76 | 1 | 0 | 0.39 | |
| 210 | 0 | 0 | 1 | 1 | 3 | 10 | 44 | 220 | 251 | 114 | 8 | 0 | 0.38 | |
| 230 | 0 | 0 | 0 | 1 | 1 | 3 | 21 | 122 | 180 | 113 | 7 | 0 | 0.25 | |
| 250 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 32 | 53 | 6 | 2 | 0.06 | |
| 270 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 2 | 17 | 78 | 34 | 22 | 0.14 | |
| User accuracy | 0.90 | 0.67 | 0.56 | 0.48 | 0.42 | 0.40 | 0.38 | 0.28 | 0.32 | 0.24 | 0.11 | 0.92 | Overall accuracy 0.36 | |
| Species | Reynolds Index | Packalén Index | Inventoried Number of Stems/ha | Predicted Number of Stems/ha |
|---|---|---|---|---|
| Oak | 32.27 | 0.17 | 76.4 | 73.7 |
| Beech | 41.22 | 0.21 | 75.0 | 74.8 |
| Spruce | 26.08 | 0.14 | 44.1 | 41.5 |
| Other | 25.00 | 0.12 | 28.8 | 28.8 |
| Species | Proportion of Basal Area (%) in the Independent Dataset | Reynolds Index | Packalén Index | Inventoried Number of Stems/ha | Predicted Number of Stems/ha |
|---|---|---|---|---|---|
| Oak | 53 | 22.38 | 0.11 | 59.5 | 60.2 |
| Beech | 41 | 65.17 | 0.32 | 77.2 | 79.1 |
| Spruce | 3 | 314.65 | 0.48 | 6.3 | 23.0 |
| Other | 3 | 247.11 | 0.43 | 8.4 | 28.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leclère, L.; Lejeune, P.; Bolyn, C.; Latte, N. Estimating Species-Specific Stem Size Distributions of Uneven-Aged Mixed Deciduous Forests Using ALS Data and Neural Networks. Remote Sens. 2022, 14, 1362. https://doi.org/10.3390/rs14061362
Leclère L, Lejeune P, Bolyn C, Latte N. Estimating Species-Specific Stem Size Distributions of Uneven-Aged Mixed Deciduous Forests Using ALS Data and Neural Networks. Remote Sensing. 2022; 14(6):1362. https://doi.org/10.3390/rs14061362
Chicago/Turabian StyleLeclère, Louise, Philippe Lejeune, Corentin Bolyn, and Nicolas Latte. 2022. "Estimating Species-Specific Stem Size Distributions of Uneven-Aged Mixed Deciduous Forests Using ALS Data and Neural Networks" Remote Sensing 14, no. 6: 1362. https://doi.org/10.3390/rs14061362
APA StyleLeclère, L., Lejeune, P., Bolyn, C., & Latte, N. (2022). Estimating Species-Specific Stem Size Distributions of Uneven-Aged Mixed Deciduous Forests Using ALS Data and Neural Networks. Remote Sensing, 14(6), 1362. https://doi.org/10.3390/rs14061362






