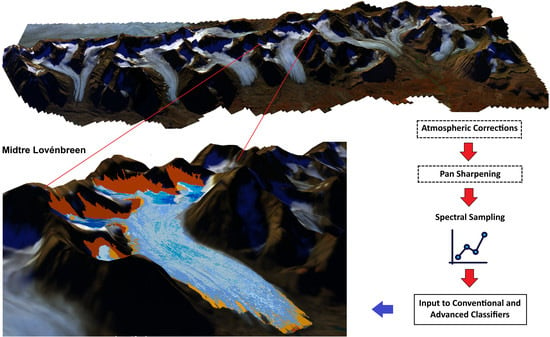
Impact of Image-Processing Routines on Mapping Glacier Surface Facies from Svalbard and the Himalayas Using Pixel-Based Methods
Abstract
:1. Introduction
1.1. Glacier Facies
1.2. Multispectral Mapping of Glacier Facies
1.3. Pansharpening
1.4. Atmospheric Correction
1.5. Research Motivation and Aim
2. Study Area and Data Used
2.1. Spatial Extent of the Test Sites
2.1.1. Site A: Ny-Ålesund, Svalbard
2.1.2. Site B: Chandra–Bhaga Basin, Himalaya
2.2. Geospatial Data
3. Data Processing Methodology
3.1. Experimental Setup
3.2. Image Processing
3.2.1. Radiometric Calibration and Atmospheric Correction
3.2.2. Pansharpening and Digitization
3.3. Glacier Facies Mapping Using Advanced Image Processing
Pixel-Based Classification
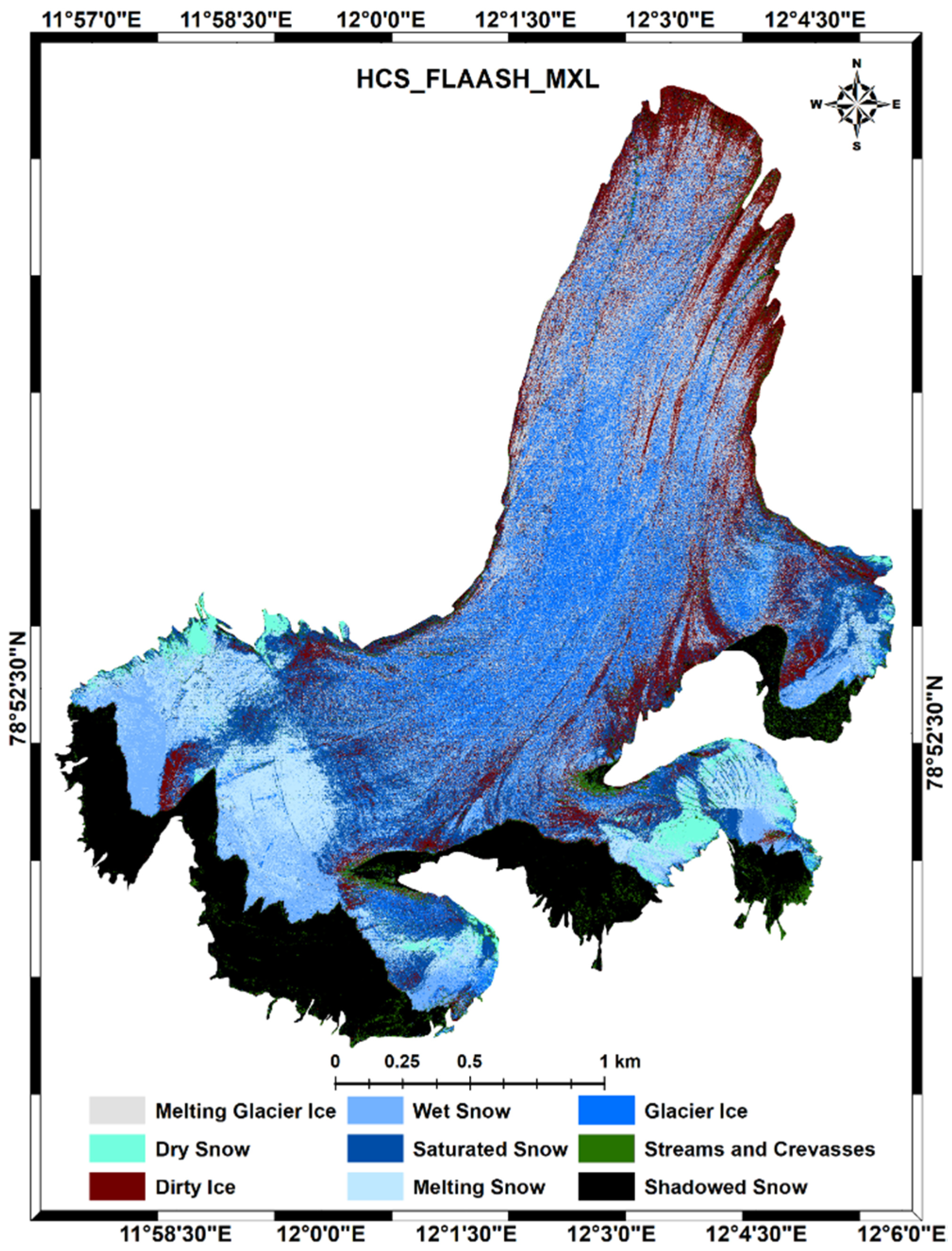
3.4. Identification of Surface Facies
3.5. Thematic Accuracy Assessment
4. Results and Discussion
4.1. Spectral Signatures
4.2. Quantitative Analysis of Mapped Facies
4.2.1. Area per Facies Produced by Each Classifier
4.2.2. Accuracy Achieved by Each Classifier
- (a)
- F1 score for classification in Ny-Ålesund
- (b)
- F1 score for classification in the Chandra–Bhaga basin
4.2.3. Comparison between Atmospheric Correction Methods
4.2.4. Effect of Pansharpening
4.3. Discussion
4.3.1. Classifiers and Surface Facies: Performance and Comparison
4.3.2. Computer Processing Time and Limitations
4.3.3. Inherent Challenges and Limitations
4.3.4. Significances and a Path Forward
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cisek, D.; Mahajan, M.; Brown, M.; Genaway, D. Remote sensing data integration for mapping glacial extents. In Proceedings of the 2017 New York Scientific Data Summit (NYSDS), IEEE Conference, New York, NY, USA, 6–9 August 2017; pp. 1–4. [Google Scholar]
- Kargel, J.S.; Abrams, M.J.; Bishop, M.P.; Bush, A.; Hamilton, G.; Jiskoot, H.; Kääb, A.; Kieffer, H.H.; Lee, E.M.; Paul, F.; et al. Multispectral imaging contributions to global land ice measurements from space. Remote Sens. Environ. 2005, 99, 187–219. [Google Scholar] [CrossRef]
- Naegeli, K.; Damm, A.; Huss, M.; Wulf, H.; Schaepman, M.; Hoelzle, M. Cross-Comparison of Albedo Products for Glacier Surfaces Derived from Airborne and Satellite (Sentinel-2 and Landsat 8) Optical Data. Remote Sens. 2017, 9, 110. [Google Scholar] [CrossRef] [Green Version]
- Pope, E.L.; Willis, I.C.; Pope, A.; Miles, E.S.; Arnold, N.S.; Rees, W.G. Contrasting snow and ice albedos derived from MODIS, Landsat ETM+ and airborne data from Langjökull, Iceland. Remote Sens. Environ. 2016, 175, 183–195. [Google Scholar] [CrossRef] [Green Version]
- Rabatel, A.; Dedieu, J.-P.; Vincent, C. Using remote-sensing data to determine equilibrium-line altitude and mass-balance time series: Validation on three French glaciers, 1994–2002. J. Glaciol. 2005, 51, 539–546. [Google Scholar] [CrossRef] [Green Version]
- Parrot, J.F.; Lyberis, N.; Lefauconnier, B.; Manby, G. SPOT multispectral data and digital terrain model for the analysis of ice-snow fields on arctic glaciers. Int. J. Remote Sens. 1993, 14, 425–440. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Shea, J.M.; Litt, M.; Steiner, J.F.; Treichler, D.; Koch, I.; Immerzeel, W. Mapping Surface Temperatures on a Debris-Covered Glacier with an Unmanned Aerial Vehicle. Front. Earth Sci. 2018, 6, 64. [Google Scholar] [CrossRef] [Green Version]
- Karimi, N.; Farokhnia, A.; Karimi, L.; Eftekhari, M.; Ghalkhani, H. Combining optical and thermal remote sensing data for mapping debris-covered glaciers (Alamkouh Glaciers, Iran). Cold Reg. Sci. Technol. 2012, 71, 73–83. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Joshi, P.; Snehmani; Sam, L.; Singh, M.; Singh, S.; Kumar, R. Applicability of Landsat 8 data for characterizing glacier facies and supraglacial debris. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 51–64. [Google Scholar] [CrossRef]
- Pope, A.; Rees, G. Using in situ spectra to explore Landsat classification of glacier surfaces. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 42–52. [Google Scholar] [CrossRef]
- Paul, F.; Winsvold, S.H.; Kääb, A.; Nagler, T.; Schwaizer, G. Glacier Remote Sensing Using Sentinel-2. Part II: Mapping Glacier Extents and Surface Facies, and Comparison to Landsat 8. Remote Sens. 2016, 8, 575. [Google Scholar] [CrossRef] [Green Version]
- Williams, R.S.; Hall, D.K.; Benson, C.S. Analysis of glacier facies using satellite techniques. J. Glaciol. 1991, 37, 120–128. [Google Scholar] [CrossRef] [Green Version]
- Barzycka, B.; Grabiec, M.; Błaszczyk, M.; Ignatiuk, D.; Laska, M.; Hagen, J.O.; Jania, J. Changes of glacier facies on Hornsund glaciers (Svalbard) during the decade 2007–2017. Remote Sens. Environ. 2020, 251, 112060. [Google Scholar] [CrossRef]
- Brown, I.A.; Kirkbride, M.P.; Vaughan, R.A. Find the firn line! The suitability of ERS-1 and ERS-2 SAR data for the analysis of glacier facies on Icelandic icecaps. Int. J. Remote Sens. 1999, 20, 3217–3230. [Google Scholar] [CrossRef]
- Yousuf, B.; Shukla, A.; Arora, M.K.; Jasrotia, A.S. Glacier facies characterization using optical satellite data: Impacts of radiometric resolution, seasonality, and surface morphology. Prog. Phys. Geogr. Earth Environ. 2019, 43, 473–495. [Google Scholar] [CrossRef]
- Pope, A.; Rees, W.G. Impact of spatial, spectral, and radiometric properties of multispectral imagers on glacier surface classification. Remote Sens. Environ. 2014, 141, 1–13. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J. Explorative Study on Mapping Surface Facies of Selected Glaciers from Chandra Basin, Himalaya Using World, View-2 Data. Remote Sens. 2019, 11, 1207. [Google Scholar] [CrossRef] [Green Version]
- Braun, M.; Schuler, T.V.; Hock, R.; Brown, I.; Jackson, M. Comparison of remote sensing derived glacier facies maps with distributed mass balance modelling at Engabreen, northern Norway. IAHS Publ. Ser. Proc. Rep. 2007, 318, 126–134. [Google Scholar]
- Benson, C. Stratigraphic Studies in the Snow and Firn of the Greenland Ice Sheet, No. RR70; Cold Regions Research and Engineering Lab: Hanover, NH, USA, 1962; Available online: http://acwc.sdp.sirsi.net/client/en_US/search/asset/1001392;jsessionid=351D596A6CE87F45BAEB04E7B9ECE897.enterprise-15000 (accessed on 17 January 2018).
- Braun, M.; Rau, F.; Saurer, H.; Gobmann, H. Development of radar glacier zones on the King George Island ice cap, Antarctica, during austral summer 1996/97 as observed in ERS-2 SAR data. Ann. Glaciol. 2000, 31, 357–363. [Google Scholar] [CrossRef] [Green Version]
- Brown, I.A. Radar Facies on the West Greenland Ice Sheet: Comparison with AVHRR Albedo Data. In Proceedings of the 22nd Symposium of the European Association of Remote Sensing Laboratories, Prague, Czech, 4–6 June 2002; Available online: http://www.earsel.org/symposia/2002-symposium-Prague/pdf/050.pdf (accessed on 18 August 2020).
- Barzycka, B.; Błaszczyk, M.; Grabiec, M.; Jania, J. Glacier facies of Vestfonna (Svalbard) based on SAR images and GPR measurements. Remote Sens. Environ. 2019, 221, 373–385. [Google Scholar] [CrossRef]
- Anderson, L.S.; Armstrong, W.H.; Anderson, R.S.; Buri, P. Debris cover and the thinning of Kennicott Glacier, Alaska: In situ measurements, automated ice cliff delineation and distributed melt estimates. Cryosphere 2021, 15, 265–282. [Google Scholar] [CrossRef]
- Alifu, H.; Johnson, B.A.; Tateishi, R. Delineation of Debris-Covered Glaciers Based on a Combination of Geomorphometric Parameters and a TIR/NIR/SWIR Band Ratio. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 781–792. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Joshi, P.K.; Snehmani; Singh, M.; Sam, L.; Gupta, R. Mapping debris-covered glaciers and identifying factors affecting the accuracy. Cold Reg. Sci. Technol. 2014, 106–107, 161–174. [Google Scholar] [CrossRef]
- Foster, L.A.; Brock, B.W.; Cutler, M.E.J.; Diotri, F. A physically based method for estimating supraglacial debris thickness from thermal band remote-sensing data. J. Glaciol. 2012, 58, 677–691. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hirabayashi, Y.; Fujita, K.; Liu, S.; Liu, Q. Heterogeneity in supraglacial debris thickness and its role in glacier mass changes of the Mount Gongga. Sci. China Earth Sci. 2015, 59, 170–184. [Google Scholar] [CrossRef]
- Pandey, A.; Rai, A.; Gupta, S.K.; Shukla, D.P.; Dimri, A. Integrated approach for effective debris mapping in glacierized regions of Chandra River Basin, Western Himalayas, India. Sci. Total Environ. 2021, 779, 146492. [Google Scholar] [CrossRef] [PubMed]
- Winsvold, S.H.; Kaab, A.; Nuth, C. Regional Glacier Mapping Using Optical Satellite Data Time Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3698–3711. [Google Scholar] [CrossRef] [Green Version]
- Dozier, J. Snow Reflectance from LANDSAT-4 Thematic Mapper. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 323–328. [Google Scholar] [CrossRef]
- Hall, D.; Ormsby, J.; Bindschadler, R.; Siddalingaiah, H. Characterization of Snow and Ice Reflectance Zones on Glaciers Using Landsat Thematic Mapper Data. Ann. Glaciol. 1987, 9, 104–108. [Google Scholar] [CrossRef] [Green Version]
- De Angelis, H.; Rau, F.; Skvarca, P. Snow zonation on Hielo Patagónico Sur, Southern Patagonia, derived from Landsat 5 TM data. Glob. Planet. Chang. 2007, 59, 149–158. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J.; Pandit, P.H.; Kumar, S. Implementing an object-based multi-index protocol for mapping surface glacier facies from Chandra-Bhaga basin, Himalaya. Czech Polar Rep. 2019, 9, 125–140. [Google Scholar] [CrossRef]
- Ali, I.; Shukla, A.; Romshoo, S. Assessing linkages between spatial facies changes and dimensional variations of glaciers in the upper Indus Basin, western Himalaya. Geomorphology 2017, 284, 115–129. [Google Scholar] [CrossRef]
- Shukla, A.; Ali, I. A hierarchical knowledge-based classification for glacier terrain mapping: A case study from Kolahoi Glacier, Kashmir Himalaya. Ann. Glaciol. 2016, 57, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Yousuf, B.; Shukla, A.; Arora, M.K.; Bindal, A.; Jasrotia, A.S. On Drivers of Subpixel Classification Accuracy—An Example from Glacier Facies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 601–608. [Google Scholar] [CrossRef]
- Rahimzadeganasl, A.; Alganci, U.; Goksel, C. An Approach for the Pan Sharpening of Very High Resolution Satellite Images Using a CIELab Color Based Component Substitution Algorithm. Appl. Sci. 2019, 9, 5234. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Smith, S.E.; Grunwald, S.; Abd-Elrahman, A.; Wani, S.P. Incorporation of satellite remote sensing pan-sharpened imagery into digital soil prediction and mapping models to characterize soil property variability in small agricultural fields. ISPRS J. Photogramm. Remote Sens. 2016, 123, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Shen, H.; Li, H.; Zhang, L.; Fu, R. Review of the pansharpening methods for remote sensing images based on the idea of meta-analysis: Practical discussion and challenges. Inf. Fusion 2019, 46, 102–113. [Google Scholar] [CrossRef]
- Jawak, S.; Luis, A.J. A spectral index ratio-based Antarctic land-cover mapping using hyperspatial 8-band World, View-2 imagery. Polar Sci. 2013, 7, 18–38. [Google Scholar] [CrossRef] [Green Version]
- Jawak, S.D.; Luis, A.J.; Fretwell, P.T.; Convey, P.; Durairajan, U.A. Semiautomated Detection and Mapping of Vegetation Distribution in the Antarctic Environment Using Spatial-Spectral Characteristics of World, View-2 Imagery. Remote Sens. 2019, 11, 1909. [Google Scholar] [CrossRef] [Green Version]
- Padwick, C.; Deskevich, M.; Pacifici, F.; Smallwood, S. World, View-2 Pan-Sharpening. In Proceedings of the ASPRS 2010 Annual Conference, San Diego, CA, USA, 26 April 2010; pp. 1–14. Available online: http://www.asprs.org/wp-content/uploads/2013/08/Padwick.pdf (accessed on 12 May 2021).
- Wyczałek, I.; Wyzcałek, E. Studies on parsharpening and object-based classification of World, View-2 multispectral image. Arch. Photogramm. Cartogr. Remote Sens. 2013, 109–117. [Google Scholar]
- Pushparaj, J.; Hegde, A.V. Evaluation of pan-sharpening methods for spatial and spectral quality. Appl. Geomat. 2016, 9, 1–12. [Google Scholar] [CrossRef]
- Snehmani, A.G.; Ganju, A.; Kumar, S.; Srivastava, P.K.; Hari Ram, R.P. A comparative analysis of pansharpening techniques on Quick, Bird and World, View-3 images. Geocarto Int. 2016, 32, 1268–1284. [Google Scholar] [CrossRef]
- Nikolakopoulos, K. Quality assessment of ten fusion techniques applied on Worldview-2. Eur. J. Remote Sens. 2015, 48, 141–167. [Google Scholar] [CrossRef]
- Rayegani, B.; Barati, S.; Goshtasb, H.; Sarkheil, H.; Ramezani, J. An effective approach to selecting the appropriate pan-sharpening method in digital change detection of natural ecosystems. Ecol. Inform. 2019, 53, 100984. [Google Scholar] [CrossRef]
- Wu, B.; Fu, Q.; Sun, L.; Wang, X. Enhanced hyperspherical color space fusion technique preserving spectral and spatial content. J. Appl. Remote Sens. 2015, 9, 097291. [Google Scholar] [CrossRef]
- Du, Y.; Teillet, P.M.; Cihlar, J. Radiometric Normalization of Multi-temporal High Resolution Satellite Images with Quality Control for Land Cover Change Detection. Remote Sens. Environ. 2002, 82, 123–134. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- Bernstein, L.S.; Jin, X.; Gregor, B.; Adler-Golden, S.M. Quick atmospheric correction code: Algorithm description and recent upgrades. Opt. Eng. 2012, 51, 111719. [Google Scholar] [CrossRef]
- Cooley, T.; Anderson, G.; Felde, G.; Hoke, M.; Ratkowski, A.; Chetwynd, J.; Gardner, J.; Adler-Golden, S.; Matthew, M.; Berk, A.; et al. FLAASH, a MODTRAN4-based atmospheric correction algorithm, its application and validation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium 2003, Toronto, ON, Canada, 24–28 June 2002; IEEE: Piscataway, NJ, USA; Volume 3, pp. 1414–1418. [Google Scholar] [CrossRef]
- Adler-Golden, S.M.; Matthew, M.W.; Bernstein, L.S.; Levine, R.Y.; Berk, A.; Richtsmeier, S.C.; Acharya, P.K.; Anderson, G.P.; Felde, J.W.; Gardner, J.A.; et al. Atmospheric correction for shortwave spectral imagery based on MODTRAN4. SPIE Proc. 1999, 3753, 61–69. [Google Scholar] [CrossRef]
- Marcello, J.; Eugenio, F.; Perdomo, U.; Medina, A. Assessment of Atmospheric Algorithms to Retrieve Vegetation in Natural Protected Areas Using Multispectral High Resolution Imagery. Sensors 2016, 16, 1624. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, L.; Mao, Z.; Chen, P.; Han, S.; Gong, F.; Zhu, Q. Comparison and evaluation of atmospheric correction algorithms of QUAC, DOS, and FLAASH for HICO hyperspectral imagery. SPIE Proc. 2016, 9999, 999917. [Google Scholar] [CrossRef]
- Dewi, E.K.; Trisakti, B. Comparing Atmospheric Correction Methods for Landsat Oli Data. Int. J. Remote Sens. Earth Sci. 2016, 13, 105–120. [Google Scholar] [CrossRef] [Green Version]
- Chakouri, M.; Lhissou, R.; El Harti, A.; Maimouni, S.; Adiri, Z. Assessment of the image-based atmospheric correction of multispectral satellite images for geological mapping in arid and semi-arid regions. Remote Sens. Appl. Soc. Environ. 2020, 20, 100420. [Google Scholar] [CrossRef]
- Guo, Z.; Geng, L.; Shen, B.; Wu, Y.; Chen, A.; Wang, N. Spatiotemporal Variability in the Glacier Snowline Altitude across High Mountain Asia and Potential Driving Factors. Remote Sens. 2021, 13, 425. [Google Scholar] [CrossRef]
- Albert, T.H. Evaluation of Remote Sensing Techniques for Ice-Area Classification Applied to the Tropical Quelccaya Ice Cap, Peru. Polar Geogr. 2002, 26, 210–226. [Google Scholar] [CrossRef]
- Luis, A.J.; Singh, S. High-resolution multispectral mapping facies on glacier surface in the Arctic using World, View-3 data. Czech Polar Rep. 2020, 10, 23–36. [Google Scholar] [CrossRef]
- Lee, K.H.; Yum, J.M. A Review on Atmospheric Correction Technique Using Satellite Remote Sensing. Korean J. Remote Sens. 2019, 35, 1011–1030. [Google Scholar] [CrossRef]
- Gore, A.; Mani, S.; HariRam, R.P.; Shekhar, C.; Ganju, A. Glacier surface characteristics derivation and monitoring using Hyperspectral datasets: A case study of Gepang Gath glacier, Western Himalaya. Geocarto Int. 2017, 34, 23–42. [Google Scholar] [CrossRef]
- Thakur, P.K.; Garg, V.; Nikam, B.; Singh, S.; Chouksey, A.; Dhote, P.R.; Aggarwal, S.P.; Chauhan, P.; Kumar, A.S. Jasmine Snow Cover and Glacier Dynamics Study Using C-And L-Band Sar Datasets in Parts of North West Himalaya. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-5, 375–382. [Google Scholar] [CrossRef] [Green Version]
- Hallikainen, M.; Pulliainen, J.; Praks, J.; Arslan, A. Progress and challenges in radar remote sensing of snow. In Proceedings of the Third International Symposium on Retrieval of Bio-and Geophysical Parameters from SAR Data for Land Applications, Sheffield, UK, 11–14 September 2001; ESA SP-475. ESA Publications Division: Noordwijk, The Netherlands; pp. 185–192, ISBN 92-9092-741-0. [Google Scholar]
- Thakur, P.K.; Aggarwal, S.P.; Garg, P.K.; Garg, R.D.; Mani, S.; Pandit, A.; Kumar, S. Snow physical parameter estimation using space-based SAR. Geocarto Int. 2012, 27, 263–288. [Google Scholar] [CrossRef]
- Dozier, J.; Painter, T.H. Multispectral and hyperspectral remote sensing of alpine snow properties. Annu. Rev. Earth Planet. Sci. 2004, 32, 465–494. [Google Scholar] [CrossRef] [Green Version]
- Racoviteanu, A.; Williams, M.W. Decision Tree and Texture Analysis for Mapping Debris-Covered Glaciers in the Kangchenjunga Area, Eastern Himalaya. Remote Sens. 2012, 4, 3078–3109. [Google Scholar] [CrossRef] [Green Version]
- Negi, H.S.; Thakur, N.K.; Ganju, A. Snehmani Monitoring of Gangotri glacier using remote sensing and ground observations. J. Earth Syst. Sci. 2012, 121, 855–866. [Google Scholar] [CrossRef] [Green Version]
- Schuler, T.V.; Kohler, J.; Elagina, N.; Hagen, J.O.M.; Hodson, A.J.; Jania, J.A.; Kääb, A.M.; Luks, B.; Małecki, J.; Moholdt, G.; et al. Reconciling Svalbard Glacier Mass Balance. Front. Earth Sci. 2020, 8, 8. [Google Scholar] [CrossRef]
- Svendsen, H.; Beszczynska-Møller, A.; Hagen, J.O.; Lefauconnier, B.; Tverberg, V.; Gerland, S.; Ørbæk, J.B.; Bischof, K.; Papucci, C.; Zajączkowski, M.; et al. The physical environment of Kongsfjorden–Krossfjorden, an Arctic fjord system in Svalbard. Polar Res. 2002, 21, 133–166. [Google Scholar] [CrossRef] [Green Version]
- Isaksen, K.; Nordli, Ø.; Førland, E.J.; Lupikasza, E.; Eastwood, S.; Niedźwiedź, T. Recent warming on Spitsbergen—Influence of atmospheric circulation and sea ice cover. J. Geophys. Res. Atmos. 2016, 121, 121. [Google Scholar] [CrossRef]
- Nuth, C.; Kohler, J.; König, M.; von Deschwanden, A.; Hagen, J.O.; Kääb, A.; Moholdt, G.; Pettersson, R. Decadal changes from a multi-temporal glacier inventory of Svalbard. Cryosphere 2013, 7, 1603–1621. [Google Scholar] [CrossRef] [Green Version]
- Van Pelt, W.J.J.; Pohjola, V.; Reijmer, C. The Changing Impact of Snow Conditions and Refreezing on the Mass Balance of an Idealized Svalbard Glacier. Front. Earth Sci. 2016, 4, 4. [Google Scholar] [CrossRef]
- Van Pelt, W.; Kohler, J. Modelling the long-term mass balance and firn evolution of glaciers around Kongsfjorden, Svalbard. J. Glaciol. 2015, 61, 731–744. [Google Scholar] [CrossRef] [Green Version]
- Hambrey, M.J.; Murray, T.; Glasser, N.; Hubbard, A.; Hubbard, B.; Stuart, G.; Hansen, S.; Kohler, J. Structure and changing dynamics of a polythermal valley glacier on a centennial timescale: Midre Lovénbreen, Svalbard. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Evans, D.J.; Strzelecki, M.; Milledge, D.; Orton, C. Hørbyebreen polythermal glacial landsystem, Svalbard. J. Maps 2012, 8, 146–156. [Google Scholar] [CrossRef] [Green Version]
- Hamberg, A. En resa till norra Ishafet sommaren 1892. J. Geol. 1895, 4, 25–61. [Google Scholar]
- Liestøl, O. The glaciers in the Kongsfjorden area, Spitsbergen. Nor. Geogr. Tidsskr.-Nor. J. Geogr. 1988, 42, 231–238. [Google Scholar] [CrossRef]
- Pandey, P.; Venkataraman, G. Changes in the glaciers of Chandra–Bhaga basin, Himachal Himalaya, India, between 1980 and 2010 measured using remote sensing. Int. J. Remote Sens. 2013, 34, 5584–5597. [Google Scholar] [CrossRef]
- Kaushik, S.; Joshi, P.K.; Singh, T. Development of glacier mapping in Indian Himalaya: A review of approaches. Int. J. Remote Sens. 2019, 40, 6607–6634. [Google Scholar] [CrossRef]
- Mir, R.A.; Jain, S.K.; Saraf, A.K.; Goswami, A. Glacier changes using satellite data and effect of climate in Tirungkhad basin located in western Himalaya. Geocarto Int. 2013, 29, 293–313. [Google Scholar] [CrossRef]
- Pandey, P.; Kulkarni, A.V.; Venkataraman, G. Remote sensing study of snowline altitude at the end of melting season, Chandra-Bhaga basin, Himachal Pradesh, 1980–2007. Geocarto Int. 2013, 28, 311–322. [Google Scholar] [CrossRef]
- Sahu, R.; Gupta, R.D. Glacier mapping and change analysis in Chandra basin, Western Himalaya, India during 1971–2016. Int. J. Remote Sens. 2020, 41, 6914–6945. [Google Scholar] [CrossRef]
- Jawak, S.D.; Wankhede, S.F.; Luis, A.J. Exploration of Glacier Surface Facies, Mapping Techniques Using Very High Resolution Worldview-2 Satellite Data. Proceedings 2018, 2, 339. [Google Scholar] [CrossRef] [Green Version]
- Shukla, A.; Arora, M.; Gupta, R. Synergistic approach for mapping debris-covered glaciers using optical–thermal remote sensing data with inputs from geomorphometric parameters. Remote Sens. Environ. 2010, 114, 1378–1387. [Google Scholar] [CrossRef]
- Shukla, A.; Gupta, R.; Arora, M. Estimation of debris cover and its temporal variation using optical satellite sensor data: A case study in Chenab basin, Himalaya. J. Glaciol. 2009, 55, 444–452. [Google Scholar] [CrossRef] [Green Version]
- Raup, B.; Racoviteanu, A.; Khalsa, S.J.; Helm, C.; Armstrong, R.; Arnaud, Y. The GLIMS geospatial glacier database: A new tool for studying glacier change. Glob. Planet. Chang. 2007, 56, 101–110. [Google Scholar] [CrossRef]
- Digital Globe Product Details. Available online: https://www.geosoluciones.cl/documentos/worldview/Digital,Globe-Core-Imagery-Products-Guide.pdf (accessed on 20 February 2020).
- ASTER GDEM v2. Available online: Gdex.cr.usgs.gov/gdex/ (accessed on 2 February 2017).
- Arctic DEM. Available online: Pgc.umn.edu/data/arcticdem/ (accessed on 21 January 2019).
- Porter, C.; Morin, P.; Howat, I.; Noh, M.-J.; Bates, B.; Peterman, K.; Keesey, S.; Schlenk, M.; Gardiner, J.; Tomko, K.; et al. “ArcticDEM”, Harvard Dataverse, V1. 2018. Available online: https://www.pgc.umn.edu/data/arcticdem/ (accessed on 13 March 2022).
- Radiative Transfer Code. Available online: https://www.harrisgeospatial.com/docs/backgroundflaash.html (accessed on 20 November 2021).
- Atmospheric Correction User Guide. Available online: https://www.l3harrisgeospatial.com/portals/0/pdfs/envi/Flaash_Module.pdf (accessed on 20 November 2021).
- Kaufman, Y.; Wald, A.; Remer, L.; Gao, B.-C.; Li, R.-R.; Flynn, L. The MODIS 2.1-μm channel-correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1286–1298. [Google Scholar] [CrossRef]
- Abreu, L.W.; Anderson, G.P. The MODTRAN 2/3 report and LOWTRAN 7 model. Contract 1996, 19628, 132. [Google Scholar]
- Teillet, P.; Fedosejevs, G. On the Dark Target Approach to Atmospheric Correction of Remotely Sensed Data. Can. J. Remote Sens. 1995, 21, 374–387. [Google Scholar] [CrossRef]
- Zhang, Z.; He, G.; Zhang, X.; Long, T.; Wang, G.; Wang, M. A coupled atmospheric and topographic correction algorithm for remotely sensed satellite imagery over mountainous terrain. GIScience Remote Sens. 2017, 55, 400–416. [Google Scholar] [CrossRef]
- Rumora, L.; Miler, M.; Medak, D. Impact of Various Atmospheric Corrections on Sentinel-2 Land Cover Classification Accuracy Using Machine Learning Classifiers. ISPRS Int. J. Geo-Inform. 2020, 9, 277. [Google Scholar] [CrossRef] [Green Version]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Rastner, P.; Bolch, T.; Notarnicola, C.; Paul, F. A Comparison of Pixel-and Object-Based Glacier Classification with Optical Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 853–862. [Google Scholar] [CrossRef]
- Description of CC and AC Algorithms. Available online: https://www.l3harrisgeospatial.com/Learn/Whitepapers/Whitepaper-Detail/ArtMID/17811/Article,ID/17299/Workflow-Tools-in-ENVI (accessed on 24 November 2021).
- Mahmon, N.A.; Ya’Acob, N.; Yusof, A.L. Differences of image classification techniques for land use and land cover classification. In Proceedings of the 2015 IEEE 11th International Colloquium on Signal Processing & Its Applications (CSPA), Kuala Lumpur, Malaysia, 6–8 March 2015; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2015; pp. 90–94. [Google Scholar]
- Hamill, P.; Giordano, M.; Ward, C.; Giles, D.; Holben, B. An AERONET-based aerosol classification using the Mahalanobis distance. Atmos. Environ. 2016, 140, 213–233. [Google Scholar] [CrossRef]
- Doma, M.I.; Gomaa, M.S.; Amer, R.A. Sensitivity of Pixel-Based Classifiers to Training Sample Size in Case of High Resolution Satellite Imagery. ERJ. Eng. Res. J. 2014, 37, 365–370. [Google Scholar] [CrossRef]
- Gao, Y.; Mas, J.F. A comparison of the performance of pixel-based and object-based classifications over images with various spatial resolutions. Online J. Earth Sci. 2008, 2, 27–35. [Google Scholar]
- Gevana, D.; Camacho, L.; Carandang, A.; Camacho, S.; Im, S. Land use characterization and change detection of a small mangrove area in Banacon Island, Bohol, Philippines using a maximum likelihood classification method. For. Sci. Technol. 2015, 11, 197–205. [Google Scholar] [CrossRef]
- Chandra Bhensle, A.; Raja, R. An efficient face recognition using PCA and Euclidean distance classification. Int. J. Comput. Sci. Mob. Comput. 2014, 3, 407–413. [Google Scholar]
- Ahmed, A.; Muaz, M.; Ali, M.; Yasir, M.; Minallah, N.; Ullah, S.; Khan, S. Comparing pixel-based classifiers for detecting tobacco crops in north-west Pakistan. In Proceedings of the 2015 7th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 16–19 June 2015; IEEE Conference: Piscataway, NJ, USA, 2015; pp. 211–216. [Google Scholar]
- Cho, M.A.; Debba, P.; Mathieu, R.; Naidoo, L.; Van Aardt, J.; Asner, G. Improving Discrimination of Savanna Tree Species Through a Multiple-Endmember Spectral Angle Mapper Approach: Canopy-Level Analysis. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4133–4142. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Vadrevu, K.P.; Xanthopoulos, G.; Karantounias, G.; Scholze, M. A Comparison of Spectral Angle Mapper and Artificial Neural Network Classifiers Combined with Landsat TM Imagery Analysis for Obtaining Burnt Area Mapping. Sensors 2010, 10, 1967–1985. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, K.; Wang, L.; Chi, H. Methods of Combining Multiple Classifiers with Different Features and Their Applications to Text-Independent Speaker Identification. Int. J. Pattern Recognit. Artif. Intell. 1997, 11, 417–445. [Google Scholar] [CrossRef]
- Mancini, A.; Frontoni, E.; Zingaretti, P. A Winner Takes All Mechanism for Automatic Object Extraction from Multi-Source Data. In Proceedings of the 2009 17th International Conference on Geoinformatics IEEE, Fairfax, VA, USA, 12–14 August 2009; pp. 1–6. [Google Scholar]
- Ni, L.; Xu, H.; Zhou, X. Mineral Identification and Mapping by Synthesis of Hyperspectral VNIR/SWIR and Multispectral TIR Remotely Sensed Data with Different Classifiers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3155–3163. [Google Scholar] [CrossRef]
- Sukcharoenpong, A.; Yilmaz, A.; Li, R. An Integrated Active Contour Approach to Shoreline Mapping Using HSI and DEM. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1586–1597. [Google Scholar] [CrossRef]
- Zou, S.; Gader, P.; Zare, A. Hyperspectral tree crown classification using the multiple instance adaptive cosine estimator. Peer J. 2019, 7, e6405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soul, M.E.; Broadwater, J.B. Featureless classification for active sonar systems. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, NSW, Australia, 24–28 May 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–5. [Google Scholar]
- Ren, H.; Du, Q.; Chang, C.-I.; Jensen, J. Comparison between constrained energy minimization based approaches for hyperspectral imagery. In Proceedings of the IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data, Greenbelt, MD, USA, 27–28 October 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 244–248. [Google Scholar]
- Du, Q.; Ren, H.; Chang, C.-I. A comparative study for orthogonal subspace projection and constrained energy minimization. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1525–1529. [Google Scholar] [CrossRef] [Green Version]
- Pour, A.B.; Park, T.-Y.S.; Park, Y.; Hong, J.K.; Pradhan, B. Application of Constrained Energy Minimization (CEM) Algorithm to ASTER Data for Alteration Mineral Mapping. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, IEEE, Yokohama, Japan, 28 July–2 August 2019; pp. 6760–6763. [Google Scholar]
- Gürsoy, Ö.; Atun, R. Investigating Surface Water Pollution by Integrated Remotely Sensed and Field Spectral Measurement Data: A Case Study. Pol. J. Environ. Stud. 2019, 28, 2139–2144. [Google Scholar] [CrossRef]
- Harris, J.R.; Rogge, D.; Hitchcock, R.; Ijewliw, O.; Wright, D. Mapping lithology in Canada’s Arctic: Application of hyperspectral data using the minimum noise fraction transformation and matched filtering. Can. J. Earth Sci. 2005, 42, 2173–2193. [Google Scholar] [CrossRef]
- Funk, C.; Theiler, J.; Roberts, D.; Borel, C. Clustering to improve matched filter detection of weak gas plumes in hyperspectral thermal imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1410–1420. [Google Scholar] [CrossRef] [Green Version]
- Mehr, S.G.; Ahadnejad, V.; Abbaspour, R.A.; Hamzeh, M. Using the mixture-tuned matched filtering method for lithological mapping with Landsat TM5 images. Int. J. Remote Sens. 2013, 34, 8803–8816. [Google Scholar] [CrossRef]
- Williams, A.P.; Hunt, E.R. Estimation of leafy spurge cover from hyperspectral imagery using mixture tuned matched filtering. Remote Sens. Environ. 2002, 82, 446–456. [Google Scholar] [CrossRef]
- Zadeh, M.; Tangestani, M.; Roldan, F.; Yusta, I. Mineral Exploration and Alteration Zone Mapping Using Mixture Tuned Matched Filtering Approach on ASTER Data at the Central Part of Dehaj-Sarduiyeh Copper Belt, SE Iran. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 284–289. [Google Scholar] [CrossRef]
- Singha, A.; Bhowmik, M.K.; Bhattacherjee, D. Akin-based Orthogonal Space (AOS): A subspace learning method for face recognition. Multimedia Tools Appl. 2020, 79, 35069–35091. [Google Scholar] [CrossRef]
- Ren, H.; Chang, C.-I. A target-constrained interference-minimized filter for subpixel target detection in hyperspectral imagery. In Proceedings of the IGARSS 2000, IEEE 2000 International Geoscience and Remote Sensing Symposium, Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Honolulu, HI, USA, 24–28 July 2000; IEEE: Piscataway, NJ, USA, 2002; Volume 4, pp. 1545–1547. [Google Scholar]
- Du, Q.; Ren, H. On the performance of CEM and TCIMF. In Proceedings of the Defense and Security, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Orlando, FL, USA, 28 March 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5806, pp. 861–869. [Google Scholar]
- Millan, V.E.G.; Pakzad, K.; Faude, U.; Teuwsen, S.; Muterthies, A. Target Detection of Mine-RELATED flooded Areas Using AISA-Eagle Data. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–4. [Google Scholar]
- Seyedain, S.A.; Valadan Zoej, M.J.; Maghsoudi, Y.; Janalipour, M. Improving the Classification Accuracy Using Combination of Target Detection Algorithms in Hyperspectral Images. J. Geomatics Sci. Technol. 2015, 4, 161–174. Available online: http://jgst.issge.ir/article-1-170-en.html (accessed on 18 September 2021).
- Kumar, C.; Shetty, A.; Raval, S.; Champatiray, P.K.; Sharma, R. Sub-pixel mineral mapping using EO-1 hyperion hyperspectral data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 455. [Google Scholar] [CrossRef] [Green Version]
- Sidike, P.; Khan, J.; Alam, M.; Bhuiyan, S. Spectral Unmixing of Hyperspectral Data for Oil Spill Detection. In Optics and Photonics for Information Processing; SPIE Optical Engineering + Applications: San Diego, CA, USA, 2012; Volume 8498, p. 84981B. [Google Scholar] [CrossRef]
- Jawak, S.D.; Devliyal, P.; Luis, A.J. A Comprehensive Review on Pixel Oriented and object Oriented Methods for Information Extraction from Remotely Sensed Satellite Images with a Special Emphasis on Cryospheric Applications. Adv. Remote Sens. 2015, 4, 177–195. [Google Scholar] [CrossRef] [Green Version]
- Keshri, A.K.; Shukla, A.; Gupta, R.P. ASTER ratio indices for supraglacial terrain mapping. Int. J. Remote Sens. 2009, 30, 519–524. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Maxwell, A.E.; Warner, T.A. Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics. Remote Sens. 2020, 12, 1905. [Google Scholar] [CrossRef]
- Casacchia, R.; Lauta, F.; Salvatori, R.; Cagnati, A.; Valt, M.; Ørbæk, J.B. Radiometric investigation of different snow covers in Svalbard. Polar Res. 2001, 20, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Hinkler, J.; Ørbæk, J.B.; Hansen, B.U. Detection of spatial, temporal, and spectral surface changes in the Ny-Ålesund area 79°, N, Svalbard, using a low cost multispectral camera in combination with spectroradiometer measurements. Phys. Chem. Earth Parts A/B/C 2003, 28, 1229–1239. [Google Scholar] [CrossRef]
- Gao, J.; Liu, Y. Applications of remote sensing, GIS and GPS in glaciology: A review. Prog. Phys. Geogr. Earth Environ. 2001, 25, 520–540. [Google Scholar] [CrossRef]
- Zeng, Q.; Cao, M.; Feng, X.; Liang, F.; Chen, X.; Sheng, W. Study on spectral reflection characteristics of snow, ice and water of northwest China. Sci. Sin. Ser. B 1984, 46, 647–656. [Google Scholar]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcântara, E. Atmospheric correction issues for retrieving total suspended matter concentrations in inland waters using OLI/Landsat-8 image. Adv. Space Res. 2017, 59, 2335–2348. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef] [Green Version]
- Binding, C.E.; Jerome, J.H.; Bukata, R.P.; Booty, W.G. Suspended particulate matter in Lake Erie derived from MODIS aquatic colour imagery. Int. J. Remote Sens. 2010, 31, 5239–5255. [Google Scholar] [CrossRef]
- Prieto-Amparan, J.A.; Villarreal-Guerrero, F.; Martinez-Salvador, M.; Manjarrez-Domínguez, C.; Santellano-Estrada, E.; Pinedo-Alvarez, A. Atmospheric and Radiometric Correction Algorithms for the Multitemporal Assessment of Grasslands Productivity. Remote Sens. 2018, 10, 219. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Assessment of atmospheric correction methods for Landsat TM data applicable to Amazon basin LBA research. Int. J. Remote Sens. 2002, 23, 2651–2671. [Google Scholar] [CrossRef]
- Gong, S.; Huang, J.; Li, Y.; Wang, H. Comparison of atmospheric correction algorithms for TM image in inland waters. Int. J. Remote Sens. 2008, 29, 2199–2210. [Google Scholar] [CrossRef]
- Manakos, I.; Manevski, K.; Kalaitzidis, C.; Edler, D. Comparison between Atmospheric Correction Modules on the Basis of Worldview-2 Imagery and In Situ spectroradiometric Measurements. In Proceedings of the 7th EARSeL SIG Imaging Spectroscopy Workshop, Edinburgh, UK, 11–13 April 2011. [Google Scholar]
- Saini, V.; Tiwari, R.; Gupta, R. Comparison of FLAASH and QUAC Atmospheric Correction Methods for Resourcesat-2 LISS-IV Data. In Proceedings of the SPIE, Earth Observing Missions and Sensors: Development, Implementation, and Characterization IV, New Delhi, India, 2 May 2016. [Google Scholar]
- Jin, X.; Paswaters, S.; Cline, H. A comparative study of target detection algorithms for hyperspectral imagery. SPIE Proc. 2009, 7, 73341W. [Google Scholar] [CrossRef]
- Jawak, S.D.; Luis, A. Very high-resolution satellite data for improved land cover extraction of Larsemann Hills, Eastern Antarctica. J. Appl. Remote Sens. 2013, 7, 73460. [Google Scholar] [CrossRef]
- Schadt, E.E.; Linderman, M.D.; Sorenson, J.; Lee, L.; Nolan, G.P. Computational solutions to large-scale data management and analysis. Nat. Rev. Genet. 2010, 11, 647–657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Racoviteanu, A.; Paul, F.; Raup, B.; Khalsa, S.J.; Armstrong, R. Challenges and recommendations in mapping of glacier parameters from space: Results of the 2008 Global Land Ice Measurements from Space (GLIMS) workshop, Boulder, Colorado, USA. Ann. Glaciol. 2009, 50, 53–69. [Google Scholar] [CrossRef] [Green Version]
- Robson, B.A.; Bolch, T.; Mac Donell, S.; Hölbling, D.; Rastner, P.; Schaffer, N. Automated detection of rock glaciers using deep learning and object-based image analysis. Remote Sens. Environ. 2020, 250, 112033. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Z.; Shangguan, D.; Yang, J. Novel Machine Learning Method Integrating Ensemble Learning and Deep Learning for Mapping Debris-Covered Glaciers. Remote Sens. 2021, 13, 2595. [Google Scholar] [CrossRef]
- De Beer, C.M.; Sharp, M.J. Topographic influences on recent changes of very small glaciers in the Monashee Mountains, British Columbia, Canada. J. Glaciol. 2009, 55, 691–700. [Google Scholar] [CrossRef] [Green Version]
- Petrou, Z.I.; Kosmidou, V.; Manakos, I.; Stathaki, T.; Adamo, M.; Tarantino, C.; Tomaselli, V.; Blonda, P.; Petrou, M. A rule-based classification methodology to handle uncertainty in habitat mapping employing evidential reasoning and fuzzy logic. Pattern Recognit. Lett. 2014, 48, 24–33. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Ansari, R.A.; Buddhiraju, K.M. Noise Filtering in High-Resolution Satellite Images Using Composite Multiresolution Transforms. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2018, 86, 249–261. [Google Scholar] [CrossRef]
- Liang, H.; Li, N.; Zhao, S. Salt and Pepper Noise Removal Method Based on a Detail-Aware Filter. Symmetry 2021, 13, 515. [Google Scholar] [CrossRef]
- Green, A.; Berman, M.; Switzer, P.; Craig, M. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Shimamura, Y.; Izumi, T.; Matsuyama, H. Evaluation of a useful method to identify snow-covered areas under vegetation–Comparisons among a newly proposed snow index, normalized difference snow index, and visible reflectance. Int. J. Remote Sens. 2006, 27, 4867–4884. [Google Scholar] [CrossRef]
- ENVI User’s Guide. 2009. Available online: https://www.tetracam.com/PDFs/Rec_Cite9.pdf (accessed on 1 March 2022).
- Ramezan, C.A.; Warner, T.A.; Maxwell, A.E.; Price, B.S. Effects of Training Set Size on Supervised Machine-Learning Land-Cover Classification of Large-Area High-Resolution Remotely Sensed Data. Remote Sens. 2021, 13, 368. [Google Scholar] [CrossRef]
- Schaaf, C.; Wang, Z. MCD43A4 MODIS/Terra+Aqua BRDF/Albedo Nadir BRDF Adjusted Ref Daily L3 Global-500m V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2018.
- Schaaf, C.; Wang, Z.; Zhang, X.; Strahler, A. VIIRS/NPP BRDF/Albedo Albedo Daily L3 Global 500m SIN Grid V001; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2018. [CrossRef]
- Schaaf, C.; Wang, Z.; Zhang, X.; Strahler, A. VIIRS/NPP BRDF/Albedo Albedo Daily L3 Global 1km SIN Grid V001; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2018. [CrossRef]
- Dierckx, W.; Sterckx, S.; Benhadj, I.; Livens, S.; Duhoux, G.; Van Achteren, T.; Francois, M.; Mellab, K.; Saint, G. PROBA-V mission for global vegetation monitoring: Standard products and image quality. Int. J. Remote Sens. 2014, 35, 2589–2614. [Google Scholar] [CrossRef]
- Download of VIIRS VNP43IA3 Datasets. Available online: https://lpdaac.usgs.gov/products/vnp43ia3v001/ (accessed on 25 February 2022).
- Download of CGLS PROBA-V Surface Albedo Data. Available online: https://land.copernicus.eu/global/products/sa (accessed on 25 February 2022).
- Knap, W.H.; Reijmer, C.H.; Oerlemans, J. Narrowband to broadband conversion of Landsat TM glacier albedos. Int. J. Remote. Sens. 1999, 20, 2091–2110. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2000, 76, 213–238. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D.; Liang, S.; Yu, Y.; He, T. Assessment of the Suomi NPP VIIRS Land Surface Albedo Data Using Station Measurements and High-Resolution Albedo Maps. Remote Sens. 2016, 8, 137. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Sun, L.; Zhu, J.; Wei, J.; Su, Q.; Sun, W.; Liu, F.; Shu, M. A simplified Suomi NPP VIIRS dust detection algorithm. J. Atmos. Sol.-Terr. Phys. 2017, 164, 314–323. [Google Scholar] [CrossRef]
- Moroni, B.; Arnalds, O.; Dagsson-Waldhauserová, P.; Crocchianti, S.; Vivani, R.; Cappelletti, D. Mineralogical and Chemical Records of Icelandic Dust Sources Upon Ny-Ålesund (Svalbard Islands). Front. Earth Sci. 2018, 6, 6080–6097. [Google Scholar] [CrossRef]
- Di Mauro, B.; Fava, F.; Ferrero, L.; Garzonio, R.; Baccolo, G.; Delmonte, B.; Colombo, R. Mineral dust impact on snow radiative properties in the European Alps combining ground, UAV, and satellite observations. J. Geophys. Res. Atmos. 2015, 120, 6080–6097. [Google Scholar] [CrossRef]
- Baddock, M.C.; Mockford, T.; Bullard, J.E.; Thorsteinsson, T. Pathways of high-latitude dust in the North Atlantic. Earth Planet. Sci. Lett. 2017, 459, 170–182. [Google Scholar] [CrossRef] [Green Version]
- Dagsson-Waldhauserova, P.; Magnusdottir, A.Ö.; Olafsson, H.; Arnalds, O. The Spatial Variation of Dust Particulate Matter Concentrations during Two Icelandic Dust Storms in 2015. Atmosphere 2016, 7, 77. [Google Scholar] [CrossRef] [Green Version]
- Casey, K.A.; Kääb, A.; Benn, D.I. Geochemical characterization of supraglacial debris via in situ and optical remote sensing methods: A case study in Khumbu Himalaya, Nepal. Cryosphere 2012, 6, 85–100. [Google Scholar] [CrossRef] [Green Version]
- Norwegian Climate Service Center: Observations and Weather Statistics. Available online: https://seklima.met.no/observations/ (accessed on 25 May 2021).
- Close, O.; Benjamin, B.; Petit, S.; Fripiat, X.; Hallot, E. Use of Sentinel-2 and LUCAS Database for the Inventory of Land Use, Land Use Change, and Forestry in Wallonia, Belgium. Land 2018, 7, 154. [Google Scholar] [CrossRef] [Green Version]
- Tsai, Y.-L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. Wet and Dry Snow Detection Using Sentinel-1 SAR Data for Mountainous Areas with a Machine Learning Technique. Remote Sens. 2019, 11, 895. [Google Scholar] [CrossRef] [Green Version]
- Charoenjit, K.; Zuddas, P.; Allemand, P.; Pattanakiat, S.; Pachana, K. Estimation of biomass and carbon stock in Para rubber plantations using object-based classification from Thaichote satellite data in Eastern Thailand. J. Appl. Remote Sens. 2015, 9, 96072. [Google Scholar] [CrossRef] [Green Version]








| Region | Glacier | Areal Extent in km2 | GLIMS Reference ID |
|---|---|---|---|
| Ny-Ålesund Svalbard | Vestre Brøggerbreen | 2.89 | G011694E78906N |
| Austre Lovénbreen | 4.64 | G012161E78870N | |
| Austre Brøggerbreen | 8.08 | G011895E78886N | |
| Midtre Lovénbreen | 4.75 | G012039E78878N | |
| Edithbreen | 3.27 | G012119E78852N | |
| Botnfjellbreen | 4.82 | G012405E78843N | |
| Pedersbreen | 5.87 | G012286E78855N | |
| Uvérsbreen | 13.85 | G012520E78787N | |
| Chandra–Bhaga basin Himalayas | Samudra Tapu | 76.00 | G077426E32511N |
| CB 1 | 27.70 | G077376E32671N | |
| CB 2 | 12.44 | G077368E32619N | |
| CB 3 | 37.43 | G077369E32564N | |
| CB 4 | 12.05 | G077421E32604N | |
| CB 5 | 24.93 | G077485E32394N | |
| CB 6 | 16.65 | G077438E32563N |
| Nomenclature/Abbreviation | Description/Definition |
|---|---|
| DOS | DOS-corrected |
| FLAASH | FLAASH-corrected |
| QUAC | QUAC-corrected |
| GS_DOS | DOS followed by GS sharpening |
| GS_FLAASH | FLAASH followed by GS sharpening |
| GS_QUAC | QUAC followed by GS sharpening |
| HCS_DOS | DOS followed by HCS sharpening |
| HCS_FLAASH | FLAASH followed by HCS sharpening |
| HCS_QUAC | QUAC followed by HCS sharpening |
| DOS_AC/CC | DOS followed by AC or CC classification |
| FLAASH_AC/CC | FLAASH followed by AC or CC classification |
| QUAC_AC/CC | QUAC followed by AC or CC classification |
| GS_DOS_AC/CC | DOS followed by GS followed by AC or CC classification |
| GS_FLAASH_AC/CC | FLAASH followed by GS followed by AC or CC classification |
| GS_QUAC_AC/CC | QUAC followed by GS followed by AC or CC classification |
| HCS_DOS_AC/CC | DOS followed by HCS followed by AC or CC classification |
| HCS_FLAASH_AC/CC | FLAASH followed by HCS followed by AC or CC classification |
| HCS_QUAC_AC/CC | QUAC followed by HCS followed by AC or CC classification |
| AC: ACE/CEM/MF/MTMF/MTTCIMF/OSP/TCIMF | Individual processing schemes are followed by the abbreviations for each advanced classifier |
| CC: MHD/MXL/MD/SAM/WTA | Individual processing schemes are followed by the abbreviations for each conventional classifier |
| Parameter | Chandra–Bhaga Basin | Ny-Ålesund | Computation |
|---|---|---|---|
| Flight date | 16 October 2014 | 10 August 2018 | Imagery metadata |
| Scene center location | Lat: 32.5324 Long: 77.4175 | Lat: 78.8816 Long: 12.0734 | Automatic computation |
| GMT | 5.6825 | 12.7456 | User-defined |
| Sensor altitude (km) | 770 | 770 | Automatic computation |
| View zenith angle (degrees) | 180.00 | 180.00 | Automatic computation |
| Initial visibility (km) | 40.00 | 40.00 | User-defined |
| Atmospheric model | 1 (Tropical) | 4 (Subarctic Summer) | User-defined [93] |
| Aerosol model | 6 (Tropospheric) | 4 (Maritime) | User-defined [93] |
| Water column multiplier | 1.00 | 1.00 | Automatic computation |
| Pixel size (m) | 2.00 | 0.90 | Automatic computation |
| Aerosol scale height | 1.50 | 1.50 | Automatic computation |
| CO2 mixing ratio (ppm) | 390.00 | 390.00 | Automatic computation |
| Spectral Bands | Mean at-Sensor Reflectance of Selected Dark Pixels | |
|---|---|---|
| Ny-Ålesund | Chandra–Bhaga Basin | |
| Coastal | 0.09 | 0.17 |
| Blue | 0.06 | 0.14 |
| Green | 0.04 | 0.11 |
| Yellow | 0.03 | 0.09 |
| Red | 0.03 | 0.08 |
| Red Edge | 0.02 | 0.08 |
| NIR1 | 0.01 | 0.06 |
| NIR2 | 0.01 | 0.06 |
| Approach/Workflow | Algorithm | Description | Reference Applications |
|---|---|---|---|
| Conventional Classifiers | Mahalanobis Distance (MHD) | Assumes equal class covariances and assigns pixels to closest training samples based on direction sensitive highest probability. | Landcover Mahmon et al. [102]; Aerosol classification: Hamill et al. [103]; Assessment: Doma et al. [104]; Gao and Mas [105]; Glacier facies: Jawak et al. [17] |
| Maximum Likelihood (MXL) | Assigns pixels according to highest probability based on an assumption of normal distribution of the statistics for each training sample in each band. | Landcover: Mahmon et al. [102]; Assessment: Doma et al. [104]; Vegetation area: Gevana et al. [106]; Glacier facies: Shukla and Ali [35]; Jawak et al. [17] | |
| Minimum Distance (MD) | Calculates the average of training samples and computes the Euclidean distance from each unknown pixel to the average sample for each class. | Face Recognition: ChandraBhensle and Raja [107]; Landcover: Mahmon et al. [102]; Assessment: Doma et al. [104]; Crop area: Ahmed et al. [108]; Glacier facies: Jawak et al. [17] | |
| Spectral Angle Mapper (SAM) | Uses an n (spectral band numbers)-D angle of spectral similarity to assign pixel spectra to training samples with the smallest angle (hence, closest probable class). | Crop area: Ahmed et al. [108]; Canopy species identification: Cho et al. [109]; Burnt area mapping: Petropoulos et al. [110]; Glacier facies: Jawak et al. [17] | |
| Winner Takes All (WTA) | A voting method that classifies pixels based on the majority compiled from all other methods in the TERCAT workflow. | Pattern recognition: Chen et al. [111]; Polar land cover mapping: Jawak and Luis [40]; Multisource object extraction: Mancini et al. [112] | |
| Advanced Classifiers | Adaptive Coherence Estimator (ACE) | Derived from the generalized likelihood ratio (GLR). It does not require knowledge of all target classes in an image. | Mineral mapping: Ni et al. [113]; Shoreline mapping: Sukcharoenpong et al. [114]; Tree crown classification: Zou et al. [115]; Sonar systems: Soules and Broadwater [116] |
| Constrained Energy Minimization (CEM) | Classifies pixels through a covariance matrix using a constrained finite impulse filter based on the provided training samples. | Assessment: Ren et al. [117]; Du et al. [118]; Mineral mapping: Pour et al. [119]; Glacier facies: Jawak et al. [17] | |
| Matched Filtering (MF) | Minimizes the unknown background spectra according to the training sample through partial unmixing, assigning classes based on mean pixel spectra abundances. | Surface water pollution: Gursoy and Atun [120]; Lithology: Harris et al. [121]; Gas plumes: Funk et al. [122]; Glacier facies: Jawak et al. [17] | |
| Mixture-Tuned Matched Filtering (MTMF) | Adds an infeasibility image to the results to reduce the number of false positives that may occur in MF results. | Lithology: Mehr et al. [123]; Hyperspectral leafy spurge cover: Williams and Hunt Jr. [124]; Mineral mapping: Zadeh et al. [125] | |
| Orthogonal Space Projection (OSP) | Matches pixels to training samples by using an orthogonal subspace projector to remove nontargets and then applying MF. | Assessment: Du et al. [118]; Face recognition: Singha et al. [126]; Glacier facies: Jawak et al. [17] | |
| Target-Constrained Interference-Minimized Filter (TCIMF) | Constrained to eliminate the response of nontargets rather than minimize their energy. It can minimize interferences in classification. | Hyperspectral subpixel target detection: Ren and Chang [127]; Assessment: Du and Ren [128]; Flood area mapping: Millan et al. [129] | |
| Mixture-Tuned Target-Constrained Interference-Minimized Filter (MTTCIMF) | Adds infeasibilty to TCIMF in order to reduce misclassification after using a minimum noise fraction transformation to perform TCIMF | Assessment: Seyedein et al. [130]; Subpixel mineral mapping: Kumar et al. [131]; Oil spill spectral unmixing: Sidike et al. [132] |
| Test Site | Facies | Variations in Spectral Reflectance | |||||
|---|---|---|---|---|---|---|---|
| Atmospheric Corrections | GS Sharpening | HCS Sharpening | |||||
| Max. | Min. | Max. | Min. | Max. | Min. | ||
| Ny-Ålesund | Dry snow | B1 (0.20) | B7 (0.06) | B2 (0.17) | B7 (0.07) | B1 (0.20) | B7 (0.07) |
| Wet snow | B1 (0.10) | B7 (0.03) | B4, B6 (0.11) | B2, B7, B9 (0.09) | B1 (0.10) | B7 (0.03) | |
| Melting snow | B1 (0.11) | B7 (0.03) | B6 (0.12) | B7 (0.08) | B1 (0.11) | B7 (0.04) | |
| Saturated snow | B1 (0.06) | B7 (0.01) | B6 (0.11) | B1 (0.06) | B1 (0.05) | B7 (0.01) | |
| Shadowed snow | B1 (0.06) | B7 (0.01) | B1, B2 (0.08) | B4 (0.01) | B1 (0.05) | B8 (0.00) | |
| Glacier ice | B1 (0.11) | B7 (0.02) | B6 (0.11) | B7, B8 (0.08) | B1 (0.11) | B7 (0.03) | |
| Melting glacier ice | B1 (0.08) | B7 (0.02) | B6 (0.11) | B1 (0.07) | B1 (0.08) | B7 (0.02) | |
| Dirty ice | B1 (0.05) | B7 (0.00) | B1, B2, B4 (0.6) | B7, B8 (0.04) | B1 (0.05) | B7 (0.00) | |
| Streams and crevasses | B1 (0.07) | B7, B8 (0.01) | B6 (0.11) | B1 (0.06) | B1 (0.07) | B7 (0.01) | |
| Chandra–Bhaga basin | Crevasses | B2, B3, B5, B6, B8 (0.08) | B1 (0.05) | B1, B2 (0.06) | B6, B7, B8 (0.02) | B2–B6, B8 (0.7) | B1 (0.05) |
| Glacier ice | B2 (0.27) | B7, B8 (0.21) | B2 (0.22) | B7 (0.15) | B1 (0.27) | B8 (0.20) | |
| Ice mixed debris | B8 (0.07) | B1 (0.02) | B6 (0.06) | B1, B2 (0.03) | B8 (0.04) | B1 (0.02) | |
| Shadowed snow | B8 (0.05) | B1 (0.01) | B1 (0.04) | B2–B8 (0.02) | B8 (0.05) | B1 (0.02) | |
| Debris | B8 (0.05) | B1 (0.01) | B2–B8 (0.02) | B1 (0.01) | B8 (0.16) | B1–B7 (0.01) | |
| Snow | B2 (0.31) | B8 (0.16) | B2 (0.29) | B7 (0.18) | B2 (0.31) | B8 (0.16) | |
| Facies | ACE | CEM | MF | MTMF | MTTCIMF | OSP | TCIMF | |
|---|---|---|---|---|---|---|---|---|
| Ny-Ålesund | Unclassified | 0.04 | 0.10 | 0.03 | 0.18 | 0.05 | 0.03 | 0.20 |
| Dry Snow | 0.64 | 0.28 | 0.31 | 0.45 | 0.14 | 0.29 | 0.43 | |
| Wet Snow | 0.46 | 0.45 | 0.47 | 0.68 | 0.47 | 0.53 | 0.63 | |
| Melting Snow | 0.31 | 0.36 | 0.44 | 0.37 | 0.63 | 0.42 | 0.33 | |
| Saturated Snow | 0.63 | 0.62 | 0.59 | 0.46 | 0.72 | 0.64 | 0.50 | |
| Shadowed Snow | 0.70 | 0.78 | 0.65 | 0.81 | 0.69 | 0.50 | 0.76 | |
| Glacier Ice | 0.38 | 0.37 | 0.44 | 0.32 | 0.42 | 0.60 | 0.29 | |
| Melting Glacier Ice | 0.74 | 0.58 | 0.70 | 0.59 | 0.63 | 0.62 | 0.67 | |
| Dirty Ice | 0.57 | 0.93 | 0.89 | 0.64 | 0.58 | 0.88 | 0.61 | |
| Streams and Crevasses | 0.29 | 0.28 | 0.23 | 0.24 | 0.42 | 0.24 | 0.33 | |
| Chandra–Bhaga basin | Unclassified | 0.59 | 0.54 | 0.81 | 0.55 | 0.81 | 0.35 | 0.78 |
| Crevasses | 4.75 | 5.58 | 4.79 | 4.05 | 6.22 | 5.17 | 4.46 | |
| Glacier Ice | 20.62 | 15.61 | 21.45 | 22.68 | 17.22 | 22.13 | 22.55 | |
| Ice Mixed Debris | 4.04 | 6.89 | 8.42 | 4.82 | 8.69 | 10.44 | 4.55 | |
| Shadowed Snow | 8.44 | 6.98 | 1.93 | 8.20 | 3.09 | 3.97 | 8.27 | |
| Debris | 8.25 | 6.23 | 8.76 | 7.81 | 10.77 | 8.35 | 7.59 | |
| Snow | 29.30 | 34.17 | 29.84 | 27.88 | 29.21 | 25.59 | 27.81 | |
| Facies | MHD | MXL | MD | SAM | WTA | |
|---|---|---|---|---|---|---|
| Ny-Ålesund | Unclassified | 0.00 | 0.00 | 0.00 | 0.76 | 0.02 |
| Dry Snow | 0.16 | 0.15 | 0.16 | 0.26 | 0.16 | |
| Wet Snow | 0.43 | 0.32 | 0.50 | 0.49 | 0.38 | |
| Melting Snow | 0.62 | 0.47 | 0.76 | 0.64 | 0.65 | |
| Saturated Snow | 0.56 | 0.79 | 0.54 | 0.40 | 0.66 | |
| Shadowed Snow | 0.69 | 0.74 | 0.88 | 0.65 | 0.79 | |
| Glacier Ice | 0.50 | 0.62 | 0.35 | 0.45 | 0.54 | |
| Melting Glacier Ice | 0.59 | 0.81 | 0.73 | 0.52 | 0.76 | |
| Dirty Ice | 0.78 | 0.43 | 0.44 | 0.32 | 0.48 | |
| Streams and Crevasses | 0.43 | 0.41 | 0.39 | 0.27 | 0.32 | |
| Chandra–Bhaga basin | Unclassified | 0.00 | 0.00 | 0.00 | 6.02 | 0.37 |
| Crevasses | 3.93 | 8.46 | 4.58 | 1.89 | 4.81 | |
| Glacier Ice | 19.20 | 24.95 | 24.42 | 35.85 | 27.71 | |
| Ice Mixed Debris | 2.84 | 2.39 | 1.72 | 0.57 | 1.84 | |
| Shadowed Snow | 3.56 | 1.47 | 0.94 | 1.90 | 1.65 | |
| Debris | 2.40 | 2.33 | 2.90 | 0.64 | 2.37 | |
| Snow | 44.07 | 36.41 | 41.45 | 29.13 | 37.26 | |
| Algorithm/Classifier | Error Rate | |
|---|---|---|
| Himalayas | Ny-Ålesund | |
| ACE | 0.60 | 0.59 |
| CEM | 0.65 | 0.75 |
| MF | 0.64 | 0.75 |
| MTMF | 0.78 | 0.82 |
| MTTCIMF | 0.82 | 0.91 |
| OSP | 0.77 | 0.88 |
| TCIMF | 0.73 | 0.87 |
| MHD | 0.47 | 0.56 |
| MXL | 0.44 | 0.49 |
| MD | 0.61 | 0.68 |
| SAM | 0.78 | 0.69 |
| WTA | 0.45 | 0.53 |
| Classifier | DOS | FLAASH | QUAC | GS | HCS | ||||
|---|---|---|---|---|---|---|---|---|---|
| DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | ||||
| ACE | 0.38 | 0.53 | 0.42 | 0.56 | 0.80 | 0.79 | 0.66 | 0.48 | 0.77 |
| CEM | 0.46 | 0.63 | 0.64 | 0.78 | 0.79 | 0.84 | 0.79 | 0.62 | 0.81 |
| MF | 0.46 | 0.63 | 0.64 | 0.78 | 0.79 | 0.84 | 0.80 | 0.52 | 0.81 |
| MTMF | 0.77 | 0.84 | 0.78 | 0.77 | 0.87 | 0.84 | 0.83 | 0.72 | 0.81 |
| MTTCI-MF | 0.99 | 0.99 | 1.00 | 0.90 | 0.89 | 0.88 | 0.91 | 0.64 | 0.59 |
| OSP | 0.71 | 0.88 | 0.81 | 0.88 | 0.85 | 0.84 | 0.85 | 0.72 | 0.88 |
| TCIMF | 0.77 | 0.88 | 0.76 | 0.89 | 0.80 | 0.87 | 0.85 | 0.54 | 0.88 |
| MHD | 0.30 | 0.40 | 0.34 | 0.42 | 0.75 | 0.81 | 0.66 | 0.48 | 0.52 |
| MXL | 0.22 | 0.28 | 0.21 | 0.25 | 0.75 | 0.77 | 0.49 | 0.78 | 0.45 |
| MD | 0.36 | 0.37 | 0.52 | 0.68 | 0.80 | 0.79 | 0.82 | 0.81 | 0.69 |
| SAM | 0.55 | 0.66 | 0.62 | 0.67 | 0.89 | 0.83 | 0.79 | 0.91 | 0.73 |
| WTA | 0.20 | 0.28 | 0.28 | 0.35 | 0.76 | 0.76 | 0.61 | 0.76 | 0.46 |
| Test Site Image Subset | Time in Hours (and Storage Space Occupied) | Total Time in h | Total Storage in GB | ||||
|---|---|---|---|---|---|---|---|
| Radiometric Calibration | Pansharpening | Band Math | Classification | Exporting Shapefiles (h) | |||
| Midtre Lovénbreen (ML) | DOS: 0.50 h (0.44 GB) | -- | TD: 1.58 h (5.04 GB) | 4.00 | 6.08 | 5.48 | |
| TERCAT: 1.08 h (1.94 GB) | 2.00 | 3.58 | 2.38 | ||||
| GS: 1.00 h (7.25 GB) | -- | TD: 56.00 h (96.80 GB) | 100.00 | 157.5 | 104.49 | ||
| TERCAT: 48.00 h (34.50 GB) | 35.00 | 84.50 | 42.19 | ||||
| HCS: 0.38 h (8.15 GB) | -- | TD: 51.00 h (90.80 GB) | 86.00 | 137.88 | 99.39 | ||
| TERCAT: 44.00 h (31.50 GB) | 29.00 | 73.88 | 40.09 | ||||
| FLAASH: 0.83 h (0.23 GB) | -- | 0.33 h (0.45 GB) | TD: 2.17 h (5.05 GB) | 9.00 | 12.33 | 5.73 | |
| TERCAT: 1.68 h (0.14 GB) | 1.00 | 3.84 | 0.82 | ||||
| GS: 1.13 h (6.57 GB) | 0.57 h (6.60 GB) | TD: 60.00 h (81.10 GB) | 83.00 | 145.53 | 94.5 | ||
| TERCAT: 50.00 h (31.30 GB) | 32.00 | 84.53 | 44.7 | ||||
| HCS: 0.42 h (9.31 GB) | 0.50 h (6.57 GB) | TD: 54.00 h (80.70 GB) | 82.00 | 137.75 | 96.81 | ||
| TERCAT: 45.00 h (31.30 GB) | 30.00 | 76.75 | 47.41 | ||||
| QUAC: 0.70 h (0.59 GB) | -- | 0.30 h (0.64 GB) | TD: 1.77 h (5.05 GB) | 9.00 | 11.77 | 6.28 | |
| TERCAT: 1.50 h (1.95 GB) | 4.00 | 6.50 | 3.18 | ||||
| GS: 1.00 h (6.57 GB) | 0.50 h (6.70 GB) | TD: 55.00 h (76.5 GB) | 64.00 | 121.20 | 90.36 | ||
| TERCAT: 46.00 h (29 GB) | 25.00 | 73.20 | 42.86 | ||||
| HCS: 0.47 h (9.31 GB) | 0.41 h (6.60 GB) | TD: 51.00 h (80.7 GB) | 74.00 | 126.58 | 97.2 | ||
| TERCAT: 43.00 h (29.9 GB) | 28.00 | 72.58 | 46.4 | ||||
| Samudra Tapu (ST) | DOS: 1.00 h (2.15 GB) | -- | TD: 3.28 h (19.80 GB) | 24.00 | 28.28 | 21.95 | |
| TERCAT: 2.45 h (6.75 GB) | 10.00 | 13.45 | 8.9 | ||||
| GS: 1.25 h (35.6 GB) | -- | TD: 65.00 h (219.00 GB) | 374.00 | 441.25 | 256.75 | ||
| TERCAT: 57.00 h (70.60 GB) | 61.00 | 120.25 | 108.35 | ||||
| HCS: 1.56 h (43.50 GB) | -- | TD: 68.00 h (221.00 GB) | 336.00 | 338.56 | 266.65 | ||
| TERCAT: 58.50 h (75.6 GB) | 71.00 | 132.06 | 121.25 | ||||
| FLAASH: 1.56 h (0.81 GB) | -- | 1.58 h (2.62 GB) | TD: 4.12 h (19.80 GB) | 24.00 | 31.26 | 23.23 | |
| TERCAT: 3.34 h (0.58 GB) | 3.00 | 9.48 | 4.01 | ||||
| GS: 2.40 h (16.50 GB) | 1.85 h (33.00 GB) | TD: 76.00 h (312.00 GB) | 512.00 | 593.81 | 362.31 | ||
| TERCAT: 66.00 h (130.00 GB) | 104.00 | 175.81 | 180.31 | ||||
| HCS: 1.00 h (50.00 GB) | 1.75 h (102.00 GB) | TD: 70.00 h (282.00 GB) | 432.00 | 506.31 | 434.81 | ||
| TERCAT: 59.10 h (109.00 GB) | 96.00 | 159.41 | 261.81 | ||||
| QUAC: 1.35 h (1.10 GB) | -- | 1.50 h (2.06 GB) | TD: 3.80 h (19.80 GB) | 24.00 | 30.65 | 22.96 | |
| TERCAT: 3.10 h (0.683 GB) | 3.00 | 8.95 | 3.843 | ||||
| GS: 2.10 h (16.50 GB) | 1.80 h (33 GB) | TD: 72.6 h (254 GB) | 418.00 | 495.85 | 304.6 | ||
| TERCAT: 64.00 h (108 GB) | 96.00 | 165.25 | 158.6 | ||||
| HCS: 0.90 h (20.50 GB) | 1.72 h (33 GB) | TD: 68.40 h (282 GB) | 432.00 | 504.37 | 336.6 | ||
| TERCAT: 56.10 h (108 GB) | 96.00 | 156.07 | 162.6 | ||||
| Total time and storage | 5247.05 h | 3909.80 GB | |||||
| Test Subset | Spectral Bands | Noise within the Processing Scheme Subsets | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Raw DN | DOS | FLAASH | QUAC | GS | HCS | ||||||
| DOS | FLAASH | QUAC | DOS | FLAASH | QUAC | ||||||
| Samudra Tapu | B1 | 443.81 | 152.56 | 290.19 | 180.59 | 834.25 | 647.47 | 493.75 | 350.27 | 179.23 | 624.17 |
| B2 | 16.72 | 15.68 | 13.11 | 15.49 | 411.80 | 207.93 | 412.07 | 172.58 | 43.79 | 312.83 | |
| B3 | 5.52 | 3.75 | 6.65 | 5.29 | 108.70 | 51.59 | 158.97 | 36.17 | 11.86 | 92.01 | |
| B4 | 2.57 | 2.42 | 2.39 | 3.07 | 58.31 | 20.20 | 88.51 | 25.48 | 6.98 | 77.26 | |
| B5 | 1.68 | 1.21 | 2.00 | 1.21 | 14.59 | 16.33 | 25.34 | 10.11 | 6.66 | 23.59 | |
| B6 | 1.18 | 1.10 | 1.16 | 1.10 | 12.83 | 15.44 | 20.81 | 9.19 | 4.18 | 19.04 | |
| B7 | 1.08 | 1.03 | 1.05 | 1.03 | 8.26 | 12.34 | 19.54 | 5.46 | 3.73 | 18.21 | |
| B8 | 0.96 | 0.94 | 0.99 | 0.95 | 2.15 | 7.62 | 14.99 | 3.01 | 3.37 | 14.01 | |
| Midtre Lovénbreen | B1 | 144.38 | 116.77 | 56.14 | 50.05 | 866.56 | 314.90 | 203.19 | 41.28 | 37.54 | 51.60 |
| B2 | 27.41 | 26.67 | 10.13 | 17.57 | 57.59 | 52.55 | 50.12 | 13.57 | 10.72 | 21.78 | |
| B3 | 2.25 | 2.05 | 2.07 | 3.04 | 47.93 | 35.13 | 30.15 | 9.32 | 8.93 | 11.77 | |
| B4 | 1.18 | 1.17 | 1.29 | 1.72 | 19.88 | 18.72 | 17.20 | 6.41 | 8.23 | 11.28 | |
| B5 | 1.15 | 1.17 | 1.18 | 1.65 | 18.79 | 18.14 | 18.02 | 8.49 | 7.69 | 10.83 | |
| B6 | 1.11 | 1.12 | 1.11 | 1.51 | 17.58 | 15.60 | 13.19 | 5.36 | 7.36 | 9.95 | |
| B7 | 1.00 | 1.00 | 1.01 | 1.24 | 13.78 | 13.90 | 14.24 | 5.21 | 6.70 | 9.48 | |
| B8 | 0.99 | 0.98 | 0.99 | 1.00 | 13.13 | 12.83 | 12.21 | 3.01 | 5.06 | 8.97 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jawak, S.D.; Wankhede, S.F.; Luis, A.J.; Balakrishna, K. Impact of Image-Processing Routines on Mapping Glacier Surface Facies from Svalbard and the Himalayas Using Pixel-Based Methods. Remote Sens. 2022, 14, 1414. https://doi.org/10.3390/rs14061414
Jawak SD, Wankhede SF, Luis AJ, Balakrishna K. Impact of Image-Processing Routines on Mapping Glacier Surface Facies from Svalbard and the Himalayas Using Pixel-Based Methods. Remote Sensing. 2022; 14(6):1414. https://doi.org/10.3390/rs14061414
Chicago/Turabian StyleJawak, Shridhar D., Sagar F. Wankhede, Alvarinho J. Luis, and Keshava Balakrishna. 2022. "Impact of Image-Processing Routines on Mapping Glacier Surface Facies from Svalbard and the Himalayas Using Pixel-Based Methods" Remote Sensing 14, no. 6: 1414. https://doi.org/10.3390/rs14061414
APA StyleJawak, S. D., Wankhede, S. F., Luis, A. J., & Balakrishna, K. (2022). Impact of Image-Processing Routines on Mapping Glacier Surface Facies from Svalbard and the Himalayas Using Pixel-Based Methods. Remote Sensing, 14(6), 1414. https://doi.org/10.3390/rs14061414