A New Method for InSAR Stratified Tropospheric Delay Correction Facilitating Refinement of Coseismic Displacement Fields of Small-to-Moderate Earthquakes
Abstract
:1. Introduction
2. Data and Methodology
2.1. Atmospheric Stratification Delay Estimation
- The turbulent delay component typically results from turbulent processes in the troposphere and leads to three-dimensional spatial heterogeneities in refractivity [20]. The stochastic model of tropospheric spatial variability shows a power-law dependence on frequency [36]. The contribution from this type of component could be reduced by averaging independent interferograms [19].
- Vertical stratified delay is caused by the different vertical refractivity profiles of two acquisitions, assuming no heterogeneity within the horizontal layers [20]. In contrast to the turbulent component, the vertical stratified delay is correlated with topography and affects regions with mountainous terrain conditions [20,21]. Additionally, as revealed by the ERA5 weather model dataset, the stratified delay features a seasonal fluctuation [35]. Many methods rely on a suite of assumptions about the spatial-temporal characteristics of InSAR signals (e.g., the linear progression of deformation over time and the zero-mean Gaussian nature of atmospheric phases) that are often not valid in cases of the stratification delay. This is of great significance for many earthquake studies using InSAR. The coupling in the temporal domain further complicates the correction of stratification delays. Thus, the estimated surface deformation may be ambiguous, and inappropriate correction may lead to an erroneous interpretation of the earthquake deformation.
2.2. Correction Working Flow
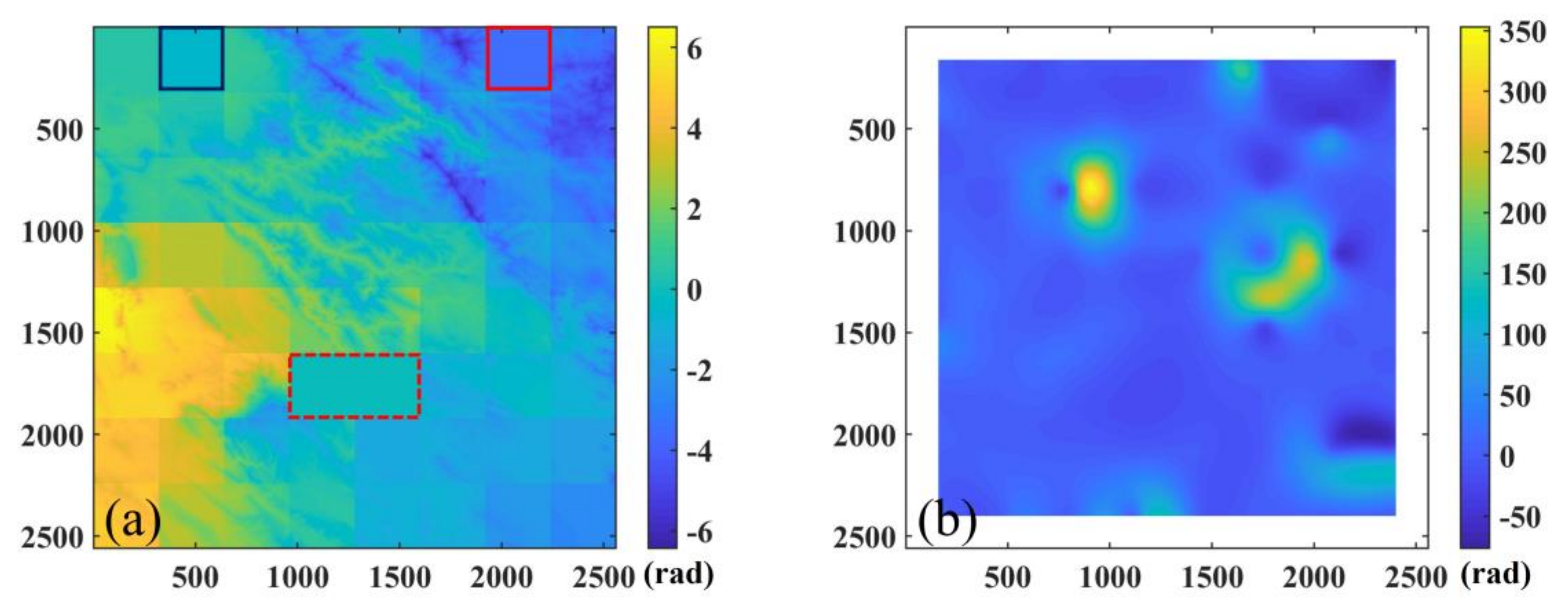
- We masked the coseismic displacement area in individual interferograms. The mask was generated based on the reported epicenter. We aimed to avoid participation of pixels dominated by coseismic displacements in estimating phase-elevation model parameters.
- We then segmented each interferogram into multiple small patches. We cropped the interferogram into by dimensions and the coseismic zone had to be included in this step. We aimed to roll-change the window numbers by a factor of 2 in a more automatic manner. The choice of the number of segmented windows was related to the scale of the estimated stratifications and the size of the earthquakes. We found that a patch number of 8 or 16 in both range and azimuth was appropriate for most of the earthquakes tested here. More scenarios on properly splitting windows will be discussed in Section 4.
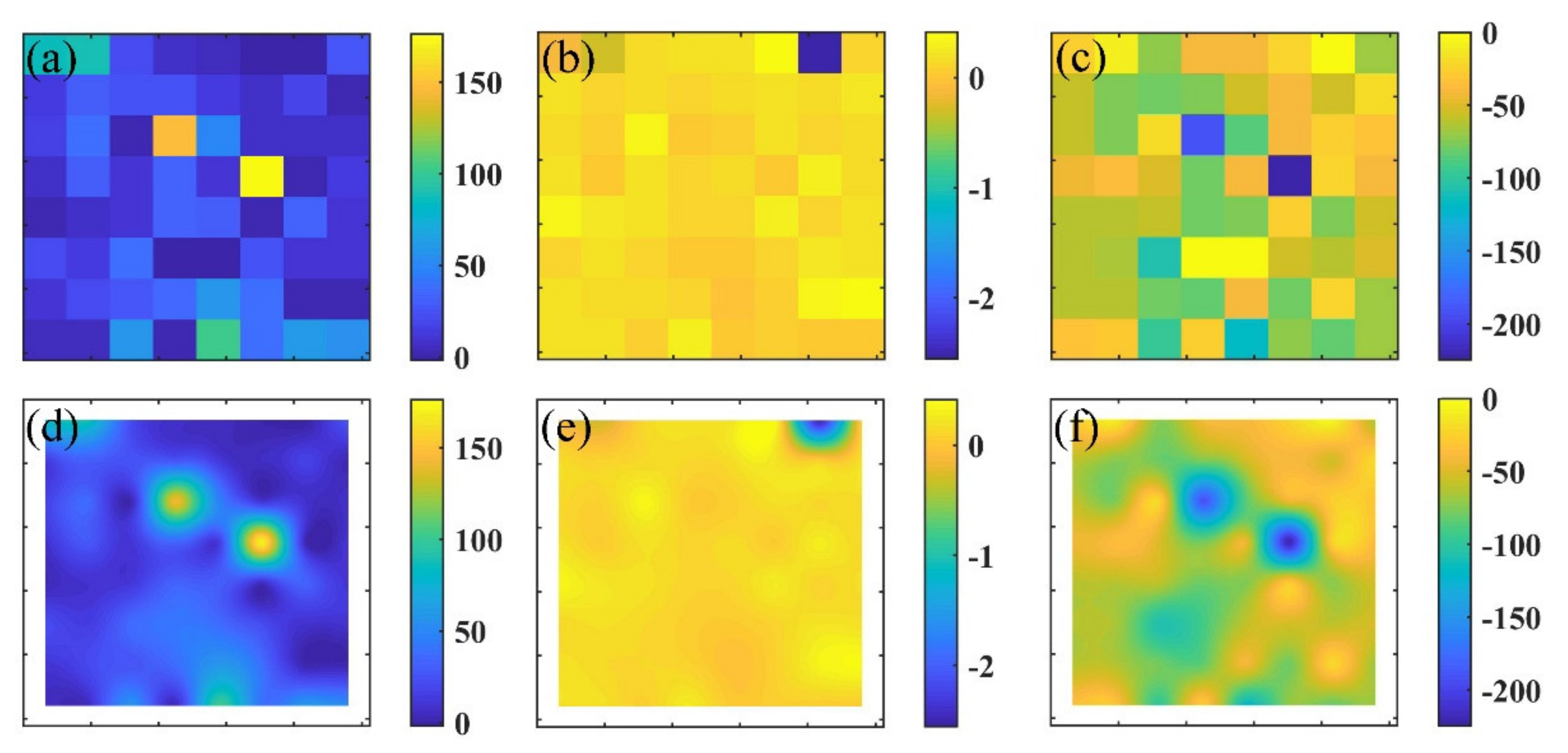
- Each window contained a cluster of pixels, which were subsequently utilized to estimate the phase-elevation model parameters via the empirical linear model (Figure 1). For a window partially impacted by coseismic deformation, the percentage of deforming pixels was computed in conjunction a with previously determined mask of the coseismic zone. The empirical threshold was 60%, meaning that if >60% pixels were not masked, they were used to estimate the phase-elevation model parameters in this window. However, if the percentage was smaller than 60%, this window was recognized as a masked one and the corresponding parameters estimation were skipped here.
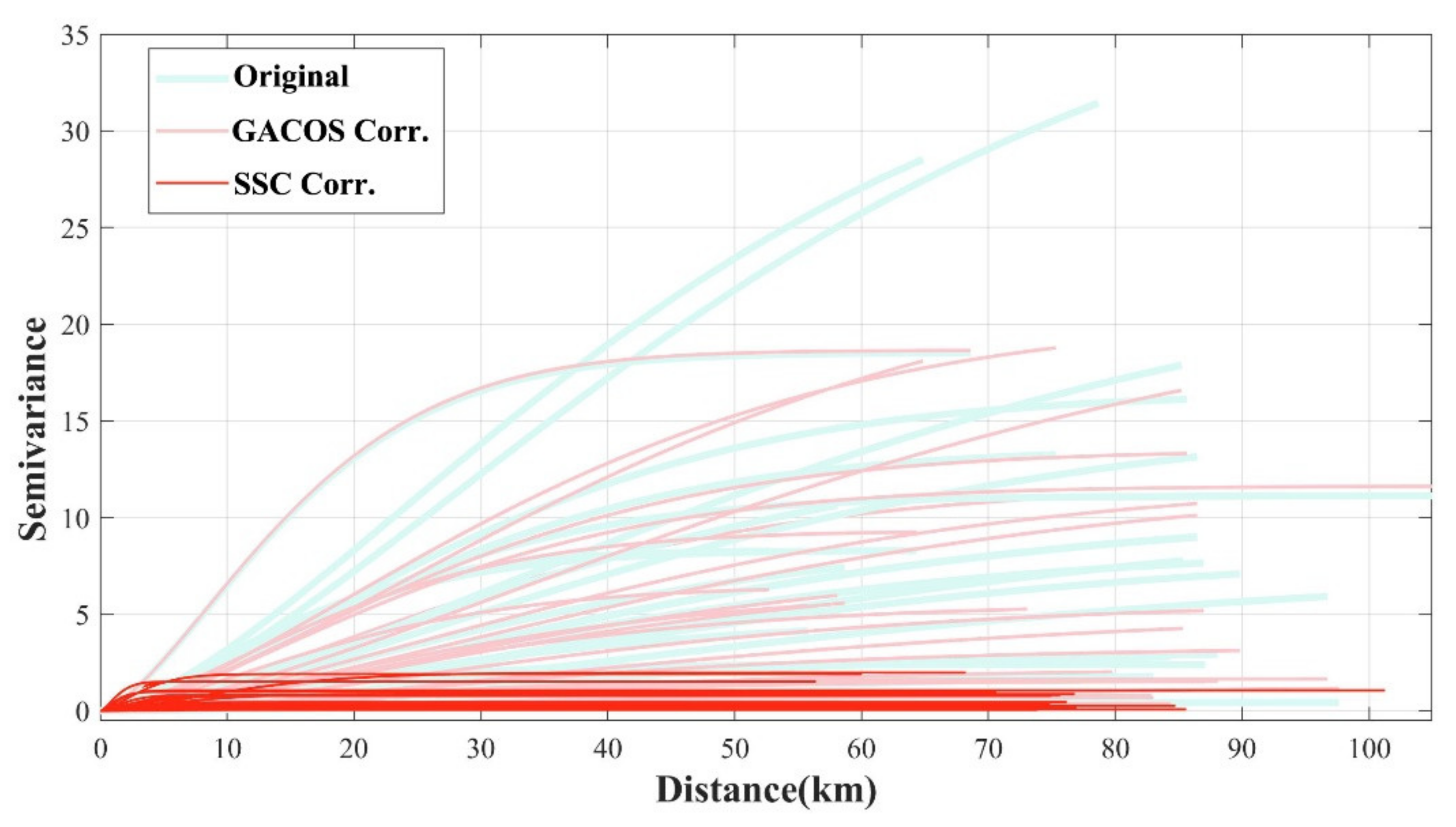
- The next step was to fill the masked windows that failed in the direct estimation in the previous step. We calculated the semi-variogram structure from the input phase over the non-deforming zone. This step aided the kriging solution in predicting the model parameters at those windows dominated by coseismic deformation zones.
- Based on the obtained sparse C (constant parameter) and K (scale parameter) grid, we applied the kriging interpolation to calculate the values at all pixels. For each pixel, we obtained a pair of K and C. Given the known height, we applied these resolved values back to the empirical phase-elevation model to calculate . Note that the estimated parameters in the last step were assigned to be at the center of each window. Therefore, after the spatial interpolation, it left an empty area that was not computable. This appears in Figure 1b as the region outside the dashed box. The width of this zone is the half of a segmented window.
- Finally, we subtracted the modeled tropospheric delay from each unwrapped interferogram to obtain the corrected coseismic displacement map.
2.3. Earthquake Catalog and Coseismic InSAR Observations
3. Results
4. Discussion
4.1. Parameter Setting
4.2. Relationship with Regional Terrain
4.3. Regression Models and Parameters
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lohman, R.B.; Simons, M. Locations of selected small earthquakes in the Zagros mountains. Geochem. Geophys. Geosyst. 2005, 6, Q03001. [Google Scholar] [CrossRef]
- Dawson, J.; Tregoning, P. Uncertainty analysis of earthquake source parameters determined from InSAR: A simulation study. J. Geophys Res.-Sol. Earth 2007, 112, B09406. [Google Scholar] [CrossRef] [Green Version]
- Funning, G.J.; Parsons, B.; Wright, T.J.; Jackson, J.A.; Fielding, E.J. Surface displacements and source parameters of the 2003 Bam (Iran) earthquake from Envisat advanced synthetic aperture radar imagery. J. Geophys. Res. Solid Earth 2005, 110, B09406. [Google Scholar] [CrossRef] [Green Version]
- Mellors, R.J.; Magistrale, H.; Earle, P.; Cogbill, A.H. Comparison of four moderate-size earthquakes in southern California using seismology and InSAR. Seismol. Soc. Am. 2004, 94, 2004–2014. [Google Scholar] [CrossRef] [Green Version]
- Kwong, K.B.; DeShon, H.R.; Kim, J.W.; Lu, Z. Resolving Teleseismic Earthquake Catalog and InSAR Data Discrepancies in Absolute Space to Explore Rupture Complexity Along the Ecuadorian Megathrust Fault. J. Geophys. Res. Solid Earth 2019, 124, 6703–6719. [Google Scholar] [CrossRef] [Green Version]
- Weston, J.; Ferreira, A.M.G.; Funning, G.J. Global compilation of interferometric synthetic aperture radar earthquake source models: 1. Comparisons with seismic catalogs. J. Geophys. Res. Solid Earth 2011, 116, B08408. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, A.M.G.; Weston, J.; Funning, G.J. Global compilation of interferometric synthetic aperture radar earthquake source models: 2. Effects of 3-D Earth structure. J. Geophys. Res. Solid Earth 2011, 116, B08409. [Google Scholar] [CrossRef]
- Wang, R.; Diao, F.; Hoechner, A. SDM—A geodetic inversion code incorporating with layered crust structure and curved fault geometry. In Proceedings of the General Assembly European Geosciences Union, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Tong, X.; Sandwell, D.T.; Fialko, Y. Coseismic slip model of the 2008 Wenchuan earthquake derived from joint inversion of interferometric synthetic aperture radar, GPS, and field data. J. Geophys. Res. Solid Earth 2010, 115, B04314. [Google Scholar] [CrossRef] [Green Version]
- Isken, M.; Sudhaus, H.; Heimann, S.; Steinberg, A.; Daout, S.; Vasyura-Bathke, H. Kite—Software for Rapid Earthquake Source Optimisation from InSAR Surface Displacement; V.0.1; GFZ Data Services: Potsdam, Germany, 2017. [Google Scholar]
- Lindsey, E.O.; Natsuaki, R.; Xu, X.; Shimada, M.; Hashimoto, M.; Melgar, D.; Sandwell, D.T. Line-of-sight displacement from ALOS-2 interferometry: Mw 7.8 Gorkha Earthquake and Mw 7.3 aftershock. Geophys. Res. Lett. 2015, 42, 6655–6661. [Google Scholar] [CrossRef]
- Elliott, J.R.; Walters, R.J.; Wright, T.J. The role of space-based observation in understanding and responding to active tectonics and earthquakes. Nat. Commun. 2016, 7, 13844. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.; Wang, C.; Zhang, B.; Qin, X.; Shan, X. Differential Interferometric Synthetic Aperture Radar data for more accurate earthquake catalogs. Remote Sens. Environ. 2021, 266, 112690. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef] [Green Version]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosystems 2005, 6, Q01007. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, X.; Gong, W.; Zhang, G. The ambiguous fault geometry derived from InSAR measurements of buried thrust earthquakes: A synthetic data based study. Geophys. J. Int. 2021, 225, 1799–1811. [Google Scholar] [CrossRef]
- Xu, W.; Dutta, R.; Jónsson, S. Identifying Active Faults by Improving Earthquake Locations with InSAR Data and Bayesian Estimation: The 2004 Tabuk (Saudi Arabia) Earthquake Sequence. Seismol. Soc. Am. 2015, 105, 765–775. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.; Bock, Y.; Fang, P. Integrated satellite interferometry: Tropospheric noise, GPS estimates and implications for interferometric synthetic aperture radar products. J. Geophys. Res. Solid Earth 1998, 103, 27051–27067. [Google Scholar] [CrossRef]
- Hanssen, R. Radar Interferometry: Data Interpretation and Error Analysis, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; Volume 2. [Google Scholar]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Emardson, T.R.; Simons, M.; Webb, F.H. Neutral atmospheric delay in interferometric synthetic aperture radar applications: Statistical description and mitigation. J. Geophys. Res.-Sol. Earth 2003, 108, 2231. [Google Scholar] [CrossRef]
- Funning, G.J.; Garcia, A. A systematic study of earthquake detectability using Sentinel-1 Interferometric Wide-Swath data. Geophys. J. Int. 2018, 216, 332–349. [Google Scholar] [CrossRef] [Green Version]
- Webley, P.W.; Bingley, R.M.; Dodson, A.H.; Wadge, G.; Waugh, S.J.; James, I.N. Atmospheric water vapour correction to InSAR surface motion measurements on mountains: Results from a dense GPS network on Mount Etna. Phys. Chem. Earth 2002, 27, 363–370. [Google Scholar] [CrossRef]
- Onn, F.; Zebker, H.A. Correction for interferometric synthetic aperture radar atmospheric phase artifacts using time series of zenith wet delay observations from a GPS network. J. Geophys. Res. Solid Earth 2006, 111, B09102. [Google Scholar] [CrossRef]
- Li, Z.H.; Muller, J.P.; Cross, P.; Fielding, E.J. Interferometric synthetic aperture radar (InSAR) atmospheric correction: GPS, moderate resolution Imaging spectroradiometer (MODIS), and InSAR integration. J. Geophys. Res.-Sol. Earth 2005, 110, B03410. [Google Scholar] [CrossRef]
- Gong, W.; Meyer, F.J.; Lee, C.W.; Lu, Z.; Freymueller, J. Measurement and interpretation of subtle deformation signals at Unimak Island from 2003 to 2010 using weather model-assisted time series InSAR. J. Geophys. Res. Solid Earth 2015, 120, 1175–1194. [Google Scholar] [CrossRef]
- Webley, P.W.; Wadge, G.; James, I.N. Determining radio wave delay by non-hydrostatic atmospheric modelling of water vapour over mountains. Phys. Chem. Earth 2004, 29, 139–148. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38, L17311. [Google Scholar] [CrossRef] [Green Version]
- Jolivet, R.; Agram, P.S.; Lin, N.N.Y.; Simons, M.; Doin, M.P.; Peltzer, G.; Li, Z.H. Improving InSAR geodesy using Global Atmospheric Models. J. Geophys. Res.-Sol. Earth 2014, 119, 2324–2341. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Luo, H.; Wang, T.; Wei, S.; Liao, M.; Gong, J. Deriving Centimeter-Level Coseismic Deformation and Fault Geometries of Small-To-Moderate Earthquakes From Time-Series Sentinel-1 SAR Images. Front. Earth Sci. 2021, 9, 32. [Google Scholar] [CrossRef]
- Hou, L.; Shan, X.; Gong, W.; Zhang, Y.; Luo, H.; Zhao, D. Characterizing seismogenic fault of 2016 Dingjie earthquake based on multitemporal DInSAR. Chin. J. Geophys. 2020, 63, 1357–1369. [Google Scholar] [CrossRef]
- Daout, S.; Sudhaus, H.; Kausch, T.; Steinberg, A.; Dini, B. Interseismic and Postseismic Shallow Creep of the North Qaidam Thrust Faults Detected with a Multitemporal InSAR Analysis. J. Geophys. Res. Solid Earth 2019, 124, 7259–7279. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Liao, M.; Gong, J. Improved correction of seasonal tropospheric delay in InSAR observations for landslide deformation monitoring. Remote Sens. Environ. 2019, 233, 111370. [Google Scholar] [CrossRef]
- Knospe, S.H.G.; Jonsson, S. Covariance Estimation for dInSAR Surface Deformation Measurements in the Presence of Anisotropic Atmospheric Noise. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2057–2065. [Google Scholar] [CrossRef]
- Agram, P.S.; Simons, M. A noise model for InSAR time series. J. Geophys. Res.-Sol. Earth 2015, 120, 2752–2771. [Google Scholar] [CrossRef]
- Lin, Y.N.N.; Simons, M.; Hetland, E.A.; Muse, P.; DiCaprio, C. A multiscale approach to estimating topographically correlated propagation delays in radar interferograms. Geochem. Geophys. Geosystems 2010, 11, Q09002. [Google Scholar] [CrossRef]
- Cavalié, O.; Doin, M.-P.; Lasserre, C.; Briole, P. Ground motion measurement in the Lake Mead area, Nevada, by differential synthetic aperture radar interferometry time series analysis: Probing the lithosphere rheological structure. J. Geophys. Res. Solid Earth 2007, 112, B03403. [Google Scholar] [CrossRef] [Green Version]
- Murray, K.D.; Lohman, R.B.; Bekaert, D.P.S. Cluster-Based Empirical Tropospheric Corrections Applied to InSAR Time Series Analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2204–2212. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A spatially-variable power-law tropospheric correction technique for InSAR data. J. Geophys. Res. Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. Reassessing the 2006 Guerrero slow slip event, Mexico: Implications for large earthquakes in the Guerrero Gap. J. Geophys. Res. Solid Earth 2015, 120, 1357–1375. [Google Scholar] [CrossRef]
- Bejar-Pizarro, M.; Socquet, A.; Armijo, R.; Carrizo, D.; Genrich, J.; Simons, M. Andean structural control on interseismic coupling in the North Chile subduction zone. Nat. Geosci. 2013, 6, 462–467. [Google Scholar] [CrossRef] [Green Version]
- Liang, H.; Zhang, L.; Ding, X.; Lu, Z.; Li, X. Toward Mitigating Stratified Tropospheric Delays in Multitemporal InSAR: A Quadtree Aided Joint Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 291–303. [Google Scholar] [CrossRef]
- Bekaert, D.P.S. InSAR Time Series Analysis of the 2006 Slow Slip Event on the Guerrero Subduction Zone, Mexico. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalie, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Meyer, F.J.; Whitley, M.; Logan, T.; McAlpin, D.B.; Hogenson, K.; Nicoll, J.B. The sarviews project: Automated processing of sentinel-1 sar data for geoscience and hazard response. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5468–5471. [Google Scholar]
- Gong, W.; Zhang, Y.; Li, T.; Wen, S.; Zhao, D.; Hou, L.; Shan, X. Multi-Sensor Geodetic Observations and Modeling of the 2017 Mw 6.3 Jinghe Earthquake. Remote Sens. 2019, 11, 2157. [Google Scholar] [CrossRef] [Green Version]
- Murray, K.D.; Bekaert, D.P.S.; Lohman, R.B. Tropospheric corrections for InSAR: Statistical assessments and applications to the Central United States and Mexico. Remote Sens. Environ. 2019, 232, 111326. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar] [CrossRef]
- Ghayournajarkar, N.; Fukushima, Y. Using InSAR for evaluating the accuracy of locations and focal mechanism solutions of local earthquake catalogues. Geophys. J. Int. 2022. [Google Scholar] [CrossRef]
- Dal Zilio, L.; Hetényi, G.; Hubbard, J.; Bollinger, L. Building the Himalaya from tectonic to earthquake scales. Nat. Rev. Earth Environ. 2021, 2, 251–268. [Google Scholar] [CrossRef]
- Michel, S.; Jolivet, R.; Rollins, C.; Jara, J.; dal Zilio, L. Seismogenic Potential of the Main Himalayan Thrust Constrained by Coupling Segmentation and Earthquake Scaling. Geophys. Res. Lett. 2021, 48, e2021GL093106. [Google Scholar] [CrossRef]
- Dal Zilio, L.; Jolivet, R.; van Dinther, Y. Segmentation of the Main Himalayan Thrust Illuminated by Bayesian Inference of Interseismic Coupling. Geophys. Res. Lett. 2020, 47, e2019GL086424. [Google Scholar] [CrossRef] [Green Version]
- Grandin, R.; Doin, M.-P.; Bollinger, L.; Pinel-Puysségur, B.; Ducret, G.; Jolivet, R.; Sapkota, S.N. Long-term growth of the Himalaya inferred from interseismic InSAR measurement. Geology 2012, 40, 1059–1062. [Google Scholar] [CrossRef] [Green Version]
- Lauknes, T.R. InSAR Tropospheric Stratification Delays: Correction Using a Small Baseline Approach. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1070–1074. [Google Scholar] [CrossRef]
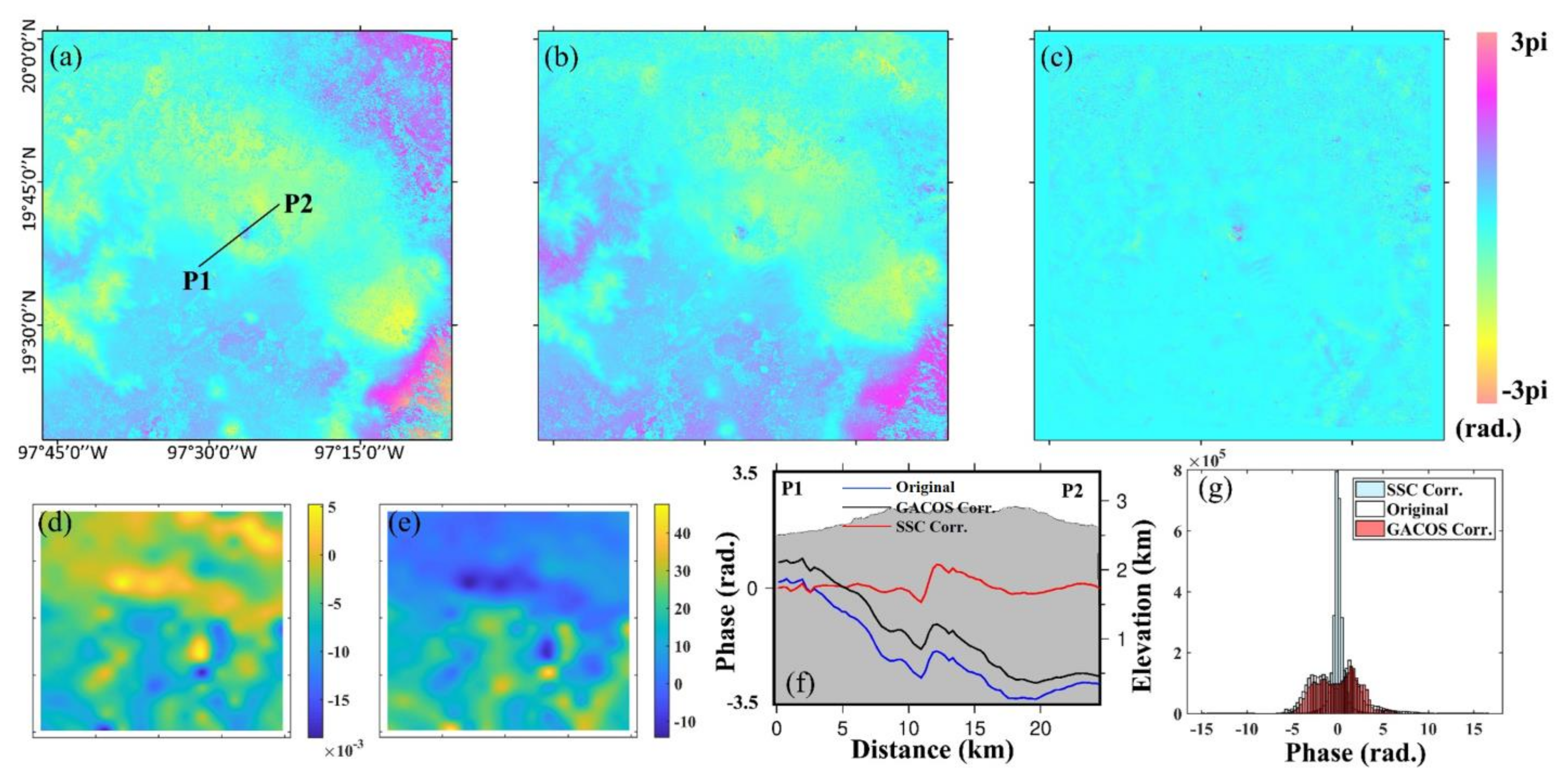
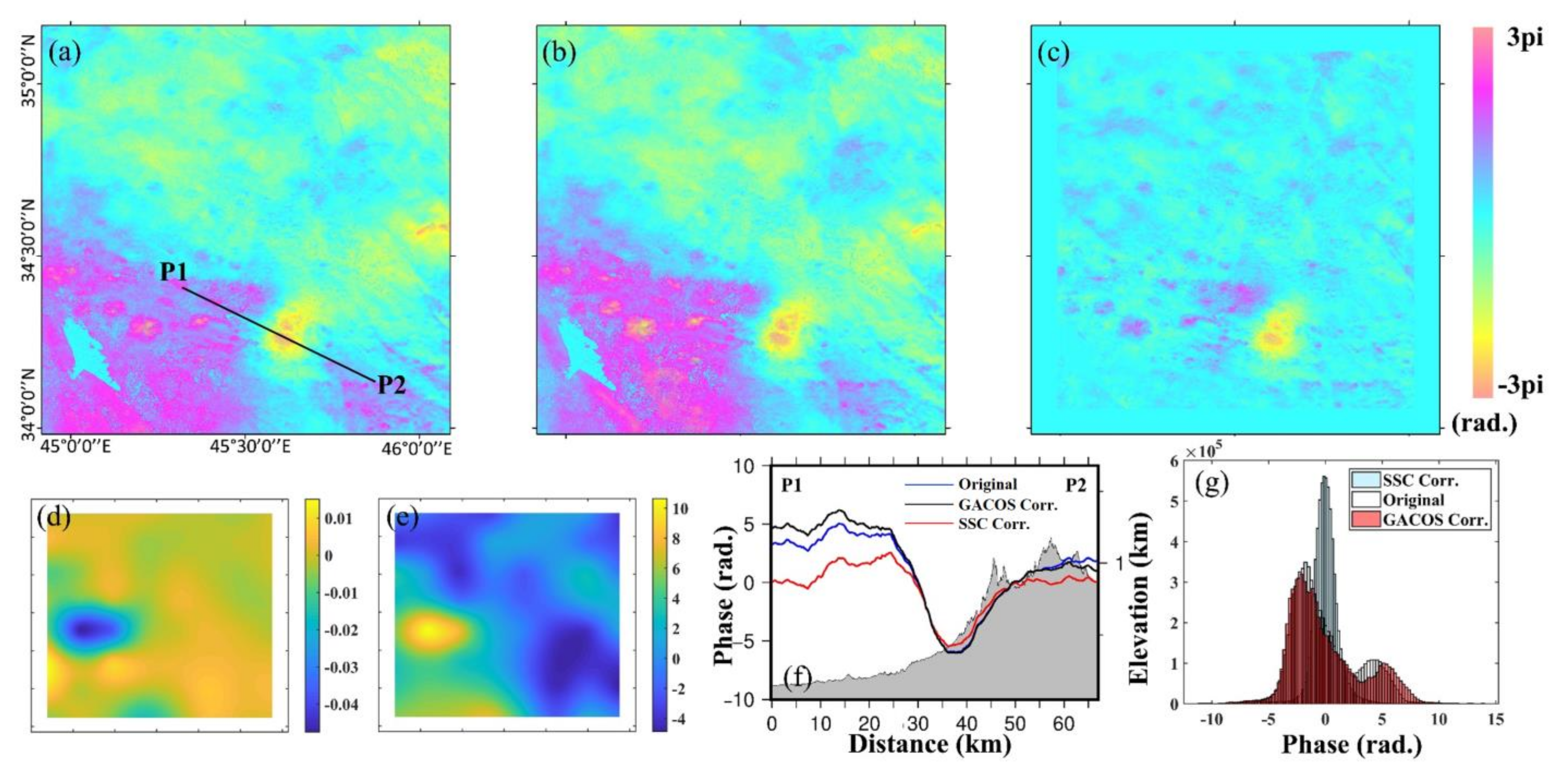
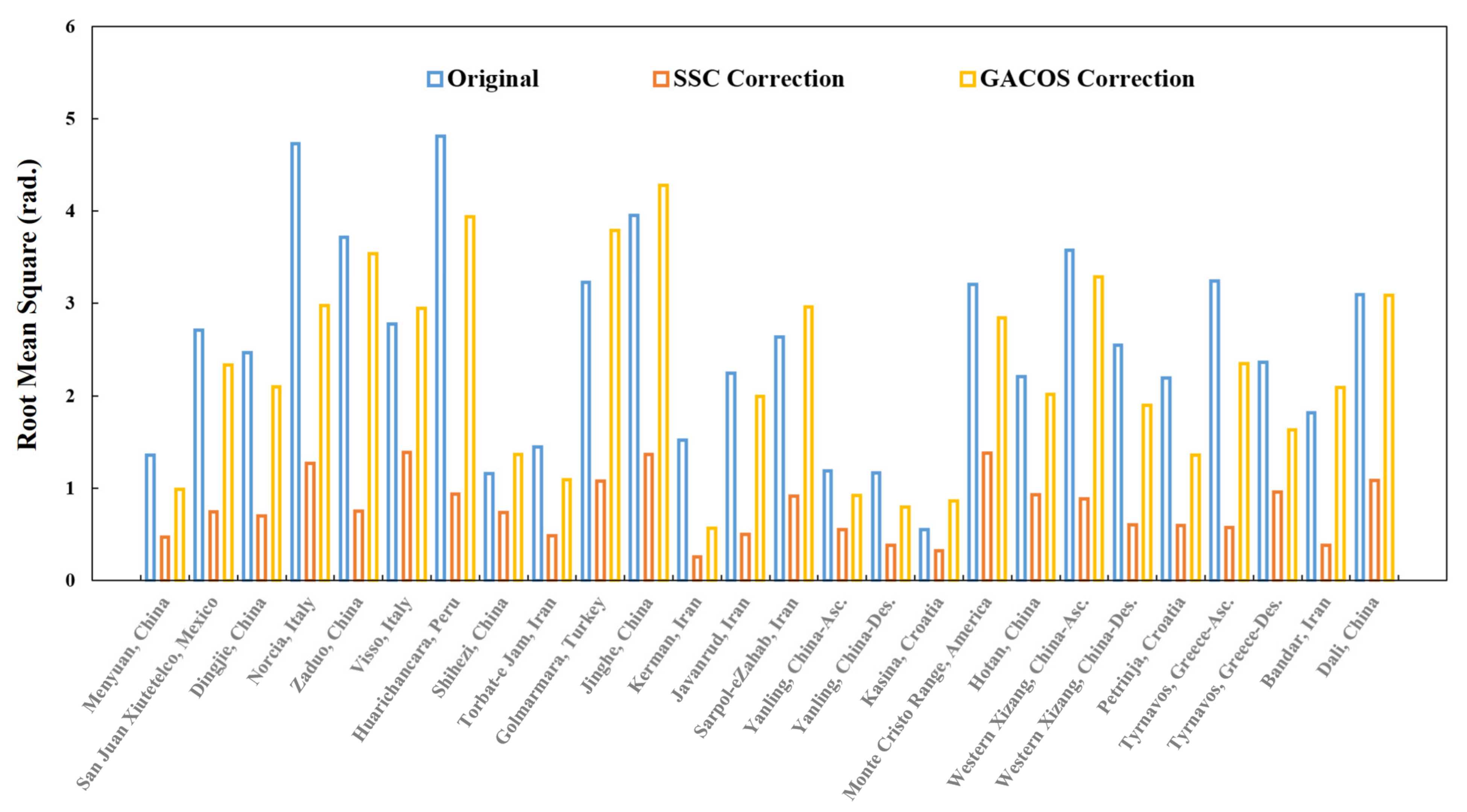

| Index | Date | Location | Lat. (deg) | Lon. (deg) | Depth (km) | Mw | Strike (deg) | Dip (deg) | Rake (deg) | Patch Number |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 20 January 2016 | Menyuan, China | 37.72 | 101.68 | 12.50 | 5.87 | 129 | 47 | 77 | 8 |
| 2 | 8 February 2016 | San Juan Xiutetelco, Mexico | 19.67 | −97.45 | 1.50 | 4.83 | 160 | 80 | 96 | 16 |
| 3 | 22 May 2016 | Dingjie, China | 28.48 | 87.61 | 2.40 | 5.58 | 188 | 43 | −78 | 8 |
| 4 | 24 August 2016 | Norcia, Italy | 42.74 | 13.29 | 5.00 | 6.16 | 168 | 50 | −83 | 8 |
| 5 | 17 October 2016 | Zaduo, China | 32.88 | 94.82 | 10.50 | 5.85 | 68 | 69 | −104 | 8 |
| 6 | 26 October 2016 | Visso, Italy | 42.97 | 13.20 | 5.00 | 6.28 | 155 | 40 | −91 | 8 |
| 7 | 1 December 2016 | Huarichancara, Peru | −15.29 | −70.84 | 5.50 | 6.18 | 150 | 44 | −92 | 8 |
| 8 | 8 December 2016 | Shihezi, China | 43.79 | 86.33 | 19.00 | 5.82 | 280 | 61 | 80 | 16 |
| 9 | 5 April 2017 | Torbat-e Jam, Iran | 35.83 | 60.44 | 8.92 | 6.14 | 124 | 42 | 62 | 8 |
| 10 # | 27 May 2017 | Golmarmara, Turkey | 38.73 | 27.79 | 5.00 | 5.58 | 304 | 60 | −89 | 16 |
| 11 | 8 August 2017 | Jinghe, China | 44.26 | 82.72 | 14.05 | 6.19 | 90 | 42 | 89.56 | 8 |
| 12 | 1 December 2017 | Kerman, Iran | 30.78 | 57.34 | 7.45 | 6.08 | 119 | 51 | 80 | 8 |
| 13 | 25 August 2018 | Javanrud, Iran | 34.63 | 46.24 | 5.50 | 5.98 | 264 | 78 | 4 | 8 |
| 14 | 25 November 2018 | Sarpol-e Zahab, Iran | 34.39 | 45.60 | 14.50 | 6.50 | 25 | 63 | −173 | 8 |
| 15 | 25 February 2019 | Yanling, China | 29.47 | 104.50 | 1.67 | 4.83 | 174 | 64 | 80 | 8 |
| 16 | 22 March 2020 | Kasina, Croatia | 45.84 | 16.04 | 9.15 | 5.55 | 46 | 16 | 9 | 8 |
| 17 | 15 May 2020 | Monte Cristo Range, America | 38.18 | −117.93 | 9.84 | 6.44 | 76 | 73 | −10 | 4 |
| 18 | 25 June 2020 | Hotan, China | 35.61 | 82.47 | 9.78 | 6.28 | 186 | 68 | −89 | 8 |
| 19 # | 22 July 2020 | Western Xizang, China | 33.20 | 86.82 | 10.00 | 6.36 | 31 | 52 | −80 | 8 |
| 20 | 29 December 2020 | Petrinja, Croatia | 45.43 | 16.22 | 5.00 | 6.48 | 120 | 78 | 174 | 8 |
| 21 # | 3 March 2021 | Tyrnavos, Greece | 39.63 | 22.15 | 6.00 | 6.39 | 292 | 35 | −98 | 8 (Asc.) 6 (Des.) |
| 22 | 18 April 2021 | Bandar, Iran | 29.72 | 50.60 | 6.50 | 6.10 | 306 | 60 | 81 | 8 |
| 23 | 21 May 2021 | Dali, China | 25.64 | 99.94 | 7.00 | 6.09 | 134 | 90 | 179 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, W.; Zhao, D.; Zhu, C.; Zhang, Y.; Li, C.; Zhang, G.; Shan, X. A New Method for InSAR Stratified Tropospheric Delay Correction Facilitating Refinement of Coseismic Displacement Fields of Small-to-Moderate Earthquakes. Remote Sens. 2022, 14, 1425. https://doi.org/10.3390/rs14061425
Gong W, Zhao D, Zhu C, Zhang Y, Li C, Zhang G, Shan X. A New Method for InSAR Stratified Tropospheric Delay Correction Facilitating Refinement of Coseismic Displacement Fields of Small-to-Moderate Earthquakes. Remote Sensing. 2022; 14(6):1425. https://doi.org/10.3390/rs14061425
Chicago/Turabian StyleGong, Wenyu, Dezheng Zhao, Chuanhua Zhu, Yingfeng Zhang, Chenglong Li, Guifang Zhang, and Xinjian Shan. 2022. "A New Method for InSAR Stratified Tropospheric Delay Correction Facilitating Refinement of Coseismic Displacement Fields of Small-to-Moderate Earthquakes" Remote Sensing 14, no. 6: 1425. https://doi.org/10.3390/rs14061425
APA StyleGong, W., Zhao, D., Zhu, C., Zhang, Y., Li, C., Zhang, G., & Shan, X. (2022). A New Method for InSAR Stratified Tropospheric Delay Correction Facilitating Refinement of Coseismic Displacement Fields of Small-to-Moderate Earthquakes. Remote Sensing, 14(6), 1425. https://doi.org/10.3390/rs14061425






