Comparing Offshore Ferry Lidar Measurements in the Southern Baltic Sea with ASCAT, FINO2 and WRF
Abstract
:1. Introduction
2. Measurements and Data Processing
2.1. Kiel Ferry Lidar
2.2. Sea Surface Temperature
2.3. FINO2
2.4. ASCAT
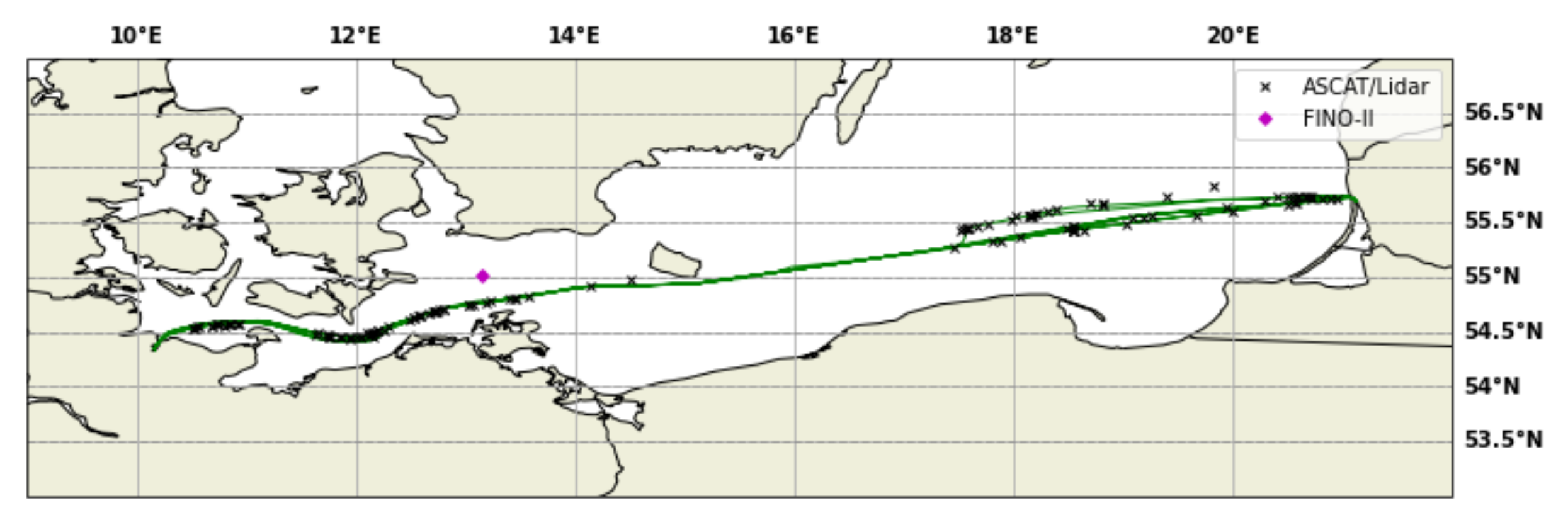
2.5. Collocation Procedure
2.6. Atmospheric Stability Calculation
2.7. Mesoscale Model Simulations
3. Results
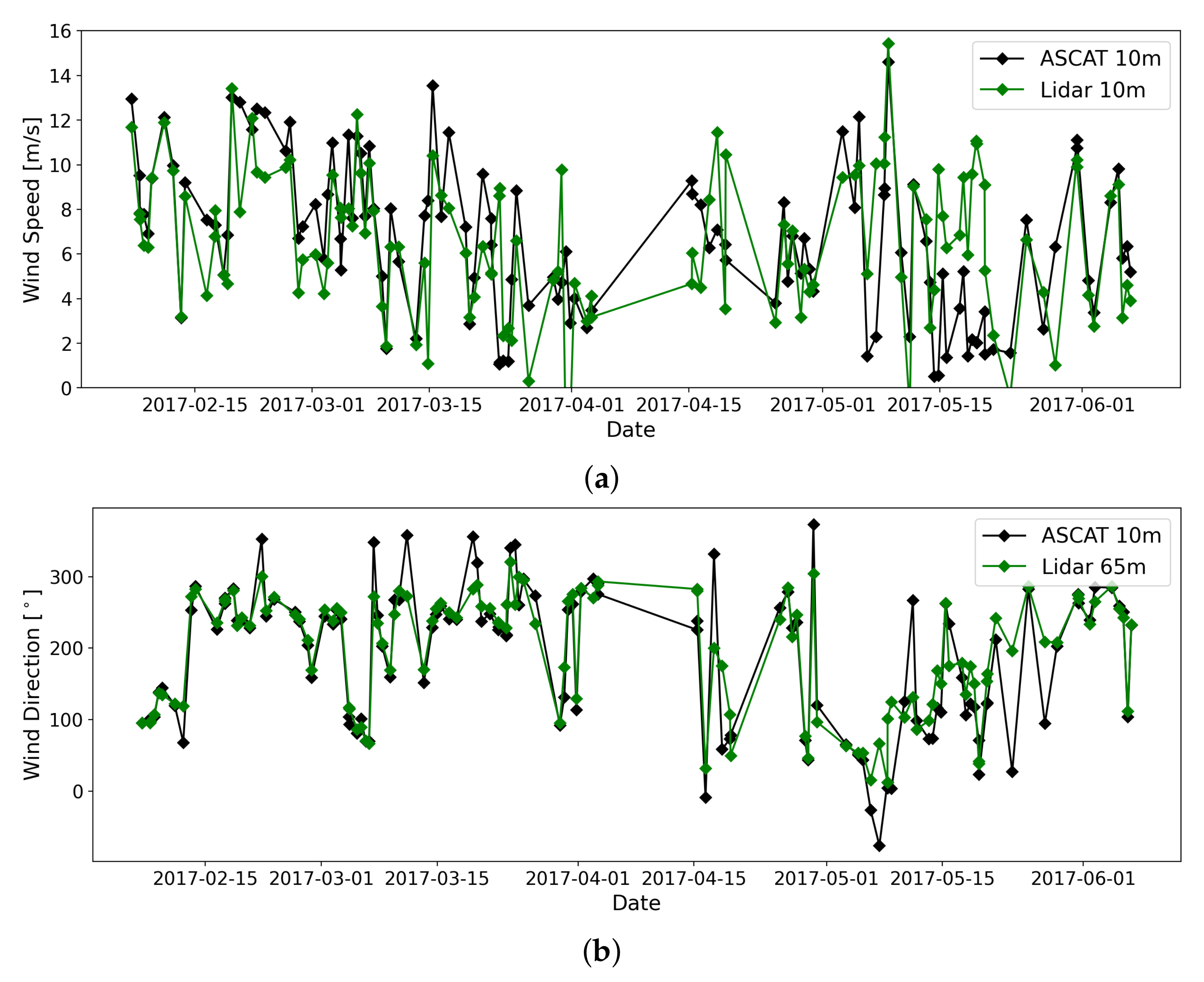
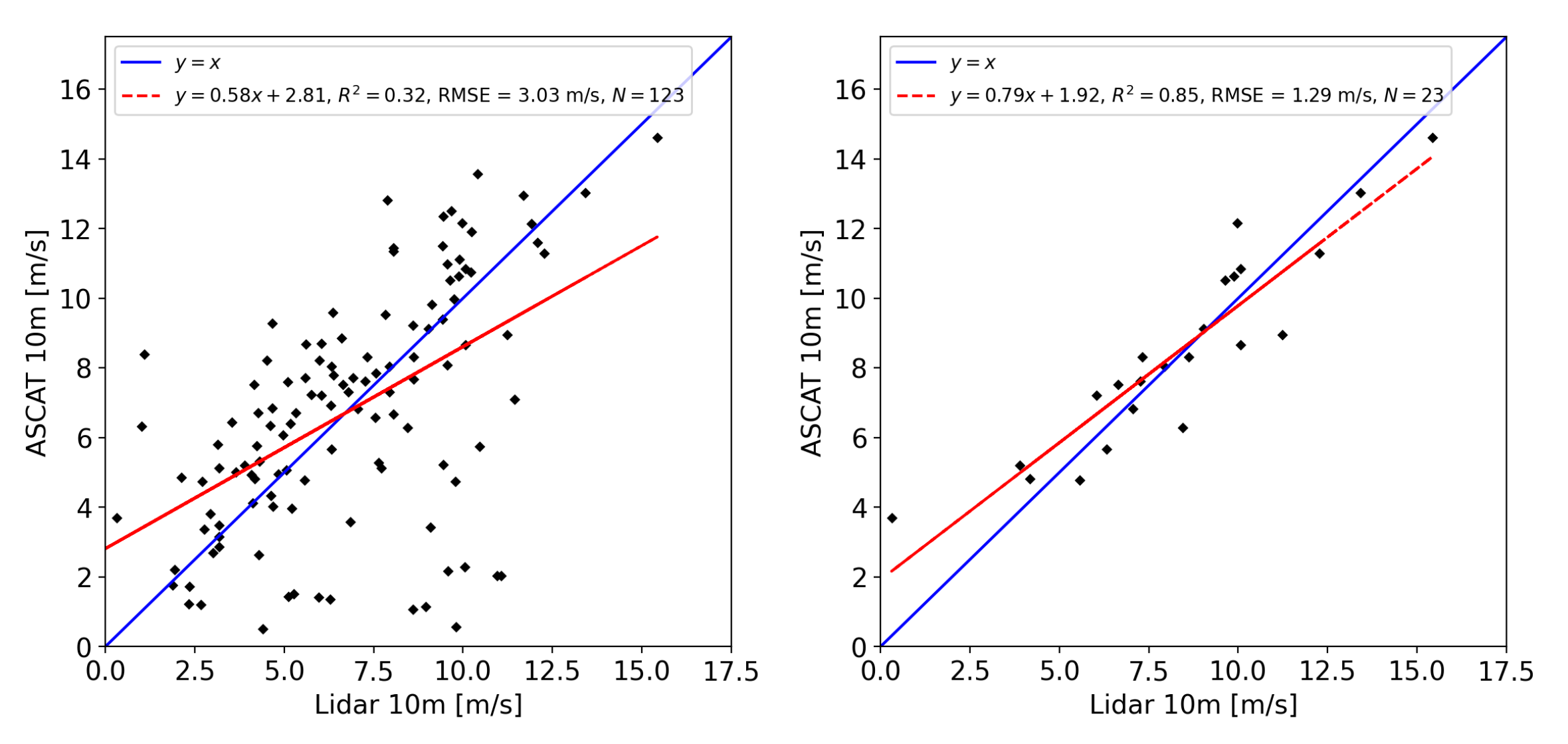
3.1. Ferry Lidar vs. ASCAT
3.2. Ferry Lidar vs. FINO2
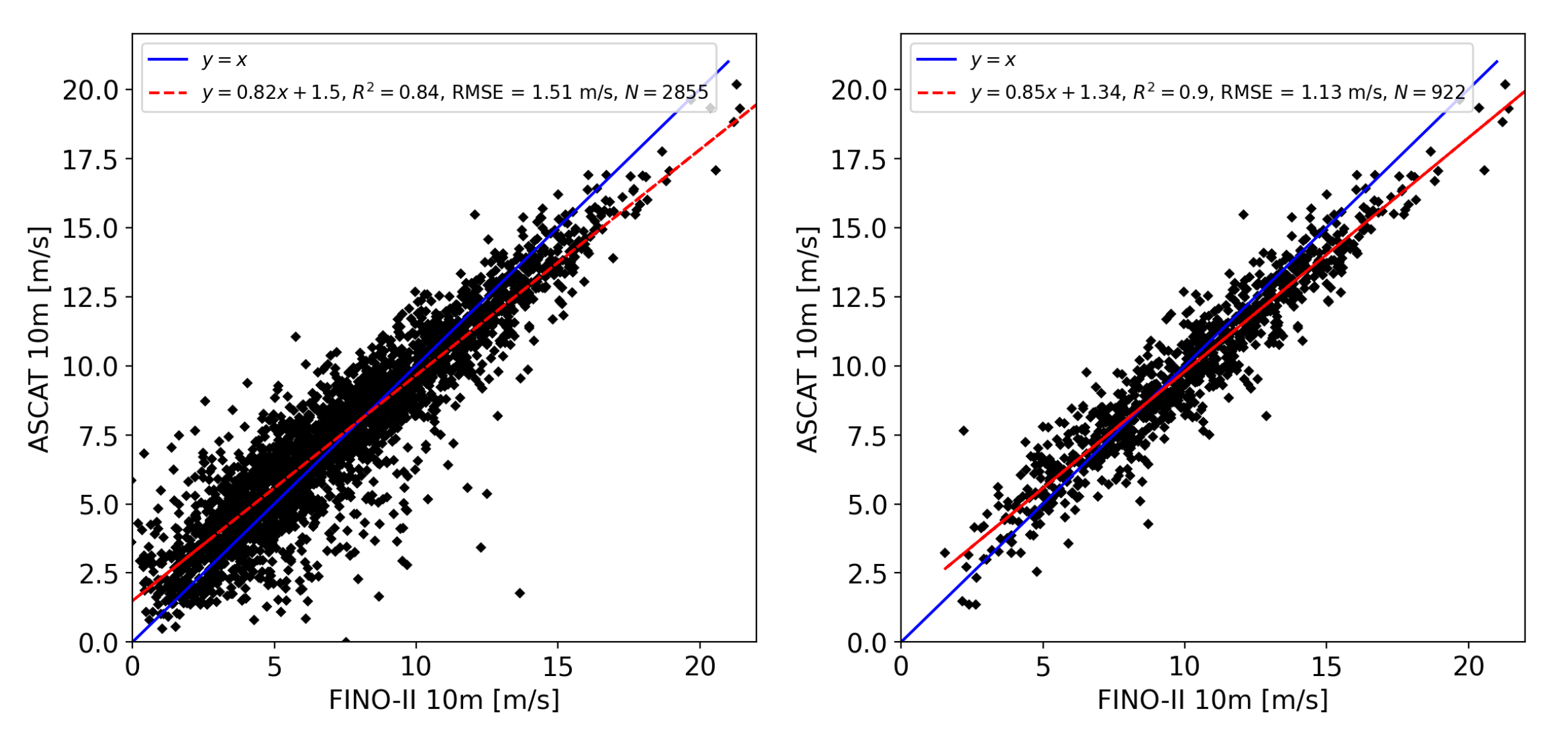
3.3. ASCAT vs. FINO2
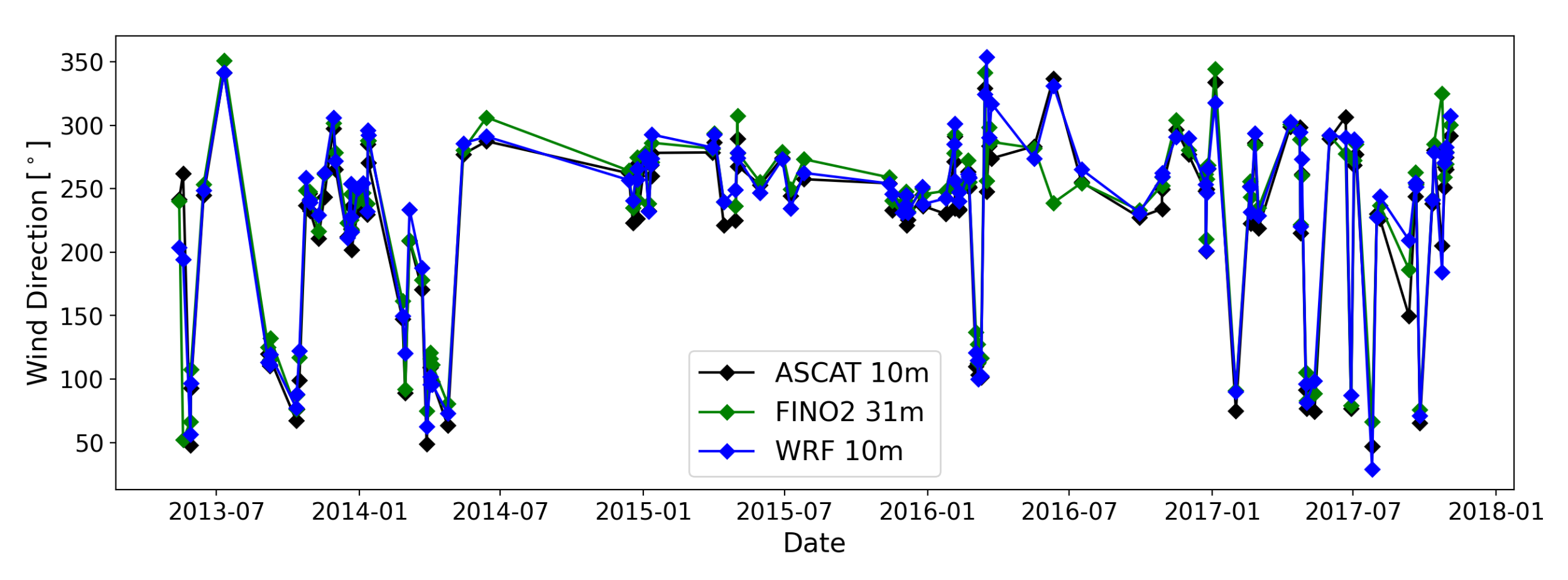
3.4. WRF
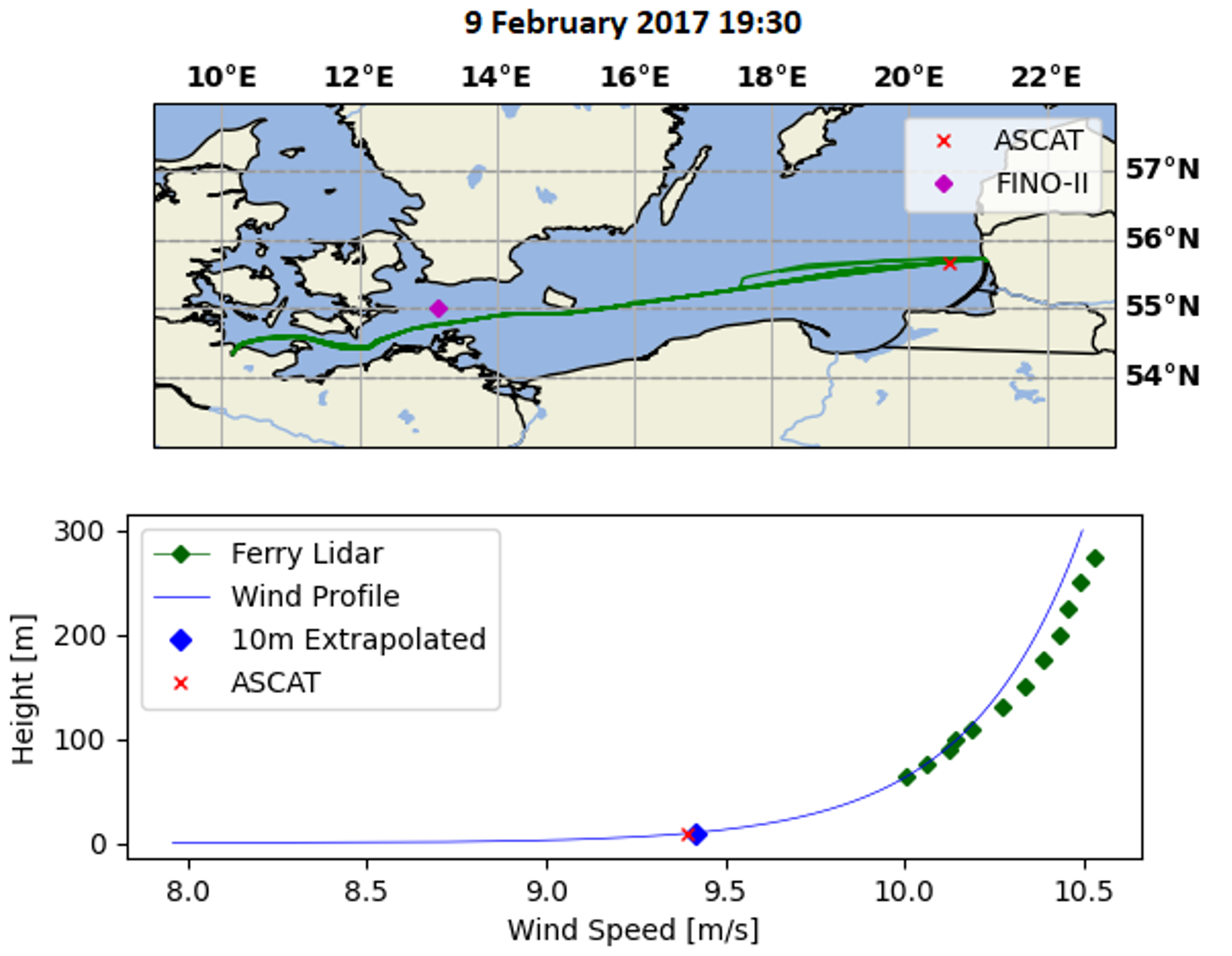
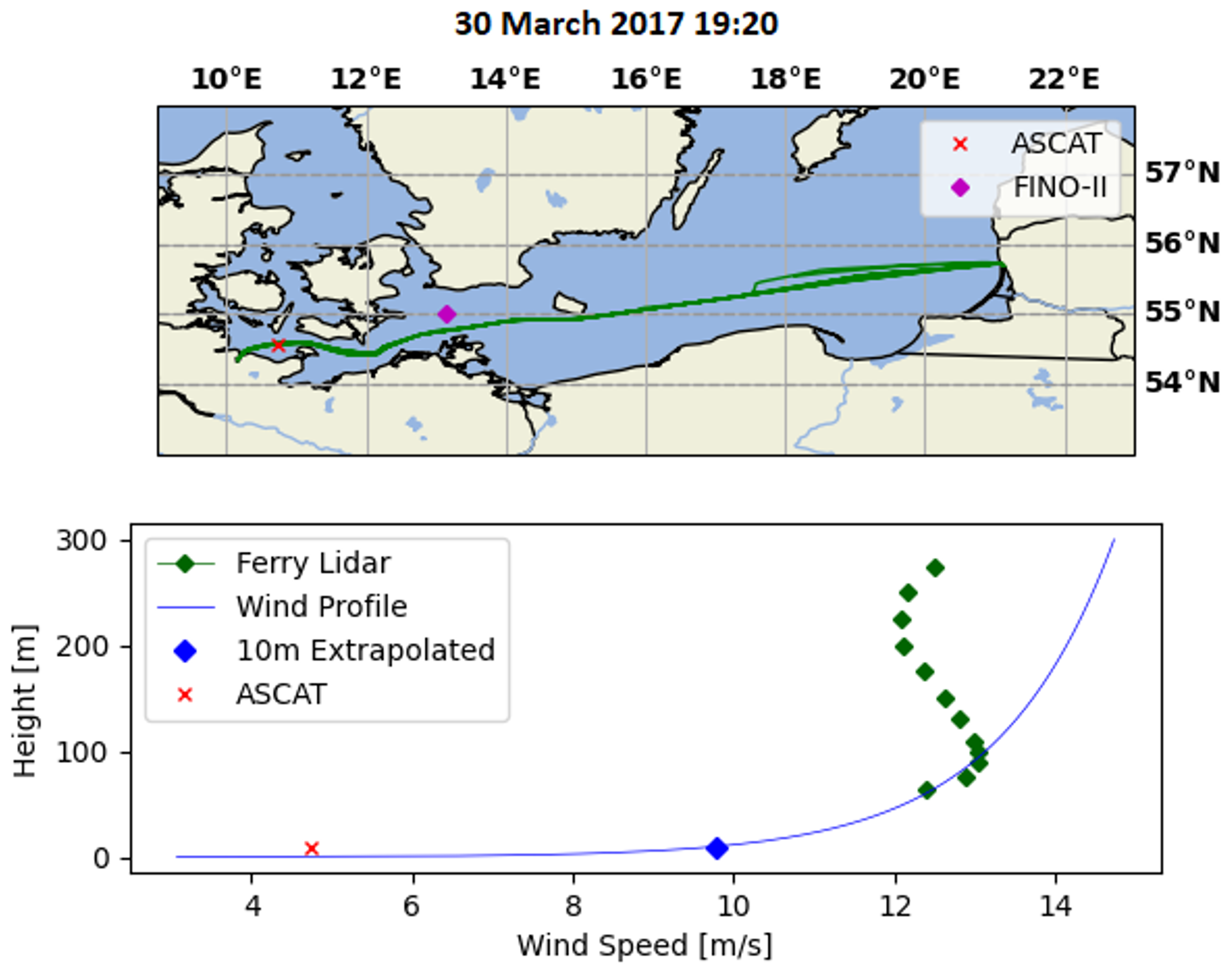
3.5. Low-Level Jet Case Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Stability Correction through Bulk Richardson Number
References
- European Commission. An EU Strategy to Harness the Potential of Offshore Renewable Energy for a Climate Neutral Future; European Commission: Brussels, Belgium, 2020. [Google Scholar]
- MacAskill, A.; Mitchell, P. Offshore wind—An overview. WIREs Energy Environ. 2013, 2, 374–383. [Google Scholar] [CrossRef]
- Skaare, B.; Nielsen, F.G.; Hanson, T.D.; Yttervik, R.; Havmøller, O.; Rekdal, A. Analysis of measurements and simulations from the Hywind Demo floating wind turbine. Wind Energy 2015, 18, 1105–1122. [Google Scholar] [CrossRef]
- Leiding, T.; Tinz, B.; Gates, L.; Rosenhagen, G.; Herklotz, K.; Senet, C.; Outzen, O.; Lindenthal, A.; Neumann, T.; Frühman, R.; et al. Standardisierung und Vergleichende Analyse der Meteorologischen FINO-Messdaten (FINO123); Technical Report; Deutscher Wetterdienst: Offenbach, Germany, 2016. [Google Scholar]
- Clifton, A.; Boquet, M.; Burin Des Roziers, E.; Westerhellweg, A.; Hofsass, M.; Klaas, T.; Vogstad, K.; Clive, P.; Harris, M.; Wylie, S.; et al. Remote Sensing of Complex Flows by Doppler Wind Lidar: Issues and Preliminary Recommendations; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2015. [Google Scholar] [CrossRef]
- Gottschall, J.; Gribben, B.; Stein, D.; Würth, I. Floating lidar as an advanced offshore wind speed measurement technique: Current technology status and gap analysis in regard to full maturity. WIREs Energy Environ. 2017, 6, e250. [Google Scholar] [CrossRef]
- Smith, M. An insight into lidars for offshore wind measurements. In Deepwind 2012; Natural Power: Trondheim, Norway, 2012; p. 35. [Google Scholar]
- Bischoff, O.; Würth, I.; Gottschall, J.; Gribben, B.; Hughes, J.; Stein, D.; Verhoef, H. IEA Wind Annex 32 Work Package 1.5 Expert Group Report on Recommended Practices: 18. Floating Lidar Systems; Issue 1.0; University of Stuttgart: Stuttgart, Germany, 2017. [Google Scholar]
- Wolken-Möhlmann, G.; Gottschall, J.; Lange, B. First Verification Test and Wake Measurement Results Using a SHIP-LIDAR System. Energy Procedia 2014, 53, 146–155. [Google Scholar] [CrossRef]
- Edson, J.B.; Hinton, A.A.; Prada, K.E.; Hare, J.E.; Fairall, C.W. Direct Covariance Flux Estimates from Mobile Platforms at Sea. J. Atmos. Ocean. Technol. 1998, 15, 547–562. [Google Scholar] [CrossRef] [Green Version]
- Strobach, E.J.; Sparling, L.C. The Impact of Coastal Terrain on Offshore Wind and Implications for Wind Energy. Ph.D. Thesis, University of Maryland, Baltimore County, MD, USA, 2017. [Google Scholar]
- Gottschall, J.; Catalano, E.; Dörenkämper, M.; Witha, B. The NEWA Ferry Lidar Experiment: Measuring mesoscalewinds in the Southern Baltic Sea. Remote Sens. 2018, 10, 1620. [Google Scholar] [CrossRef] [Green Version]
- Zentek, R.; Kohnemann, S.H.E.; Heinemann, G. Analysis of the performance of a ship-borne scanning wind lidar in the Arctic and Antarctic. Atmos. Meas. Tech. 2018, 11, 5781–5795. [Google Scholar] [CrossRef] [Green Version]
- Witha, B.; Hahmann, A.; Sile, T.; Dörenkämper, M.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Leroy, G.; Navarro, J. WRF Model Sensitivity Studies and Specifications for the NEWA Mesoscale Wind Atlas Production Runs; Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- González-Rouco, J.; Bustamante, E.; Hahmann, A.; Karagili, I.; Navarro, J.; Olsen, B.; Sile, T.; Witha, B. NEWA Report on Uncertainty Quantification Deliverable D4.4; NEWA—New European Wind Atlas; Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Belmonte Rivas, M.; Stoffelen, A. Characterizing ERA-Interim and ERA5 surface wind biases using ASCAT. Ocean Sci. 2019, 15, 831–852. [Google Scholar] [CrossRef] [Green Version]
- Karagali, I.; Badger, M.; Hasager, C. Spaceborne Earth Observation for Offshore Wind Energy Applications. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 172–175. [Google Scholar] [CrossRef]
- Badger, M.; Peña, A.; Hahmann, A.N.; Mouche, A.A.; Hasager, C.B. Extrapolating satellite winds to turbine operating heights. J. Appl. Meteorol. Climatol. 2016, 55, 975–991. [Google Scholar] [CrossRef]
- Karagali, I.; Hahmann, A.N.; Badger, M.; Hasager, C.; Mann, J. Offshore new European wind atlas. J. Phys. Conf. Ser. 2018, 1037, 052007. [Google Scholar] [CrossRef]
- Hasager, C.B.; Hahmann, A.N.; Ahsbahs, T.; Karagali, I.; Sile, T.; Badger, M.; Mann, J. Europe’s offshore winds assessed with synthetic aperture radar, ASCAT and WRF. Wind Energy Sci. 2020, 5, 375–390. [Google Scholar] [CrossRef] [Green Version]
- Kelly, M.; Gryning, S.E. Long-Term Mean Wind Profiles Based on Similarity Theory. Bound.-Layer Meteorol. 2010, 136, 377–390. [Google Scholar] [CrossRef] [Green Version]
- Sempreviva, A.; Barthelmie, R.; Pryor, S. Review of Methodologies for Offshore Wind Resource Assessment in European Seas. Surv. Geophys. 2008, 29, 471–497. [Google Scholar] [CrossRef]
- Smedman, A.S.; Bergström, H.; Grisogono, B. Evolution of stable internal boundary layers over a cold sea. J. Geophys. Res. Ocean. 1997, 102, 1091–1099. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Optis, M.; Monahan, A.; Steinfeld, G. On the Offshore Advection of Boundary-Layer Structures and the Influence on Offshore Wind Conditions. Bound.-Layer Meteorol. 2015, 155, 459–482. [Google Scholar] [CrossRef]
- Svensson, N. Mesoscale Processes over the Baltic Sea. Ph.D. Thesis, Uppsala Universitet, Uppsala, Sweden, 2018. [Google Scholar]
- Hasager, C.B.; Badger, M.; Peña, A.; Larsén, X.G.; Bingöl, F. SAR-Based Wind Resource Statistics in the Baltic Sea. Remote Sens. 2011, 3, 117–144. [Google Scholar] [CrossRef] [Green Version]
- Služenikina, J.; Mžnnik, A. A comparison of ASCAT wind measurements and the HIRLAM model over the Baltic Sea. Oceanologia 2011, 53, 229–244. [Google Scholar] [CrossRef] [Green Version]
- Catalano, E. Assessment of Offshore Wind Resources through Measurements from a Ship-Based LiDAR System. Master’s Thesis, University of Genoa, Genoa, Italy, 2017. [Google Scholar]
- Worsfold, M.; Good, S.; Martin, M.; Mclaren, A.; Fiedler, E. Global Ocean OSTIA Sea Surface Temperature Reprocessing, SST-GLO-SST-L4-REP-OBSERVATIONS-010-011; Technical Report 1.3; Copernicus Marine Service: Southampton, UK, 2021. [Google Scholar]
- Verhoef, A.; Stoffelen, A. EUMETSAT Advanced Retransmission Service ASCAT Wind Product User Manual; Technical Report October; EUMETSAT: Darmstadt, Germany, 2019. [Google Scholar]
- Stoffelen, A. Error Modelling of Scatterometer In-Situ, and ECMWF Model Winds: A Calibration Refinement; Technical Report; Koninklijk Nederlands Meteorologisch Instituut (KNMI): De Bilt, The Netherlands, 1996. [Google Scholar]
- Martin, S. An Introduction to Ocean Remote Sensing, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Chelton, D.B.; Ries, J.C.; Haines, B.J.; Fu, L.L.; Callahan, P.S. Chapter 1 Satellite Altimetry. Int. Geophys. 2001, 69, 1–183. [Google Scholar] [CrossRef]
- Stoffelen, A.; Verspeek, J.A.; Vogelzang, J.; Verhoef, A. The CMOD7 Geophysical Model Function for ASCAT and ERS Wind Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2123–2134. [Google Scholar] [CrossRef]
- Verhoef, A.; Stoffelen, A. Algorithm Theoretical Basis Document for the OSI SAF Wind Products; Technical Report; EUMETSAT: Darmstadt, Germany, 2019. [Google Scholar]
- Grachev, A.A.; Fairall, C.W. Dependence of the Monin–Obukhov Stability Parameter on the Bulk Richardson Number over the Ocean. J. Appl. Meteorol. 1997, 36, 406–414. [Google Scholar] [CrossRef]
- Emeis, S. Wind Energy Meteorology: Atmospheric Physics for Wind Power Generation, 2nd ed.; Green Energy and Technology; Springer: Berlin/Heidelberg, Germany, 2018; p. 276. [Google Scholar]
- Paulson, C.A. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. Climatol. 1970, 9, 857–861. [Google Scholar] [CrossRef]
- Högström, U. Non-dimensional wind and temperature profiles in the atmospheric surface layer: A re-evaluation. In Topics in Micrometeorology. A Festschrift for Arch Dyer; Springer: Berlin/Heidelberg, Germany, 1988; pp. 55–78. [Google Scholar]
- Karagali, I.; Peña, A.; Badger, M.; Hasager, C.B. Wind characteristics in the North and Baltic Seas from the QuikSCAT satellite. Wind Energy 2014, 17, 123–140. [Google Scholar] [CrossRef]
- Sorbjan, Z.; Grachev, A.A. An evaluation of the flux-gradient relationship in the stable boundary layer. Bound.-Layer Meteorol. 2010, 135, 385–405. [Google Scholar] [CrossRef]
- Peña, A.; Hahmann, A.; Hasager, C.; Bingöl, F.; Karagali, I.; Badger, J. South Baltic Wind Atlas: South Baltic Offshore Wind Energy Regions Project; Technical Report; Risø-Report: Roskilde, Denmark, 2011. [Google Scholar]
- Baas, P.; Bosveld, F.; Klein, B.H.; Holtslag, B. A Climatology of Nocturnal Low-Level Jets at Cabauw. J. Appl. Meteorol. Climatol. 2009, 48, 1627–1642. [Google Scholar] [CrossRef]
- Optis, M.; Bodini, N.; Debnath, M.; Doubrawa, P. New methods to improve the vertical extrapolation of near-surface offshore wind speeds. Wind Energy Sci. 2021, 6, 935–948. [Google Scholar] [CrossRef]
- Optis, M.; Monahan, A.; Bosveld, F.C. Moving Beyond Monin–Obukhov Similarity Theory in Modelling Wind-Speed Profiles in the Lower Atmospheric Boundary Layer under Stable Stratification. Bound.-Layer Meteorol. 2014, 153, 497–514. [Google Scholar] [CrossRef]
- Optis, M.; Monahan, A. The Extrapolation of Near-Surface Wind Speeds under Stable Stratification Using an Equilibrium-Based Single-Column Model Approach. J. Appl. Meteorol. Climatol. 2016, 55, 923–943. [Google Scholar] [CrossRef]
- Schneemann, J.; Rott, A.; Dörenkämper, M.; Steinfeld, G.; Kühn, M. Cluster wakes impact on a far-distant offshore wind farm’s power. Wind Energy Sci. 2020, 5, 29–49. [Google Scholar] [CrossRef] [Green Version]
- Stull, R. An Introduction to Boundary Layer Meteorology, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; p. 670. [Google Scholar]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile Relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Dyer, A. A review of flux-profile relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Holtslag, A.A.M.; Bruin, H.A.R.D. Applied Modeling of the Nighttime Surface Energy Balance over Land. J. Appl. Meteorol. Climatol. 1988, 27, 689–704. [Google Scholar] [CrossRef] [Green Version]

| Stability Classification | Range |
|---|---|
| Very stable | 0.6 2.0 |
| Stable | 0.2 0.6 |
| Weakly stable | 0.02 0.2 |
| Neutral | −0.02 0.02 |
| Weakly unstable | −0.2 −0.02 |
| Unstable | −0.6 −0.2 |
| Very Unstable | −2.0 −0.6 |
| Period of Collocation | Number of Samples | |
|---|---|---|
| FINO2 | 16 April 2013 to 30 November 2017 | 31,256 |
| ASCAT | 2 January 2007 to 29 December 2017 | 2395 |
| Ferry lidar | 13 February 2017 to 6 June 2017 | 1181 |
| Lidar Height (m) | Height (m) | R | RMSE (m s) | Bias (m s) | N | |
|---|---|---|---|---|---|---|
| Ferry lidar vs. ASCAT (collocated) | 10 | 10 | 0.85 | 1.29 | 0.02 | 23 |
| Ferry lidar vs. WRF (collocated) | 10 | 10 | 0.55 | 2.41 | 0.01 | 23 |
| 65 | 50 | 0.76 | 1.90 | −0.01 | 3671 | |
| 75 | 75 | 0.76 | 1.93 | −0.02 | 3671 | |
| 100 | 100 | 0.77 | 2.04 | −0.00 | 3671 | |
| 200 | 200 | 0.79 | 2.27 | −0.02 | 3671 | |
| 250 | 250 | 0.80 | 2.32 | −0.03 | 3671 | |
| Ferry lidar vs. FINO2 (30 km distance) | 65 | 62 | 0.87 | 1.71 | −0.11 | 134 |
| 75 | 72 | 0.87 | 1.79 | −0.11 | 134 | |
| 90 | 92 | 0.87 | 1.81 | −0.07 | 134 | |
| 100 | 102 | 0.89 | 1.69 | −0.06 | 134 |
| Lidar Height (m) | Height (m) | R | RMSE () | Bias () | N | |
|---|---|---|---|---|---|---|
| Ferry lidar vs. ASCAT (collocated) | 65 | 10 | 0.83 | 34.8 | 0.06 | 119 |
| Ferry lidar vs. WRF (collocated) | 65 | 10 | 0.81 | 53.8 | 0.04 | 119 |
| 65 | 50 | 0.79 | 26.3 | 0.01 | 3671 | |
| 75 | 75 | 0.78 | 25.6 | 0.01 | 3671 | |
| 100 | 100 | 0.76 | 25.4 | 0.01 | 3671 | |
| 200 | 200 | 0.73 | 28.1 | −0.01 | 3671 | |
| 250 | 250 | 0.75 | 27.2 | −0.00 | 3671 | |
| Ferry lidar vs. FINO2 (30 km distance) | 75 | 71 | 0.86 | 32.8 | 0.04 | 134 |
| 90 | 91 | 0.97 | 14.5 | 0.02 | 134 |
| WRF Height (m) | Height (m) | R | RMSE (m s) | Bias (m s) | N | |
|---|---|---|---|---|---|---|
| WRF vs. ASCAT | 10 | 10 | 0.78 | 1.87 | 0.03 | 129 |
| WRF vs. FINO2 | 50 | 52 | 0.67 | 2.45 | 0.00 | 2867 |
| 100 | 102 | 0.70 | 2.61 | −0.03 | 2867 | |
| WRF vs. Ferry Lidar | 50 | 65 | 0.76 | 1.90 | −0.01 | 3671 |
| 100 | 100 | 0.77 | 2.04 | −0.00 | 3671 | |
| 200 | 200 | 0.79 | 2.27 | −0.02 | 3671 | |
| 250 | 250 | 0.80 | 2.32 | −0.03 | 3671 |
| WRF Height (m) | Height (m) | R | RMSE () | Bias () | N | |
|---|---|---|---|---|---|---|
| WRF vs. ASCAT | 10 | 10 | 0.95 | 17.6 | −0.01 | 129 |
| WRF vs. FINO2 | 50 | 51 | 0.58 | 41.8 | 0.02 | 2867 |
| 100 | 91 | 0.58 | 42.6 | 0.02 | 2867 | |
| WRF vs. Ferry Lidar | 50 | 65 | 0.79 | 26.3 | 0.01 | 3671 |
| 100 | 100 | 0.76 | 25.4 | 0.01 | 3671 | |
| 200 | 200 | 0.73 | 28.1 | −0.01 | 3671 | |
| 250 | 250 | 0.75 | 27.2 | −0.00 | 3671 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatfield, D.; Hasager, C.B.; Karagali, I. Comparing Offshore Ferry Lidar Measurements in the Southern Baltic Sea with ASCAT, FINO2 and WRF. Remote Sens. 2022, 14, 1427. https://doi.org/10.3390/rs14061427
Hatfield D, Hasager CB, Karagali I. Comparing Offshore Ferry Lidar Measurements in the Southern Baltic Sea with ASCAT, FINO2 and WRF. Remote Sensing. 2022; 14(6):1427. https://doi.org/10.3390/rs14061427
Chicago/Turabian StyleHatfield, Daniel, Charlotte Bay Hasager, and Ioanna Karagali. 2022. "Comparing Offshore Ferry Lidar Measurements in the Southern Baltic Sea with ASCAT, FINO2 and WRF" Remote Sensing 14, no. 6: 1427. https://doi.org/10.3390/rs14061427
APA StyleHatfield, D., Hasager, C. B., & Karagali, I. (2022). Comparing Offshore Ferry Lidar Measurements in the Southern Baltic Sea with ASCAT, FINO2 and WRF. Remote Sensing, 14(6), 1427. https://doi.org/10.3390/rs14061427







