Farmland Shelterbelt Age Mapping Using Landsat Time Series Images
Abstract
:1. Introduction
2. Materials and Methods
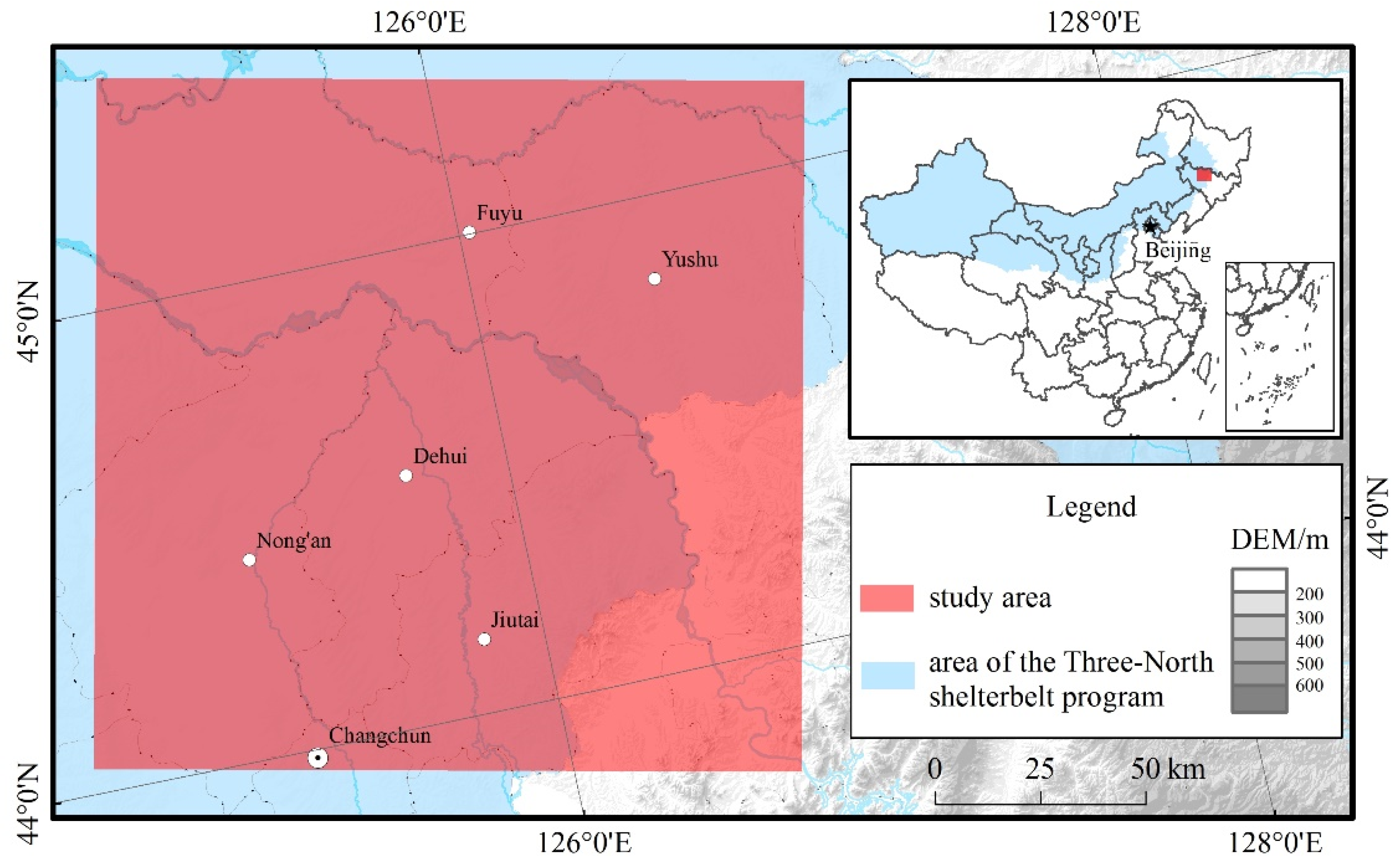
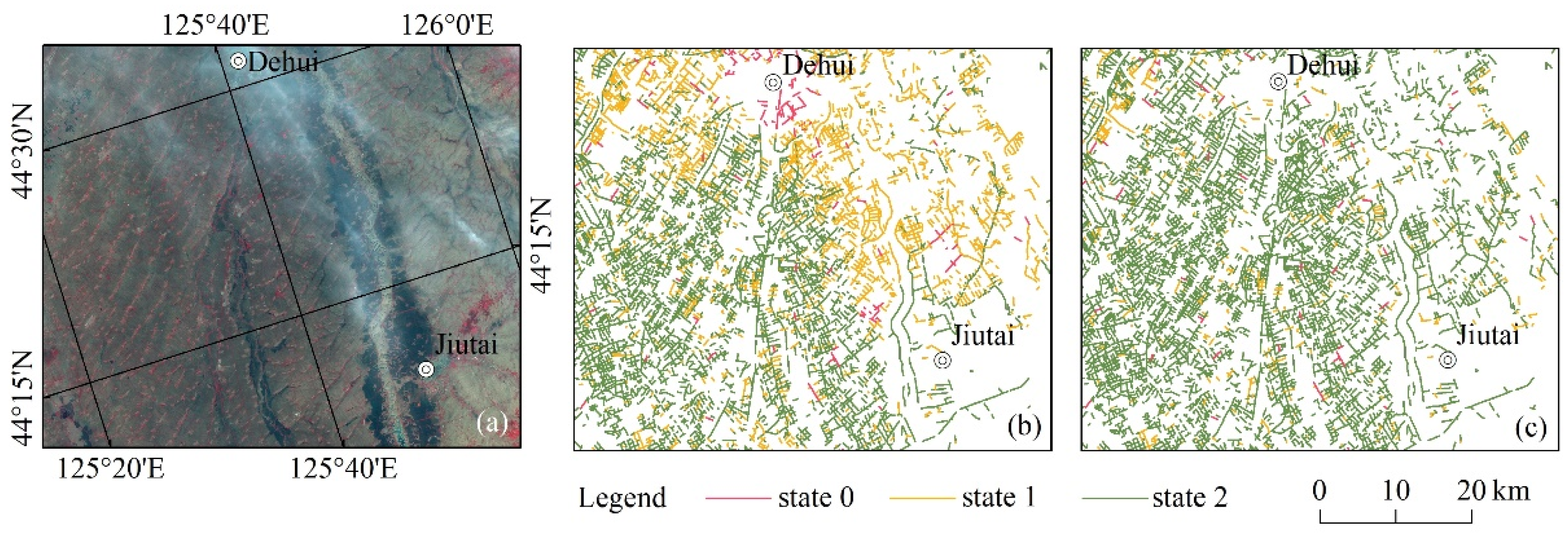
2.1. Study Area
2.2. Data Source
2.2.1. Selection of Remote Sensing Images
2.2.2. Extraction of Vector Information in the Farmland Shelterbelt
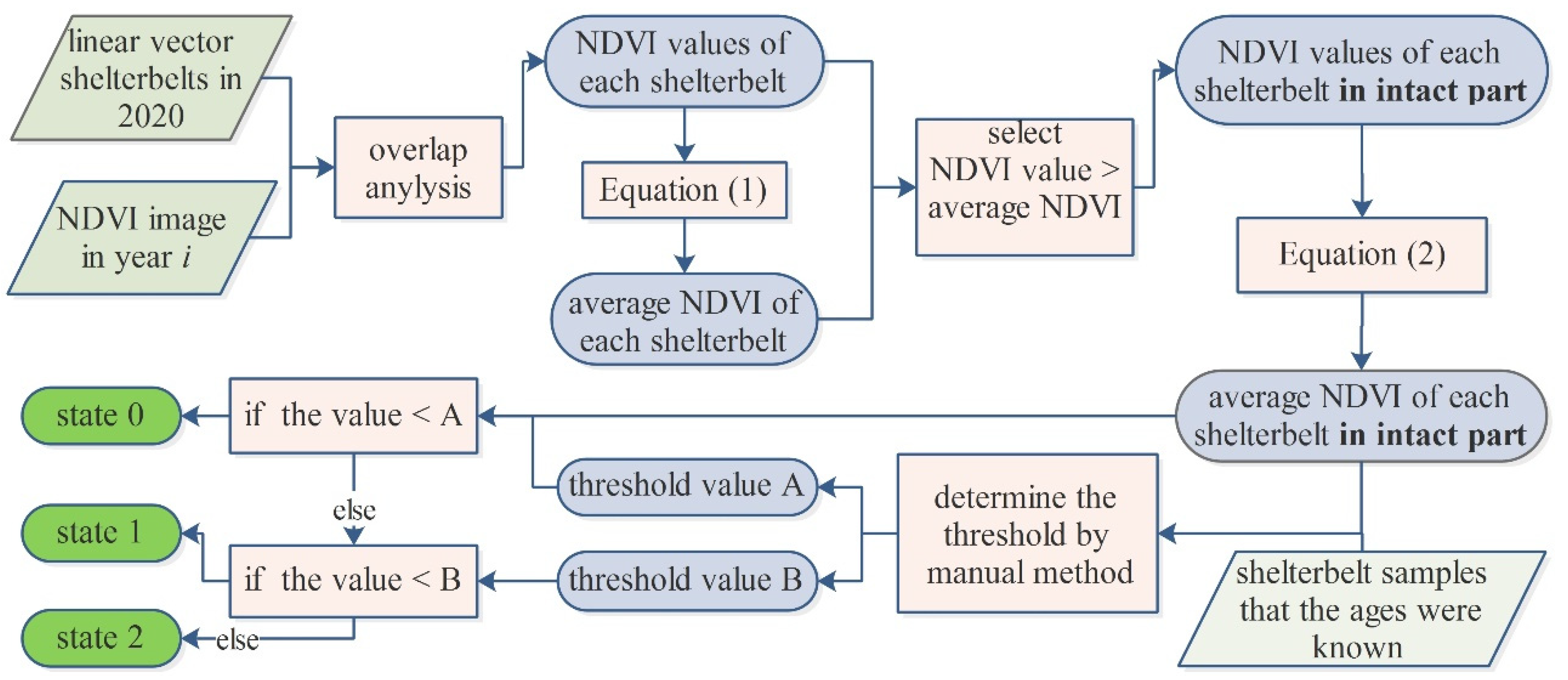
2.3. Dividing Shelterbelts into Three States Using a Single Remote Sensing Image
2.4. Establishing a Three-Stage Growth Process Using Time Series Remote Sensing Image
2.4.1. Shelterbelt Growth Process from Time Series Images
2.4.2. Three-Stage Growth of Farmland Shelterbelt Derived from Time Series Remote Sensing Images
2.5. Algorithm for the Identification of Shelterbelt Ages Based on Time Series Remote Sensing Images
3. Results
3.1. Modification and Predication of the Shelterbelt States
3.2. Identification Result and Validation
3.2.1. Identification Result
3.2.2. Validation
4. Discussion
4.1. Uncertainty Analysis
4.2. Method Comparison
4.3. Implications of the Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brandle, J.; Hodges, L.; Zhou, X. Windbreaks in North American agricultural systems. Agrofor. Syst. 2004, 61–62, 65–78. [Google Scholar] [CrossRef]
- Stange, C. Windbreak Management; Papers in Natural Resources; University of Nebraska-Lincoln: Lincoln, NE, USA, 1996; p. 124. [Google Scholar]
- Helama, S. Expressing Tree-Ring Chronology as Age-Standardized Growth Measurements. For. Sci. 2015, 61, 817–828. [Google Scholar] [CrossRef]
- Sun, J.; Hamel, J.-F.; Gianasi, B.L.; Mercier, A. Age determination in echinoderms: First evidence of annual growth rings in holothuroids. Proc. R. Soc. B Boil. Sci. 2019, 286, 20190858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nascimbene, J.; Marini, L.; Motta, R.; Nimis, P.L. Influence of tree age, tree size and crown structure on lichen communities in mature Alpine spruce forests. Biodivers. Conserv. 2009, 18, 1509–1522. [Google Scholar] [CrossRef]
- Trotsiuk, V.; Hobi, M.; Commarmot, B. Age structure and disturbance dynamics of the relic virgin beech forest Uholka (Ukrainian Carpathians). For. Ecol. Manag. 2012, 265, 181–190. [Google Scholar] [CrossRef]
- Dey, D.C.; Dwyer, J.; Wiedenbeck, J. Relationship between Tree Value, Diameter, and Age in High-Quality Sugar Maple (Acer saccharum) on the Menominee Reservation, Wisconsin. J. For. 2017, 115, 397–405. [Google Scholar] [CrossRef]
- Briseño-Reyes, J.; Corral-Rivas, J.J.; Solis-Moreno, R.; Padilla-Martínez, J.R.; Vega-Nieva, D.J.; López-Serrano, P.M.; Vargas-Larreta, B.; Diéguez-Aranda, U.; Quiñonez-Barraza, G.; López-Sánchez, C.A. Individual Tree Diameter and Height Growth Models for 30 Tree Species in Mixed-Species and Uneven-Aged Forests of Mexico. Forests 2020, 11, 429. [Google Scholar] [CrossRef] [Green Version]
- Ojoatre, S.; Zhang, C.; Hussin, Y.A.; Kloosterman, H.E.; Ismail, M.H. Assessing the Uncertainty of Tree Height and Aboveground Biomass from Terrestrial Laser Scanner and Hypsometer Using Airborne LiDAR Data in Tropical Rainforests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4149–4159. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Liu, Q.; Luo, P.; Ye, Q.; Duan, G.; Sharma, R.; Zhang, H.; Wang, G.; Fu, L. Prediction of Individual Tree Diameter and Height to Crown Base Using Nonlinear Simultaneous Regression and Airborne LiDAR Data. Remote Sens. 2020, 12, 2238. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, W.; Di, L.; Lu, L.; Guo, L. Estimation of Tree Height by Combining Low Density Airborne LiDAR Data and Images Using the 3D Tree Model: A Case Study in a Subtropical Forest in China. Forests 2020, 11, 1252. [Google Scholar] [CrossRef]
- Kobal, M.; Hladnik, D. Tree Height Growth Modelling Using LiDAR-Derived Topography Information. ISPRS Int. J. Geo-Inf. 2021, 10, 419. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Wu, Z.; Yu, Y.; Li, F.; Fan, W. Forest age mapping based on multiple-resource remote sensing data. Environ. Monit. Assess. 2020, 192, 734. [Google Scholar] [CrossRef] [PubMed]
- Dye, M.; Mutanga, O.; Ismail, R. Combining Spectral and Textural Remote Sensing Variables Using Random Forests: Predicting the Age of Pinus Patula Forests in KwaZulu-Natal, South Africa. J. Spat. Sci. 2012, 57, 193–211. [Google Scholar] [CrossRef]
- Chemura, A.; van Duren, I.; van Leeuwen, L.M. Determination of the Age of Oil Palm from Crown Projection Area Detected from WorldView-2 Multispectral Remote Sensing Data: The Case of Ejisu-Juaben District, Ghana. ISPRS-J. Photogramm. Remote Sens. 2015, 100, 118–127. [Google Scholar] [CrossRef]
- Cao, X.; Liu, Y.; Liu, Q.; Cui, X.; Chen, X.; Chen, J. Estimating the age and population structure of encroaching shrubs in arid/semiarid grasslands using high spatial resolution remote sensing imagery. Remote Sens. Environ. 2018, 216, 572–585. [Google Scholar] [CrossRef]
- Qiao, C.; Sun, R.; Xu, Z.; Zhang, L.; Liu, L.; Hao, L.; Jiang, G. A Study of Shelterbelt Transpiration and Cropland Evapotranspiration in an Irrigated Area in the Middle Reaches of the Heihe River in Northwestern China. IEEE Geosci. Remote Sens. Lett. 2015, 12, 369–373. [Google Scholar] [CrossRef]
- Xing, Z.F.; Li, Y.; Deng, R.X.; Zhu, H.L.; Fu, B.L. Extracting Farmland Shelterbelt Automatically Based on ZY-3 Remote Sensing Images. Sci. Silv. Sin. 2016, 52, 11–20. [Google Scholar]
- Zheng, X.; Zhu, J.; Xing, Z. Assessment of the effects of shelterbelts on crop yields at the regional scale in Northeast China. Agric. Syst. 2016, 143, 49–60. [Google Scholar] [CrossRef]
- Deng, R.X.; Li, Y.; Xu, X.L.; Wang, W.J.; Wei., Y.C. Remote estimation of shelterbelt width from SPOT5 imagery. Agrofor. Syst. 2017, 91, 161–172. [Google Scholar] [CrossRef]
- Yu, T.; Liu, P.; Zhang, Q.; Ren, Y.; Yao, J. Detecting Forest Degradation in the Three-North Forest Shelterbelt in China from Multi-Scale Satellite Images. Remote Sens. 2021, 13, 1131. [Google Scholar] [CrossRef]
- De Fries, R.S.; Townshend, J.R.G. NDVI-Derived Land Cover Classifications at Global Scale. Int. J. Remote Sens. 1994, 15, 3567–3586. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Pan, Z.; Huang, J.; Zhou, Q.; Wang, L.; Cheng, Y.; Zhang, H.; Blackburn, G.A.; Yan, J.; Liu, J. Mapping crop phenology using NDVI time-series derived from HJ-1 A/B data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 188–197. [Google Scholar] [CrossRef] [Green Version]
- Guan, X.; Huang, C.; Liu, G.; Meng, X.; Liu, Q. Mapping Rice Cropping Systems in Vietnam Using an NDVI-Based Time-Series Similarity Measurement Based on DTW Distance. Remote Sens. 2016, 8, 19. [Google Scholar] [CrossRef] [Green Version]
- Antonucci, S.; Rossi, S.; Deslauriers, A.; Morin, H.; Lombardi, F.; Marchetti, M.; Tognetti, R. Large-scale estimation of xylem phenology in black spruce through remote sensing. Agric. For. Meteorol. 2017, 233, 92–100. [Google Scholar] [CrossRef]
- Khare, S.; Drolet, G.; Sylvain, J.-D.; Paré, M.C.; Rossi, S. Assessment of Spatio-Temporal Patterns of Black Spruce Bud Phenology across Quebec Based on MODIS-NDVI Time Series and Field Observations. Remote Sens. 2019, 11, 2745. [Google Scholar] [CrossRef] [Green Version]
- Li, X.F.; Tian, Y.C.; Zheng, X.; Cong, J.X.; Song, L.N. Characterizing 40 Years of Natural Pinus Sylvestris Var. Mongolica Carbon Stocks in Northeast China Using Stand Age from Remote Sensing Time Series. Int. J. Remote Sens. 2020, 41, 2391–2409. [Google Scholar] [CrossRef]
- Ji, Z.; Pan, Y.; Zhu, X.; Wang, J.; Li, Q. Prediction of Crop Yield Using Phenological Information Extracted from Remote Sensing Vegetation Index. Sensors 2021, 21, 1406. [Google Scholar] [CrossRef]
- Shi, X.; Li, Y.; Deng, R. A method for spatial heterogeneity evaluation on landscape pattern of farmland shelterbelt networks: A case study in midwest of Jilin Province, China. Chin. Geogr. Sci. 2011, 21, 48–56. [Google Scholar] [CrossRef]
- USGS. Available online: https://www.usgs.gov/landsat-missions/using-usgs-landsat-level-1-data-product (accessed on 13 March 2022).
- Deng, R.; Li, Y.; Wang, W.; Zhang, S. Recognition of shelterbelt continuity using remote sensing and waveform recognition. Agrofor. Syst. 2013, 87, 827–834. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, J.; Zeng, D.; Fan, Z.; Du, X.; Cao, Y. Management for Protective Plantations; China Forestry Publisher: Beijing, China, 2003; pp. 75–86. [Google Scholar]
- Jiang, F.Q.; Zhu, J.J. Phase-Directional Management of Protective Plantations. I. Fundamentals. Chin. J. Appl. Ecol. 2002, 13, 1352–1355. [Google Scholar]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The ice, cloud, and land elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The global ecosystem dynamics investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Liu, A.B.; Cheng, X.; Chen, Z.Q. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Xu, C.; Manley, B.; Morgenroth, J. Evaluation of modelling approaches in predicting forest volume and stand age for small-scale plantation forests in New Zealand with RapidEye and LiDAR. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 386–396. [Google Scholar] [CrossRef]
- Lucas, R.M.; Xiao, X.; Hagen, S.; Frolking, S. Evaluating TERRA-1 MODIS data for discrimination of tropical secondary forest regeneration stages in the Brazilian Legal Amazon. Geophys. Res. Lett. 2002, 29, 42-1–42-4. [Google Scholar] [CrossRef] [Green Version]
- Sader, S.A.; Waide, R.B.; Lawrence, W.T.; Joyce, A.T. Tropical forest biomass and successional age class relationships to a vegetation index derived from landsat TM data. Remote Sens. Environ. 1989, 28, 143–198. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Castillo-Santiago, M.Á; Mas, J.F.; Wheeler, C.E.; Andres-Mauricio, J.; Tun-Dzul, F.; George-Chacón, S.P.; Reyes-Palomeque, G.; Castellanos-Basto, B.; Vaca, R.; et al. Improving aboveground biomass maps of tropical dry forests by integrating LiDAR, ALOS PALSAR, climate and field data. Carbon Balance Manag. 2020, 15, 15. [Google Scholar] [CrossRef]
- Ma, S.B.; Zhou, Z.F.; Zhang, Y.R.; An, Y.L.; Yang, G.B. Identification of Forest Disturbance and Estimation of Forest Age in Subtropical Mountainous Areas Based on Landsat Time Series Data. Earth Sci. Inform. 2022, 15, 321–334. [Google Scholar] [CrossRef]
- Fujiki, S.; Okada, K.-I.; Nishio, S.; Kitayama, K. Estimation of the stand ages of tropical secondary forests after shifting cultivation based on the combination of WorldView-2 and time-series Landsat images. ISPRS J. Photogramm. Remote Sens. 2016, 119, 280–293. [Google Scholar] [CrossRef]
- Read, L.; Lawrence, D. Recovery of Biomass Following Shifting Cultivation in Dry Tropical Forests of The Yucatan. Ecol. Appl. 2003, 13, 85–97. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Peng, D.; Wang, Z.; Hu, Y. Improving artificial forest biomass estimates using afforestation age information from time series Landsat stacks. Environ. Monit. Assess. 2014, 186, 7293–7306. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Guo, Z.; Piao, S.; Fang, J. Biomass carbon stocks in China’s forests between 2000 and 2050: A prediction based on forest biomass-age relationships. Sci. China Life Sci. 2010, 53, 776–783. [Google Scholar] [CrossRef] [PubMed]


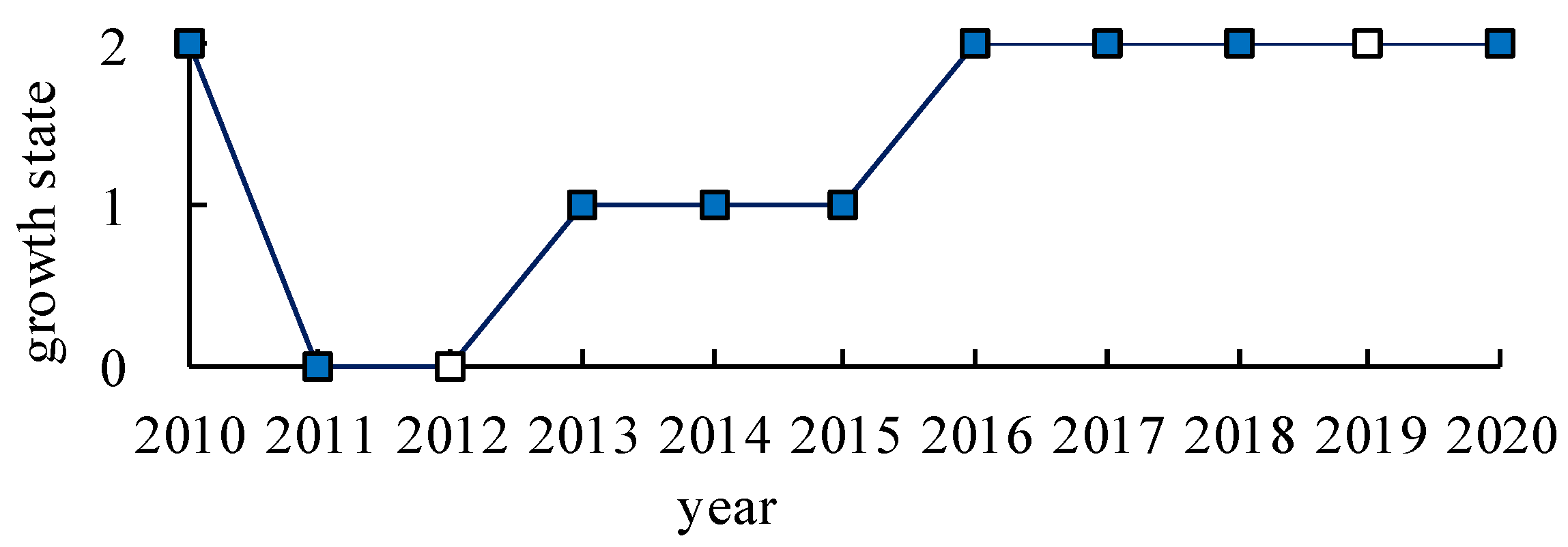
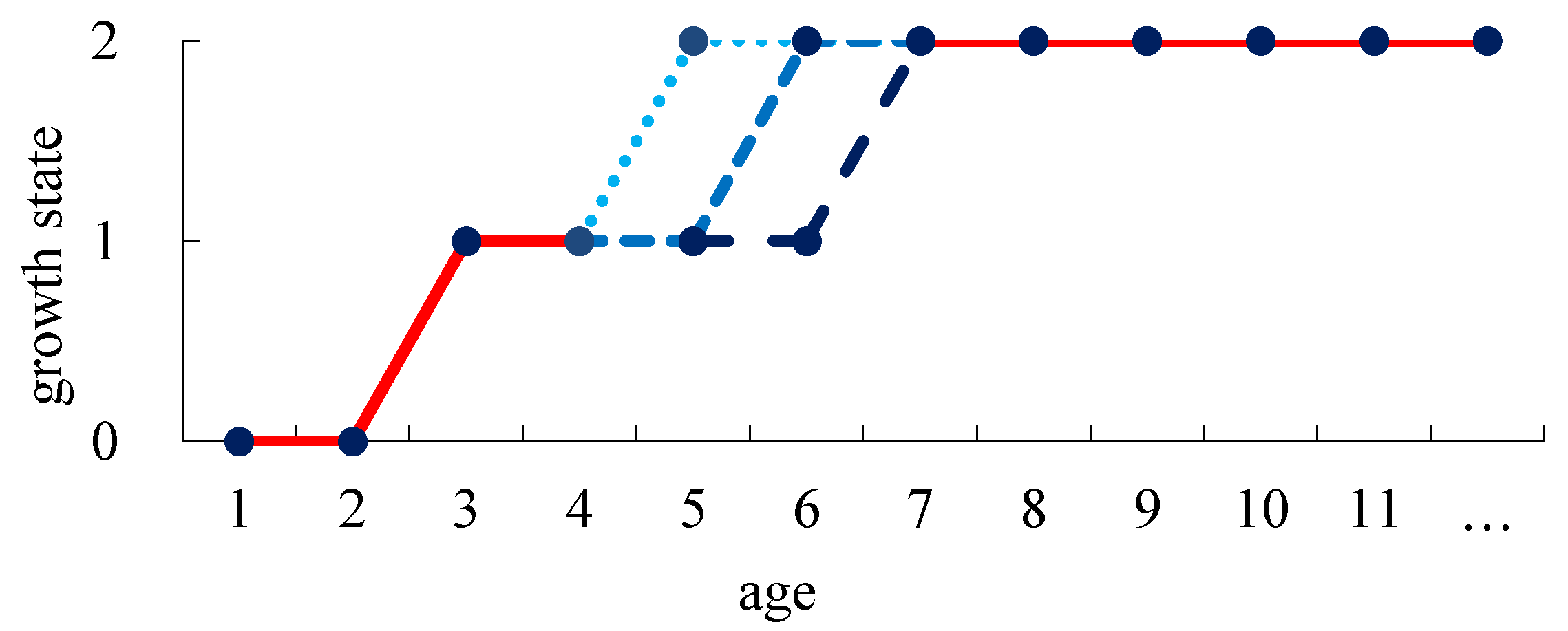

| Year | Data Source | Date (Month-Day) | Cloud Cover (%) |
|---|---|---|---|
| 1984 | No available | ||
| 1985 | Landsat-5 | 28 May | 0 |
| 1986 | Landsat-5 | 31 May | 8 |
| 1987 | Landsat-5 | 18 May | 0 |
| 1988 | Landsat-5 | 20 May | 3 |
| 1989 | No available | ||
| 1990 | No available | ||
| 1991 | Landsat-5 | 14 June | 2 |
| 1992 | No available | ||
| 1993 | No available | ||
| 1994 | Landsat-5 | 21 May | 19 |
| 1995 | Landsat-5 | 9 June | 30 |
| 1996 | Landsat-5 | 11 June | 5 |
| 1997 | Landsat-5 | 14 June | 0 |
| 1998 | Landsat-5 | 16 May | 0 |
| 1999 | Landsat-5 | 4 June | 4 |
| 2000 | No available | ||
| 2001 | Landsat-5 | 9 June | 10 |
| 2002 | No available | ||
| 2003 | Landsat-5 | 14 May | 0 |
| 2004 | Landsat-5 | 1 June | 0 |
| 2005 | Landsat-5 | 19 May | 0 |
| 2006 | Landsat-5 | 6 May | 7 |
| 2007 | Landsat-5 | 10 June | 20 |
| 2008 | Landsat-5 | 12 June | 0 |
| 2009 | Landsat-5 | 14 May | 0 |
| 2010 | Landsat-5 | 1 May | 1 |
| 2011 | Landsat-5 | 5 June | 3 |
| 2012 | No available | ||
| 2013 | Landsat-8 | 25 May | 0 |
| 2014 | Landsat-8 | 13 June | 0 |
| 2015 | Landsat-8 | 15 May | 0 |
| 2016 | Landsat-8 | 17 May | 2 |
| 2017 | Landsat-8 | 5 June | 1 |
| 2018 | Landsat-8 | 23 May | 6 |
| 2019 | No available | ||
| 2020 | Landsat-8 | 28 May | 1 |
| 2021 | No available |
| i − 2 | Missing Year (i) | i + 2 | |
|---|---|---|---|
| Growth state | 0 | 0 | 0 |
| 0 | if I − 4 = 2, statei = 1; if I + 4 = 1, statei = 0 | 1 | |
| 0 | 1 | 2 | |
| 1 | × | 0 | |
| 1 | × | 1 | |
| 1 | 1 or 2 | 2 | |
| 2 | 0 or 2 | 0 | |
| 2 | 0 | 1 | |
| 2 | 2 | 2 |
| Ground Truth Data | |||||||
|---|---|---|---|---|---|---|---|
| Class | 1–3a | 4–15a | 16–33a | >33a | Total | Commission | |
| Estimated data | 1–3a | 23 | 10 | 0 | 0 | 33 | 30.3% |
| 4–15a | 5 | 103 | 5 | 2 | 115 | 10.4% | |
| 16–33a | 0 | 15 | 33 | 3 | 51 | 35.3% | |
| >33a | 3 | 13 | 4 | 24 | 44 | 45.5% | |
| Total | 31 | 141 | 42 | 29 | 243 | ||
| Omission | 25.8% | 27.0% | 21.4% | 17.2% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, R.; Xu, Z.; Li, Y.; Zhang, X.; Li, C.; Zhang, L. Farmland Shelterbelt Age Mapping Using Landsat Time Series Images. Remote Sens. 2022, 14, 1457. https://doi.org/10.3390/rs14061457
Deng R, Xu Z, Li Y, Zhang X, Li C, Zhang L. Farmland Shelterbelt Age Mapping Using Landsat Time Series Images. Remote Sensing. 2022; 14(6):1457. https://doi.org/10.3390/rs14061457
Chicago/Turabian StyleDeng, Rongxin, Zhengran Xu, Ying Li, Xing Zhang, Chunjing Li, and Lu Zhang. 2022. "Farmland Shelterbelt Age Mapping Using Landsat Time Series Images" Remote Sensing 14, no. 6: 1457. https://doi.org/10.3390/rs14061457
APA StyleDeng, R., Xu, Z., Li, Y., Zhang, X., Li, C., & Zhang, L. (2022). Farmland Shelterbelt Age Mapping Using Landsat Time Series Images. Remote Sensing, 14(6), 1457. https://doi.org/10.3390/rs14061457





