Range Gate Pull-Off Mainlobe Jamming Suppression Approach with FDA-MIMO Radar: Theoretical Formalism and Numerical Study
Abstract
:1. Introduction
2. Signal Model of FDA-MIMO Radar
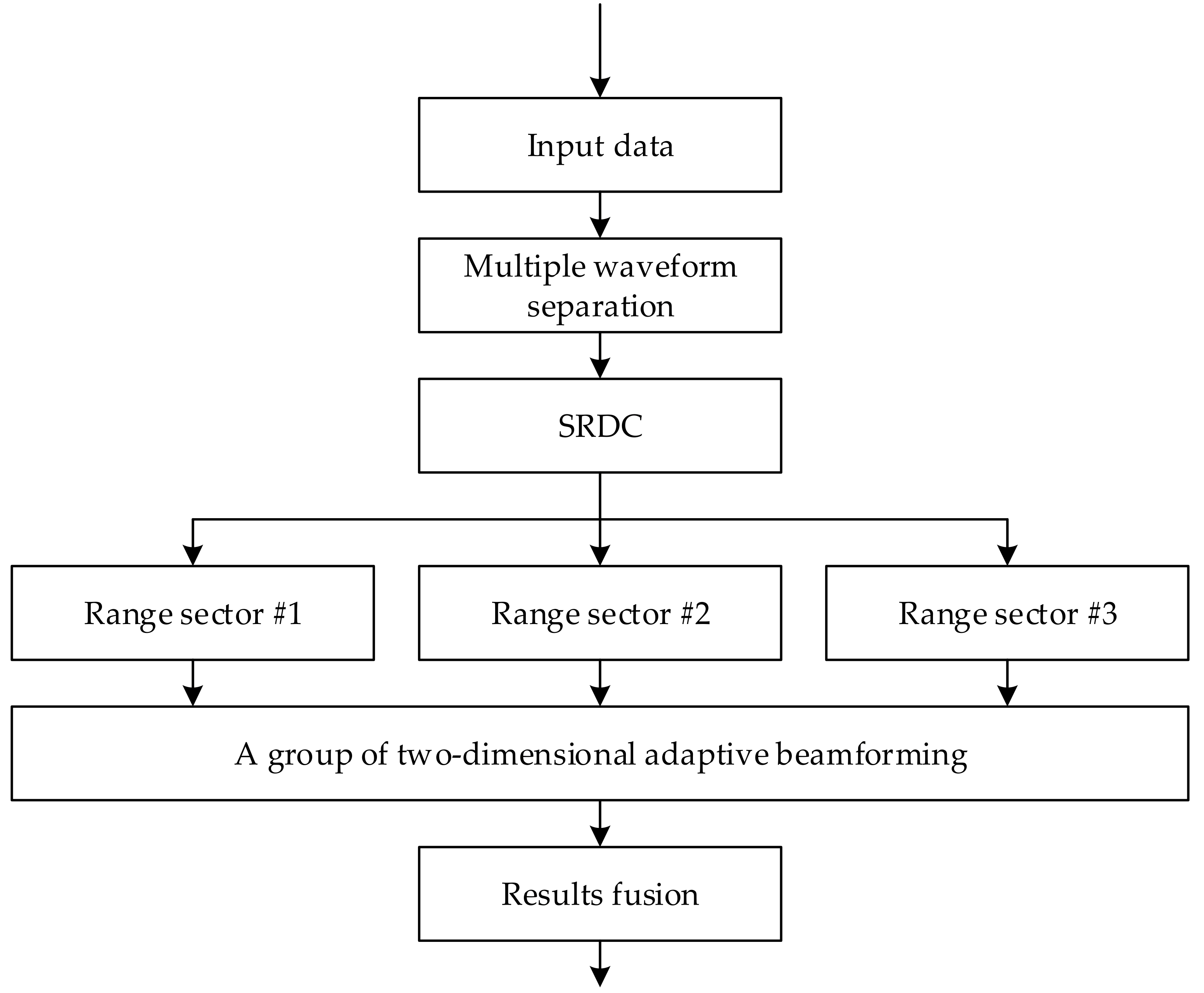
3. Mainlobe RGPO Jamming Suppression for FDA-MIMO Radar
4. Simulations
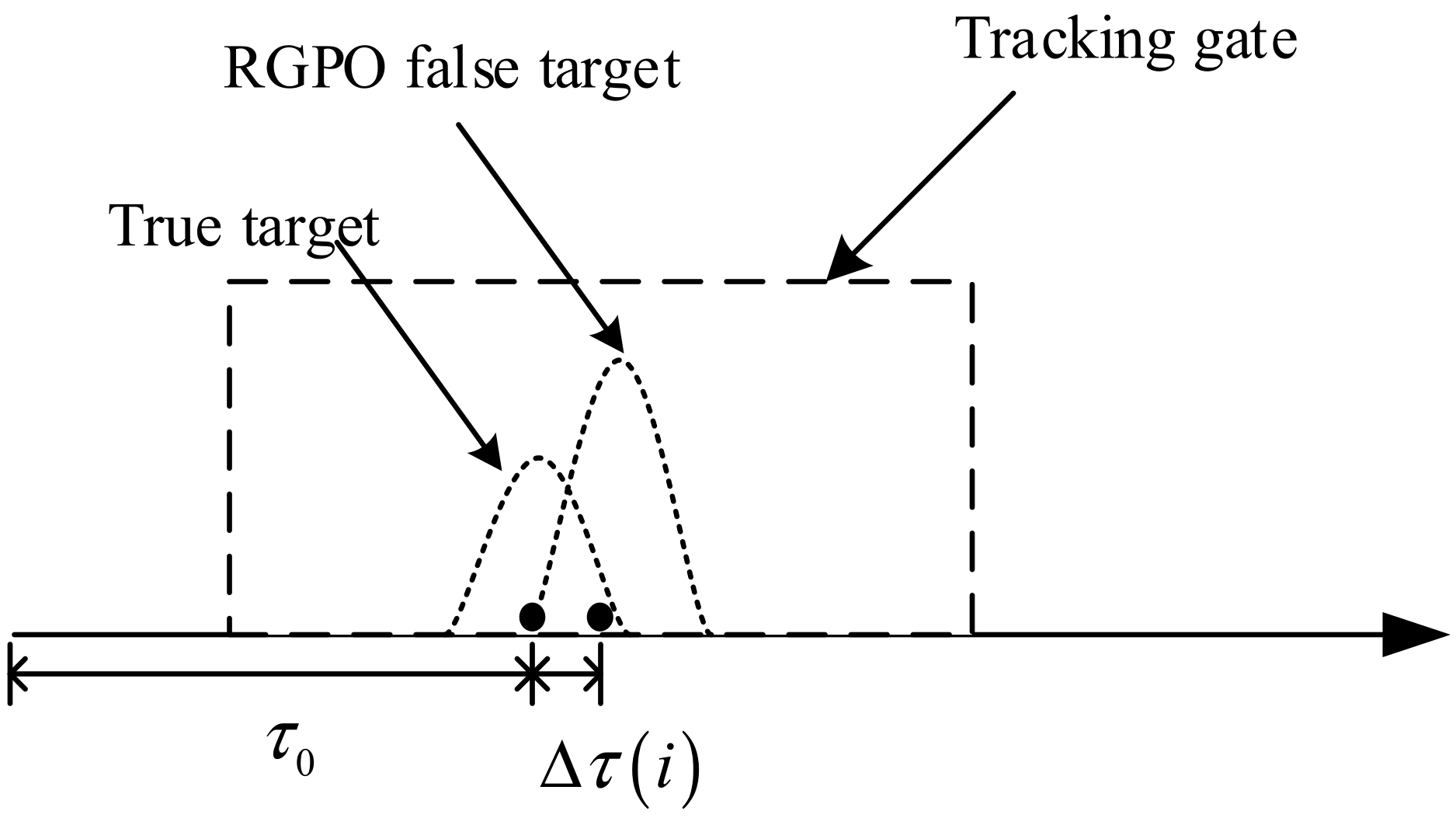
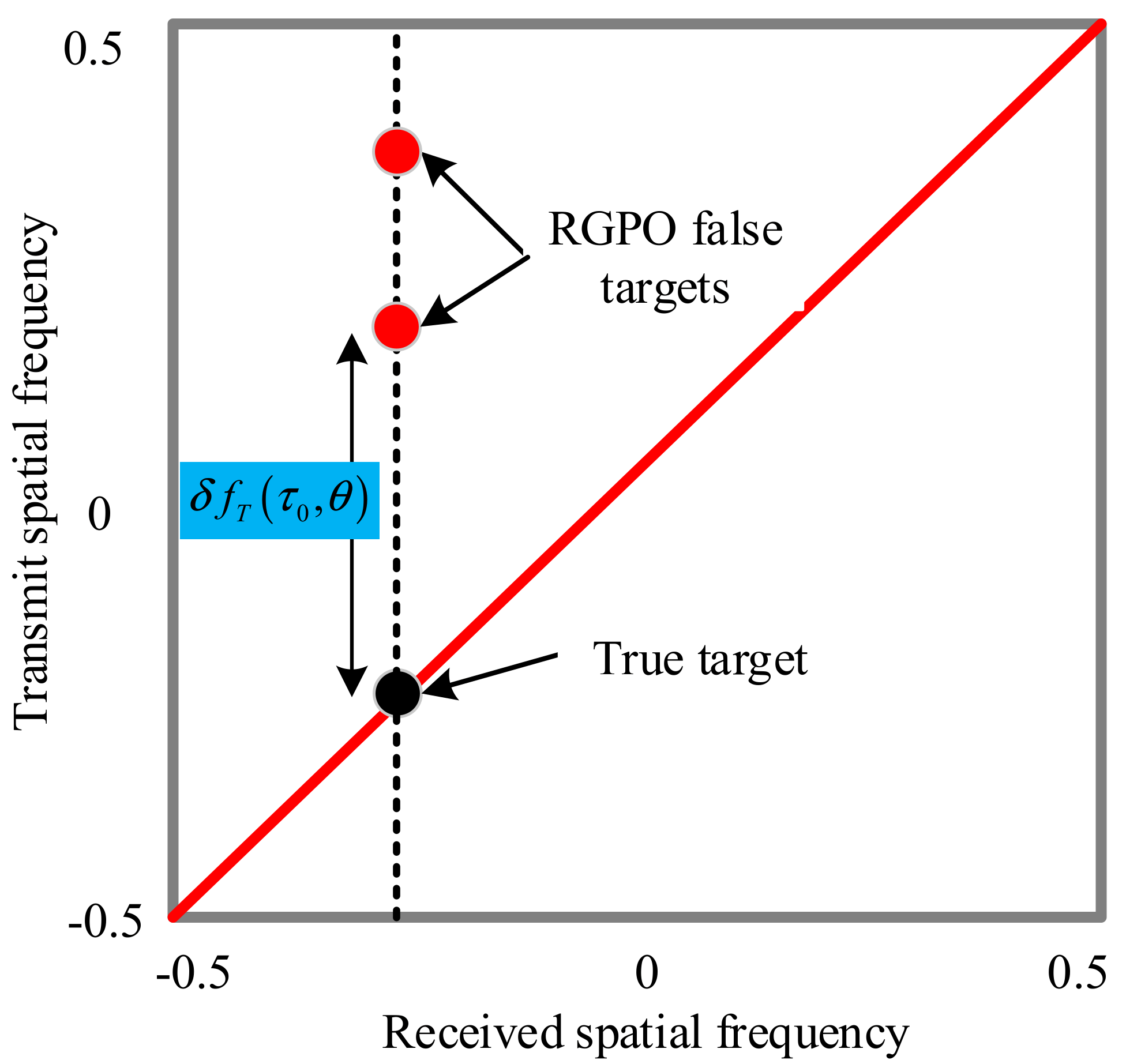
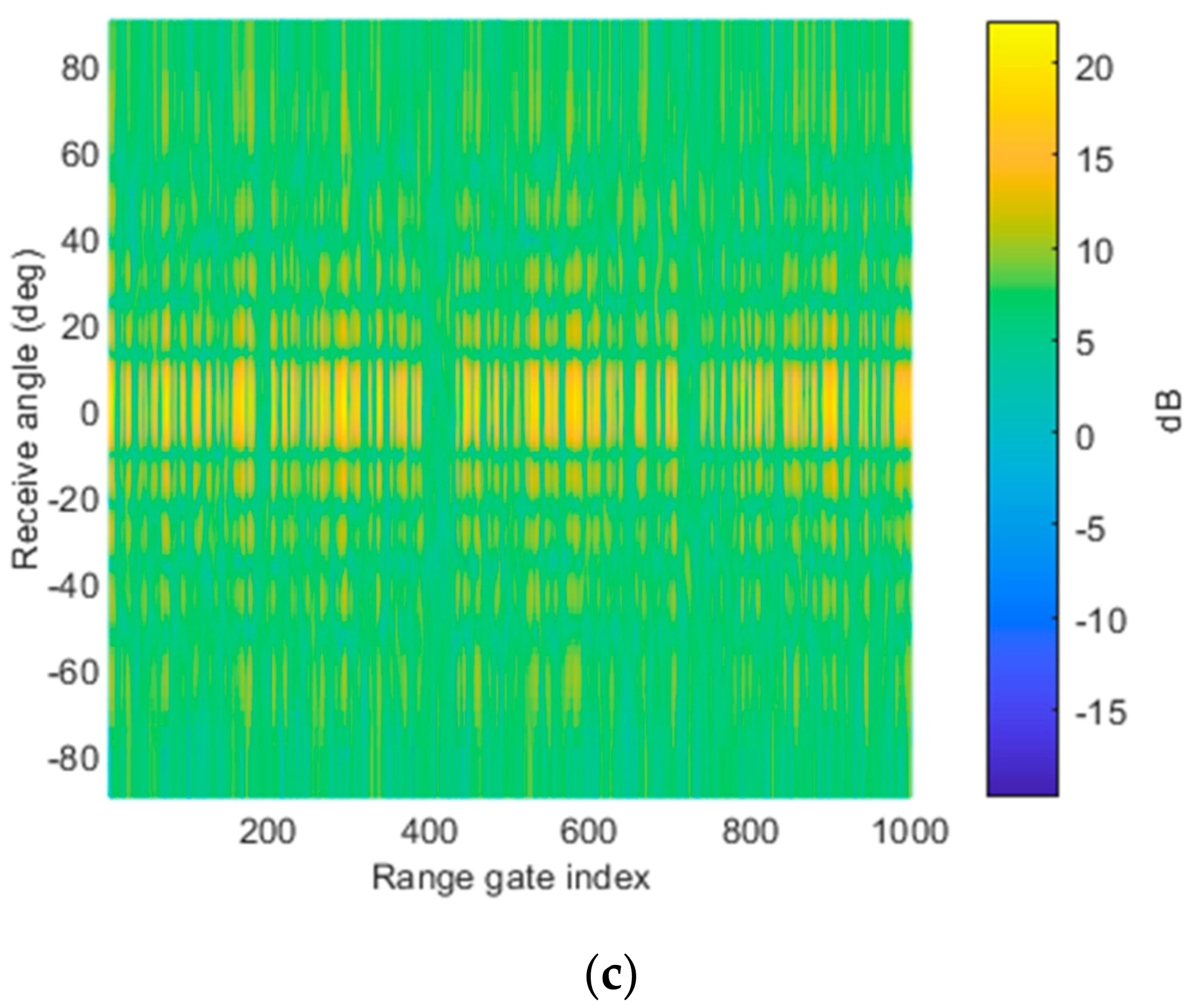
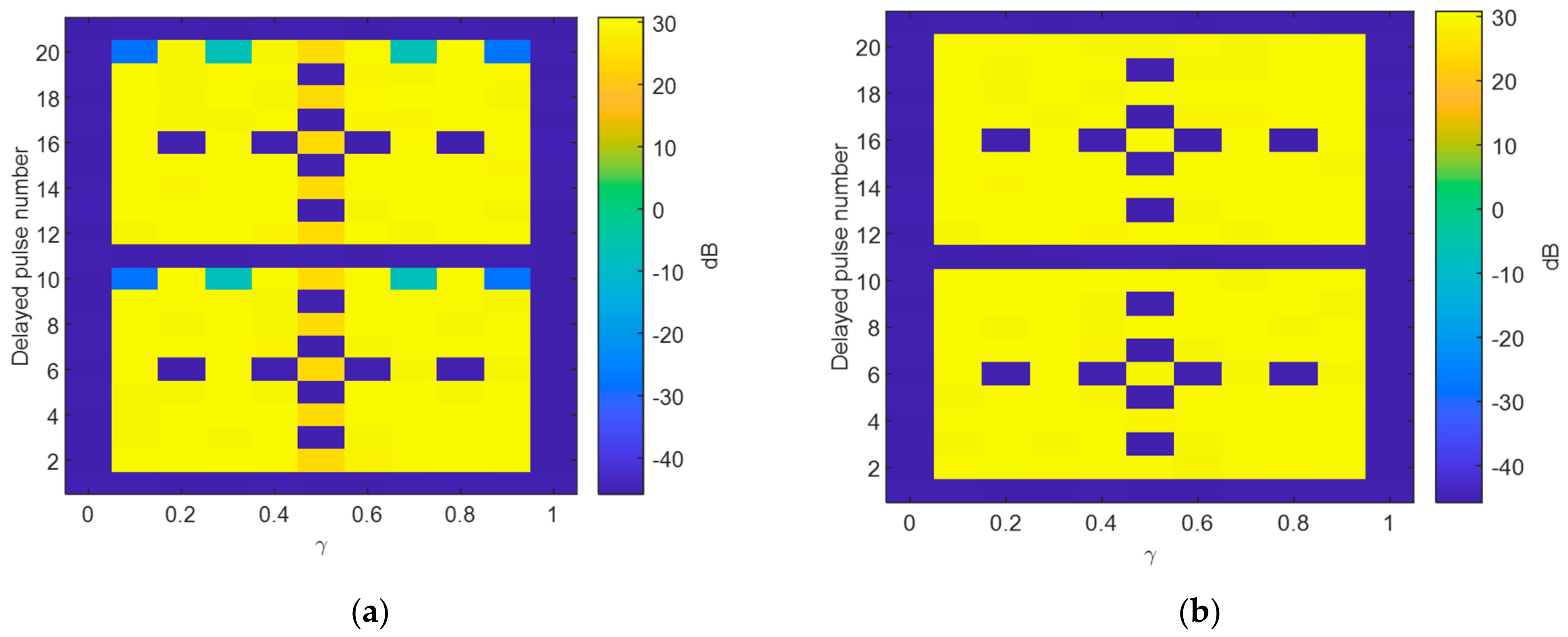
4.1. Property Analysis of RGPO Jamming
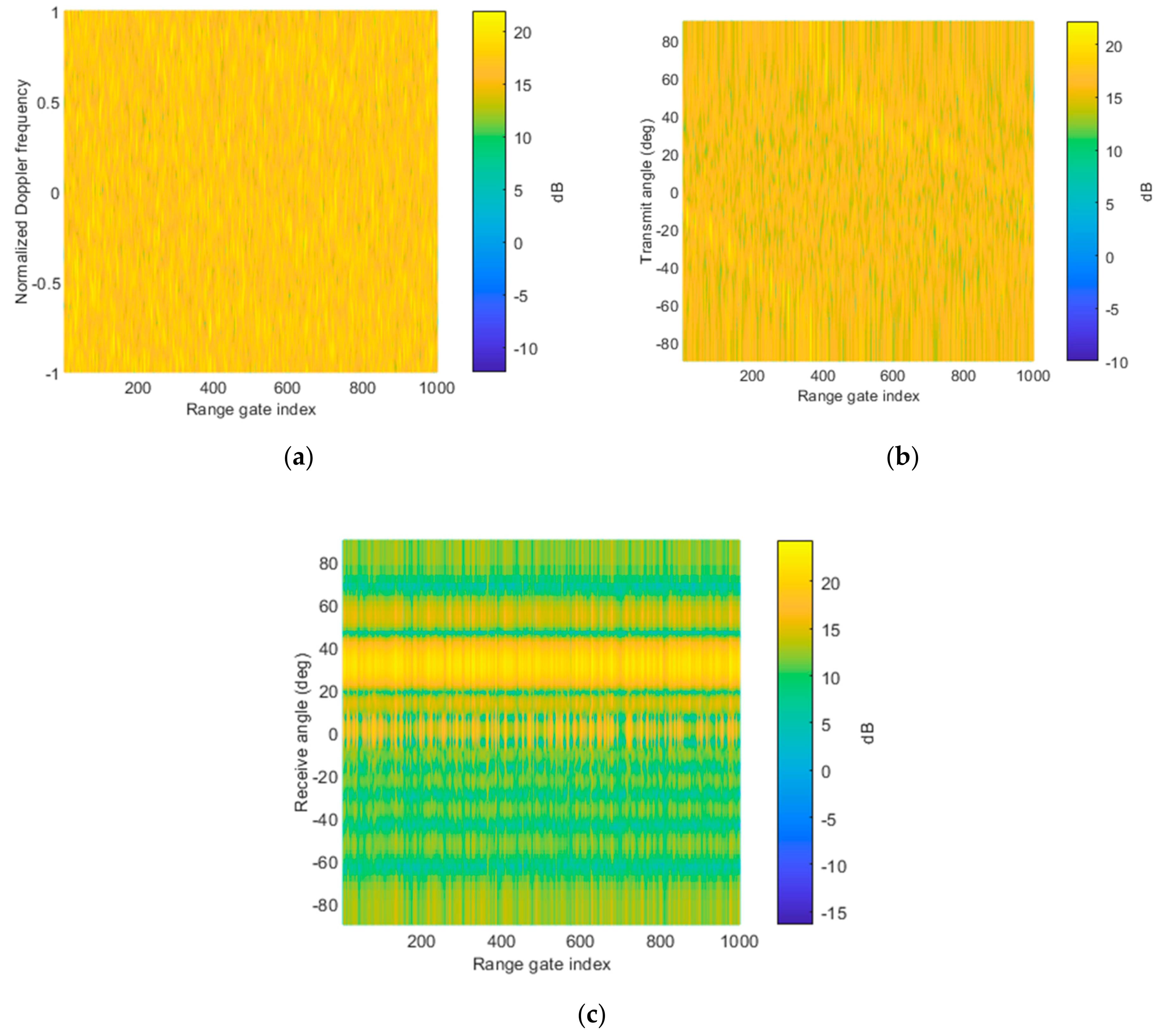
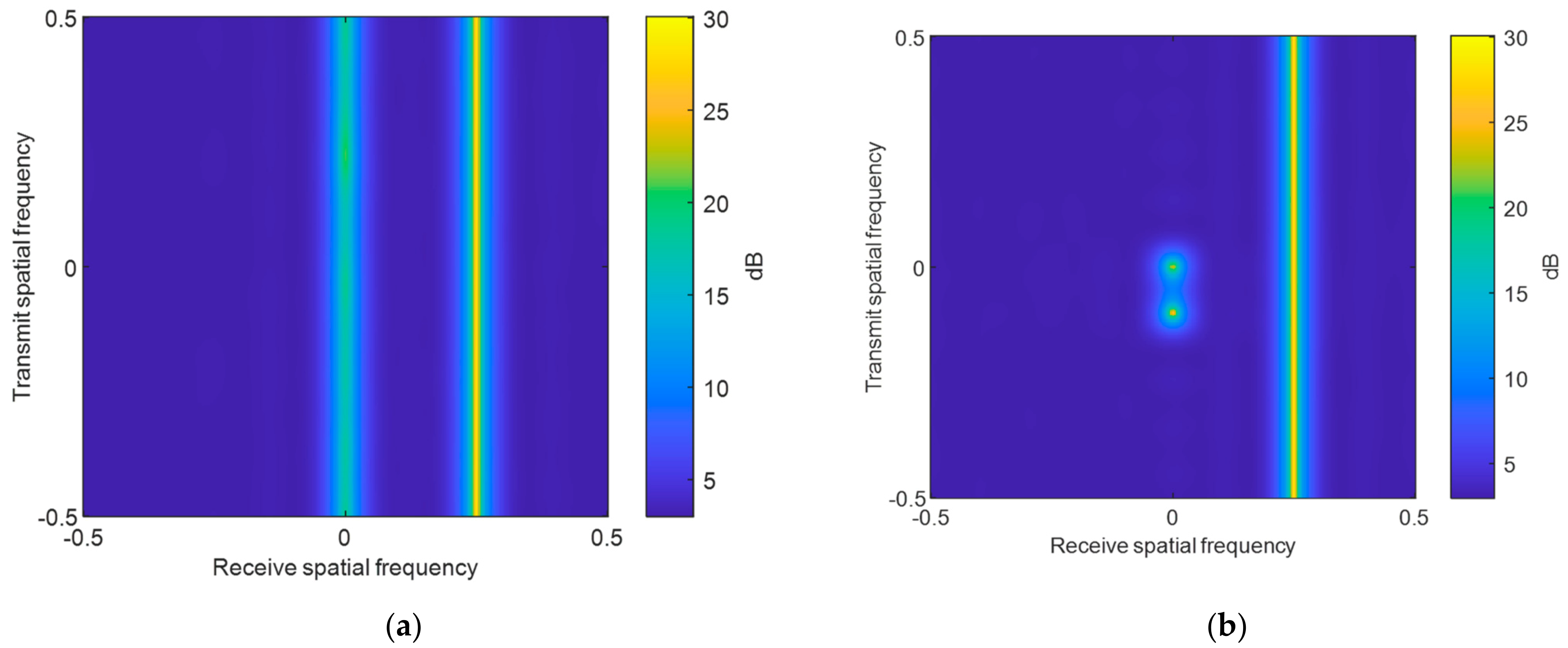
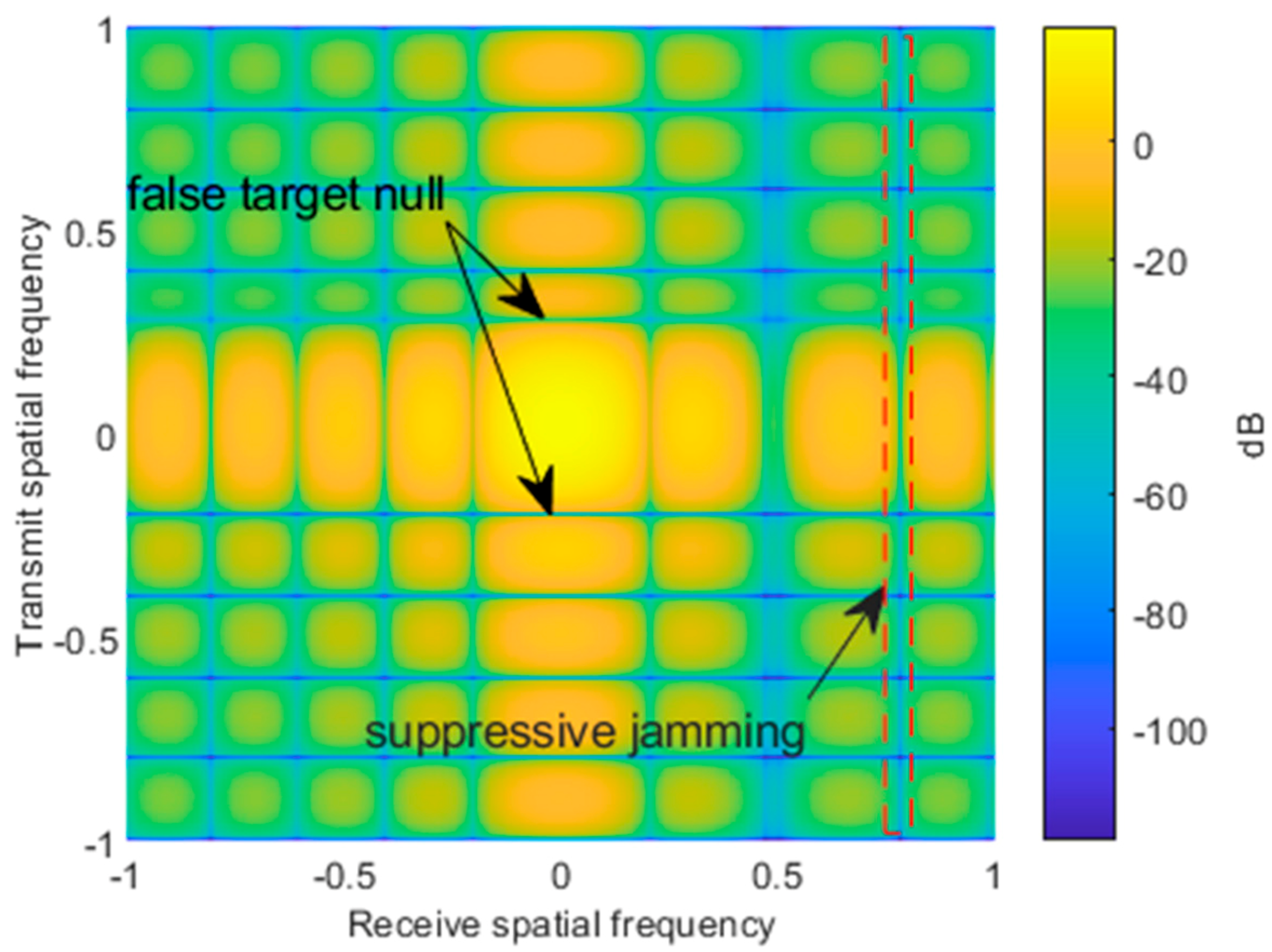
4.2. Transmit–Receive Two-Dimensional Adaptive Beamforming
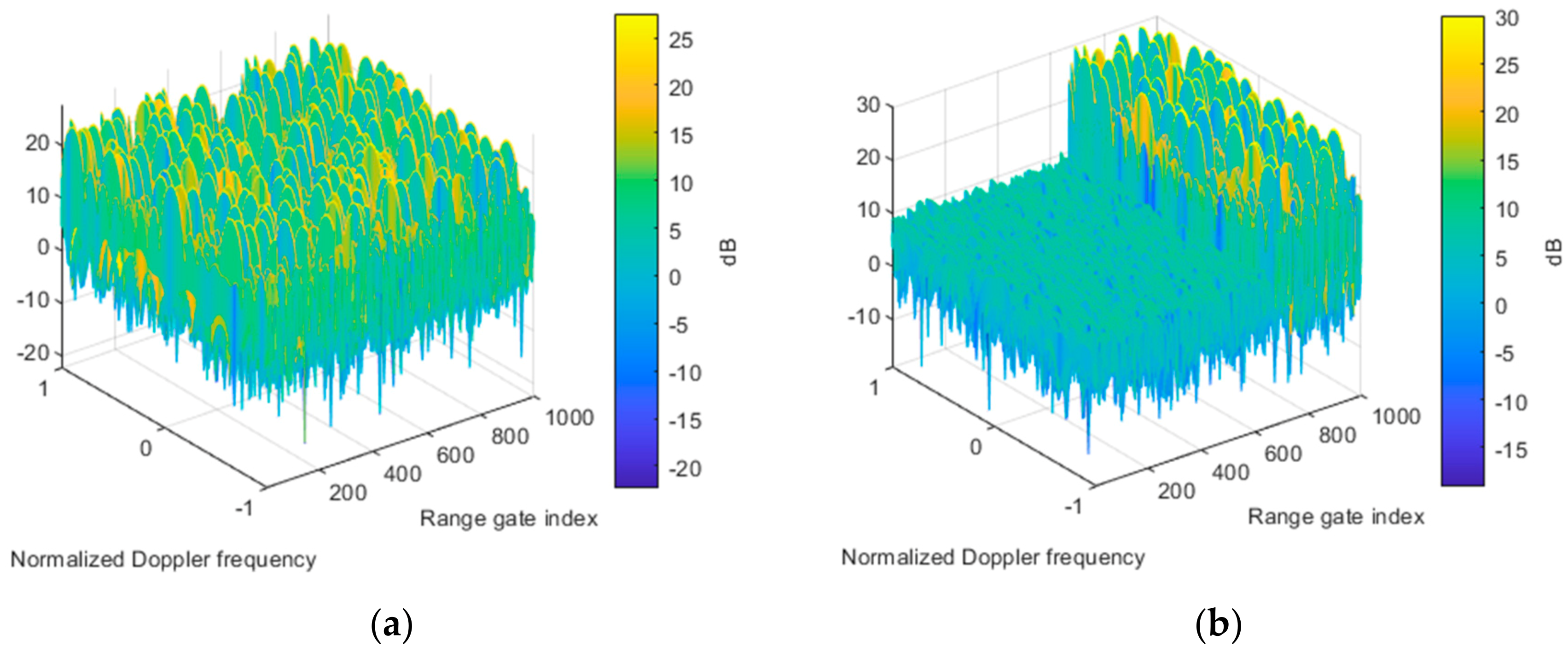
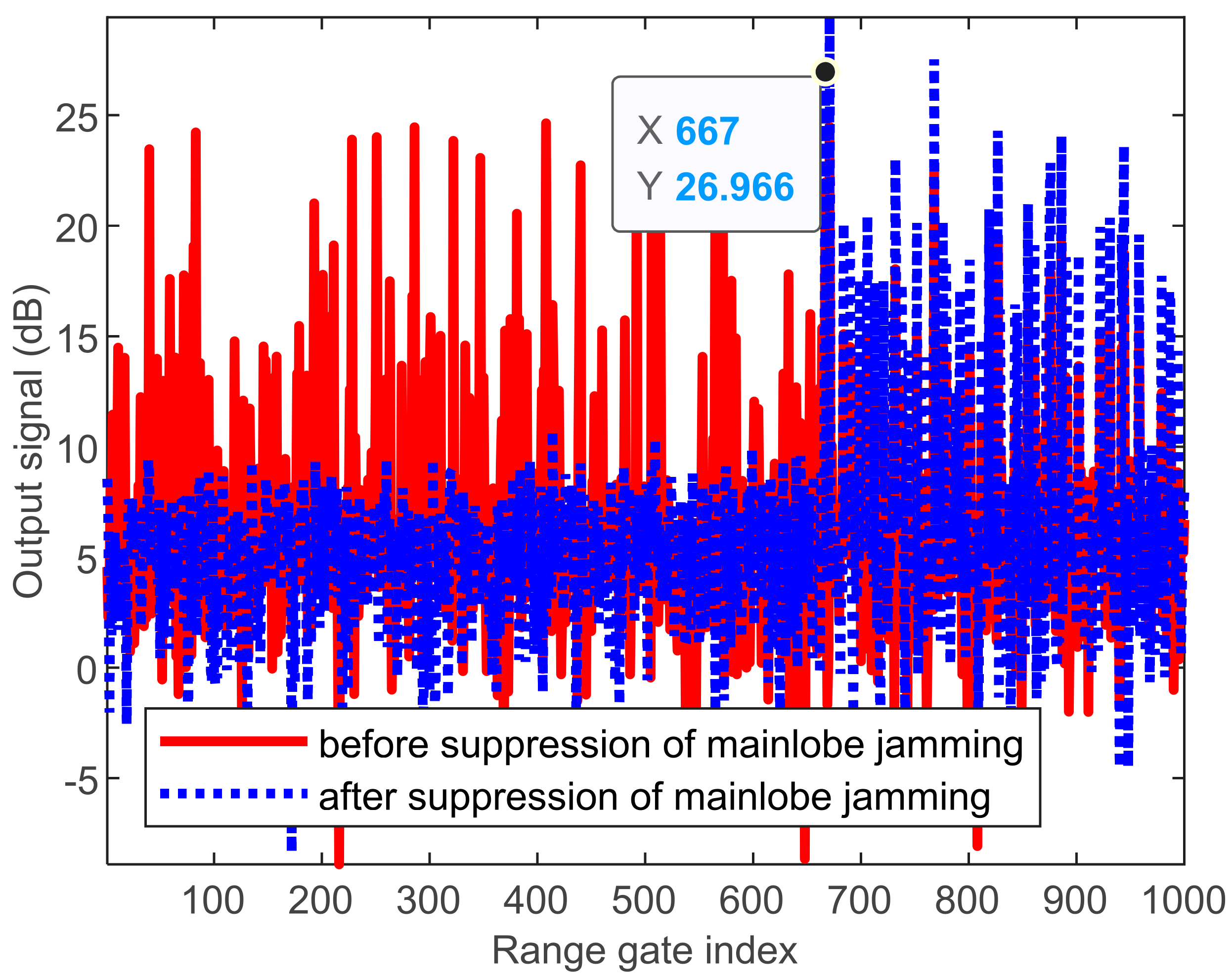
4.3. RGPO Mainlobe Jamming Suppression Performance Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tarchi, D.; Oliveri, F.; Sammartino, P.F. MIMO Radar and Ground-Based SAR Imaging Systems: Equivalent Approaches for Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2012, 51, 425–435. [Google Scholar] [CrossRef]
- Li, X.; Wang, D.; Ma, X.; Wang, W.-Q. FDS-MIMO Radar Low-Altitude Beam Coverage Performance Analysis and Optimization. IEEE Trans. Signal Process. 2018, 66, 2494–2506. [Google Scholar] [CrossRef]
- Soumkh, M. SAR-ECCM using phase-pertured LFM chirp signals an DRFM repeat jammer jenmlization. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 191–205. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, Z. Main-Lobe Jamming Suppression Method in Multiple-Radar System. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2276–2279. [Google Scholar] [CrossRef]
- Xiang, Z.; Chen, B.; Yang, M. Polarization optimization for mainlobe interference suppression. In Proceedings of the International Conference on Radar Systems (Radar 2017), Belfast, Northern Ireland, 23–26 October 2017. [Google Scholar] [CrossRef]
- Wang, J.; Xu, X.; Dai, H. Method for four-channel monopulse radar to resist dual-source angle deception jamming. J. Eng. 2019, 21, 7493–7497. [Google Scholar]
- Shi, J.; Sun, J.; Yang, Y.; Wang, N. Mainlobe Jamming Suppression with Frequency Diverse Array Radar. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Luo, W.; Jin, H.; Li, H.; Duan, K. Radar Main-Lobe Jamming Suppression Based on Adaptive Opposite Fireworks Algorithm. IEEE Open J. Antennas Propag. 2020, 2, 138–150. [Google Scholar] [CrossRef]
- He, S.; Guo, T. Main-lobe jamming suppression for missile-borne phased array high-repetition stepped frequency radar. In Proceedings of the 2012 IEEE International Conference on Information Science and Technology, Wuhan, China, 23–25 March 2012; pp. 866–872. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y.; Guan, S.Y.; Qiang, W.Y.; Zhang, K. Study of cooperative operation effectiveness for UAV with escort free-flight decoys. J. Astronaut. 2007, 3, 498–502. [Google Scholar]
- Nouri, M.; Mivehchy, M.; Aghdam, S.A. Adaptive time-frequency Kernel Local Fisher Discriminant Analysis to distinguish range deception jamming. In Proceedings of the 2015 6th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Dallas-Fortworth, TX, USA, 13–15 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Jia, R.; Zhang, T. An intelligent generation method of range gate pull-off (RGPO) jamming strategy. J. Signal Process. 2021, 2, 276–283. [Google Scholar]
- Cheng, T.; He, Z.; Li, Y. An effective target tracking algorithm with anti-RGPO ability. In Proceedings of the 10th IEEE International NEWCAS Conference, Montreal, QC, Canada, 17–20 June 2012; pp. 117–120. [Google Scholar] [CrossRef]
- Greco, M.; Gini, F.; Farina, A. Combined effect of phase and range gate pull-off delay quantization on jammer signal. IEEE Proc. -Radar Sonar Navig. 2006, 153, 454–459. [Google Scholar] [CrossRef]
- Xie, M.; Liu, L.; Zhang, C.; Fu, X. Bidirectional false targets RGPO jamming. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 2345–2348. [Google Scholar]
- Zhang, J.; Zhu, D.; Zhang, G. New anti-velocity deception jamming technique using pulses with adaptive initial phases. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1290–1300. [Google Scholar] [CrossRef]
- Schuerger, J.; Garmatyuk, D. Performance of random OFDM radar signals in deception jamming scenarios. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–6. [Google Scholar]
- Rao, B.; Xiao, S.; Wang, X. Joint tracking and discrimination of exoatmospheric active decoys using nine-dimensional parameter-augmented EKF. Signal Process. 2011, 91, 2247–2258. [Google Scholar] [CrossRef]
- Rao, B.; Xiao, S.; Wang, X.; Wang, T. Maximum Likelihood Approach to the Estimation and Discrimination of Exoatmospheric Active Phantom Tracks using Motion Features. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 794–819. [Google Scholar] [CrossRef]
- Xiang, Z.; Chen, B.; Yang, M. Transmitter/receiver polarisation optimization based on oblique projection filtering for mainlobe interference suppression in polarimetric multiple-input multiple-output radar. IET Radar Sonar Navig. 2018, 12, 137–144. [Google Scholar] [CrossRef]
- Dai, H.; Wang, X.; Li, Y.; Liu, Y.; Xiao, S. Main-Lobe Jamming Suppression Method of using Spatial Polarization Characteristics of Antennas. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2167–2179. [Google Scholar] [CrossRef]
- Antonik, P.; Wicks, M.C.; Griffiths, H.D.; Baker, C.J. Range-dependent beamforming using element level waveform diversity. In Proceedings of the 2006 International Waveform Diversity & Design Conference, Lihue, HI, USA, 22–27 January 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, W.-Q. Range-Angle Dependent Transmit Beampattern Synthesis for Linear Frequency Diverse Arrays. IEEE Trans. Antennas Propag. 2013, 61, 4073–4081. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, S.; Liao, G.; Zhang, Y. An overview of frequency diverse array radar technology. J. Radars 2018, 7, 167–182. [Google Scholar]
- Shao, H.; Dai, J.; Xiong, J.; Chen, H.; Wang, W.-Q. Dot-Shaped Range-Angle Beampattern Synthesis for Frequency Diverse Array. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1703–1706. [Google Scholar] [CrossRef]
- Wang, W.-Q. Subarray-based frequency diverse array radar for target range-angle estimation. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3057–3067. [Google Scholar] [CrossRef]
- Tang, W.-G.; Jiang, H.; Zhang, Q. Range-Angle Decoupling and Estimation for FDA-MIMO Radar via Atomic Norm Minimization and Accelerated Proximal Gradient. IEEE Signal Process. Lett. 2020, 27, 366–370. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhu, S.; Huang, L.; So, H.C. Joint Range and Angle Estimation Using MIMO Radar with Frequency Diverse Array. IEEE Trans. Signal Process. 2015, 63, 3396–3410. [Google Scholar] [CrossRef]
- Sammartino, P.F.; Baker, C.J.; Griffiths, H.D. Frequency diverse MIMO techniques for radar. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 201–222. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhu, S.; So, H.C. Deceptive jamming suppression with frequency diverse MIMO radar. Signal Process. 2015, 113, 9–17. [Google Scholar] [CrossRef]
- Shi, J.; Liu, X.; Yang, Y.; Sun, J.; Wang, N. Comments on “deceptive jamming suppression with frequency diverse MIMO radar”. Signal Process. 2019, 158, 1–3. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Liu, N.; Zhang, J.; Zhao, S. Adaptive detection with conic rejection to suppress deceptive jamming for frequency diverse MIMO radar. Digit. Signal Process. 2017, 69, 32–40. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Ge, Q.; Xue, B. A robust deceptive jamming suppression method based on covariance matrix reconstruction with frequency diverse array MIMO radar. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, J.; Kang, J.; Liao, G.; So, H.C. Mainlobe deceptive jammer suppression with FDA-MIMO radar. In Proceedings of the 2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM), Sheffield, UK, 8–11 July 2018; pp. 504–508. [Google Scholar]
- Xu, J.; Lan, L.; He, X.; Zhu, S.; Zeng, C.; Liao, G.; Zhang, Y. System Design and Signal Processing for Frequency Diverse Array Radar. J. Beijing Inst. Technol. 2021, 30, 1–19. [Google Scholar]
- Lan, L.; Liao, G.; Xu, J.; Zhang, Y.; Liao, B. Transceive Beamforming with Accurate Nulling in FDA-MIMO Radar for Imaging. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4145–4159. [Google Scholar] [CrossRef]
- Lan, L.; Xu, J.; Liao, G.; Zhang, Y.; Fioranelli, F.; So, H.C. Suppression of Mainbeam Deceptive Jammer with FDA-MIMO Radar. IEEE Trans. Veh. Technol. 2020, 69, 11584–11598. [Google Scholar] [CrossRef]
- Gao, X.; Quan, Y.; Li, Y.; Zhu, S.; Xing, M. Main-lobe deceptive Jamming Suppression with FDA-MIMO Radar Based on BSS. Syst. Eng. Electron. 2020, 42, 1927–1934. [Google Scholar]
- Tan, M.; Wang, C.; Xue, B.; Xu, J. A Novel Deceptive Jamming Approach Against Frequency Diverse Array Radar. IEEE Sens. J. 2020, 21, 8323–8332. [Google Scholar] [CrossRef]
- Feng, Y.; Liao, G.; Xu, J.; Zhu, S.; Zeng, C. Robust adaptive beamforming against large steering vector mismatch using multiple uncertainty sets. Signal Process. 2018, 152, 320–330. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, P.; Weng, Y.; Xu, J.; Liao, G. Range Gate Pull-Off Mainlobe Jamming Suppression Approach with FDA-MIMO Radar: Theoretical Formalism and Numerical Study. Remote Sens. 2022, 14, 1499. https://doi.org/10.3390/rs14061499
Wan P, Weng Y, Xu J, Liao G. Range Gate Pull-Off Mainlobe Jamming Suppression Approach with FDA-MIMO Radar: Theoretical Formalism and Numerical Study. Remote Sensing. 2022; 14(6):1499. https://doi.org/10.3390/rs14061499
Chicago/Turabian StyleWan, Pengfei, Yuanlong Weng, Jingwei Xu, and Guisheng Liao. 2022. "Range Gate Pull-Off Mainlobe Jamming Suppression Approach with FDA-MIMO Radar: Theoretical Formalism and Numerical Study" Remote Sensing 14, no. 6: 1499. https://doi.org/10.3390/rs14061499
APA StyleWan, P., Weng, Y., Xu, J., & Liao, G. (2022). Range Gate Pull-Off Mainlobe Jamming Suppression Approach with FDA-MIMO Radar: Theoretical Formalism and Numerical Study. Remote Sensing, 14(6), 1499. https://doi.org/10.3390/rs14061499






