Multifunctional Signal Design for Measurement, Navigation and Communication Based on BOC and BPSK Modulation
Abstract
:1. Introduction
2. The Transmitting and Receiving System of the Composite Signal
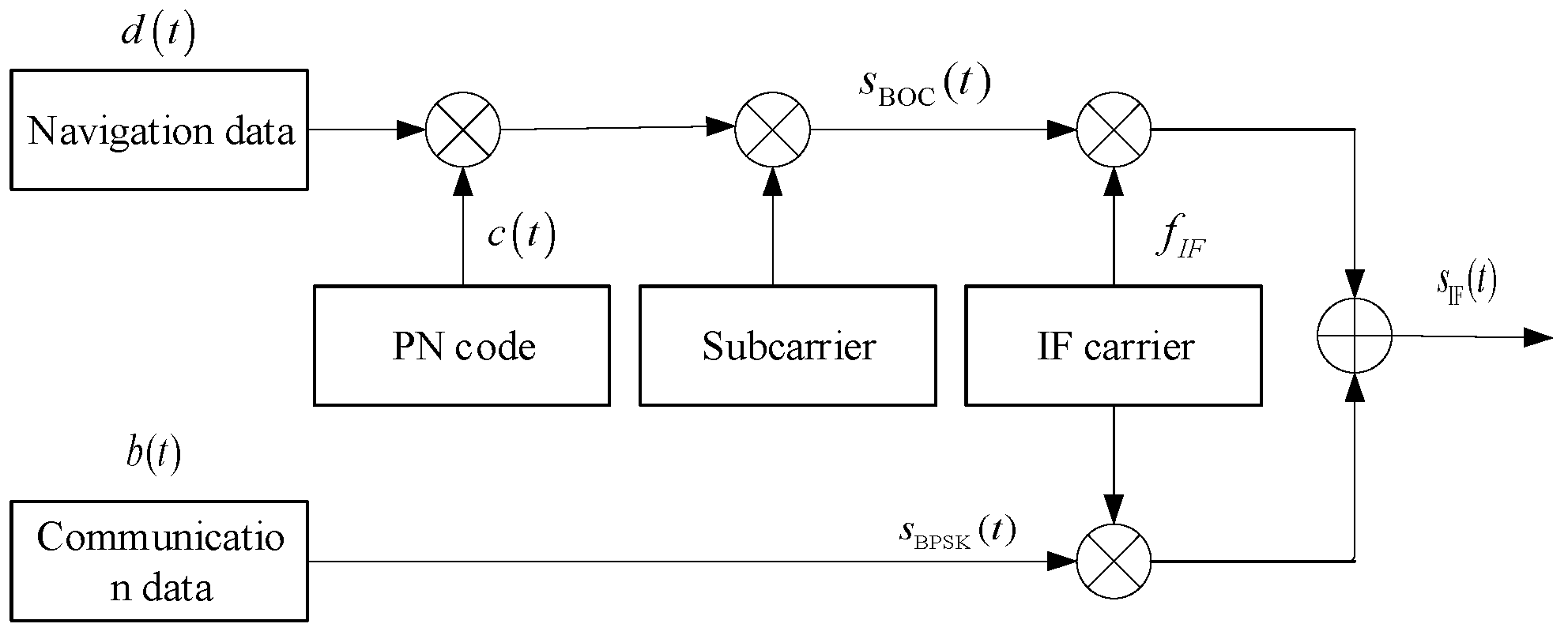
2.1. Signal Model
2.2. The Reception of the Composite Signal
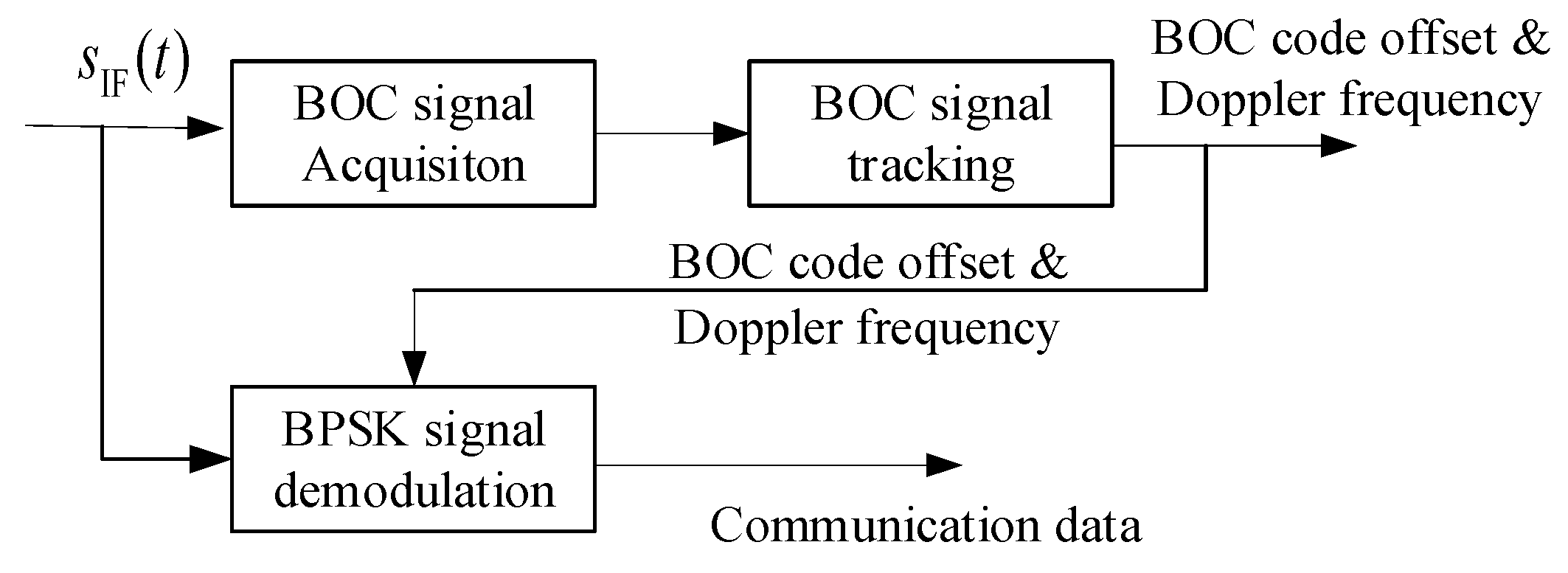
3. The Receiving Process of the Composite Signal
3.1. The Receiving Independence of a BOC Signal and BPSK Signal
3.2. The Tracking Process of a BOC Signal
3.3. The Tracking Process of a BPSK Signal
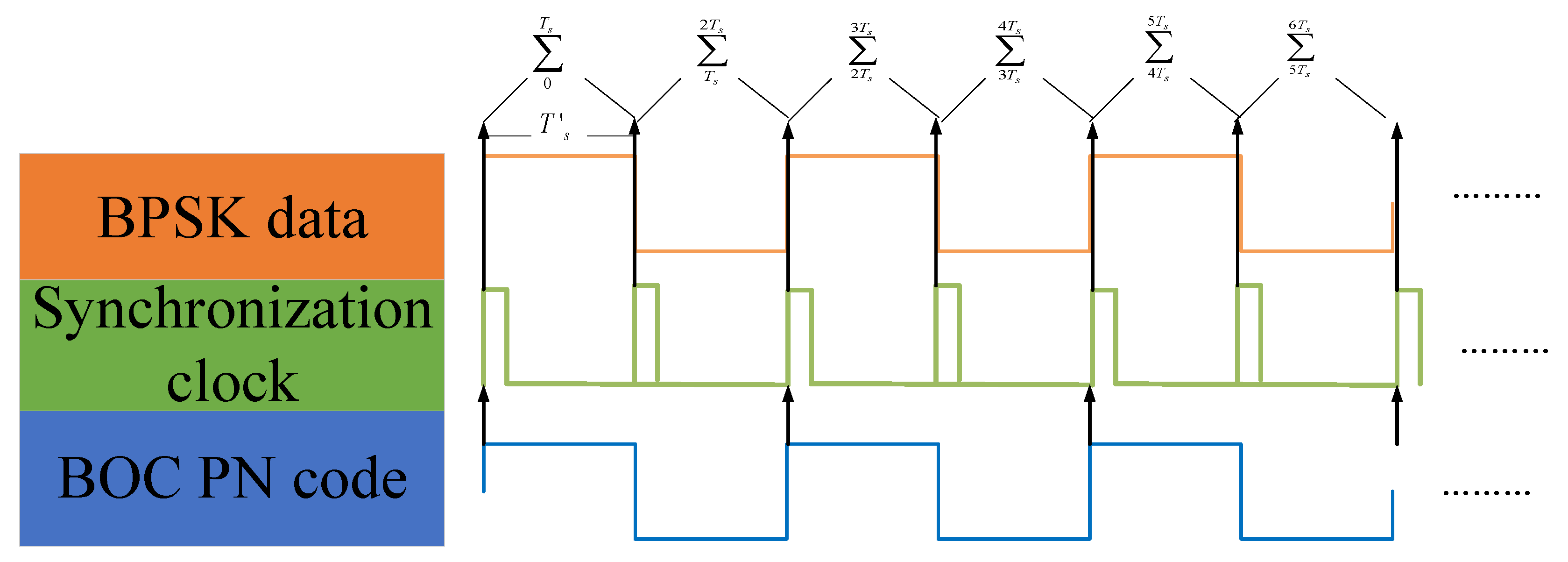
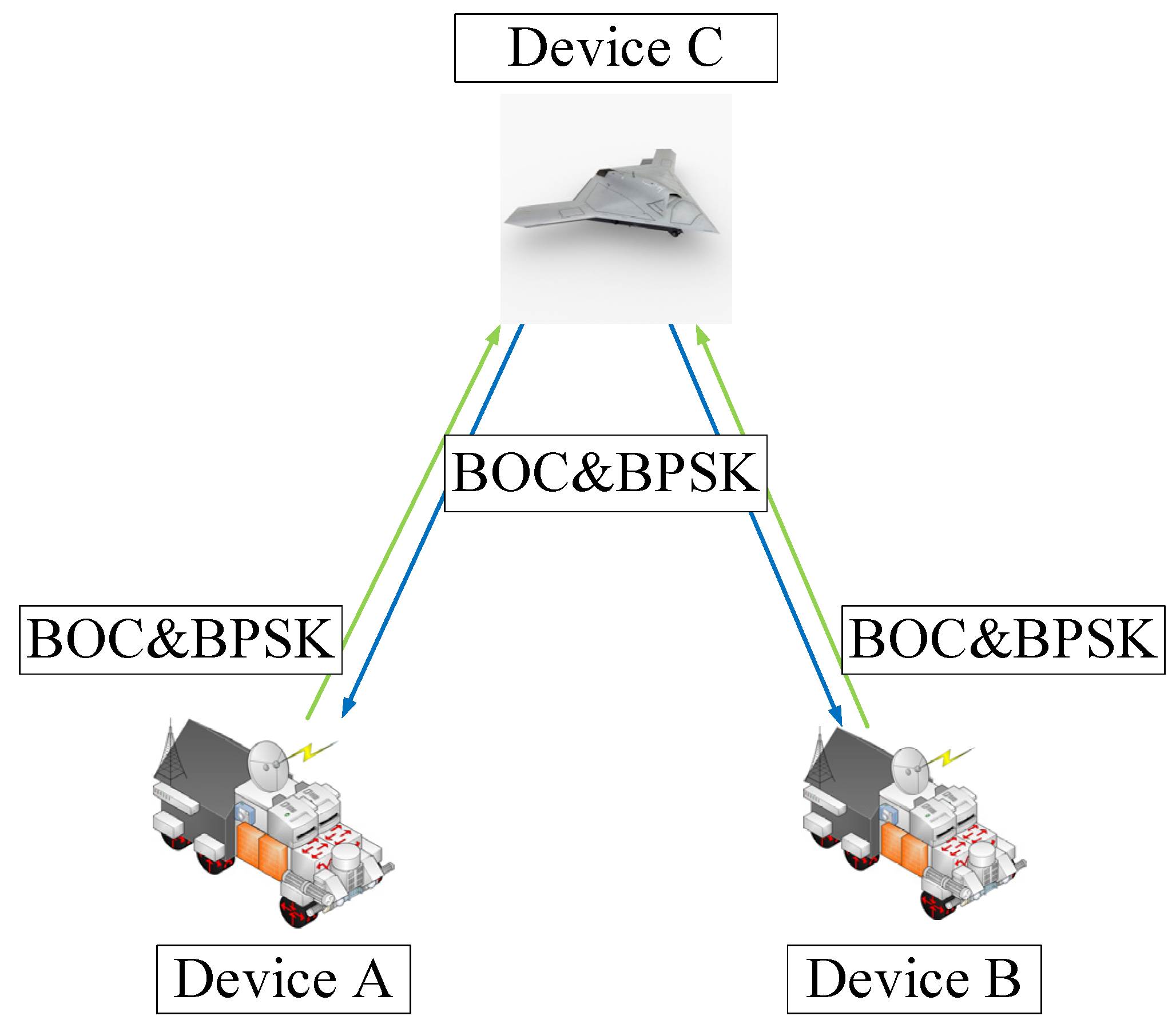
3.4. The Application Scenario
3.5. The Fast Switching of the Composite Signal
- (1)
- The BOC signal is continuously transmitted; and
- (2)
- The transmission of uplink BPSK signals is controlled by the master device.
- The master device starts communication with device A. The links contain the BOC signal and BPSK signal.
- Before switching, device C transmits one frame of data to control device A to stop transmitting the BPSK signal. In addition, the frame can control device B to start transmitting the BPSK signal to device C.
- Master device C uses the code offset and Doppler frequency in the BOC signal of device B to demodulate the BPSK signal from device B.
- If master device C needs to communicate with device A, the process is the same as steps 2 and step 3.
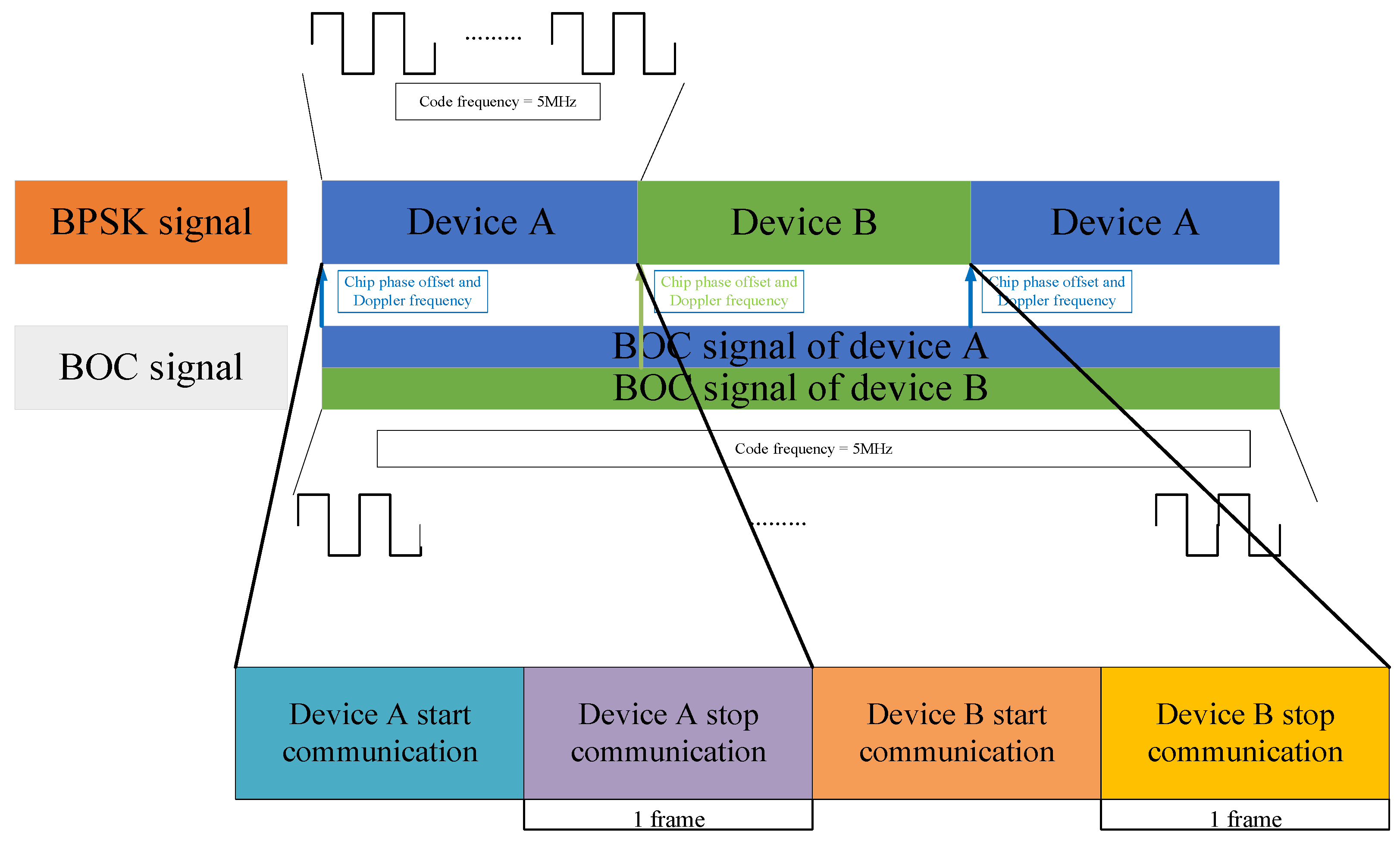
4. Performance Analysis of the BOC Signal and BPSK Signal
4.1. The Design of the Signal Channel
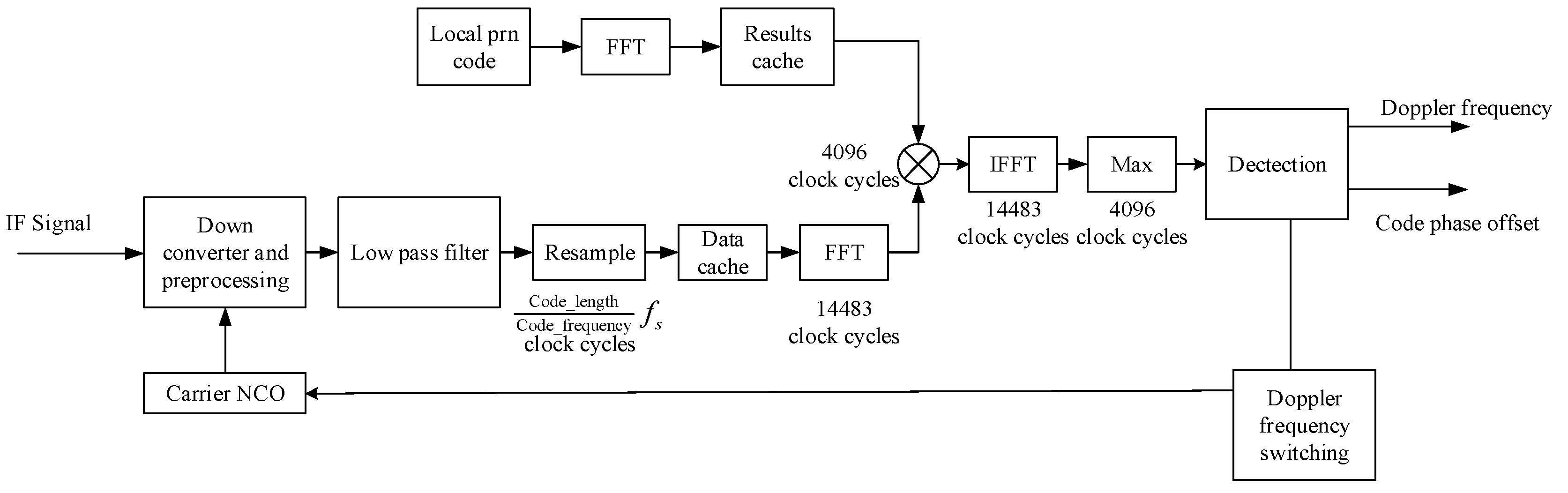
4.2. Acquisition Performance of the BOC Signal
4.3. Tracking Performance for the BOC Signal
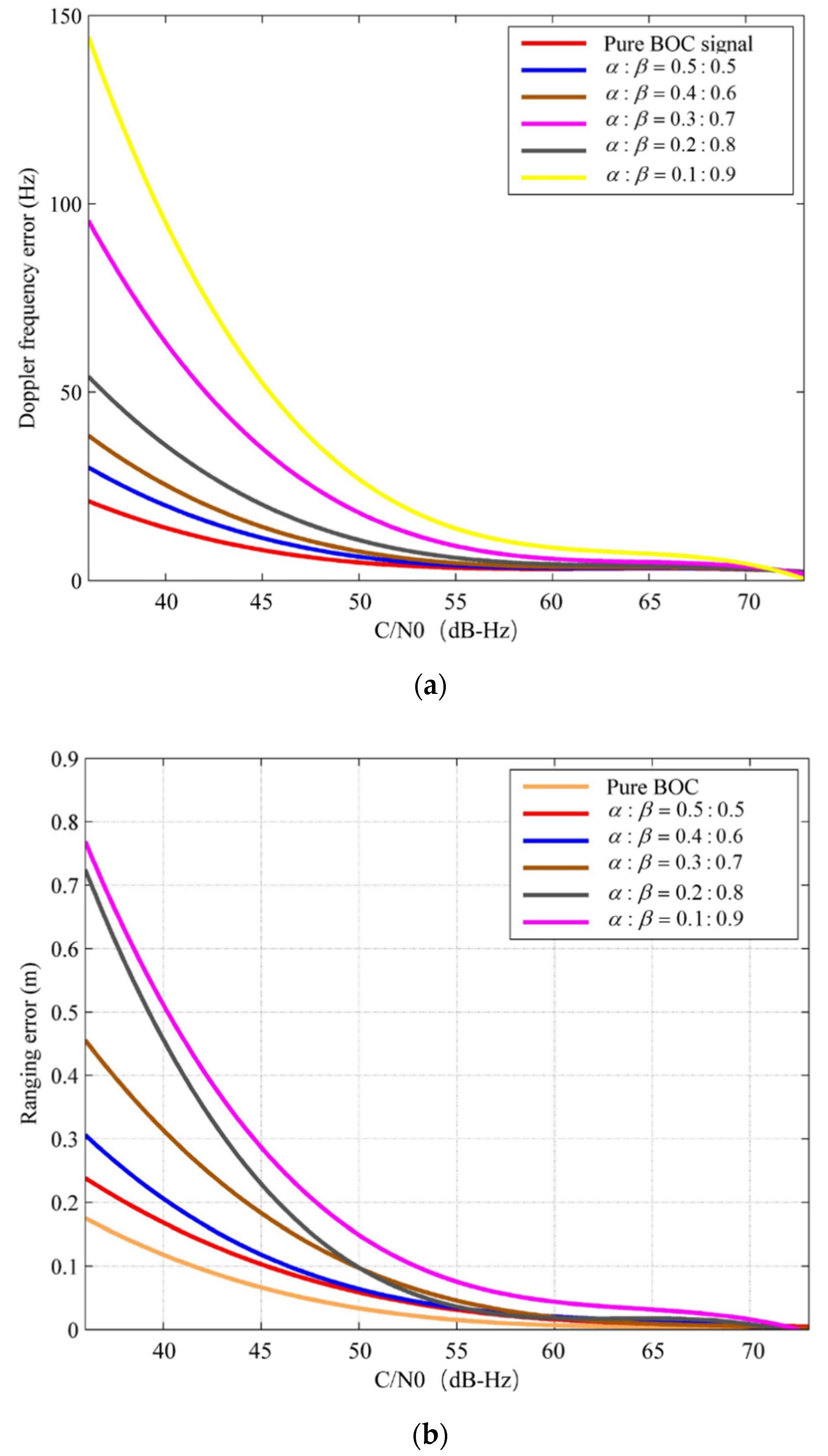
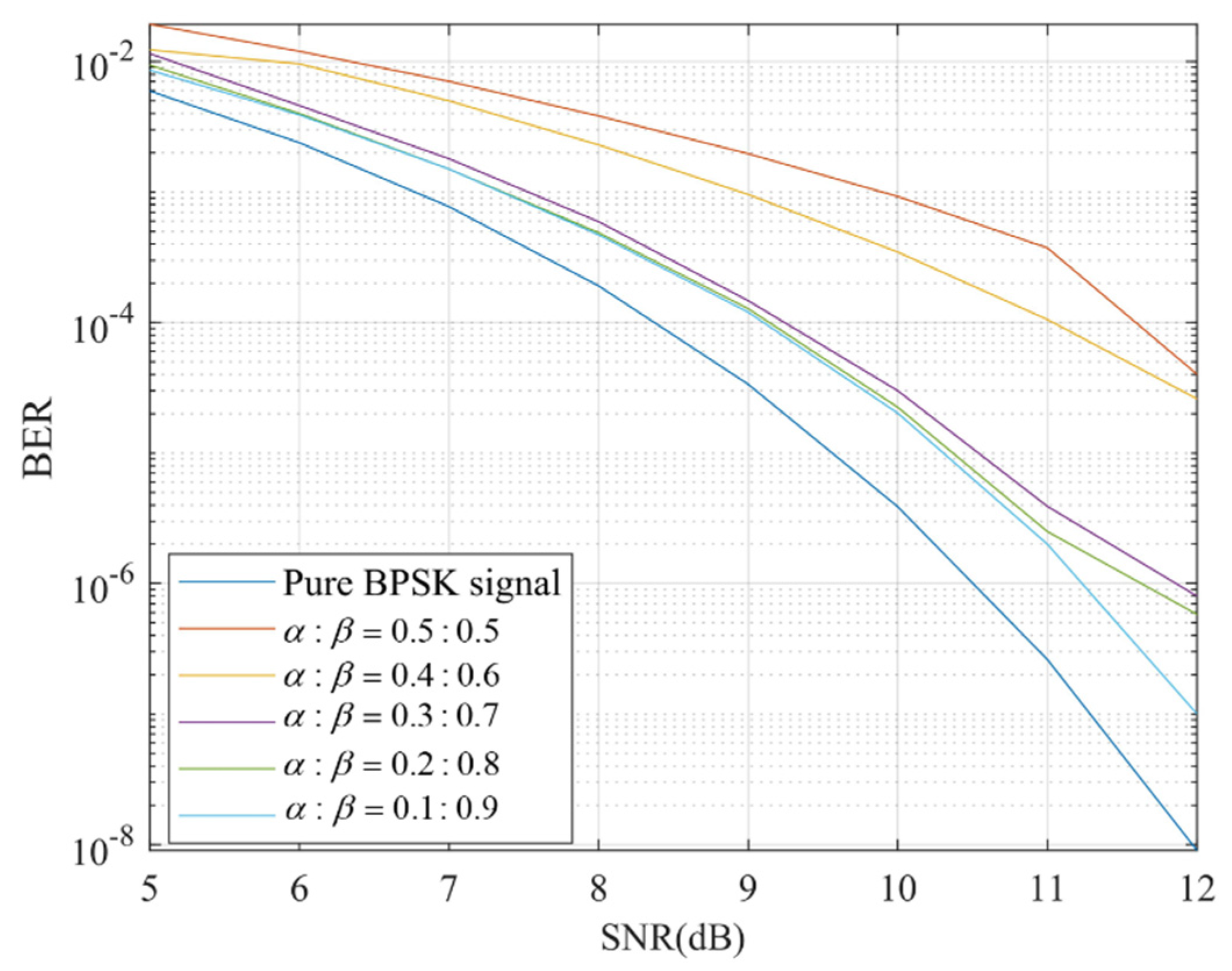
4.4. Data Demodulation with Diffferent BOC and BPSK Ratios
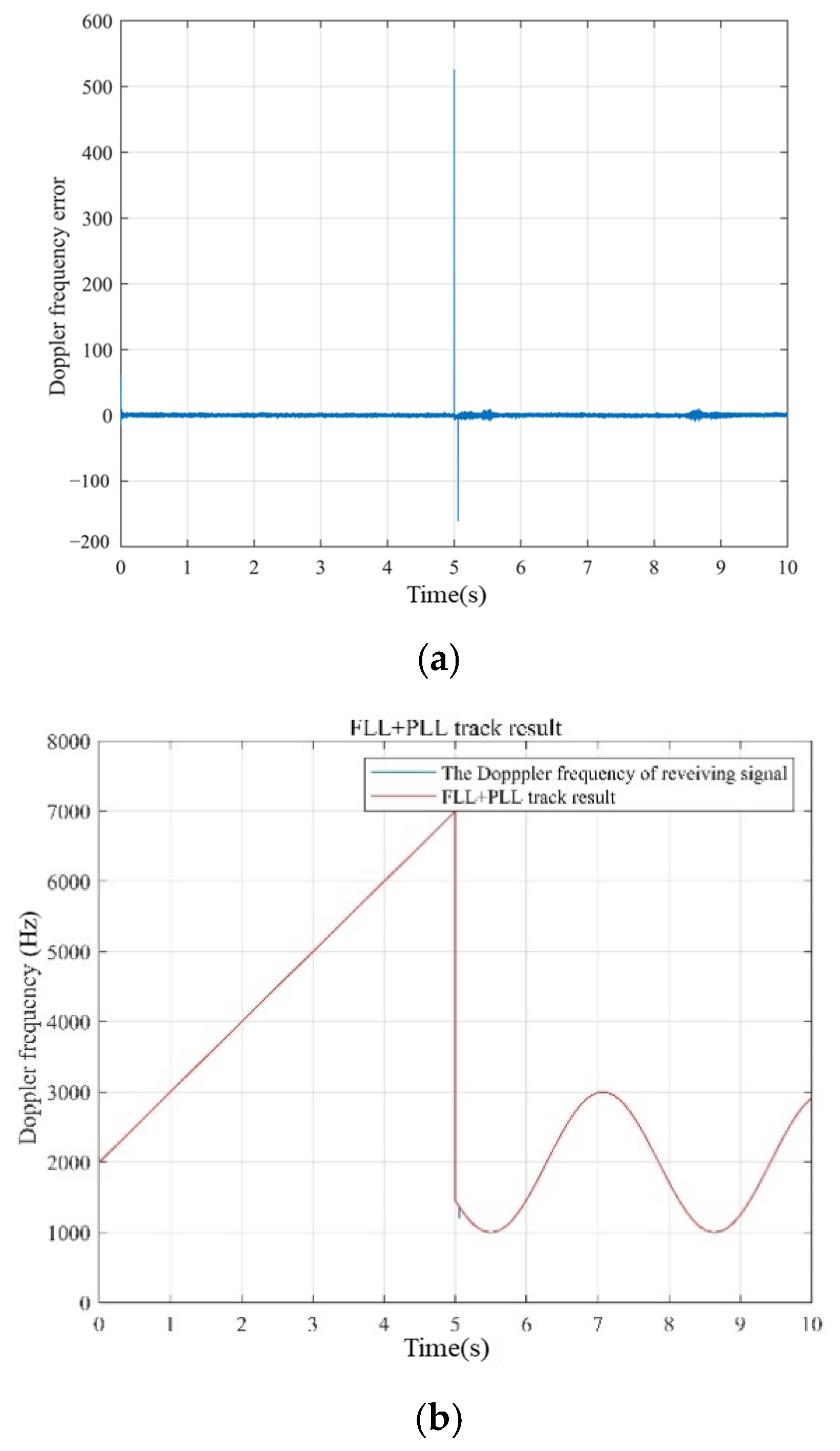
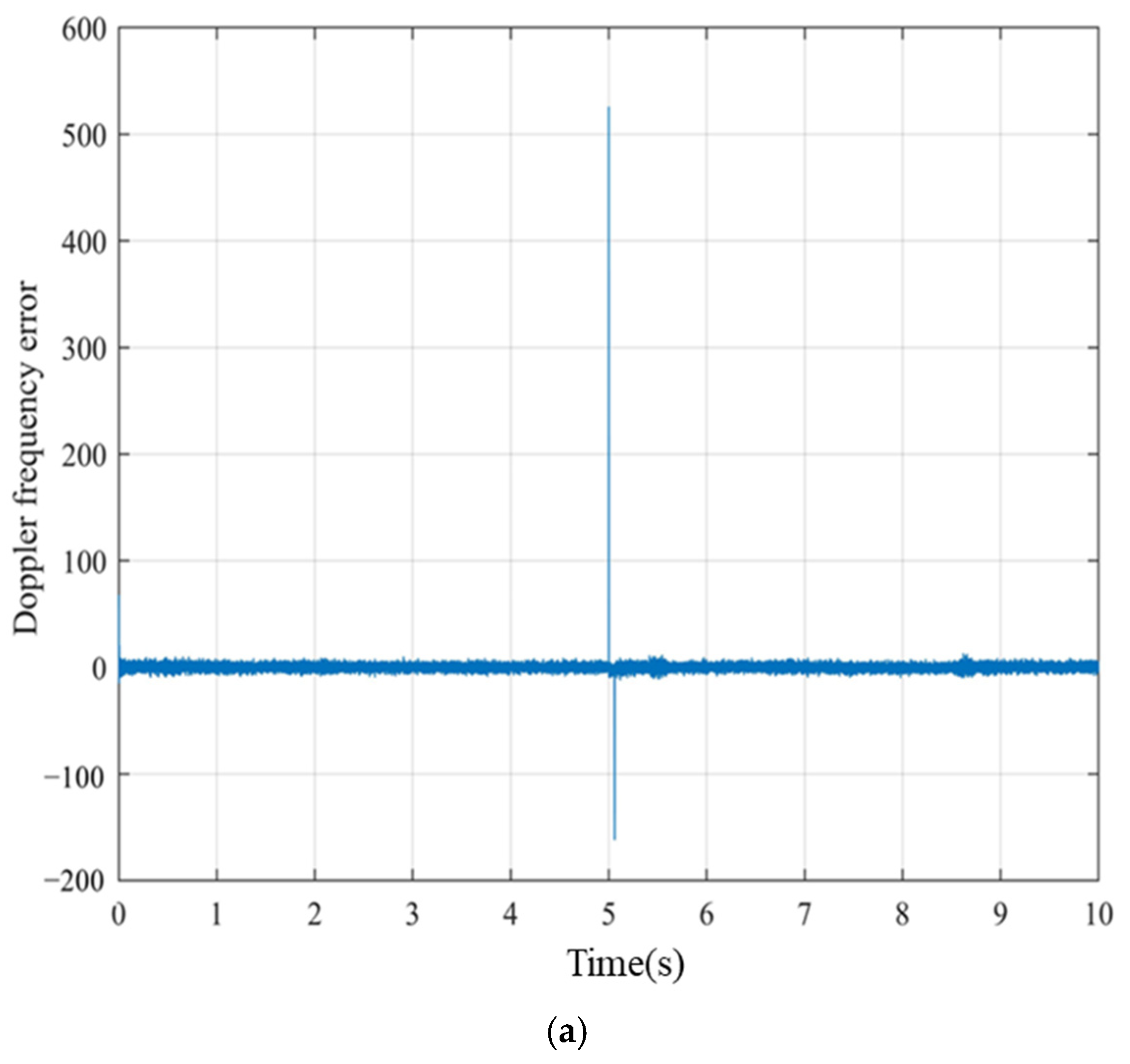
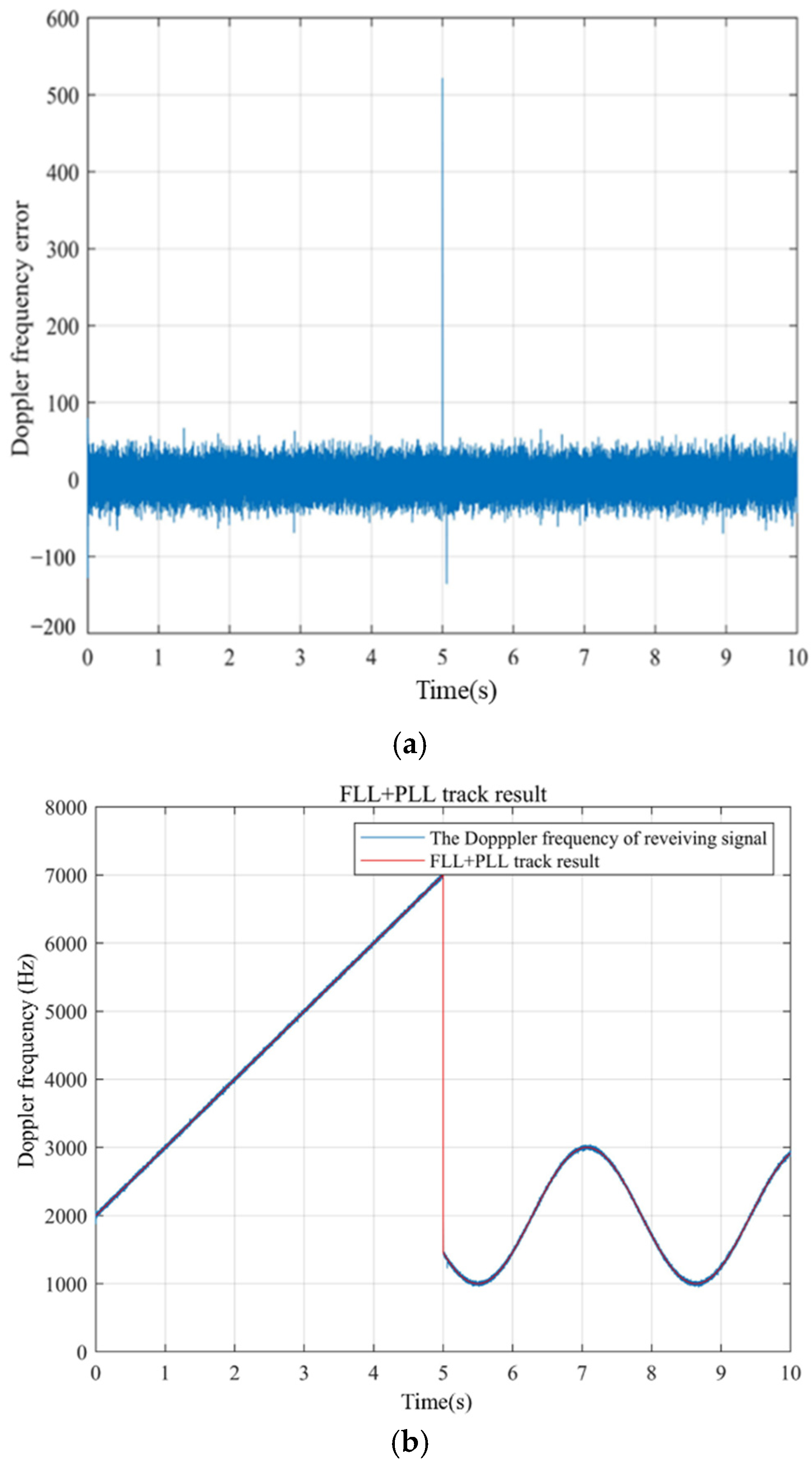
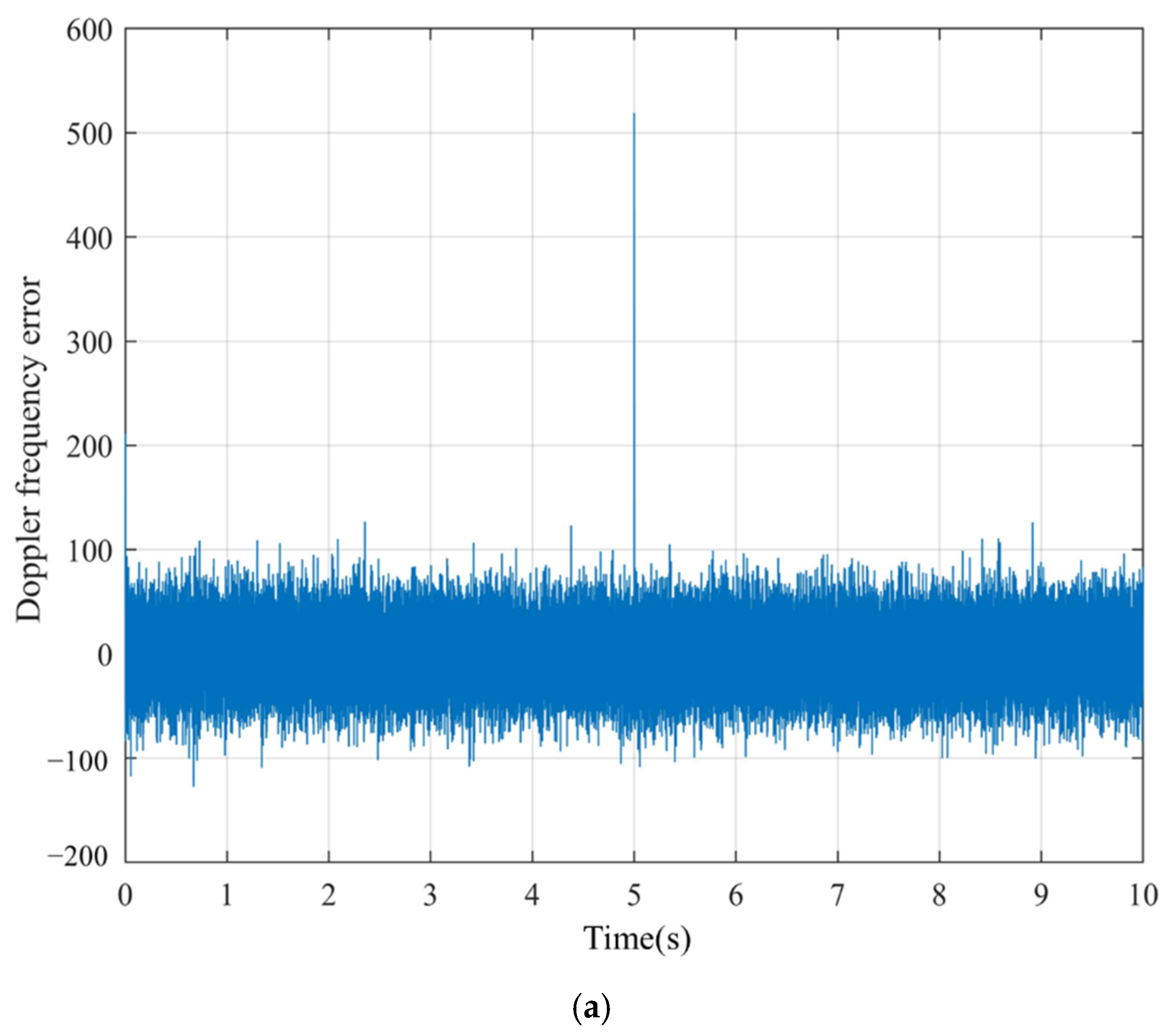
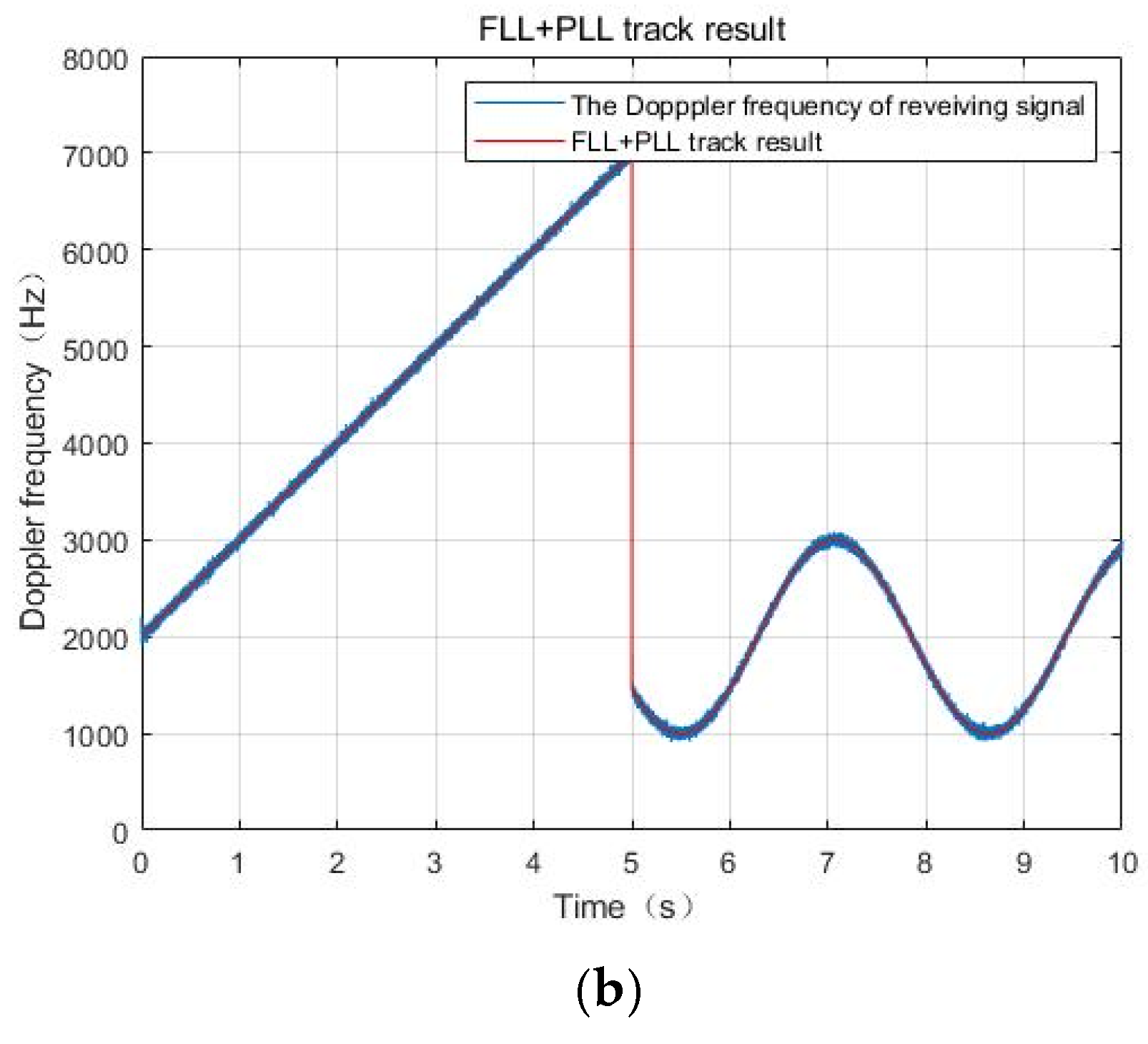
4.5. The Performance of the Fast Switching Algorithm
- (1)
- Device A performs uniform acceleration;
- (2)
- Device B performs sinusoidal motion; and
- (3)
- In the fifth second, the device communicates with the master device from A to B.
4.6. The Hardware Application and Test
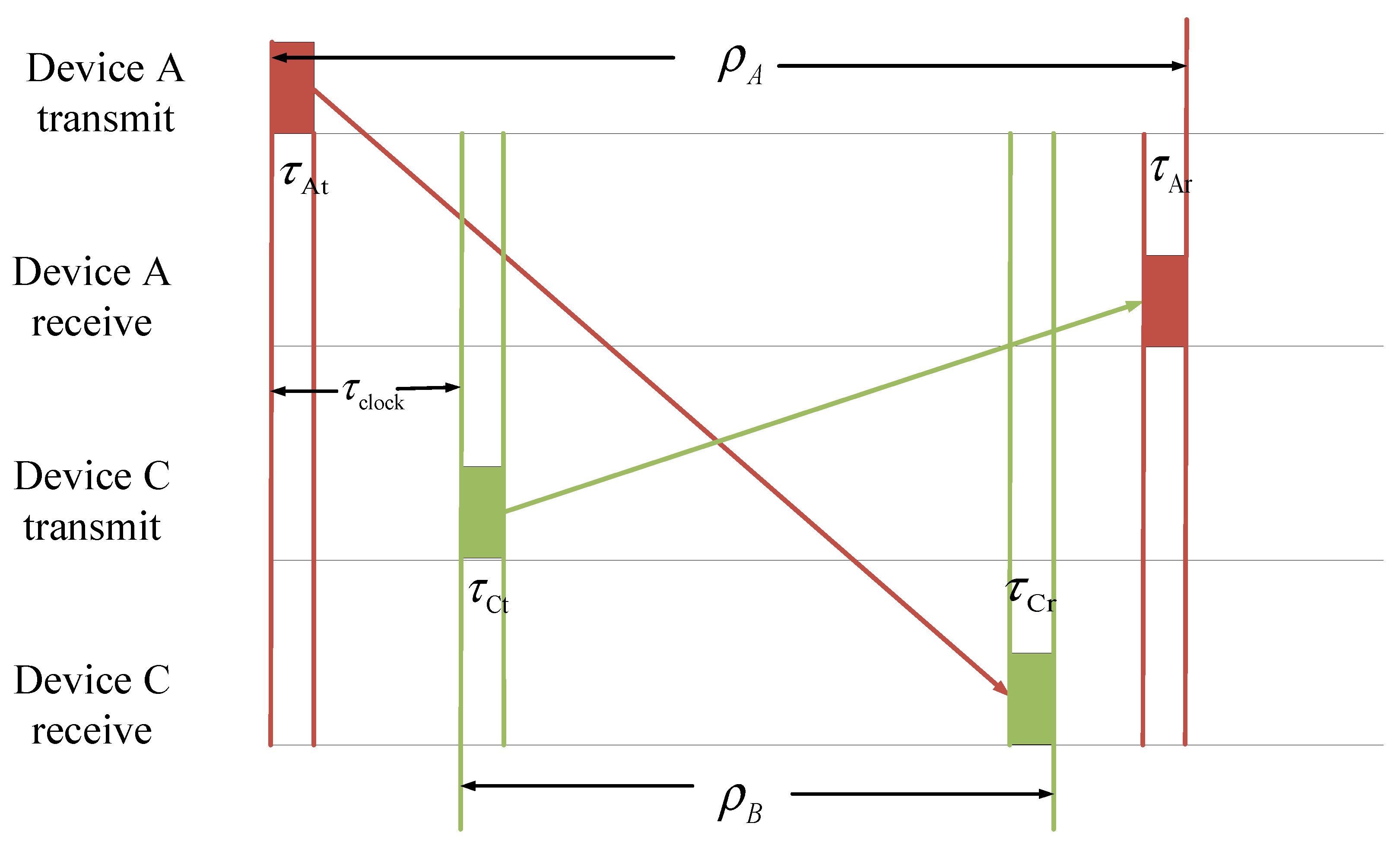
5. Discussion
- (1)
- The composite BOC signal can perform Doppler frequency measurement and high-speed communication at the same frequency. In addition, the communication signal and BOC signal are orthogonal in the time domain, which minimizes the influence of the BOC signal on the communication signal.
- (2)
- The paper gives the receiving algorithm of the composite signal. The algorithm includes the acquisition and tracking of the BOC signal and demodulation of the BPSK signal. By using the synchronization clock of the BOC signal for BPSK demodulation, the tolerance of the BPSK signal to a highly dynamic environment is increased, and the receiver design is simplified.
- (3)
- We discuss the fast-switching algorithm used to make the composite signal have better performance in spacecraft formation or UAVs. The reacquisition time after switching is reduced to one clock cycle.
- (4)
- We simulate and analyze the Doppler measurement and BER performance under different BOC and BPSK signal power ratios, as well as under different C/N0s. This shows that the BPSK signal will interfere with the BOC signal at low C/N0s. In this situation, the power ratio of the BOC signal needs to be improved. However, the performance of the BPSK signal is influenced only by its own power in the composite signal.
- (5)
- The fast-switching algorithm can operate at different C/N0s and signal power ratios in the case of the receiver regenerating local BOC signal to cancel the cross-correlation interference or the different nodes at similar distances.
- (6)
- The hardware platform can achieve all the functions of the composite BOC signal, which shows that the platform is feasible in the physical environment.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Chang, Q.; Zhao, N. A method of GMSK demodulation in inter-satellite link integration technology. In Proceedings of the 11th China Satellite Navigation Conference, Chengdu, China, 23–25 November 2020. [Google Scholar]
- Bai, Y.; Guo, Y.; Wang, X.; Lu, X. Satellite-Ground Two-Way Measuring Method and Performance Evaluation of BDS-3 Inter-Satellite Link System. IEEE Access 2020, 8, 157530–157540. [Google Scholar] [CrossRef]
- Yu, X.; Li, S.; Zhang, J.; Wang, Q.; Qiu, Y. Research on Unified Channel Method of Inter Satellite Radio TT&C and Data Transmission. In Proceedings of the 2021 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Nanjing, China, 23–26 May 2021. [Google Scholar]
- Sessler, G.; Vassallo, E.; Visintin, M. Performance of GMSK for Telemetry and PN Ranging under Realistic Conditions. In Proceedings of the 6th ESA International Workshop on Tracking, Telemetry and Command Systems for Space Applications, Darmstadt, Germany, 10–13 September 2013. [Google Scholar]
- Sessler, G.; Vassallo, E.; Calzolari, G.P. GMSK/PN for High Rate Telemetry and High Accuracy Ranging of Lagrange and Mars Missions. In Proceedings of the 13th International Conference on Space Operations 2014, Pasadena, CA, USA, 5–9 May 2014. [Google Scholar]
- Zhao, N.; Chang, Q.; Wang, H.; Zhang, Z. An Unbalanced QPSK-Based Integrated Communication-Ranging System for Distributed Spacecraft Networking. Sensors 2020, 20, 5803. [Google Scholar] [CrossRef]
- Xia, X.Y.; Gao, F.; Han, X.D. An Improved Digital Carrier Synchronization Method for UQPSK. In Proceedings of the 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 20–22 July 2018; pp. 1076–1080. [Google Scholar]
- Ma, J.; Yang, Y. A generalized anti-interference low-ambiguity dual-frequency multiplexing modulation based on the frequency-hopping technique. IEEE Access 2020, 8, 95288–95300. [Google Scholar] [CrossRef]
- Xiong, H.; Wang, S.; Gong, S.; Peng, M.; Shi, J.; Tang, J. Improved synchronisation algorithm based on reconstructed correlation function for BOC modulation in satellite navigation and positioning system. IET Commun. 2018, 12, 743–750. [Google Scholar] [CrossRef]
- Juang, J.C.; Lin, C.T.; Tsai, Y.F. Comparison and Synergy of BPSK and BOC Modulations in GNSS Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1959–1971. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Y.; Li, H.; Li, J. Expressions for the Autocorrelation Function and Power Spectral Density of BOC Modulation Based on Convolution Operation. Math. Probl. Eng. 2020, 2020, 2063563. [Google Scholar] [CrossRef]
- Lohan, E.S.; Lakhzouri, A.; Renfors, M. Binary-offset-carrier modulation techniques with applications in satellite navigation systems. Wirel. Commun. Mob. Comput. 2007, 7, 767–779. [Google Scholar] [CrossRef]
- Wang, C.; Cui, X.; Zhu, Y.; Lu, M. Thermal noise performance analysis for dual binary phase-shift keying tracking of standard BOC signals. IET Radar Sonar Navig. 2020, 14, 1019–1028. [Google Scholar] [CrossRef]
- Li, M.; Qu, L.; Zhao, Q.; Guo, J.; Su, X.; Li, X. Precise Point Positioning with the BeiDou Navigation Satellite System. Sensors 2014, 14, 927–943. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Zhou, Q.; Ji, Y.; Fu, Q.; Miao, Q.; Wu, S. An Unambiguous Acquisition Algorithm for BOC (n, n) Signal Based on Sub-correlation Combination. Wirel. Pers. Commun. 2019, 106, 1609–1628. [Google Scholar] [CrossRef]
- Wang, B.; Li, T.; Wei, J.; Tang, Z. A new unambiguous tracking algorithm for sine-BOC(m, n) signals. GPS Solut. 2019, 23, 58. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Y.; Li, H.; Li, J. FH-BOC: Generalized low-ambiguity anti-interference spread spectrum modulation based on frequency-hopping binary offset carrier. GPS Solut. 2020, 24, 70. [Google Scholar] [CrossRef]
- Julien, O.; Macabiau, C.; Cannon, M.E.; Lachapelle, G. ASPeCT: Unambiguous sine-BOC (n, n) acquisition/tracking technique for navigation applications. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 150–162. [Google Scholar] [CrossRef] [Green Version]
- Benedetto, F.; Giunta, G.; Lohan, E.S.; Renfors, M. A Fast Unambiguous Acquisition Algorithm for BOC-Modulated Signals. IEEE Trans. Veh. Technol. 2013, 62, 1350–1355. [Google Scholar] [CrossRef]
- Tang, Z.; Zhou, H.; Wei, J.; Yan, T.; Liu, Y.; Ran, Y.; Zhou, Y. TD-AltBOC: A new COMPASS B2 modulation. Sci. China-Phys. Mech. Astron. 2011, 54, 1014–1021. [Google Scholar] [CrossRef]
- Lee, Y.; Chong, D.; Song, I.; Kim, S.Y.; Jee, G.I.; Yoon, S. Cancellation of Correlation Side-Peaks for Unambiguous BOC Signal Tracking. IEEE Commun. Lett. 2012, 16, 569–572. [Google Scholar] [CrossRef]
- Feng, T. Decimation Double-Phase Estimator: An Efficient and Unambiguous High-Order Binary Offset Carrier Tracking Algorithm. IEEE Signal Processing Lett. 2016, 23, 905–909. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, W.; Chen, H.; Yu, D. Insight to Double Estimator Technique: The concept of subcarrier aided code tracking. In Proceedings of the 2015 International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 3–5 April 2015. [Google Scholar]
- Mishra, D.; Kumar, M. Design and Implementation of a Novel Digital Interplex Modulator for Future Navigation Satellite System. In Proceedings of the 2014 International Conference on Signal Processing and Integrated Networks (SPIN), Noida, Delhi, India, 20–21 February 2014. [Google Scholar]
- Dafesh, P.A.; Khadge, G.K. Phase Optimized Constant Envelope Transmission (POCET) and the Method of Phantom Signals. In Proceedings of the ION 2017 Pacific PNT Meeting, Honolulu, HI, USA, 1–4 May 2017; pp. 100–117. [Google Scholar]
- He, T.; Ma, Z. Proposed OFDM modulation for future generations of GNSS signal system. J. Navig. 2016, 69, 971–990. [Google Scholar] [CrossRef] [Green Version]
- Saxena, T.; Jadon, J.S. Spectral analysis of Sine and Cosine BOC modulated signals. In Proceedings of the 2014 International Conference on Signal Processing and Composite Networks (SPIN), Noida, India, 20–21 February 2014; pp. 734–738. [Google Scholar]
- Zitouni, S.; Rouabah, K.; Chikouche, D.; Mokrani, K.; Atia, S.; Harba, R.; Ravier, P. General analytical models characterizing MBOC modulated signal. Aerosp. Sci. Technol. 2016, 50, 112–126. [Google Scholar] [CrossRef]
- Nie, S.J.; He, B.Z.; Wang, H.Z.; Qin, Y.F. Design of integration channel of ranging and data transmission. Mod. Electron. Tech. 2013, 36, 57–62. [Google Scholar]
- Kinman, P.W. Doppler tracking of planetary spacecraft. IEEE Trans. Microw. Theory Tech. 1992, 40, 1199–1204. [Google Scholar] [CrossRef]
- Lin, K.; Zhan, X.; Yang, R.; Shao, F.; Huang, J. BDS Space Service Volume characterizations considering side-lobe signals and 3D antenna pattern. Aerosp. Sci. Technol. 2020, 106, 106071. [Google Scholar] [CrossRef]
- Yoon, S.; Chae, K.; Kim, S.Y. A New Approach to Local Signal Design for Enhanced TMBOC Signal Tracking. J. Electr. Eng. Technol. 2020, 15, 1837–1845. [Google Scholar] [CrossRef]
- Lu, B.; Zhong, J.; Zhao, M.; Li, L. A near-far effect canceller for GPS high sensitivity receiver. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012. [Google Scholar]
- Yang, W.; Meng, S.; Wang, J.; Liu, J. Acquisition performance analysis of a synchronizati. In Proceedings of the 2009 9th International Conference on Electronic Measurement & Instrumentson scheme of DS/FH hybrid spread spectrum signals for TT&C, Beijing, China, 16–19 August 2009; pp. 4-395–4-399. [Google Scholar]
- Crisan, A.M.; Martian, A.; Cacoveanu, R.; Coltuc, D. Evaluation of synchronization techniques for inter-satellite links. In Proceedings of the 2016 International Conference on Communications (COMM), Bucharest, Romania, 9–10 June 2016; pp. 463–468. [Google Scholar]
- Meng, S.; Yang, W.; Lu, W.; Liu, J.; Yu, J. Code tracking performance of DS/FH spread spectrum signal for TT&C. In Proceedings of the 2010 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16–18 April 2010; pp. 491–495. [Google Scholar]
- Li, T.; Tang, Z.; Wei, J.; Zhou, Z.; Wang, B. Unambiguous Tracking Technique Based on Combined Correlation Functions for Sine BOC Signals. J. Navig. 2019, 72, 140–154. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Distance between different nodes | Within 100 km |
| Relative movement speed | 1020 m/s |
| Radio frequency of VHF band | Uplink 200 MHz/ Downlink 300 MHz |
| Radio frequency of S band | Uplink 2.9 GHz/ Downlink 3.1 GHz |
| Maximum Doppler frequency of VHF band | Uplink 2550 Hz/ Downlink 3825 Hz |
| Maximum Doppler frequency of S band | Uplink 9860 Hz/ Downlink 10,540 Hz |
| Equivalent isotropically radiated power (EIRP) of VHF band | 45 dBm |
| Equivalent isotropically radiated power (EIRP) of S band | 47 dBm |
| VHF band receiving antenna gain | 8 dBi |
| S band receiving antenna gain | 28 dBi |
| Parameter | Value |
|---|---|
| Acquisition time | 0.034489 s |
| Acquisition frequency | 8950 Hz |
| Radio frequency of S band | Uplink 2.9 GHz/ Downlink 3.1 GHz |
| The SNR of communication signal at receiving end | 11 dB |
| The C/N0 of navigation and measurement signal at receiving end | 65 dB-Hz |
| The Doppler frequency | Sinusoidal variation with amplitude 12 kHz, period 3 s |
| Channel attenuation | Rice fading channel |
| Doppler measurement accuracy | <0.01 m/s |
| Ranging accuracy | <0.1 m |
| BER | 8.964 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, L.; Li, X.; Wu, W.; Dong, J. Multifunctional Signal Design for Measurement, Navigation and Communication Based on BOC and BPSK Modulation. Remote Sens. 2022, 14, 1653. https://doi.org/10.3390/rs14071653
Xue L, Li X, Wu W, Dong J. Multifunctional Signal Design for Measurement, Navigation and Communication Based on BOC and BPSK Modulation. Remote Sensing. 2022; 14(7):1653. https://doi.org/10.3390/rs14071653
Chicago/Turabian StyleXue, Linshan, Xue Li, Weiren Wu, and Jialin Dong. 2022. "Multifunctional Signal Design for Measurement, Navigation and Communication Based on BOC and BPSK Modulation" Remote Sensing 14, no. 7: 1653. https://doi.org/10.3390/rs14071653
APA StyleXue, L., Li, X., Wu, W., & Dong, J. (2022). Multifunctional Signal Design for Measurement, Navigation and Communication Based on BOC and BPSK Modulation. Remote Sensing, 14(7), 1653. https://doi.org/10.3390/rs14071653





