An Experimental Study on Measuring Breaking-Wave Bubbles with LiDAR Remote Sensing
Abstract
:1. Introduction
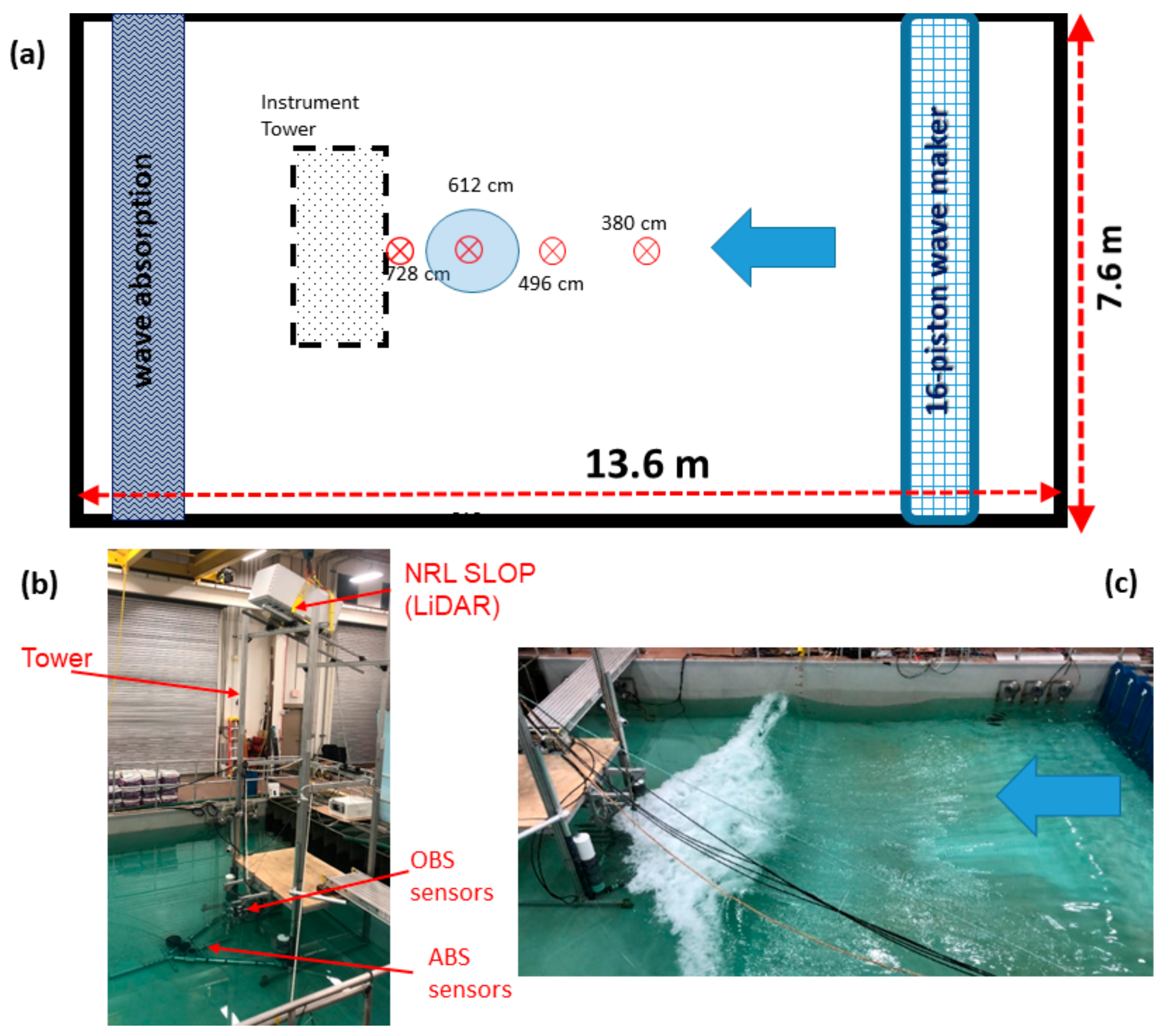
2. Experimental Setup
2.1. Wave Tank and Breaking Wave Generation
2.2. Breaking-Wave Bubble Mesurements Setup
2.2.1. In-Water OBS and ABS Measurement Systems
2.2.2. Above-Water LiDAR System
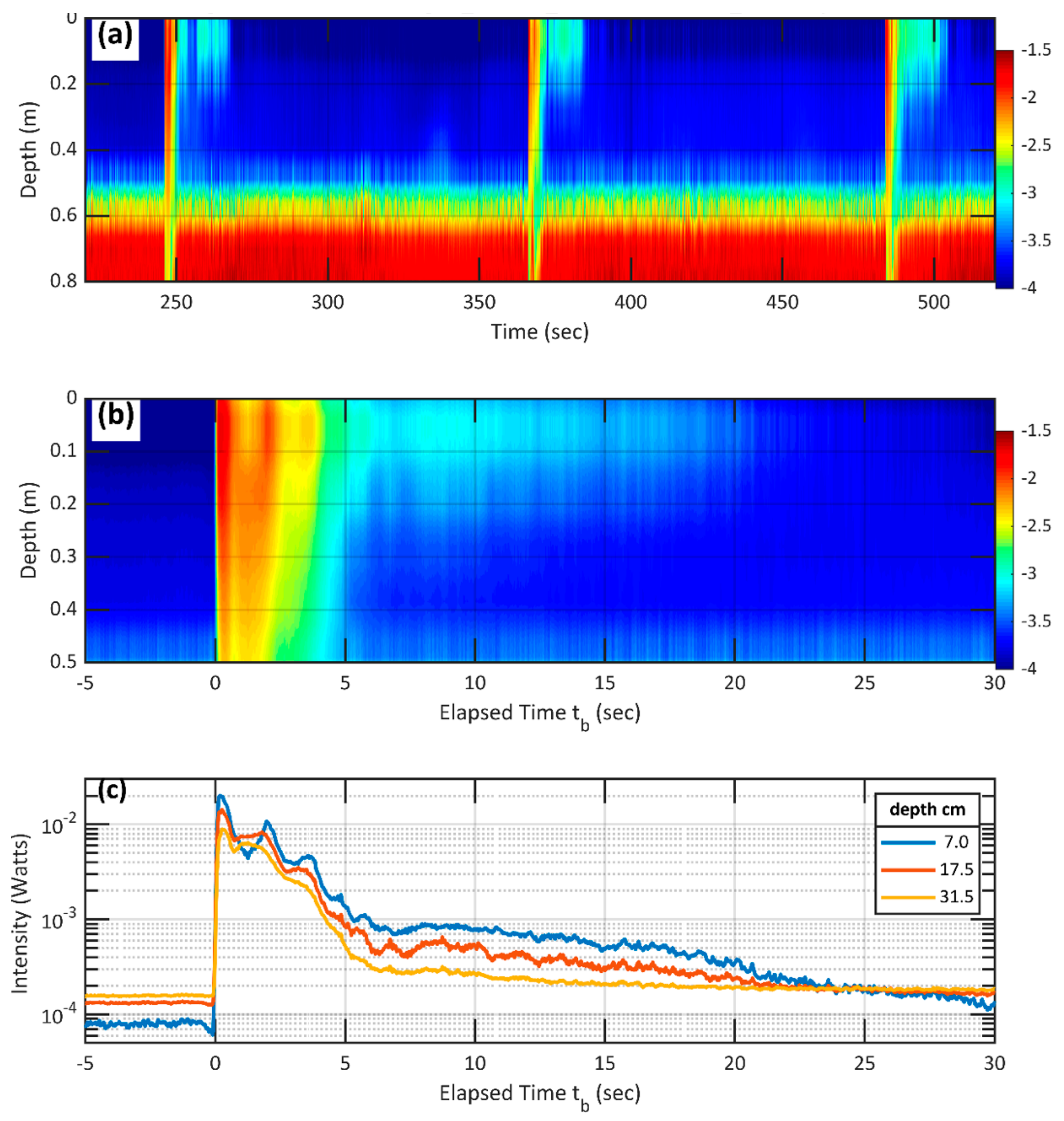
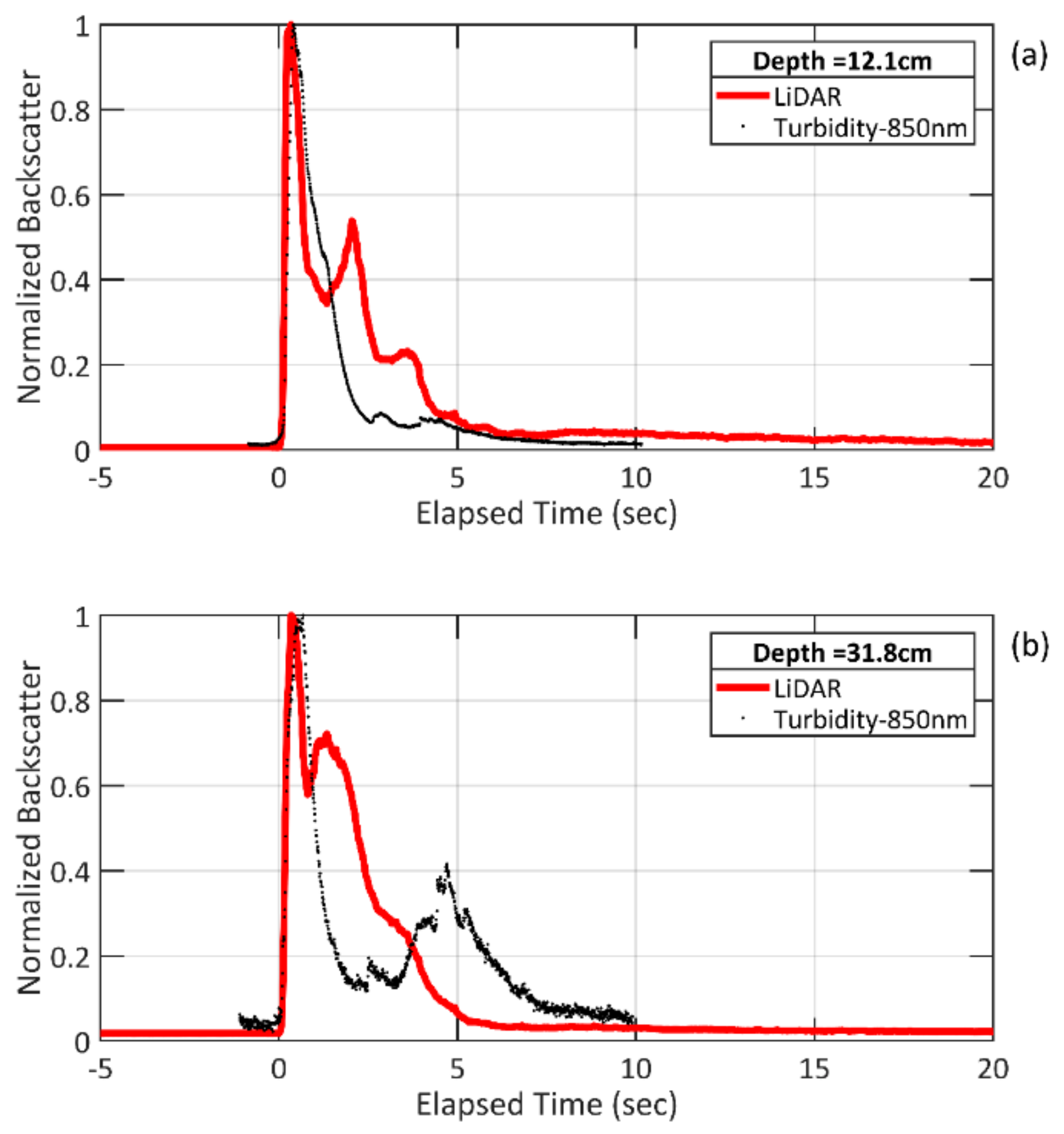
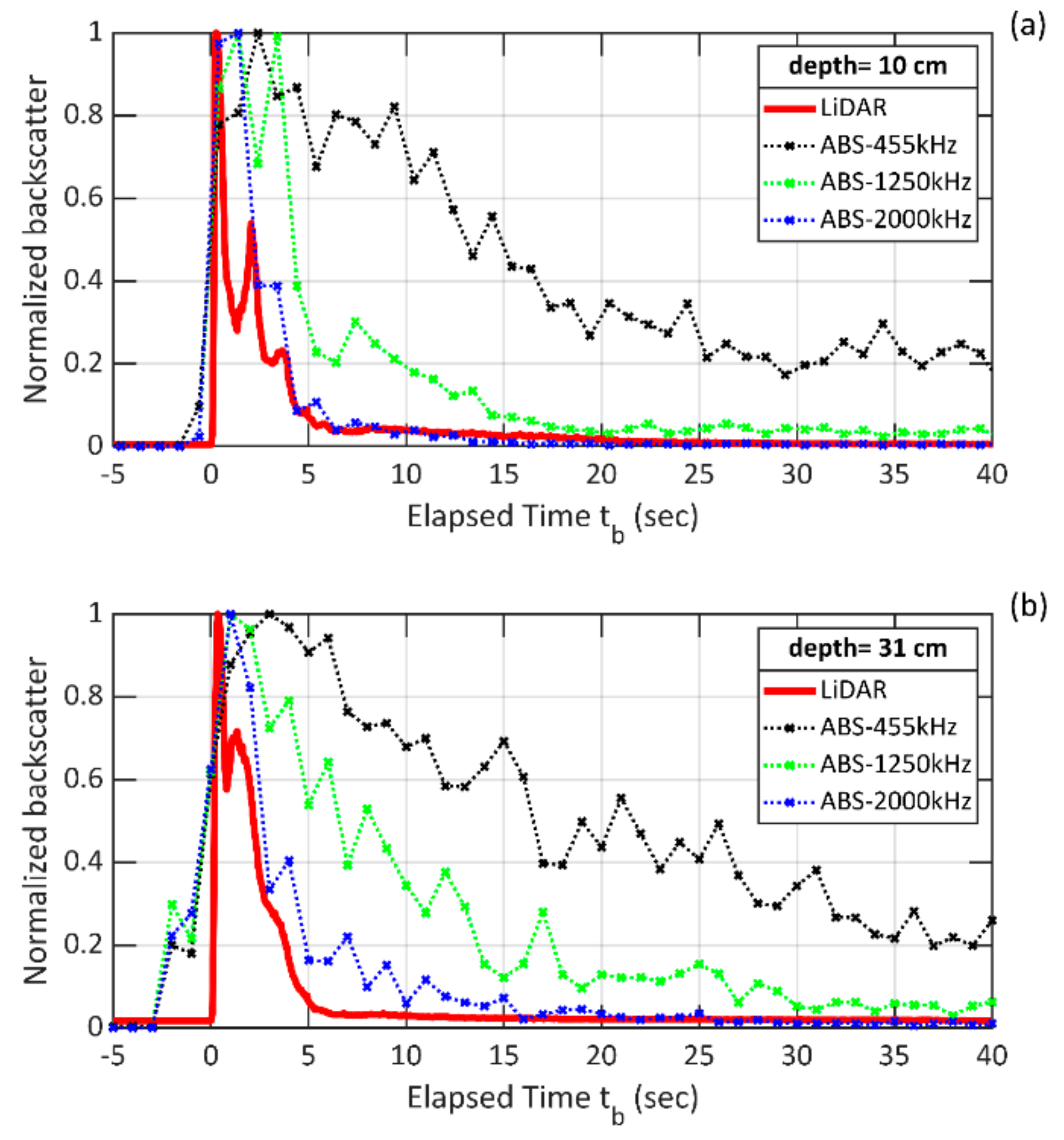
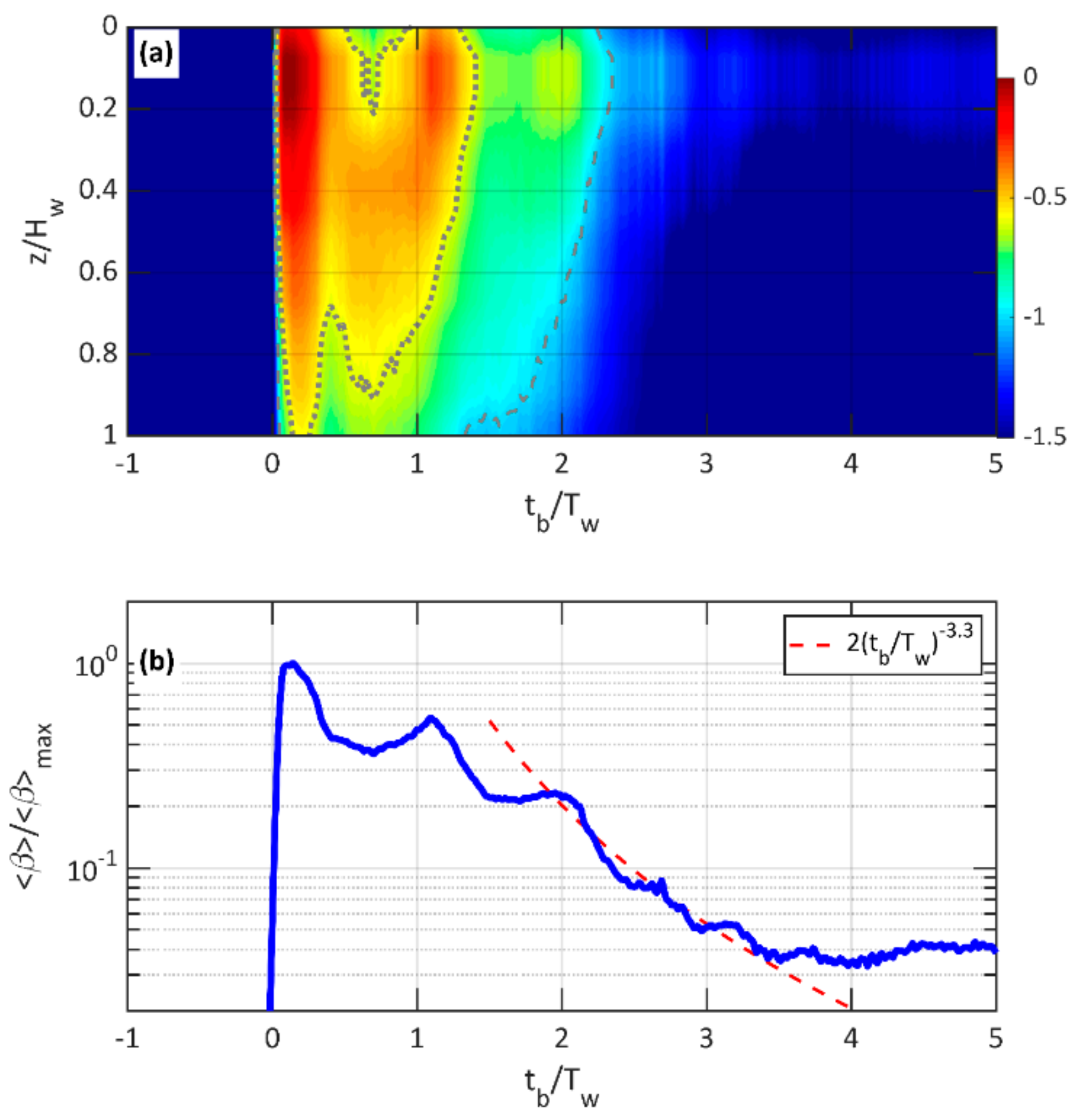
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thorpe, S.A. On the clouds of bubbles formed by breaking wind-waves in deep water, and their role in air-sea gas transfer. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1982, 304, 155–210. [Google Scholar] [CrossRef]
- Deane, G.B.; Stokes, M.D. Model calculations of the underwater noise of breaking waves and comparison with experiment. J. Acoust. Soc. Am. 2010, 127, 3394–3410. [Google Scholar] [CrossRef] [PubMed]
- Longuet-Higgins, M.S.; Turner, J.S. An ‘entraining plume’ model of a spilling breaker. J. Fluid Mech. 1974, 63, 1–20. [Google Scholar] [CrossRef]
- Banner, M.L.; Cato, D.H. Physical mechanisms of noise generation by breaking waves—A laboratory study. In Sea Surface Sound; Springer: Dordrecht, The Netherlands, 1988; pp. 429–436. [Google Scholar]
- Lamarre, E.; Melville, W.K. Void-fraction measurements and sound-speed fields in bubble plumes generated by breaking waves. J. Acoust. Soc. Am. 1994, 95, 1317–1328. [Google Scholar] [CrossRef]
- Churnside, J.H. Lidar signature from bubbles in the sea. Opt. Express 2010, 18, 8294–8299. [Google Scholar] [CrossRef]
- Cipriano, R.J.; Blanchard, D.C. Bubble and aerosol spectra produced by a laboratory ‘breaking wave’. J. Geophys. Res. Earth Surf. 1981, 86, 8085–8092. [Google Scholar] [CrossRef]
- Medwin, H.; Daniel, A.C. Acoustical measurements of bubble production by spilling breakers. J. Acoust. Soc. Am. 1990, 88, 408–412. [Google Scholar] [CrossRef]
- Loewen, M.R.; O’Dor, M.A.; Skafel, M.G. Bubbles entrained by mechanically generated breaking waves. J. Geophys. Res. Earth Surf. 1996, 101, 20759–20769. [Google Scholar] [CrossRef]
- Leifer, I.; De Leeuw, G.; Cohen, L.H. Optical Measurement of Bubbles: System Design and Application. J. Atmos. Ocean. Technol. 2003, 20, 1317–1332. [Google Scholar] [CrossRef] [Green Version]
- Medwin, H. In situ acoustic measurements of bubble populations in coastal ocean waters. J. Geophys. Res. Earth Surf. 1970, 75, 599–611. [Google Scholar] [CrossRef]
- Vagle, S.; Farmer, D.M. The Measurement of Bubble-Size Distributions by Acoustical Backscatter. J. Atmos. Ocean. Technol. 1992, 9, 630–644. [Google Scholar] [CrossRef]
- Wang, D.W.; Wijesekera, H.W.; Jarosz, E.; Teague, W.J.; Pegau, W.S. Turbulent Diffusivity under High Winds from Acoustic Measurements of Bubbles. J. Phys. Oceanogr. 2016, 46, 1593–1613. [Google Scholar] [CrossRef]
- Strand, K.O.; Breivik, Ø.; Pedersen, G.; Vikebø, F.B.; Sundby, S.; Christensen, K.H. Long-Term Statistics of Observed Bubble Depth Versus Modeled Wave Dissipation. J. Geophys. Res. Oceans 2020, 125, e2019JC015906. [Google Scholar] [CrossRef]
- Josset, D.B.; Wang, D.W.; Savelyev, I.; Anguelova, M.D.; Keiffer, R.S.; Fabre, J.P. On the retrieval of bubble properties from space lidar and their impact on acoustic transmission loss. In Ocean Sciences Meeting; AGU: San Diego, CA, USA, 2020. [Google Scholar]
- Salisbury, D.J.; Anguelova, M.D.; Brooks, I.M. On the variability of whitecap fraction using satellite-based observations. J. Geophys. Res. Oceans 2013, 118, 6201–6222. [Google Scholar] [CrossRef] [Green Version]
- Anguelova, M.D.; Bettenhausen, M.H. Whitecap Fraction from Satellite Measurements: Algorithm Description. J. Geophys. Res. Oceans 2019, 124, 1827–1857. [Google Scholar] [CrossRef]
- Burrage, D.M.; Anguelova, M.D.; Wang, D.W.; Wesson, J.C. Predicting radiometric effects of a Rough Sea surface, whitecaps, foam, and spray using SURFER 2D. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3194–3207. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Gaiser, P.W. Skin depth at microwave frequencies of sea foam layers with vertical profile of void fraction. J. Geophys. Res. Earth Surf. 2011, 116, C11002. [Google Scholar] [CrossRef] [Green Version]
- Churnside, J.H. Review of profiling oceanographic lidar. Opt. Eng. 2013, 53, 051405. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Pan, D. Ocean Optical Profiling in South China Sea Using Airborne LiDAR. Remote Sens. 2019, 11, 1826. [Google Scholar] [CrossRef] [Green Version]
- Krekova, M.M.; Krekov, G.M.; Shamanaev, V.S. Influence of Air Bubbles in Seawater on the Formation of Lidar Returns. J. Atmos. Ocean. Technol. 2004, 21, 819–824. [Google Scholar] [CrossRef]
- Li, W.; Yang, K.; Xia, M.; Rao, J.; Zhang, W. Influence of characteristics of micro-bubble clouds on backscatter lidar signal. Opt. Express 2009, 17, 17772–17783. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, D.; Bai, J.; Liu, N.; Zhang, Y.; Shen, X. Influence of ocean surface waves and air bubbles on the polarization characteristics of spaceborne oceanographic lidar returns. In Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10784, p. 107840O. [Google Scholar] [CrossRef]
- Handler, R.A.; Savelyev, I.; Lindsey, M. Infrared imagery of streak formation in a breaking wave. Phys. Fluids 2012, 24, 121701. [Google Scholar] [CrossRef]
- Gould, R.; Josset, D.; Anderson, S.; Goode, W. Estimating Oil Slick Thickness with LiDAR Remoter Sensing Technology; Final Report; Bureau of Safety and Environmental Enforcement (BSEE): Washington, DC, USA, 2019.
- Josset, D.; Cayula, S.; Concannon, B.; Sova, S.; Weidemann, A. On the bubble-bubbleless ocean continuum: Lidar measurement of underwater bubble properties during storm conditions. J. Atmos. Ocean. Technol. 2022, unpublished work. [Google Scholar]
- Rapp, R.J.; Melville, W.K. Laboratory measurements of deep-water breaking waves. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Sci. 1990, 331, 735–800. [Google Scholar]
- Deane, G.B.; Stokes, M.D. Air Entrainment Processes and Bubble Size Distributions in the Surf Zone. J. Phys. Oceanogr. 1999, 29, 1393–1403. [Google Scholar] [CrossRef]
- Anguelova, M.D.; Huq, P. Characteristics of bubble clouds at various wind speeds. J. Geophys. Res. Earth Surf. 2012, 117, C03036. [Google Scholar] [CrossRef] [Green Version]
- Leifer, I.; De Leeuw, G. Bubbles generated from wind-steepened breaking waves: 1. Bubble plume bubbles. J. Geophys. Res. Ocean. 2006, 111, C06020. [Google Scholar] [CrossRef] [Green Version]
- Deike, L.; Melville, W.K.; Popinet, S. Air entrainment and bubble statistics in breaking waves. J. Fluid Mech. 2016, 801, 91–129. [Google Scholar] [CrossRef] [Green Version]
- Cox, D.T.; Shin, S. Laboratory Measurements of Void Fraction and Turbulence in the Bore Region of Surf Zone Waves. J. Eng. Mech. 2003, 129, 1197–1205. [Google Scholar] [CrossRef]
- Lamarre, E.; Melville, W.K. Air entrainment and dissipation in breaking waves. Nature 1991, 351, 469–472. [Google Scholar] [CrossRef]
- Rojas, G.; Loewen, M.R. Void fraction measurements beneath plunging and spilling breaking waves. J. Geophys. Res. Earth Surf. 2010, 115, C08001. [Google Scholar] [CrossRef]


| Parameter | Values |
|---|---|
| Wavelength | 532 nm |
| Pulse energy | 1 mJ |
| Repetition rate | 50 Hz |
| Beam divergence | 12 mrad (after beam expander) |
| Parameter | Values |
|---|---|
| Telescope diameter | 5 cm (6 units) |
| Field of view | 140 mrad |
| Digitizer sample rate | 800 MHz |
| Vertical sampling spacing | 0.14 m (underwater) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Josset, D.; Savelyev, I.; Anguelova, M.; Cayula, S.; Abelev, A. An Experimental Study on Measuring Breaking-Wave Bubbles with LiDAR Remote Sensing. Remote Sens. 2022, 14, 1680. https://doi.org/10.3390/rs14071680
Wang D, Josset D, Savelyev I, Anguelova M, Cayula S, Abelev A. An Experimental Study on Measuring Breaking-Wave Bubbles with LiDAR Remote Sensing. Remote Sensing. 2022; 14(7):1680. https://doi.org/10.3390/rs14071680
Chicago/Turabian StyleWang, David, Damien Josset, Ivan Savelyev, Magdalena Anguelova, Stephanie Cayula, and Anna Abelev. 2022. "An Experimental Study on Measuring Breaking-Wave Bubbles with LiDAR Remote Sensing" Remote Sensing 14, no. 7: 1680. https://doi.org/10.3390/rs14071680





