Design of an FPGA-Based High-Quality Real-Time Autonomous Dehazing System
Abstract
:1. Introduction
1.1. Image Dehazing in Remote Sensing
1.2. Real-Time Processing
1.3. Contributions
- An FPGA-based implementation of an autonomous dehazing algorithm that can satisfactorily handle high-quality clean and hazy/cloudy images in real time.
- An in-depth discussion of FPGA implementation techniques to achieve real-time processing on high-resolution images (DCI 4K in particular).
- An efficient method for synthesizing cloudy images from a clean dataset (AID).
2. Literature Review
2.1. Representative Single-Image Dehazing Algorithms
2.1.1. Image Processing
- The scene radiance exhibits an extremely dark channel whose intensities approach zero in non-sky patches;
- The transmission map t is locally homogeneous.
- , where denotes an image patch centered at x, and c denotes a color channel;
- .
2.1.2. Machine Learning
2.1.3. Deep Learning
2.2. Summary
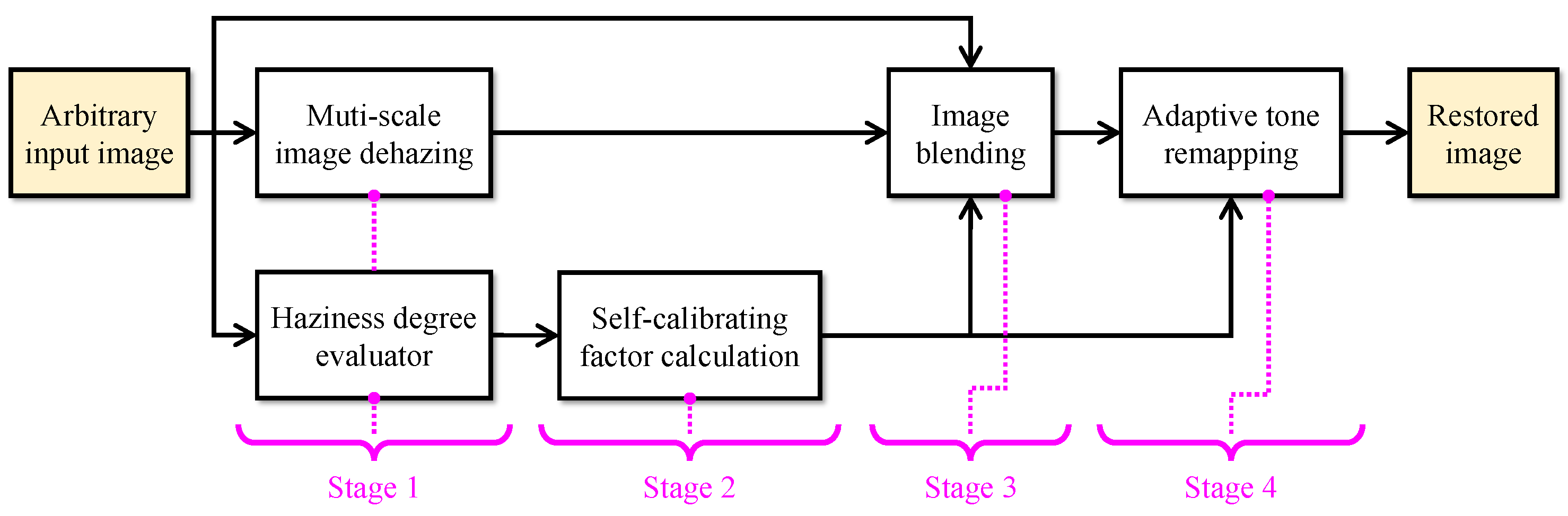
3. Autonomous Dehazing System
- How can the haze condition be determined from a single input image?
- How can an input image be dehazed according to its haze condition?
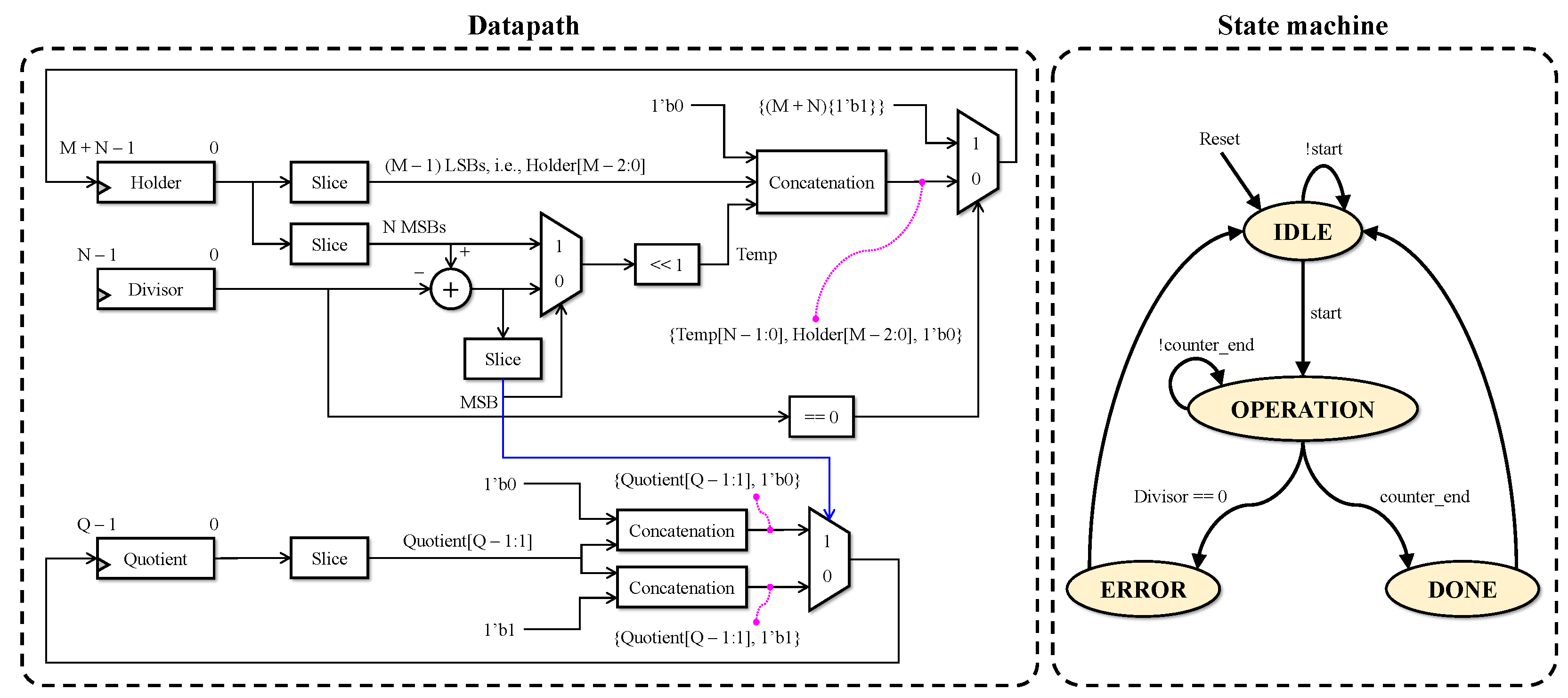
3.1. Base Algorithm
| Algorithm 1 Multi-scale image dehazing |
| Input: An RGB image , the number of artificially underexposed images and corresponding gamma values , and the number of scales Output: The restored image Auxiliary functions: and denote upsampling and downsampling by a factor of two BEGIN
|
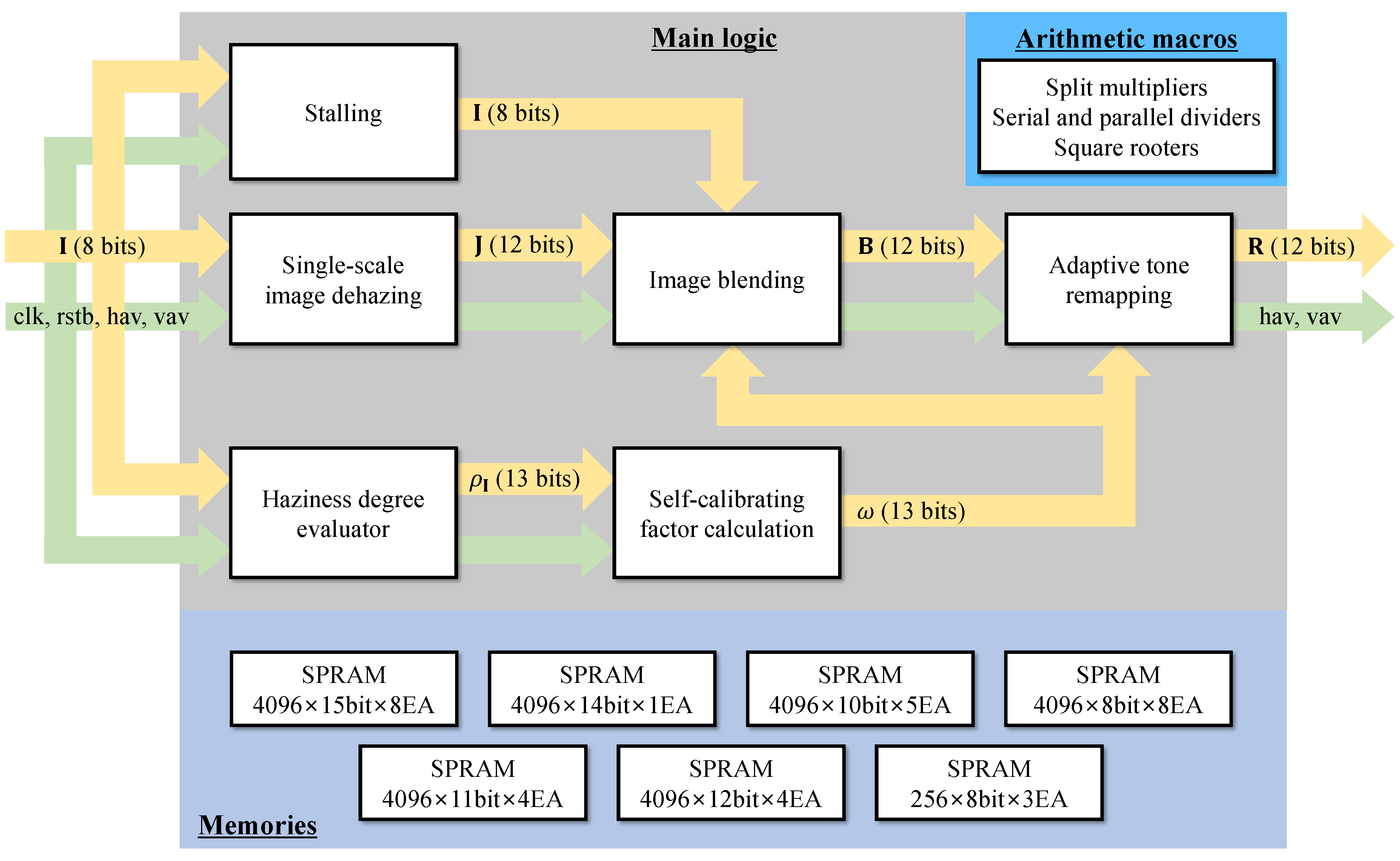
3.2. FPGA Implementation
3.2.1. Pipelined Architecture
- Fixed-point design for minimizing the signal’s word length to reduce the size of CLCs;
- Split multiplying for breaking large multiplications (represented by a large CLC) into smaller ones and inserting pipeline registers (PRs) between them, thus reducing propagation delay.
3.2.2. Fixed-Point Design
3.2.3. Customized Split Multiplier
4. Evaluation
4.1. Hardware Resources
4.1.1. Implementation Results
4.1.2. Comparison with Benchmark Designs
4.2. Performance
4.2.1. Outdoor Images
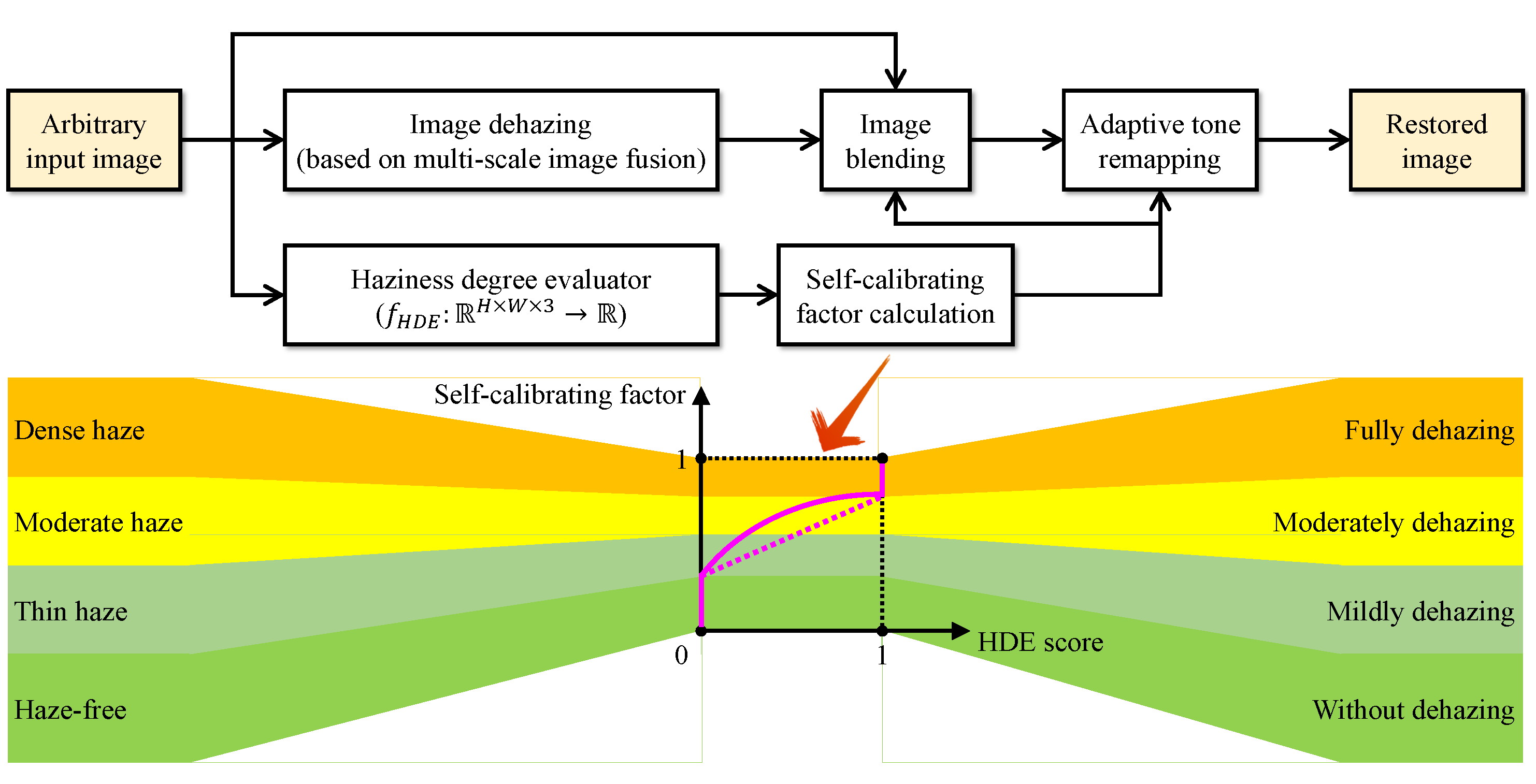
- Haze-free if ;
- Thin haze if ;
- Moderate haze if ;
- Dense haze if .
4.2.2. Aerial Images
| Algorithm 2 Synthetic haze/cloud generation |
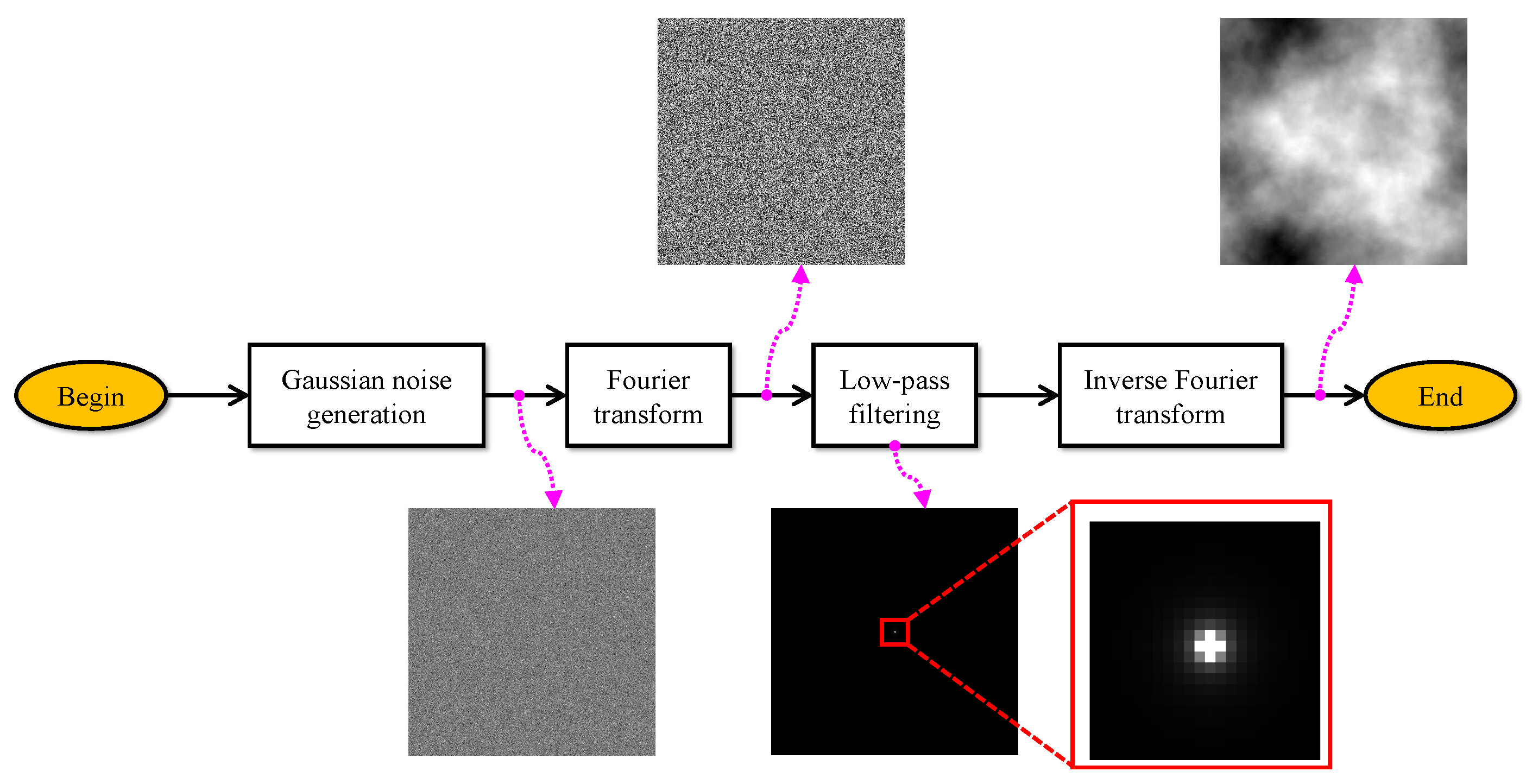
| Input: Image size and cut-off frequency Output: Transmission map Auxiliary functions: generates a image of random Gaussian noise, denote forward and inverse Fourier transforms, and denotes low-pass filtering the image X with the cut-off frequency BEGIN
|
| Algorithm 3 Synthetic hazy/cloudy image generation |
| Input: Clean image , cut-off frequency , haze density control and its step , desirable HDE score , HDE tolerance , and maximum iteration Output: Synthetic hazy/cloudy image Auxiliary functions: generates a transmission map described in Algorithm 2, generates a uniformly distributed number in the range , calculates the HDE score of the image , and is the sign function defined in Equation (11) BEGIN
|
4.3. Limitations
- Misclassifying haze-free images with a broad and smooth background as mildly hazy;
- Misclassifying hazy night-time images as haze-free.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B

References
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A Benchmark Data Set for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef] [Green Version]
- Cho, Y.; Jeong, J.; Kim, A. Model-Assisted Multiband Fusion for Single Image Enhancement and Applications to Robot Vision. IEEE Robot. Autom. Lett. 2018, 3, 2822–2829. [Google Scholar] [CrossRef]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Ngo, D.; Lee, G.; Kang, B. Haziness degree evaluator: A knowledge-driven approach for haze density estimation. Sensors 2021, 21, 3896. [Google Scholar] [CrossRef] [PubMed]
- Adimec. Technical Specifications for S-65A35 CoaXPress. Available online: https://www.adimec.com/cameras/machine-vision-cameras/sapphire-series/s-65a35-with-gpixel-gmax3265-65mp-sensor/ (accessed on 16 December 2021).
- Azimi, S. ShuffleDet: Real-Time Vehicle Detection Network in On-Board Embedded UAV Imagery. In Computer Vision—ECCV 2018, Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; Leal-Taixe, L., Roth, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; pp. 88–99. [Google Scholar] [CrossRef] [Green Version]
- Ngo, D.; Lee, S.; Lee, G.D.; Kang, B. Automating a Dehazing System by Self-Calibrating on Haze Conditions. Sensors 2021, 21, 6373. [Google Scholar] [CrossRef]
- Tarel, J.; Hautiere, N. Fast visibility restoration from a single color or gray level image. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–2 October 2009; pp. 2201–2208. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar] [CrossRef]
- Ngo, D.; Lee, S.; Nguyen, Q.; Ngo, T.; Lee, G.; Kang, B. Single Image Haze Removal from Image Enhancement Perspective for Real-Time Vision-Based Systems. Sensors 2020, 20, 5170. [Google Scholar] [CrossRef]
- Zhu, Q.; Mai, J.; Shao, L. A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior. IEEE Trans. Image Process. 2015, 24, 3522–3533. [Google Scholar] [CrossRef] [Green Version]
- Berman, D.; Treibitz, T.; Avidan, S. Non-local Image Dehazing. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1674–1682. [Google Scholar] [CrossRef]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. DehazeNet: An End-to-End System for Single Image Haze Removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.; Liu, S.; Zhang, H.; Pan, J.; Cao, X.; Yang, M. Single Image Dehazing via Multi-scale Convolutional Neural Networks. In Proceedings of the 2016 European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 154–169. [Google Scholar] [CrossRef]
- Nvidia. Jetson TX2 Module. Available online: https://developer.nvidia.com/embedded/jetson-tx2 (accessed on 16 December 2021).
- Wielage, M.; Cholewa, F.; Fahnemann, C.; Pirsch, P.; Blume, H. High Performance and Low Power Architectures: GPU vs. FPGA for Fast Factorized Backprojection. In Proceedings of the 2017 Fifth International Symposium on Computing and Networking (CANDAR), Aomori, Japan, 19–22 November 2017; pp. 351–357. [Google Scholar] [CrossRef]
- Vincent, R. An ERTS Multispectral Scanner experiment for mapping iron compounds. In Proceedings of the Eight International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 2–6 October 1972; pp. 1239–1247. [Google Scholar]
- Chavez, P.S., Jr. Atmospheric, solar, and MTF corrections for ERTS digital imagery. In Proceedings of the American Society of Photogrammetry, Fall Technical Meeting, Phoenix, AZ, USA, 26–31 October 1975; p. 69. [Google Scholar]
- Liang, J.; Ju, H.; Ren, L.; Yang, L.; Liang, R. Generalized Polarimetric Dehazing Method Based on Low-Pass Filtering in Frequency Domain. Sensors 2020, 20, 1729. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Ren, L.; Liang, R. Low-pass filtering based polarimetric dehazing method for dense haze removal. Opt. Express 2021, 29, 28178–28189. [Google Scholar] [CrossRef]
- Ancuti, C.; Ancuti, C. Single Image Dehazing by Multi-Scale Fusion. IEEE Trans. Image Process. 2013, 22, 3271–3282. [Google Scholar] [CrossRef] [PubMed]
- Ancuti, C.; Ancuti, C.; De Vleeschouwer, C.; Bovik, A. Day and Night-Time Dehazing by Local Airlight Estimation. IEEE Trans. Image Process. 2020, 29, 6264–6275. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Shang, S. Visibility: How Applicable is the Century-Old Koschmieder Model? J. Atmos. Sci. 2016, 73, 4573–4581. [Google Scholar] [CrossRef]
- Zhang, J.; Tao, D. FAMED-Net: A Fast and Accurate Multi-Scale End-to-End Dehazing Network. IEEE Trans. Image Process. 2020, 29, 72–84. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Pan, J.; He, M.; Li, Z.; Tang, J. Task-Oriented Network for Image Dehazing. IEEE Trans. Image Process. 2020, 29, 6523–6534. [Google Scholar] [CrossRef]
- Ngo, D.; Lee, S.; Ngo, T.; Lee, G.D.; Kang, B. Visibility Restoration: A Systematic Review and Meta-Analysis. Sensors 2021, 21, 2625. [Google Scholar] [CrossRef]
- Tang, K.; Yang, J.; Wang, J. Investigating Haze-Relevant Features in a Learning Framework for Image Dehazing. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2995–3002. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Sun, C.; Zhao, Y.; Yang, L. Fog Density Estimation and Image Defogging Based on Surrogate Modeling for Optical Depth. IEEE Trans. Image Process. 2017, 26, 3397–3409. [Google Scholar] [CrossRef]
- Li, B.; Ren, W.; Fu, D.; Tao, D.; Feng, D.; Zeng, W.; Wang, Z. Benchmarking Single Image Dehazing and Beyond. IEEE Trans. Image Process. 2019, 28, 492–505. [Google Scholar] [CrossRef] [Green Version]
- Levin, A.; Lischinski, D.; Weiss, Y. A Closed-Form Solution to Natural Image Matting. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 228–242. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Zhu, Z.; Yao, W.; Wu, S. Weighted guided image filtering. IEEE Trans. Image Process. 2015, 24, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Han, B.; Li, J.; Zhang, J.; Gao, X. Weighted Guided Image Filtering with Steering Kernel. IEEE Trans. Image Process. 2020, 29, 500–508. [Google Scholar] [CrossRef] [PubMed]
- Ngo, D.; Lee, G.; Kang, B. Improved Color Attenuation Prior for Single-Image Haze Removal. Appl. Sci. 2019, 9, 4011. [Google Scholar] [CrossRef] [Green Version]
- Ngo, D.; Lee, S.; Lee, G.; Kang, B. Single-Image Visibility Restoration: A Machine Learning Approach and Its 4K-Capable Hardware Accelerator. Sensors 2020, 20, 5795. [Google Scholar] [CrossRef] [PubMed]
- Galdran, A. Image dehazing by artificial multiple-exposure image fusion. Signal Process. 2018, 149, 135–147. [Google Scholar] [CrossRef]
- Amdahl, G. Validity of the single processor approach to achieving large scale computing capabilities. In Proceedings of the Spring Joint Computer Conference, Atlantic City, NJ, USA, 18–20 April 1967; pp. 483–485. [Google Scholar] [CrossRef]
- IEEE Std 1364-2005 (Revision of IEEE Std 1374-2001); IEEE Standard for Verilog Hardware Description Language. IEEE: New York, NY, USA, 2006; pp. 1–590. [CrossRef]
- Cho, H.; Kim, G.J.; Jang, K.; Lee, S.; Kang, B. Color Image Enhancement Based on Adaptive Nonlinear Curves of Luminance Features. J. Semicond. Technol. Sci. 2015, 15, 60–67. [Google Scholar] [CrossRef]
- Xilinx. Zynq-7000 SoC Data Sheet: Overview (DS190). Available online: https://www.xilinx.com/support/documentation/data_sheets/ds190-Zynq-7000-Overview.pdf (accessed on 30 December 2021).
- Xilinx. Vivado Design Suite User Guide: Release Notes, Installation, and Licensing (UG973). Available online: https://www.xilinx.com/support/documentation/sw_manuals/xilinx2019_1/ug973-vivado-release-notes-install-license.pdf (accessed on 31 December 2021).
- Ngo, D.; Lee, G.; Kang, B. A 4K-Capable FPGA Implementation of Single Image Haze Removal Using Hazy Particle Maps. Appl. Sci. 2019, 9, 3443. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.; Kim, T. A video dehazing system based on fast airlight estimation. In Proceedings of the 2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Montreal, QC, Canada, 14–16 November 2017; pp. 779–783. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [Green Version]
- Tarel, J.; Hautiere, N.; Caraffa, L.; Cord, A.; Halmaoui, H.; Gruyer, D. Vision Enhancement in Homogeneous and Heterogeneous Fog. IEEE Intell. Transp. Syst. Mag. 2012, 4, 6–20. [Google Scholar] [CrossRef] [Green Version]
- Ancuti, C.; Ancuti, C.; Vleeschouwer, C. D-HAZY: A dataset to evaluate quantitatively dehazing algorithms. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2226–2230. [Google Scholar] [CrossRef]
- Ancuti, C.; Ancuti, C.; Timofte, R.; Vleeschouwer, C. O-HAZE: A Dehazing Benchmark with Real Hazy and Haze-Free Outdoor Images. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 867–8678. [Google Scholar] [CrossRef] [Green Version]
- Ancuti, C.; Ancuti, C.; Timofte, R.; De Vleeschouwer, C. I-HAZE: A dehazing benchmark with real hazy and haze-free indoor images. arXiv 2018, arXiv:1804.05091. [Google Scholar]
- Ancuti, C.; Ancuti, C.; Sbert, M.; Timofte, R. Dense-Haze: A Benchmark for Image Dehazing with Dense-Haze and Haze-Free Images. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1014–1018. [Google Scholar] [CrossRef] [Green Version]







| Resolution | ||||||
|---|---|---|---|---|---|---|
| Method | ||||||
| Tarel and Hautiere [8] | 0.28 | 0.59 | 0.76 | 1.51 | 9.02 | |
| He et al. [9] | 12.64 | 19.94 | 32.37 | 94.25 | 470.21 | |
| Ngo et al. [10] | 0.26 | 0.39 | 0.64 | 1.68 | 7.18 | |
| Zhu et al. [11] | 0.22 | 0.34 | 0.55 | 1.51 | 6.39 | |
| Berman et al. [12] | 2.65 | 5.54 | 6.61 | 5.74 | 34.39 | |
| Cho et al. [2] | 0.51 | 0.66 | 1.24 | 3.60 | 11.62 | |
| Cai et al. [13] | 1.53 | 2.39 | 3.88 | 10.68 | 47.35 | |
| Ren et al. [14] | 0.54 | 0.88 | 1.53 | 3.43 | 17.90 | |
| Ngo et al. [7] | 0.65 | 1.12 | 1.88 | 4.94 | 20.36 | |
| Category | Description | Representative Studies |
|---|---|---|
| Image processing | Uses traditional computer vision techniques and only the input RGB image | [7,8,9,10] |
| Machine learning | Uses machine learning techniques additionally to exploit the hidden regularities in relevant image datasets | [11,12,27,28] |
| Deep learning | Uses deep neural networks with powerful representation capability to learn relevant mapping functions | [13,14,24,25] |
| Xilinx Vivado v2019.1 | |||
|---|---|---|---|
| Device | XC7Z045-2FFG900 | ||
| Slice Logic Utilization | Available | Used | Utilization |
| Slice registers (#) | 437,200 | 53,216 | 12.17% |
| Slice LUTs (#) | 218,600 | 49,799 | 22.78% |
| RAM36E1/FIFO36E1s | 545 | 45 | 8.26% |
| RAM18E1/FIFO18E1s | 1090 | 22 | 2.02% |
| Minimum period | 3.685 ns | ||
| Maximum frequency | 271.37 MHz | ||
| Standard | Resolution | Required Clock Cycles (#) | Processing Speed () | |
|---|---|---|---|---|
| Full HD | 2,076,601 | 130.68 | ||
| Quad HD | 3,690,401 | 73.53 | ||
| 4K | UW4K | 6,149,441 | 44.13 | |
| UHD TV | 8,300,401 | 32.69 | ||
| DCI 4K | 8,853,617 | 30.65 | ||
| Hardware Utilization | Park and Kim [43] | Ngo et al. [42] | Ngo et al. [35] | Proposed Design |
|---|---|---|---|---|
| Registers (#) | 53,400 | 70,864 | 57,848 | 53,216 |
| LUTs (#) | 64,000 | 56,664 | 53,569 | 49,799 |
| DSPs (#) | 42 | 0 | 0 | 0 |
| Memory (Mbits) | 3.2 | 1.5 | 2.4 | 1.4 |
| Maximum frequency (MHz) | 88.70 | 236.29 | 271.67 | 271.37 |
| Maximum resolution | SVGA | DCI 4K | DCI 4K | DCI 4K |
| Autonomous dehazing | Unequipped | Unequipped | Unequipped | Equipped |
| Method | He et al. [9] | Zhu et al. [11] | Cai et al. [13] | Berman et al. [12] | Cho et al. [2] | Proposed System | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | |
| FRIDA2 | Hazy | 0.0744 | 0.5969 | 0.7746 | 0.0744 | 0.5473 | 0.7918 | 0.0679 | 0.6289 | 0.7963 | 0.0705 | 0.6603 | 0.7323 | 0.1559 | 0.5517 | 0.6792 | 0.0636 | 0.7378 | 0.8007 |
| Haze-free | 0.0295 | 0.7870 | 0.9586 | 0.0705 | 0.4414 | 0.9102 | 0.0430 | 0.5901 | 0.9703 | 0.0264 | 0.7338 | 0.8770 | 0.2261 | 0.5357 | 0.6668 | 0.0016 | 0.9890 | 0.9977 | |
| D-HAZY | Hazy | 0.0309 | 0.8348 | 0.9002 | 0.0483 | 0.7984 | 0.8880 | 0.0528 | 0.7916 | 0.8874 | 0.0492 | 0.7473 | 0.8395 | 0.0606 | 0.7212 | 0.8316 | 0.0669 | 0.7614 | 0.8691 |
| Haze-free | 0.0211 | 0.9049 | 0.9541 | 0.0317 | 0.7957 | 0.8968 | 0.0111 | 0.8823 | 0.9843 | 0.0359 | 0.7994 | 0.8681 | 0.0336 | 0.7252 | 0.8281 | 0.0017 | 0.9911 | 0.9953 | |
| O-HAZE | Hazy | 0.0200 | 0.7709 | 0.8423 | 0.0226 | 0.6647 | 0.7738 | 0.0266 | 0.6999 | 0.7865 | 0.0255 | 0.8024 | 0.8605 | 0.0196 | 0.7745 | 0.8504 | 0.0272 | 0.7562 | 0.8277 |
| Haze-free | 0.0086 | 0.9221 | 0.9645 | 0.0335 | 0.6508 | 0.8679 | 0.0135 | 0.8384 | 0.9839 | 0.0257 | 0.7054 | 0.8253 | 0.0227 | 0.6731 | 0.8158 | 0.0000 | 1.0000 | 1.0000 | |
| I-HAZE | Hazy | 0.0535 | 0.6580 | 0.8208 | 0.0362 | 0.6864 | 0.8252 | 0.0320 | 0.7116 | 0.8482 | 0.0275 | 0.7959 | 0.8823 | 0.0344 | 0.7693 | 0.8607 | 0.0281 | 0.7793 | 0.8611 |
| Haze-free | 0.0361 | 0.8030 | 0.9335 | 0.0441 | 0.6353 | 0.8716 | 0.0273 | 0.6704 | 0.9751 | 0.0311 | 0.7491 | 0.8608 | 0.0317 | 0.7184 | 0.8324 | 0.0001 | 0.9997 | 0.9998 | |
| Dense-Haze | Hazy | 0.0549 | 0.4662 | 0.6419 | 0.0646 | 0.4171 | 0.5773 | 0.0793 | 0.3923 | 0.5573 | 0.0597 | 0.5225 | 0.7169 | 0.0549 | 0.5254 | 0.6867 | 0.0652 | 0.4318 | 0.5939 |
| Haze-free | 0.0212 | 0.8790 | 0.9414 | 0.0458 | 0.6077 | 0.8508 | 0.0203 | 0.7767 | 0.9776 | 0.0347 | 0.7321 | 0.8339 | 0.0241 | 0.7147 | 0.8237 | 0.0002 | 0.9993 | 0.9996 | |
| 500IMG | Haze-free | 0.0117 | 0.9350 | 0.9563 | 0.0320 | 0.7668 | 0.8795 | 0.0070 | 0.8967 | 0.9870 | 0.0242 | 0.8193 | 0.8855 | 0.0196 | 0.7852 | 0.8605 | 0.0001 | 0.9994 | 0.9996 |
| Total | Hazy | 0.0621 | 0.6207 | 0.7746 | 0.0634 | 0.5764 | 0.7693 | 0.0615 | 0.6203 | 0.7725 | 0.0600 | 0.6720 | 0.7608 | 0.1139 | 0.5973 | 0.7228 | 0.0575 | 0.7037 | 0.7845 |
| Haze-free | 0.0150 | 0.9079 | 0.9548 | 0.0364 | 0.7122 | 0.8798 | 0.0127 | 0.8458 | 0.9840 | 0.0254 | 0.7956 | 0.8764 | 0.0418 | 0.7463 | 0.8378 | 0.0003 | 0.9982 | 0.9993 | |
| Overall | 0.0323 | 0.8025 | 0.8886 | 0.0463 | 0.6623 | 0.8392 | 0.0306 | 0.7630 | 0.9063 | 0.0381 | 0.7502 | 0.8340 | 0.0682 | 0.6916 | 0.7964 | 0.0213 | 0.8901 | 0.9204 | |
| Method | He et al. [9] | Zhu et al. [11] | Cai et al. [13] | Berman et al. [12] | Cho et al. [2] | Proposed System | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | MSE | SSIM | FSIMc | |
| Figure 9 | Haze-free | 0.0271 | 0.7261 | 0.8254 | 0.0193 | 0.8570 | 0.9507 | 0.0615 | 0.6187 | 0.9663 | 0.0581 | 0.4902 | 0.7528 | 0.0387 | 0.5233 | 0.7132 | 0.0000 | 1.0000 | 1.0000 |
| Thin | 0.0269 | 0.7754 | 0.8735 | 0.0124 | 0.9093 | 0.9616 | 0.0434 | 0.7539 | 0.9678 | 0.0324 | 0.6271 | 0.7605 | 0.0319 | 0.5848 | 0.7407 | 0.0028 | 0.9685 | 0.9778 | |
| Moderate | 0.0206 | 0.8298 | 0.9134 | 0.0121 | 0.8848 | 0.9572 | 0.0148 | 0.8740 | 0.9591 | 0.0346 | 0.5990 | 0.7791 | 0.0211 | 0.6660 | 0.7842 | 0.0081 | 0.8888 | 0.9387 | |
| Dense | 0.0317 | 0.7486 | 0.8769 | 0.0570 | 0.7305 | 0.8733 | 0.0457 | 0.7534 | 0.8719 | 0.0480 | 0.6448 | 0.7961 | 0.0466 | 0.6502 | 0.7923 | 0.0581 | 0.7450 | 0.8641 | |
| Figure 10 | Haze-free | 0.0110 | 0.9595 | 0.9653 | 0.0824 | 0.6984 | 0.8792 | 0.0131 | 0.9578 | 0.9860 | 0.0471 | 0.7363 | 0.8169 | 0.0506 | 0.7720 | 0.8719 | 0.0000 | 1.0000 | 1.0000 |
| Thin | 0.0110 | 0.9512 | 0.9560 | 0.0681 | 0.7546 | 0.9133 | 0.0099 | 0.9644 | 0.9826 | 0.0330 | 0.7650 | 0.8211 | 0.0473 | 0.7773 | 0.8717 | 0.0016 | 0.9836 | 0.9823 | |
| Moderate | 0.0108 | 0.9493 | 0.9542 | 0.0550 | 0.8052 | 0.9286 | 0.0079 | 0.9693 | 0.9824 | 0.0365 | 0.7590 | 0.8184 | 0.0429 | 0.7955 | 0.8803 | 0.0041 | 0.9646 | 0.9648 | |
| Dense | 0.0425 | 0.8062 | 0.8664 | 0.0247 | 0.8629 | 0.9037 | 0.0157 | 0.8838 | 0.9086 | 0.1046 | 0.6309 | 0.8178 | 0.0268 | 0.8508 | 0.9027 | 0.0185 | 0.8564 | 0.8724 | |
| Case | Haze-Free | Thin | Moderate | Dense | |||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Airplane (#) | Failure (#) | Airplane (#) | Failure (#) | Airplane (#) | Failure (#) | Airplane (#) | Failure (#) | |
| Input | 9 | 1 | 9 | 1 | 9 | 0 | 3 | 0 | |
| He et al. [9] | 9 | 1 | 8 | 2 | 7 | 4 | 9 | 1 | |
| Zhu et al. [11] | 9 | 1 | 9 | 3 | 6 | 2 | 6 | 0 | |
| Cai et al. [13] | 7 | 2 | 8 | 3 | 8 | 2 | 6 | 0 | |
| Berman et al. [12] | 0 | 1 | 2 | 3 | 6 | 4 | 7 | 1 | |
| Cho et al. [2] | 4 | 1 | 5 | 3 | 8 | 4 | 7 | 2 | |
| Proposed system | 9 | 1 | 10 | 1 | 10 | 0 | 7 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Ngo, D.; Kang, B. Design of an FPGA-Based High-Quality Real-Time Autonomous Dehazing System. Remote Sens. 2022, 14, 1852. https://doi.org/10.3390/rs14081852
Lee S, Ngo D, Kang B. Design of an FPGA-Based High-Quality Real-Time Autonomous Dehazing System. Remote Sensing. 2022; 14(8):1852. https://doi.org/10.3390/rs14081852
Chicago/Turabian StyleLee, Seungmin, Dat Ngo, and Bongsoon Kang. 2022. "Design of an FPGA-Based High-Quality Real-Time Autonomous Dehazing System" Remote Sensing 14, no. 8: 1852. https://doi.org/10.3390/rs14081852
APA StyleLee, S., Ngo, D., & Kang, B. (2022). Design of an FPGA-Based High-Quality Real-Time Autonomous Dehazing System. Remote Sensing, 14(8), 1852. https://doi.org/10.3390/rs14081852







