Analyzing the Error Pattern of InSAR-Based Mining Subsidence Estimation Caused by Neglecting Horizontal Movements

Abstract

It is common to estimate underground mining-induced subsidence from interferometric synthetic aperture radar (InSAR) displacement observations by Neglecting hOrizontal moVements (NOV). Such a strategy would cause large errors in the NOV-estimated subsidence. This issue was proven and the theoretical equation of the resulting errors has been deduced before. However, the systematic analysis of the error pattern (e.g., spatial distribution) and its relationship between some critical influence factors (e.g., lithology of overlying rock strata) is lacking to date. To circumvent this, a method was first presented to assess the errors of the NOV-estimated mining subsidence in this study. Then, the error pattern and the influence factors of the NOV-estimated mining subsidence were discussed. The results suggest that the errors of the NOV-estimated mining subsidence spatially follow a “peak-to-valley” shape, with an absolute “peak-to-valley angle” of 5–15°. In addition, for the same underground mining geometry, the error magnitudes of the NOV-estimated mining subsidence under hard lithology of overlying rock strata are smaller than those under soft lithology, and vice versa. These results would be beneficial to guide the scientific use of the NOV method for understanding the deformation mechanism and controlling the geohazards associated with underground mining and other similar anthropogenic activities.

1. Introduction

Reasonably using coal mine subsidence zones (e.g., install photovoltaic station) becomes emerging demand for improving mining environment. Since mining subsidence possibly impose damage to infrastructures located in subsidence zones, it is essential to monitoring surface subsidence for assessing the potential mining-induced damage. Interferometric synthetic aperture radar (InSAR) is a useful remote sensing technique to monitor ground surface displacements associated with underground mining activities [1,2,3,4,5,6]. However, InSAR observation is a projection of the real mining-induced deformation vector onto the radar line-of-sight (LOS) direction [7]. Hence, it is challenging to reveal the complex spatio-temporal evolution of mining-induced displacements from InSAR one-dimensional observations of LOS displacements. In the past two decades, some algorithms have been proposed to reconstruct the complete three-dimensional (3D) components of the real deformation vector in the vertical, west–east, and north–south directions from InSAR observations [8,9,10,11,12,13,14,15]. These algorithms, to some extent, can overcome the limitation of InSAR LOS displacements in practical uses. Nevertheless, some of the prerequisites required by these algorithms (e.g., requiring three or more independent InSAR observations, or knowledge of the constraint parameters) usually hinder their practical applications (see [16] for more details). As a consequence, only a few cases of successfully estimating 3D mining displacements from InSAR observations have been reported to date.

When the complete 3D components of mining deformation are hard to be estimated from InSAR, it is a common strategy to resolve the vertical component from InSAR 1D observations by Neglecting hOrizontal moVements (NOV) in both the east–west and north–south directions. For simplification, we referred to the strategy as NOV (see a brief overview of it in Section 2.1). The NOV-estimated mining subsidence is practically used in mining engineering, e.g., to delimitate subsidence boundary [17,18], assess mining-related building damage [19,20], and analyze the spatial-temporal evolution analysis of mining subsidence [21,22] or mining-induced shocks [23]. Theoretically, the NOV method holds well under the assumption that mining-induced horizontal movements are negligible. In fact, besides subsidence, considerable horizontal movements are also induced due to underground mining, and the magnitude of the induced horizontal movements can reach up to 40~50% of the vertical component [24,25]. This implies that large errors can possibly result from NOV-estimated subsidence, due to neglecting the considerable horizontal movements.

The issue that neglecting horizontal movements would cause errors in the estimated subsidence from InSAR observations was recognized, and some attempts were made to analyze the resulting errors. For instance, Samieie-Esfahany et al. [26] deduced the theoretical error equation of the subsidence due to neglecting horizontal movements in the year 2009. Based on the deduced theoretical equation, Fuhrmann and Garthwaite [27] found that the errors due to neglecting horizontal movements primarily depend on the incidence angle of the SAR sensors and the magnitudes of horizontal movements. In addition, the case study in the Sydney Region, Australia, showed that the resulting error can reach up to 67% of the maximum subsidence [27]. These studies primarily focused on the deduction analysis of theoretical errors of the estimated subsidence, but, to the best of our knowledge, rarely focused on assessing the resulting errors and further analyzing the error pattern in specific deformation cases (e.g., associated with underground mining characterized by considerable horizontal movements).

In this paper, we first presented a pixel-wise method for assessing the error of the NOV-estimated mining subsidence in Section 2. The presented method was then tested with real datasets in Section 3. In Section 4 the pattern and some influence factors (e.g., SAR imaging view, interferometric coherence, and the lithology of overlying rock strata) of the NOV-estimated subsidence errors were discussed. Finally, a conclusion was drawn in Section 5.

2. Methods

2.1. Overview of the NOV Method and Its Theoretical Errors

InSAR-measured LOS displacement, namely $d_{\mathrm{los}}$, is a projection of the real deformation vector onto the radar LOS direction by [28]

$$d_{\mathrm{los}}=\cos \theta \cdot d_{\mathrm{u}}-\sin \alpha \cdot d_{\mathrm{e}}+\sin \theta \sin \alpha \cdot d_{\mathrm{n}}$$

(1)

where $\left[d_{\mathrm{u}},d_{\mathrm{e}},d_{\mathrm{n}}\right]$ are the vertical, west–east, and north–south components of the real deformation vector; $\theta$ stands for the incidence angle of the resolution cell; $\alpha$ denotes the flight angle of the selected SAR sensor. The NOV method estimates subsidence (vertical component of mining displacements) from InSAR observations based on two steps. Firstly, it assumes that mining-induced 2D horizontal movements are both equal to zeros (i.e., $d_{\mathrm{e}}\equiv 0$ and $d_{\mathrm{n}}\equiv 0$), and yields

$$-\sin \theta \cos \alpha \cdot d_{\mathrm{e}}+\sin \theta \sin \alpha \cdot d_{\mathrm{n}}=0$$

(2)

Then, it estimates the subsidence (namely ${\widehat{d}}_{\mathrm{u}}$) by substituting Equation (2) into (1), i.e.,

$${\widehat{d}}_{\mathrm{u}}={\widehat{d}}_{\mathrm{los}}/\cos \theta$$

(3)

where ${\widehat{d}}_{\mathrm{los}}=d_{\mathrm{los}}+{\delta }_{\mathrm{los}}$ denotes InSAR observation of LOS displacement, with ${\delta }_{\mathrm{los}}$ being the observation error (caused by noise, orbital error, atmospheric delay, unwrapping error, etc.).

According to Equation (1), subsidence can be rigorously expressed in math as

$$d_{\mathrm{u}}=d_{\mathrm{los}}/\cos \theta +\tan \theta \left[\sin \alpha \cdot d_{\mathrm{n}}-\cos \alpha \cdot d_{\mathrm{e}}\right]$$

(4)

By comparing Equations (3) and (4), the theoretical error of the NOV-estimated subsidence (denoted by δ_u) can be written as

$${\delta }_{\mathrm{u}}={\delta }_{\mathrm{L}}+{\delta }_{\mathrm{H}}$$

(5)

with

$${\delta }_{\mathrm{L}}={\delta }_{\mathrm{los}}/\cos \theta$$

(6)

$${\delta }_{\mathrm{H}}=-\tan \theta \cos \alpha \cdot d_{\mathrm{e}}+\tan \theta \sin \alpha \cdot d_{\mathrm{n}}$$

(7)

Equation (5) suggests that the theoretical error structure of the NOV-estimated mining subsidence consists of two parts: (i) the error term due to the InSAR observation uncertainties of LOS displacements, namely ${\delta }_{\mathrm{L}}$, and (ii) the error term caused by neglecting horizontal movement components, namely ${\delta }_{\mathrm{H}}$.

It can be observed from Equation (5) that the error of the NOV-estimated mining subsidence theoretically depends on three factors: (i) uncertainty of InSAR observations (${\delta }_{\mathrm{los}}$), (ii) SAR imaging view ($\theta$ and $\alpha$), and (iii) mining-induced 2D horizontal movements ($d_{\mathrm{e}}$ and $d_{\mathrm{n}}$) [27], in which, except for the parameters of SAR imaging view (that can readily be obtained from SAR head files), the remaining two factors are difficult to be accurately determined from a single InSAR observation. Therefore, it is challenging to assess the errors of the NOV-estimated mining subsidence in a pixel-wise manner based on Equation (5). Considering the error assessment is an indispensable step for the error analyses of the NOV-estimated mining subsidence, especially for real datasets, we presented a pixel-wise method for assessing the errors in Section 2.2.

2.2. Pixel-Wise Method for Assessing the Errors of the NOV-Estimated Mining Subsidence

2.2.1. Generating a Reference Subsidence Assisted by a Prior Constraint

The core idea of the presented pixel-wise method is firstly offering a reference subsidence field based on a method named SIP (single InSAR pair). The SIP method, which was originally developed by Li et al. [29], can decompose subsidence from a single InSAR pair assisted by a prior deformation model with an acceptable accuracy level. More specifically, the prior deformation model is described as that there exists a linearly proportional relationship between surface horizontal movement components and the corresponding gradients of vertical subsidence components for extracting underground horizontal or nearly horizontal mineral seams [30]. Based on this prior model, horizontal movements in the east and north directions (namely $d_{\mathrm{e}}$ and $d_{\mathrm{n}}$) at a pixel $\left(i,j\right)$ can be expressed as two formulas relating to vertical subsidence, i.e.,

$$\{\begin{array}{l}{d}_{\mathrm{e}}\left(i,j\right)=C_{\mathrm{e}}\cdot G_{\mathrm{e}}\left(i,j\right)\hfill \\ d_{\mathrm{n}}\left(i,j\right)=C_{\mathrm{n}}\cdot G_{\mathrm{n}}\left(i,j\right)\hfill \end{array}$$

(8)

where $C_{\mathrm{e}}$ denotes the proportional coefficient between the horizontal movement component and the gradient of vertical subsidence in the east direction (namely $G_{\mathrm{e}}$); $C_{\mathrm{n}}$ and $G_{\mathrm{n}}$ represent the same things as the $C_{\mathrm{e}}$ and $G_{\mathrm{e}}$ but in the north direction, in which, the parameters $C_{\mathrm{e}}$ and $C_{\mathrm{n}}$ can be determined by three in situ parameters, i.e., mining depth, the tangent of major influence angle, and the constant of horizontal movement.

By substituting Equation (8) into Equation (1), reference subsidence (denoted by ${\widehat{d}}_{\mathrm{u\_ref}}$ can then be solved on the basis of pixel-by-pixel using

$${\widehat{d}}_{\mathrm{u\_ref}}(i,j)={\widehat{d}}_{\mathrm{los}}(i,j)/\cos \theta +\tan \theta [\sin \alpha ·C_{\mathrm{n}}·G_{\mathrm{n}}(i,j)-\cos \alpha ·C_{\mathrm{e}}·G_{\mathrm{e}}(i,j)]$$

(9)

In Equation (9) the gradients of subsidence at pixel (i,j) in the east and north directions have involved the subsidence at the pixels $\left(i+1,j\right)$ and $\left(i,j+1\right)$. Therefore, the reference subsidence of the whole subsidence basin will be solved with a back-substitution strategy. Please refer to [29] for more details.

2.2.2. Assessing the Errors of NOV-Estimated Mining Subsidence

Having obtained the reference subsidence, the error of the NOV-estimated mining subsidence ${\widehat{d}}_{\mathrm{u}}\left(i,j\right)$ at a pixel $\left(i,j\right)$ (namely ${\delta }_{\mathrm{u}}\left(i,j\right)$) can then be estimated by

$${\delta }_{\mathrm{u}}\left(i,j\right)={\widehat{d}}_{\mathrm{u}}\left(i,j\right)-{\widehat{d}}_{\mathrm{u}\_\mathrm{ref}}\left(i,j\right)$$

(10)

where ${\widehat{d}}_{\mathrm{u}\_\mathrm{ref}}\left(i,j\right)$ denotes the SIP-retrieved subsidence at the pixel $\left(i,j\right)$. The relative error of the NOV-estimated subsidence ${\widehat{d}}_{\mathrm{u}}\left(i,j\right)$ to the maximum subsidence (a very common error indicator in mining engineering) can be calculated by

$$\frac{{\delta }_{\mathrm{u}}\left(i,j\right)}{\max \left({\widehat{d}}_{\mathrm{u}\_\mathrm{ref}}\right)}\times 100\%$$

(11)

where ${\widehat{d}}_{\mathrm{u}\_\mathrm{ref}}$ is a vector of the SIP-retrieved reference subsidence in the concerned mining area.

It should be pointed out that three model parameters involved in the SIP method are needed to be in situ collected for solving the reference subsidence in this study. Once these three model parameters are unknown in practice, the SIP-assisted method for the error assessment cannot be performed (see Li, et al. [29] for more details). Since the main aim of this paper is to analyze the errors of the NOV-estimated subsidence, however, we tested the presented pixel-wise method and analyzed the error patterns of the NOV-estimated mining subsidence over those areas where the involved model parameters are known in the following sections.

3. Results

The presented method for error assessment was tested over the Huaibei coalfield, China, in which, two Phased Array type L-band Synthetic Aperture Radar (PALSAR) images, acquired on 13 January and 28 February 2010, respectively, were firstly collected to form a single InSAR pair. Figure 1a presents the InSAR-measured LOS displacements caused by an active working panel over the Huaibei coalfield. Note that it is challenging to obtain the LOS displacements over low-coherent areas [31], thus we interpolated them by inverse distance weighting interpolation for the sake of the following SIP-based subsidence estimation. Figure 1b–d show the NOV-estimated mining subsidence from the InSAR-measured LOS displacements, the SIP-solved reference subsidence, and the assessed errors using the SIP-assisted method, respectively, in which, three model parameters involved in the SIP method, i.e., mining depth, the tangent of major influence angle, and the constant of horizontal movements, were given by 620 m, 1.7, and 0.32. As is seen in Figure 1, significant errors ranging from −0.18 m to 0.23 m were contained in the NOV-estimated mining subsidence, indicating the relative errors to the solved maximum subsidence (about 0.5 m) from −35% to 45%. This result further proves that neglecting horizontal movements in the NOV method could cause large errors in the mining subsidence estimation.

The right panel in Figure 2 shows a scatter plot between the “real” and the assessed errors of the NOV-estimated mining subsidence at 34 field points (i.e., along the profile AB, marked by black crosses in Figure 1d). The “real” errors were obtained by comparing the precise levelling observations of mining subsidence at these 34 field points with the NOV-estimated subsidence there (see the left panel in Figure 2). As is shown, the assessed errors nearly well agree with the “real” ones, with a standard deviation (STD) of the differences between them of about 0.011 m. This result indicates that the assessed errors of the NOV-estimated mining subsidence are reliable.

4. Discussions

4.1. Error Pattern Analyses of the NOV-Estimated Mining Subsidence

4.1.1. Histogram Analysis of the Errors

The error pattern of the NOV-estimated mining subsidence was firstly analyzed using histogram statistics with simulated datasets. Specifically, we first simulated the 3D displacements (see Figure 3) caused by six simulated working panels using the probability integral method (PIM, a widely-used mathematical model in mining subsidence engineering) [32,33]. The mining width, length, thickness, and depth of the six simulated working panels are the same (i.e., 200 m, 300 m, 2 m, and 500 m, respectively). However, the mining directions (the angle between the mining direction and the north direction, which is denoted by $\phi$) of the six simulated working panels were 0°, 30°, 60°, 90°, 120°, and 150°, respectively (marked by black arrows in Figure 3). Then, the simulated 3D displacements were projected onto the ascending (i.e., $\theta =38°$ and $\alpha =190°$) and descending (i.e., $\theta =38°$ and $\alpha =350°$) LOS directions of the PALSAR-1 sensor (in StripMap mode). Finally, the NOV method was utilized to estimate mining subsidence from the simulated LOS displacements and the presented pixel-wise method was applied to assess the errors of the NOV-estimated mining subsidence (see Figure 4).

Figure 5 plots the histograms of the errors of the NOV-estimated mining subsidence, with respect to the varied mining directions and the flight angles (ascending or descending). As is observed from Figure 5, the errors of the NOV-estimated mining subsidence approximately follow a normal distribution with a mean of zero (marked by the red solid lines) and the STDs from 0.10 m to 0.12 m, with respect to the varied mining directions or flight angles. This fact was validated using the Z-test, which is a statistical test for the null hypothesis that the tested samples come from a normal distribution [34]. This result indicates that the errors of the NOV-estimated mining subsidence are not spatially heterogeneous; that is, nearly half of the NOV-estimated subsidence in the subsidence region would be under-estimated and the remaining half would be over-estimated.

Figure 6 shows the histogram of the assessed relative errors of the NOV-estimated mining subsidence (using Equation (11)) over the region of interest over the Huaibei coalfield. The areas where the subsidence was less than 0.03 m (i.e., three times the STD of the differences between the “real” and assessed errors) were masked out before the histogram statistics were performed. The red curve in Figure 6 shows the fitted frequency of a normal distribution, which does not show a good agreement with the real frequency. The possible reason for this is likely due to the more complex error components (e.g., uncertainties of LOS displacements and the error assessment method) and displacement patterns in the real cases compared to the simulated ones.

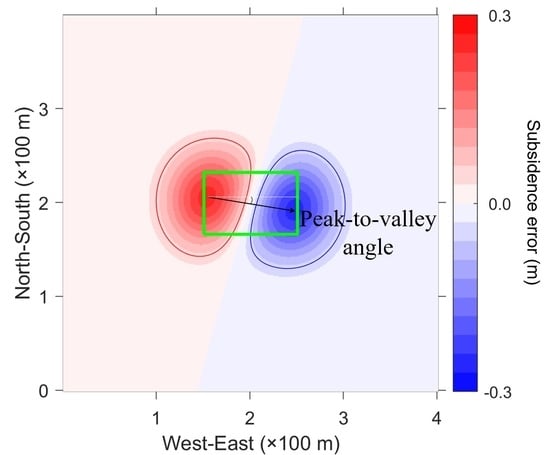
4.1.2. Spatial Pattern of the Errors

As can be visually observed from the error maps of NOV-estimated mining subsidence (e.g., see Figure 1d and Figure 4), the errors are spatially auto-correlated. This is expected due to the following factors. As stated in Section 2.2, the errors of NOV-estimated mining subsidence depend on the geometry of SAR imaging, uncertainties of InSAR LOS displacements, and 3D mining displacements. Consequently, for a certain mining area where SAR image series and InSAR processing methods are selected, the errors of NOV-estimated mining subsidence should theoretically be auto-correlated in space because of the spatial correlation of 3D mining displacements.

As is shown in Figure 1d and Figure 4, there were two areas where mining subsidence is under-estimated (positive values) and over-estimated (negative values) by the NOV method, respectively. For an LEO descending SAR imaging view ($\alpha \approx 190°$), the under-estimated and over-estimated errors of the NOV-estimated subsidence are primarily distributed in the northwest “peak” (positive values) and the southeast “valley” (negative values), respectively. On the other hand, for an LEO ascending SAR imaging view ($\alpha \approx 350°$), the under-estimated and over-estimated errors of the NOV-estimated subsidence are primarily distributed in the northeast “peak” and the southwest “valley”, respectively. In summary, the errors of the NOV-estimated mining subsidence approximately follow a “peak-to-valley” shape.

It is also can be found in Figure 4 that there exist two extrema (i.e., the highest and lowest errors), and their geolocations were changed with respect to underground mining directions. For the sake of the following analysis, we refer to the angle between the line of the peak summit to the valley bottom and the east direction (positive clockwise, and vice versa) as the “peak-to-valley angle”. Figure 7 plots the peak-to-valley angles of the NOV-estimated subsidence errors with respect to the changes in underground mining directions from 0° to 180° (i.e., $\phi =0^{\circ }\sim 180°$). As is seen, the absolute values of the peak-to-valley angles varied in the ranges of 5° to 15° for the LEO ascending (clockwise from the east) and descending (anti-clockwise from the east) SAR orbits, when the underground mining direction changes from 0° to 180°. In summary, the errors of the NOV-estimated mining subsidence spatially follow a “peak-to-valley” shape with peak-to-valley angles from 5° to 15° (for LEO ascending view) and −5° to −15° (for LEO descending view).

4.2. Impact Factors on the NOV-Estimated Subsidence Errors

In this section, the factors on the error magnitudes of the NOV-estimated mining subsidence were qualitatively discussed. As analyzed in Section 2.2, the errors of the NOV-estimated subsidence theoretically depend on the InSAR parameters (i.e., SAR imaging view and the uncertainty of InSAR-measured LOS displacements) and the 2D horizontal movements $d_{\mathrm{e}}$ and $d_{\mathrm{n}}$ from which, the parameters of SAR imaging views (i.e., $\theta$ and $\alpha$) can be readily obtained from the head files of SAR images. Meanwhile, the uncertainties of InSAR LOS displacements can be empirically assessed by interferometric coherence [7]. According to Peng [35], for the same underground mining geometry, surface 2D horizontal movements in the west–east and north–south directions are mainly related to the lithology of rock strata overlying underground mining. Hence, we discussed the influence of SAR imaging views, interferometric coherence, and the lithology of overlying rock strata on the errors of the NOV-estimated mining subsidence.

4.2.1. Influence of Interferometric Coherence

The standard deviation of InSAR LOS displacement (namely ${\delta }_{\mathrm{los}}$) can be empirically expressed as [36,37]

$${\delta }_{\mathrm{los}}\approx \frac{\lambda }{4\pi \gamma }\sqrt{\frac{1-{\left|\gamma \right|}^2}{2N}}$$

(12)

if other error components of InSAR (e.g., due to orbital inaccuracy, atmospheric phase screen, and phase unwrapping) were reasonably mitigated, where $\gamma$ denotes interferometric coherence, $N$ is the number of independent pixels, and $\lambda$ represents the wavelength of the SAR sensor. Figure 8 shows the relationship of the error of the NOV-estimated subsidence with respect to interferometric coherence (i.e., using ${\delta }_{los}\cdot \sec \theta$ based on Equation (12)), where the involved parameters were designated as $\gamma =0.1\sim 1.0$, $\theta ={20}^{\circ }\sim {55}^{\circ }$, $\lambda =0.056 \mathrm{m}$ (C band) and $N=6$. Note that, the 2D horizontal movements were assumed to be zeros (i.e., $d_{\mathrm{e}}=0 \mathrm{m}$ and $d_{\mathrm{n}}=0 \mathrm{m}$) for the analysis of the influence of interferometric coherence only.

As can be observed from Figure 8, for a fixed incidence angle, the error of the NOV-estimated subsidence exponentially climbs to the peak of about 2.3 cm, with a linear decrease of interferometric coherence from 1 to 0.1. This is expected because of the fact that the relationship between the uncertainties of InSAR LOS displacements and interferometric coherence is a monotone decreasing function (see Equation (12)); that is, the larger the coherence is, the smaller the uncertainty is, and vice versa.

4.2.2. Influence of SAR Imaging Views

The current LEO SAR satellites usually fly along near-polar orbits with a fixed flight angle of $\alpha \approx 350°$ for ascending and $\alpha \approx 190°$ for descending configurations. In addition, the incidence angles of the current LEO SAR sensors are usually variable in the range of $\theta =20~55°$. Figure 9 plots an example of the errors of the NOV-estimated subsidence with respect to the imaging view configuration of the current SAR sensors (i.e., $\alpha \approx 350°\hspace{0.17em}\mathrm{or}\hspace{0.17em}190°$ and $\theta =20~55°$) using Equation (5). In which, the error of InSAR LOS displacements was given by ${\delta }_{\mathrm{los}}=0.01 \mathrm{m}$, and the 2D horizontal movements were designated as $d_{\mathrm{e}}=0.2 \mathrm{m}$ and $d_{\mathrm{n}}=0.2 \mathrm{m}$, respectively.

As is seen in Figure 9, the absolute error of the NOV-estimated subsidence nonlinearly increases from 0.07 m to the maximum of 0.31 m, with the increase of the incidence angles from 20° to 55°. This is expected because of the following reason. As can be seen from Equations (5)–(7), the two error sources of the NOV-estimated mining subsidence, i.e., ${\delta }_{\mathrm{L}}={\delta }_{\mathrm{los}}\sec \theta$ and ${\delta }_{\mathrm{H}}=\tan \theta \left(-\cos \alpha \cdot d_{\mathrm{e}}+\sin \alpha \cdot d_{\mathrm{n}}\right)$, are all related to the incidence angle, in which, the incidence angle-related propagation coefficients of these two error sources (i.e., $\sec \theta$ and $\tan \theta$) are all monotonically increasing in the common range of the incidence angles from 20° to 55°. This result suggests that, for the same error level of InSAR LOS displacements and the same 2D horizontal movements, the larger the incidence angles of SAR sensors are, the larger the error of the NOV-estimated subsidence is, and vice versa.

4.2.3. Influence of the Lithology of Overlying Rock Strata

Besides the uncertainties of InSAR LOS displacements and SAR imaging views, 2D horizontal movements have a significant influence on the error of the NOV-estimated mining subsidence. In theory, ground surface displacements caused by underground mining primarily depend on the mining geometry (e.g., mining size, depth, width, thickness) and the lithology of overlying rock strata [38]. Since the mining geometry has a significant difference, even in the same mining area, we did not discuss its influence on the error of the NOV-estimated mining subsidence in this paper. Although the lithology of overlying rock strata is also different in different mining areas, it can be roughly classified into three categories, i.e., soft, medium, and hard. The composites of the classified three categories of overlying rock strata can be found in the State Bureau of Coal Industry of China [39]. In addition, the main parameter ranges of the PIM relating to these three categories of overlying rock strata (i.e., subsidence factor q and tangent of major influence angle tanβ) are listed in

Table 1. The common ranges of the subsidence factor (q) and tangent of major influence angle (tanβ) for the hard, medium, and soft overlying rock strata.

Parameters of the PIM	Lithology of Overlying Rock Strata
	Hard	Medium	Soft
q	0.27~0.54	0.55~0.85	0.86~1.0
tanβ	1.2~1.91	1.92~2.4	2.41~3.54

[39]. This allows us to analyze the influence of the lithology of overlying rock strata on the error of the NOV-estimated mining subsidence.

More specifically, we first took the means of the subsidence factor q and tangent of major influence angle tanβ from their common ranges under the three categories of overlying rock strata; that is, q = 0.4 and tanβ = 1.5 for the hard rock, q = 0.7 and tanβ = 2.2 for the medium rock, and q = 0.9 and tanβ = 2.9 for the soft rock, respectively. The error simulation and assessment procedure, described in Section 4.1.1, was performed to assess the errors of the NOV-estimated mining subsidence under the different lithology of overlying rock strata. Figure 10 shows an example of the assessed errors associated with an underground working panel with an advancing direction of $\phi =90°$(the same as the one described in Section 4.1.1).

Table 2. Standard deviations (STD) and the influence areas of the errors of the NOV-estimated mining subsidence under different overlying rock strata.

Indicators	Lithology of Overlying Rock Strata
	Hard	Medium	Soft
STD	0.05 m	0.11 m	0.17 m
Influence area	0.40 m2	0.33 m2	0.26 m2

lists two indicators that are used to qualitatively analyze the influence of the lithology of overlying rock strata on the errors of the NOV-estimated mining subsidence in this case, in which, the influence area is defined as the area where the errors of the NOV-estimated mining subsidence are larger than 0.01 m (the common level of InSAR displacement uncertainties). The STDs denote the standard deviations of the errors over the influence area.

It can be seen from Table 2 and Figure 10 that the influence areas of the errors of the NOV-estimated mining subsidence gradually decrease when the lithology of overlying rock strata changes from hard to soft (e.g., from 0.40 km² to 0.26 km² in this case). On the other hand, the STDs of the NOV-estimated subsidence errors dramatically increase with the changes from hard to soft (e.g., 0.05 m to 0.17 m in this case). This result implies that, for the same mining geometry, larger errors distributed in a smaller area would result in the NOV-estimated mining subsidence for the soft overlying rock strata, compared with those under the hard overlying rock strata. Consequently, more attention should be paid to scientifically using the NOV-estimated mining subsidence, especially in a mining area with soft overlying rock strata, due to the resulting large errors.

4.3. Influence of the Error of the NOV-Estimated Mining Subsidence on Its Typical Uses

4.3.1. Influence on the Boundary Delimitation of Mining Subsidence

Delimitating the boundary of ground surface subsidence is a typical use of subsidence observations [35]. To intuitively demonstrate the influence of the error of the NOV-estimated mining subsidence on the boundary delimitation, we projected the simulated 3D displacements caused by an underground working panel with φ = 90° (see Figure 3) onto the descending (i.e., α = 190°) and ascending (i.e., α = 350°) SAR LOS directions (θ = 38°), respectively. The NOV method was then applied to estimate mining subsidence from the projected ascending and descending LOS displacements, respectively. Finally, the subsidence boundary (generally defined as the area where surface subsidence is larger than 0.01 m [30]) was delimitated from the ascending and descending NOV-estimated mining subsidence estimates (see Figure 11).

As is shown in Figure 11, compared with the “real” boundary (black dashed line), all of the delimitated boundaries that are based on the ascending (red line) and descending (blue line) NOV-estimated mining subsidence shrank (e.g., about 8% in this case). More specifically, for the ascending SAR imaging view, the delimitated boundary shifted to the west–south direction and insignificantly shrank in the east–north region, with respect to the “real” boundary. This is mainly due to the “peak-to-valley” error pattern of the NOV-estimated mining subsidence; that is, for the ascending SAR imaging view, the NOV-retrieved subsidence is under- and over-estimated in the regions of the north–east and south–west peaks, respectively. A similar shift and shrink phenomenon of the delimitated boundary (but in different regions and different directions) can be observed for the descending NOV-estimated mining subsidence.

4.3.2. Influence on the Assessment of Mining-Induced Building Damage Risk

Another typical application of mining subsidence observations is used to assess the categories of mining-induced damage to buildings [40]. In this section, a simulation analysis was conducted to intuitively show the influence of the error of the NOV-estimated mining subsidence on the assessment of building damage risk, in which, the simulated 3D mining displacements and the ascending NOV-estimated subsidence were the same as those in Section 4.1.1. Then, we assumed that 660 buildings (marked by the circles in Figure 12a) were randomly located in the simulated mining subsidence basin (the boundary is denoted by a gray line in Figure 12). Finally, the damage categories of the assumed 660 buildings caused by the simulated underground extraction (see black solid rectangle) were then assessed on the basis of the ascending NOV-estimated mining subsidence. Readers can refer to He, et al. [32] for more details about the assessment procedure. For the sake of comparison, the “real” damage categories assessed by the simulated subsidence are presented in Figure 12b. Figure 12c plots the differences between the assessed and “real” building damage categories.

The results show that the damage categories of 72 and 28 buildings are overestimated (i.e., +I in Figure 12a) and underestimated (i.e., −I in Figure 12a), respectively. In other words, the damage risks of 100 buildings, representing 15.2% of all 660 buildings, are inaccurately assessed due to the errors of the NOV-estimated subsidence. In fact, one can observe from Figure 12c that those buildings with inaccurately assessed damage risks are located in the error clustering peak and valley of the NOV-estimated mining subsidence (marked by the blue and red ellipses in the base map in Figure 12c), respectively. This result suggests that the NOV-estimated subsidence located in the error peak and valley should be used prudently in practice.

5. Conclusions

In this paper, we systematically analyzed the error of NOV-estimated mining subsidence from InSAR observations due to neglecting 2D horizontal movements with simulated and real datasets. The results indicate that the errors can reach up to 45.1% of the maximum subsidence in this study. In addition, two areas where mining subsidence was under-estimated (“peak” errors) and over-estimated (“valley” errors), respectively, were observed in the mining subsidence basin, and the absolute angles between the summit-to-bottom line and the east direction usually vary from 5° to 15°. For the same InSAR datasets and underground mining geometry, the errors of the NOV-estimated subsidence primarily depend on the lithology of overlying rock strata; that is, the harder the lithology is, the smaller the error magnitude is but the wider the error area is, and vice versa. Therefore, prior to the use of NOV-estimated mining subsidence, it is preferable to approximately assess the errors due to neglecting 2D horizontal movements (e.g., using the presented method in this study if possible), in order to scientifically guide the use of subsidence observations.

Note that the presented pixel-wise method for assessing the errors of the NOV-estimated mining subsidence relies on three in situ parameters (e.g., mining depth, angle of major influence, and constant of horizontal movement) [29]. This may limit the use of the presented method if these three parameters are unavailable. In addition, the above-analyzed patterns of the NOV-estimated mining subsidence generally hold well over those mining areas where nearly horizontal mineral seams are extracted (very common currently), since the assisted SIP and PIM methods work well in this scenario. Nevertheless, as suggested by Dai et al. [41] and Franks et al. [42], several special mining situations (e.g., extracting steep inclined mineral seams) or geological conditions (rugged surface terrain) would cause significant discrepancies with the error pattern analyzed based on the SIP and PIM. Future research efforts should be devoted to address this issue.