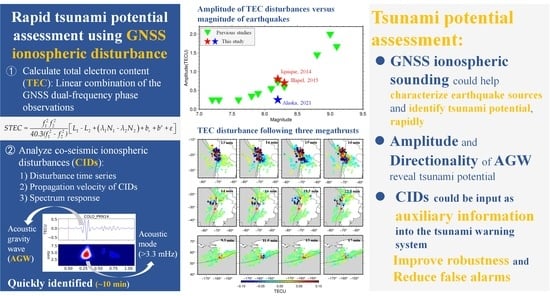
Rapid Tsunami Potential Assessment Using GNSS Ionospheric Disturbance: Implications from Three Megathrusts
Abstract
:1. Introduction
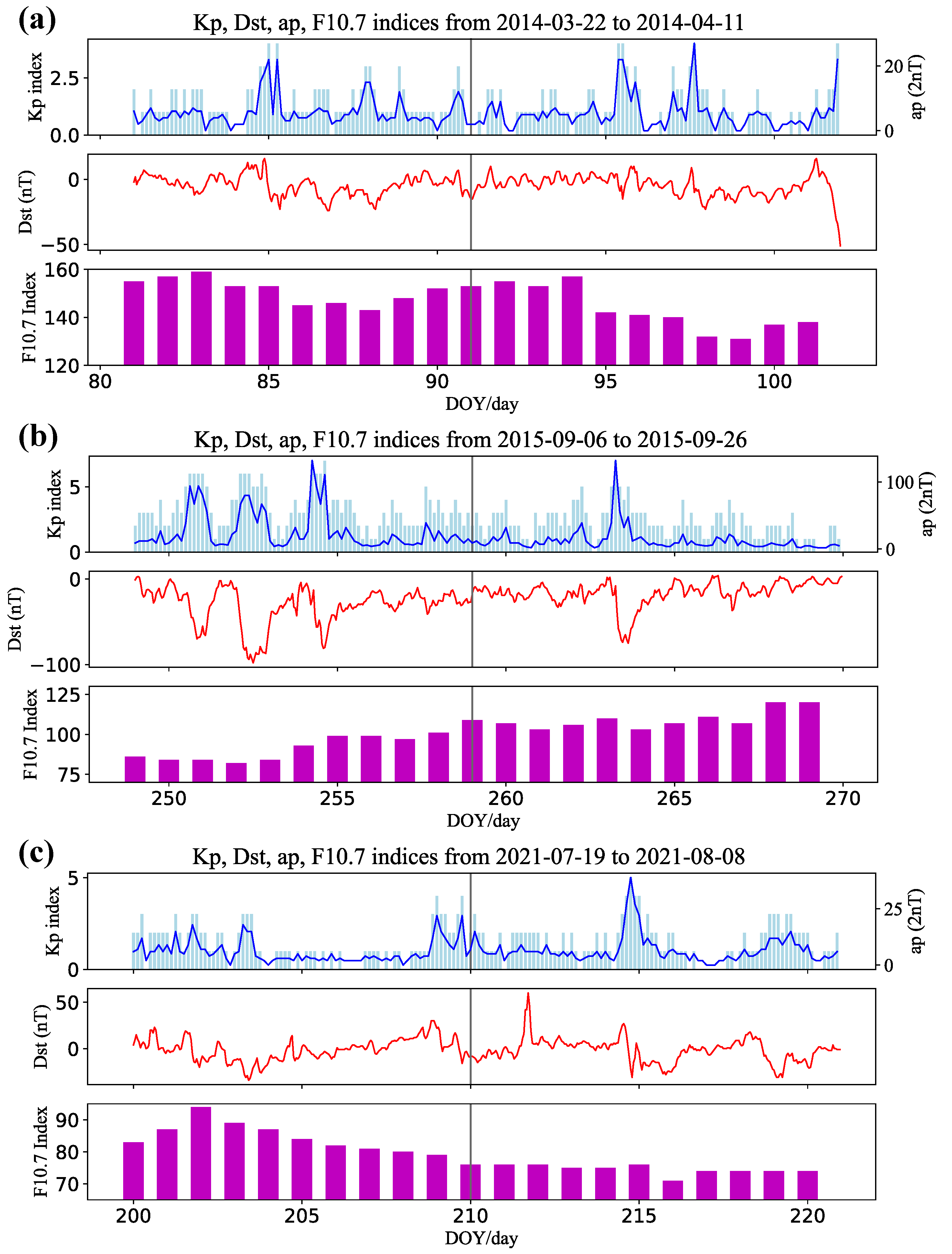
2. Materials and Methods
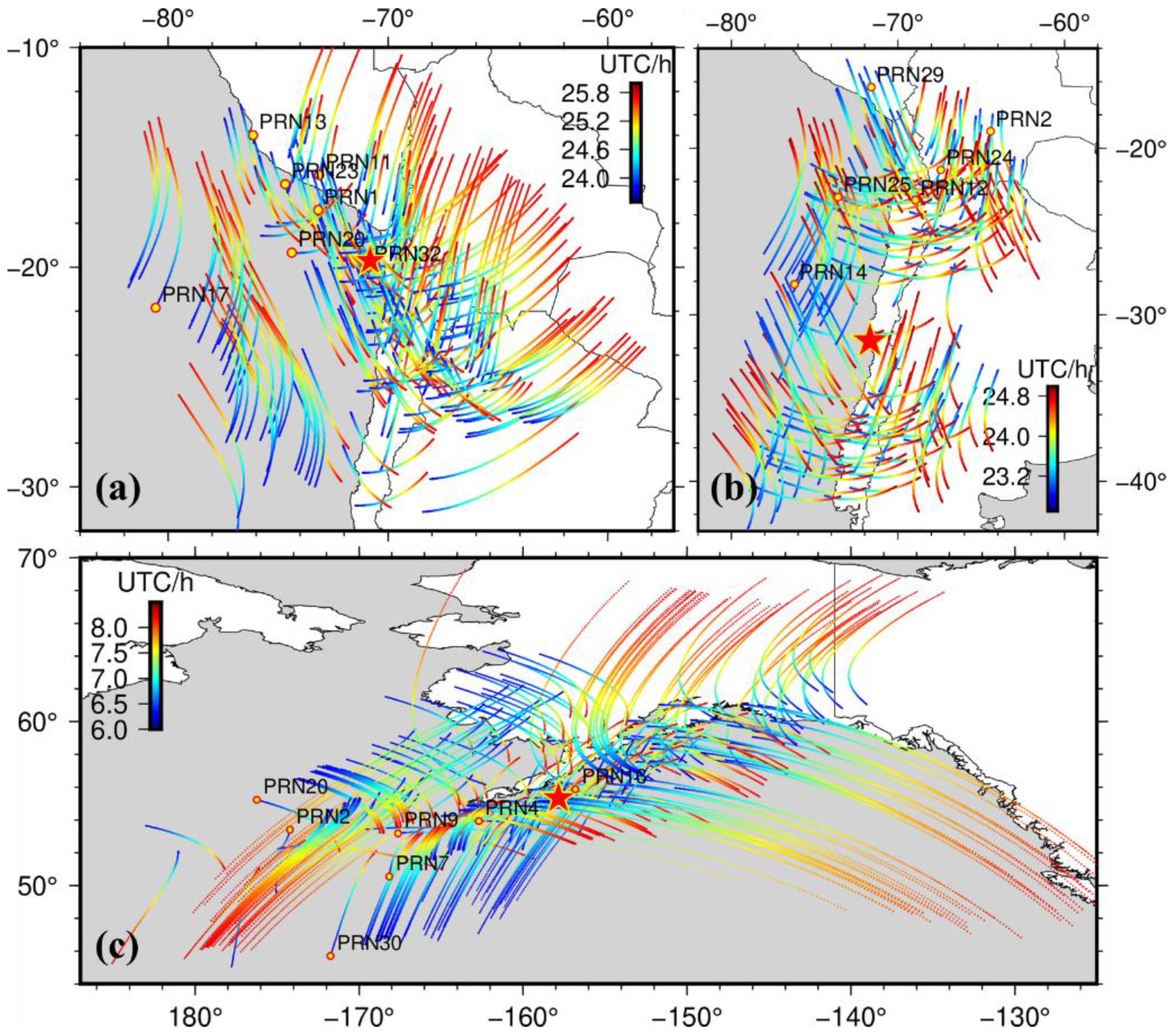
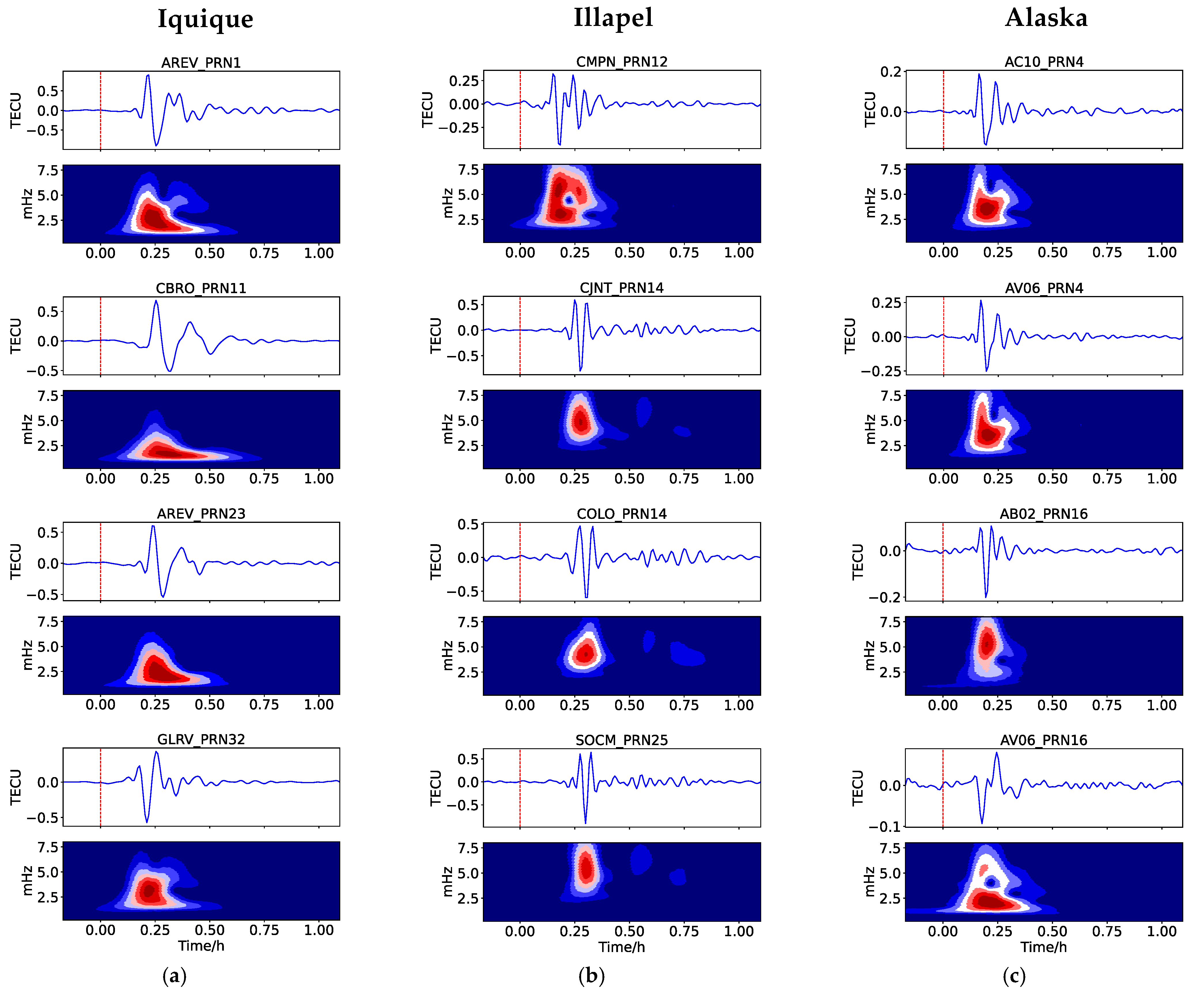
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sobolev, S.V.; Babeyko, A.Y.; Wang, R.; Hoechner, A.; Galas, R.; Rothacher, M.; Sein, D.V.; Schroter, J.; Lauterjung, J.; Subarya, C. Tsunami early warning using GPS-Shield arrays. J. Geophys. Res. Solid Earth 2007, 112, B08415. [Google Scholar] [CrossRef]
- Song, Y.T. Detecting tsunami genesis and scales directly from coastal GPS stations. Geophys. Res. Lett. 2007, 34, L19602. [Google Scholar] [CrossRef] [Green Version]
- Hooper, A.; Pietrzak, J.; Simons, W.; Cui, H.; Riva, R.; Naeije, M.; van Scheltinga, A.T.; Schrama, E.; Stelling, G.; Socquet, A. Importance of horizontal seafloor motion on tsunami height for the 2011 Mw = 9.0 Tohoku-Oki earthquake. Earth Planet. Sci. Lett. 2013, 361, 469–479. [Google Scholar] [CrossRef]
- Kanamori, H.; Rivera, L. Source inversion of W phase: Speeding up seismic tsunami warning. Geophys. J. Int. 2008, 175, 222–238. [Google Scholar] [CrossRef]
- Melgar, D.; Bock, Y. Near-field tsunami models with rapid earthquake source inversions from land- and ocean-based observations: The potential for forecast and warning. J. Geophys. Res. Solid Earth 2013, 118, 5939–5955. [Google Scholar] [CrossRef]
- Chen, K.J.; Liu, Z.; Song, Y.T. Automated GNSS and Teleseismic Earthquake Inversion (AutoQuake Inversion) for Tsunami Early Warning: Retrospective and Real-Time Results. Pure Appl. Geophys. 2020, 177, 1403–1423. [Google Scholar] [CrossRef] [Green Version]
- Government Accountability Office. Tsunami Preparedness: Federal and State Partners Collaborate to Help Communities Reduce Potential Impacts, but Significant Challenges Remain; Government Accountability Office, Ed.; U.S. Government Printing Office: Washington, DC, USA, 2006; Volume 06-519, pp. 1–65.
- Dautermann, T.; Calais, E.; Lognonne, P.; Mattioli, G.S. Lithosphere-atmosphere-ionosphere coupling after the 2003 explosive eruption of the Soufriere Hills Volcano, Montserrat. Geophys. J. Int. 2009, 179, 1537–1546. [Google Scholar] [CrossRef] [Green Version]
- Rakoto, V.; Lognonne, P.; Rolland, L.; Coisson, P. Tsunami Wave Height Estimation from GPS-Derived Ionospheric Data. J. Geophys. Res. Space Phys. 2018, 123, 4329–4348. [Google Scholar] [CrossRef]
- Rakoto, V.; Lognonne, P.; Rolland, L. Tsunami modeling with solid Earth-ocean-atmosphere coupled normal modes. Geophys. J. Int. 2017, 211, 1119–1138. [Google Scholar] [CrossRef]
- Artru, J.; Ducic, V.; Kanamori, H.; Lognonne, P.; Murakami, M. Ionospheric detection of gravity waves induced by tsunamis. Geophys. J. Int. 2005, 160, 840–848. [Google Scholar] [CrossRef] [Green Version]
- Afraimovich, E.L.; Terekhov, A.I.; Udodov, M.Y.; Fridman, S.V. Refraction Distortions of Transionospheric Radio Signals Caused by Changes in a Regular Ionosphere and by Traveling Ionospheric Disturbances. J. Atmos. Terr. Phys. 1992, 54, 1013–1020. [Google Scholar] [CrossRef]
- Manta, F.; Occhipinti, G.; Feng, L.J.; Hill, E.M. Rapid identification of tsunamigenic earthquakes using GNSS ionospheric sounding. Sci. Rep. 2020, 10, 11054. [Google Scholar] [CrossRef] [PubMed]
- Satake, K.; Nishimura, Y.; Putra, P.S.; Gusman, A.R.; Sunendar, H.; Fujii, Y.; Tanioka, Y.; Latief, H.; Yulianto, E. Tsunami Source of the 2010 Mentawai, Indonesia Earthquake Inferred from Tsunami Field Survey and Waveform Modeling. Pure Appl. Geophys. 2013, 170, 1567–1582. [Google Scholar] [CrossRef] [Green Version]
- Tu, R.; Zhang, H.; Ge, M.; Huang, G. A real-time ionospheric model based on GNSS Precise Point Positioning. Adv. Space Res. 2013, 52, 1125–1134. [Google Scholar] [CrossRef]
- Brunini, C.; Azpilicueta, F.J. Accuracy assessment of the GPS-based slant total electron content. J. Geod. 2009, 83, 773–785. [Google Scholar] [CrossRef]
- Jin, S.G.; Occhipinti, G.; Jin, R. GNSS ionospheric seismology: Recent observation evidences and characteristics. Earth-Sci. Rev. 2015, 147, 54–64. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, 23, 325–331. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tsai, H.F.; Lin, C.H.; Kamogawa, M.; Chen, Y.I.; Huang, B.S.; Yu, S.B.; Yeh, Y.H. Coseismic ionospheric disturbances triggered by the Chi-Chi earthquake. J. Geophys. Res. Space Phys. 2010, 115, A08303. [Google Scholar] [CrossRef]
- Liu, J.Y.; Lin, C.Y.; Tsai, Y.L.; Liu, T.C.; Hattori, K.; Sun, Y.Y.; Wu, T.R. Ionospheric GNSS Total Electron Content for Tsunami Warning. J. Earthq. Tsunami 2019, 13, 1941007. [Google Scholar] [CrossRef]
- Li, Z.; Wang, N.; Liu, A.; Yuan, Y.; Wang, L.; Hernández-Pajares, M.; Krankowski, A.; Yuan, H. Status of CAS global ionospheric maps after the maximum of solar cycle 24. Satell. Navig. 2021, 2, 19. [Google Scholar] [CrossRef]
- Coster, A.; Williams, J.; Weatherwax, A.; Rideout, W.; Herne, D. Accuracy of GPS total electron content: GPS receiver bias temperature dependence. Radio Sci. 2013, 48, 190–196. [Google Scholar] [CrossRef]
- Kong, J.; Yao, Y.B.; Zhou, C.; Liu, Y.; Zhai, C.Z.; Wang, Z.M.; Liu, L. Tridimensional reconstruction of the Co-Seismic Ionospheric Disturbance around the time of 2015 Nepal earthquake. J. Geod. 2018, 92, 1255–1266. [Google Scholar] [CrossRef]
- Nicolls, M.J.; Kelley, M.C.; Coster, A.J.; Gonzalez, S.A.; Makela, J.J. Imaging the structure of a large-scale TID using ISR and TEC data. Geophys. Res. Lett. 2004, 31, L09812. [Google Scholar] [CrossRef]
- Perevalova, N.P.; Sankov, V.A.; Astafyeva, E.I.; Zhupityaeva, A.S. Threshold magnitude for Ionospheric TEC response to earthquakes. J. Atmos. Sol.-Terr. Phys. 2014, 108, 77–90. [Google Scholar] [CrossRef]
- Richmond, A.D.; Matsushita, S. Thermospheric Response to a Magnetic Substorm. J. Geophys. Res. Space Phys. 1975, 80, 2839–2850. [Google Scholar] [CrossRef]
- Occhipinti, G.; Kherani, E.A.; Lognonne, P. Geomagnetic dependence of ionospheric disturbances induced by tsunamigenic internal gravity waves. Geophys. J. Int. 2008, 173, 753–765. [Google Scholar] [CrossRef]
- Dautermann, T.; Calais, E.; Mattioli, G.S. Global Positioning System detection and energy estimation of the ionospheric wave caused by the 13 July 2003 explosion of the Soufriere Hills Volcano, Montserrat. J. Geophys. Res. Solid Earth 2009, 114, B02202. [Google Scholar] [CrossRef]
- Shrivastava, M.N.; Maurya, A.K.; Gonzalez, G.; Sunil, P.S.; Gonzalez, J.; Salazar, P.; Aranguiz, R. Tsunami detection by GPS-derived ionospheric total electron content. Sci. Rep. 2021, 11, 12978. [Google Scholar] [CrossRef]
- Catalan, P.A.; Aranguiz, R.; Gonzalez, G.; Tomita, T.; Cienfuegos, R.; Gonzalez, J.; Shrivastava, M.N.; Kumagai, K.; Mokrani, C.; Cortes, P.; et al. The 1 April 2014 Pisagua tsunami: Observations and modeling. Geophys. Res. Lett. 2015, 42, 2918–2925. [Google Scholar] [CrossRef]
- Aranguiz, R.; Gonzalez, G.; Gonzalez, J.; Catalan, P.A.; Cienfuegos, R.; Yagi, Y.; Okuwaki, R.; Urra, L.; Contreras, K.; Del Rio, I.; et al. The 16 September 2015 Chile Tsunami from the Post-Tsunami Survey and Numerical Modeling Perspectives. Pure Appl. Geophys. 2016, 173, 333–348. [Google Scholar] [CrossRef]
- Astafyeva, E.; Heki, K.; Kiryushkin, V.; Afraimovich, E.; Shalimov, S. Two-mode long-distance propagation of coseismic ionosphere disturbances. J. Geophys. Res. Space Phys. 2009, 114, A10307. [Google Scholar] [CrossRef] [Green Version]
- Afraimovich, E.L.; Ding, F.; Kiryushkin, V.V.; Astafyeva, E.I.; Jin, S.G.; Sankov, V.A. TEC response to the 2008 Wenchuan Earthquake in comparison with other strong earthquakes. Int. J. Remote Sens. 2010, 31, 3601–3613. [Google Scholar] [CrossRef] [Green Version]
- Astafyeva, E.; Heki, K. Dependence of waveform of near-field coseismic ionospheric disturbances on focal mechanisms. Earth Planets Space 2009, 61, 939–943. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.T.; Zhang, K.K.; Imtiaz, N.; Song, Q.; Zhang, Y. Relating Far-Field Coseismic Ionospheric Disturbances to Geological Structures. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029209. [Google Scholar] [CrossRef]
- Astafyeva, E. Ionospheric Detection of Natural Hazards. Rev. Geophys. 2019, 57, 1265–1288. [Google Scholar] [CrossRef]
- Reddy, C.D.; Sunil, A.S.; Gonzalez, G.; Shrivastava, M.N.; Moreno, M. Near-field co-seismic ionospheric response due to the northern Chile Mw 8.1 Pisagua earthquake on April 1, 2014 from GPS observations. J. Atmos. Sol.-Terr. Phys. 2015, 134, 1–8. [Google Scholar] [CrossRef]
- Occhipinti, G.; Rolland, L.; Lognonne, P.; Watada, S. From Sumatra 2004 to Tohoku-Oki 2011: The systematic GPS detection of the ionospheric signature induced by tsunamigenic earthquakes. J. Geophys. Res. Space Phys. 2013, 118, 3626–3636. [Google Scholar] [CrossRef]
- Nishitani, N.; Ogawa, T.; Otsuka, Y.; Hosokawa, K.; Hori, T. Propagation of large amplitude ionospheric disturbances with velocity dispersion observed by the SuperDARN Hokkaido radar after the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 891–896. [Google Scholar] [CrossRef] [Green Version]
- Cahyadi, M.N.; Heki, K. Coseismic ionospheric disturbance of the large strike-slip earthquakes in North Sumatra in 2012: M-w dependence of the disturbance amplitudes. Geophys. J. Int. 2015, 200, 116–129. [Google Scholar] [CrossRef] [Green Version]
- Zettergren, M.D.; Snively, J.B. Ionospheric response to infrasonic-acoustic waves generated by natural hazard events. J. Geophys. Res. Space Phys. 2015, 120, 8002–8024. [Google Scholar] [CrossRef] [Green Version]
- Nishida, K.; Kobayashi, N.; Fukao, Y. Resonant oscillations between the solid Earth and the atmosphere. Science 2000, 287, 2244–2246. [Google Scholar] [CrossRef] [PubMed]
- Saito, A.; Tsugawa, T.; Otsuka, Y.; Nishioka, M.; Iyemori, T.; Matsumura, M.; Saito, S.; Chen, C.H.; Goi, Y.; Choosakul, N. Acoustic resonance and plasma depletion detected by GPS total electron content observation after the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 863–867. [Google Scholar] [CrossRef] [Green Version]
- Richmond, A.D. Gravity-Wave Generation, Propagation, and Dissipation in Thermosphere. J. Geophys. Res. Space Phys. 1978, 83, 4131–4145. [Google Scholar] [CrossRef]
- Mao, T.; Wang, J.S.; Yang, G.L.; Yu, T.; Ping, J.S.; Suo, Y.C. Effects of typhoon Matsa on ionospheric TEC. Chin. Sci. Bull. 2010, 55, 712–717. [Google Scholar] [CrossRef]
- Reddy, C.D.; Shrivastava, M.N.; Seemala, G.K.; Gonzalez, G.; Baez, J.C. Ionospheric Plasma Response to M (w) 8.3 Chile Illapel Earthquake on September 16, 2015. Pure Appl. Geophys. 2016, 173, 1451–1461. [Google Scholar] [CrossRef]
- Wan, X.; Xiong, C.; Gao, S.Z.; Huang, F.Q.; Liu, Y.W.; Aa, E.C.; Yin, F.; Cai, H.T. The nighttime ionospheric response and occurrence of equatorial plasma irregularities during geomagnetic storms: A case study. Satell. Navig. 2021, 2, 23. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Dubey, S.; Tiwari, R.; Purohit, P.K.; Gwal, A.K. Effect of magnetic activity on ionospheric time delay at low latitude. J. Astrophys. Astron. 2008, 29, 269–274. [Google Scholar] [CrossRef]
- Bartels, J.; Veldkamp, J. International Data on Magnetic Disturbances, 4th Quarter, 1955. J. Geophys. Res. 1956, 61, 285–292. [Google Scholar]
- Astafyeva, E.; Shalimov, S.; Olshanskaya, E.; Lognonne, P. Ionospheric response to earthquakes of different magnitudes: Larger quakes perturb the ionosphere stronger and longer. Geophys. Res. Lett. 2013, 40, 1675–1681. [Google Scholar] [CrossRef] [Green Version]
- Ye, L.L.; Lay, T.; Kanamori, H.; Koper, K.D. Reply to: Comment by Rodrigo Cienfuegos on “Rapidly Estimated Seismic Source Parameters for the 16 September 2015 Illapel, Chile, Mw 8.3 Earthquake” by Lingling Ye, Thorne Lay, Hiroo Kanamori, and Keith D. Koper. Pure Appl. Geophys. 2019, 176, 2753. [Google Scholar] [CrossRef] [Green Version]
- Heidarzadeh, M.; Murotani, S.; Satake, K.; Ishibe, T.; Gusman, A.R. Source model of the 16 September 2015 Illapel, Chile, M-w 8.4 earthquake based on teleseismic and tsunami data. Geophys. Res. Lett. 2016, 43, 643–650. [Google Scholar] [CrossRef] [Green Version]



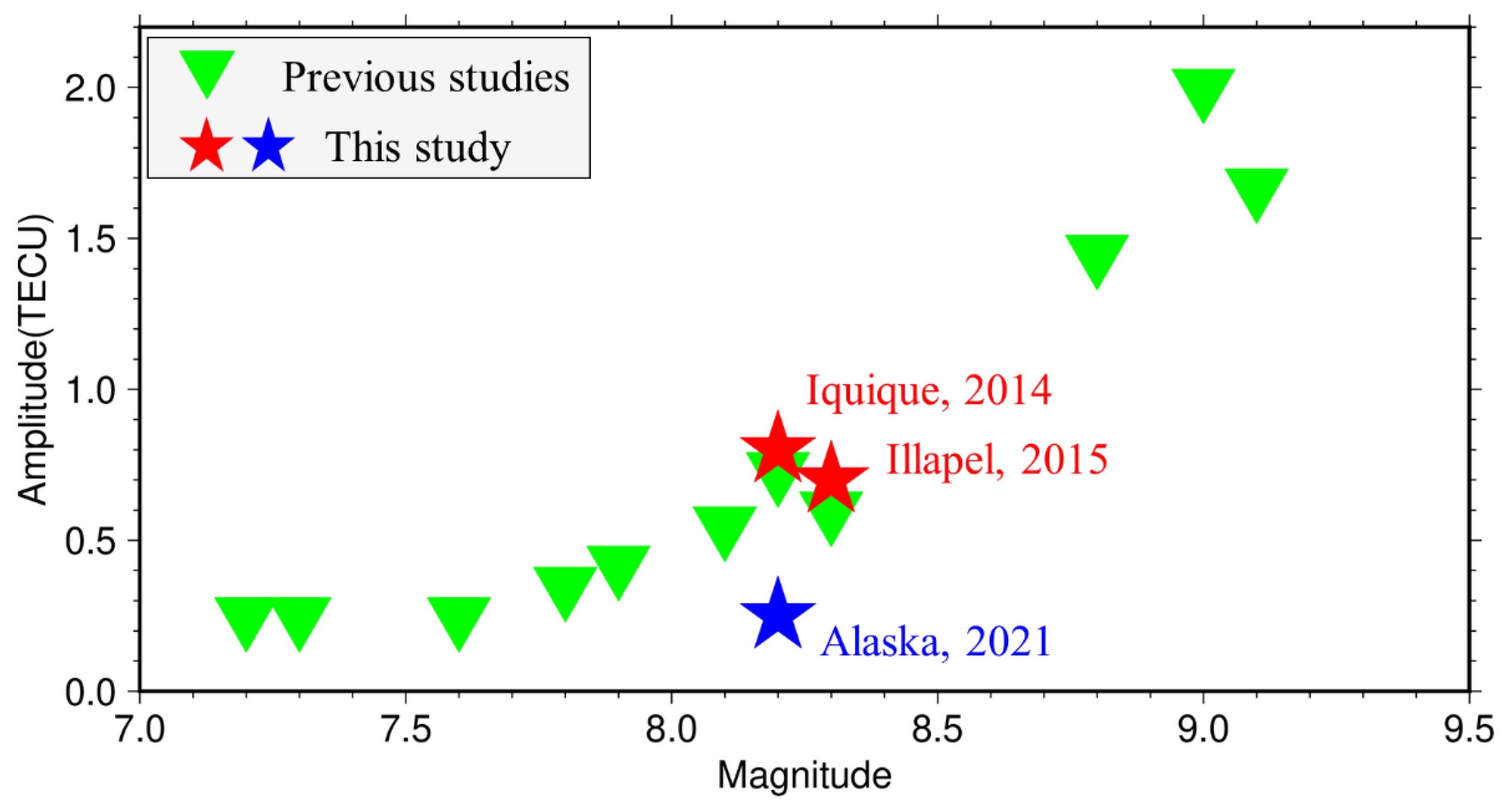
| Number | Date | UTC | Location (B, L) | D, km | Mw | Amp, TECU | Water, m |
|---|---|---|---|---|---|---|---|
| #1 | 4 October 1994 | 13:23:28 | 43.60; 147.63 | 61.0 | 8.1 | 0.4 −0.7 | 10.40 |
| #2 | 20 September 1999 | 17:47:35 | 23.87; 120.75 | 21.0 | 7.6 | 0.25 | - |
| #3 | 25 September 2003 | 19:50:06 | 41.78; 143.90 | 28.0 | 8.3 | 0.5 −0.7 | 4.40 |
| #4 | 5 September 2004 | 10:07:07 | 33.10, 136.60 | 14.0 | 7.2 | 0.2 −0.3 | 0.93 |
| #5 | 26 December 2004 | 00:58:53 | 3.32; 95.85 | 30.0 | 9.1 | 1.67 | 50.90 |
| #6 | 3 May 2006 | 15:26:39 | −20.13, −174.16 | 55.0 | 7.9 | 0.35 -0.5 | 0.27 |
| #7 | 15 November 2006 | 11:14:13 | 46.61, 153.23 | 30.3 | 8.2 | 0.73 | 21.90 |
| #8 | 15 July 2009 | 09:22:29 | −45.75, 166.58 | 12.0 | 7.8 | 0.28 −0.4 | 0.47 |
| #9 | 27 February 2010 | 06:34:14 | 35.91; 72.73 | 23.0 | 8.8 | 1.1 −1.8 | 29.00 |
| #10 | 9 March 2011 | 02:45:20 | 38.44, 142.84 | 32.0 | 7.3 | 0.2 −0.3 | 0.60 |
| #11 | 11 March 2011 | 05:46:24 | 38.30, 142.37 | 32.0 | 9.0 | 1.2–3.0 | 39.26 |
| This study #1 | 1 April 2014 | 23:46:47 | −19.61, −70.77 | 25.0 | 8.2 | 0.8 | 4.63 |
| This study #2 | 16 September 2015 | 22:54:32 | −31.57, −71.60 | 22.4 | 8.3 | 0.7 | 13.60 |
| This study #3 | 29 July 2021 | 06:15:47 | 55.33, −157.84 | 32.2 | 8.2 | 0.25 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Chen, K.; Chai, H.; Wei, G. Rapid Tsunami Potential Assessment Using GNSS Ionospheric Disturbance: Implications from Three Megathrusts. Remote Sens. 2022, 14, 2018. https://doi.org/10.3390/rs14092018
Li J, Chen K, Chai H, Wei G. Rapid Tsunami Potential Assessment Using GNSS Ionospheric Disturbance: Implications from Three Megathrusts. Remote Sensing. 2022; 14(9):2018. https://doi.org/10.3390/rs14092018
Chicago/Turabian StyleLi, Jiafeng, Kejie Chen, Haishan Chai, and Guoguang Wei. 2022. "Rapid Tsunami Potential Assessment Using GNSS Ionospheric Disturbance: Implications from Three Megathrusts" Remote Sensing 14, no. 9: 2018. https://doi.org/10.3390/rs14092018
APA StyleLi, J., Chen, K., Chai, H., & Wei, G. (2022). Rapid Tsunami Potential Assessment Using GNSS Ionospheric Disturbance: Implications from Three Megathrusts. Remote Sensing, 14(9), 2018. https://doi.org/10.3390/rs14092018