Optimization of Numerical Methods for Transforming UTM Plane Coordinates to Lambert Plane Coordinates
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Methods
2.1.1. Linear Rule Approximation (LRA) Method
2.1.2. Improved Linear Rule Approximation (ILRA) Method
2.1.3. Hyperbolic Transformation (HT) Method
2.1.4. Conformal Transformation (CT) Method
2.2. Test Scenarios
- In the first step, for a particular numerical method, the four vertices of each subzone are used as control points to calculate their corresponding polynomial parameters. The polynomial parameters are stored in a memory array.
- In the second step, all sample points are grouped according to the spatial extent of the subzone. Sample points within the same subzone are assigned to the same group.
- In the third step, for each group, the polynomial parameters are called from the memory array, and the coordinate transformation is performed in bulk for the sample points belonging to that group.
2.3. Hardware and Software Environment
3. Results
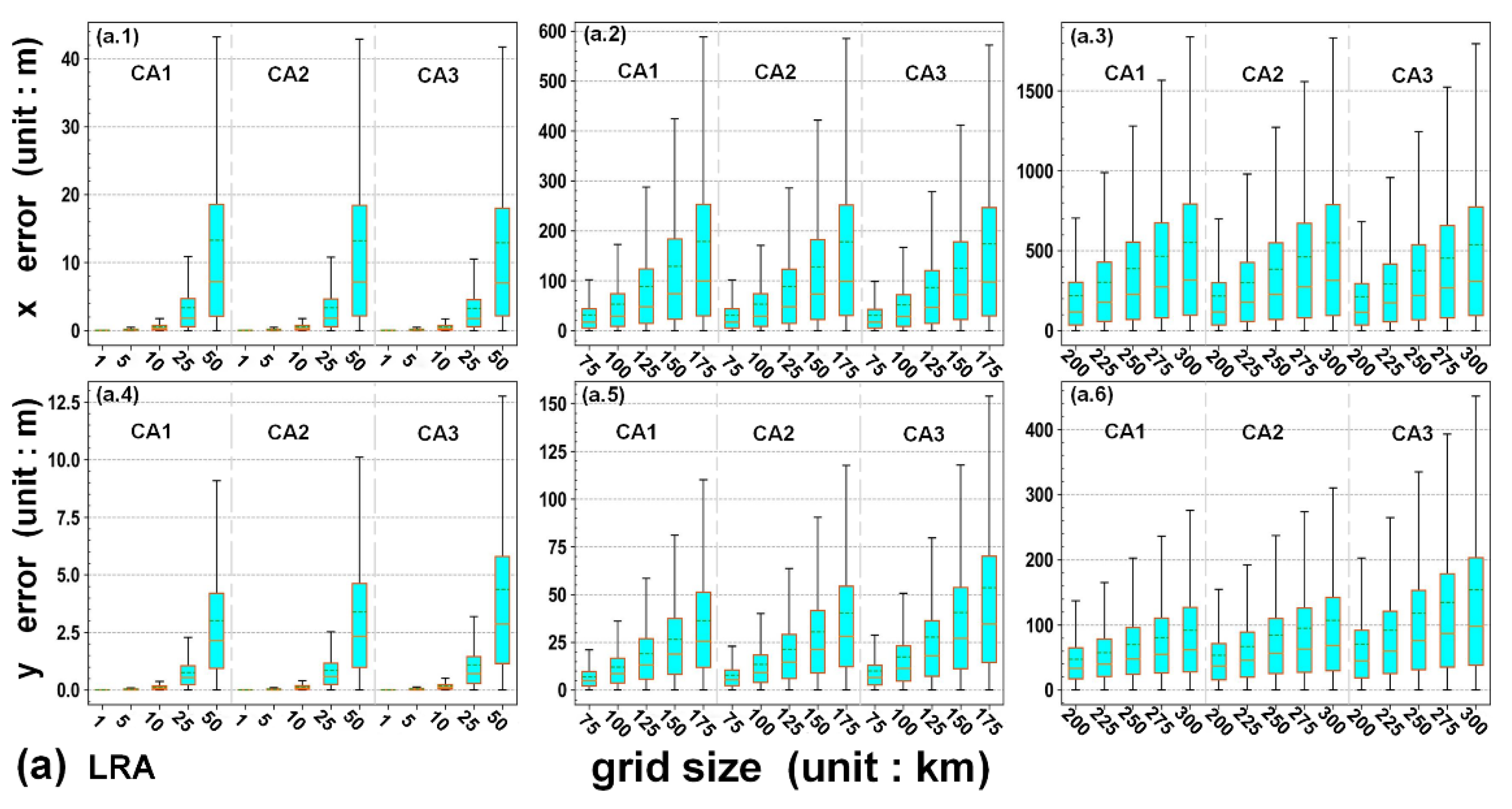
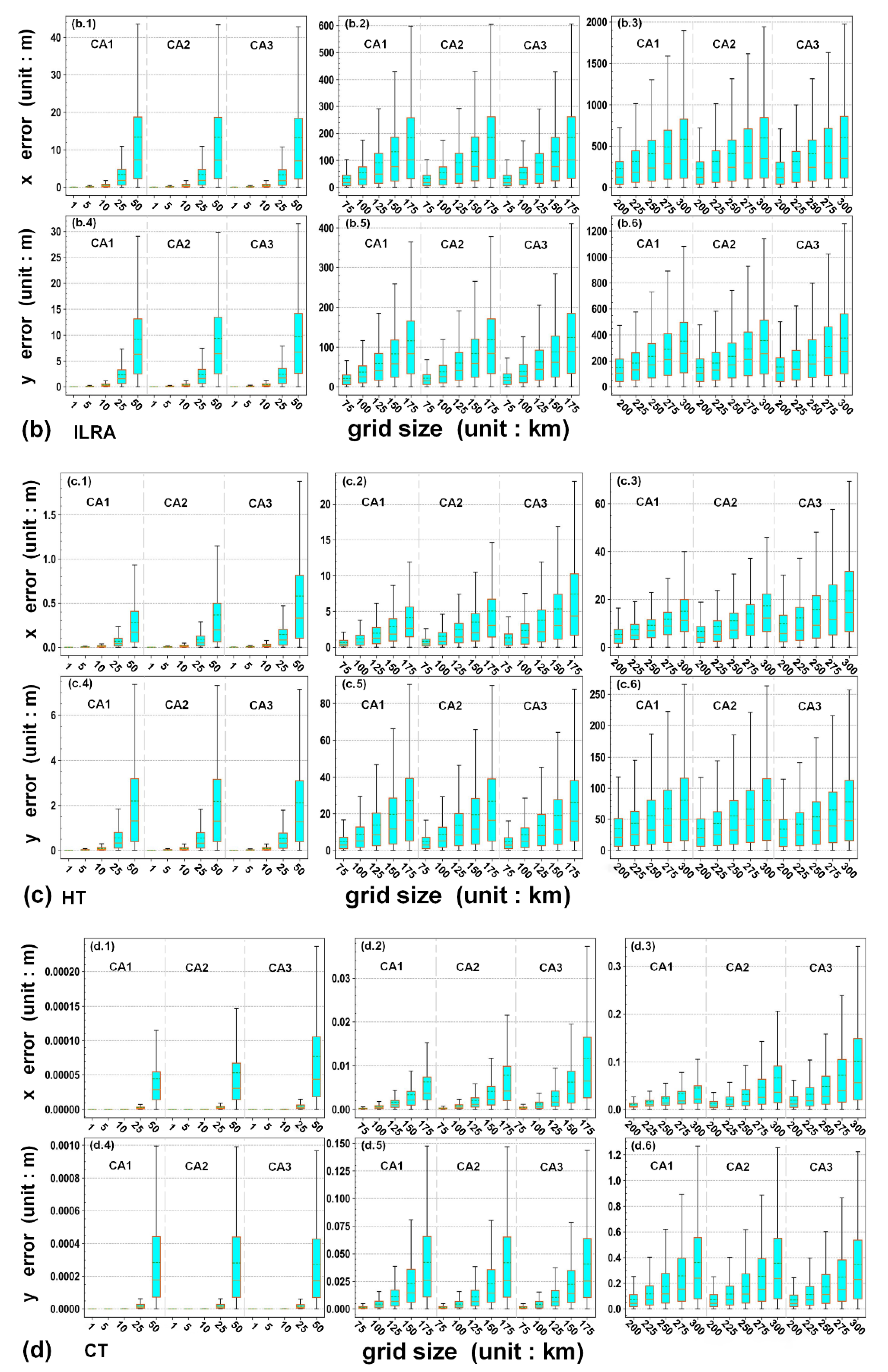
3.1. Error Statistics of Multiple Numerical Methods
3.2. Comparison of the Transformation Efficiency of Multiple Numerical Methods
3.3. Effect of Grid Shape Change on the Maximum Coordinate Transformation Error of the CT Method
3.4. Spatial Distribution of Coordinate Transformation Error of the CT Method
4. Discussion
4.1. Comparison of Multiple Numerical Methods
4.2. Analysis of Potential Application Scenario
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ye, S.; Song, C.; Gao, P.; Liu, C.; Cheng, C. Visualizing Clustering Characteristics of Multidimensional Arable Land Quality Indexes at the County Level in Mainland China. Environ. Plan. A Econ. Space 2022, 54, 222–225. [Google Scholar] [CrossRef]
- Ye, S.; Ren, S.; Song, C.; Cheng, C.; Shen, S.; Yang, J.; Zhu, D. Spatial Patterns of County-level Arable Land Productive-capacity and Its Coordination with Land-use Intensity in Mainland China. Agric. Ecosyst. Environ. 2022, 326, 107757. [Google Scholar]
- Fang, L.; Wang, M.; Li, D.; Pan, J. CPU/GPU Near Real-time Preprocessing for ZY-3 Satellite Images: Relative Radiometric Correction, MTF Compensation, and Geocorrection. ISPRS J. Photogramm. Remote Sens. 2014, 87, 229–240. [Google Scholar] [CrossRef]
- Yu, H.; Cao, N.; Lan, Y.; Xing, M. Multisystem Interferometric Data Fusion Framework: A Three-Step Sensing Approach. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8501–8509. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G. Motion Compensation/Autofocus in Airborne Synthetic Aperture Radar: A Review. IEEE Geosci. Remote Sens. Mag. 2021, 2–23. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, M.; Cheng, Y.; He, L.; Xue, L. An Improved Jitter Detection Method Based on Parallax Observation of Multispectral Sensors for Gaofen-1 02/03/04 Satellites. Remote Sens. 2019, 11, 16. [Google Scholar] [CrossRef] [Green Version]
- Ipbuker, C. An Inverse Solution to the Winkel Tripel Projection Using Partial Derivatives. Cartogr. Geogr. Inf. Sci. 2002, 29, 37–42. [Google Scholar] [CrossRef]
- Wu, Z. How to Transform the Coordinates of One Kind of Map Projection Point to Another Kind of Map Projection Point Coordinate Problem. Acta Geogr. Sin. 1979, 1, 55–68. [Google Scholar]
- Yang, Q.; Snyder, J.; Tobler, W. Map Projection Transformation: Principles and Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Liu, X.; Liu, H. A Comprehensive Appraisial of Numerical Transformation Method for Map Projection. J. Inst. Surv. Mapp. 2002, 19, 150–153. [Google Scholar]
- Liu, D.; Zhou, G.; Huang, J.; Zhang, R.; Shu, L.; Zhou, X.; Xin, C. On-board Georeferencing Using FPGA-based Optimized Second-order Polynomial Equation. Remote Sens. 2019, 11, 124. [Google Scholar] [CrossRef] [Green Version]
- Bildirici, I. Numerical Inverse Transformation for Map Projections. Comput. Geosci. 2003, 29, 1003–1011. [Google Scholar] [CrossRef]
- Ye, S.; Yan, T.; Yue, Y.; Lin, W.; Li, L.; Yao, X.; Mu, Q.; Li, Y.; Zhu, D. Developing a Reversible Rapid Coordinate Transformation Model for the Cylindrical Projection. Comput. Geosci. 2016, 89, 44–56. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric Equations of Topography and Other Irregular Surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Hardy, R.L. Theory and Applications of the Multiquadric-biharmonic Method 20 Years of Discovery 1968–1988. Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Duan, M.; Yin, C.; Qin, C. Rapid algorithm of raster map projection transformation. In Proceedings of the Second International Conference on Image and Graphics, Hefei, China, 31 July 2002; pp. 154–159. [Google Scholar]
- Mu, C.; Chou, T.; Hoang, T.V.; Kung, P.; Fang, Y.; Chen, M.; Yeh, M. Development of Multilayer-Based Map Matching to Enhance Performance in Large Truck Fleet Dispatching. ISPRS Int. J. Geo-Inf. 2021, 10, 79. [Google Scholar] [CrossRef]
- Yang, Q. On the Numerical Method For transforming The Zones of Gauss Projection. Acta Geod. Cartogr. Sin. 1982, 11, 18–31. [Google Scholar]
- Yang, Q. A Research on Numerical Transformation between Conformal Projections. Acta Geod. Cartogr. Sin. 1982, 11, 268–282. [Google Scholar]
- Li, J. A Research on Transformation of Finiteelembnt between Conformal Projections. Acta Geod. Cartogr. Sin. 1985, 14, 214–225. [Google Scholar]
- Liu, H. The Numerical Method of Transformation of Conformal Projection. Acta Geod. Cartogr. Sin. 1985, 14, 61–72. [Google Scholar]
- Jiang, B. Head/tail Breaks: A New Classification Scheme for Data with a Heavy-tailed Distribution. Prof. Geogr. 2013, 65, 482–494. [Google Scholar] [CrossRef]
- Ye, S.; Liu, D.; Yao, X.; Tang, H.; Xiong, Q.; Zhuo, W.; Du, Z.; Huang, J.; Su, W.; Shen, S. RDCRMG: A Raster Dataset Clean & Reconstitution Multi-grid Architecture for Remote Sensing Monitoring of Vegetation Dryness. Remote Sens. 2018, 10, 1376. [Google Scholar]
- Yang, N.; Liu, D.; Feng, Q.; Xiong, Q.; Zhang, L.; Ren, T.; Zhao, Y.; Zhu, D.; Huang, J. Large-Scale Crop Mapping Based on Machine Learning and Parallel Computation with Grids. Remote Sens. 2019, 11, 1500. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Liu, Z.; Liu, D.; Xiong, Q.; Yang, N.; Ren, T.; Zhang, C.; Zhang, X.; Li, S. Crop Mapping Based on Historical Samples and New Training Samples Generation in Heilongjiang Province, China. Sustainability 2019, 11, 5052. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Li, G.; Xia, J.; Ben, J.; Cao, Q.; Zhao, L.; Ma, Y.; Zhang, L.; Zhu, D. Enabling the Big Earth Observation Data via Cloud Computing and DGGS: Opportunities and Challenges. Remote Sens. 2020, 12, 62. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Song, C.; Shen, S.; Gao, P.; Cheng, C.; Cheng, F.; Wan, C.; Zhu, D. Spatial Pattern of Arable Land-use Intensity in China. Land Use Policy 2020, 99, 104845. [Google Scholar] [CrossRef]
- Yan, S.; Yao, X.; Zhu, D.; Liu, D.; Zhang, L.; Yu, G.; Gao, B.; Yang, J.; Yun, W. Large-scale Crop Mapping from Multi-source Optical Satellite Imageries Using Machine Learning with Discrete Grids. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102485. [Google Scholar] [CrossRef]
- Ye, S.; Zhu, D.; Yao, X.; Zhang, N.; Fang, S.; Li, L. Development of a Highly Flexible Mobile GIS-Based System for Collecting Arable Land Quality Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4432–4441. [Google Scholar] [CrossRef]
- Wan, C.; Kuzyakov, Y.; Cheng, C.; Ye, S.; Gao, B.; Gao, P.; Ren, S.; Yun, W. A Soil Sampling Design for Arable Land Quality Observation by Using SPCOSA-CLHS Hybrid Approach. Land Degrad. Dev. 2021, 32, 4889–4906. [Google Scholar] [CrossRef]







| Parameter Name | Parameter Value |
|---|---|
| False easting | 0.00° |
| False northing | 0.00° |
| Central meridian | 105.00°E |
| Standard parallel 1 | 25.00°N |
| Standard parallel 2 | 47.00°N |
| Scale factor | 1.00 |
| Latitude of origin | 0.00° |
| Parameter Name | Parameter Value |
|---|---|
| CPU | AMD Ryzen 7 4700U @ 2.00 GHz (8 cores 8 threads) |
| Internal storage | 16 GB (Micron 8 GB DDR4 3200 MHz × 2) |
| Operating system | Windows 10 pro 64 bit |
| Development platform | Microsoft Visual Studio 2019 |
| Programming language | C# |
| Method | Origin Coordinate System | Target Coordinate System | Test Scenario | x/Lon Error | y/Lat Error | Application | Reference |
|---|---|---|---|---|---|---|---|
| Quartic CT | Mercator projection | Lambert projection | Conversion area: 15 × 15° | ≤10.00 m | ≤10.00 m | Coordinate transformation for topographic map | [9] |
| Cubic CT | Mercator projection | Lambert projection | The control points are all on the central meridian, conversion area: 10° × 10° | ≤30.00 m | ≤30.00 m | Coordinate transformation for topographic map | [9] |
| HT | Lambert projection | WGS84 | Conversion area: 22° × 8°, grid size: 2° × 2° | ≤25.25″ | ≤19.01″ | Digitization for paper maps | [12] |
| HT | Lambert projection | WGS84 | Conversion area: 22° × 8°, grid size: 0.5° × 0.5° | ≤1.49″ | ≤1.25″ | Digitization for paper maps | [12] |
| LRA | WGS84 | UTM projection | Conversion area: 3° × 3°, grid size: 1′ × 1′ | ≤0.59 m | ≤0.27 m | Large amount of data, high efficiency requirements | [13] |
| LRA | WGS84 | UTM projection | Conversion area: 3° × 3°, grid size: 5′ × 5′ | ≤6.25 m | ≤1.07 m | Large amount of data, high efficiency requirements | [13] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Ye, S.; Gao, P.; Yao, X.; Zhao, Z. Optimization of Numerical Methods for Transforming UTM Plane Coordinates to Lambert Plane Coordinates. Remote Sens. 2022, 14, 2056. https://doi.org/10.3390/rs14092056
Wang K, Ye S, Gao P, Yao X, Zhao Z. Optimization of Numerical Methods for Transforming UTM Plane Coordinates to Lambert Plane Coordinates. Remote Sensing. 2022; 14(9):2056. https://doi.org/10.3390/rs14092056
Chicago/Turabian StyleWang, Kuangxu, Sijing Ye, Peichao Gao, Xiaochuang Yao, and Zuliang Zhao. 2022. "Optimization of Numerical Methods for Transforming UTM Plane Coordinates to Lambert Plane Coordinates" Remote Sensing 14, no. 9: 2056. https://doi.org/10.3390/rs14092056
APA StyleWang, K., Ye, S., Gao, P., Yao, X., & Zhao, Z. (2022). Optimization of Numerical Methods for Transforming UTM Plane Coordinates to Lambert Plane Coordinates. Remote Sensing, 14(9), 2056. https://doi.org/10.3390/rs14092056









