Semi-Supervised Classification for Intra-Pulse Modulation of Radar Emitter Signals Using Convolutional Neural Network
Abstract
:1. Introduction
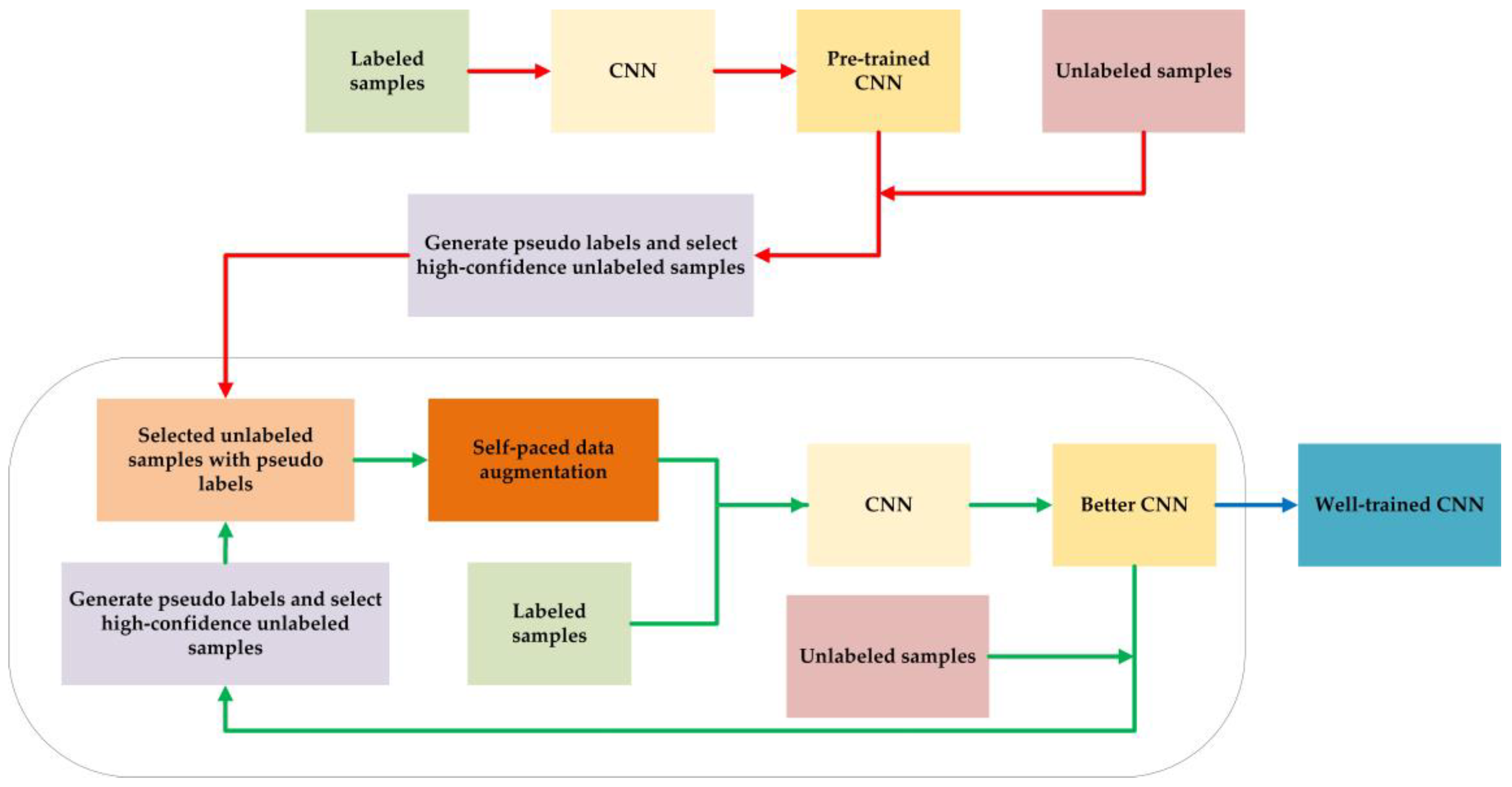
2. The Proposed Method
- (1)
- Preprocess the original raw radar emitter signal samples.
- (2)
- Generate pseudo labels of unlabeled samples and their confidence. Select the high-confidence unlabeled samples.
- (3)
- Make self-paced data augmentation for the selected unlabeled samples. Train the CNN model with the true-label samples and the selected pseudo-label samples.
2.1. The Structure of CNN
2.2. Preprocessing of Data
2.3. Generating Pseudo Labels and Selecting Unlabeled Samples
| Algorithm 1. The algorithm of accomplishing the semi-supervised classification task based on CNN and selecting samples according to the threshold of confidence | |
| Step 1 | Train a CNN model: with labeled samples . Thus, the pre-trained CNN model can be obtained. |
| Step 2 | Generate pseudo labels for unlabeled samples by the latest trained CNN. This can be written as: |
| Step 3 | Set the threshold and select high-confidence samples based on Equation (15). We can obtain a sub-collection of samples from . |
| Step 4 | Train a better CNN model: with and . |
| Step 5 | Perform Step 2 to Step 4 until the threshold meets the stop condition or other conditions. |
| Algorithm 2. The algorithm of accomplishing the semi-supervised classification task based on CNN and selecting samples by controlling the number | |
| Step 1 | Train a CNN model: with labeled samples . The pre-trained CNN model: can be obtained. |
| Step 2 | Generate pseudo labels for unlabeled samples by the latest trained CNN according to mentioned Equation (16): where refers to the latest trained CNN and refers to the pseudo label. If it is the first time to generate pseudo labels, will be . Otherwise, will be in Step 4. |
| Step 3 | Set the number of selected samples: and select samples with highest confidence. Through this process, the selected pseudo-labeled samples in this session can be obtained, where the number of samples in is . |
| Step 4 | Train a better CNN model: with and . |
| Step 5 | Perform Step 2 to Step 4 until meets the stop condition or other conditions. |
2.4. Self-Paced Data Augmentation
| Algorithm 3. The algorithm of accomplishing the semi-supervised classification task based on CNN and selecting samples by controlling the number and self-paced data augmentation | |
| Step 1 | Train a CNN model: with labeled samples . Thus, the pre-trained CNN model: can be obtained. |
| Step 2 | Generate pseudo labels for unlabeled samples by the latest trained CNN according to mentioned Equation (16): where refers to the latest trained CNN and refers to the pseudo label. If it is the first time to generate pseudo labels, will be . Otherwise, will be in Step 4. |
| Step 3 | Set the number of selected samples: and select samples with highest confidence. Through this process, the selected pseudo-labeled samples in this session can be obtained, where the number of samples in is . |
| Step 4 | Set the value of d. Augment the selected samples and normalize the results based on Equations (17) and (18). Then, the selected pseudo-labeled augmented samples can be obtained. |
| Step 5 | Train a better CNN model: with and . |
| Step 6 | Perform Step 3 to Step 5 until meets the stop condition or other conditions. |
3. Dataset and Parameters of MA-CNN
3.1. Dataset
- (1)
- For the testing dataset, we select 400 samples for each type of intra-pulse modulation at each value of SNR from the original dataset.
- (2)
- For the labeled dataset, we select 30 samples for each type of intra-pulse modulation at each value of SNR from the original dataset.
- (3)
- The labeled dataset is divided into training dataset and validation dataset. For the training dataset, we select 15 samples for each type of intra-pulse modulation at each value of SNR from the labeled dataset. Similarly, for the validation dataset, we select 15 samples for each type of intra-pulse modulation at each value of SNR from the labeled dataset.
- (4)
- For the unlabeled dataset, we select 770 samples for each type of intra-pulse modulation at each value of SNR from the original dataset.
- (5)
- The unlabeled dataset is divided into two datasets: the 1th unlabeled dataset and the 2nd unlabeled dataset. For the 1th unlabeled dataset, we select 385 samples for each type of intra-pulse modulation at each value of SNR from the unlabeled dataset. Similarly, for the 2nd unlabeled dataset, we select 385 samples for each type of intra-pulse modulation at each value of SNR from the unlabeled dataset.
3.2. Parameters of MA-CNN
4. Experiments
4.1. Implementation Details
| Algorithm 4. The framework of our proposed method | |
| Step 1 | Train a MA-CNN model: with labeled samples and obtain the pre-trained CNN model: . |
| Step 2 | Set the value of training cycles: . Set the value of and d in each round of training cycle. |
| Step 3 | Generate pseudo labels for unlabeled samples by the latest well-trained MA-CNN: and obtain the pseudo-labeled samples . Note that refers to the latest trained MA-CNN. If it is the first time to generate pseudo labels, will be . Otherwise, will be in Step 7. |
| Step 4 | Based on the value of the current round of training cycle, select the samples with highest confidence in this round. |
| Step 5 | Augment the selected pseudo-labeled samples and normalize the results based on the value of d in this round. |
| Step 6 | Train a better MA-CNN model: with the selected pseudo-labeled augmented samples and the labeled samples. |
| Step 7 | Perform Step 3 to Step 7 until the training cycle reaches . |
4.2. Experiments of Fully Supervised Baseline Methods
4.3. Experiments of the Proposed Method
5. Discussion
5.1. Ablation Study on the Value of and
5.2. Ablation Study on Data Augmentation
5.3. Ablation Study on the Strategy of Self-Paced Data Augmentation
5.4. Generality Study on Generating Pseudo Labels, Selecting Unlabeled Samples and Augmenting Self-Paced Data
5.5. Application Scenarios
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. The Classification Results of the Experiments
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9200 | 0.9375 | 0.9350 | 0.9700 | 0.9750 | 0.9650 | 0.9675 | 0.9875 | 0.9650 | 0.9650 | 0.9675 | 0.9675 | 0.9600 | 0.9602 |
| LFM | 0.2300 | 0.2125 | 0.2525 | 0.2425 | 0.2175 | 0.2650 | 0.2650 | 0.2925 | 0.3125 | 0.3775 | 0.4600 | 0.5325 | 0.5225 | 0.3217 |
| SFM | 0.7450 | 0.8475 | 0.9025 | 0.9275 | 0.9525 | 0.9550 | 0.9500 | 0.9600 | 0.9875 | 0.9775 | 0.9775 | 0.9775 | 0.9825 | 0.9340 |
| BFSK | 0.6900 | 0.7550 | 0.7900 | 0.8525 | 0.8650 | 0.8675 | 0.8725 | 0.8750 | 0.8900 | 0.9025 | 0.8825 | 0.9275 | 0.9225 | 0.8533 |
| QFSK | 0.7975 | 0.8700 | 0.9025 | 0.9275 | 0.9125 | 0.9275 | 0.9150 | 0.9050 | 0.9350 | 0.9575 | 0.9525 | 0.9625 | 0.9500 | 0.9165 |
| EQFM | 0.2900 | 0.3925 | 0.4825 | 0.5425 | 0.6450 | 0.7025 | 0.8100 | 0.8325 | 0.9025 | 0.9275 | 0.9250 | 0.9250 | 0.9425 | 0.7169 |
| DLFM | 0.2550 | 0.2550 | 0.3325 | 0.3425 | 0.4550 | 0.5375 | 0.6625 | 0.6750 | 0.7900 | 0.8125 | 0.8600 | 0.8950 | 0.8725 | 0.5958 |
| MLFM | 0.2100 | 0.1900 | 0.2125 | 0.2525 | 0.2675 | 0.2500 | 0.3325 | 0.3350 | 0.3475 | 0.4175 | 0.4400 | 0.4875 | 0.4875 | 0.3254 |
| BPSK | 0.9550 | 0.9475 | 0.9725 | 0.9625 | 0.9425 | 0.9400 | 0.9525 | 0.9550 | 0.9600 | 0.9200 | 0.9475 | 0.9525 | 0.9500 | 0.9506 |
| FRANK | 0.8575 | 0.9300 | 0.9500 | 0.9750 | 0.9875 | 0.9825 | 0.9900 | 0.9950 | 0.9775 | 0.9900 | 0.9975 | 0.9925 | 0.9925 | 0.9706 |
| LFM-BPSK | 0.2375 | 0.2300 | 0.2750 | 0.2325 | 0.2825 | 0.3150 | 0.3900 | 0.3875 | 0.4350 | 0.4850 | 0.4700 | 0.4750 | 0.4300 | 0.3573 |
| Average | 0.5625 | 0.5970 | 0.6370 | 0.6570 | 0.6820 | 0.7007 | 0.7370 | 0.7455 | 0.7730 | 0.7939 | 0.8073 | 0.8268 | 0.8193 | 0.7184 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9950 | 0.9925 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9990 |
| LFM | 0.4500 | 0.5725 | 0.6775 | 0.7725 | 0.8075 | 0.9000 | 0.9600 | 0.9700 | 0.9800 | 0.9900 | 0.9975 | 0.9975 | 0.9975 | 0.8517 |
| SFM | 0.9250 | 0.9700 | 0.9850 | 0.9925 | 0.9950 | 0.9975 | 0.9975 | 0.9950 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 0.9925 | 0.9879 |
| BFSK | 0.9800 | 0.9875 | 0.9950 | 0.9950 | 0.9975 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9954 |
| QFSK | 0.9800 | 0.9875 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9969 |
| EQFM | 0.8825 | 0.9425 | 0.9775 | 0.9825 | 0.9950 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9829 |
| DLFM | 0.5125 | 0.6000 | 0.7325 | 0.8375 | 0.9075 | 0.9300 | 0.9500 | 0.9600 | 0.9875 | 0.9900 | 0.9975 | 0.9950 | 1.0000 | 0.8769 |
| MLFM | 0.5200 | 0.5150 | 0.6400 | 0.6775 | 0.7400 | 0.8275 | 0.8800 | 0.9275 | 0.9475 | 0.9675 | 0.9675 | 0.9650 | 0.9725 | 0.8113 |
| BPSK | 0.9925 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9990 |
| FRANK | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9996 |
| LFM-BPSK | 0.4400 | 0.4425 | 0.5100 | 0.5650 | 0.6000 | 0.6375 | 0.7175 | 0.7900 | 0.8925 | 0.9275 | 0.9550 | 0.9675 | 0.9900 | 0.7258 |
| Average | 0.7884 | 0.8189 | 0.8650 | 0.8925 | 0.9130 | 0.9345 | 0.9548 | 0.9673 | 0.9823 | 0.9882 | 0.9923 | 0.9932 | 0.9957 | 0.9297 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9996 |
| LFM | 0.4425 | 0.5575 | 0.6400 | 0.7200 | 0.7525 | 0.7975 | 0.8750 | 0.9300 | 0.9600 | 0.9775 | 0.9825 | 0.9975 | 0.9950 | 0.8175 |
| SFM | 0.9150 | 0.9475 | 0.9825 | 0.9850 | 0.9975 | 0.9900 | 0.9900 | 0.9925 | 1.0000 | 0.9925 | 0.9950 | 0.9950 | 0.9875 | 0.9823 |
| BFSK | 0.9750 | 0.9800 | 0.9900 | 0.9950 | 0.9950 | 0.9950 | 0.9925 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9950 | 0.9933 |
| QFSK | 0.9675 | 0.9800 | 0.9950 | 0.9925 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9938 |
| EQFM | 0.9250 | 0.9850 | 0.9950 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9925 |
| DLFM | 0.7125 | 0.7900 | 0.8700 | 0.9225 | 0.9550 | 0.9700 | 0.9850 | 0.9875 | 1.0000 | 0.9950 | 0.9925 | 0.9975 | 1.0000 | 0.9367 |
| MLFM | 0.5600 | 0.5775 | 0.6250 | 0.6600 | 0.7325 | 0.7900 | 0.8625 | 0.9000 | 0.9150 | 0.9350 | 0.9625 | 0.9575 | 0.9800 | 0.8044 |
| BPSK | 0.9850 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9985 |
| FRANK | 0.9950 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9925 | 0.9950 | 0.9875 | 0.9971 |
| LFM-BPSK | 0.4650 | 0.4725 | 0.5300 | 0.6175 | 0.6625 | 0.7325 | 0.8325 | 0.8725 | 0.9600 | 0.9625 | 0.9725 | 0.9800 | 0.9975 | 0.7737 |
| Average | 0.8127 | 0.8439 | 0.8750 | 0.8989 | 0.9173 | 0.9339 | 0.9577 | 0.9709 | 0.9848 | 0.9870 | 0.9907 | 0.9927 | 0.9948 | 0.9354 |
Appendix A.2. The Classification Results of the Experiments
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9975 | 0.9900 | 0.9975 | 0.9975 | 0.9900 | 0.9950 | 0.9975 | 0.9925 | 0.9925 | 0.9900 | 0.9925 | 0.9925 | 0.9900 | 0.9935 |
| LFM | 0.4075 | 0.5025 | 0.5450 | 0.6300 | 0.6300 | 0.6875 | 0.7675 | 0.7900 | 0.7700 | 0.7950 | 0.8050 | 0.8350 | 0.8375 | 0.6925 |
| SFM | 0.8600 | 0.9375 | 0.9700 | 0.9800 | 0.9875 | 0.9975 | 0.9925 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9975 | 0.9781 |
| BFSK | 0.9675 | 0.9750 | 0.9700 | 0.9850 | 0.9875 | 0.9950 | 0.9975 | 0.9950 | 0.9975 | 0.9950 | 0.9950 | 0.9925 | 0.9975 | 0.9885 |
| QFSK | 0.9825 | 0.9750 | 0.9900 | 0.9850 | 0.9950 | 0.9925 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9938 |
| EQFM | 0.7850 | 0.8675 | 0.9300 | 0.9500 | 0.9925 | 0.9775 | 0.9925 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9610 |
| DLFM | 0.3900 | 0.4225 | 0.5500 | 0.6000 | 0.6975 | 0.7875 | 0.8325 | 0.8650 | 0.8975 | 0.8850 | 0.9325 | 0.9175 | 0.9000 | 0.7444 |
| MLFM | 0.5000 | 0.5250 | 0.6175 | 0.6675 | 0.6125 | 0.6600 | 0.6475 | 0.6325 | 0.6650 | 0.6425 | 0.6450 | 0.6525 | 0.5975 | 0.6204 |
| BPSK | 0.9925 | 0.9900 | 0.9925 | 0.9950 | 0.9950 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9950 | 0.9965 |
| FRANK | 0.9825 | 0.9950 | 0.9975 | 1.0000 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 0.9950 | 0.9975 | 0.9925 | 0.9975 | 0.9850 | 0.9950 |
| LFM-BPSK | 0.2725 | 0.3600 | 0.3900 | 0.4700 | 0.5725 | 0.6325 | 0.7075 | 0.7700 | 0.8325 | 0.8750 | 0.8875 | 0.8825 | 0.9400 | 0.6610 |
| Average | 0.7398 | 0.7764 | 0.8136 | 0.8418 | 0.8595 | 0.8839 | 0.9030 | 0.9125 | 0.9225 | 0.9255 | 0.9318 | 0.9334 | 0.9309 | 0.8750 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9998 |
| LFM | 0.2975 | 0.3475 | 0.3500 | 0.3775 | 0.4400 | 0.4975 | 0.5075 | 0.5350 | 0.6025 | 0.6775 | 0.6975 | 0.7475 | 0.7375 | 0.5242 |
| SFM | 0.9075 | 0.9525 | 0.9725 | 0.9850 | 0.9900 | 0.9975 | 0.9900 | 0.9900 | 1.0000 | 0.9950 | 0.9975 | 0.9975 | 0.9925 | 0.9821 |
| BFSK | 0.8400 | 0.9400 | 0.9550 | 0.9750 | 0.9775 | 0.9875 | 0.9925 | 0.9850 | 1.0000 | 0.9950 | 0.9900 | 0.9975 | 0.9925 | 0.9713 |
| QFSK | 0.9750 | 0.9850 | 1.0000 | 0.9925 | 0.9950 | 0.9900 | 0.9950 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9940 |
| EQFM | 0.8550 | 0.9475 | 0.9650 | 0.9850 | 0.9975 | 0.9875 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9798 |
| DLFM | 0.3600 | 0.4500 | 0.5900 | 0.6625 | 0.7625 | 0.8275 | 0.8950 | 0.9175 | 0.9375 | 0.9550 | 0.9800 | 0.9700 | 0.9625 | 0.7900 |
| MLFM | 0.5275 | 0.5125 | 0.6075 | 0.6575 | 0.6175 | 0.6750 | 0.7275 | 0.6900 | 0.6575 | 0.6650 | 0.7250 | 0.7325 | 0.6375 | 0.6487 |
| BPSK | 0.9750 | 0.9825 | 0.9900 | 0.9875 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9948 |
| FRANK | 0.9700 | 0.9875 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9950 | 0.9975 | 0.9975 | 0.9925 | 0.9948 |
| LFM-BPSK | 0.3275 | 0.4125 | 0.5575 | 0.6325 | 0.7375 | 0.7700 | 0.8250 | 0.8850 | 0.9100 | 0.9350 | 0.9600 | 0.9625 | 0.9700 | 0.7604 |
| Average | 0.7305 | 0.7741 | 0.8168 | 0.8411 | 0.8650 | 0.8845 | 0.9030 | 0.9089 | 0.9186 | 0.9286 | 0.9407 | 0.9459 | 0.9350 | 0.8764 |
Appendix A.3. The Classification Results of the Experiments
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9750 | 0.9675 | 0.9625 | 0.9625 | 0.9650 | 0.9750 | 0.9675 | 0.9800 | 0.9700 | 0.9550 | 0.9525 | 0.9625 | 0.9500 | 0.9650 |
| LFM | 0.4725 | 0.4925 | 0.5675 | 0.6625 | 0.7075 | 0.7325 | 0.7600 | 0.7825 | 0.7675 | 0.8000 | 0.7875 | 0.8300 | 0.7975 | 0.7046 |
| SFM | 0.8925 | 0.9400 | 0.9700 | 0.9775 | 0.9875 | 0.9900 | 0.9850 | 0.9900 | 0.9950 | 0.9975 | 0.9975 | 0.9950 | 0.9925 | 0.9777 |
| BFSK | 0.9425 | 0.9675 | 0.9925 | 0.9750 | 0.9900 | 0.9875 | 0.9950 | 0.9950 | 0.9950 | 0.9950 | 0.9975 | 0.9950 | 0.9950 | 0.9863 |
| QFSK | 0.9500 | 0.9750 | 0.9850 | 0.9775 | 0.9875 | 0.9925 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 0.9890 |
| EQFM | 0.8800 | 0.9525 | 0.9625 | 0.9850 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9829 |
| DLFM | 0.3350 | 0.3775 | 0.5600 | 0.6200 | 0.6975 | 0.8100 | 0.8850 | 0.9025 | 0.9150 | 0.9100 | 0.9250 | 0.9325 | 0.9125 | 0.7525 |
| MLFM | 0.4250 | 0.4775 | 0.5575 | 0.6400 | 0.5800 | 0.6450 | 0.6475 | 0.6975 | 0.6525 | 0.6625 | 0.6500 | 0.6825 | 0.6175 | 0.6104 |
| BPSK | 0.9325 | 0.9525 | 0.9500 | 0.9600 | 0.9775 | 0.9675 | 0.9875 | 0.9875 | 0.9875 | 0.9800 | 0.9850 | 0.9825 | 0.9700 | 0.9708 |
| FRANK | 0.9675 | 0.9825 | 0.9825 | 0.9975 | 0.9975 | 0.9950 | 0.9950 | 0.9975 | 0.9975 | 0.9950 | 0.9975 | 0.9975 | 0.9975 | 0.9923 |
| LFM-BPSK | 0.2675 | 0.2975 | 0.3675 | 0.4300 | 0.4925 | 0.5875 | 0.6550 | 0.7500 | 0.8400 | 0.8825 | 0.8925 | 0.9225 | 0.9475 | 0.6410 |
| Average | 0.7309 | 0.7620 | 0.8052 | 0.8352 | 0.8530 | 0.8800 | 0.8977 | 0.9161 | 0.9200 | 0.9252 | 0.9257 | 0.9364 | 0.9255 | 0.8702 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9750 | 0.9650 | 0.9675 | 0.9575 | 0.9600 | 0.9600 | 0.9700 | 0.9875 | 0.9625 | 0.9425 | 0.9575 | 0.9650 | 0.9500 | 0.9631 |
| LFM | 0.3650 | 0.4200 | 0.4350 | 0.4550 | 0.5300 | 0.5425 | 0.6075 | 0.6525 | 0.7100 | 0.7500 | 0.7725 | 0.8100 | 0.8225 | 0.6056 |
| SFM | 0.8400 | 0.9050 | 0.9450 | 0.9550 | 0.9750 | 0.9900 | 0.9775 | 0.9900 | 1.0000 | 0.9925 | 0.9950 | 0.9975 | 0.9850 | 0.9652 |
| BFSK | 0.9300 | 0.9225 | 0.9200 | 0.9525 | 0.9625 | 0.9700 | 0.9800 | 0.9775 | 0.9875 | 0.9850 | 0.9800 | 0.9875 | 0.9825 | 0.9644 |
| QFSK | 0.8950 | 0.9150 | 0.9500 | 0.9300 | 0.9550 | 0.9800 | 0.9850 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 0.9694 |
| EQFM | 0.8700 | 0.9400 | 0.9575 | 0.9775 | 0.9950 | 0.9775 | 0.9950 | 0.9950 | 1.0000 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 0.9769 |
| DLFM | 0.2925 | 0.3300 | 0.5450 | 0.6500 | 0.6925 | 0.7550 | 0.8375 | 0.8775 | 0.9025 | 0.8975 | 0.9150 | 0.9350 | 0.9325 | 0.7356 |
| MLFM | 0.4300 | 0.4650 | 0.5600 | 0.5850 | 0.5250 | 0.6450 | 0.6050 | 0.6675 | 0.6100 | 0.6375 | 0.6625 | 0.6550 | 0.6100 | 0.5890 |
| BPSK | 0.9500 | 0.9600 | 0.9550 | 0.9725 | 0.9625 | 0.9700 | 0.9875 | 0.9850 | 0.9825 | 0.9925 | 0.9950 | 0.9825 | 0.9875 | 0.9756 |
| FRANK | 0.9400 | 0.9750 | 0.9950 | 0.9875 | 0.9925 | 0.9900 | 0.9850 | 0.9900 | 0.9850 | 0.9725 | 0.9675 | 0.9550 | 0.9750 | 0.9777 |
| LFM-BPSK | 0.2925 | 0.3850 | 0.4850 | 0.5825 | 0.6600 | 0.7375 | 0.7700 | 0.8275 | 0.8550 | 0.8675 | 0.8650 | 0.9125 | 0.9125 | 0.7040 |
| Average | 0.7073 | 0.7439 | 0.7923 | 0.8186 | 0.8373 | 0.8652 | 0.8818 | 0.9043 | 0.9084 | 0.9123 | 0.9186 | 0.9270 | 0.9234 | 0.8570 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 0.9950 | 1.0000 | 0.9950 | 0.9800 | 0.9750 | 0.9925 | 0.9750 | 0.9927 |
| LFM | 0.3250 | 0.3600 | 0.3850 | 0.4875 | 0.5575 | 0.5400 | 0.6200 | 0.6800 | 0.6750 | 0.7325 | 0.7375 | 0.7725 | 0.7650 | 0.5875 |
| SFM | 0.9175 | 0.9375 | 0.9775 | 0.9900 | 0.9925 | 0.9975 | 0.9950 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9950 | 0.9842 |
| BFSK | 0.9725 | 0.9700 | 0.9850 | 0.9825 | 0.9950 | 0.9925 | 0.9850 | 0.9950 | 0.9975 | 0.9975 | 0.9950 | 0.9925 | 0.9900 | 0.9885 |
| QFSK | 0.9000 | 0.9250 | 0.9525 | 0.9775 | 0.9850 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9790 |
| EQFM | 0.9175 | 0.9700 | 0.9725 | 0.9925 | 0.9975 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9879 |
| DLFM | 0.3300 | 0.4000 | 0.5250 | 0.5925 | 0.6900 | 0.7275 | 0.7800 | 0.8100 | 0.8875 | 0.8900 | 0.9225 | 0.9525 | 0.9500 | 0.7275 |
| MLFM | 0.4475 | 0.4975 | 0.5775 | 0.6750 | 0.7025 | 0.7125 | 0.7625 | 0.7850 | 0.8050 | 0.8075 | 0.8650 | 0.8575 | 0.7900 | 0.7142 |
| BPSK | 0.9200 | 0.9175 | 0.9375 | 0.9525 | 0.9425 | 0.9500 | 0.9650 | 0.9725 | 0.9575 | 0.9500 | 0.9500 | 0.9350 | 0.9250 | 0.9442 |
| FRANK | 0.9750 | 0.9975 | 0.9925 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9965 |
| LFM-BPSK | 0.3000 | 0.3925 | 0.4375 | 0.5450 | 0.5950 | 0.6800 | 0.7650 | 0.8375 | 0.8700 | 0.9125 | 0.9375 | 0.9400 | 0.9650 | 0.7060 |
| Average | 0.7275 | 0.7607 | 0.7945 | 0.8357 | 0.8591 | 0.8718 | 0.8964 | 0.9157 | 0.9261 | 0.9334 | 0.9439 | 0.9491 | 0.9414 | 0.8735 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9950 | 0.9975 | 0.9975 | 0.9925 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9950 | 0.9950 | 0.9975 | 0.9950 | 0.9967 |
| LFM | 0.2225 | 0.3350 | 0.3325 | 0.3900 | 0.4475 | 0.5550 | 0.6250 | 0.6675 | 0.6850 | 0.7825 | 0.7900 | 0.8000 | 0.8250 | 0.5737 |
| SFM | 0.8600 | 0.9275 | 0.9475 | 0.9700 | 0.9925 | 0.9950 | 0.9950 | 0.9925 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 0.9900 | 0.9742 |
| BFSK | 0.8175 | 0.9000 | 0.9100 | 0.9550 | 0.9675 | 0.9825 | 0.9850 | 0.9850 | 0.9850 | 0.9750 | 0.9850 | 0.9775 | 0.9800 | 0.9542 |
| QFSK | 0.9975 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9950 | 0.9985 |
| EQFM | 0.8575 | 0.9225 | 0.9525 | 0.9725 | 0.9925 | 0.9750 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9742 |
| DLFM | 0.4050 | 0.3825 | 0.5050 | 0.6175 | 0.6975 | 0.7400 | 0.8475 | 0.8650 | 0.9275 | 0.9275 | 0.9625 | 0.9575 | 0.9550 | 0.7531 |
| MLFM | 0.4475 | 0.4925 | 0.5575 | 0.6475 | 0.6675 | 0.6975 | 0.7325 | 0.7450 | 0.7800 | 0.8300 | 0.8450 | 0.8250 | 0.8050 | 0.6979 |
| BPSK | 0.9825 | 0.9875 | 0.9775 | 0.9650 | 0.9750 | 0.9775 | 0.9925 | 0.9950 | 0.9975 | 1.0000 | 0.9975 | 0.9950 | 1.0000 | 0.9879 |
| FRANK | 0.9775 | 0.9950 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9969 |
| LFM-BPSK | 0.2325 | 0.3275 | 0.4175 | 0.5450 | 0.6275 | 0.6825 | 0.7900 | 0.7950 | 0.8775 | 0.9300 | 0.9400 | 0.9375 | 0.9600 | 0.6971 |
| Average | 0.7086 | 0.7511 | 0.7809 | 0.8227 | 0.8509 | 0.8730 | 0.9057 | 0.9132 | 0.9314 | 0.9486 | 0.9559 | 0.9536 | 0.9550 | 0.8731 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9900 | 0.9979 |
| LFM | 0.2625 | 0.3825 | 0.4275 | 0.5300 | 0.5975 | 0.6400 | 0.7300 | 0.7275 | 0.7600 | 0.8000 | 0.8050 | 0.8175 | 0.8175 | 0.6383 |
| SFM | 0.8925 | 0.9475 | 0.9750 | 0.9800 | 0.9875 | 1.0000 | 0.9950 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 0.9900 | 0.9813 |
| BFSK | 0.9175 | 0.9300 | 0.9500 | 0.9750 | 0.9825 | 0.9850 | 0.9900 | 0.9800 | 0.9975 | 0.9925 | 0.9875 | 0.9900 | 0.9850 | 0.9740 |
| QFSK | 0.9900 | 0.9925 | 0.9950 | 0.9950 | 0.9950 | 0.9900 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9967 |
| EQFM | 0.9075 | 0.9400 | 0.9725 | 0.9825 | 0.9975 | 0.9925 | 0.9975 | 1.0000 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 0.9835 |
| DLFM | 0.3550 | 0.4375 | 0.6050 | 0.6800 | 0.7675 | 0.8725 | 0.9050 | 0.9500 | 0.9875 | 0.9950 | 0.9925 | 0.9950 | 0.9800 | 0.8094 |
| MLFM | 0.5825 | 0.5625 | 0.6725 | 0.6750 | 0.7050 | 0.7175 | 0.7725 | 0.7375 | 0.7250 | 0.7400 | 0.7450 | 0.7600 | 0.6725 | 0.6975 |
| BPSK | 0.9550 | 0.9675 | 0.9750 | 0.9950 | 0.9950 | 0.9950 | 1.0000 | 0.9975 | 0.9950 | 0.9975 | 0.9875 | 0.9725 | 0.9675 | 0.9846 |
| FRANK | 0.9700 | 0.9825 | 0.9900 | 0.9900 | 0.9950 | 1.0000 | 0.9950 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 0.9925 | 0.9927 |
| LFM-BPSK | 0.3250 | 0.4075 | 0.4400 | 0.5175 | 0.6050 | 0.6900 | 0.7675 | 0.8250 | 0.8850 | 0.9200 | 0.9150 | 0.9450 | 0.9575 | 0.7077 |
| Average | 0.7414 | 0.7773 | 0.8182 | 0.8470 | 0.8752 | 0.8982 | 0.9225 | 0.9282 | 0.9407 | 0.9489 | 0.9480 | 0.9523 | 0.9411 | 0.8876 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 0.9875 | 0.9825 | 0.9950 | 0.9775 | 0.9948 |
| LFM | 0.3325 | 0.4375 | 0.5150 | 0.5600 | 0.6125 | 0.6850 | 0.7500 | 0.7550 | 0.7925 | 0.8075 | 0.8075 | 0.8275 | 0.8200 | 0.6694 |
| SFM | 0.8175 | 0.9100 | 0.9475 | 0.9800 | 0.9875 | 0.9975 | 0.9975 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 0.9950 | 0.9708 |
| BFSK | 0.9275 | 0.9575 | 0.9750 | 0.9925 | 0.9950 | 0.9900 | 0.9925 | 0.9975 | 1.0000 | 0.9950 | 0.9975 | 0.9900 | 0.9975 | 0.9852 |
| QFSK | 0.9925 | 0.9900 | 0.9925 | 0.9950 | 0.9950 | 0.9925 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9967 |
| EQFM | 0.8675 | 0.9450 | 0.9775 | 0.9800 | 0.9975 | 0.9900 | 0.9975 | 0.9900 | 0.9900 | 1.0000 | 0.9950 | 0.9975 | 1.0000 | 0.9790 |
| DLFM | 0.4075 | 0.4475 | 0.5950 | 0.6750 | 0.7450 | 0.8475 | 0.8800 | 0.9100 | 0.9450 | 0.9200 | 0.9500 | 0.9750 | 0.9550 | 0.7887 |
| MLFM | 0.5625 | 0.5125 | 0.5950 | 0.5900 | 0.5750 | 0.6325 | 0.6450 | 0.6900 | 0.6525 | 0.7100 | 0.7275 | 0.7200 | 0.6550 | 0.6360 |
| BPSK | 0.9325 | 0.9525 | 0.9775 | 0.9800 | 0.9875 | 0.9800 | 0.9875 | 0.9950 | 0.9975 | 0.9925 | 0.9975 | 0.9975 | 0.9975 | 0.9827 |
| FRANK | 0.9850 | 0.9925 | 0.9950 | 1.0000 | 0.9925 | 0.9950 | 0.9975 | 0.9925 | 0.9950 | 0.9950 | 0.9950 | 0.9975 | 1.0000 | 0.9948 |
| LFM-BPSK | 0.3575 | 0.3900 | 0.4600 | 0.5850 | 0.6450 | 0.7250 | 0.7750 | 0.8275 | 0.8700 | 0.9125 | 0.9150 | 0.9325 | 0.9500 | 0.7188 |
| Average | 0.7436 | 0.7757 | 0.8209 | 0.8489 | 0.8666 | 0.8941 | 0.9109 | 0.9227 | 0.9307 | 0.9380 | 0.9425 | 0.9484 | 0.9407 | 0.8834 |
Appendix A.4. The Classification Results of the Experiments
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9996 |
| LFM | 0.1725 | 0.2175 | 0.2200 | 0.2475 | 0.3425 | 0.3850 | 0.4425 | 0.4875 | 0.5275 | 0.5475 | 0.5875 | 0.6050 | 0.6050 | 0.4144 |
| SFM | 0.8950 | 0.9350 | 0.9525 | 0.9750 | 0.9675 | 0.9800 | 0.9825 | 0.9850 | 1.0000 | 0.9900 | 0.9900 | 0.9875 | 0.9825 | 0.9710 |
| BFSK | 0.9700 | 0.9825 | 0.9700 | 0.9850 | 0.9975 | 0.9900 | 0.9925 | 0.9900 | 1.0000 | 0.9925 | 0.9925 | 0.9975 | 0.9950 | 0.9888 |
| QFSK | 0.9750 | 0.9750 | 0.9775 | 0.9675 | 0.9950 | 0.9925 | 0.9975 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9902 |
| EQFM | 0.8125 | 0.8925 | 0.9500 | 0.9775 | 0.9900 | 0.9850 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9692 |
| DLFM | 0.3650 | 0.3950 | 0.5000 | 0.6325 | 0.7525 | 0.8200 | 0.8950 | 0.9025 | 0.9575 | 0.9575 | 0.9875 | 0.9825 | 0.9925 | 0.7800 |
| MLFM | 0.4600 | 0.4300 | 0.4550 | 0.4900 | 0.4900 | 0.5150 | 0.4575 | 0.4775 | 0.4275 | 0.5125 | 0.4800 | 0.5175 | 0.5000 | 0.4779 |
| BPSK | 0.9625 | 0.9800 | 0.9825 | 0.9850 | 0.9875 | 0.9700 | 0.9900 | 0.9925 | 0.9825 | 0.9800 | 0.9800 | 0.9900 | 0.9950 | 0.9829 |
| FRANK | 0.9800 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9981 |
| LFM-BPSK | 0.1150 | 0.0825 | 0.1450 | 0.1450 | 0.1450 | 0.1625 | 0.1725 | 0.2700 | 0.2600 | 0.2875 | 0.3050 | 0.3475 | 0.3375 | 0.2135 |
| Average | 0.7005 | 0.7170 | 0.7409 | 0.7641 | 0.7880 | 0.8000 | 0.8114 | 0.8273 | 0.8318 | 0.8423 | 0.8475 | 0.8570 | 0.8552 | 0.7987 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9950 | 0.9875 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9977 |
| LFM | 0.3125 | 0.3225 | 0.3750 | 0.3800 | 0.4025 | 0.4025 | 0.4725 | 0.4450 | 0.4700 | 0.4900 | 0.4775 | 0.4875 | 0.4750 | 0.4240 |
| SFM | 0.9225 | 0.9500 | 0.9725 | 0.9825 | 0.9825 | 0.9900 | 0.9825 | 0.9975 | 1.0000 | 0.9900 | 0.9950 | 0.9900 | 0.9875 | 0.9802 |
| BFSK | 0.9125 | 0.9600 | 0.9625 | 0.9925 | 0.9950 | 0.9950 | 0.9975 | 0.9900 | 0.9975 | 0.9950 | 0.9925 | 0.9975 | 0.9950 | 0.9833 |
| QFSK | 0.9800 | 0.9875 | 0.9950 | 0.9900 | 1.0000 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9958 |
| EQFM | 0.8425 | 0.9025 | 0.9475 | 0.9675 | 0.9950 | 0.9775 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9715 |
| DLFM | 0.2475 | 0.2800 | 0.3925 | 0.5025 | 0.6375 | 0.7475 | 0.8275 | 0.8825 | 0.9425 | 0.9700 | 0.9875 | 0.9950 | 0.9975 | 0.7238 |
| MLFM | 0.4725 | 0.4675 | 0.4225 | 0.4675 | 0.4325 | 0.4500 | 0.4475 | 0.4350 | 0.4125 | 0.4525 | 0.4775 | 0.5150 | 0.4725 | 0.4558 |
| BPSK | 0.9300 | 0.9400 | 0.9425 | 0.9375 | 0.9550 | 0.9350 | 0.9625 | 0.9375 | 0.9425 | 0.9450 | 0.9300 | 0.9200 | 0.9225 | 0.9385 |
| FRANK | 0.9725 | 0.9950 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9971 |
| LFM-BPSK | 0.1925 | 0.1850 | 0.2300 | 0.2175 | 0.2325 | 0.2600 | 0.2925 | 0.3525 | 0.4350 | 0.3900 | 0.4225 | 0.4925 | 0.4125 | 0.3165 |
| Average | 0.7073 | 0.7252 | 0.7482 | 0.7668 | 0.7843 | 0.7959 | 0.8161 | 0.8218 | 0.8361 | 0.8393 | 0.8439 | 0.8543 | 0.8420 | 0.7986 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| LFM | 0.2900 | 0.2750 | 0.3300 | 0.3500 | 0.3325 | 0.3325 | 0.3450 | 0.3750 | 0.4425 | 0.4275 | 0.4725 | 0.5000 | 0.5025 | 0.3827 |
| SFM | 0.8825 | 0.9325 | 0.9550 | 0.9775 | 0.9800 | 0.9900 | 0.9825 | 0.9875 | 1.0000 | 0.9925 | 0.9925 | 0.9875 | 0.9825 | 0.9725 |
| BFSK | 0.9425 | 0.9700 | 0.9850 | 0.9925 | 0.9950 | 0.9950 | 0.9975 | 0.9925 | 1.0000 | 0.9950 | 1.0000 | 0.9975 | 0.9950 | 0.9890 |
| QFSK | 0.9950 | 0.9900 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9985 |
| EQFM | 0.8225 | 0.9125 | 0.9450 | 0.9750 | 0.9975 | 0.9850 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9719 |
| DLFM | 0.1775 | 0.2050 | 0.3500 | 0.4800 | 0.5800 | 0.6900 | 0.7650 | 0.8275 | 0.9075 | 0.9350 | 0.9725 | 0.9925 | 0.9675 | 0.6808 |
| MLFM | 0.5825 | 0.5225 | 0.5200 | 0.5100 | 0.4825 | 0.4700 | 0.4250 | 0.4450 | 0.3975 | 0.4575 | 0.4250 | 0.4375 | 0.4050 | 0.4677 |
| BPSK | 0.9775 | 0.9825 | 0.9875 | 0.9850 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 0.9937 |
| FRANK | 0.9750 | 0.9925 | 0.9950 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9967 |
| LFM-BPSK | 0.1875 | 0.1850 | 0.2600 | 0.2550 | 0.3100 | 0.3525 | 0.3475 | 0.4075 | 0.4000 | 0.4125 | 0.4225 | 0.4150 | 0.3900 | 0.3342 |
| Average | 0.7120 | 0.7243 | 0.7570 | 0.7745 | 0.7884 | 0.8009 | 0.8052 | 0.8211 | 0.8314 | 0.8382 | 0.8439 | 0.8482 | 0.8402 | 0.7989 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9992 |
| LFM | 0.3075 | 0.2650 | 0.2975 | 0.2850 | 0.3750 | 0.3300 | 0.3275 | 0.3700 | 0.3950 | 0.4375 | 0.4500 | 0.4525 | 0.4475 | 0.3646 |
| SFM | 0.8825 | 0.9175 | 0.9675 | 0.9750 | 0.9775 | 0.9850 | 0.9875 | 0.9950 | 1.0000 | 0.9950 | 1.0000 | 0.9925 | 0.9875 | 0.9740 |
| BFSK | 0.8550 | 0.9200 | 0.9400 | 0.9550 | 0.9800 | 0.9900 | 0.9925 | 0.9725 | 0.9950 | 0.9900 | 0.9900 | 0.9925 | 0.9925 | 0.9665 |
| QFSK | 0.9825 | 0.9925 | 0.9950 | 0.9850 | 0.9850 | 0.9975 | 0.9925 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9946 |
| EQFM | 0.8150 | 0.9025 | 0.9425 | 0.9675 | 0.9950 | 0.9825 | 0.9975 | 0.9975 | 0.9975 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 0.9685 |
| DLFM | 0.0875 | 0.0750 | 0.1600 | 0.3150 | 0.4550 | 0.6175 | 0.7425 | 0.8100 | 0.8875 | 0.8950 | 0.9500 | 0.9675 | 0.9600 | 0.6094 |
| MLFM | 0.5025 | 0.5325 | 0.6075 | 0.6200 | 0.6050 | 0.6350 | 0.6675 | 0.6600 | 0.5875 | 0.6825 | 0.6775 | 0.6550 | 0.6350 | 0.6206 |
| BPSK | 0.9900 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9985 |
| FRANK | 0.9600 | 0.9850 | 0.9850 | 0.9875 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9931 |
| LFM-BPSK | 0.1425 | 0.1600 | 0.1800 | 0.2200 | 0.2100 | 0.2575 | 0.2875 | 0.3400 | 0.3625 | 0.3875 | 0.4125 | 0.4625 | 0.4325 | 0.2965 |
| Average | 0.6836 | 0.7041 | 0.7336 | 0.7552 | 0.7800 | 0.7993 | 0.8177 | 0.8314 | 0.8384 | 0.8532 | 0.8614 | 0.8657 | 0.8593 | 0.7987 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9998 |
| LFM | 0.1875 | 0.1850 | 0.2600 | 0.2650 | 0.3325 | 0.3450 | 0.3925 | 0.3900 | 0.4175 | 0.4150 | 0.4725 | 0.4700 | 0.5175 | 0.3577 |
| SFM | 0.9250 | 0.9450 | 0.9800 | 0.9800 | 0.9800 | 0.9925 | 0.9825 | 0.9925 | 1.0000 | 0.9950 | 1.0000 | 0.9900 | 0.9875 | 0.9808 |
| BFSK | 0.9525 | 0.9700 | 0.9750 | 0.9975 | 0.9950 | 0.9900 | 0.9950 | 0.9950 | 0.9975 | 0.9975 | 0.9950 | 0.9950 | 0.9975 | 0.9887 |
| QFSK | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9998 |
| EQFM | 0.8100 | 0.9100 | 0.9375 | 0.9675 | 0.9875 | 0.9900 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9694 |
| DLFM | 0.1375 | 0.2050 | 0.3600 | 0.4825 | 0.5950 | 0.7300 | 0.8125 | 0.8675 | 0.9275 | 0.9275 | 0.9650 | 0.9900 | 0.9875 | 0.6913 |
| MLFM | 0.5500 | 0.5800 | 0.6200 | 0.6225 | 0.5825 | 0.6075 | 0.6100 | 0.6050 | 0.5800 | 0.6325 | 0.6025 | 0.6325 | 0.5800 | 0.6004 |
| BPSK | 0.9800 | 0.9925 | 0.9950 | 0.9950 | 0.9975 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9965 |
| FRANK | 0.9775 | 0.9950 | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9973 |
| LFM-BPSK | 0.2475 | 0.2325 | 0.2700 | 0.2975 | 0.2900 | 0.3450 | 0.3400 | 0.4125 | 0.3850 | 0.4250 | 0.3925 | 0.4400 | 0.4375 | 0.3473 |
| Average | 0.7057 | 0.7286 | 0.7632 | 0.7825 | 0.7961 | 0.8180 | 0.8298 | 0.8420 | 0.8461 | 0.8539 | 0.8570 | 0.8652 | 0.8643 | 0.8117 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9900 | 0.9875 | 0.9900 | 0.9875 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 0.9950 | 0.9850 | 0.9500 | 0.9325 | 0.9856 |
| LFM | 0.3850 | 0.3275 | 0.4050 | 0.3600 | 0.3625 | 0.3200 | 0.3650 | 0.3600 | 0.4300 | 0.4300 | 0.4300 | 0.4425 | 0.4725 | 0.3915 |
| SFM | 0.8400 | 0.9100 | 0.9400 | 0.9575 | 0.9775 | 0.9775 | 0.9700 | 0.9825 | 1.0000 | 0.9875 | 0.9850 | 0.9850 | 0.9825 | 0.9612 |
| BFSK | 0.9225 | 0.9375 | 0.9525 | 0.9850 | 0.9800 | 0.9850 | 0.9875 | 0.9850 | 0.9975 | 0.9925 | 0.9900 | 0.9950 | 0.9925 | 0.9771 |
| QFSK | 0.9575 | 0.9575 | 0.9775 | 0.9750 | 0.9850 | 0.9825 | 0.9850 | 0.9975 | 0.9925 | 0.9925 | 1.0000 | 1.0000 | 1.0000 | 0.9848 |
| EQFM | 0.9125 | 0.9550 | 0.9650 | 0.9725 | 0.9975 | 0.9900 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9840 |
| DLFM | 0.2550 | 0.2925 | 0.5050 | 0.6500 | 0.7650 | 0.8800 | 0.9350 | 0.9600 | 0.9925 | 0.9875 | 0.9925 | 1.0000 | 1.0000 | 0.7858 |
| MLFM | 0.4025 | 0.4625 | 0.5400 | 0.5750 | 0.5650 | 0.6075 | 0.6200 | 0.6025 | 0.6150 | 0.6450 | 0.6275 | 0.6725 | 0.6375 | 0.5825 |
| BPSK | 0.9525 | 0.9700 | 0.9900 | 0.9925 | 0.9950 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9919 |
| FRANK | 0.9800 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9981 |
| LFM-BPSK | 0.2175 | 0.2275 | 0.2325 | 0.2725 | 0.3325 | 0.3700 | 0.4125 | 0.4725 | 0.4900 | 0.4550 | 0.5150 | 0.5750 | 0.5550 | 0.3944 |
| Average | 0.7105 | 0.7295 | 0.7723 | 0.7934 | 0.8145 | 0.8280 | 0.8427 | 0.8509 | 0.8652 | 0.8623 | 0.8659 | 0.8745 | 0.8702 | 0.8215 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9925 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9985 |
| LFM | 0.2350 | 0.2150 | 0.2300 | 0.2450 | 0.2750 | 0.2850 | 0.3375 | 0.3525 | 0.3575 | 0.4150 | 0.4125 | 0.4425 | 0.4150 | 0.3244 |
| SFM | 0.8950 | 0.9425 | 0.9725 | 0.9775 | 0.9825 | 0.9950 | 0.9825 | 0.9900 | 1.0000 | 0.9950 | 0.9975 | 0.9875 | 0.9825 | 0.9769 |
| BFSK | 0.8800 | 0.9350 | 0.9600 | 0.9850 | 0.9950 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 0.9975 | 0.9975 | 0.9975 | 0.9796 |
| QFSK | 0.9950 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9988 |
| EQFM | 0.8325 | 0.8725 | 0.9325 | 0.9600 | 0.9825 | 0.9675 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 0.9646 |
| DLFM | 0.1775 | 0.1875 | 0.2975 | 0.4300 | 0.5175 | 0.6900 | 0.7925 | 0.8525 | 0.9250 | 0.9600 | 0.9675 | 0.9825 | 0.9975 | 0.6752 |
| MLFM | 0.5275 | 0.5450 | 0.6675 | 0.7200 | 0.7125 | 0.7750 | 0.8250 | 0.8350 | 0.8675 | 0.8900 | 0.9025 | 0.8900 | 0.8900 | 0.7729 |
| BPSK | 0.9775 | 0.9850 | 0.9975 | 0.9875 | 0.9925 | 0.9900 | 0.9950 | 0.9975 | 0.9925 | 0.9975 | 0.9950 | 0.9925 | 0.9975 | 0.9921 |
| FRANK | 0.9850 | 0.9975 | 0.9975 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9971 |
| LFM-BPSK | 0.3400 | 0.3250 | 0.4025 | 0.4000 | 0.3725 | 0.4725 | 0.4800 | 0.5100 | 0.5000 | 0.5400 | 0.5825 | 0.6050 | 0.5775 | 0.4698 |
| Average | 0.7125 | 0.7266 | 0.7686 | 0.7905 | 0.8025 | 0.8332 | 0.8550 | 0.8664 | 0.8764 | 0.8907 | 0.8957 | 0.8995 | 0.8961 | 0.8318 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9996 |
| LFM | 0.3300 | 0.2650 | 0.2850 | 0.2675 | 0.2950 | 0.2350 | 0.3075 | 0.2575 | 0.2825 | 0.2875 | 0.3000 | 0.2900 | 0.2900 | 0.2840 |
| SFM | 0.8400 | 0.9075 | 0.9300 | 0.9600 | 0.9700 | 0.9825 | 0.9775 | 0.9900 | 0.9975 | 0.9875 | 0.9850 | 0.9825 | 0.9800 | 0.9608 |
| BFSK | 0.9125 | 0.9425 | 0.9575 | 0.9850 | 0.9800 | 0.9875 | 0.9950 | 0.9875 | 0.9925 | 0.9900 | 0.9900 | 0.9950 | 0.9950 | 0.9777 |
| QFSK | 0.9675 | 0.9675 | 0.9850 | 0.9825 | 0.9950 | 0.9850 | 0.9875 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 0.9975 | 0.9892 |
| EQFM | 0.7850 | 0.8950 | 0.9600 | 0.9650 | 0.9975 | 0.9800 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9677 |
| DLFM | 0.2325 | 0.2825 | 0.4200 | 0.5650 | 0.6775 | 0.7775 | 0.8300 | 0.8500 | 0.9150 | 0.9575 | 0.9700 | 0.9925 | 0.9925 | 0.7279 |
| MLFM | 0.4900 | 0.4525 | 0.5450 | 0.5900 | 0.5575 | 0.6550 | 0.7125 | 0.7475 | 0.7575 | 0.8300 | 0.8525 | 0.8650 | 0.8775 | 0.6871 |
| BPSK | 0.9875 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9988 |
| FRANK | 0.9725 | 0.9800 | 0.9950 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9958 |
| LFM-BPSK | 0.2700 | 0.3175 | 0.3800 | 0.4025 | 0.4750 | 0.5225 | 0.6100 | 0.6450 | 0.6850 | 0.6675 | 0.6700 | 0.7150 | 0.6650 | 0.5404 |
| Average | 0.7075 | 0.7282 | 0.7686 | 0.7923 | 0.8134 | 0.8295 | 0.8561 | 0.8611 | 0.8755 | 0.8834 | 0.8880 | 0.8945 | 0.8907 | 0.8299 |
Appendix A.5. The Classification Results of the Experiments
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9725 | 0.9650 | 0.9525 | 0.9625 | 0.9550 | 0.9575 | 0.9425 | 0.9750 | 0.9450 | 0.9225 | 0.9250 | 0.9425 | 0.9425 | 0.9508 |
| LFM | 0.3475 | 0.3025 | 0.3175 | 0.3700 | 0.3600 | 0.3600 | 0.4525 | 0.5075 | 0.5950 | 0.6675 | 0.6975 | 0.7700 | 0.8075 | 0.5042 |
| SFM | 0.8125 | 0.8750 | 0.9275 | 0.9425 | 0.9575 | 0.9675 | 0.9825 | 0.9775 | 1.0000 | 0.9875 | 0.9900 | 0.9925 | 0.9850 | 0.9537 |
| BFSK | 0.9350 | 0.9450 | 0.9650 | 0.9625 | 0.9525 | 0.9450 | 0.9475 | 0.9600 | 0.9650 | 0.9825 | 0.9575 | 0.9475 | 0.9550 | 0.9554 |
| QFSK | 0.7625 | 0.8225 | 0.8900 | 0.9125 | 0.9200 | 0.9300 | 0.9250 | 0.9575 | 0.9525 | 0.9775 | 0.9750 | 0.9900 | 0.9675 | 0.9217 |
| EQFM | 0.6150 | 0.7650 | 0.8225 | 0.8875 | 0.9500 | 0.9425 | 0.9700 | 0.9800 | 0.9875 | 0.9900 | 0.9900 | 0.9975 | 0.9975 | 0.9150 |
| DLFM | 0.1925 | 0.2700 | 0.3275 | 0.3725 | 0.4675 | 0.5600 | 0.7150 | 0.7175 | 0.8425 | 0.8825 | 0.9350 | 0.9325 | 0.9450 | 0.6277 |
| MLFM | 0.3575 | 0.3525 | 0.4275 | 0.4225 | 0.4025 | 0.4975 | 0.5250 | 0.5775 | 0.6125 | 0.6200 | 0.6225 | 0.6025 | 0.5825 | 0.5079 |
| BPSK | 0.8625 | 0.8625 | 0.8550 | 0.9025 | 0.8850 | 0.8400 | 0.8500 | 0.8625 | 0.8425 | 0.8000 | 0.8200 | 0.7975 | 0.8050 | 0.8450 |
| FRANK | 0.9450 | 0.9775 | 0.9700 | 0.9825 | 0.9925 | 0.9925 | 0.9900 | 0.9950 | 0.9950 | 0.9900 | 0.9975 | 0.9925 | 0.9925 | 0.9856 |
| LFM-BPSK | 0.3600 | 0.4175 | 0.4625 | 0.5625 | 0.5775 | 0.6775 | 0.7675 | 0.8000 | 0.8575 | 0.9250 | 0.9125 | 0.9375 | 0.9750 | 0.7102 |
| Average | 0.6511 | 0.6868 | 0.7198 | 0.7527 | 0.7655 | 0.7882 | 0.8243 | 0.8464 | 0.8723 | 0.8859 | 0.8930 | 0.9002 | 0.9050 | 0.8070 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9275 | 0.9050 | 0.9075 | 0.9050 | 0.9125 | 0.9000 | 0.9150 | 0.9125 | 0.9125 | 0.8800 | 0.8825 | 0.8825 | 0.9025 | 0.9035 |
| LFM | 0.3375 | 0.4025 | 0.4325 | 0.4900 | 0.4875 | 0.4925 | 0.5850 | 0.6250 | 0.7000 | 0.7225 | 0.7400 | 0.7600 | 0.8150 | 0.5838 |
| SFM | 0.8500 | 0.8925 | 0.9250 | 0.9325 | 0.9475 | 0.9650 | 0.9775 | 0.9725 | 0.9900 | 0.9850 | 0.9900 | 0.9850 | 0.9800 | 0.9533 |
| BFSK | 0.9350 | 0.9275 | 0.9400 | 0.9425 | 0.9275 | 0.9325 | 0.9225 | 0.8875 | 0.9175 | 0.9375 | 0.9300 | 0.9000 | 0.9025 | 0.9233 |
| QFSK | 0.8425 | 0.8300 | 0.9025 | 0.9325 | 0.9300 | 0.9300 | 0.9450 | 0.9600 | 0.9600 | 0.9775 | 0.9650 | 0.9850 | 0.9800 | 0.9338 |
| EQFM | 0.7075 | 0.8350 | 0.8925 | 0.9375 | 0.9725 | 0.9550 | 0.9750 | 0.9950 | 0.9875 | 0.9875 | 0.9925 | 0.9875 | 0.9900 | 0.9396 |
| DLFM | 0.2325 | 0.2400 | 0.3425 | 0.3825 | 0.4950 | 0.5925 | 0.6900 | 0.7075 | 0.7975 | 0.8325 | 0.8850 | 0.8700 | 0.8725 | 0.6108 |
| MLFM | 0.2850 | 0.2900 | 0.3550 | 0.3175 | 0.3850 | 0.4375 | 0.4600 | 0.5300 | 0.5600 | 0.5725 | 0.6200 | 0.6200 | 0.5550 | 0.4606 |
| BPSK | 0.9150 | 0.9250 | 0.9050 | 0.9025 | 0.9175 | 0.8800 | 0.9075 | 0.8825 | 0.8550 | 0.8625 | 0.8400 | 0.8600 | 0.8800 | 0.8871 |
| FRANK | 0.9450 | 0.9725 | 0.9825 | 0.9700 | 0.9750 | 0.9850 | 0.9650 | 0.9850 | 0.9650 | 0.9725 | 0.9725 | 0.9825 | 0.9625 | 0.9719 |
| LFM-BPSK | 0.1850 | 0.2250 | 0.3200 | 0.4500 | 0.4525 | 0.5800 | 0.6625 | 0.7675 | 0.8350 | 0.9025 | 0.9075 | 0.9375 | 0.9700 | 0.6304 |
| Average | 0.6511 | 0.6768 | 0.7186 | 0.7420 | 0.7639 | 0.7864 | 0.8186 | 0.8386 | 0.8618 | 0.8757 | 0.8841 | 0.8882 | 0.8918 | 0.7998 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9800 | 0.9625 | 0.9650 | 0.9525 | 0.9475 | 0.9500 | 0.9550 | 0.9725 | 0.9425 | 0.9200 | 0.9250 | 0.9450 | 0.9300 | 0.9498 |
| LFM | 0.2100 | 0.2125 | 0.3075 | 0.3525 | 0.4125 | 0.4525 | 0.5525 | 0.6500 | 0.6300 | 0.7025 | 0.7550 | 0.7700 | 0.7900 | 0.5229 |
| SFM | 0.7525 | 0.8300 | 0.8875 | 0.9325 | 0.9550 | 0.9650 | 0.9675 | 0.9800 | 1.0000 | 0.9875 | 0.9950 | 0.9875 | 0.9875 | 0.9406 |
| BFSK | 0.9375 | 0.9575 | 0.9800 | 0.9875 | 0.9950 | 0.9875 | 0.9950 | 0.9925 | 0.9875 | 0.9925 | 0.9800 | 0.9900 | 0.9750 | 0.9813 |
| QFSK | 0.9650 | 0.9650 | 0.9850 | 0.9850 | 0.9875 | 0.9875 | 0.9850 | 0.9875 | 0.9875 | 0.9975 | 0.9925 | 0.9950 | 0.9900 | 0.9854 |
| EQFM | 0.7525 | 0.8625 | 0.9050 | 0.9125 | 0.9800 | 0.9775 | 0.9825 | 0.9900 | 0.9975 | 1.0000 | 0.9950 | 0.9900 | 0.9950 | 0.9492 |
| DLFM | 0.2675 | 0.2775 | 0.4025 | 0.4575 | 0.6100 | 0.7025 | 0.7625 | 0.8375 | 0.8900 | 0.8850 | 0.9475 | 0.9500 | 0.9575 | 0.6883 |
| MLFM | 0.4800 | 0.5125 | 0.5250 | 0.5275 | 0.5275 | 0.6100 | 0.6800 | 0.7100 | 0.7500 | 0.7275 | 0.7950 | 0.8100 | 0.7300 | 0.6450 |
| BPSK | 0.9325 | 0.9550 | 0.9650 | 0.9675 | 0.9650 | 0.9575 | 0.9575 | 0.9675 | 0.9475 | 0.9375 | 0.9450 | 0.9450 | 0.9475 | 0.9531 |
| FRANK | 0.9225 | 0.9700 | 0.9600 | 0.9650 | 0.9850 | 0.9825 | 0.9750 | 0.9825 | 0.9800 | 0.9750 | 0.9750 | 0.9775 | 0.9700 | 0.9708 |
| LFM-BPSK | 0.2525 | 0.3650 | 0.3875 | 0.5050 | 0.5475 | 0.6650 | 0.7175 | 0.7600 | 0.8125 | 0.8675 | 0.9000 | 0.9025 | 0.9550 | 0.6644 |
| Average | 0.6775 | 0.7155 | 0.7518 | 0.7768 | 0.8102 | 0.8398 | 0.8664 | 0.8936 | 0.9023 | 0.9084 | 0.9277 | 0.9330 | 0.9298 | 0.8410 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9850 | 0.9575 | 0.9600 | 0.9625 | 0.9525 | 0.9575 | 0.9475 | 0.9850 | 0.9500 | 0.9250 | 0.9300 | 0.9425 | 0.9400 | 0.9535 |
| LFM | 0.3325 | 0.3275 | 0.3500 | 0.4200 | 0.4925 | 0.5250 | 0.6175 | 0.6500 | 0.6850 | 0.7325 | 0.7175 | 0.7625 | 0.7875 | 0.5692 |
| SFM | 0.8125 | 0.8825 | 0.9300 | 0.9500 | 0.9600 | 0.9775 | 0.9625 | 0.9800 | 1.0000 | 0.9875 | 0.9925 | 0.9950 | 0.9925 | 0.9556 |
| BFSK | 0.9325 | 0.9500 | 0.9700 | 0.9725 | 0.9825 | 0.9850 | 0.9800 | 0.9675 | 0.9825 | 0.9875 | 0.9825 | 0.9750 | 0.9650 | 0.9717 |
| QFSK | 0.9625 | 0.9500 | 0.9675 | 0.9775 | 0.9800 | 0.9725 | 0.9800 | 0.9900 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 0.9823 |
| EQFM | 0.7425 | 0.8625 | 0.8825 | 0.9225 | 0.9625 | 0.9650 | 0.9700 | 0.9825 | 0.9925 | 0.9900 | 0.9800 | 0.9950 | 0.9875 | 0.9412 |
| DLFM | 0.3300 | 0.3850 | 0.4525 | 0.5150 | 0.6525 | 0.7300 | 0.8000 | 0.8175 | 0.8900 | 0.8700 | 0.9275 | 0.9450 | 0.9250 | 0.7108 |
| MLFM | 0.3950 | 0.4000 | 0.4750 | 0.5550 | 0.5025 | 0.6000 | 0.6500 | 0.6475 | 0.6775 | 0.6800 | 0.7075 | 0.7475 | 0.6875 | 0.5942 |
| BPSK | 0.9375 | 0.9625 | 0.9750 | 0.9650 | 0.9500 | 0.9525 | 0.9700 | 0.9700 | 0.9575 | 0.9350 | 0.9475 | 0.9550 | 0.9550 | 0.9563 |
| FRANK | 0.9600 | 0.9725 | 0.9775 | 0.9625 | 0.9675 | 0.9750 | 0.9725 | 0.9875 | 0.9825 | 0.9650 | 0.9675 | 0.9675 | 0.9650 | 0.9710 |
| LFM-BPSK | 0.2375 | 0.2475 | 0.2975 | 0.4500 | 0.4975 | 0.5700 | 0.7050 | 0.7850 | 0.8475 | 0.9075 | 0.9525 | 0.9425 | 0.9650 | 0.6465 |
| Average | 0.6934 | 0.7180 | 0.7489 | 0.7866 | 0.8091 | 0.8373 | 0.8686 | 0.8875 | 0.9057 | 0.9070 | 0.9184 | 0.9298 | 0.9243 | 0.8411 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9800 | 0.9800 | 0.9950 | 0.9950 | 0.9975 | 1.0000 | 0.9975 | 0.9925 | 0.9925 | 0.9850 | 0.9850 | 0.9875 | 0.9800 | 0.9898 |
| LFM | 0.1700 | 0.2175 | 0.2500 | 0.3275 | 0.3825 | 0.4625 | 0.5450 | 0.6650 | 0.7450 | 0.8025 | 0.8325 | 0.8850 | 0.8825 | 0.5513 |
| SFM | 0.8500 | 0.9100 | 0.9500 | 0.9725 | 0.9775 | 0.9925 | 0.9850 | 0.9875 | 0.9975 | 0.9925 | 1.0000 | 0.9975 | 0.9925 | 0.9696 |
| BFSK | 0.9300 | 0.9500 | 0.9475 | 0.9750 | 0.9825 | 0.9850 | 0.9925 | 0.9850 | 0.9975 | 0.9925 | 0.9925 | 0.9975 | 0.9975 | 0.9788 |
| QFSK | 0.9900 | 0.9825 | 0.9950 | 0.9875 | 0.9900 | 0.9950 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 0.9946 |
| EQFM | 0.7250 | 0.8600 | 0.9425 | 0.9550 | 0.9925 | 0.9850 | 0.9950 | 1.0000 | 0.9950 | 1.0000 | 0.9975 | 0.9950 | 0.9850 | 0.9560 |
| DLFM | 0.1575 | 0.2100 | 0.3375 | 0.4650 | 0.5675 | 0.7150 | 0.8125 | 0.8875 | 0.9400 | 0.9675 | 0.9875 | 0.9950 | 0.9875 | 0.6946 |
| MLFM | 0.5650 | 0.5800 | 0.5875 | 0.6000 | 0.5525 | 0.6200 | 0.6275 | 0.6800 | 0.7200 | 0.7350 | 0.7325 | 0.7075 | 0.6925 | 0.6462 |
| BPSK | 0.9850 | 0.9825 | 0.9800 | 0.9900 | 0.9850 | 0.9825 | 0.9925 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 0.9900 | 0.9975 | 0.9904 |
| FRANK | 0.9825 | 0.9950 | 0.9925 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 0.9950 | 0.9965 |
| LFM-BPSK | 0.3175 | 0.3350 | 0.4650 | 0.5875 | 0.6500 | 0.7175 | 0.7575 | 0.8275 | 0.8975 | 0.9325 | 0.9475 | 0.9650 | 0.9925 | 0.7225 |
| Average | 0.6957 | 0.7275 | 0.7675 | 0.8048 | 0.8252 | 0.8595 | 0.8820 | 0.9109 | 0.9343 | 0.9459 | 0.9516 | 0.9561 | 0.9548 | 0.8628 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9875 | 0.9875 | 0.9875 | 0.9925 | 0.9850 | 0.9950 | 0.9725 | 0.9925 | 0.9350 | 0.9025 | 0.9100 | 0.9025 | 0.9150 | 0.9588 |
| LFM | 0.2275 | 0.2525 | 0.3375 | 0.4050 | 0.4900 | 0.5025 | 0.5450 | 0.5975 | 0.6925 | 0.7225 | 0.7525 | 0.8175 | 0.8425 | 0.5527 |
| SFM | 0.8425 | 0.9125 | 0.9400 | 0.9625 | 0.9725 | 0.9925 | 0.9875 | 0.9900 | 1.0000 | 0.9925 | 0.9975 | 0.9975 | 0.9900 | 0.9675 |
| BFSK | 0.9625 | 0.9700 | 0.9750 | 0.9850 | 0.9900 | 0.9900 | 0.9950 | 0.9900 | 0.9900 | 0.9925 | 0.9900 | 0.9950 | 0.9925 | 0.9860 |
| QFSK | 0.9675 | 0.9650 | 0.9850 | 0.9775 | 0.9825 | 0.9825 | 0.9675 | 0.9900 | 0.9900 | 0.9925 | 0.9950 | 1.0000 | 1.0000 | 0.9842 |
| EQFM | 0.8400 | 0.8950 | 0.9450 | 0.9575 | 0.9875 | 0.9775 | 0.9925 | 0.9975 | 0.9950 | 0.9950 | 1.0000 | 0.9975 | 0.9975 | 0.9675 |
| DLFM | 0.4100 | 0.3600 | 0.4850 | 0.5175 | 0.5975 | 0.7350 | 0.8050 | 0.8500 | 0.9200 | 0.9675 | 0.9775 | 0.9975 | 1.0000 | 0.7402 |
| MLFM | 0.4675 | 0.4450 | 0.5650 | 0.5650 | 0.5550 | 0.6550 | 0.6850 | 0.7075 | 0.6550 | 0.6875 | 0.6775 | 0.6550 | 0.6250 | 0.6112 |
| BPSK | 0.9850 | 0.9900 | 0.9825 | 0.9925 | 0.9950 | 0.9900 | 0.9900 | 0.9875 | 0.9900 | 0.9950 | 0.9950 | 0.9775 | 0.9800 | 0.9885 |
| FRANK | 0.9800 | 0.9950 | 0.9925 | 0.9925 | 0.9950 | 0.9950 | 0.9950 | 0.9975 | 0.9975 | 0.9950 | 0.9950 | 0.9850 | 0.9750 | 0.9915 |
| LFM-BPSK | 0.1750 | 0.2525 | 0.3425 | 0.4825 | 0.5725 | 0.6800 | 0.8025 | 0.8300 | 0.9400 | 0.9550 | 0.9775 | 0.9750 | 0.9900 | 0.6904 |
| Average | 0.7132 | 0.7295 | 0.7761 | 0.8027 | 0.8293 | 0.8632 | 0.8852 | 0.9027 | 0.9186 | 0.9270 | 0.9334 | 0.9364 | 0.9370 | 0.8580 |
Appendix A.6. The Parameters of 1-D SKCNN
| Input | Input Layer | Shape: 16384 |
| Main Block 1 | Selective Convolutional Block | Filters: 16 First kernel size: 9 Second kernel size: 16 Nodes of first hidden layer in MLP: 8 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Main Block 2 | Selective Convolutional Block | Filters: 32 First kernel size: 9 Second kernel size: 16 Nodes of first hidden layer in MLP: 8 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Main Block 3 | Selective Convolutional Block | Filters: 64 First kernel size: 9 Second kernel size: 16 Nodes of first hidden layer in MLP: 8 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Main Block 4 | Selective Convolutional Block | Filters: 128 First kernel size: 9 Second kernel size: 16 Nodes of first hidden layer in MLP: 8 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Full Connection Unit | Full Connection Layer | Nodes: 512 Activation function: “ReLU” |
| Output | Full Connection Layer | Nodes: 11 Activation function = “SoftMax” |
| Total Parameters: 1,096,467 | Floating point operations: 2,191,445 | Training time/10000 iterations with 64 batch size: 485 s |
Appendix A.7. The Classification Results of the Experiments
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9725 | 0.9725 | 0.9850 | 0.9925 | 0.9900 | 0.9950 | 0.9900 | 1.0000 | 0.9800 | 0.9850 | 0.9875 | 0.9875 | 0.9750 | 0.9856 |
| LFM | 0.2525 | 0.2400 | 0.2750 | 0.2350 | 0.3025 | 0.3475 | 0.3550 | 0.3850 | 0.4375 | 0.5100 | 0.5300 | 0.5850 | 0.4925 | 0.3806 |
| SFM | 0.7975 | 0.8550 | 0.9100 | 0.9350 | 0.9600 | 0.9675 | 0.9750 | 0.9800 | 0.9975 | 0.9875 | 0.9900 | 0.9900 | 0.9850 | 0.9485 |
| BFSK | 0.7650 | 0.8225 | 0.8550 | 0.9000 | 0.8950 | 0.9425 | 0.9175 | 0.9225 | 0.9250 | 0.9250 | 0.9150 | 0.9475 | 0.9275 | 0.8969 |
| QFSK | 0.8825 | 0.9275 | 0.9500 | 0.9500 | 0.9450 | 0.9600 | 0.9650 | 0.9500 | 0.9825 | 0.9675 | 0.9675 | 0.9800 | 0.9750 | 0.9540 |
| EQFM | 0.2600 | 0.3875 | 0.4600 | 0.5400 | 0.6200 | 0.7025 | 0.8200 | 0.8875 | 0.9275 | 0.9500 | 0.9575 | 0.9850 | 0.9925 | 0.7300 |
| DLFM | 0.2575 | 0.2175 | 0.3150 | 0.3425 | 0.5350 | 0.5900 | 0.6750 | 0.7075 | 0.8100 | 0.8575 | 0.8750 | 0.8950 | 0.8875 | 0.6127 |
| MLFM | 0.3025 | 0.3275 | 0.2975 | 0.2950 | 0.2925 | 0.3450 | 0.3525 | 0.3450 | 0.3750 | 0.3775 | 0.3925 | 0.4025 | 0.4025 | 0.3467 |
| BPSK | 0.9550 | 0.9675 | 0.9775 | 0.9800 | 0.9850 | 0.9850 | 0.9900 | 0.9900 | 0.9875 | 0.9825 | 0.9750 | 0.9875 | 0.9925 | 0.9812 |
| FRANK | 0.8800 | 0.9400 | 0.9750 | 0.9775 | 0.9975 | 0.9950 | 1.0000 | 0.9925 | 0.9925 | 0.9925 | 0.9975 | 0.9925 | 0.9750 | 0.9775 |
| LFM-BPSK | 0.1950 | 0.2200 | 0.1850 | 0.2075 | 0.2375 | 0.2850 | 0.2800 | 0.3150 | 0.3150 | 0.3250 | 0.4125 | 0.4375 | 0.4225 | 0.2952 |
| Average | 0.5927 | 0.6252 | 0.6532 | 0.6686 | 0.7055 | 0.7377 | 0.7564 | 0.7705 | 0.7936 | 0.8055 | 0.8182 | 0.8355 | 0.8207 | 0.7372 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9900 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9987 |
| LFM | 0.3675 | 0.4375 | 0.5550 | 0.6200 | 0.6700 | 0.7875 | 0.8425 | 0.9075 | 0.9400 | 0.9575 | 0.9675 | 0.9925 | 0.9850 | 0.7715 |
| SFM | 0.9300 | 0.9575 | 0.9825 | 0.9925 | 1.0000 | 0.9950 | 0.9975 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 0.9950 | 0.9879 |
| BFSK | 0.8575 | 0.9025 | 0.9350 | 0.9775 | 0.9600 | 0.9750 | 0.9750 | 0.9750 | 0.9850 | 0.9775 | 0.9725 | 0.9875 | 0.9850 | 0.9588 |
| QFSK | 0.9925 | 0.9875 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9983 |
| EQFM | 0.9175 | 0.9575 | 0.9825 | 0.9800 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 0.9867 |
| DLFM | 0.6150 | 0.7125 | 0.8350 | 0.8850 | 0.9200 | 0.9425 | 0.9725 | 0.9825 | 0.9825 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 0.9108 |
| MLFM | 0.5900 | 0.6400 | 0.6575 | 0.7250 | 0.7825 | 0.8225 | 0.8850 | 0.9150 | 0.9175 | 0.9600 | 0.9750 | 0.9650 | 0.9550 | 0.8300 |
| BPSK | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9950 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9992 |
| FRANK | 0.9850 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9987 |
| LFM-BPSK | 0.5050 | 0.5450 | 0.6325 | 0.6775 | 0.7400 | 0.8075 | 0.8775 | 0.9225 | 0.9750 | 0.9750 | 1.0000 | 0.9925 | 1.0000 | 0.8192 |
| Average | 0.7955 | 0.8305 | 0.8707 | 0.8961 | 0.9157 | 0.9384 | 0.9586 | 0.9727 | 0.9811 | 0.9875 | 0.9916 | 0.9941 | 0.9927 | 0.9327 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| LFM | 0.4950 | 0.5950 | 0.6325 | 0.7550 | 0.7375 | 0.8275 | 0.8900 | 0.9400 | 0.9750 | 0.9750 | 0.9925 | 0.9975 | 1.0000 | 0.8317 |
| SFM | 0.9050 | 0.9575 | 0.9875 | 0.9925 | 0.9925 | 0.9950 | 0.9925 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 0.9925 | 0.9850 |
| BFSK | 0.9775 | 0.9925 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 0.9963 |
| QFSK | 0.9925 | 0.9950 | 0.9950 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 0.9979 |
| EQFM | 0.9075 | 0.9550 | 0.9775 | 0.9800 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9858 |
| DLFM | 0.6350 | 0.7500 | 0.8350 | 0.8900 | 0.9300 | 0.9725 | 0.9775 | 0.9975 | 0.9925 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 0.9210 |
| MLFM | 0.6000 | 0.5800 | 0.6375 | 0.6625 | 0.7350 | 0.7950 | 0.8325 | 0.9225 | 0.9300 | 0.9525 | 0.9625 | 0.9725 | 0.9775 | 0.8123 |
| BPSK | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9996 |
| FRANK | 0.9925 | 1.0000 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9990 |
| LFM-BPSK | 0.4000 | 0.4875 | 0.5675 | 0.6675 | 0.7075 | 0.8025 | 0.8600 | 0.9025 | 0.9575 | 0.9700 | 0.9825 | 0.9875 | 1.0000 | 0.7917 |
| Average | 0.8093 | 0.8466 | 0.8750 | 0.9039 | 0.9182 | 0.9443 | 0.9589 | 0.9780 | 0.9866 | 0.9900 | 0.9939 | 0.9952 | 0.9970 | 0.9382 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9950 | 0.9875 | 0.9987 |
| LFM | 0.3600 | 0.3475 | 0.4225 | 0.4075 | 0.4650 | 0.5350 | 0.5925 | 0.6650 | 0.7425 | 0.8000 | 0.8375 | 0.8900 | 0.8900 | 0.6119 |
| SFM | 0.8700 | 0.9300 | 0.9475 | 0.9750 | 0.9875 | 1.0000 | 0.9975 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9950 | 0.9767 |
| BFSK | 0.9750 | 0.9950 | 0.9825 | 0.9925 | 0.9900 | 0.9925 | 0.9925 | 0.9950 | 1.0000 | 0.9950 | 0.9900 | 0.9925 | 0.9950 | 0.9913 |
| QFSK | 0.9900 | 0.9950 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9979 |
| EQFM | 0.8950 | 0.9700 | 0.9825 | 0.9825 | 1.0000 | 0.9875 | 0.9925 | 0.9950 | 0.9975 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9846 |
| DLFM | 0.3700 | 0.4175 | 0.5700 | 0.7150 | 0.8050 | 0.8750 | 0.9075 | 0.9425 | 0.9300 | 0.9550 | 0.9575 | 0.9475 | 0.9625 | 0.7965 |
| MLFM | 0.5050 | 0.5500 | 0.5975 | 0.6400 | 0.6800 | 0.7550 | 0.8200 | 0.7850 | 0.8100 | 0.8300 | 0.8450 | 0.8650 | 0.8350 | 0.7321 |
| BPSK | 0.9825 | 0.9850 | 0.9875 | 0.9925 | 0.9950 | 0.9950 | 0.9950 | 0.9875 | 0.9875 | 0.9975 | 0.9950 | 0.9950 | 0.9900 | 0.9912 |
| FRANK | 0.9875 | 0.9975 | 0.9925 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 0.9975 | 0.9977 |
| LFM-BPSK | 0.3800 | 0.4300 | 0.5425 | 0.6775 | 0.7275 | 0.8525 | 0.9075 | 0.9475 | 0.9825 | 0.9775 | 0.9775 | 0.9925 | 0.9900 | 0.7988 |
| Average | 0.7559 | 0.7834 | 0.8200 | 0.8527 | 0.8770 | 0.9084 | 0.9275 | 0.9377 | 0.9495 | 0.9593 | 0.9636 | 0.9707 | 0.9675 | 0.8980 |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SCF | 0.9925 | 0.9875 | 0.9975 | 0.9875 | 0.9900 | 0.9975 | 0.9875 | 0.9950 | 0.9875 | 0.9725 | 0.9650 | 0.9750 | 0.9625 | 0.9844 |
| LFM | 0.5050 | 0.5000 | 0.5725 | 0.6250 | 0.6850 | 0.7150 | 0.8175 | 0.8150 | 0.8500 | 0.8575 | 0.8875 | 0.9275 | 0.9175 | 0.7442 |
| SFM | 0.8875 | 0.9500 | 0.9725 | 0.9825 | 0.9875 | 0.9975 | 0.9975 | 0.9950 | 0.9975 | 1.0000 | 1.0000 | 0.9975 | 0.9950 | 0.9815 |
| BFSK | 0.9550 | 0.9775 | 1.0000 | 0.9900 | 0.9975 | 0.9975 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9925 | 0.9929 |
| QFSK | 0.9700 | 0.9925 | 0.9900 | 0.9975 | 1.0000 | 0.9950 | 0.9950 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9952 |
| EQFM | 0.8650 | 0.9275 | 0.9600 | 0.9600 | 0.9875 | 0.9925 | 0.9975 | 1.0000 | 1.0000 | 0.9975 | 1.0000 | 1.0000 | 1.0000 | 0.9760 |
| DLFM | 0.3850 | 0.5000 | 0.6425 | 0.7825 | 0.8700 | 0.9350 | 0.9425 | 0.9725 | 0.9775 | 0.9875 | 0.9850 | 0.9900 | 0.9800 | 0.8423 |
| MLFM | 0.3825 | 0.4125 | 0.5150 | 0.5125 | 0.6250 | 0.6375 | 0.7350 | 0.7400 | 0.7725 | 0.8150 | 0.8475 | 0.8525 | 0.8250 | 0.6671 |
| BPSK | 0.9400 | 0.9225 | 0.9575 | 0.9750 | 0.9800 | 0.9900 | 0.9775 | 0.9700 | 0.9850 | 0.9900 | 0.9550 | 0.9900 | 0.9850 | 0.9706 |
| FRANK | 0.9850 | 0.9875 | 0.9975 | 0.9900 | 0.9950 | 0.9950 | 0.9975 | 0.9950 | 1.0000 | 1.0000 | 0.9975 | 0.9950 | 0.9975 | 0.9948 |
| LFM-BPSK | 0.3100 | 0.3325 | 0.4550 | 0.5625 | 0.5825 | 0.7250 | 0.8150 | 0.8700 | 0.9225 | 0.9350 | 0.9725 | 0.9700 | 0.9875 | 0.7262 |
| Average | 0.7434 | 0.7718 | 0.8236 | 0.8514 | 0.8818 | 0.9070 | 0.9330 | 0.9409 | 0.9539 | 0.9593 | 0.9645 | 0.9725 | 0.9675 | 0.8977 |
Appendix A.8. The Time Usage for Training the Proposed MA-CNN Based on Different Pairs of and
| (,) | (26, 2145) | (50, 1102) | (100, 551) | (200, 276) |
| Iterations in total | 610 k | 1181 k | 2341 k | 4977 k |
| Training time | 7 h | 14 h | 27 h | 58 h |
References
- Barton, D.K. Radar System Analysis and Modeling; Artech: London, UK, 2004. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Wiley, R.G.; Ebrary, I. ELINT: The Interception and Analysis of Radar Signals; Artech: London, UK, 2006. [Google Scholar]
- Qu, Z.; Hou, C.; Hou, C.; Wang, W. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Neural Network and Deep Q-Learning Network. IEEE Access 2020, 8, 49125–49136. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks; NIPS Curran Associates Inc.: New York, NY, USA, 2012. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Highway networks. arXiv 2015, arXiv:1505.00387. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, W.; Hu, X.; Yang, J. Selective Kernel Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 510–519. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Bai, X.; Gong, C.; Zhou, F. Hybrid Inference Network for Few-Shot SAR Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9257–9269. [Google Scholar] [CrossRef]
- Kong, S.; Kim, M.; Hoang, L.M.; Kim, E. Automatic LPI Radar Waveform Recognition Using CNN. IEEE Access 2018, 6, 4207–4219. [Google Scholar] [CrossRef]
- Yu, Z.; Tang, J. Radar Signal Intra-Pulse Modulation Recognition Based on Contour Extraction. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2783–2786. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Yin, J. Modulation classification method for frequency modulation signals based on the time–frequency distribution and CNN. IET Radar Sonar Navigat. 2017, 12, 244–249. [Google Scholar] [CrossRef]
- Huynh-The, T.; Hua, C.; Pham, Q.; Kim, D. MCNet: An Efficient CNN Architecture for Robust Automatic Modulation Classification. IEEE Commun. Lett. 2020, 24, 811–815. [Google Scholar] [CrossRef]
- Peng, S.; Jiang, H.; Wang, H.; Alwageed, H.; Zhou, Y.; Sebdani, M.M.; Yao, Y.-D. Modulation Classification Based on Signal Constellation Diagrams and Deep Learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 718–727. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Tang, J.; Wang, Z. GCPS: A CNN Performance Evaluation Criterion for Radar Signal Intrapulse Modulation Recognition. IEEE Commun. Lett. 2021, 25, 2290–2294. [Google Scholar] [CrossRef]
- Wu, B.; Yuan, S.; Li, P.; Jing, Z.; Huang, S.; Zhao, Y. Radar Emitter Signal Recognition Based on One-Dimensional Convolutional Neural Network with Attention Mechanism. Sensors 2020, 20, 6350. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Wu, B.; Li, P. Intra-Pulse Modulation Classification of Radar Emitter Signals Based on a 1-D Selective Kernel Convolutional Neural Network. Remote Sens. 2021, 13, 2799. [Google Scholar] [CrossRef]
- Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Workshop on Challenges in Representation Learning; ICML: Atlanta, GA, USA, 2013; Volume 3, p. 2. [Google Scholar]
- Berthelot, D.; Carlini, N.; Goodfellow, I.; Papernot, N.; Oliver, A.; Raffel, C.A. Mixmatch: A holistic approach to semi-supervised learning. arXiv 2019, arXiv:1905.02249. [Google Scholar]
- Sohn, K.; Berthelot, D.; Li, C.L.; Zhang, Z.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Zhang, H.; Raffel, C. FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence. arXiv 2020, arXiv:2001.07685. [Google Scholar]
- Bachman, P.; Alsharif, O.; Precup, D. Learning with pseudo-ensembles. Adv. Neural Inf. Process. Syst. 2014, 3365–3373. [Google Scholar]
- Sajjadi, M.; Javanmardi, M.; Tasdizen, T. Regularization with stochastic transformations and perturbations for deep semi-supervised learning. Adv. Neural Inf. Process. Syst. 2016, 1171–1179. [Google Scholar]
- Laine, S.; Aila, T. Temporal ensembling for semi-supervised learning. arXiv 2016, arXiv:1610.02242. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, L.; Zhang, H.; Xiao, J.; Nie, L.; Shao, J.; Liu, W.; Chua, T.-S. SCA-CNN: Spatial and Channel-Wise Attention in Convolutional Networks for Image Captioning. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6298–6306. [Google Scholar] [CrossRef] [Green Version]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]



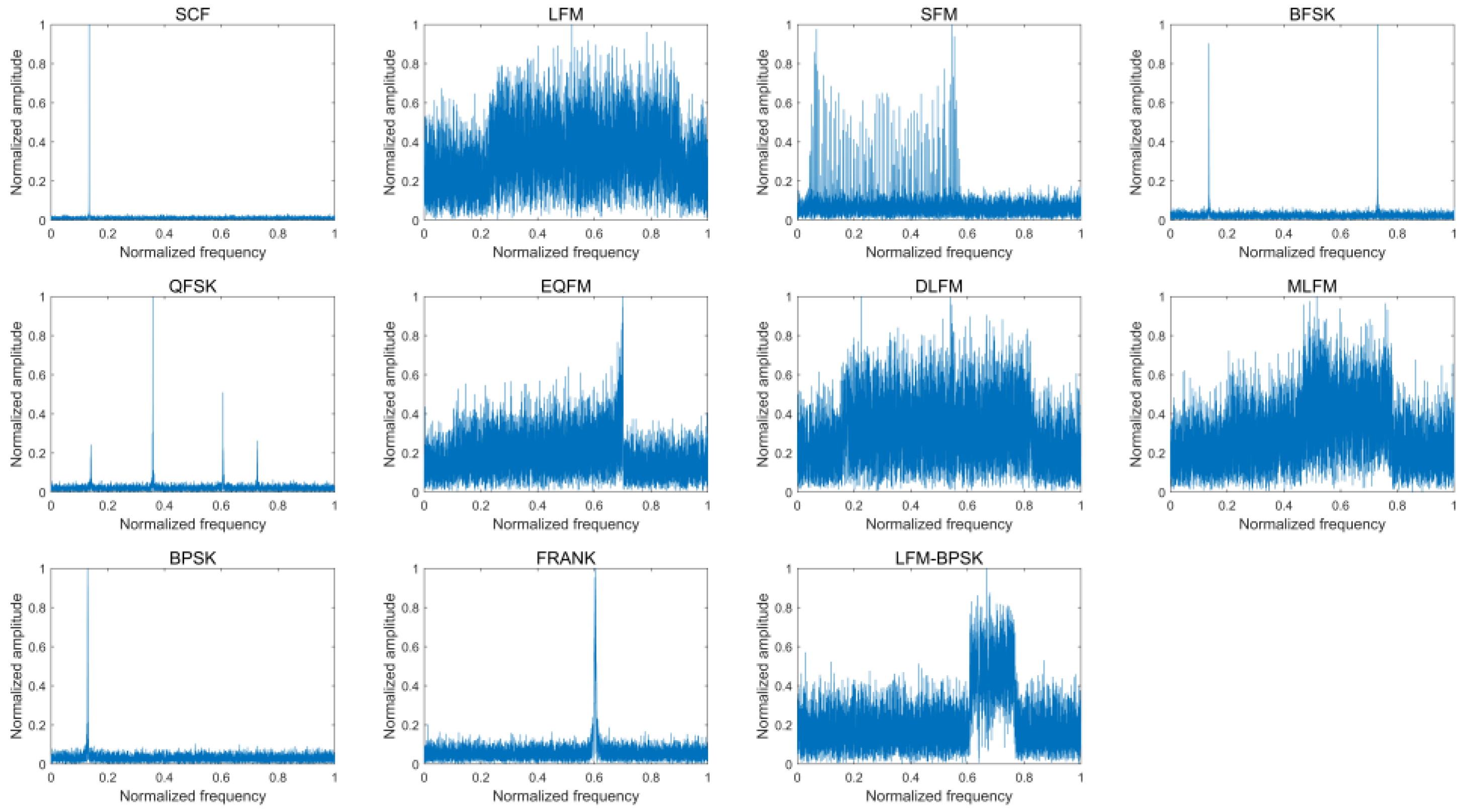


| Class ID | Type | Carrier Frequency | Parameters | Details |
|---|---|---|---|---|
| 1 | SCF | 0.05–0.95 | None | None |
| 2 | LFM | 0.05–0.95 | Bandwidth: 0.05–0.8 | 1. Up LFM and down LFM are included 2. Both max value and min value of the instantaneous frequency for LFM range from 0.05 to 0.95 |
| 3 | SFM | 0.05–0.95 | Bandwidth: 0.05–0.8 | Both max value and min value of the instantaneous frequency for LFM range from 0.05 to 0.95 |
| 4 | BFSK | 0.05–0.95 0.05–0.95 | 5, 7, 11, 13-bit Barker code | The distance of two-carrier frequency is longer than 0.05 |
| 5 | QFSK | 0.05–0.95 0.05–0.95 0.05–0.95 0.05–0.95 | 16-bit Frank code | The distance of each two-carrier frequency is longer than 0.05 |
| 6 | EQFM | 0.05–0.95 | Bandwidth: 0.05–0.8 | 1. The instantaneous frequency increases first and then decreases, or decreases first and then increases2. Both max value and min value of the instantaneous frequency for EQFM range from 0.05 to 0.95 |
| 7 | DLFM | 0.05–0.95 | Bandwidth: 0.05–0.8 | 1. The instantaneous frequency increases first and then decreases, or decreases first and then increases 2. Both max value and min value of the instantaneous frequency for EQFM range from 0.05 to 0.95 |
| 8 | MLFM | 0.05–0.95 0.05–0.95 | Bandwidth: 0.05–0.8 Bandwidth: 0.05–0.8 Segment: 20–80% | 1. Up LFM and down LFM are included in each of the two parts 2. Both max value and min value of the instantaneous frequency for each part of the MLFM range from 0.05 to 0.95 3. The distance of the instantaneous frequency in the end of first part and the instantaneous frequency in the start of last part is longer than 0.05 |
| 9 | BPSK | 0.05–0.95 | 5, 7, 11, 13-bit Barker code | 5, 7, 11, 13-bit Barker code |
| 10 | FRANK | 0.05–0.95 | Phase number: 6, 7, 8 | Phase number: 6, 7, 8 |
| 11 | LFM-BPSK | 0.05–0.95 | Bandwidth: 0.05–0.8 5, 7, 11, 13-bit Barker code | 1. Up LFM and down LFM are included 2. Both max value and min value of the instantaneous frequency for LFM range from 0.05 to 0.95 |
| Input | Input Layer | Shape: 16384 |
|---|---|---|
| Main Block 1 | Convolutional Layer | Filters: 16 Kernel size: 16 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Mixed Attention Block | MLP_1: Hidden layer 1: 16 nodes, activation: “ReLU” Hidden layer 2: 4 nodes, activation: “Sigmoid” MLP_2: Hidden layer 1: 32 nodes, activation: “ReLU” Hidden layer 2: 4 nodes, activation: “Sigmoid” Convolution Layer_1: Kernel size: 9, activation: “Sigmoid” Convolution Layer_2: Kernel size: 16, activation: “Sigmoid” | |
| Main Block 2 | Selective Convolutional Block | Filters: 32 First kernel size: 9 Second kernel size: 16 Nodes of first hidden layer in MLP: 8 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Mixed Attention Block | MLP_1: Hidden layer 1: 32 nodes, activation: “ReLU” Hidden layer 2: 8 nodes, activation: “Sigmoid” MLP_2: Hidden layer 1: 64 nodes, activation: “ReLU” Hidden layer 2: 8 nodes, activation: “Sigmoid” Convolution Layer_1: Kernel size: 9, activation: “Sigmoid” Convolution Layer_2: Kernel size: 16, activation: “Sigmoid” | |
| Main Block 3 | Selective Convolutional Block | Filters: 64 First kernel size: 9 Second kernel size: 16 Nodes of first hidden layer in MLP: 8 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Mixed Attention Block | MLP_1: Hidden layer 1: 64 nodes, activation: “ReLU” Hidden layer 2: 16 nodes, activation: “Sigmoid” MLP_2: Hidden layer 1: 128 nodes, activation: “ReLU” Hidden layer 2: 16 nodes, activation: “Sigmoid” Convolution Layer_1: Kernel size: 5, activation: “Sigmoid” Convolution Layer_2: Kernel size: 9, activation: “Sigmoid” | |
| Main Block 4 | Selective Convolutional Block | Filters: 128 First kernel size: 9 Second kernel size: 16 Nodes of first hidden layer in MLP: 8 |
| Max-Pooling | Stride: 6 Pooling_size: 6 | |
| BatchNormalization | BatchNormalization | |
| Mixed Attention Block | MLP_1: Hidden layer 1: 128 nodes, activation: “ReLU” Hidden layer 2: 32 nodes, activation: “Sigmoid” MLP_2: Hidden layer 1: 256 nodes, activation: “ReLU” Hidden layer 2: 32 nodes, activation: “Sigmoid” Convolution Layer_1: Kernel size: 3, activation: “Sigmoid” Convolution Layer_2: Kernel size: 5, activation: “Sigmoid” | |
| Full Connection Unit | Full Connection layer | Nodes: 512 Activation: “ReLU” |
| Output | Full Connection layer | Nodes: 11 Activation: “SoftMax” |
| Total Parameters: 1,033,195 | Floating point operations: 2,063,221 | Training time/10,000 iterations with 64 batch size: 410 s |
| Situation | Details |
|---|---|
| Situation Dataset1 | Labeled dataset |
| Situation Dataset2 | Labeled dataset + 1-st unlabeled dataset with true labels |
| Situation Dataset3 | Labeled dataset + 2nd unlabeled dataset with true labels |
| Situation Dataset4 | Labeled dataset + 1-st unlabeled dataset without true labels |
| Situation Dataset5 | Labeled dataset + 2nd unlabeled dataset without true labels |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Situation Dataset 1 | 0.5625 | 0.5970 | 0.6370 | 0.6570 | 0.6820 | 0.7007 | 0.7370 | 0.7455 | 0.7730 | 0.7939 | 0.8073 | 0.8268 | 0.8193 | 0.7184 |
| Situation Dataset 2 | 0.7884 | 0.8189 | 0.8650 | 0.8925 | 0.9130 | 0.9345 | 0.9548 | 0.9673 | 0.9823 | 0.9882 | 0.9923 | 0.9932 | 0.9957 | 0.9297 |
| Situation Dataset 3 | 0.8127 | 0.8439 | 0.8750 | 0.8989 | 0.9173 | 0.9339 | 0.9577 | 0.9709 | 0.9848 | 0.9870 | 0.9907 | 0.9927 | 0.9948 | 0.9354 |
| Situation | Situation Dataset 1 | Situation Dataset 2 | Situation Dataset 3 | |
|---|---|---|---|---|
| Class | ||||
| SCF | 0.9602 | 0.9990 | 0.9996 | |
| LFM | 0.3217 | 0.8517 | 0.8175 | |
| SFM | 0.9340 | 0.9879 | 0.9823 | |
| BFSK | 0.8533 | 0.9954 | 0.9933 | |
| QFSK | 0.9165 | 0.9969 | 0.9938 | |
| EQFM | 0.7169 | 0.9829 | 0.9925 | |
| DLFM | 0.5958 | 0.8769 | 0.9367 | |
| MLFM | 0.3254 | 0.8113 | 0.8044 | |
| BPSK | 0.9506 | 0.9990 | 0.9985 | |
| FRANK | 0.9706 | 0.9996 | 0.9971 | |
| LFM-BPSK | 0.3573 | 0.7258 | 0.7737 | |
| Average | 0.7184 | 0.9297 | 0.9354 | |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Situation Dataset 4 | 0.7398 | 0.7764 | 0.8136 | 0.8418 | 0.8595 | 0.8839 | 0.9030 | 0.9125 | 0.9225 | 0.9255 | 0.9318 | 0.9334 | 0.9309 | 0.8750 |
| Situation Dataset 5 | 0.7305 | 0.7741 | 0.8168 | 0.8411 | 0.8650 | 0.8845 | 0.9030 | 0.9089 | 0.9186 | 0.9286 | 0.9407 | 0.9459 | 0.9350 | 0.8764 |
| Situation | Situation Dataset 4 | Situation Dataset 5 | |
|---|---|---|---|
| Class | |||
| SCF | 0.9935 | 0.9998 | |
| LFM | 0.6925 | 0.5242 | |
| SFM | 0.9781 | 0.9821 | |
| BFSK | 0.9885 | 0.9713 | |
| QFSK | 0.9938 | 0.9940 | |
| EQFM | 0.9610 | 0.9798 | |
| DLFM | 0.7444 | 0.7900 | |
| MLFM | 0.6204 | 0.6487 | |
| BPSK | 0.9965 | 0.9948 | |
| FRANK | 0.9950 | 0.9948 | |
| LFM-BPSK | 0.6610 | 0.7604 | |
| Average | 0.8750 | 0.8764 | |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Situation Dataset 4 | (26, 2145) | 0.7309 | 0.7620 | 0.8052 | 0.8352 | 0.8530 | 0.8800 | 0.8977 | 0.9161 | 0.9200 | 0.9252 | 0.9257 | 0.9364 | 0.9255 | 0.8702 |
| (50, 1102) | 0.7275 | 0.7607 | 0.7945 | 0.8357 | 0.8591 | 0.8718 | 0.8964 | 0.9157 | 0.9261 | 0.9334 | 0.9439 | 0.9491 | 0.9414 | 0.8735 | |
| (100, 551) | 0.7398 | 0.7764 | 0.8136 | 0.8418 | 0.8595 | 0.8839 | 0.9030 | 0.9125 | 0.9225 | 0.9255 | 0.9318 | 0.9334 | 0.9309 | 0.8750 | |
| (200, 276) | 0.7414 | 0.7773 | 0.8182 | 0.8470 | 0.8752 | 0.8982 | 0.9225 | 0.9282 | 0.9407 | 0.9489 | 0.9480 | 0.9523 | 0.9411 | 0.8876 | |
| Situation Dataset 5 | (26, 2145) | 0.7073 | 0.7439 | 0.7923 | 0.8186 | 0.8373 | 0.8652 | 0.8818 | 0.9043 | 0.9084 | 0.9123 | 0.9186 | 0.9270 | 0.9234 | 0.8570 |
| (50, 1102) | 0.7086 | 0.7511 | 0.7809 | 0.8227 | 0.8509 | 0.8730 | 0.9057 | 0.9132 | 0.9314 | 0.9486 | 0.9559 | 0.9536 | 0.9550 | 0.8731 | |
| (100, 551) | 0.7305 | 0.7741 | 0.8168 | 0.8411 | 0.8650 | 0.8845 | 0.9030 | 0.9089 | 0.9186 | 0.9286 | 0.9407 | 0.9459 | 0.9350 | 0.8764 | |
| (200, 276) | 0.7436 | 0.7757 | 0.8209 | 0.8489 | 0.8666 | 0.8941 | 0.9109 | 0.9227 | 0.9307 | 0.9380 | 0.9425 | 0.9484 | 0.9407 | 0.8834 | |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Situation Dataset 4 | (26, 2145) | 0.7005 | 0.7170 | 0.7409 | 0.7641 | 0.7880 | 0.8000 | 0.8114 | 0.8273 | 0.8318 | 0.8423 | 0.8475 | 0.8570 | 0.8552 | 0.7987 |
| (50, 1102) | 0.7120 | 0.7243 | 0.7570 | 0.7745 | 0.7884 | 0.8009 | 0.8052 | 0.8211 | 0.8314 | 0.8382 | 0.8439 | 0.8482 | 0.8402 | 0.7989 | |
| (100, 551) | 0.7057 | 0.7286 | 0.7632 | 0.7825 | 0.7961 | 0.8180 | 0.8298 | 0.8420 | 0.8461 | 0.8539 | 0.8570 | 0.8652 | 0.8643 | 0.8117 | |
| (200, 276) | 0.7125 | 0.7266 | 0.7686 | 0.7905 | 0.8025 | 0.8332 | 0.8550 | 0.8664 | 0.8764 | 0.8907 | 0.8957 | 0.8995 | 0.8961 | 0.8318 | |
| Situation Dataset 5 | (26, 2145) | 0.7073 | 0.7252 | 0.7482 | 0.7668 | 0.7843 | 0.7959 | 0.8161 | 0.8218 | 0.8361 | 0.8393 | 0.8439 | 0.8543 | 0.8420 | 0.7986 |
| (50, 1102) | 0.6836 | 0.7041 | 0.7336 | 0.7552 | 0.7800 | 0.7993 | 0.8177 | 0.8314 | 0.8384 | 0.8532 | 0.8614 | 0.8657 | 0.8593 | 0.7987 | |
| (100, 551) | 0.7105 | 0.7295 | 0.7723 | 0.7934 | 0.8145 | 0.8280 | 0.8427 | 0.8509 | 0.8652 | 0.8623 | 0.8659 | 0.8745 | 0.8702 | 0.8215 | |
| (200, 276) | 0.7075 | 0.7282 | 0.7686 | 0.7923 | 0.8134 | 0.8295 | 0.8561 | 0.8611 | 0.8755 | 0.8834 | 0.8880 | 0.8945 | 0.8907 | 0.8299 | |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Situation Dataset 4 | d = 1 constant | 0.6511 | 0.6868 | 0.7198 | 0.7527 | 0.7655 | 0.7882 | 0.8243 | 0.8464 | 0.8723 | 0.8859 | 0.8930 | 0.9002 | 0.9050 | 0.8070 |
| d = 0.5 constant | 0.6775 | 0.7155 | 0.7518 | 0.7768 | 0.8102 | 0.8398 | 0.8664 | 0.8936 | 0.9023 | 0.9084 | 0.9277 | 0.9330 | 0.9298 | 0.8410 | |
| d = 0.5 decreasing linearly | 0.6957 | 0.7275 | 0.7675 | 0.8048 | 0.8252 | 0.8595 | 0.8820 | 0.9109 | 0.9343 | 0.9459 | 0.9516 | 0.9561 | 0.9548 | 0.8628 | |
| Situation Dataset 5 | d = 1 constant | 0.6511 | 0.6768 | 0.7186 | 0.7420 | 0.7639 | 0.7864 | 0.8186 | 0.8386 | 0.8618 | 0.8757 | 0.8841 | 0.8882 | 0.8918 | 0.7998 |
| d = 0.5 constant | 0.6934 | 0.7180 | 0.7489 | 0.7866 | 0.8091 | 0.8373 | 0.8686 | 0.8875 | 0.9057 | 0.9070 | 0.9184 | 0.9298 | 0.9243 | 0.8411 | |
| d = 0.5 decreasing linearly | 0.7132 | 0.7295 | 0.7761 | 0.8027 | 0.8293 | 0.8632 | 0.8852 | 0.9027 | 0.9186 | 0.9270 | 0.9334 | 0.9364 | 0.9370 | 0.8580 | |
| SNR | −12 | −11 | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Situation Dataset 1 | 0.5927 | 0.6252 | 0.6532 | 0.6686 | 0.7055 | 0.7377 | 0.7564 | 0.7705 | 0.7936 | 0.8055 | 0.8182 | 0.8355 | 0.8207 | 0.7372 |
| Situation Dataset 2 | 0.7955 | 0.8305 | 0.8707 | 0.8961 | 0.9157 | 0.9384 | 0.9586 | 0.9727 | 0.9811 | 0.9875 | 0.9916 | 0.9941 | 0.9927 | 0.9327 |
| Situation Dataset 3 | 0.8093 | 0.8466 | 0.8750 | 0.9039 | 0.9182 | 0.9443 | 0.9589 | 0.9780 | 0.9866 | 0.9900 | 0.9939 | 0.9952 | 0.9970 | 0.9382 |
| Situation Dataset 4 | 0.7559 | 0.7834 | 0.8200 | 0.8527 | 0.8770 | 0.9084 | 0.9275 | 0.9377 | 0.9495 | 0.9593 | 0.9636 | 0.9707 | 0.9675 | 0.8980 |
| Situation Dataset 5 | 0.7434 | 0.7718 | 0.8236 | 0.8514 | 0.8818 | 0.9070 | 0.9330 | 0.9409 | 0.9539 | 0.9593 | 0.9645 | 0.9725 | 0.9675 | 0.8977 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, S.; Li, P.; Wu, B.; Li, X.; Wang, J. Semi-Supervised Classification for Intra-Pulse Modulation of Radar Emitter Signals Using Convolutional Neural Network. Remote Sens. 2022, 14, 2059. https://doi.org/10.3390/rs14092059
Yuan S, Li P, Wu B, Li X, Wang J. Semi-Supervised Classification for Intra-Pulse Modulation of Radar Emitter Signals Using Convolutional Neural Network. Remote Sensing. 2022; 14(9):2059. https://doi.org/10.3390/rs14092059
Chicago/Turabian StyleYuan, Shibo, Peng Li, Bin Wu, Xiao Li, and Jie Wang. 2022. "Semi-Supervised Classification for Intra-Pulse Modulation of Radar Emitter Signals Using Convolutional Neural Network" Remote Sensing 14, no. 9: 2059. https://doi.org/10.3390/rs14092059
APA StyleYuan, S., Li, P., Wu, B., Li, X., & Wang, J. (2022). Semi-Supervised Classification for Intra-Pulse Modulation of Radar Emitter Signals Using Convolutional Neural Network. Remote Sensing, 14(9), 2059. https://doi.org/10.3390/rs14092059






