Multi-Rotor UAV-Borne PolInSAR Data Processing and Preliminary Analysis of Height Inversion in Urban Area
Abstract
:1. Introduction
- (1)
- An imaging and polarimetric interferometric processing method for a Ku-band small UAV-borne PolInSAR is proposed, and the impact model of the system parameters on the relative elevation results is provided, while a good urban DSM is obtained, whose Root Mean Squared Error (RMSE) in building areas is 2.88 m;
- (2)
- The differences in elevation results between Pauli decomposition and polarimetric interferometric optimal decomposition on buildings, lampposts, and trees are compared and analyzed through simulation. A reasonable explanation is given and the conditions for using PolInSAR to improve coherence and height estimation precision are given, which provides a valuable reference for the application of UAV-borne PolInSAR in urban areas.
2. Materials and Methods
2.1. Model Basis
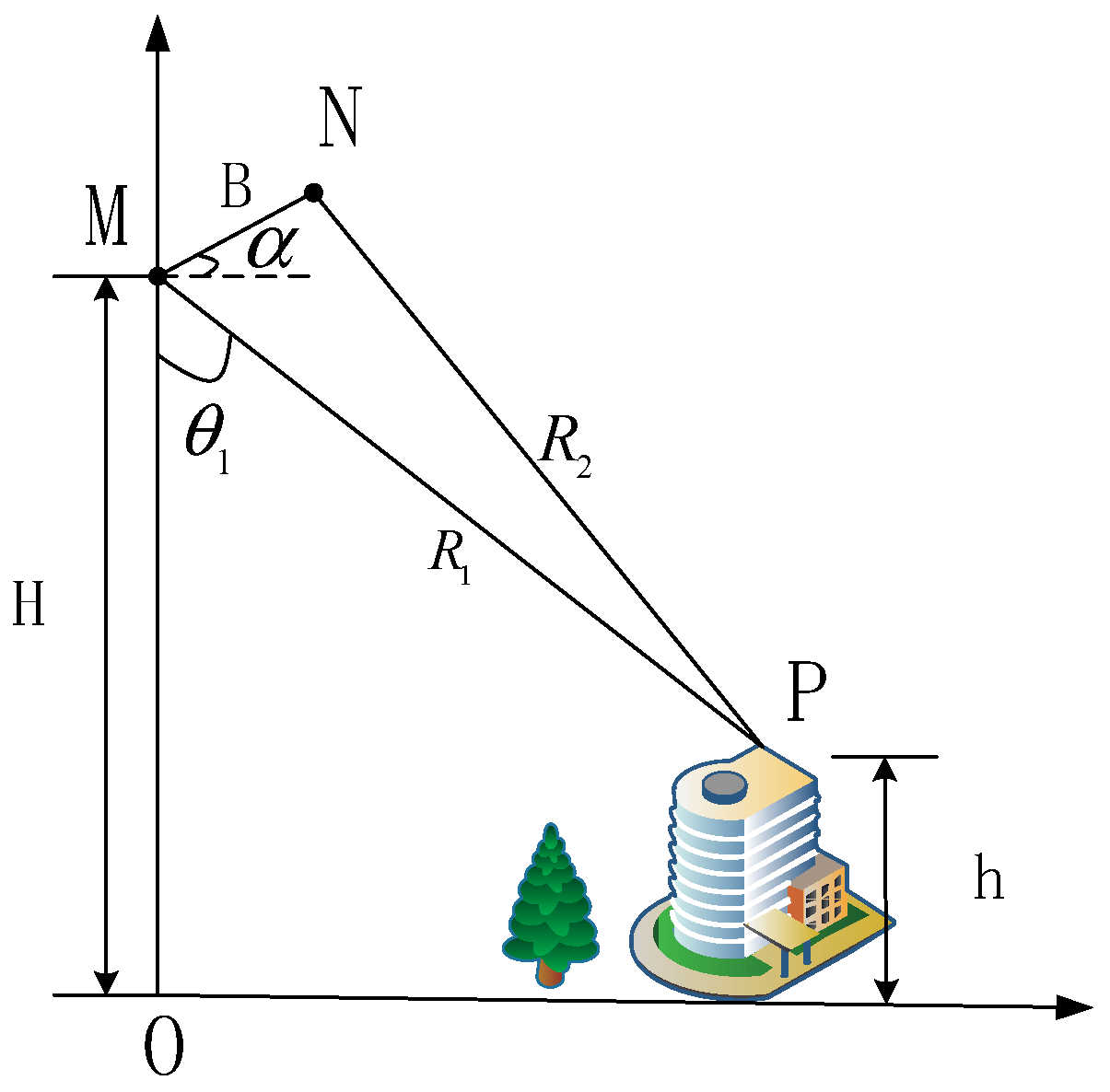
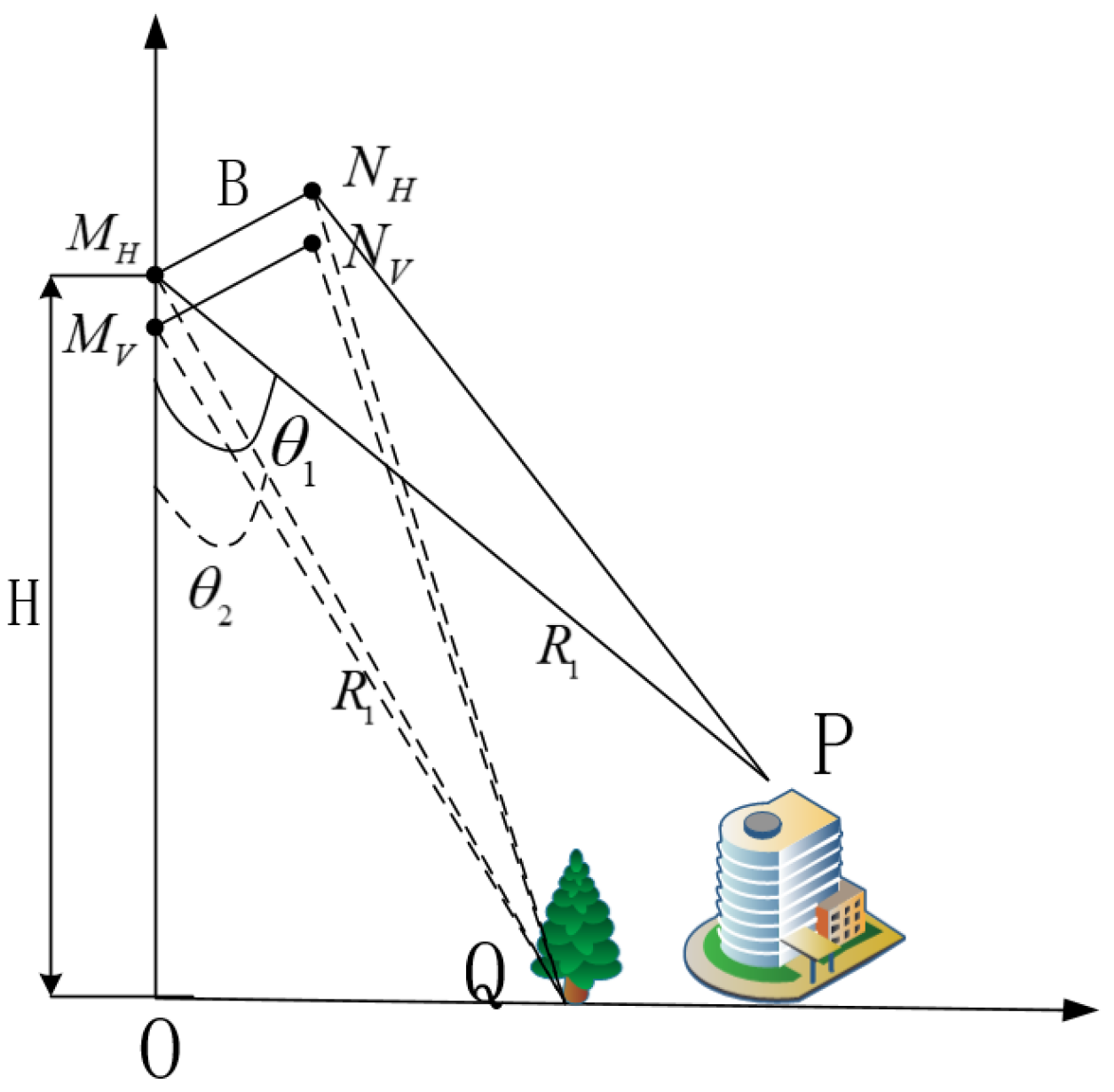
2.1.1. Interferometric SAR Model
2.1.2. PolInSAR Optimal Coherence Model
2.1.3. Height Difference
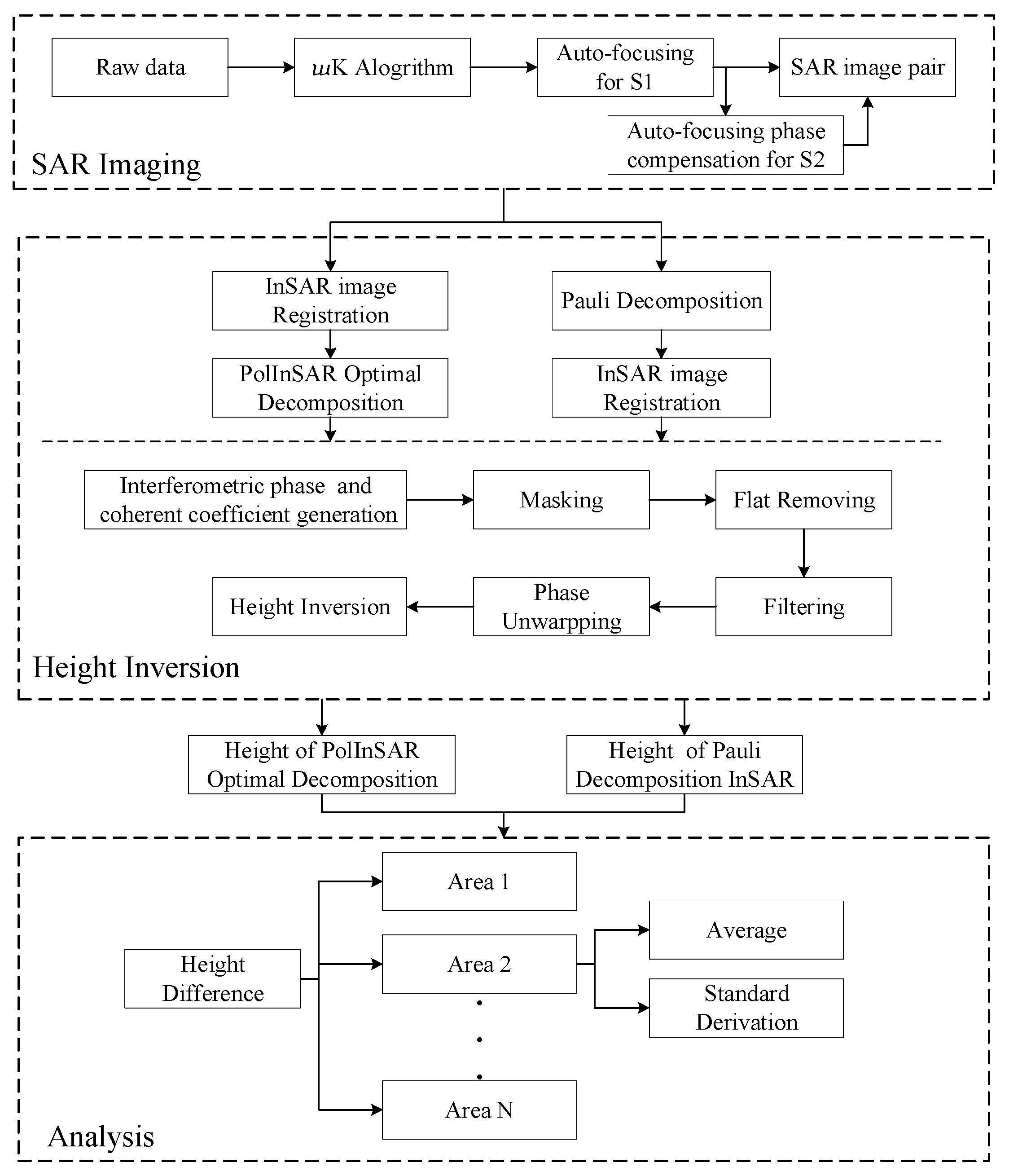
2.2. Data Processing Methodology
2.2.1. Imaging
2.2.2. Pauli Decomposition and Optimal Coherence Decomposition
2.2.3. Height Inversion
- Interferometric Phase and Coherent Coefficient Generation
- 2.
- Masking
- 3.
- Flat Removing and Filtering
- 4.
- Phase Unwrapping
- 5.
- Height Inversion
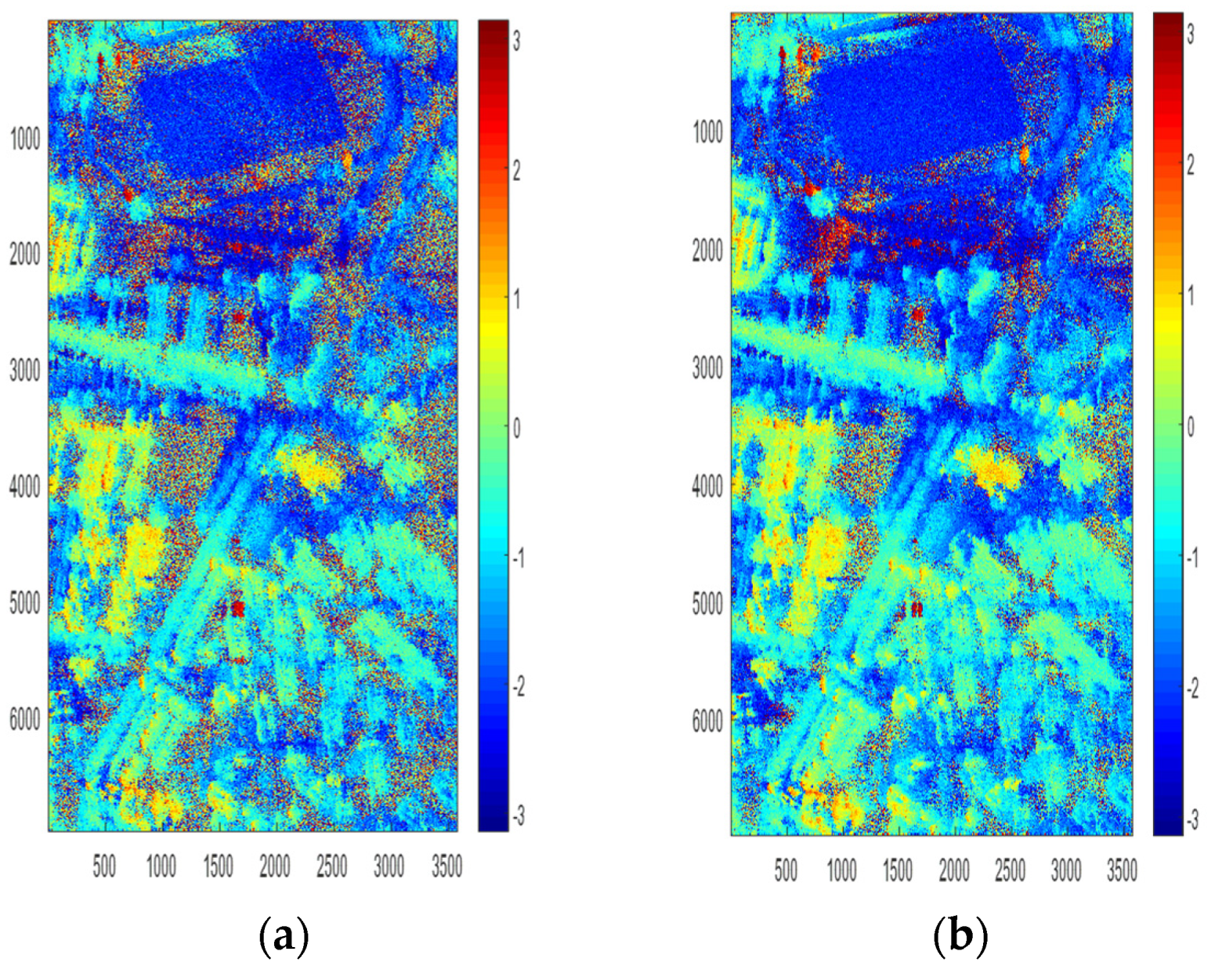
2.2.4. Height Difference Analysis
3. Results
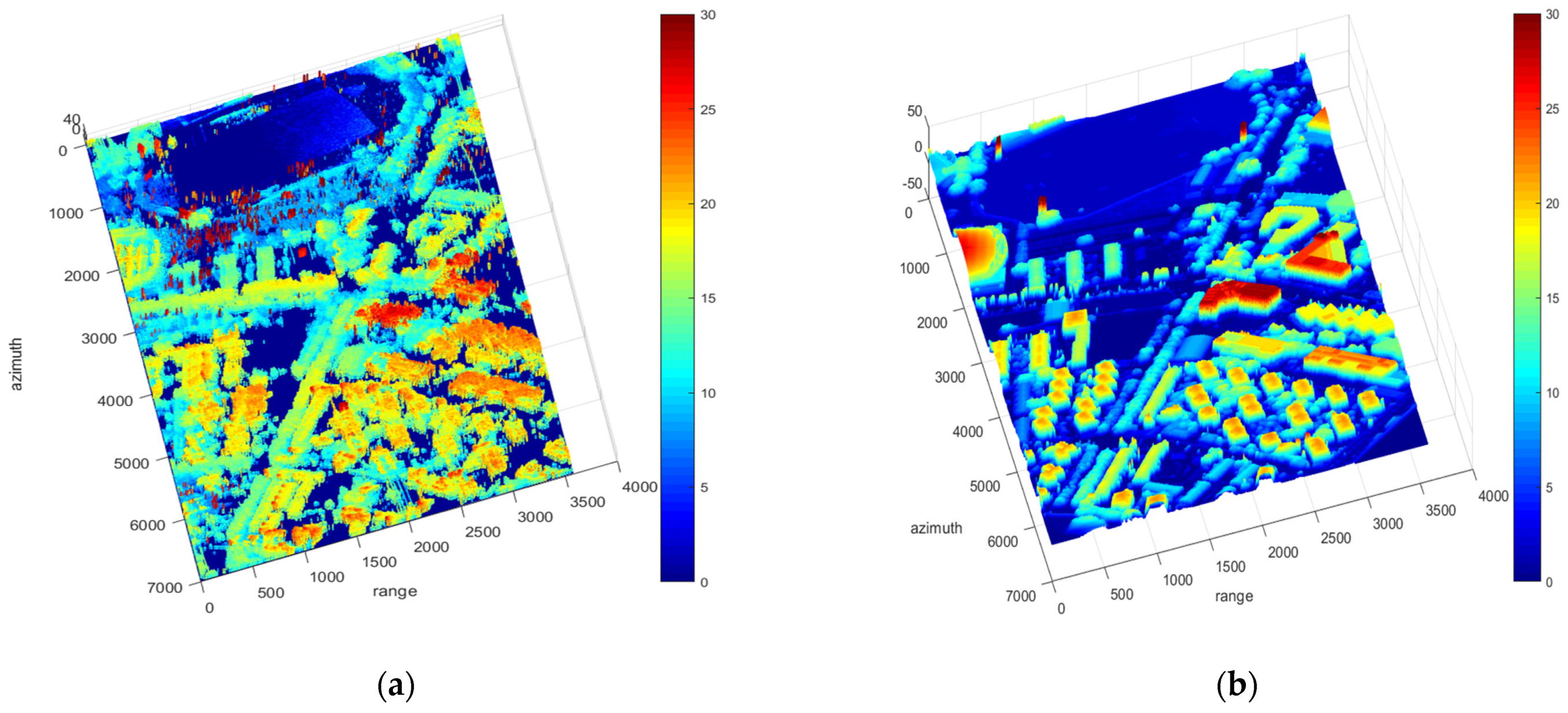
3.1. System and Experimental Data
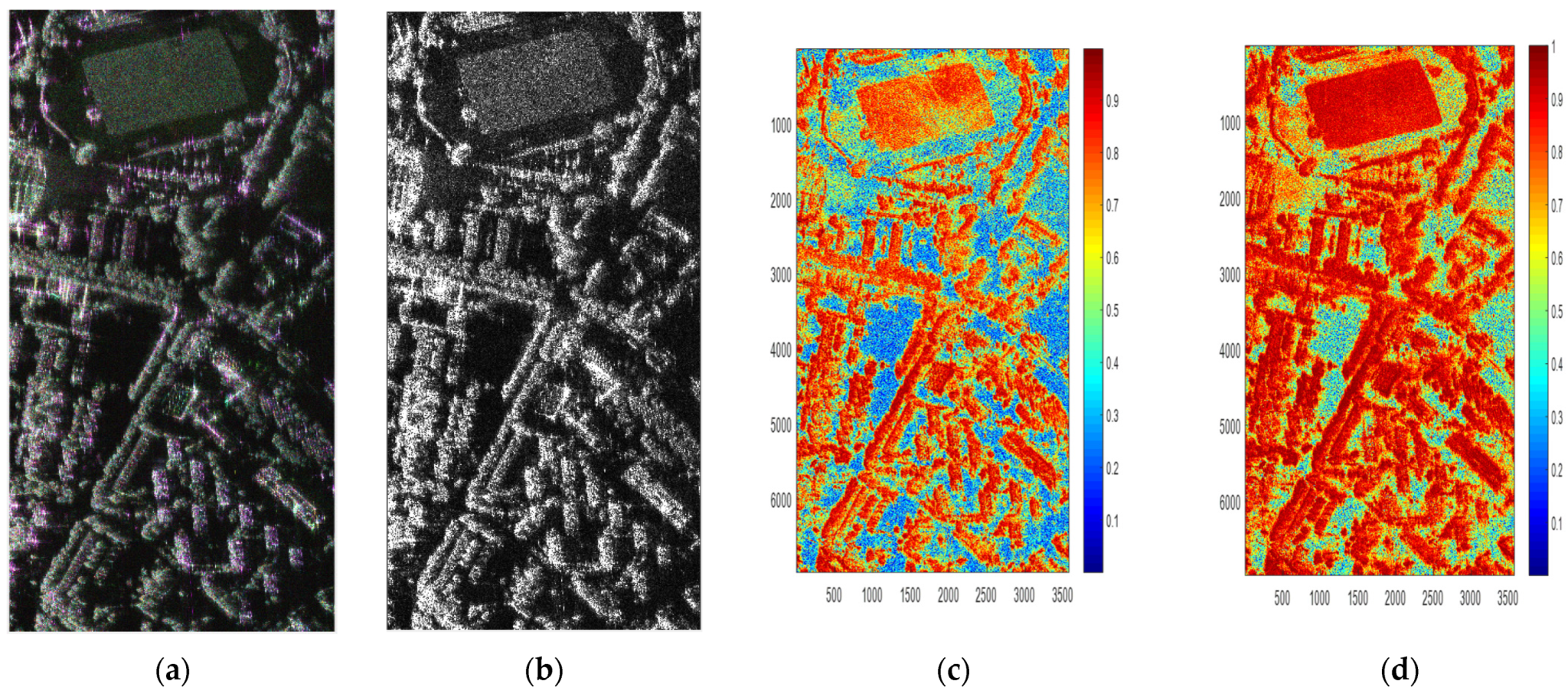
3.2. Pauli Decomposition and Optimal Coherence Decomposition Results
3.3. Interferometric Phase and Height Inversion Results
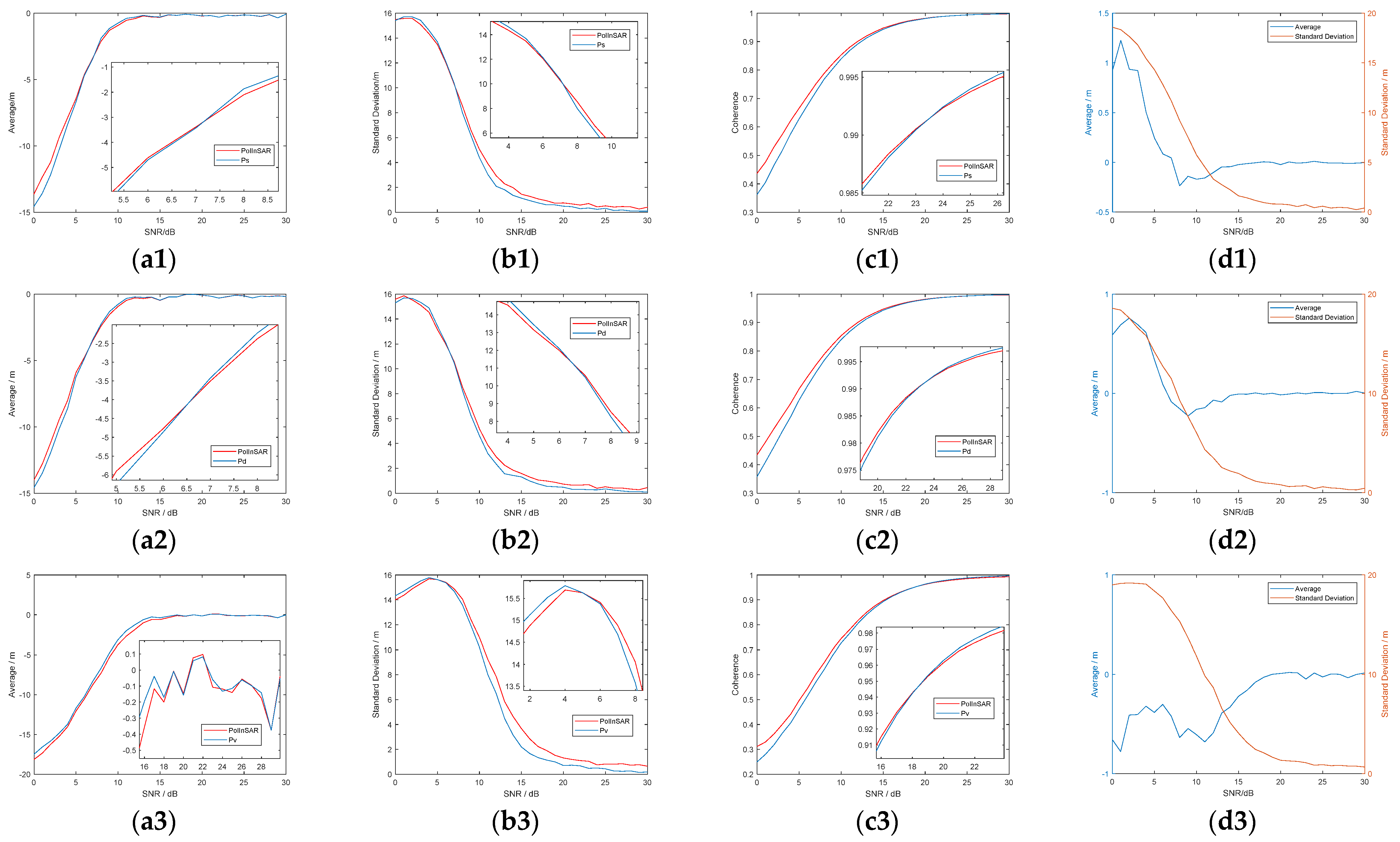
3.4. Height Inversion Results of Typical Targets
3.5. Analysis
3.5.1. One Scattering Mechanism in a Pixel
3.5.2. Mixed-Scattering Mechanisms in a Pixel
3.5.3. Mixed-Scattering Mechanism with A Main Scattering Mechanism in a Pixel
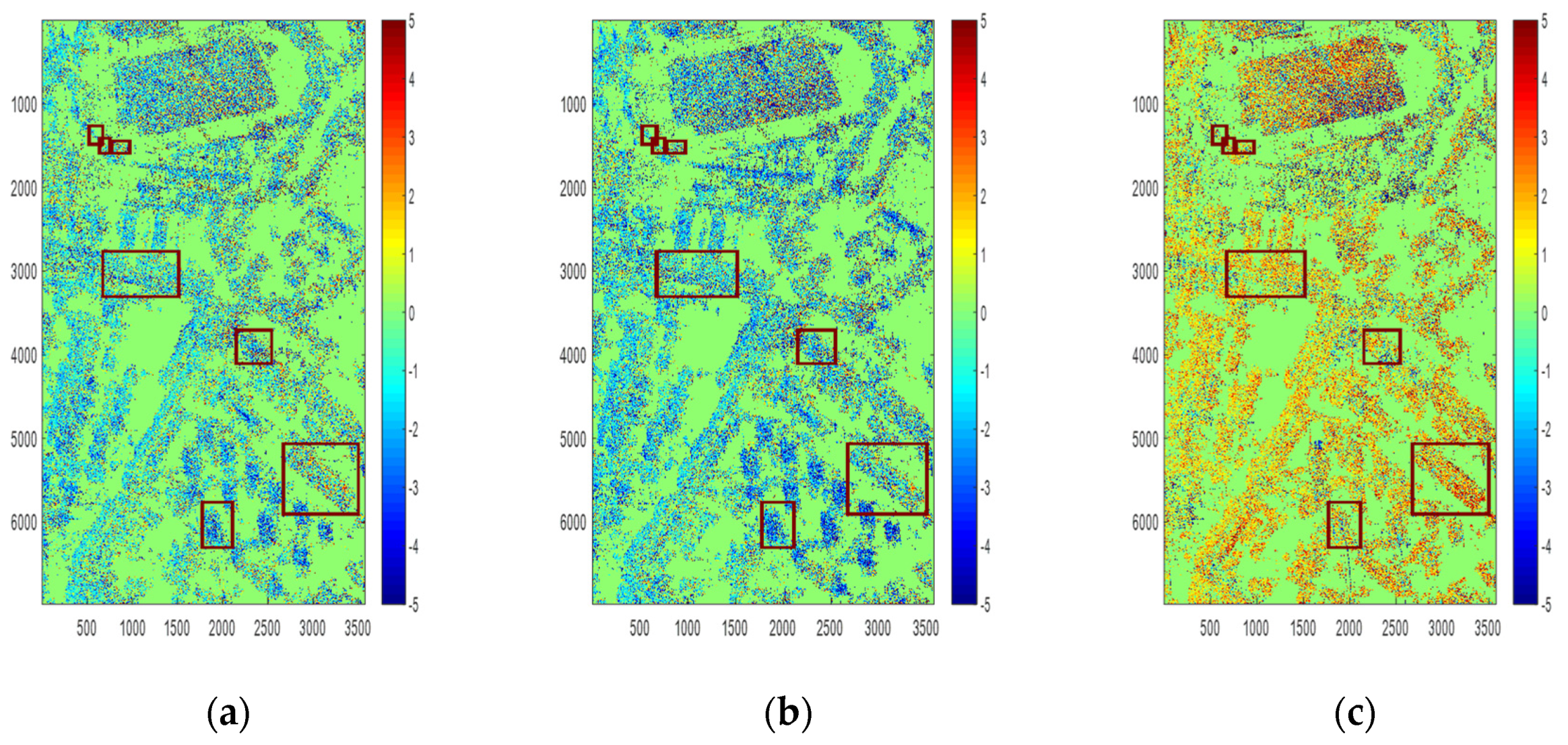
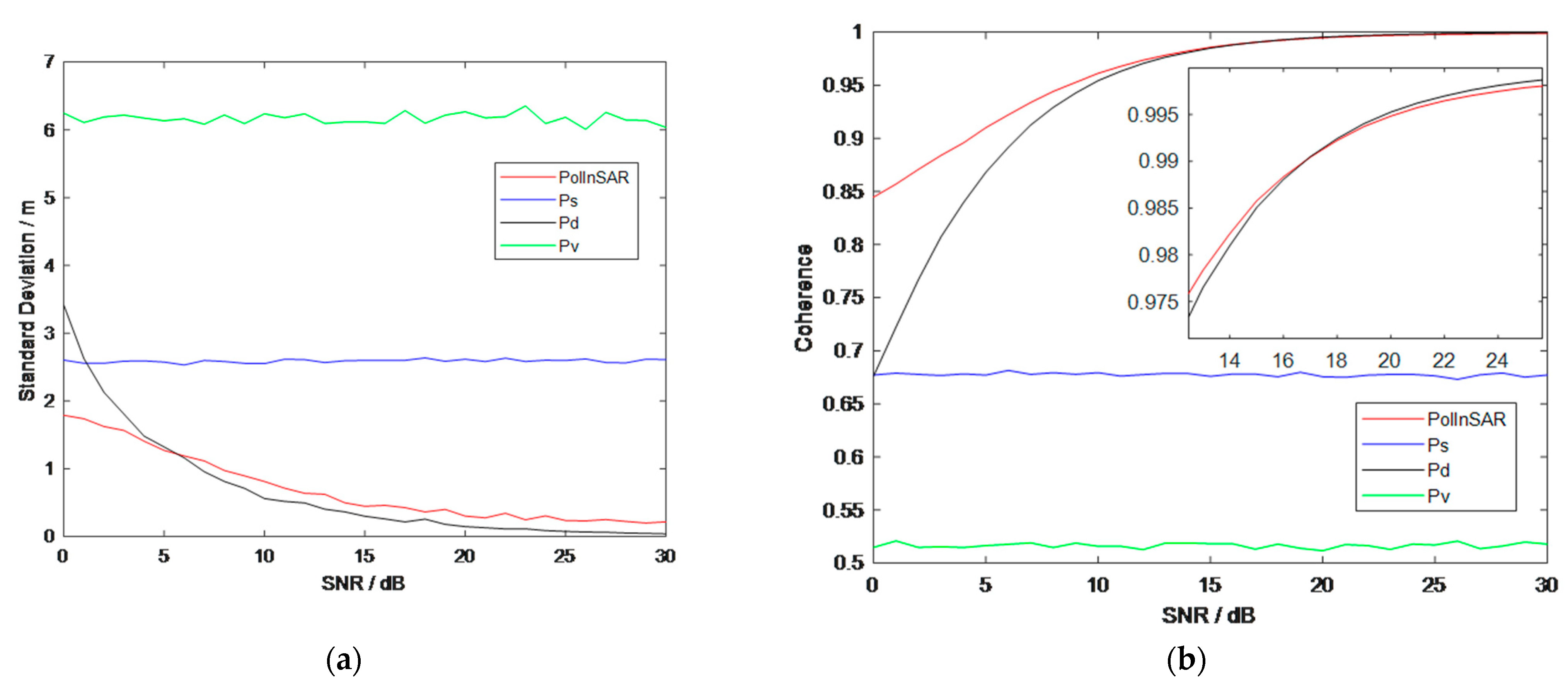
3.5.4. Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Relationship of Interferometric Phase between PolInSAR and Pauli Decomposition
Appendix B

Appendix C
References
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2002, 88, 333–382. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Essen, H.; Johannes, W.; Stanko, S.; Sommer, R.; Wahlen, A.; Wilcke, J. High resolution W-band UAV SAR. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5033–5036. [Google Scholar] [CrossRef]
- Yan, J.; Guo, J.; Lu, Q.; Wang, K.; Liu, X. X-band mini-SAR radar on eight-rotor mini-UAV. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6702–6705. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.; Lee, W.; Shin, S.; Choi, Y.; Ka, M.-H. Design and implemetation of Compact 77 GHz Synthetic aperture radar for drone based applications. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ding, M.; Tang, L.; Zhou, L.; Wang, X.; Weng, Z.; Qu, J. W Band mini-SAR on multi rotor UAV platform. In Proceedings of the 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, Germany, 20–22 January 2019; pp. 416–418. [Google Scholar] [CrossRef]
- Ding, M.-L.; Ding, C.-B.; Tang, L.; Wang, X.-M.; Qu, J.-M.; Wu, R. A W-Band 3-D Integrated mini-SAR system with high imaging resolution on UAV platform. IEEE Access 2020, 8, 113601–113609. [Google Scholar] [CrossRef]
- Engel, M.; Heinzel, A.; Schreiber, E.; Dill, S.; Peichl, M. Recent results of a UAV-based Synthetic Aperture Radar for remote sensing applications. In Proceedings of the 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021. [Google Scholar]
- Svedin, J.; Bernland, A.; Gustafsson, A. Small UAV-based high-resolution SAR using low-cost radar, GNSS/RTK and IMU sensors. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021; pp. 186–189. [Google Scholar] [CrossRef]
- Liu, W.X.; Feng, H.C.; Aye, S.Y.; Ng, B.; Lu, Y. Design and testing of multi-rotor UAV full-pol SAR system. In Proceedings of the International Conference on Radar Systems (Radar 2017), Belfast, UK, 23–26 October 2017. [Google Scholar] [CrossRef]
- Frey, O.; Werner, C.L. UAV-borne repeat-pass SAR interferometry and SAR tomography with a compact L-band SAR system. In Proceedings of the 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021. [Google Scholar]
- Shimada, M.; Kouno, T. L-band interferometric UA VSAR: Dual L-band FMCW SAR experiment for repeat pass interferometry in Taikicho, Hokkaido. In Proceedings of the 2017 IEEE Conference on Antenna Measurements and Applications (CAMA), Tsukuba, Japan, 4–6 December 2017; pp. 155–156. [Google Scholar] [CrossRef]
- Burr, R.; Schartel, M.; Grathwohl, A.; Mayer, W.; Walter, T.; Waldschmidt, C. UAV-borne FMCW InSAR for focusing buried objects. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4014505. [Google Scholar] [CrossRef]
- Bekar, A.; Antoniou, M.; Baker, C.J. Low-cost, high-resolution, drone-borne SAR imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5208811. [Google Scholar] [CrossRef]
- Fu, X.K.; Xiang, M.S.; Wang, B.N.; Jiang, S.; Wang, J. Preliminary result of a novel yaw and pitch error estimation method for UAV-based FMCW InSAR. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 463–465. [Google Scholar] [CrossRef]
- Li, F.-F.; Qiu, X.-L.; Meng, D.-D.; Hu, D.-H.; Ding, C.-B. Effects of motion compensation errors on performance of airborne dual-antenna InSAR. J. Electron. Inf. Technol. 2013, 35, 559–567. [Google Scholar] [CrossRef]
- Lv, Z.X.; Li, F.F.; Qiu, X.L.; Ding, C.B. Effects of motion compensation residual error and polarization distortion on UAV-borne PolInSAR. Remote Sens. 2021, 13, 618. [Google Scholar] [CrossRef]
- Till, N.; Luciano, V.D.; dos Santos, J.R.; Freitas, C.D.C.; Araujo, L.S. Tropical forest measurement by interferometric height modeling and P-band radar backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar] [CrossRef]
- Kenyi, L.W.; Dubayah, R.; Hofton, M.; Schardt, M. Comparative analysis of SRTM–NED vegetation canopy height to LIDAR-derived vegetation canopy metrics. Int. J. Remote Sens. 2009, 30, 2797–2811. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Coherence optimisation in polarimetric SAR interferometry. In Proceedings of the 1997 IEEE International Geoscience and Remote Sensing Symposium, Singapore, 3–8 August 1997. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarization Applications in Remote Sensing; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Yamada, H.; Yamaguchi, Y.; Rodriguez, E.; Kim, Y.; Boerner, W. Polarimetric SAR interferometry for forest canopy analysis by using the super-resolution method. In Proceedings of the 2001 IEEE Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001; pp. 1101–1103. [Google Scholar] [CrossRef]
- Tabb, M.; Orrey, J.; Flynn, T.; Carande, R. Phase diversity: A decomposition for vegetation parameter estimation using polarimetric SAR interferometry. In Proceedings of the 4th European Synthetic Aperture Radar Conference, Cologne, Germany, 4–6 June 2002. [Google Scholar]
- Guillaso, S.; Ferro-Famil, L.; Reigber, A.; Pottier, E. Analysis of built-up areas from polarimetric interferometric SAR images. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 1727–1729. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Wang, C.; Fu, H.; Xie, Q.; Xiong, W. Building scattering centers analysis with polarimetric SAR interferometry based on ESPRIT algorithm. In Proceedings of the 2014 Third International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Changsha, China, 11–14 June 2014; pp. 171–175. [Google Scholar] [CrossRef]
- Colin, E.; Titin-Schnaider, C.; Tabbara, W. An interferometric coherence optimization method in radar polarimetry for high-resolution imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 167–175. [Google Scholar] [CrossRef]
- Colin-Koeniguer, E.; Trouve, N. Performance of building height estimation using high-resolution PolInSAR images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5870–5879. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.; Dupuis, X.; Paillou, P.; Hajnsek, I. PolInSAR analysis of X-band data over vegetated and urban areas. IEEE Trans. Geosci. Remote Sens. 2006, 44, 356–364. [Google Scholar] [CrossRef]
- Wang, P.; Wang, C.C.; Peng, X. Building height information extraction method on three-component decomposition for PolInSAR data. Eng. Surv. Mapp. 2014, 23, 16–20. [Google Scholar] [CrossRef]
- Papathanassiou, K.P. POL-IN-SAR. Available online: http://cobalt.cneas.tohoku.ac.jp/users/sato/10%20POL_InSAR.pdf (accessed on 19 February 2022).
- Meng, D.D.; Hu, D.H.; Ding, C.B. Precise focusing of airborne SAR data with wide apertures large trajectory deviations: A chirp modulated back-projection approach. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2510–2519. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Baran, I.; Stewart, M.P.; Kampes, B.M.; Perski, Z.; Lilly, P. A modification to the Goldstein radar interferogram filter. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2114–2118. [Google Scholar] [CrossRef] [Green Version]
- Shimada, T.; Natsuaki, R.; Hirose, A. Pixel-by-pixel scattering mechanism vector optimization in high-resolution PolInSAR. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2587–2596. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Frequency | 15.2 GHz |
| Baseline | 0.62 m |
| Bandwidth | 1.2 GHz |
| Platform Height | 206 m |
| Incidence Angle | 70° |
| Resolution | 0.3 m |
| Area | Average | ||||
|---|---|---|---|---|---|
| 1 | −0.23 | −0.33 | 1.15 | 0.10 | −1.39 |
| 2 | −0.85 | −1.07 | 1.02 | 0.22 | −1.87 |
| 3 | −0.26 | −0.69 | 1.42 | 0.43 | −1.68 |
| 4 | −1.69 | −2.25 | 1.02 | 0.56 | −2.71 |
| 5 | −1.13 | −1.24 | 0.94 | 0.10 | −2.07 |
| 6 | −0.64 | −0.87 | 0.48 | 0.24 | −1.12 |
| 7 | −0.77 | −0.84 | 1.27 | 0.07 | −2.04 |
| Case | Mode | Preset Height (m) | Simulated Height (m) |
|---|---|---|---|
| 2.1 | 9.43 | ||
| 6 | 5.86 | ||
| 12 | 11.85 | ||
| 15 | 14.85 | ||
| 2.2 | 9.54 | ||
| 12 | 11.85 | ||
| 6 | 5.85 | ||
| 15 | 14.84 | ||
| 2.3 | 10.64 | ||
| 6 | 5.93 | ||
| 15 | 14.92 | ||
| 12 | 11.93 |
| Case | Mode | Amplitude Ratio | Experimental Height (m) | Height Result of Simulation (m) | Height Result of Derivation (m) |
|---|---|---|---|---|---|
| 1 | 25.44 | 25.89 | 24.96 | ||
| 1.00 | 26.20 | 25.96 | 26.15 | ||
| 0.77 | 26.80 | 26.56 | 26.27 | ||
| 1.20 | 23.83 | 23.59 | 23.80 | ||
| 2 | 22.19 | 22.85 | 22.69 | ||
| 1.00 | 23.07 | 22.96 | 23.89 | ||
| 0.75 | 23.98 | 23.88 | 23.89 | ||
| 1.88 | 20.98 | 20.88 | 21.17 | ||
| 3 | 18.25 | 18.90 | 18.75 | ||
| 1.00 | 18.48 | 18.44 | 19.64 | ||
| 0.87 | 19.34 | 19.30 | 19.65 | ||
| 0.74 | 17.66 | 17.62 | 17.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Qiu, X.; Cheng, Y.; Shangguan, S.; Li, F.; Ding, C. Multi-Rotor UAV-Borne PolInSAR Data Processing and Preliminary Analysis of Height Inversion in Urban Area. Remote Sens. 2022, 14, 2161. https://doi.org/10.3390/rs14092161
Lv Z, Qiu X, Cheng Y, Shangguan S, Li F, Ding C. Multi-Rotor UAV-Borne PolInSAR Data Processing and Preliminary Analysis of Height Inversion in Urban Area. Remote Sensing. 2022; 14(9):2161. https://doi.org/10.3390/rs14092161
Chicago/Turabian StyleLv, Zexin, Xiaolan Qiu, Yao Cheng, Songtao Shangguan, Fangfang Li, and Chibiao Ding. 2022. "Multi-Rotor UAV-Borne PolInSAR Data Processing and Preliminary Analysis of Height Inversion in Urban Area" Remote Sensing 14, no. 9: 2161. https://doi.org/10.3390/rs14092161
APA StyleLv, Z., Qiu, X., Cheng, Y., Shangguan, S., Li, F., & Ding, C. (2022). Multi-Rotor UAV-Borne PolInSAR Data Processing and Preliminary Analysis of Height Inversion in Urban Area. Remote Sensing, 14(9), 2161. https://doi.org/10.3390/rs14092161






