Next Article in Journal
Urban Area Mapping Using Multitemporal SAR Images in Combination with Self-Organizing Map Clustering and Object-Based Image Analysis
Previous Article in Journal
Cooperative Electromagnetic Data Annotation via Low-Rank Matrix Completion
Previous Article in Special Issue
A Comparison of Spectral Bin Microphysics versus Bulk Parameterization in Forecasting Typhoon In-Fa (2021) before, during, and after Its Landfall
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 1
10.3390/rs15010119
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

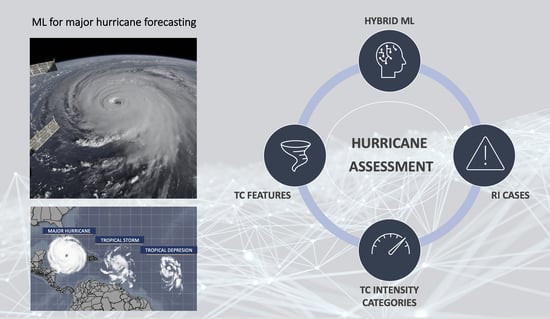
Advanced Machine Learning Methods for Major Hurricane Forecasting

by
Javier Martinez-Amaya
,
Cristina Radin
and
Veronica Nieves
*
Image Processing Laboratory, University of Valencia, 46980 Valencia, Spain
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(1), 119; https://doi.org/10.3390/rs15010119
Submission received: 17 November 2022 / Revised: 12 December 2022 / Accepted: 24 December 2022 / Published: 26 December 2022
(This article belongs to the Special Issue Tropical Cyclone Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Hurricanes, rapidly increasing in complexity and strength in a warmer world, are one of the worst natural disasters in the 21st century. Further studies integrating the changing hurricane features are thus crucial to aid in the prediction of major hurricanes. With this in mind, we present a new framework based on automated decision tree analysis, which has the capability to identify the most important cloud structural parameters from GOES imagery as predictors for hurricane intensification potential in the Atlantic and Pacific oceans. The proposed framework has been proved effective for predicting major hurricanes with an overall accuracy of 73% from 6 to 54 h in advance (both regions combined).

Graphical Abstract

1. Introduction

With rising global temperatures, it is more difficult to gauge complex ocean and atmospheric interactions, and hence the potential of a tropical cyclone (TC) to become much stronger in the short term [1,2,3,4]. It has been long disputed whether there is a positive trend in intensity-related studies given the limited quality and temporal length of the data (e.g., [5]). However, it is becoming increasingly apparent in the literature that a variety of TC properties have changed over the past 40 years [2]. Moreover, there are particularities regarding both the shape and levels of strength, depending on the region where they form (e.g., [2]). Hurricanes are strong TCs that occur in the Atlantic or northeastern (NE) Pacific oceans and behave differently than other types of storms. In the face of this complexity, it is a challenging task to disentangle which hurricane-related parameters or combinations of parameters and pre-existing factors are fundamental in the hurricane’s growth. Advanced methods should hence be set up to reflect this complexity to improve early prediction and enhanced decision-making [6]. A wider comprehension of the most robust hurricane features and precursors to the formation of a hurricane could certainly help us to be better prepared for future destructive storms. Without a doubt, the impact of an intensified hurricane can cause catastrophic damage not only to coastlines, but also hundreds of miles inland in terms of regional economic impacts and human losses [7].
Over the last two decades a number of different approaches have been proposed to predict hurricane genesis and intensity evolution (https://www.nhc.noaa.gov/modelsummary.shtml, accessed on 16 November 2022). The dynamical (or numerical), statistical, and the blended statistical-dynamical models are the most commonly used ones for intensity prediction. For example, dynamical models, such as the hurricane weather research and forecast (HWRF) system [8,9], which use numerical models to account for the underlying physical processes governing the atmosphere with all the adjustments and difficulties that this entails. These models are also computationally expensive and show a limited range of intensities that can be simulated [10]. In contrast, statistical models like the multiple linear regression (MLR) forecast model [11] are based on historical linear relationships between storm behavior and storm-specific details. Nevertheless, it would be desirable to consider the possibility of a complex nonlinearity in this context. Finally, the statistical-dynamical approaches, such as the statistical hurricane intensity prediction scheme (SHIPS) [12] and others [13], can also provide guidance in the prediction of future events by combining the strengths of probabilistic forecasts and dynamical models. Even so, these models still have some limitations, such as incomplete understanding of air-sea interaction processes and the absence of high-quality observations of the inner core [13]. They also often use fairly simple statistical methods, such as multiple linear regression, linear discriminant analysis, and logistic regression [14]. Another drawback is that these models usually fail for cases where rapid intensification (RI) occurs (i.e., increase in the maximum sustained winds of a TC of at least 55 km/h in a 24-h period) [15,16]. In addition to this, most of these models produce a notable high number of false positives (from 17–50% and up to 90–100% in the Atlantic basin for intensification rates of about 102 km/h in 48 h or larger), frequently incorrectly forecasting RI [e.g., 14]. This is a critical disadvantage since most major TCs globally rapidly intensify at some point in their life cycle [17].
The past few years have seen remarkable advances by incorporating machine learning (ML) [18], from traditional ML algorithms, including neural networks [19,20,21], to more advanced deep learning techniques with complex architectures [13,22]. There are also ensemble learning methods, such as random forests (RF) or random decision forests. for classification, regression, and other problems [23], which are less tedious than setting up a neural network. Yet, they can identify the most important features from the training dataset and learn complex nonlinear patterns of change over time as the number of trees in the forest grows [24,25]. Fundamentally, each of the outcomes leads to additional nodes (outputs of those decisions), which branch off into other possibilities with a “treelike shape” [26]. The more trees a forest contains, the more accurate it is. Therefore, in this study, we propose to use RF for major hurricane prediction, and treat the predictability as a supervised classification problem. A further advantage is that RF is less sensitive to overfitting compared to other classification techniques [25]. This is because with RF classifiers, the errors stabilize before a large number of trees is achieved. Perhaps the only downside to this framework is the fact that such a classification approach does not provide specific wind intensities, but classes that represent main groups of hurricane categories over their life cycle (each of which corresponds to a range of intensity values).
Regardless of the method, the majority of studies that investigate TC intensity evolution are focused on the surrounding large-scale environment (either in terms of complicated dynamic and thermodynamic processes that have not been fully resolved or key physical variables in the statistical behavior of the storms). Thus far, less progress has been made towards integrating the anatomy of the storms in the forecast models [27,28,29]. In these studies, instead of dealing directly with environmental dynamics, the focus is on structural properties from satellite image measurements that can indirectly reflect those environmental changes (e.g., [30]). Ultimately, the environmental processes clearly leave some fingerprints in the size, shape, and temperature features of the TC cloud. For instance, some studies have pointed to a connection between the storm/TC size (and other anatomical structural parameters) and the intensity changes [31,32,33,34,35]. The same applies to other parameters, including the temperature structure of the storm, which could be just as much, if not more, important to TC intensity growth. In fact, a basis exists for using the brightness temperature (BT) information (from GOES imagery), estimated in the outer bands and central features of TCs for each TC intensity category (tropical storm, minor hurricane, and major hurricane) [36]. But, nonetheless, the forecasting capability of a model based on all these (temperature and anatomical cloud) structural properties combined together have not yet been fully explored in terms of categories [37].
From this perspective, here, we present a novel ML framework to determine an optimal set of TC cloud properties to assess the hurricane’s growth to a major hurricane. ML is capable of adapting and making (not always obvious) nonlinear connections between what it sees in the TC satellite information and the severity categories (based on the maximum intensity that the TC attained during its lifetime). To establish this complex relationship, we use an RF classification model trained to accurately predict classes and categorize the output into different groups, according to changes in the temperature and anatomical characteristics of the TC cloud for different lead-times (defined as the time to maximum development from when the computation is initiated). The classifiers are intrinsically designed to be trained and simultaneously tested for its accuracy against an actual portion of the dataset to improve prediction of the classes. Since our intent is to predict major hurricanes only, to simplify analyses, we have only considered two classes: tropical storms that remained just below hurricane category 1 status (TSs herein) and TSs that developed to major hurricane (MH) strength (i.e., hurricanes with category 3, 4 or 5). A detailed description of the approach can be found in the Materials and Methods section.
This is the first study that explores a unique combination of satellite cloud properties for major hurricane prediction, and one of the few focused on the use of an RF approach to this intent. This approach provides a powerful complementary assessment tool for forecasters, especially when intensification is more dramatic, such as when a tropical storm becomes a high-intensity TC. It also allows inclusion of additional parameters and (environmental or other) conditions for additional investigations in the future.

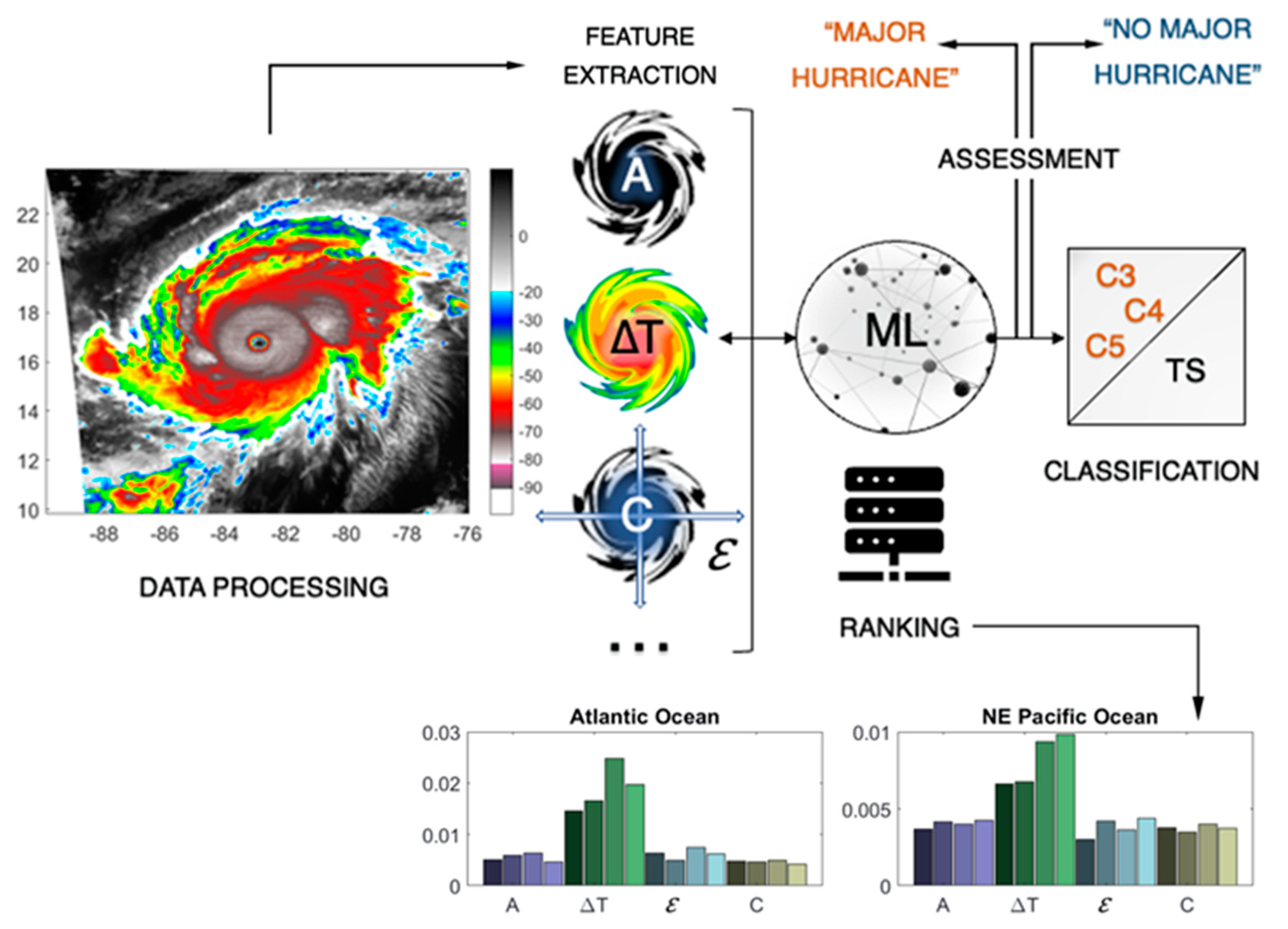
2. Materials and Methods

2.1. Data Products

The International Best Track Archive for Climate Stewardship (IBTrACS) provided by NOAA [38] was used to obtain the (location and intensity) information of the TCs, which is available every 3 h. The composite GOES series satellites, such as the infrared band 4 GOES-8-15 and band 13 GOES-16-17 imagery (https://www.avl.class.noaa.gov/saa/products/welcome, accessed on 16 November 2022), were converted to brightness temperature [39,40] to obtain temperature information of the TC cloud’s system at 15 or 30 min intervals. Then, the IBTrACS data was interpolated to the same time resolution as the one of the satellite images. The period of train/test was set from 1995 (when the first significantly improved series of GOES was operational) to 2019. The data from 2020 onwards was reserved to explore additional cases of TCs that underwent RI beyond the period of analysis. The regions of study are the North Atlantic Ocean (from −110° to 0°E and from 5° to 50°N) and the NE Pacific Ocean (from −180° to −75°E and from 5° to 50°N), based on the typical TC formation regions (https://www.nhc.noaa.gov/climo/, accessed on 16 November 2022).

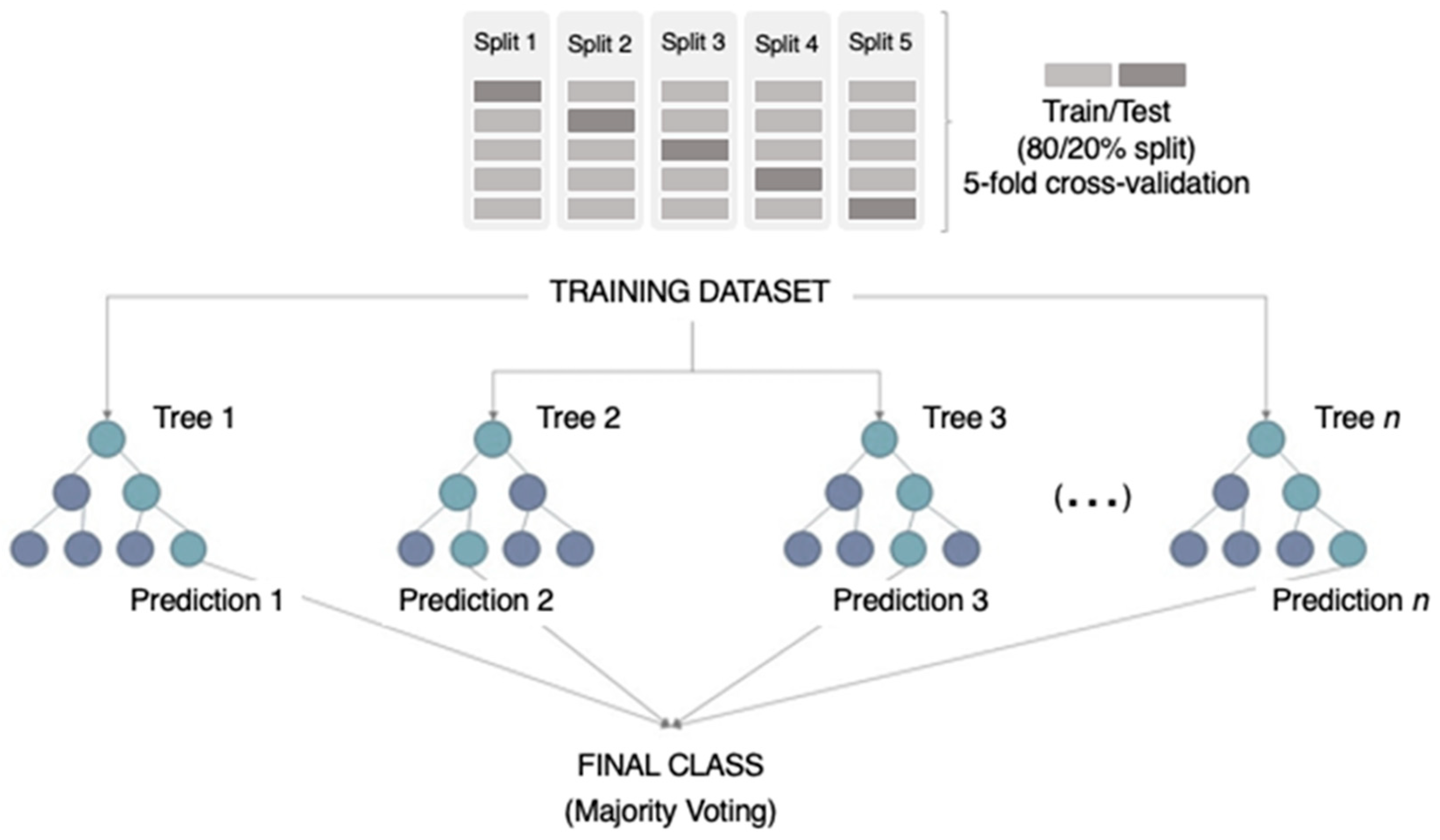
2.2. Model Construction and Evaluation Metrics

For each lead-time, a classification prediction model was built on the ensemble of RF, performed via 5-fold randomized cross-validation as discussed in this paper (see Figure 1). Alternatively, other non-parametric supervised methods, such as support vector machine or k-nearest neighbors, were also explored. However, the best-compromise between bias and variance [41] was found with our proposed model, according to the output metrics of the model (also discussed next).
We focus on Cohen’s kappa (k) and precision (pMH) for the model evaluation [42]. The first metric, defined as k = 2 × (TP × TN − FN × FP)/[(TP + FP) × (FP + TN) + (TP + FN) × (FN + TN)], is a measure of the observed non-chance agreement between all classifiers (to categorize the events) divided by the possible amount of non-chance agreement. Note that a true positive (negative), or TP (TN), is an outcome where the model correctly predicts the positive (negative) class, i.e., a MH (TS) event (using the MATLAB confusionmat function). Similarly, a false positive (negative), or FP (FN), indicates that the model incorrectly predicts the positive (negative) class. The resulting k estimates are interpretable as probabilities of agreement [43]. The higher the k value, the better the model correctly classifies the events into the two classes, within its range of [−1, +1]. In addition, the precision or positive predictive value, defined as pMH = (TP)/(TP + FP), was computed to assess the probability that an event predicted as positive is positive, as we prioritize the prediction of MHs.
Furthermore, to improve the computational efficiency of our RF models, the main hyper-parameter (the number of iterations, aka trees) was tuned by establishing a stopping criterion based on the mean k score. The general strategy is to update the RF with a new tree, for each iteration, until there is little-to-no change. This is when each model reaches “performance saturation” (i.e., the model does not improve significantly in terms of predictive power). Here, we consider that the accuracy stabilizes when the k metric has a value just above, and relative to, the mean value for a number of five consecutive iterations. We find that, although the k scores initially fluctuate over the iterations, the RF generally saturates no later than with 100 trees. On this account, the number of iterations was initialized randomly and assessed in increments of 5 trees until it reached 100 iterations. Throughout these iterations, the algorithm chooses the best k-value over the 100 iterations meeting that saturation condition. This prior analysis eliminates an arbitrary selection of the maximum number of iterations, and yields improvements in terms of computational efficiency as the learning times are reduced.

3. Results and Discussion

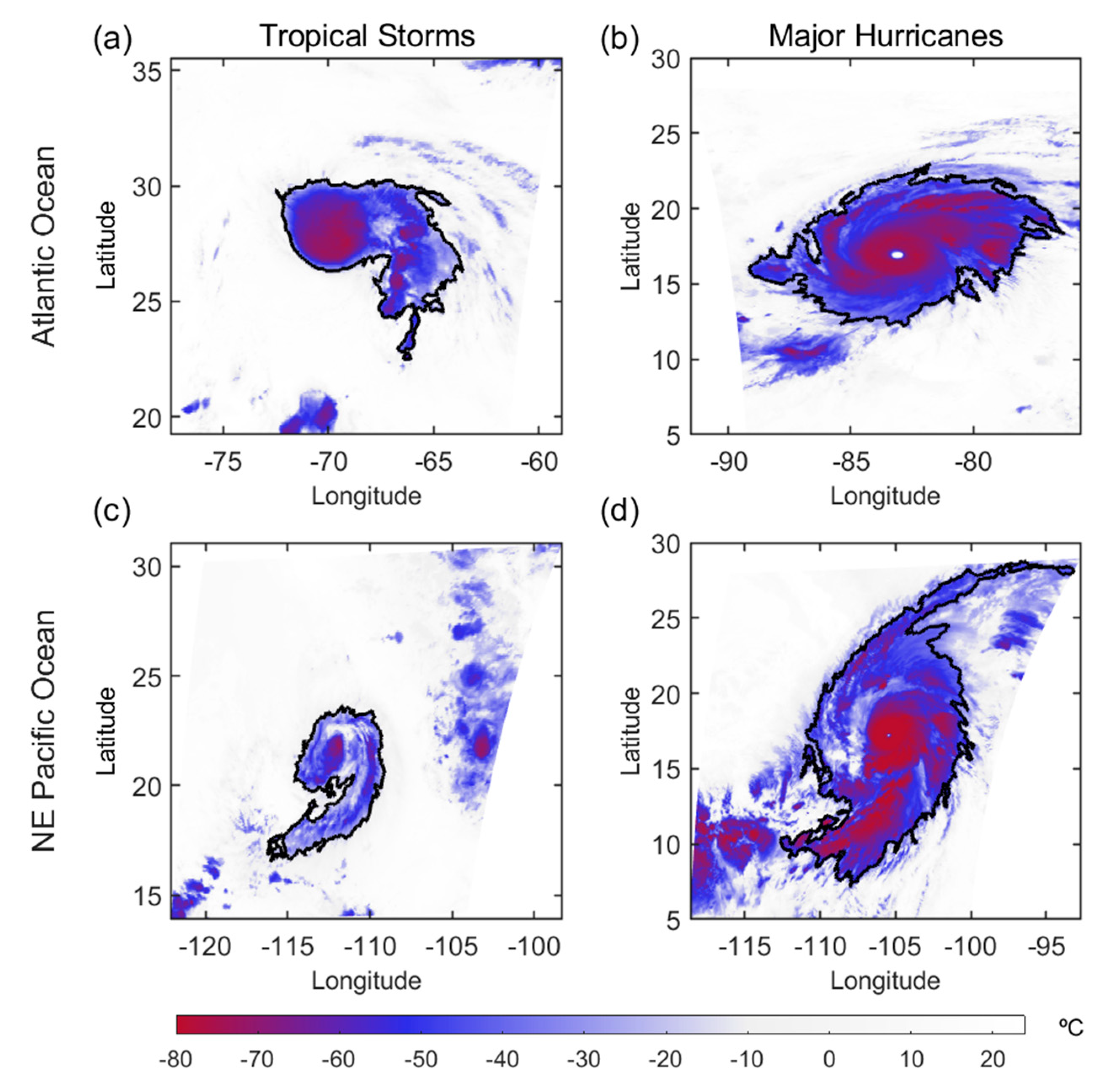
3.1. Optimal Combination of Key Structural Parameters Linked to Tropical Storm Intensification

To determine whether the TC severity categories have a positive association with the anatomical and temperature behavior of the cloud system, we analyzed their size, shape, and inner-outer core temperature evolution every 6 h (going backwards in time starting from the time of maximum intensity peak). Analysis for a range of lead-times is given in the following subsection. Here, we discuss the methods for extracting the cloud parameters from GOES measurements and the relative importance of the parameters role for predicting MHs. The following parameters were considered (see Figure 2): (1) the area of the associated cloud; (2) the temperature difference between the inner eye and outer edges of the cloud; (3) the morphological features (circularity and eccentricity).
The boundary map depicting the spatial pattern of the TC cloud was first generated using a standard unsupervised k-means clustering method [44] applied to GOES BT images from 1995 (see Materials and Methods), by assuming that the TC is in the region with the most cloud cover (as in the following Matlab demo: https://blogs.mathworks.com/loren/2011/01/20/tracking-a-hurricane-using-web-map-service-wms/, accessed on 16 November 2022). Then, the area parameter was calculated from the specified boundary (using the MATLAB areaint function). In this way, there is no compelling need to conform to any predetermined definition or criteria for storm size [45,46,47,48,49].
Next, the difference between the median temperature within the internal (eye) region and at the external boundary was calculated. For the internal region of the TC cloud, a 0.6° × 0.6° (0.7° × 0.7°) window was selected in its center, given by IBTrACS (see Materials and Methods). This optimal window size in between the internal-to-external temperature bands was identified after processing all images, and we noted that similar or slightly bigger windows can still capture the greatest temperature changes between these contrasting regions. Other parameters representing temperature change within the TCs, such as the temperature gradient, were compared and also yielded similar results.
Lastly, the morphological aspects of the system tied to the external boundary were measured (with the MATLAB regionprops function), as it is already known that storms tend to gain symmetry and a circular structure as they intensify [37,49]. Mainly, we examined the circularity (“roundness”) and eccentricity (deviation from a perfect circle), individually and together. These are standard parameters, defined as (4*Area*pi)/(Perimeter2) and the ratio of the distance between the foci of the ellipse and its major axis length, respectively. Both parameters range between 0 and 1.
We observed that, while the satellite portrait of a TS or MH is unmistakable (see Figure 3), the shape and radial profiles of BT temperature for a hurricane are less recognizable before it reaches category 3 and higher. This reinforces the idea of examining only two classes (as discussed in the introduction), as opposed to all possible groups of categories, as a way to distinguish simple TSs from those that can potentially become devastating hurricanes within days (if not hours). Moreover, this binary classification of events [23,50], often used in the detection of extreme rare events [51], makes the training easier.
All the TC cloud features were then integrated into our RF models together with the intensity information of the TC using (the MATLAB fitensemble function with) a novel configuration (see Materials and Methods), which we implemented in an automated manner to predict the two classes, TSs and MHs. First, due to some imbalance between the two classes, we resample the data into an equal percentage of samples for each class (and lead-time). Primarily, we undersampled the majority class (TS) by randomly removing samples, thereby increasing the presence of the minority class of the samples (MH) in the training set [52]. The total number of samples for each case are shown in Table 1, Table 2 and Table 3.
The next step was to perform the train-test procedure on an 80/20 split (the best of all tested splits), where 80% of the dataset is held for training and 20% for testing with no overlapping cases. Given that the dataset available is relatively small, it was deemed not appropriate to split the training part again into validation and train to re-test the model configuration. Nonetheless, our RF classifier consists of many decision trees, and it uses bootstrap aggregation (or bagging) and feature randomness, a method to randomly select subsets from the original training set when building each tree to combine the predictions from all models, which reduces the variance of the performance while maintaining the low bias of decision trees. The optimal number of trees (or iterations) was established based on Cohen’s kappa (k) metric (also described in Materials and Methods section).
From the combination of ensemble predictions, a measure of variable importance was computed (using the MATLAB predictorImportance function). We identified that the most important predictor variables are the temperature features, the area, and the morphology of the TC system (in order of importance, see Figure 2). We also determined that the dramatic differences in the shape of the cloud were slightly better captured by combining both the circularity and eccentricity, rather than with either one of them individually (not shown). The highest performance was achieved with all the grouped variables in the models as it helps “balance” every feature of the TC.
For further robustness, the stochastic nature of our models was evaluated using a cross-validation iterator, such as k-fold, for the Atlantic Ocean, NE Pacific Ocean, and both regions combined. This resampling procedure divides the data into k random groups of samples, called folds [41]. As our data was set to k = 5, the 80/20 split for training and testing data was repeated 5 times, each time with a different subset (using the MATLAB cvpartition function). All analysis led to the same conclusions above.

3.2. Anticipating Major Hurricane Events

In-depth analysis of the capability of our RF models to predict MHs is given below for several forecasting lead-times. Considering that generally the average ‘maturity time’ of a developing major TC event is no more than 2–3 days [53,54], tests were run to deliver predictions (running backwards) from the maximum sustained wind speed (referred to as 0 h) up to 54 h using a time step of 6 h. A lead-time of, for example, 18 h means that the prediction of MH is done based on the TC features at 18 h ahead of the time of peak.
Test statistics for MH prediction show that the precision (pMH) ranged between 72% and 93% (67% and 82%) in the Atlantic (NE Pacific) Ocean, and between 69% and 77% with both basins combined over the entire forecasting window (see Table 1, Table 2 and Table 3). The k-values were (also respectively) 0.58 (and 0.46) on average, meaning overall substantial (moderate) agreement between each model prediction and the actual class values for both TSs and MHs. The total number of events goes from 114 (Atlantic) to 192 (Pacific) up to 42 h, but, beyond this time frame, the numbers are somewhat reduced (with 80 events as the lowest-case scenario for 54 h in the Atlantic region). As a result, the model forecasting performance is slightly compromised in these cases. Lastly, close to the (first) maximum intensity peak (up to 6 h), although the number of cases is relatively large, the TC cloud shows mixed or less distinct traits, a limiting factor that also affects the learning process of the models to some extent. Nevertheless, in this case, the forecast accuracy is still fairly high with precision values of 72% and 67% for the Atlantic and NE Pacific regions, respectively. Combining datasets from both regions (see Table 3) helps overcome the small dataset problem and leads to more generalized models, but a somewhat lower forecast precision is found when applying the resulting models to Atlantic hurricanes (not shown). These results reveal some differences among regions, despite tropical cyclones having several traits in common, as described in the present study.
Predictions made with our RF models were also examined for individual cases that achieved RI. We include here seven examples (see Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10): category 4 Iota (2020), category 4 Laura (2020), category 5 Emily (2005), and category 4 Ian (2022) for the Atlantic, and category 5 Willa (2018), category 4 Odile (2014), and category 5 Patricia (2015) for the NE Pacific region. Emily and Patricia were of special interest as they were difficult to forecast by numerical weather prediction models [15,43]. Notably, Patricia, a MH that rapidly intensified at a rare rate, was the strongest hurricane on record in the NE Pacific and North Atlantic basins. At least 80% of our models were able to predict a MH (up to 48 h ahead). Emily, the earliest-forming category 5 hurricane on record in the Atlantic basin, which went through two RI stages, was predicted by 100% of our models (up to 54 h ahead). All of our RF models also predicted that the MH status would remain as such throughout its maximum development. Odile is another example of RI that was not anticipated by the official forecasts because of the poor organization of the cyclone’s inner core and the large size of the cyclone, but that was predicted again by at least 80% of our models (66 h ahead). Willa was predicted by 100% of our models (up to 18 h ahead). Another interesting aspect is that from 60% to 100% of our models anticipated MH status even when applying them on new data beyond the training period (1995–2019), like in the case of Iota and Laura in 2020 (up to 42 h) or Ian in 2022 (up to 60 h in advance). Note that these three cases, some of the most devastating hurricanes in U.S. history, underwent RI within 24 h. In all studied cases here, the predictive ability of our models was tested outside the range of typical lead-times (6–54 h). As expected, the RF models are less reliable when the number of trained/tested data cases decreases (i.e., for lead-times higher than 54 h).
Finally, it is also worth highlighting that our models have a relatively low computational cost, as a full run (100 trees with 5-fold cross-validation and 9 lead-times) takes about 20 min in the Atlantic (and about 2 min for a specific lead-time).

4. Summary and Conclusions

In summary, this study presents some innovations regarding the definition of the hurricane features, related to the anatomy (size, shape) and temperature (change between the outer edges and inner-core) of the cloud’s system, obtained using a k-means clustering algorithm applied to GOES data. Furthermore, these parameters were optimally combined and linked to the maximum intensity of the TC system in a nonlinear fashion using a novel random forest algorithm (trained in a 5-fold cross-validation) to predict major hurricanes events in advance. The final prediction precision is 79% (74%) in the Atlantic (NE Pacific) Ocean on average for up to 54 h in advance. Thus, our findings demonstrate that the integration of the prominent cloud features of an incipient tropical cyclone, including the anatomy and temperature, in a machine learning approach is suitable as a benchmark for diagnosing a possible transition into a major hurricane. The proposed assessment procedure also enables the integration of other candidate features or factors (to be progressively explored). Thus far, there is not enough cases in different seasons for model training and testing. However, when more data is available in the future, analysis can also be performed to study the effects of environmental variations, such as seasonality. Moreover, this design could help towards a decision support system beyond its usefulness regarding major hurricanes.

Author Contributions

Conceptualization, V.N.; methodology, V.N.; investigation, V.N., J.M-A. and C.R.; analysis, validation, and data curation, J.M.-A. and C.R.; visualization, J.M.-A. and V.N.; writing—original draft preparation, J.M.-A. and C.R.; writing—review and editing, V.N.; supervision, V.N.; funding acquisition, resources, and project administration, V.N. All authors have read and agreed to the published version of the manuscript.

Funding

This research is jointly supported by the European Space Agency (contract 4000134529/21/NL/GLC/my) and Ministry of Culture, Education, and Science of the Generalitat Valenciana (grant CIDEGENT/2019/055).

Data Availability Statement

All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supporting Information. Additional data related to this paper supporting the findings of this study is available at https://github.com/AI4OCEANS/, accessed on 16 November 2022.

Acknowledgments

We thank T. Girona for discussions on classification methods.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bhatia, K.T.; Vecchi, G.A.; Knutson, T.R.; Murakami, H.; Kossin, J.; Dixon, K.W.; Whitlock, C.E. Recent increases in tropical cyclone intensification rates. Nat. Commun. 2019, 10, 635. [Google Scholar] [CrossRef] [PubMed]
  2. Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.; Iskandar, I.; Kossin, J.; Lewis, S.; et al. Weather and Climate Extreme Events in a Changing Climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1513–1766. Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_Chapter11.pdf (accessed on 16 November 2022).
  3. Knutson, T.; Camargo, S.J.; Chan, J.C.L.; Emanuel, K.; Ho, C.-H.; Kossin, J.; Mohapatra, M.; Satoh, M.; Sugi, M.; Walsh, K.; et al. Tropical Cyclones and Climate Change Assessment: Part I: Detection and Attribution. Bull. Amer. Meteor. Soc. 2019, 100, 1987–2007. [Google Scholar] [CrossRef] [Green Version]
  4. Reed, K.A.; Stansfield, A.M.; Wehner, M.F.; Zarzycki, C.M. Forecasted attribution of the human influence on Hurricane Florence. Sci. Adv. 2020, 6, eaaw9253. [Google Scholar] [CrossRef] [Green Version]
  5. Landsea, C.W. Comments on “Monitoring and Understanding Trends in Extreme Storms: State of Knowledge”. Bull. Am. Meteorol. Soc. 2015, 96, 1175–1176. [Google Scholar] [CrossRef]
  6. Alley, R.B.; Emanuel, K.A.; Zhang, F. Advances in weather prediction. Science 2019, 363, 342–344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Coch, N.K. Inland damage from hurricanes. J. Coast. Res. 2020, 36, 1093–1105. [Google Scholar] [CrossRef]
  8. Tallapragada, V.; Bernardet, L.; Biswas, M.K.; Gopalakrishnan, S.; Kwon, Y.; Liu, Q.; Zhang, X. Hurricane Weather Research and Forecasting (HWRF) Model: 2013 Scientific Documentation; Developmental Testbed Center: Boulder, CO, USA, 2014. Available online: http://www.emc.ncep.noaa.gov/gc_wmb/vxt/pubs/HWRFScientificDocumentation2013.pdf (accessed on 16 November 2022).
  9. Biswas, M.K.; Bernardet, L.; Abarca, S.; Ginis, I.; Grell, E.; Kalina, E.; Kwon, Y.; Liu, B.; Liu, Q.; Marchok, T.; et al. 2017: Hurricane Weather Research and Forecasting (HWRF) Model: 2017 Scientific Documentation. In NCAR Technical Note NCAR/TN-544+STR; Developmental Testbed Center: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
  10. Kieu, C.; Keshavamurthy, K.; Tallapragada, V.; Gopalakrishnan, S.; Trahan, S. On the growth of intensity forecast errors in the operational hurricane weather research and forecasting (HWRF) model. Q J R Meteorol. Soc. 2018, 144, 1803–1819. [Google Scholar] [CrossRef]
  11. Lee, C.Y.; Tippett, M.K.; Camargo, S.J.; Sobel, A.H. Probabilistic Multiple Linear Regression Modeling for Tropical Cyclone Intensity. Mon. Weather Rev. 2015, 143, 933–954. [Google Scholar] [CrossRef]
  12. DeMaria, M.; Mainelli, M.; Shay, L.K.; Knaff, J.A.; Kaplan, J. Further improvements to the Statistical Hurricane Intensity Prediction Scheme (SHIPS). Weather Forecast. 2005, 20, 531–543. [Google Scholar] [CrossRef]
  13. Xu, W.; Balaguru, K.; August, A.; Lalo, N.; Hodas, N.; DeMaria, M.; Judi, D. Deep Learning Experiments for Tropical Cyclone Intensity Forecasts. Weather Forecast. 2021, 36, 1453–1470. [Google Scholar] [CrossRef]
  14. DeMaria, M.; Franklin, J.L.; Onderlinde, M.J.; Kaplan, J. Operational Forecasting of Tropical Cyclone Rapid Intensification at the National Hurricane Center. Atmosphere 2021, 12, 683. [Google Scholar] [CrossRef]
  15. Nystrom, R.G.; Zhang, F. Practical Uncertainties in the Limited Predictability of the Record-Breaking Intensification of Hurricane Patricia (2015). Mon. Weather Rev. 2019, 147, 3535–3556. [Google Scholar] [CrossRef]
  16. Cangialosi, J.P.; Blake, E.; DeMaria, M.; Penny, A.; Latto, A.; Rappaport, E.; Tallapragada, V. Recent Progress in Tropical Cyclone Intensity Forecasting at the National Hurricane Center. Weather 2020, 35, 1913–1922. [Google Scholar] [CrossRef]
  17. Lee, C.Y.; Tippett, M.; Sobel, A.; Camargo, S.J. Rapid intensification and the bimodal distribution of tropical cyclone intensity. Nat. Commun. 2016, 7, 10625. [Google Scholar] [CrossRef] [Green Version]
  18. Chen, R.; Zhang, W.; Wang, X. Machine Learning in Tropical Cyclone Forecast Modeling: A Review. Atmosphere 2020, 11, 676. [Google Scholar] [CrossRef]
  19. Pradhan, R.; Aygun, R.; Maskey, M.; Ramachandran, R.; Cecil, D. Tropical cyclone intensity estimation using a deep convolutional neural network. IEEE Trans. Image Process. 2018, 27, 692–702. [Google Scholar] [CrossRef]
  20. Lee, J.; Im, J.; Cha, D.-H.; Park, H.; Sim, S. Tropical Cyclone Intensity Estimation Using Multi-Dimensional Convolutional Neural Networks from Geostationary Satellite Data. Remote Sens. 2020, 12, 108. [Google Scholar] [CrossRef] [Green Version]
  21. Maskey, M.; Ramachandran, R.; Ramasubramanian, M.; Gurung, I.; Freitag, B.; Kaulfus, A.; Bollinger, D.; Cecil, D.J.; Miller, J. Deepti: Deep-Learning-Based Tropical Cyclone Intensity Estimation System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4271–4281. [Google Scholar] [CrossRef]
  22. Chen, R.; Wang, X.; Zhang, W.; Zhu, X.; Li, A.; Yang, C. A hybrid CNN-LSTM model for typhoon formation forecasting. Geoinformatica 2019, 23, 375–396. [Google Scholar] [CrossRef]
  23. Kim, S.-H.; Moon, I.-J.; Won, S.-H.; Kang, H.-W.; Kang, S.K. Decision-Tree-Based Classification of Lifetime Maximum Intensity of Tropical Cyclones in the Tropical Western North Pacific. Atmosphere 2021, 12, 802. [Google Scholar] [CrossRef]
  24. Auret, L.; Aldrich, C. Interpretation of nonlinear relationships between process variables by use of random forests. Miner. Eng. 2012, 35, 27–42. [Google Scholar] [CrossRef]
  25. Belgiu, M.; Drăguţ, L. Random Forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
  26. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  27. Carrasco, C.A.; Landsea, C.  W.; Lin, Y.-L. The influence of tropical cyclone size on its intensification. Weather Forecast. 2014, 29, 582–590. [Google Scholar] [CrossRef] [Green Version]
  28. Bender, M.A.; Marchok, T.P.; Sampson, C.R.; Knaff, J.A.; Morin, M.J. Impact of Storm Size on Prediction of Storm Track and Intensity Using the 2016 Operational GFDL Hurricane Model. Weather Forecast. 2017, 32, 1491–1508. [Google Scholar] [CrossRef]
  29. Chen, B.-F.; Chen, B.; Lin, H.-T.; Elsberry, R.L. Estimating tropical cyclone intensity by satellite imagery utilizing convolutional neural networks. Weather Forecast. 2019, 34, 447–465. [Google Scholar] [CrossRef]
  30. Zehr, R.M. Environmental Vertical Wind Shear with Hurricane Bertha (1996). Weather. Forecast. 2003, 18, 345–356. [Google Scholar] [CrossRef]
  31. Wu, L.; Tian, W.; Liu, Q.; Cao, J.; Knaff, J.A. Implications of the observed relationship between tropical cyclone size and intensity over the western North Pacific. J. Clim. 2015, 28, 9501–9506. [Google Scholar] [CrossRef]
  32. Guo, X.; Tan, Z.-M. Tropical cyclone fullness: A new concept for interpreting storm intensity. Geophys. Res. Lett. 2017, 44, 4324–4331. [Google Scholar] [CrossRef]
  33. Xu, J.; Wang, Y. Dependence of Tropical Cyclone Intensification Rate on Sea Surface Temperature, Storm Intensity, and Size in the Western North Pacific. Weather Forecast. 2018, 33, 523–537. [Google Scholar] [CrossRef]
  34. Song, J.; Duan, Y.; Klotzbach, P.J. Revisiting the relationship between tropical cyclone size and intensity over the western North Pacific. Geophys. Res. Lett. 2020, 47, e2020GL088217. [Google Scholar] [CrossRef]
  35. Chen, K.; Chen, G.; Rao, C.; Wang, Z. Relationship of tropical cyclone size change rate with size and intensity over the western North Pacific. Atmos. Ocean. Sci. Lett. 2021, 14, 100040. [Google Scholar] [CrossRef]
  36. Knaff, J.A.; Longmore, S.P.; Molenear, D.A. An Objective Satellite-Based Tropical Cyclone Size Climatology. J. Clim. 2014, 27, 455–476. [Google Scholar] [CrossRef]
  37. Asif, A.; Dawood, M.; Jan, B.; Khurshid, J.; DeMaria, M.; Minhas, F.A.A. PHURIE: Hurricane intensity estimation from infrared satellite imagery using machine learning. Neural Comput. Appl. 2020, 32, 4821–4834. [Google Scholar] [CrossRef]
  38. Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone best track data. Bull. Amer. Meteor. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef] [Green Version]
  39. Yang, C.; Liu, Z.; Gao, F.; Childs, P.P.; Min, J. Impact of assimilating GOES imager clear-sky radiance with a rapid refresh assimilation system for convection-permitting forecast over Mexico. J. Geophys. Res. Atmos. 2017, 122, 5472–5490. [Google Scholar] [CrossRef] [Green Version]
  40. Product Definition and User’s Guide (PUG), Volume 5: Level 2+ Products, DCN 7035538, GOES-R/Code 416 (NOAA, 2019). Available online: https://www.goes-r.gov/products/docs/PUG-L2+-vol5.pdf (accessed on 16 November 2022).
  41. James, G.; Witten, D.; Hastie, T.; Tibshirami, R. Resampling Methods. In An Introduction to Statistical Learning, 2nd ed.; Springer Texts in Statistics: New York, NY, USA, 2013; p. 181. Available online: https://link.springer.com/content/pdf/10.1007/978-1-0716-1418-1_5.pdf (accessed on 16 November 2022).
  42. Landis, J.; Koch, G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [Green Version]
  43. Pu, Z.; Li, X.; Zipser, E.J. Diagnosis of the Initial and Forecast Errors in the Numerical Simulation of the Rapid Intensification of Hurricane Emily (2005). Weather Forecast. 2009, 24, 1236–1251. [Google Scholar] [CrossRef] [Green Version]
  44. Gupta, U.; Jitkajornwanich, K.; Elmasri, R.; Fegaras, L. Adapting K-means clustering to identify spatial patterns in storms. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 2646–2654. [Google Scholar]
  45. Wang, Y.; Rosowsky, D. Joint distribution model for prediction of hurricane wind speed and size. Struct. Saf. 2012, 35, 40–51. [Google Scholar] [CrossRef]
  46. Drake, L. Scientific prerequisites to comprehension of the tropical cyclone forecast, intensity, track, and size. Weather Forecast. 2012, 27, 462–472. [Google Scholar] [CrossRef]
  47. Chan, K.T.F.; Chan, J.C.L. Global climatology of tropical cyclone size as inferred from QuikSCAT data. Int. J. Climatol. 2015, 35, 4843–4848. [Google Scholar] [CrossRef]
  48. Dolling, K.; Ritchie, E.; Tyo, J. The use of the deviation angle variance technique on geostationary satellite imagery to estimate tropical cyclone size parameters. Weather Forecast. 2016, 31, 1625–1642. [Google Scholar] [CrossRef]
  49. Zhang, G.; Perrie, W.; Zhang, B.; Yang, J.; He, Y. Monitoring of tropical cyclone structures in ten years of RADARSAT-2 SAR images. Remote Sens. Environ. 2020, 236, 111449. [Google Scholar] [CrossRef]
  50. Wei, Y.; Yang, R. An Advanced Artificial Intelligence System for Investigating Tropical Cyclone Rapid Intensification with the SHIPS Database. Atmosphere 2021, 12, 484. [Google Scholar] [CrossRef]
  51. Jiang, J.; Huang, Z.G.; Grebogi, C.; Lai, Y.C. Predicting extreme events from data using deep machine learning: When and where. Phys. Rev. Res. 2020, 4, 023028. [Google Scholar] [CrossRef]
  52. Chawla, N.V. C4.5 and Imbalanced Datasets: Investigating the Effect of Sampling Method Probabilistic Estimate and Decision tree Structure. In Proceedings of the International Conference on Machine Learning, Workshop on Learning from Imbalanced Datasets, Washington, DC, USA, 21 August 2003; pp. 1–8. Available online: https://www3.nd.edu/~dial/publications/chawla2003c45.pdf (accessed on 16 November 2022).
  53. Gu, Y.; Wu, L.; Zhan, R. Climatology of developing and nondeveloping disturbances for tropical cyclone genesis over the western North Pacific. Terr. Atmos. Ocean. Sci. 2022, 33, 13. [Google Scholar] [CrossRef]
  54. Kishtawal, C.M.; Jaiswal, N.; Singh, R.; Niyogi, D. Tropical cyclone intensification trends during satellite era (1986–2010). Geophys. Res. Lett. 2012, 39, L10810. [Google Scholar] [CrossRef]
Remotesensing 15 00119 g001 550
Figure 1. RF model architecture to forecast storm intensification to major hurricane. The model consists of an ensemble of trained decision trees with a feature importance function and a k-fold iterator. The input parameters are fed into the model, which outputs the feature importance vector about the relative importance of each predictor (see Figure 2) and 2-way class probabilities (TSs and MHs). The model performance is evaluated using Cohen’s kappa (k) and precision (pMH) metrics.
Figure 1. RF model architecture to forecast storm intensification to major hurricane. The model consists of an ensemble of trained decision trees with a feature importance function and a k-fold iterator. The input parameters are fed into the model, which outputs the feature importance vector about the relative importance of each predictor (see Figure 2) and 2-way class probabilities (TSs and MHs). The model performance is evaluated using Cohen’s kappa (k) and precision (pMH) metrics.
Remotesensing 15 00119 g001
Remotesensing 15 00119 g002 550
Figure 2. Exemplification of our hybrid ML approach. After all the GOES images are converted to BT, some hurricane-related parameters are extracted using a k-means clustering method. Then, the most important parameters, according to our RF classifier, are used to predict the intensification of a TS to MH status. Among all considered parameters, the most relevant ones are the following: the area, or A, estimated from the shape (displayed as white contour line); the temperature difference between the inner core and outer part of the storm cloud, or ∆T; and the morphology (circularity, or C; eccentricity, or ε). This ML framework sets the basis for the classification-oriented categorization of hurricanes based on key criteria (related to the anatomical and temperature features of a TC, in this study). The ability of ML in dealing with different types of ever-shifting TC features and with missing knowledge is highly important under the impact of climate change. The image (on the left side) corresponds to Hurricane Mitch (26 October 1998, at 14:45 UTC) in the Atlantic. The variable-importance plots (on the bottom) are for several lead-times (in colors) before the TCs reach their maximum intensity in the Atlantic and NE Pacific oceans. C3, C4, C5 stand for category 3, 4, 5 hurricanes, respectively, and make up the MH class.
Figure 2. Exemplification of our hybrid ML approach. After all the GOES images are converted to BT, some hurricane-related parameters are extracted using a k-means clustering method. Then, the most important parameters, according to our RF classifier, are used to predict the intensification of a TS to MH status. Among all considered parameters, the most relevant ones are the following: the area, or A, estimated from the shape (displayed as white contour line); the temperature difference between the inner core and outer part of the storm cloud, or ∆T; and the morphology (circularity, or C; eccentricity, or ε). This ML framework sets the basis for the classification-oriented categorization of hurricanes based on key criteria (related to the anatomical and temperature features of a TC, in this study). The ability of ML in dealing with different types of ever-shifting TC features and with missing knowledge is highly important under the impact of climate change. The image (on the left side) corresponds to Hurricane Mitch (26 October 1998, at 14:45 UTC) in the Atlantic. The variable-importance plots (on the bottom) are for several lead-times (in colors) before the TCs reach their maximum intensity in the Atlantic and NE Pacific oceans. C3, C4, C5 stand for category 3, 4, 5 hurricanes, respectively, and make up the MH class.
Remotesensing 15 00119 g002
Remotesensing 15 00119 g003 550
Figure 3. Overview of the main features common to most tropical storms. The images show the typical shape, dimension, and BT distribution for a TS and MH at their intensity peak over the Atlantic and the NE Pacific oceans. All figures shown are for illustration purposes only and correspond to: (a) TS Chantal (1995); (b) category 5 Hurricane Mitch (1998), (c) TS Elida (1996); and (d) category 5 Hurricane Patricia (2015). Units in degrees Celsius.
Figure 3. Overview of the main features common to most tropical storms. The images show the typical shape, dimension, and BT distribution for a TS and MH at their intensity peak over the Atlantic and the NE Pacific oceans. All figures shown are for illustration purposes only and correspond to: (a) TS Chantal (1995); (b) category 5 Hurricane Mitch (1998), (c) TS Elida (1996); and (d) category 5 Hurricane Patricia (2015). Units in degrees Celsius.
Remotesensing 15 00119 g003
Remotesensing 15 00119 g004 550
Figure 4. Analysis of the hit ratio (HR) for the different prediction models for hurricane Iota (Atlantic Ocean, 13–18 November 2018). The image shows the track of the TC under consideration for each lead time since the TS was formed (13 November 2020, at 21:00 UTC) until it reached its maximum intensity peak, or wind speed (Max WS) (16 November 2020, at 12:00 UTC). The arrow indicates the rapid increase in scale category as the TC progressed. The table shows the hit ratio (the number of times that a correct prediction was made out of the total number of predictions) of our RF classifier for each lead time (as in Table 1, Table 2 and Table 3). TS and C1-5 stand for tropical storm and category 1–5 hurricanes, respectively.
Figure 4. Analysis of the hit ratio (HR) for the different prediction models for hurricane Iota (Atlantic Ocean, 13–18 November 2018). The image shows the track of the TC under consideration for each lead time since the TS was formed (13 November 2020, at 21:00 UTC) until it reached its maximum intensity peak, or wind speed (Max WS) (16 November 2020, at 12:00 UTC). The arrow indicates the rapid increase in scale category as the TC progressed. The table shows the hit ratio (the number of times that a correct prediction was made out of the total number of predictions) of our RF classifier for each lead time (as in Table 1, Table 2 and Table 3). TS and C1-5 stand for tropical storm and category 1–5 hurricanes, respectively.
Remotesensing 15 00119 g004
Remotesensing 15 00119 g005 550
Figure 5. As in Figure 4, but for hurricane Laura (Atlantic Ocean, 20–29 August 2020). Here, the TS was formed on 21 August 2020, at 09:00 UTC and it reached the Max WS on 27 August 2020, at 00:00 UTC.
Figure 5. As in Figure 4, but for hurricane Laura (Atlantic Ocean, 20–29 August 2020). Here, the TS was formed on 21 August 2020, at 09:00 UTC and it reached the Max WS on 27 August 2020, at 00:00 UTC.
Remotesensing 15 00119 g005
Remotesensing 15 00119 g006 550
Figure 6. As in Figure 4, but for hurricane Emily (Atlantic Ocean, 11–21 July 2005). Here, the TS was formed on 12 July 2005, at 00:00 UTC and it reached the Max WS on 17 July 2005, at 00:00 UTC.
Figure 6. As in Figure 4, but for hurricane Emily (Atlantic Ocean, 11–21 July 2005). Here, the TS was formed on 12 July 2005, at 00:00 UTC and it reached the Max WS on 17 July 2005, at 00:00 UTC.
Remotesensing 15 00119 g006
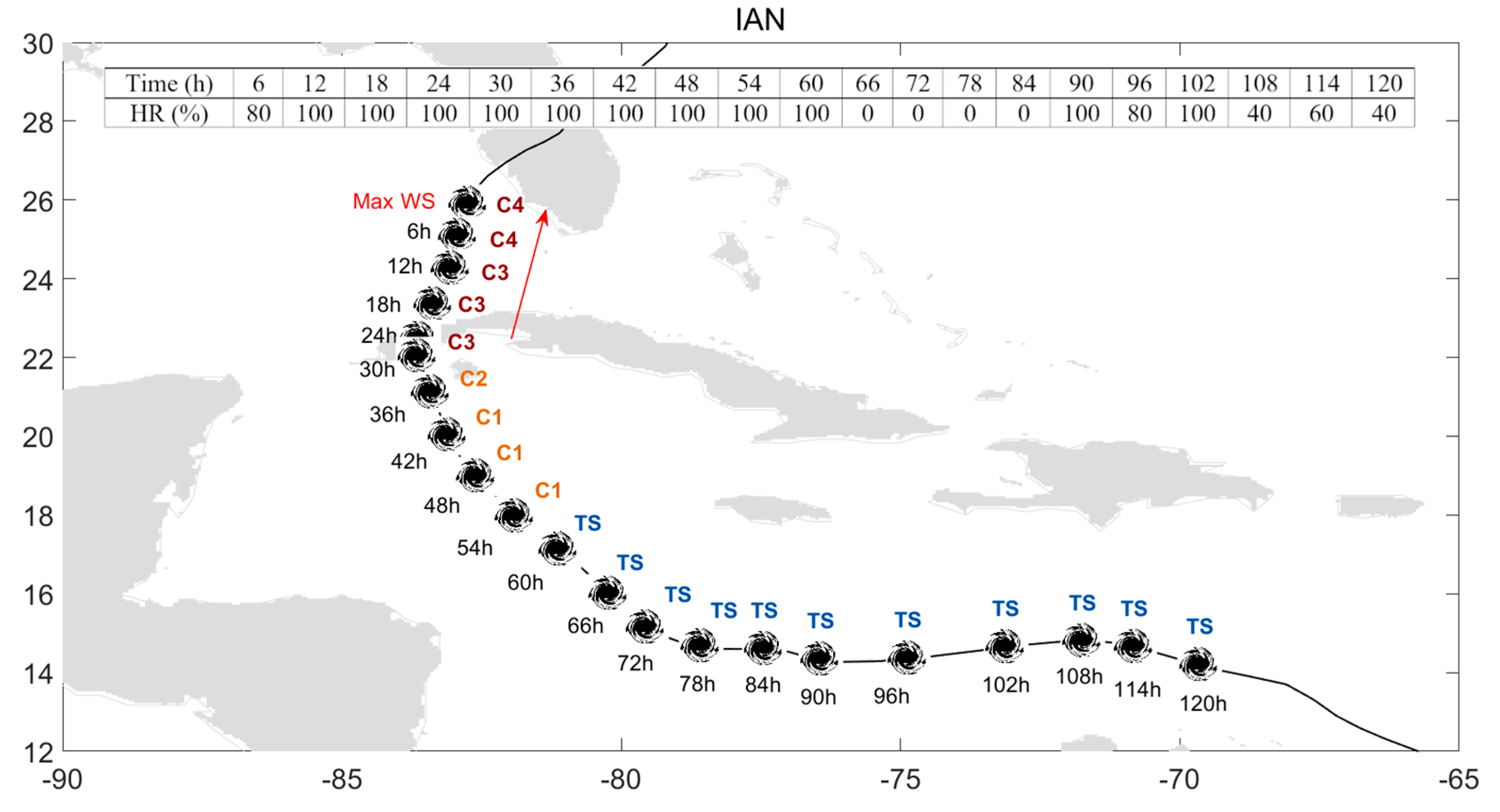
Remotesensing 15 00119 g007 550
Figure 7. As in Figure 4, but for hurricane Ian (NE Atlantic Ocean, 19 September–2 October 2022). Here, the TS was formed on 19 September 2022, at 12:00 UTC and it reached the Max WS on 28 September 2022, at 12:00 UTC.
Figure 7. As in Figure 4, but for hurricane Ian (NE Atlantic Ocean, 19 September–2 October 2022). Here, the TS was formed on 19 September 2022, at 12:00 UTC and it reached the Max WS on 28 September 2022, at 12:00 UTC.
Remotesensing 15 00119 g007
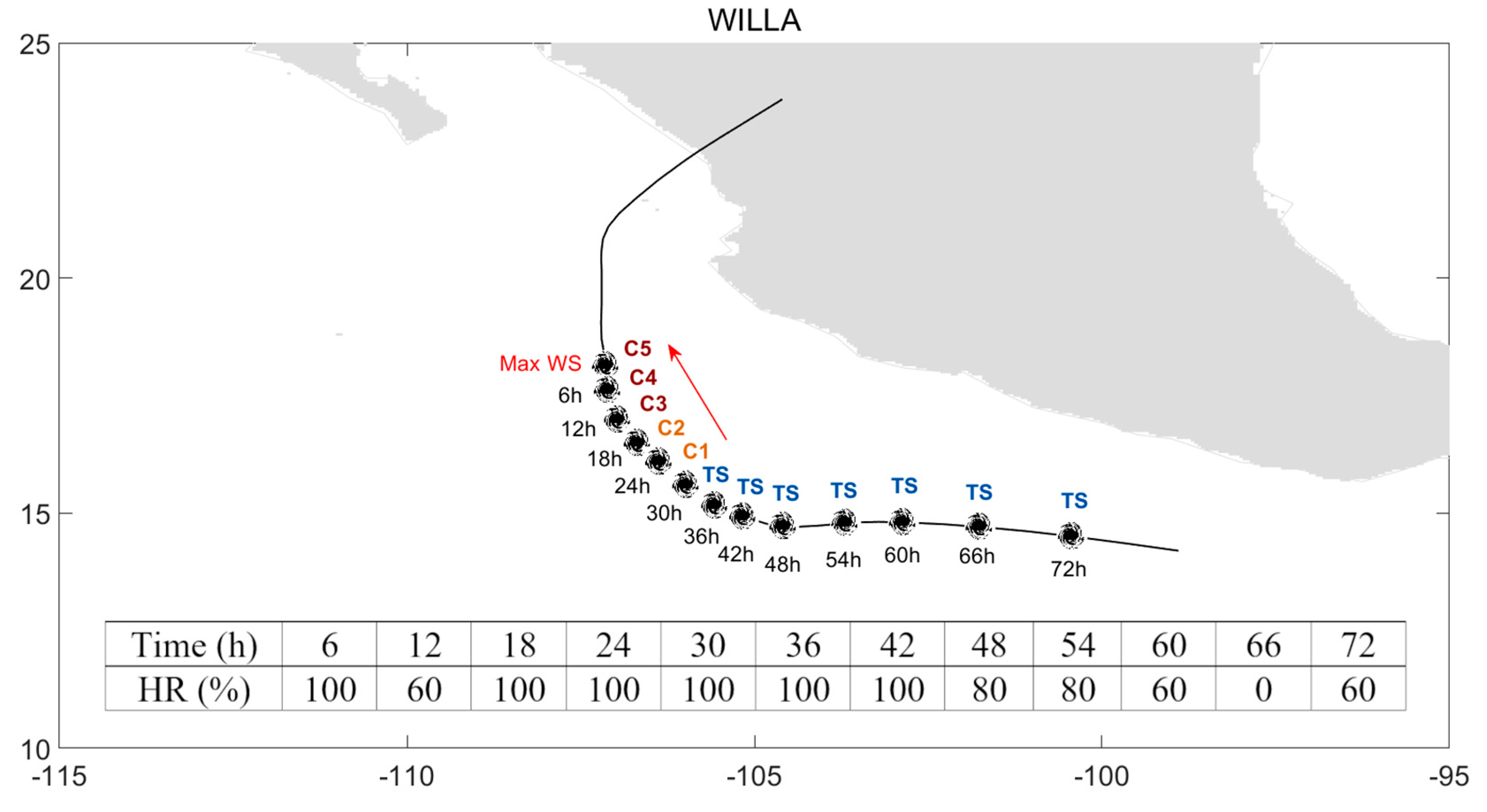
Remotesensing 15 00119 g008 550
Figure 8. As in Figure 4, but for hurricane Willa (NE Pacific Ocean, 20–24 October 2018). Here, the TS was formed on 20 October 2018, at 12:00 UTC and it reached the Max WS on 22 October 2018, at 06:00 UTC.
Figure 8. As in Figure 4, but for hurricane Willa (NE Pacific Ocean, 20–24 October 2018). Here, the TS was formed on 20 October 2018, at 12:00 UTC and it reached the Max WS on 22 October 2018, at 06:00 UTC.
Remotesensing 15 00119 g008
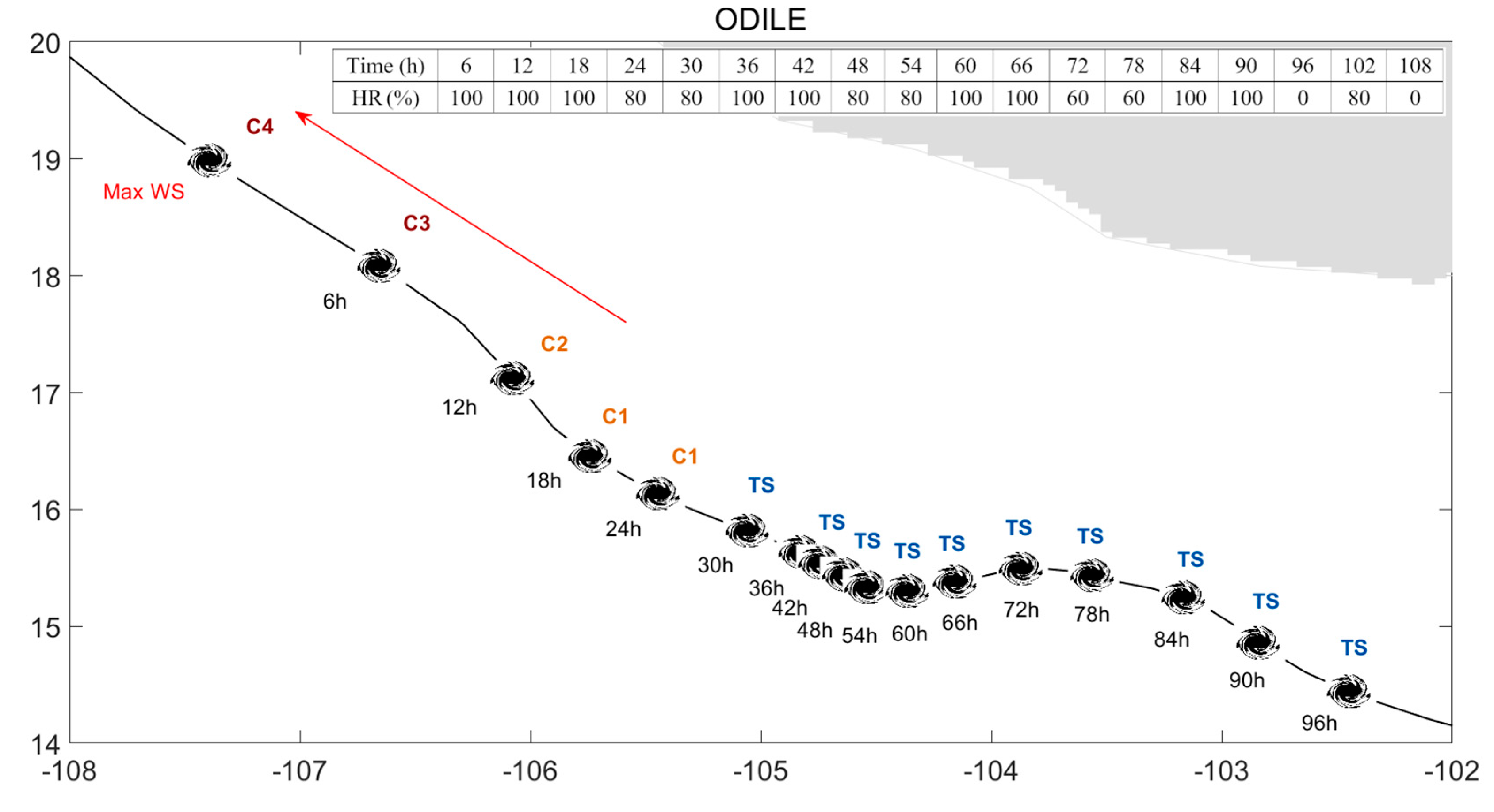
Remotesensing 15 00119 g009 550
Figure 9. As in Figure 4, but for hurricane Odile (NE Pacific Ocean, 10–18 September 2014). Here, the TS was formed on 10 September 2014, at 06:00 UTC and it reached the Max WS on 14 September 2018, at 06:00 UTC.
Figure 9. As in Figure 4, but for hurricane Odile (NE Pacific Ocean, 10–18 September 2014). Here, the TS was formed on 10 September 2014, at 06:00 UTC and it reached the Max WS on 14 September 2018, at 06:00 UTC.
Remotesensing 15 00119 g009
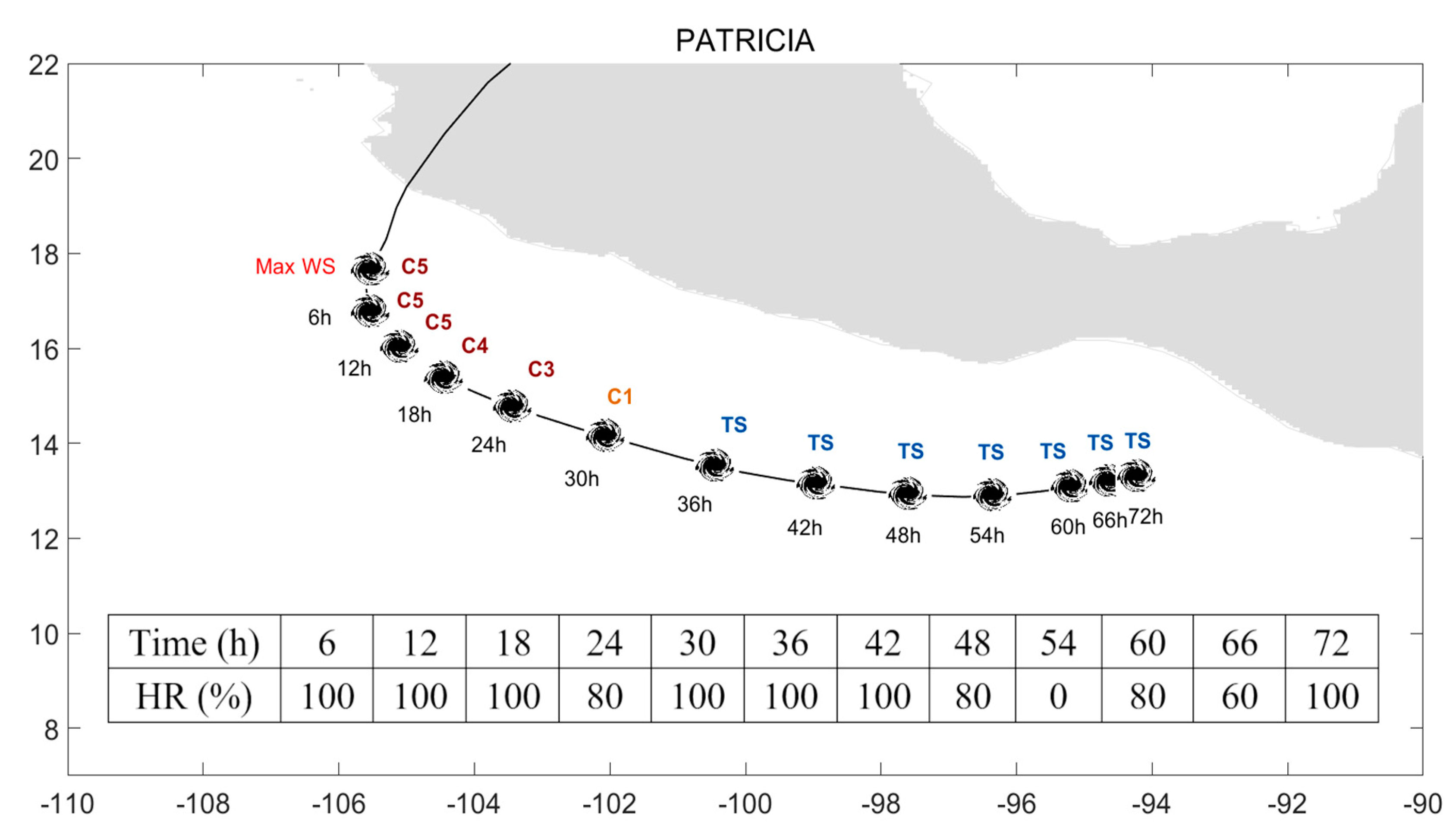
Remotesensing 15 00119 g010 550
Figure 10. As in Figure 4, but for hurricane Patricia (NE Pacific Ocean, 20–24 October 2015). Here, the TS was formed on 21 October 2015, at 00:00 UTC and it reached the Max WS on 23 October 2015, at 12:00 UTC.
Figure 10. As in Figure 4, but for hurricane Patricia (NE Pacific Ocean, 20–24 October 2015). Here, the TS was formed on 21 October 2015, at 00:00 UTC and it reached the Max WS on 23 October 2015, at 12:00 UTC.
Remotesensing 15 00119 g010
Table
Table 1. Performance metrics of our classification model for each lead-time (in hours, h) in the Atlantic Ocean. The positive and negative predictive power of the model for both classes (TSs and MHs) has been assessed using Cohen’s kappa statistic (k). The model precision (pMH) reflects the accuracy for predicting the MH class. The values for each metric report the mean result across all folds from all runs. The number of trees (# Trees) corresponds to the number of trees when the “performance saturation” condition is met. The number of samples (# Samples) is the total number of events (50% were TSs and 50% MHs).
Table 1. Performance metrics of our classification model for each lead-time (in hours, h) in the Atlantic Ocean. The positive and negative predictive power of the model for both classes (TSs and MHs) has been assessed using Cohen’s kappa statistic (k). The model precision (pMH) reflects the accuracy for predicting the MH class. The values for each metric report the mean result across all folds from all runs. The number of trees (# Trees) corresponds to the number of trees when the “performance saturation” condition is met. The number of samples (# Samples) is the total number of events (50% were TSs and 50% MHs).
Time (h)61218243036424854
# Samples12212812813412611411810080
# Trees29.8034.2035.0027.6022.2034.2012.6054.0028.60
pMH (%)72.1075.6584.3876.7880.5876.0992.6776.2277.12
k0.470.500.690.550.640.580.710.580.48
Table
Table 2. As in Table 1, but for the NE Pacific Ocean.
Table 2. As in Table 1, but for the NE Pacific Ocean.
Time (h)61218243036424854
# Samples188190192192182170148136106
# Trees39.2039.8037.8018.4017.2048.2014.6048.4015.80
pMH (%)66.7870.5567.7274.5572.3179.7977.8870.5481.79
k0.340.400.350.490.460.570.590.400.53
Table
Table 3. As in Table 1, but for the Atlantic and NE Pacific oceans combined.
Table 3. As in Table 1, but for the Atlantic and NE Pacific oceans combined.
Time (h)61218243036424854
# Samples310318320326308284276236186
# Trees32.6036.4046.2047.0071.8036.0022.4051.2051.00
pMH (%)69.1270.9472.5473.7171.9471.0177.4974.5873.14
k0.400.420.460.490.460.450.570.470.44
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Martinez-Amaya, J.; Radin, C.; Nieves, V. Advanced Machine Learning Methods for Major Hurricane Forecasting. Remote Sens. 2023, 15, 119. https://doi.org/10.3390/rs15010119

AMA Style

Martinez-Amaya J, Radin C, Nieves V. Advanced Machine Learning Methods for Major Hurricane Forecasting. Remote Sensing. 2023; 15(1):119. https://doi.org/10.3390/rs15010119

Chicago/Turabian Style

Martinez-Amaya, Javier, Cristina Radin, and Veronica Nieves. 2023. "Advanced Machine Learning Methods for Major Hurricane Forecasting" Remote Sensing 15, no. 1: 119. https://doi.org/10.3390/rs15010119

APA Style

Martinez-Amaya, J., Radin, C., & Nieves, V. (2023). Advanced Machine Learning Methods for Major Hurricane Forecasting. Remote Sensing, 15(1), 119. https://doi.org/10.3390/rs15010119

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop