Blending Sea Surface Winds from the HY-2 Satellite Scatterometers Based on a 2D-Var Method
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. 2D-Var Method
3. Data Verification
4. Results
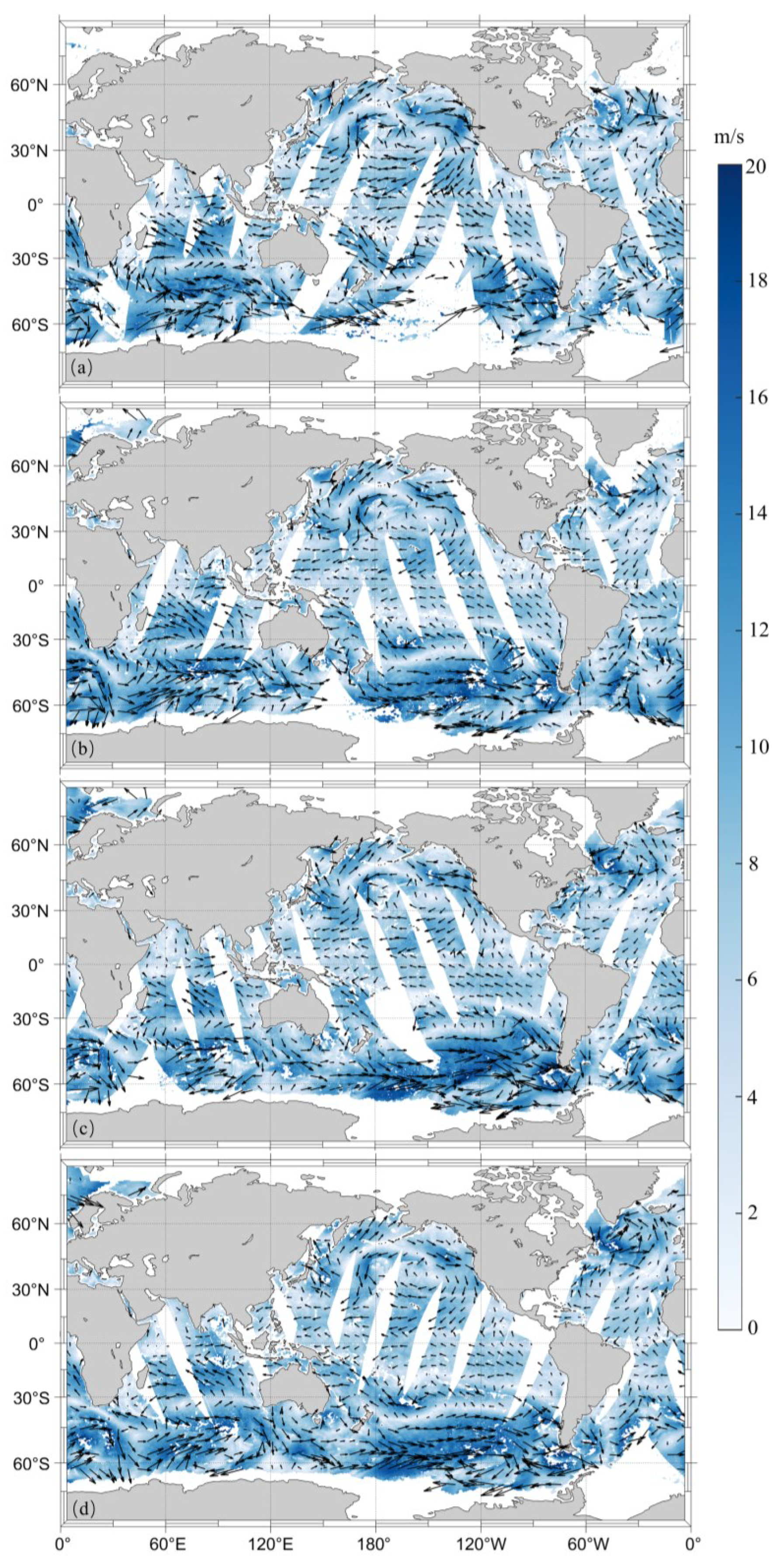
4.1. Test Case
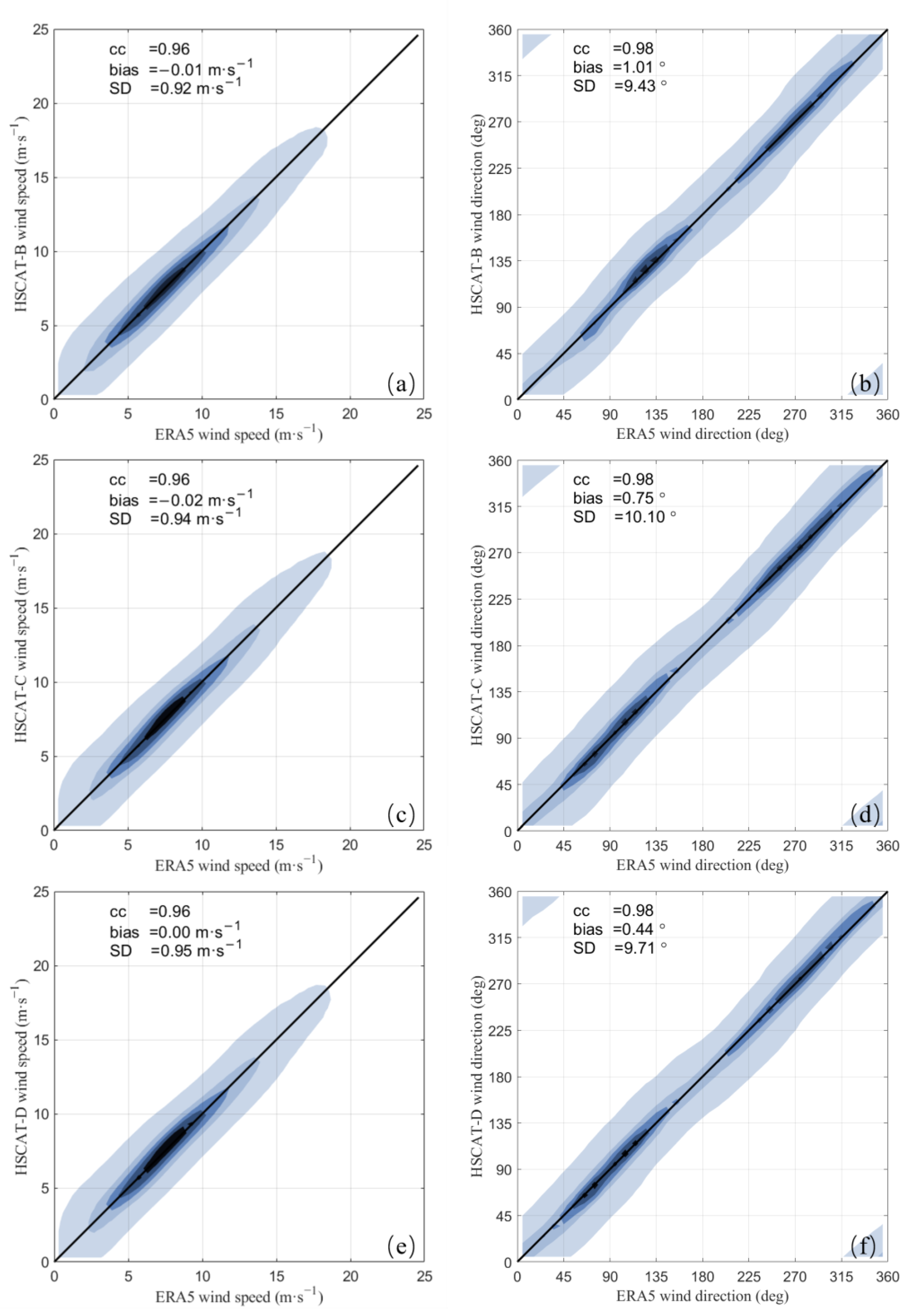
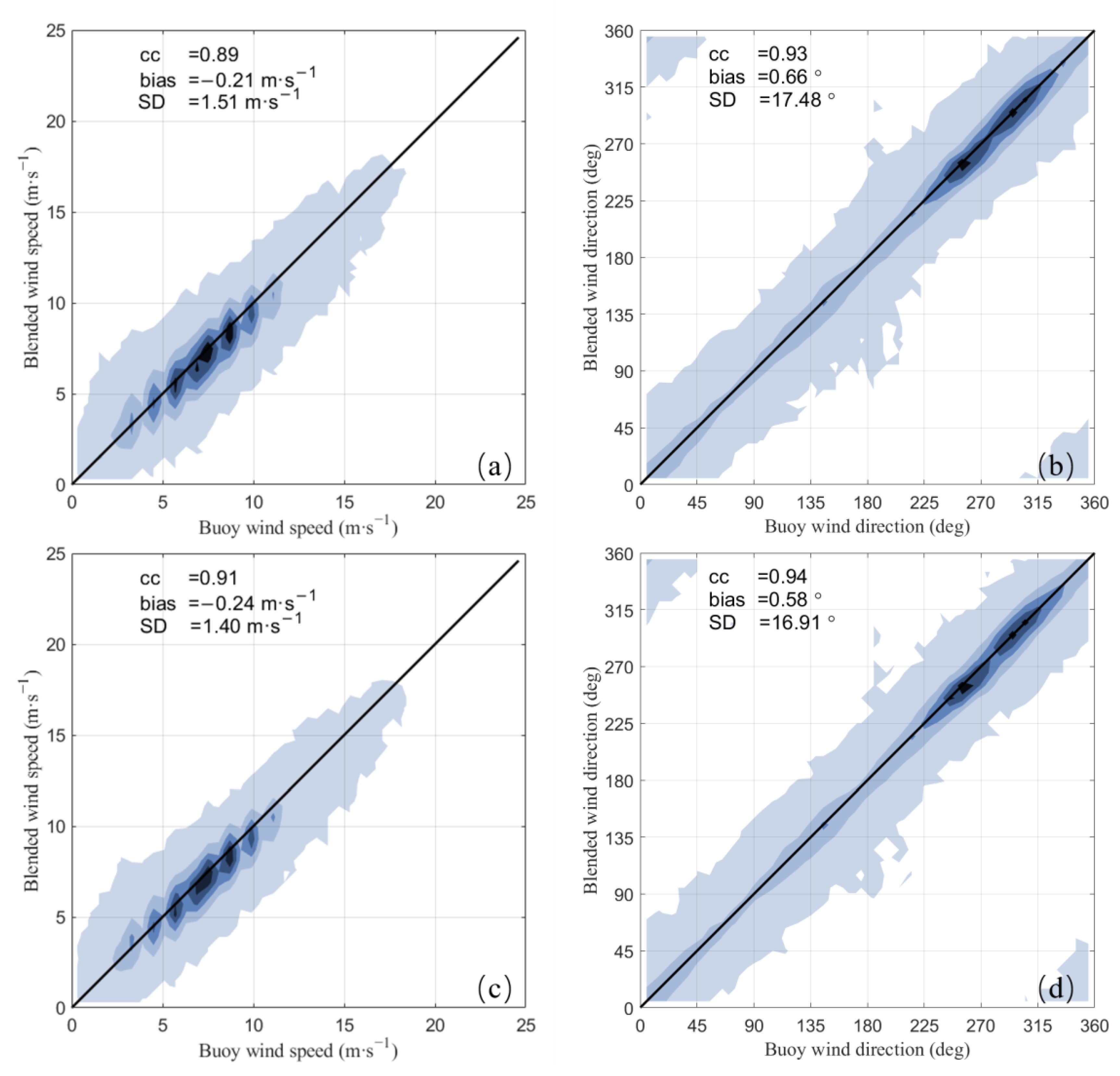
4.2. General Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mason, P.J.; Zillman, J.W.; Simmons, A.; Lindstrom, E.; Harrison, D.E.; Dolman, H.; Bojinski, S.; Fischer, A.; Latham, J.; Rasmussen, J. Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (2010 Update); World Meteorological Organization (WMO): Geneva, Switzerland, 2010; Available online: https://www.gruan.org/gruan/editor/documents/gcos/gcos-138.pdf (accessed on 12 November 2022).
- Verhoef, A.; Vogelzang, J.; Verspeek, J.; Stoffelen, A. Long-Term Scatterometer Wind Climate Data Records. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2186–2194. [Google Scholar] [CrossRef]
- Young, I.R.; Sanina, E.; Babanin, A.V. Calibration and Cross Validation of a Global Wind and Wave Database of Altimeter, Radiometer, and Scatterometer Measurements. J. Atmos. Ocean. Technol. 2017, 34, 1285–1306. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Meissner, T.; Cerovecki, I.; Chang, P.S.; Dong, X.; De Chiara, G.; Donlon, C.; Dukhovskoy, D.S.; Elya, J.; Fore, A.; et al. Remotely Sensed Winds and Wind Stresses for Marine Forecasting and Ocean Modeling. Front. Mar. Sci. 2019, 6, 443. [Google Scholar] [CrossRef] [Green Version]
- Mears, C.A.; Scott, J.; Wentz, F.J.; Ricciardulli, L.; Leidner, S.M.; Hoffman, R.; Atlas, R. A Near-Real-Time Version of the Cross-Calibrated Multiplatform (CCMP) Ocean Surface Wind Velocity Data Set. J. Geophys. Res. Ocean. 2019, 124, 6997–7010. [Google Scholar] [CrossRef]
- Mears, C.; Lee, T.; Ricciardulli, L.; Wang, X.; Wentz, F. Improving the Accuracy of the Cross-Calibrated Multi-Platform (CCMP) Ocean Vector Winds. Remote Sens. 2022, 14, 4230. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A Cross-Calibrated, Multiplatform Ocean Surface Wind Velocity Product for Meteorological and Oceanographic Applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Desbiolles, F.; Bentamy, A.; Blanke, B.; Roy, C.; Mestas-Nuñez, A.M.; Grodsky, S.A.; Herbette, S.; Cambon, G.; Maes, C. Two Decades [1992–2012] of Surface Wind Analyses Based on Satellite Scatterometer Observations. J. Mar. Syst. 2017, 168, 38–56. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Jin, X. Buoy Perspective of a High-Resolution Global Ocean Vector Wind Analysis Constructed from Passive Radiometers and Active Scatterometers (1987–Present). J. Geophys. Res. Ocean. 2012, 117, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Bentamy, A.; Fillon, D.C. Gridded Surface Wind Fields from Metop/ASCAT Measurements. Int. J. Remote Sens. 2012, 33, 1729–1754. [Google Scholar] [CrossRef] [Green Version]
- Zou, J.; Wang, Z.; Lin, M. Analysis of the High-Latitude Sea Surface Wind Acquisition Ability of Seven Satellite Scatterometers. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Trindade, A.; Portabella, M.; Stoffelen, A.; Lin, W.; Verhoef, A. ERAstar: A High-Resolution Ocean Forcing Product. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1337–1347. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhu, J.; Lin, M.; Zhang, Y.; Chang, Y. Chang Evaluating Chinese HY-2B HSCAT Ocean Wind Products Using Buoys and Other Scatterometers. IEEE Geosci. Remote Sens. Lett. 2020, 17, 923–927. [Google Scholar] [CrossRef]
- Lin, M.; Jia, Y. Past, Present and Future Marine Microwave Satellite Missions in China. Remote Sens. 2022, 14, 1330. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, J.; Stoffelen, A.; Lin, W.; Verhoef, A.; Li, X.; He, Y.; Zhang, Y.; Lin, M. Scatterometer Sea Surface Wind Product Validation for HY-2C. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6156–6164. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, J.; Zhang, Y.; Stoffelen, A.; Lin, W.; He, Y.; Feng, Q.; Zhang, Y.; Mu, B.; Lin, M. Intercalibration of Backscatter Measurements among Ku-Band Scatterometers Onboard the Chinese HY-2 Satellite Constellation. Remote Sens. 2021, 13, 4783. [Google Scholar] [CrossRef]
- Liu, W.T.; Katsaros, K.B.; Businger, J.A. Bulk Parameterization of Air-Sea Exchanges of Heat and Water Vapor Including the Molecular Constraints at the Interface. J. Atmos. Sci. 1979, 36, 1722–1735. [Google Scholar] [CrossRef]
- De Vries, J.; Stoffelen, A.; Beysens, J. Ambiguity Removal and Product Monitoring for SeaWinds. Technical Report, NWPSAF-KN-TR-001 Version 1.2; KNMI: De Bilt, The Netherlands, 2005; Available online: https://knmi-scatterometer-website-prd.s3-eu-west-1.amazonaws.com/publications/nwpsaf_td_ar_1.2.pdf (accessed on 12 November 2022).
- Vogelzang, J.; Stoffelen, A.; Verhoef, A.; de Vries, J.; Bonekamp, H. Validation of Two-Dimensional Variational Ambiguity Removal on SeaWinds Scatterometer Data. J. Atmos. Ocean. Technol. 2009, 26, 1229–1245. [Google Scholar] [CrossRef]
- Stoffelen, A.; Anderson, D. Ambiguity Removal and Assimilation of Scatterometer Data. Q. J. R. Meteorol. Soc. 1997, 123, 491–518. [Google Scholar] [CrossRef]
- Lin, W.; Portabella, M.; Stoffelen, A.; Vogelzang, J.; Verhoef, A. On Mesoscale Analysis and ASCAT Ambiguity Removal. Q. J. R. Meteorol. Soc. 2016, 142, 1745–1756. [Google Scholar] [CrossRef] [Green Version]
- Vogelzang, J.; Stoffelen, A. NWP Model Error Structure Functions Obtained From Scatterometer Winds. IEEE Trans. Geosci. Remote Sens. 2011, 50, 2525–2533. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S. Variational Bias Correction of Satellite Radiance Data in the ERA-Interim Reanalysis. Q. J. R. Meteorol. Soc. 2009, 135, 1830–1841. [Google Scholar] [CrossRef]




| Satellite | Altitude (km) | Inclination (°) | LTDN * | Repeat Cycle | |
|---|---|---|---|---|---|
| The Early Stage | The End Stage | ||||
| HY-2B | 971 | 99.3 | 6:00 am | 14 days | 168 days |
| HY-2C | 957 | 66 | Drifting | 10 days | 400 days |
| HY-2D | 957 | 66 | Drifting | 10 days | 400 days |
| Scatterometer | Wind Speed (m/s) | Wind Direction (°) | |||||
|---|---|---|---|---|---|---|---|
| HSCAT-B | HSCAT-C | HSCAT-D | HSCAT-B | HSCAT-C | HSCAT-D | ||
| Time difference | 0.0–0.5 h | −0.28 | −0.19 | −0.18 | 0.5 | 1.6 | 0.3 |
| 0.5–1.0 h | −0.26 | −0.19 | −0.16 | 0.5 | 0.9 | 1.3 | |
| 1.0–1.5 h | −0.28 | −0.23 | −0.15 | 0.8 | 1.5 | 1.2 | |
| 1.5–2.0 h | −0.31 | −0.24 | −0.20 | 0.3 | 0.1 | 0.2 | |
| 2.0–2.5 h | −0.30 | −0.20 | −0.18 | 1.0 | 0.9 | 0.8 | |
| 2.5–3.0 h | −0.25 | −0.25 | −0.18 | 1.3 | 1.0 | 1.1 | |
| Scatterometer | Wind Speed (m/s) | Wind Direction (°) | |||||
|---|---|---|---|---|---|---|---|
| HSCAT-B | HSCAT-C | HSCAT-D | HSCAT-B | HSCAT-C | HSCAT-D | ||
| Time difference | 0.0–0.5 h | 1.11 | 1.05 | 1.20 | 17.7 | 17.9 | 18.1 |
| 0.5–1.0 h | 1.20 | 1.06 | 1.21 | 16.6 | 18.0 | 17.4 | |
| 1.0–1.5 h | 1.18 | 1.16 | 1.13 | 17.1 | 16.6 | 17.0 | |
| 1.5–2.0 h | 1.24 | 1.28 | 1.38 | 17.0 | 18.1 | 17.6 | |
| 2.0–2.5 h | 1.40 | 1.45 | 1.42 | 18.7 | 19.9 | 19.3 | |
| 2.5–3.0 h | 1.39 | 1.53 | 1.55 | 20.3 | 21.1 | 22.1 | |
| u component (m/s) | v component (m/s) | ||||||
| HSCAT-B | HSCAT-C | HSCAT-D | HSCAT-B | HSCAT-C | HSCAT-D | ||
| Time difference | 0.0–0.5 h | 1.65 | 1.69 | 1.75 | 1.85 | 2.22 | 2.19 |
| 0.5–1.0 h | 1.70 | 1.65 | 1.71 | 1.76 | 2.05 | 2.22 | |
| 1.0–1.5 h | 1.62 | 1.64 | 1.60 | 2.01 | 1.96 | 1.77 | |
| 1.5–2.0 h | 1.75 | 1.82 | 1.67 | 1.77 | 2.10 | 1.89 | |
| 2.0–2.5 h | 1.95 | 1.93 | 1.96 | 2.08 | 2.21 | 2.49 | |
| 2.5–3.0 h | 2.00 | 2.06 | 2.23 | 2.28 | 2.33 | 2.45 | |
| Scatterometer | u Component | v Component | |||||
|---|---|---|---|---|---|---|---|
| HSCAT-B | HSCAT-C | HSCAT-D | HSCAT-B | HSCAT-C | HSCAT-D | ||
| Time difference | 0.0–0.5 h | 1.00 | 1.02 | 1.06 | 0.97 | 1.17 | 1.15 |
| 0.5–1.0 h | 1.03 | 1.00 | 1.03 | 0.93 | 1.08 | 1.17 | |
| 1.0–1.5 h | 0.98 | 0.99 | 0.97 | 1.06 | 1.03 | 0.93 | |
| 1.5–2.0 h | 1.05 | 1.10 | 1.00 | 0.93 | 1.11 | 0.99 | |
| 2.0–2.5 h | 1.18 | 1.16 | 1.18 | 1.10 | 1.16 | 1.31 | |
| 2.5–3.0 h | 1.20 | 1.24 | 1.34 | 1.20 | 1.23 | 1.29 | |
| Statistical Scores | Speed (m/s) | Direction (°) | u (m/s) | v (m/s) | |
|---|---|---|---|---|---|
| GSF | Obs | 1.20 | 15.6 | 1.61 | 1.89 |
| No Obs | 1.77 | 19.3 | 2.16 | 2.31 | |
| Overall | 1.51 | 17.5 | 1.90 | 2.11 | |
| EBEC | Obs | 1.17 | 15.8 | 1.62 | 1.89 |
| No Obs | 1.60 | 18.0 | 1.99 | 2.15 | |
| Overall | 1.40 | 16.9 | 1.81 | 2.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, S.; Lin, W.; Wang, Z.; Zou, J. Blending Sea Surface Winds from the HY-2 Satellite Scatterometers Based on a 2D-Var Method. Remote Sens. 2023, 15, 193. https://doi.org/10.3390/rs15010193
Lv S, Lin W, Wang Z, Zou J. Blending Sea Surface Winds from the HY-2 Satellite Scatterometers Based on a 2D-Var Method. Remote Sensing. 2023; 15(1):193. https://doi.org/10.3390/rs15010193
Chicago/Turabian StyleLv, Sirui, Wenming Lin, Zhixiong Wang, and Juhong Zou. 2023. "Blending Sea Surface Winds from the HY-2 Satellite Scatterometers Based on a 2D-Var Method" Remote Sensing 15, no. 1: 193. https://doi.org/10.3390/rs15010193
APA StyleLv, S., Lin, W., Wang, Z., & Zou, J. (2023). Blending Sea Surface Winds from the HY-2 Satellite Scatterometers Based on a 2D-Var Method. Remote Sensing, 15(1), 193. https://doi.org/10.3390/rs15010193






