Bouguer Anomaly Re-Reduction and Interpretative Remarks of the Phlegraean Fields Caldera Structures (Southern Italy)
Abstract
:1. Introduction
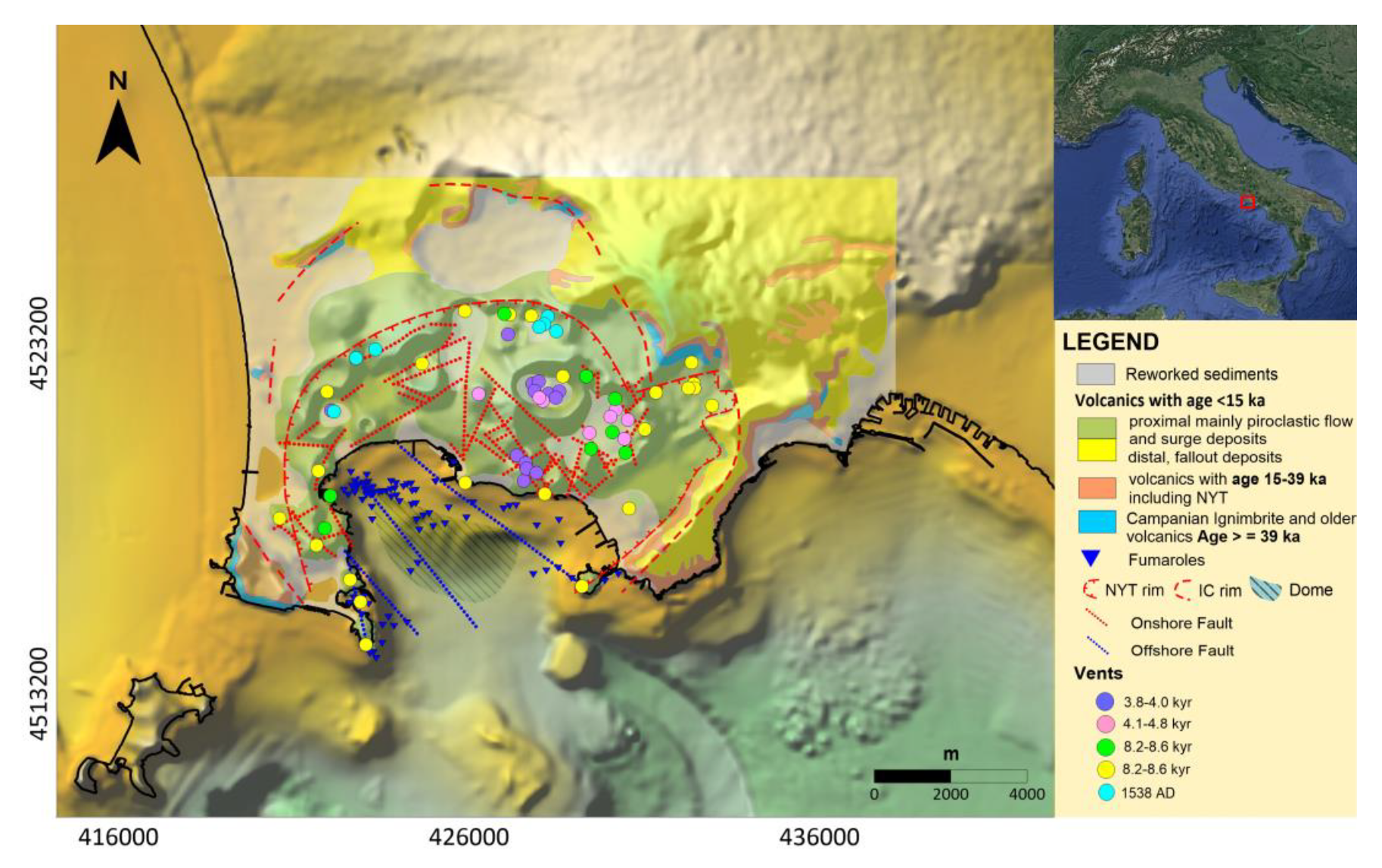
2. Geological Background
3. Data and Methods
3.1. Data
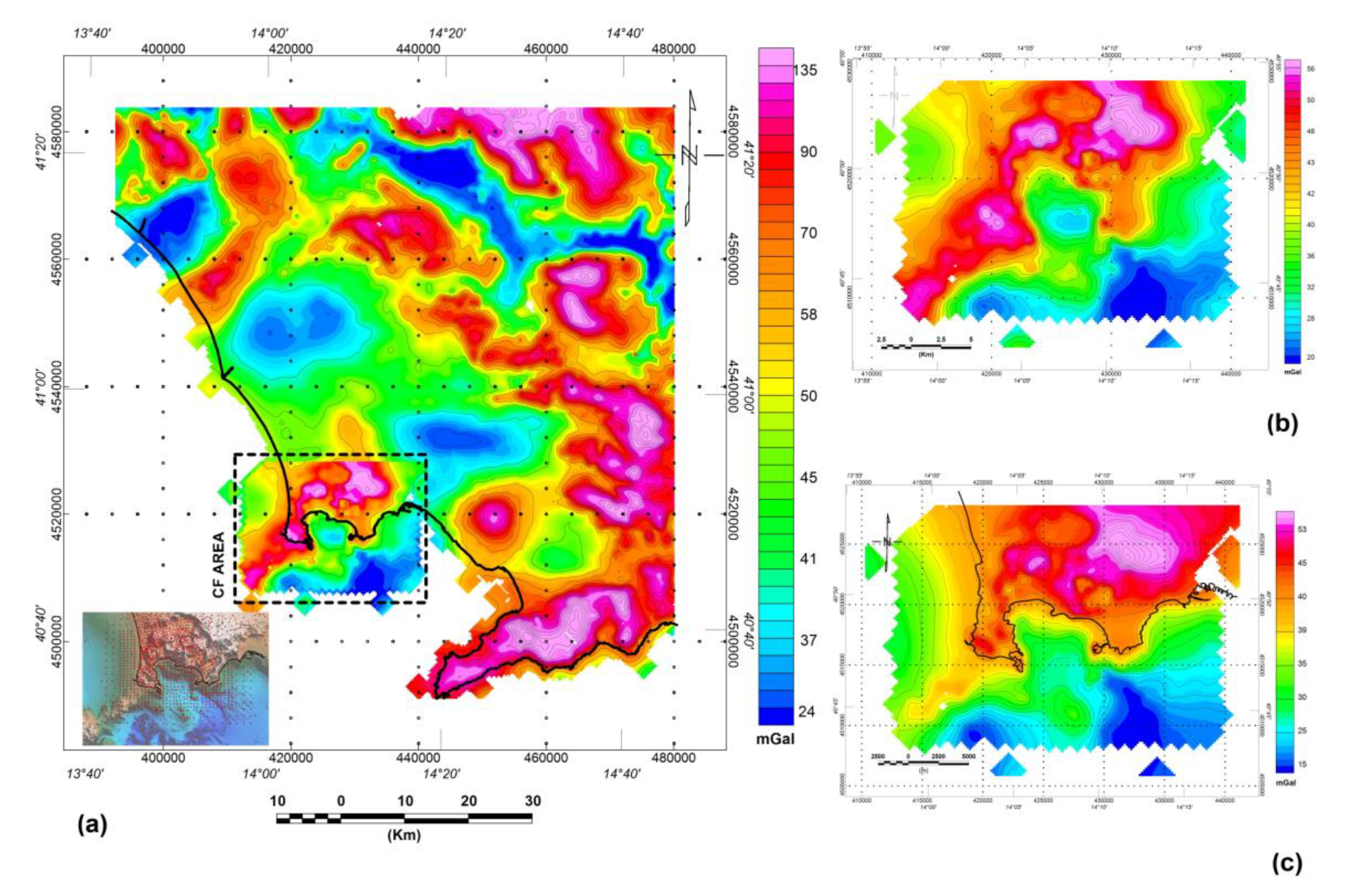
3.1.1. ISPRA—Digital Gravimetric Map of Italy at the Scale of 1:250,000
3.1.2. Campanian Plain and Phlegraean Fields ENI Gravimetric Data
3.1.3. Digital Elevation Model
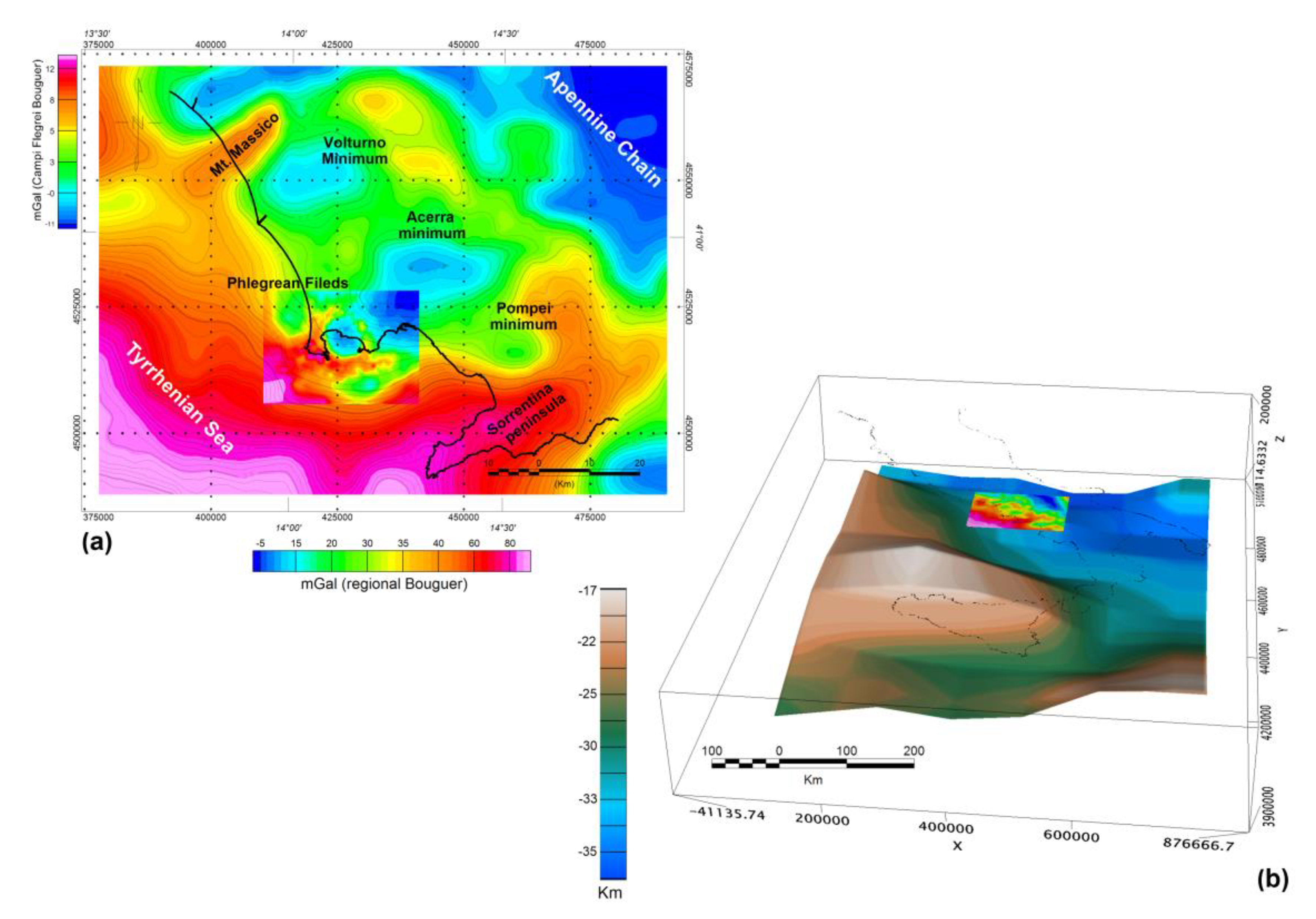
3.2. Methods
3.2.1. VPmg Geologically Constrained Terrain Correction
3.2.2. Data Detrending
3.2.3. Correlation Coefficient: Bouguer Anomaly vs. Elevation
4. Results
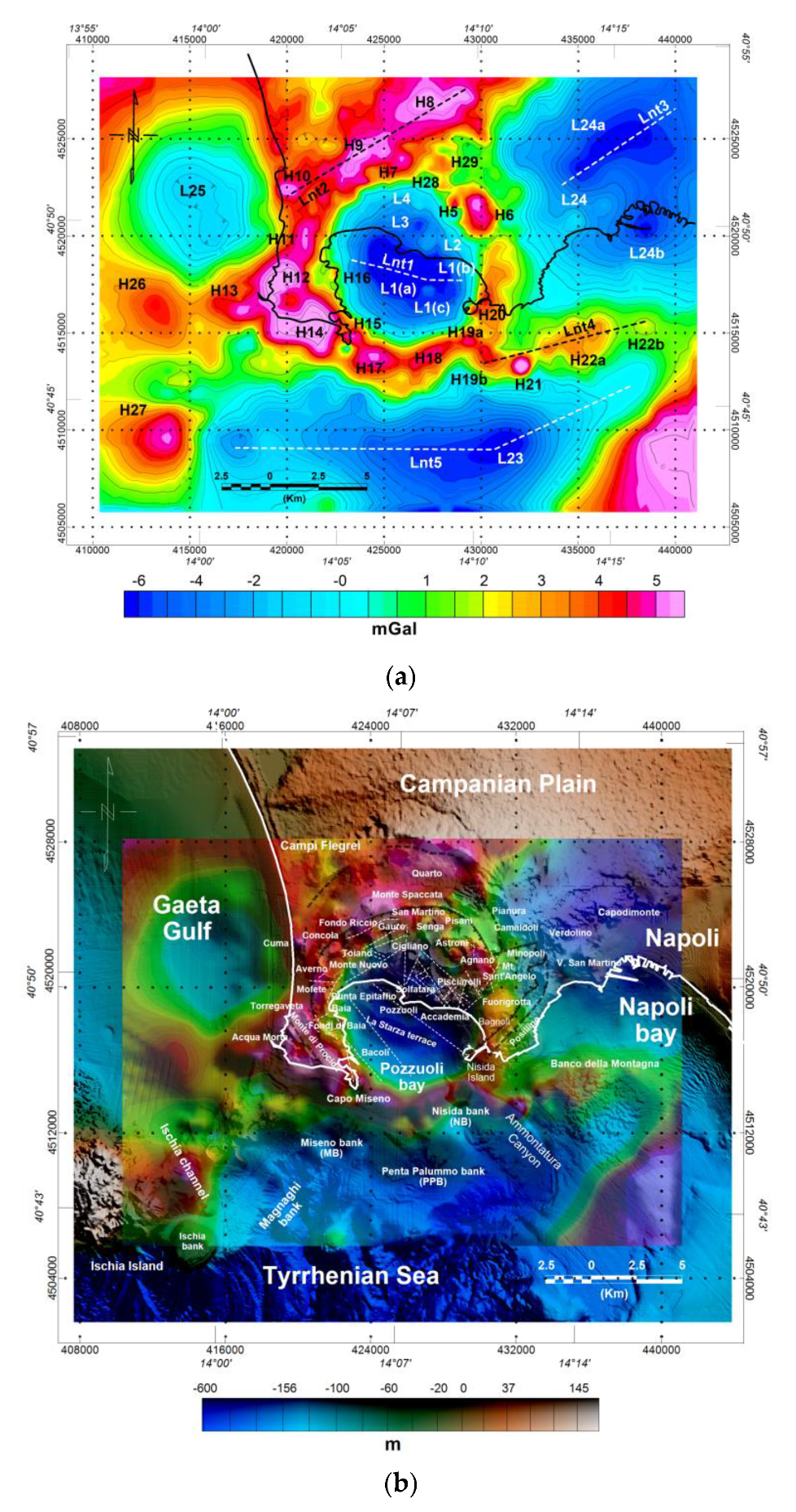
4.1. Description of the Gravity Anomaly Patterns
4.1.1. Central Gravimetric Minima
4.1.2. Annular Ring of Gravimetric Highs
4.1.3. Outer Caldera Gravimetric Signatures
4.1.4. Regional Components
4.2. Interpretative Remarks
- (1)
- The caldera refilling of low-density pyroclastic deposits;
- (2)
- The existence of a high-heat flux, triggered by deep sources (160 mWm−2 at Mofete, 120 mWm−2 at Agnano and 80 mWm−2 at S. Vito and Mt. Nuovo) [69];
- (3)
- The presence of a wide geothermal system. At the local scale, the shorter gravimetric wavelength minima (L2–4 in Figure 8a) may be related to the effects of the short wavelength variation of the isotherms caused by the local upwelling of shallow fluids. In fact, L2–4 features lay in correspondence with the most active CFc hydrothermal vents (i.e., Solfatara, Pisciarelli and Agnano).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Gebauer, S.K.; Schmitt, A.K.; Pappalardo, L.; Stockli, D.F.; Lovera, O.M. Crystallization and eruption ages of Breccia Museo (Campi Flegrei caldera, Italy) plutonic clasts and their relation to the Campanian ignimbrite. Contrib. Mineral. Petrol. 2014, 167, 953. [Google Scholar] [CrossRef]
- Deino, A.L.; Orsi, G.; de Vita, S.; Piochi, M. The age of the Neapolitan Yellow Tuff caldera-forming eruption (Campi Flegrei caldera–Italy) assessed by 40Ar/39Ar dating method. J. Volcanol. Geotherm. Res. 2004, 133, 157–170. [Google Scholar] [CrossRef]
- Barberi, F.; Cassano, E.; la Torre, P.; Sbrana, A. Structural evolution of Campi Flegrei caldera in light of volcanological and geophysical data. J. Volcanol. Geotherm. Res. 1991, 48, 33–49. [Google Scholar] [CrossRef]
- Di Vito, M.A.; Isaia, R.; Orsi, G.; Southon, J.; de Vita, S.; D’Antonio, M.; Pappalardo, L.; Piochi, M. Volcanism and deformation since 12,000 years at the Campi Flegrei caldera (Italy). J. Volcanol. Geotherm. Res. 1999, 91, 221–246. [Google Scholar] [CrossRef]
- Scandone, R.; Giacomelli, L.; Speranza, F. The volcanological history of the volcanoes of Naples: A review. Dev. Volcanol. 2006, 9, 1–26. [Google Scholar]
- Albert, P.G.; Giaccio, B.; Isaia, R.; Costa, A.; Niespolo, E.M.; Nomade, S.; Smith, V.C. Evidence for a large-magnitude eruption from Campi Flegrei caldera (Italy) at 29 ka. Geology 2019, 47, 595–599. [Google Scholar] [CrossRef] [Green Version]
- Fedi, M.; Nunziata, C.; Rapolla, A. The Campania-Campi Flegrei area: A contribution to discern the best structural model from gravity interpretation. J. Volcanol. Geotherm. Res. 1991, 48, 51–59. [Google Scholar] [CrossRef]
- Nunziata, C.; Rapolla, A. Interpretation of gravity and magnetic data in the Phlegraean Fields geothermal area, Naples, Italy. J. Volcanol. Geotherm. Res. 1981, 10, 209–225. [Google Scholar] [CrossRef]
- Cassano, E.; la Torre, P. Geophysics; Santacroce, R., Ed.; Somma-Vesuvius, Quaderni De La Ricerca Scientifica, 114, 8 Edited; Consiglio Nazionale delle Ricerche: Rome, Italy, 1987; pp. 175–195. [Google Scholar]
- Rosi, M.; Sbrana, A. Phlegraean Fields: (CNR Quaderni de “La Ricerca Scientifica” 9); Consiglio Nazionale delle Ricerche: Rome, Italy, 1987; p. 175. [Google Scholar]
- Florio, G.; Fedi, M.; Cella, F.; Rapolla, A. The Campanian Plain and Phlegrean Fields: Structural setting from potential field data. J. Volcanol. Geotherm. Res. 1999, 91, 361–379. [Google Scholar] [CrossRef]
- Berrino, G.; Corrado, G.; Riccardi, U. Sea gravity data in the Gulf of Naples. A contribution to delineating the structural pattern of the Vesuvian area. J. Volcanol. Geotherm. Res. 1998, 82, 139–150. [Google Scholar] [CrossRef]
- Berrino, G.; Corrado, G.; Riccardi, U. Sea gravity data in the Gulf of Naples. A contribution to delineating the structural pattern of the Phlegraean Volcanic District. J. Volcanol. Geotherm. Res. 2008, 175, 241–252. [Google Scholar] [CrossRef]
- Judenherc, S.; Zollo, A. The Bay of Naples (southern Italy): Constraints on the volcanic structures inferred from a dense seismic survey. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Zollo, A.; Maercklin, N.; Vassallo, M.; Iacono, D.D.; Virieux, J.; Gasparini, P. Seismic reflections reveal a massive melt layer feeding Campi Flegrei caldera. Geophys. Res. Lett. 2008, 35, 12. [Google Scholar] [CrossRef] [Green Version]
- De Siena, L.; del Pezzo, E.; Bianco, F. Seismic attenuation imaging of Campi Flegrei: Evidence of gas reservoirs, hydrothermal basins, and feeding systems. J. Geophys. Res. Solid Earth 2010, 115, B09312. [Google Scholar] [CrossRef]
- Calò, M.; Tramelli, A. Anatomy of the Campi Flegrei caldera using enhanced seismic tomography models. Sci. Rep. 2018, 8, 16254. [Google Scholar] [CrossRef] [Green Version]
- Capuano, P.; Russo, G.; Civetta, L.; Orsi, G.; D’Antonio, M.; Moretti, R. The active portion of the Campi Flegrei caldera structure imaged by 3-D inversion of gravity data. Geochem. Geophys. Geosystems 2013, 14, 4681–4697. [Google Scholar] [CrossRef] [Green Version]
- Imbò, G. Considerazioni sismo-gravimetriche sulle manifestazioni vesuviane del maggio 1964. In Proceedings of the XIV Convegno nazionale Associazione Geofisica Italiana, Naples, Italy, 1965; pp. 291–300. [Google Scholar]
- Maino, A. Rilevamento Gravimetrico di Dettaglio dell’isola D’Ischia. Boll. Serv. Geol. It. 1971, 92. [Google Scholar]
- Hinze, W.J.; von Frese, R.R.B.; Saad, A.H. Gravity and Magnetic Exploration: Principles, Practices, and Applications; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Vitale, S.; Isaia, R. Fractures and faults in volcanic rocks (Campi Flegrei, southern Italy): Insight into volcano-tectonic processes. Int. J. Earth Sci. 2014, 103, 801–819. [Google Scholar] [CrossRef]
- Steinmann, L.; Spiess, V.; Sacchi, M. The Campi Flegrei caldera (Italy): Formation and evolution in interplay with sea-level variations since the Campanian Ignimbrite eruption at 39 ka. J. Volcanol. Geotherm. Res. 2016, 327, 361–374. [Google Scholar] [CrossRef]
- Piochi, M.; Kilburn, C.R.J.; di Vito, M.A.; Mormone, A.; Tramelli, A.; Troise, C.; de Natale, G. The volcanic and geothermally active Campi Flegrei caldera: An integrated multidisciplinary image of its buried structure. Int. J. Earth Sci. 2014, 103, 401–421. [Google Scholar] [CrossRef]
- De Bonitatibus, A.; Latmiral, G.; Mirabile, L. Rilievi sismici per riflessione: Strutturali, ecografici (fumarole) e batimetrici nel Golfo di Pozzuoli. Boll. Soc. Nat. Napoli 1970, 79, 15. [Google Scholar]
- Mira Geoscience. Available online: https://mirageoscience.com (accessed on 1 October 2022).
- Fullagar, P.K.; Pears, G.A.; Milkereit, B. Towards geologically realistic inversion. In Proceedings of the Exploration 07: Fifth Decennial International Conference on Mineral Exploration, Toronto, ON, Canada, 9–12 September 2007; pp. 444–460. [Google Scholar]
- Carrozzo, M.T.; Luzio, D.; Margiotta, C.; Quarta, T. Gravity Anomaly Map of Italy. In CNR Progett Final Geodin Model Strutt Tridimensionale; CNR Edizioni: Rome, Italy, 1986. [Google Scholar]
- Doglioni, C. A proposal for the kinematic modelling of W-dipping subductions-possible applications to the Tyrrhenian-Apennines system. Terra Nova 1991, 3, 423–434. [Google Scholar] [CrossRef]
- EMODnet Consortium. Available online: https://www.emodnet-bathymetry.eu/ (accessed on 1 October 2022).
- Passaro, S.; Tamburrino, S.; Vallefuoco, M.; Gherardi, S.; Sacchi, M.; Ventura, G. High-resolution morpho-bathymetry of the Gulf of Naples, Eastern Tyrrhenian Sea. J. Maps 2016, 12, 203–210. [Google Scholar] [CrossRef]
- D’Argenio, B.; Pescatore, T.; Scandone, P. Schema Geologico dell’Appennino Meriodionale (Campania e Lucania). Verl. Nicht Ermittelbar Atti Accad. Naz. Dei Lincei 1973, 183, 220–248. [Google Scholar]
- Brocchini, D.; Principe, C.; Castradori, D.; Laurenzi, M.A.; Gorria, L. Quaternary evolution of the southern sector of the Campanian Plain and early Somma-Vesuvius activity: Insights from the Trecase 1 well. Miner. Pet. 2001, 73, 67–91. [Google Scholar] [CrossRef]
- Bruno, P.P.G.; Cippitelli, G.; Rapolla, A. Seismic study of the Mesozoic carbonate basement around Mt. Somma-Vesuvius, Italy. J. Volcanol. Geotherm. Res. 1998, 84, 311–322. [Google Scholar] [CrossRef]
- Piochi, M.; Bruno, P.P.; de Astis, G. Relative roles of rifting tectonics and magma ascent processes: Inferences from geophysical, structural, volcanological, and geochemical data for the Neapolitan volcanic region (southern Italy). Geochem. Geophys. Geosystems 2005, 6, Q07005. [Google Scholar] [CrossRef]
- De Vivo, B.; Rolandi, G.; Gans, P.B.; Calvert, A.; Bohrson, W.A.; Spera, F.J.; Belkin, H.E. New constraints on the pyroclastic eruptive history of the Campanian volcanic Plain (Italy). Miner. Pet. 2001, 73, 47–65. [Google Scholar] [CrossRef]
- Di Vito, M.A.; Sulpizio, R.; Zanchetta, G.; D’Orazio, M. The late Pleistocene pyroclastic deposits of the Campanian Plain: New insights into the explosive activity of Neapolitan volcanoes. J. Volcanol. Geother. Res. 2008, 177, 19–48. [Google Scholar] [CrossRef]
- Finetti, I.; Morelli, C. Esplorazione geofisica dell’aera mediterranea circostante il Blocco Sardo-Corso. In Paleogeografia Del Terziario Sardo Nell’ambito Del Mediterraneo Occidentale; Rendiconti del Seminario della Facoltà di Scienze—Università di Cagliari: Cagliari, Italy, 1974; Volume 43, pp. 213–238. [Google Scholar]
- Milia, A.; Torrente, M.M. Fold uplift and synkinematic stratal architectures in a region of active transtensional tectonics and volcanism, eastern Tyrrhenian Sea. Geol. Soc. Am. Bull. 2000, 112, 1531–1542. [Google Scholar] [CrossRef]
- Bruno, P.P.G.; Rapolla, A.; di Fiore, V. Structural setting of the Bay of Naples (Italy) seismic reflection data: Implications for Campanian volcanism. Tectonophysics 2003, 372, 193–213. [Google Scholar] [CrossRef]
- Bruno, P.P.G. Structure and evolution of the Bay of Pozzuoli (Italy) using marine seismic reflection data: Implications for collapse of the Campi Flegrei caldera. Bull. Volcanol. 2004, 66, 342–355. [Google Scholar] [CrossRef]
- Somma, R.; Iuliano, S.; Matano, F.; Molisso, F.; Passaro, S.; Sacchi, M.; de Natale, G. High-resolution morpho-bathymetry of Pozzuoli Bay, Southern Italy. J. Maps 2016, 12, 222–230. [Google Scholar] [CrossRef]
- Cole, P.D.; Scarpati, C. A facies interpretation of the eruption and emplacement mechanisms of the upper part of the Neapolitan Yellow Tuff, Campi Flegrei, Southern Italy. Bull. Volcanol. 1993, 55, 311–326. [Google Scholar] [CrossRef]
- Lirer, L.; Luongo, G.; Scandone, R. On the volcanological evolution of Campi Flegrei. Eos Trans. Am. Geophys. Union 1987, 68, 226–234. [Google Scholar] [CrossRef]
- Orsi, G.; de Vita, S.; di Vito, M. The restless, resurgent Campi Flegrei nested caldera (Italy): Constraints on its evolution and configuration. J. Volcanol. Geotherm. Res. 1996, 74, 179–214. [Google Scholar] [CrossRef]
- Fedele, L.; Scarpati, C.; Sparice, D.; Perrotta, A.; Laiena, F. A chemostratigraphic study of the Campanian Ignimbrite eruption (Campi Flegrei, Italy): Insights on magma chamber withdrawal and deposit accumulation as revealed by compositionally zoned stratigraphic and facies framework. J. Volcanol. Geotherm. Res. 2016, 324, 105–117. [Google Scholar] [CrossRef]
- Rolandi, G.; Bellucci, F.; Heizler, M.T.; Belkin, H.E.; de Vivo, B. Tectonic controls on the genesis of ignimbrites from the Campanian. Volcanic Zone, Southern Italy. Miner. Pet. 2003, 79, 3–31. [Google Scholar] [CrossRef]
- Rolandi, G.; de Natale, G.; Kilburn, C.R.J.; Troise, C.; Somma, R.; di Lascio, M.; Fedele, A.; Rolandi, R. The 39 ka Campanian Ignimbrite eruption: New data on source area in the Campanian Plain. In Vesuvius, Campi Flegrei, and Campanian Volcanism; Elsevier: Amsterdam, The Netherlands, 2020; pp. 175–205. [Google Scholar]
- Isaia, R.; Marianelli, P.; Sbrana, A. Caldera unrest prior to intense volcanism in Campi Flegrei (Italy) at 4.0 ka BP: Implications for caldera dynamics and future eruptive scenarios. Geophys. Res. Lett. 2009, 36, 21. [Google Scholar] [CrossRef]
- D’antonio, M.; Civetta, L.; Orsi, G. The present state of the magmatic system of the Campi Flegrei caldera based on a reconstruction of its behavior in the past 12 ka. J. Volcanol. Geotherm. Res. 1999, 91, 247–268. [Google Scholar] [CrossRef]
- Insinga, D.; Calvert, A.T.; Lanphere, M.A.; Morra, V.; Perrotta, A.; Sacchi, M.; Scarpati, C.; Saburomaru, J.; Fedele, L. The Late-Holocene evolution of the Miseno area (south-western Campi Flegrei) as inferred by stratigraphy, petrochemistry and 40Ar/39Ar geochronology. In Developments in Volcanology; Elsevier: Amsterdam, The Netherlands, 2006; pp. 97–124. [Google Scholar]
- Fedele, L.; Insinga, D.D.; Calvert, A.T.; Morra, V.; Perrotta, A.; Scarpati, C. 40 Ar/39 Ar dating of tuff vents in the Campi Flegrei caldera (Southern Italy): Toward a new chronostratigraphic reconstruction of the Holocene volcanic activity. Bull. Volcanol. 2011, 73, 1323–1336. [Google Scholar] [CrossRef]
- Sacchi, M.; Pepe, F.; Corradino, M.; Insinga, D.D.; Molisso, F.; Lubritto, C. The Neapolitan Yellow Tuff caldera offshore the Campi Flegrei: Stratal architecture and kinematic reconstruction during the last 15ky. Mar. Geol. 2014, 354, 15–33. [Google Scholar] [CrossRef] [Green Version]
- Sacchi, M.; Passaro, S.; Molisso, F.; Matano, F.; Steinmann, L.; Spiess, V.; Pepe, F.; Corradino, M.; Caccavale, M.; Taburrino, S.; et al. The Holocene Marine Record of Unrest, Volcanism, and Hydrothermal Activity of Campi Flegrei and Somma–Vesuvius: Vesuvius, Campi Flegrei, and Campanian Volcanism; Elsevier: Amsterdam, The Netherlands, 2020; pp. 435–469. [Google Scholar]
- De Natale, G.; Troise, C.; Mark, D.; Mormone, A.; Piochi, M.; di Vito, M.A.; Isaia, R.; Carlino, S.; Barra, D.; Somma, R. The Campi Flegrei Deep Drilling Project (CFDDP): New insight on caldera structure, evolution and hazard implications for the Naples area (Southern Italy). Geochem. Geophys. Geosystems 2016, 17, 4836–4847. [Google Scholar] [CrossRef]
- Perrotta, A.; Scarpati, C. The dynamics of the Breccia Museo eruption (Campi Flegrei, Italy) and the significance of spatter clasts associated with lithic breccias. J. Volcanol. Geotherm. 1994, 59, 335–355. [Google Scholar] [CrossRef]
- Passaro, S.; Barra, M.; Saggiomo, R.; di Giacomo, S.; Leotta, A.; Uhle, H.; Mazzola, S. Multi-resolution morpho-bathymetric survey results at the Pozzuoli–Baia underwater archaeological site (Naples, Italy). J. Archaeol. Sci. 2013, 40, 1268–1278. [Google Scholar] [CrossRef]
- Chiodini, G.; Frondini, F.; Cardellini, C.; Granieri, L.; Marini, L.; Ventura, G. CO2 degassing and energy release at Solfatara Volcano, Campi Flegrei, Italy. J. Geophys. Res. 2001, 106, 16213–16221. [Google Scholar] [CrossRef]
- Chiodini, G. CO2/CH4 ratio in fumaroles a powerful tool to detect magma degassing episodes at quiescent volcanoes. Geophys Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Acocella, V. Activating and reactivating pairs of nested collapses during caldera-forming eruptions: Campi Flegrei (Italy). Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Tramelli, A.; Giudicepietro, F.; Ricciolino, P.; Chiodini, G. The seismicity of Campi Flegrei in the contest of an evolving long term unrest. Sci. Rep. 2022, 12, 2900. [Google Scholar] [CrossRef]
- Di Luccio, F.; Pino, N.A.; Piscini, A.; Ventura, G. Significance of the 1982–2014 Campi Flegrei seismicity: Preexisting structures, hydrothermal processes, and hazard assessment. Geophys. Res. Lett. 2015, 42, 7498–7506. [Google Scholar] [CrossRef] [Green Version]
- CRUST 1.0. A New Global Crustal Model at 1 × 1 Degrees. Available online: https://igppweb.ucsd.edu/~gabi/crust1.html (accessed on 19 January 2021).
- Artemieva, I.M.; Mooney, W.D. Thermal thickness and evolution of Precambrian lithosphere: A global study. J. Geophys. Res. 2001, 106, 16387–16414. [Google Scholar] [CrossRef] [Green Version]
- Vallius, H.T.V.; Kotilainen, A.T.; Asch, K.C.; Fiorentino, A.; Judge, M.; Stewart, H.A.; Pjetursson, B. Discovering Europe’s seabed geology: The EMODnet concept of uniform collection and harmonization of marine data. Geol. Soc. Spec. Publ. 2022, 505, 7–18. [Google Scholar] [CrossRef]
- Passaro, S.; Genovese, S.; Sacchi, M.; Barra, M.; Rumolo, P.; Tamburino, S.; Mazzola, S.; Basilone, G.; Placenti, F.; Aronica, S.; et al. First hydroacoustic evidence of marine, active fluid vents in the Naples Bay continental shelf (Southern Italy). J. Volcanol. Geotherm. Res. 2014, 285, 29–35. [Google Scholar] [CrossRef]
- Fullagar, P.K.; Pears, G.A.; McMonnies, B. Constrained inversion of geological surfaces-pushing the boundaries. Lead. Edge 2008, 27, 98–105. [Google Scholar] [CrossRef]
- Carlino, S.; Somma, R.; Troise, C.; Natale, G. The geothermal exploration of Campanian volcanoes: Historical review and future development. Renew. Sustain. Energy Rev. 2012, 16, 1004–1030. [Google Scholar] [CrossRef]
- Mallick, K.; Vasanthi, A.; Sharma, K.K. Bouguer Gravity Regional and Residual Separation: Application to Geology and Environment; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Chapin, D.A. A deterministic approach toward isostatic gravity residuals: A case study from South America. Geophysics 1996, 4, 1022–1033. [Google Scholar] [CrossRef]
- Nettleton, L.L. Determination of density for reduction of gravimeter observations. Geophysics 1939, 4, 176–183. [Google Scholar] [CrossRef]
- Thorarinsson, F.; Magnusson, S.G. Bouguer density determination by fractal analysis. Geophysics 1990, 55, 932–935. [Google Scholar] [CrossRef]
- Caratori Tontini, F.; Graziano, F.; Cocchi, L.; Carmisciano, C.; Stefanelli, P. Determining the optimal Bouguer density for a gravity data set: Implications for the isostatic setting of the Mediterranean Sea. Geophys. J. Int. 2007, 169, 380–388. [Google Scholar] [CrossRef] [Green Version]
- Cocchi, L.; Tontini, F.C.; Carmisciano, C.; Stefanelli, P.; Anzidei, M.; Esposito, A.; del Negro, C.; Greco, F.; Napoli, R. Looking inside the Panarea Island (Aeolian Archipelago, Italy) by gravity and magnetic data. Ann. Geophys 2008, 51, 25–38. [Google Scholar] [CrossRef]
- Jilinski, P.; Fontes, S.L.; Meju, M.A. Estimating optimum density for regional Bouguer reduction by morphological correlation of gravity and bathymetric maps: Examples from offshore south-eastern Brazil. Geo-Mar. Lett. 2013, 33, 67–73. [Google Scholar] [CrossRef]
- De Marchi, A.C.P.; Ghidella, M.E.; Tocho, C.N. Analysis of Different Methodologies to Calculate Bouguer Gravity Anomalies in the Argentine Continental Margin. Geosciences 2014, 4, 33–41. [Google Scholar] [CrossRef]
- Scandone, R.; Bellucci, F.; Lirer, L.; Rolandi, G. The structure of the Campanian Plain and the activity of the Neapolitan volcanoes (Italy). J. Volcanol. Geotherm. Res. 1991, 48, 1–31. [Google Scholar] [CrossRef]
- Sartori, R.; Torelli, L.; Zitellini, N.; Carrara, G.; Magaldi, M.; Mussoni, P. 2004. Crustal features along a W–E Tyrrhenian transect from Sardinia to Campania margins (Central Mediterranean). Tectonophysics 2004, 383, 171–192. [Google Scholar] [CrossRef]
- Peccerillo, A.; Terre, A. Cenozoic Volcanism in the Tyrrhenian Sea Region; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Milia, A.; Torrente, M.M. Coeval Miocene development of thrust belt-backarc and forearc extension during the subduction of a continental margin (Western-Central Mediterranean Sea). J. Geodyn. 2022, 149, 101882. [Google Scholar] [CrossRef]
- Gilbert, L.A.; McDuff, R.E.; Paul Johnson, H. Porosity of the upper edifice of Axial Seamount. Geology 2007, 35, 49–52. [Google Scholar] [CrossRef]
- Zhu, Z.; Tian, H.; Jiang, G.; Dou, B. Effects of high temperature on rock bulk density. Geomech. Geoengin. 2022, 17, 647–657. [Google Scholar] [CrossRef]
- Miller, C.A.; Williams-Jones, G. Internal structure and volcanic hazard potential of Mt Tongariro, New Zealand, from 3D gravity and magnetic models. J. Volcanol. Geotherm. Res. 2016, 319, 12–28. [Google Scholar] [CrossRef]
- Luiso, P.; Paoletti, V.; Nappi, R.; la Manna, M.; Cella, F.; Gaudiosi, G.; Fedi, M.; Iorio, M. A multidisciplinary approach to characterize the geometry of active faults: The example of Mt. Massico, Southern Italy. Geophys. J. Int. 2018, 213, 1673–1681. [Google Scholar] [CrossRef]
- Sbrana, A.; Marianelli, P.; Pasquini, G. The phlegrean fields volcanological evolution. J. Maps 2021, 17, 557–570. [Google Scholar] [CrossRef]
- Bartole, R.; Savelli, D.; Tramontana, M.; Wezel, F.-C. 1984. Structural and sedimentary features in the Tyrrhenian margin off Campania, Southern Italy. Mar. Geol. 1984, 55, 163–180. [Google Scholar] [CrossRef]
- Milia, A.; Torrente, M.M.; Russo, M.; Zuppetta, A. Tectonics and crustal structure of the Campania continental margin: Relationships with volcanism. Miner. Pet. 2003, 79, 33–47. [Google Scholar] [CrossRef]





| Bouguer Reduction Methods | Correlation Coefficient |
|---|---|
| Vpmg | −0.4107 |
| Residual Vpmg | 0.1471 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Ritis, R.; Cocchi, L.; Passaro, S.; Campagne, T.; Gabriellini, G. Bouguer Anomaly Re-Reduction and Interpretative Remarks of the Phlegraean Fields Caldera Structures (Southern Italy). Remote Sens. 2023, 15, 209. https://doi.org/10.3390/rs15010209
De Ritis R, Cocchi L, Passaro S, Campagne T, Gabriellini G. Bouguer Anomaly Re-Reduction and Interpretative Remarks of the Phlegraean Fields Caldera Structures (Southern Italy). Remote Sensing. 2023; 15(1):209. https://doi.org/10.3390/rs15010209
Chicago/Turabian StyleDe Ritis, Riccardo, Luca Cocchi, Salvatore Passaro, Thomas Campagne, and Gianluca Gabriellini. 2023. "Bouguer Anomaly Re-Reduction and Interpretative Remarks of the Phlegraean Fields Caldera Structures (Southern Italy)" Remote Sensing 15, no. 1: 209. https://doi.org/10.3390/rs15010209
APA StyleDe Ritis, R., Cocchi, L., Passaro, S., Campagne, T., & Gabriellini, G. (2023). Bouguer Anomaly Re-Reduction and Interpretative Remarks of the Phlegraean Fields Caldera Structures (Southern Italy). Remote Sensing, 15(1), 209. https://doi.org/10.3390/rs15010209








