A Novel Cross-Correlation Algorithm Based on the Differential for Target Detection of Passive Radar
Abstract
:1. Introduction
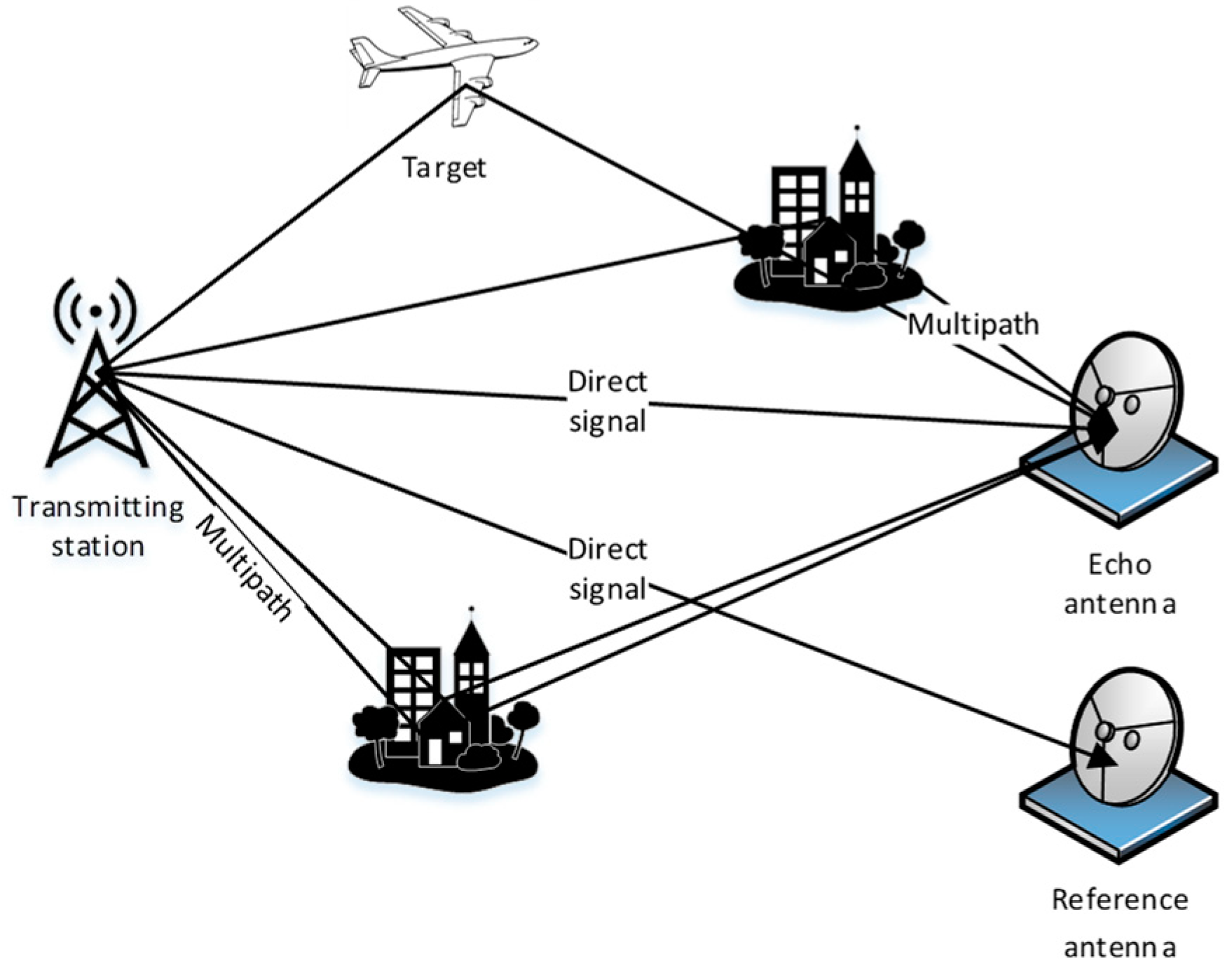
2. Materials and Methods
2.1. Signal Model
2.2. Algorithm Description and Analysis
2.2.1. Traditional Cross-Correlation Algorithm
2.2.2. Novel Cross Correlation Algorithm
3. Result
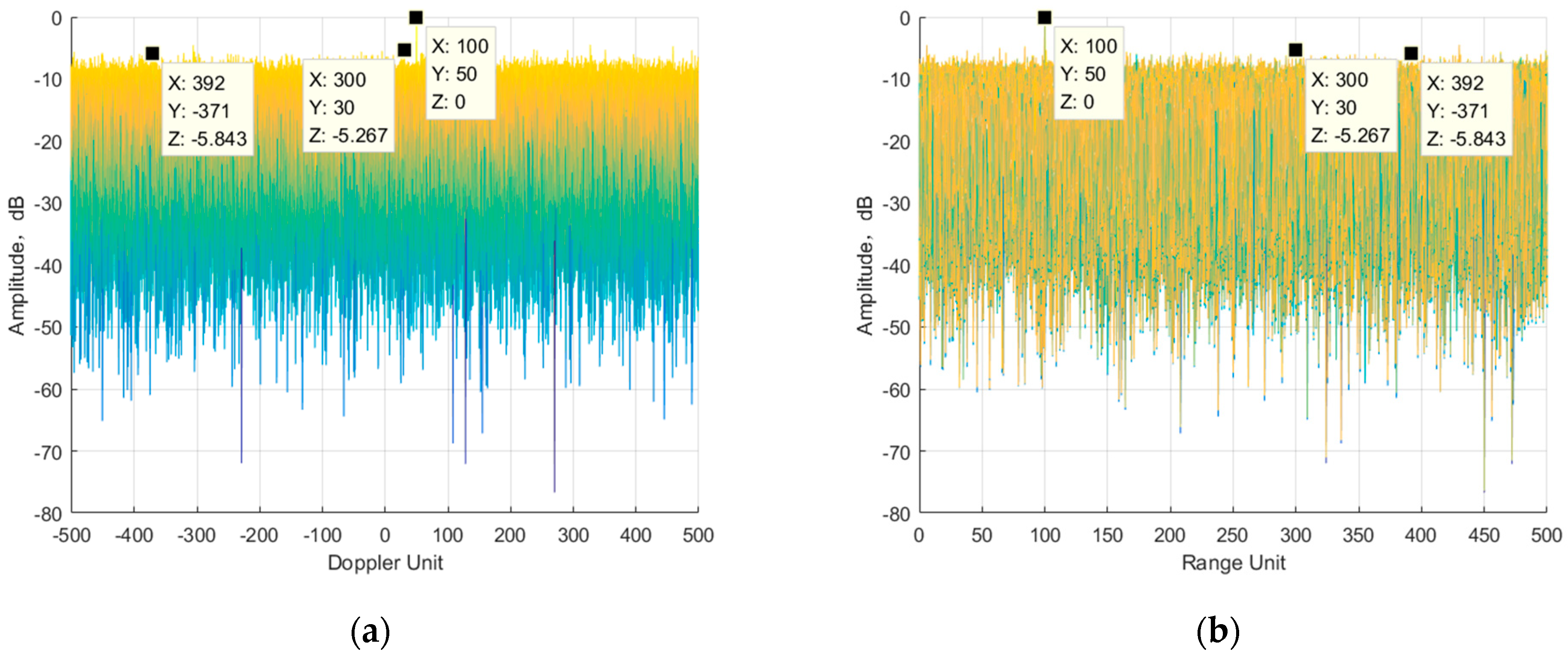
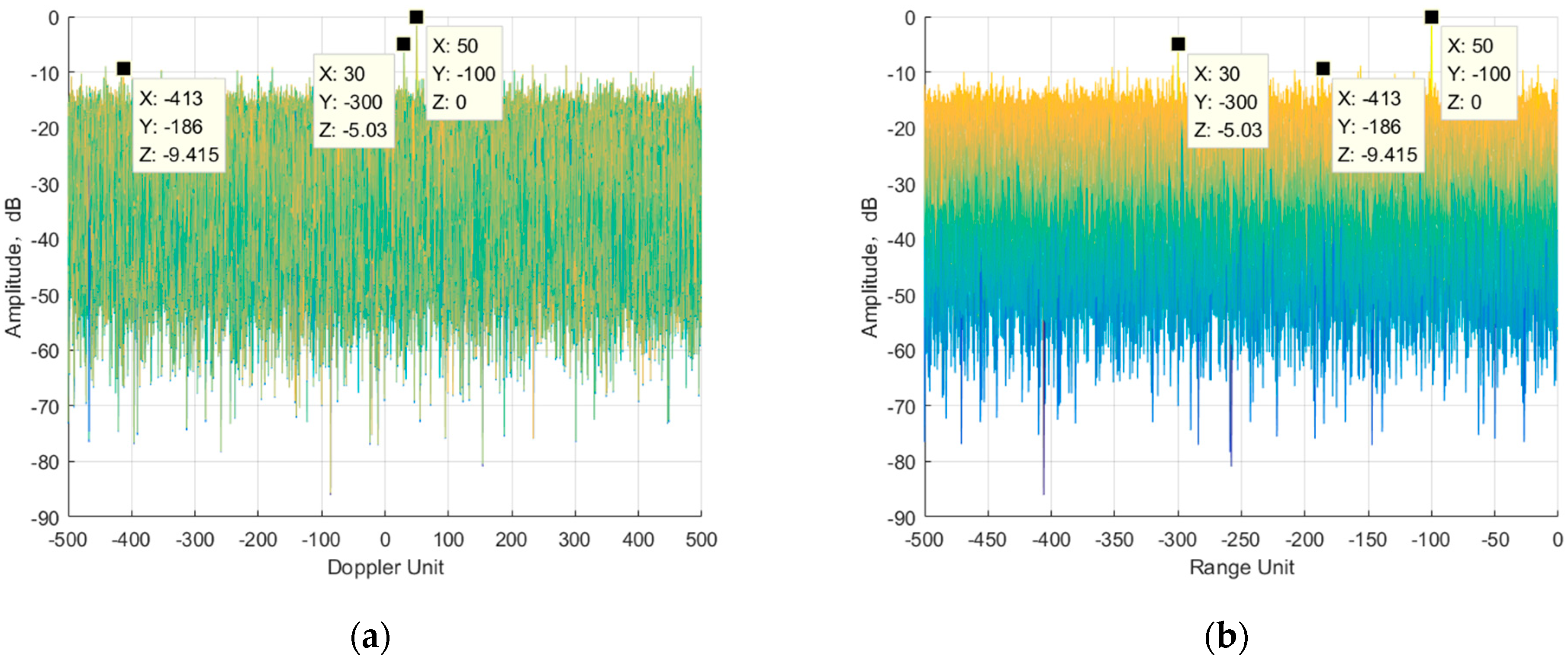
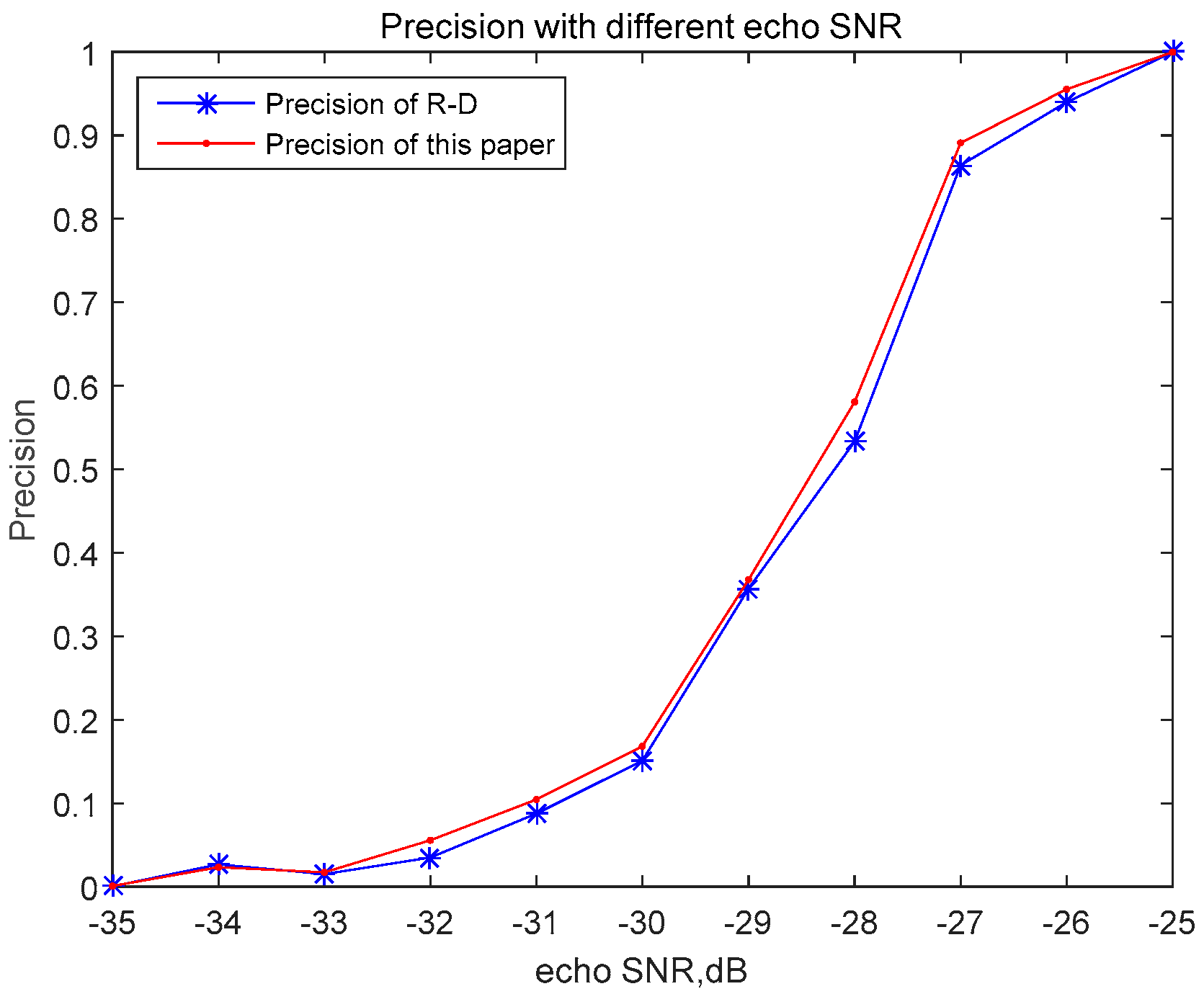
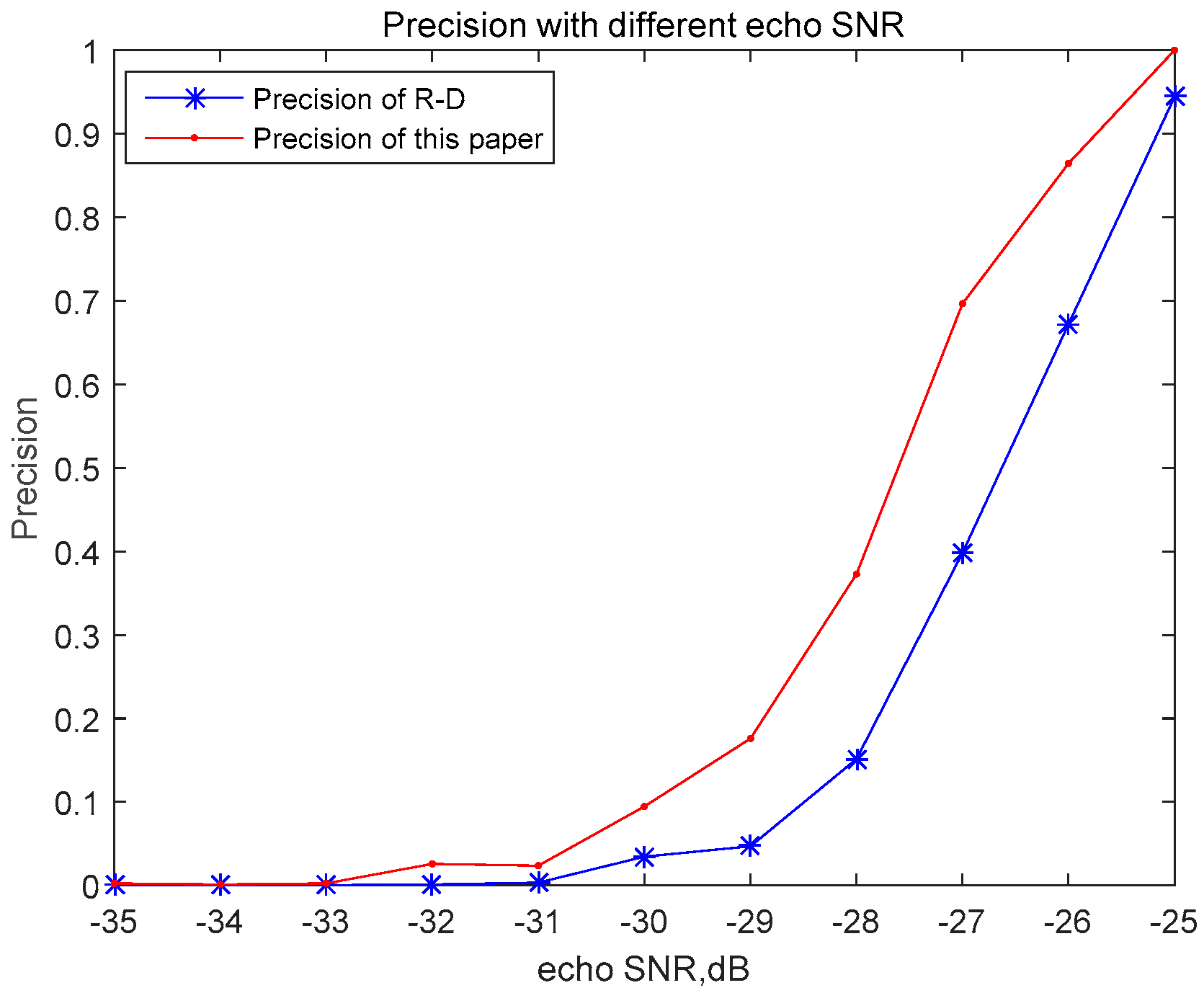
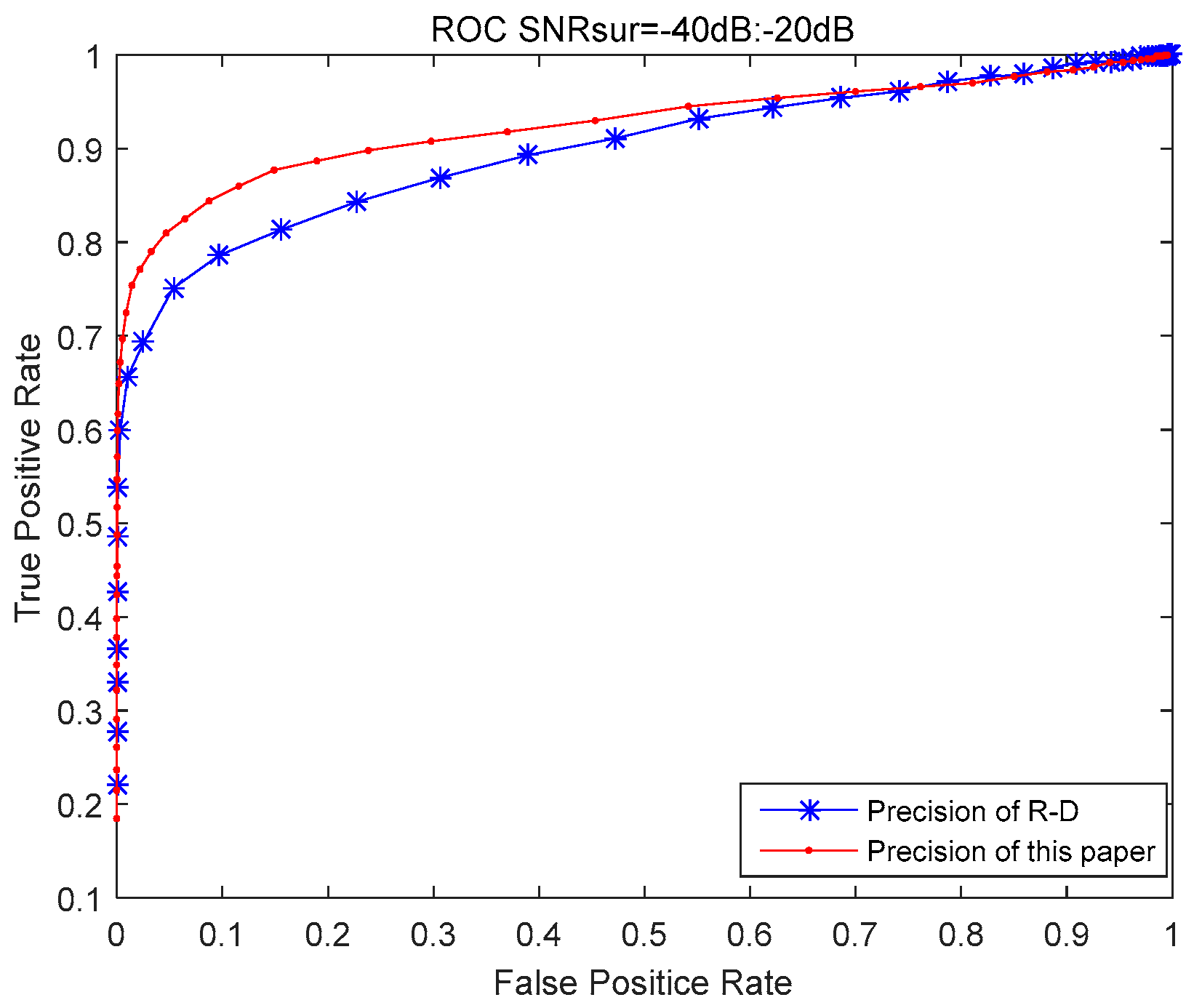
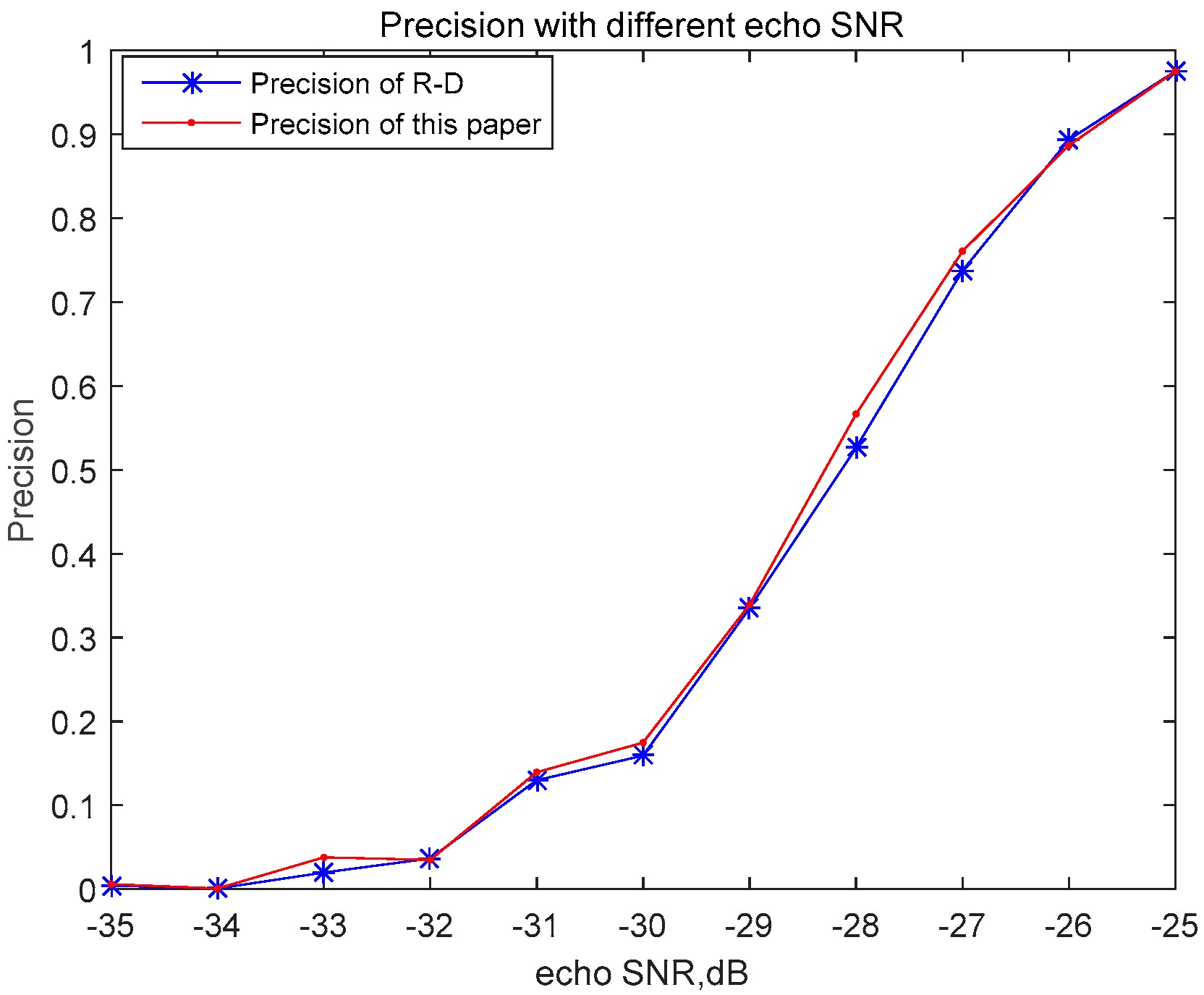
3.1. Simulation Data, Simulation Results, and Analysis
3.1.1. Simulation Analysis of Algorithm Performance with Pure Reference Signal
3.1.2. Simulation Analysis of the Algorithm’s Performance with Impure Reference Signal
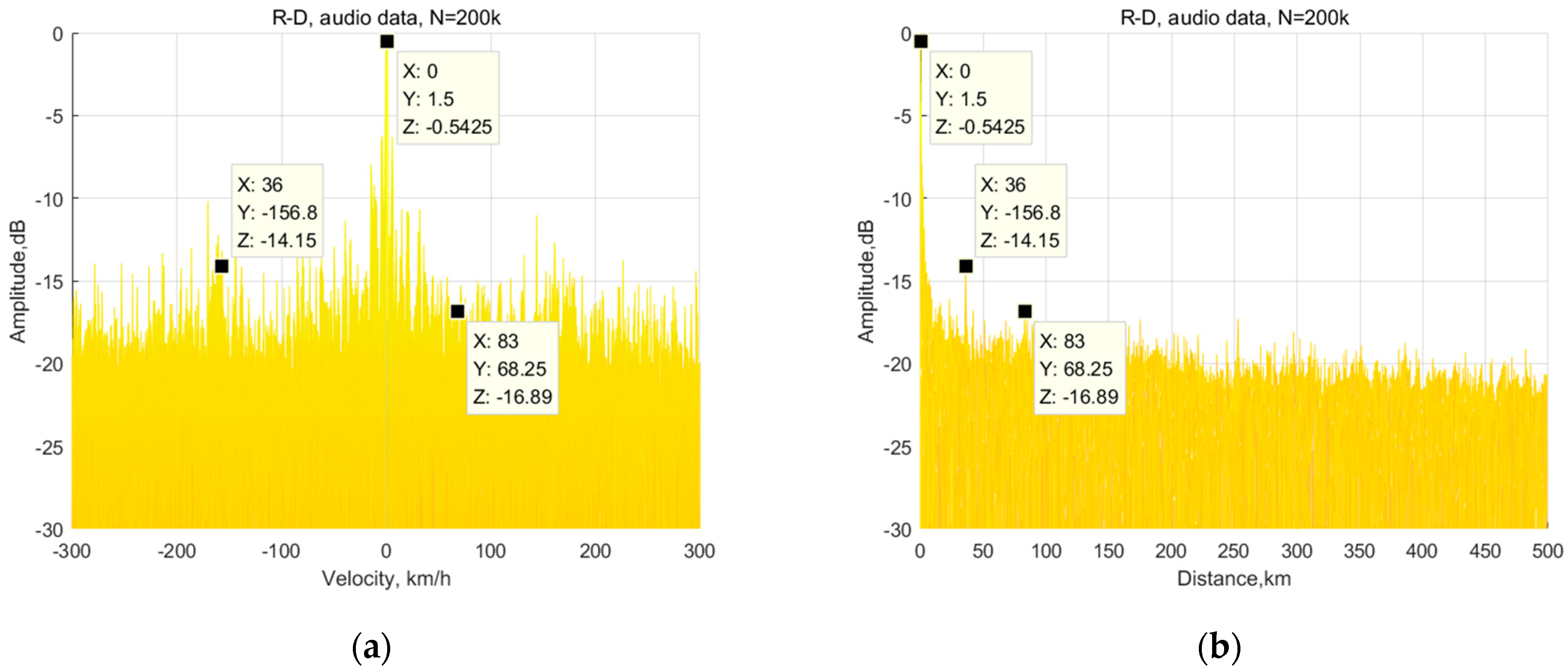
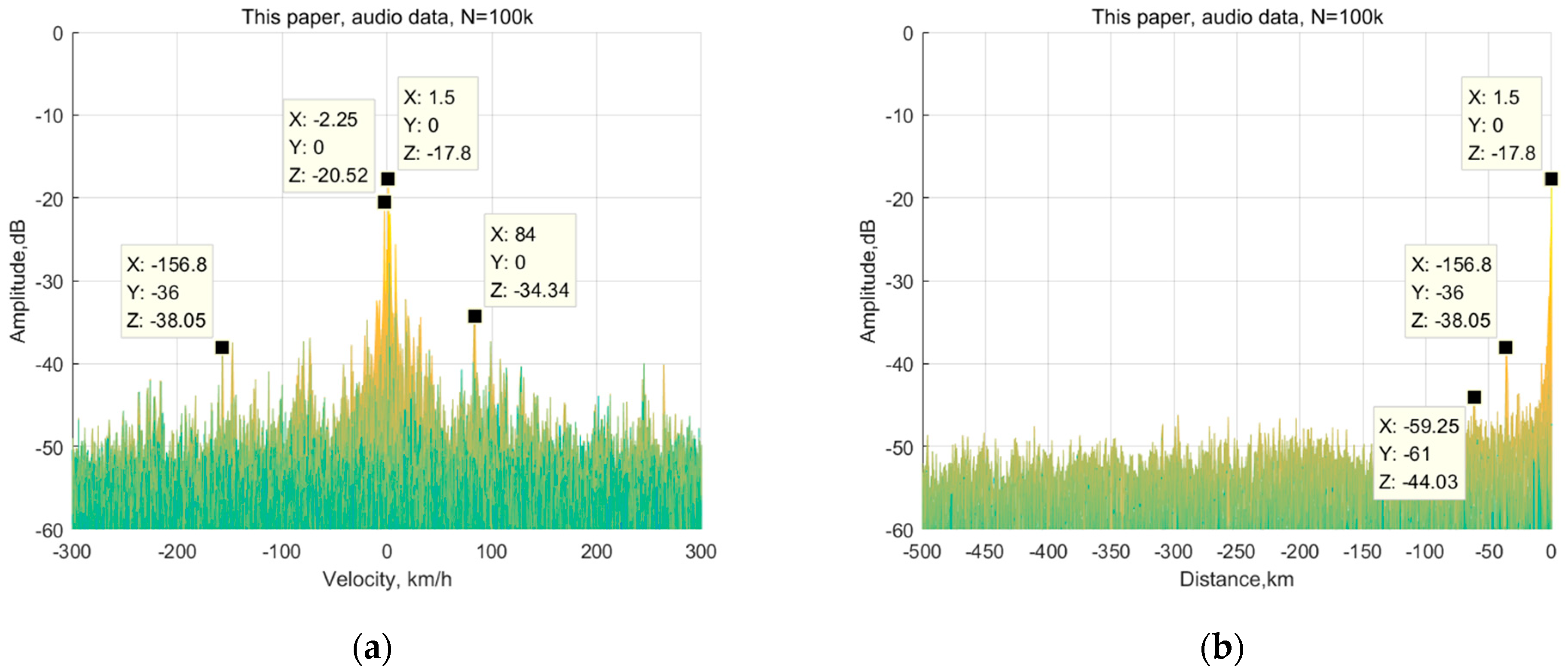
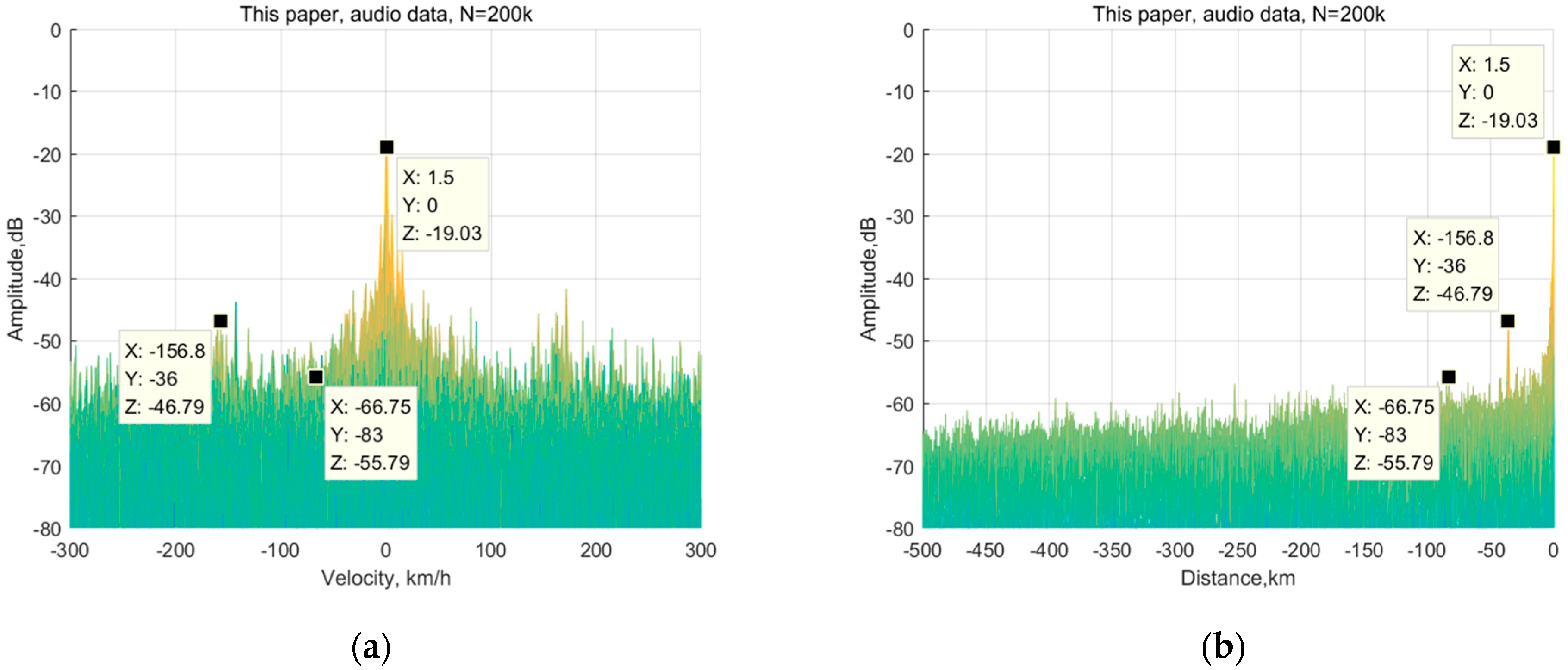
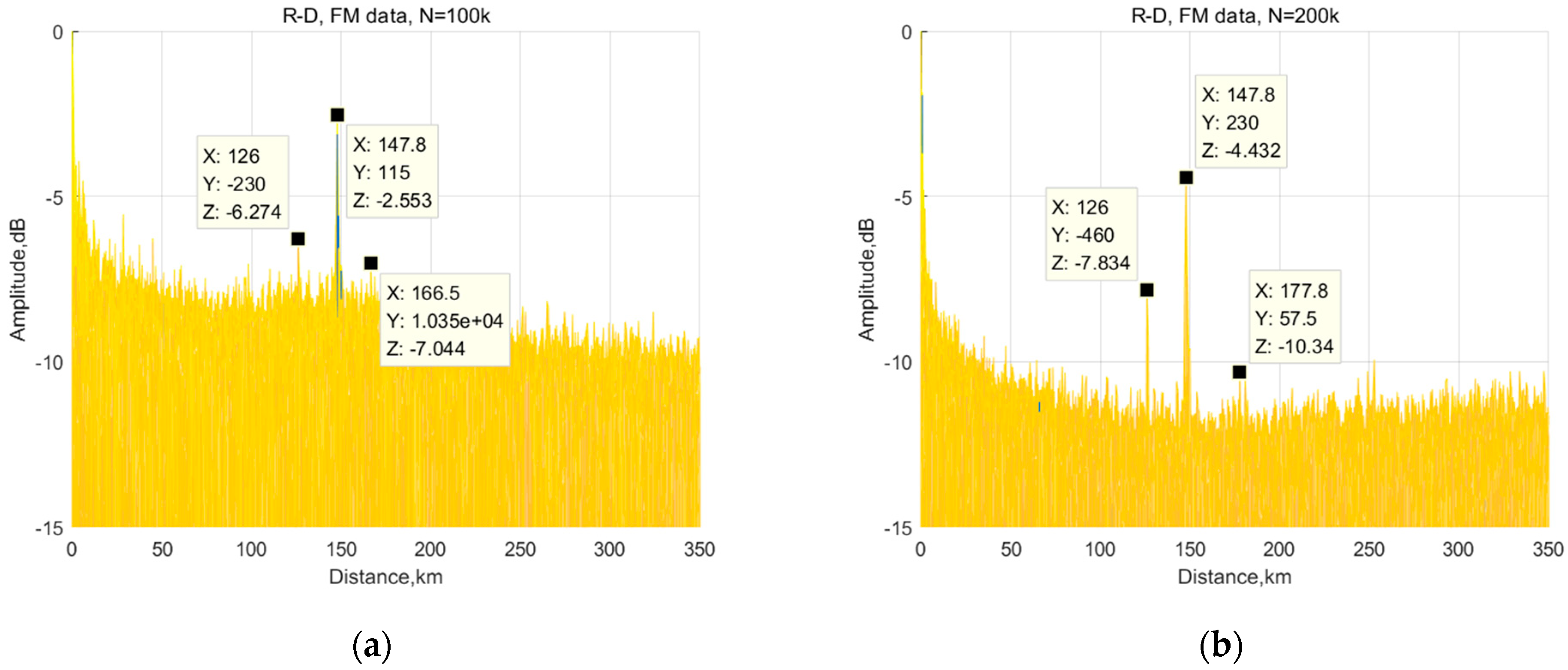
3.2. Measured Data, Measured Results, and Analysis
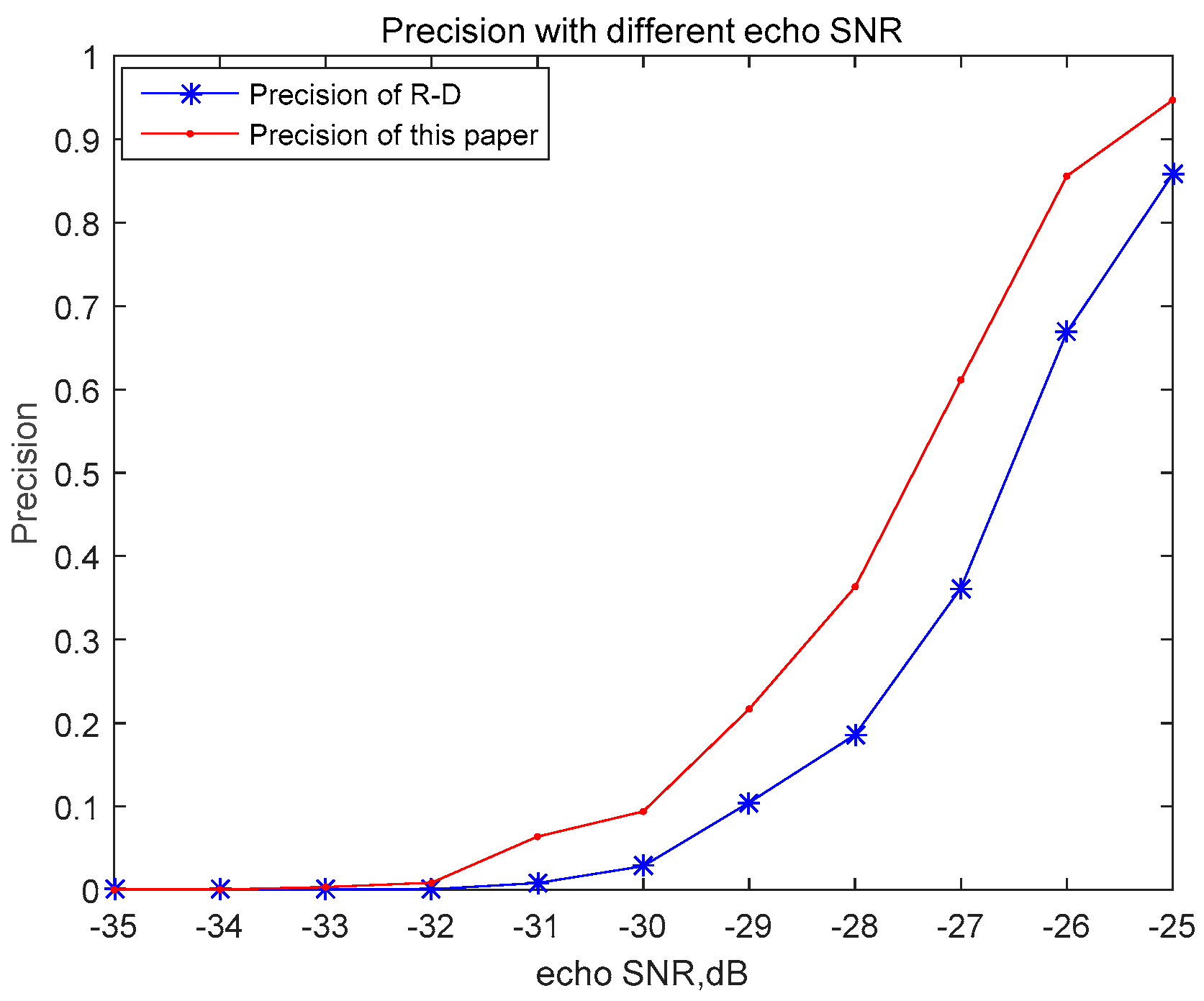
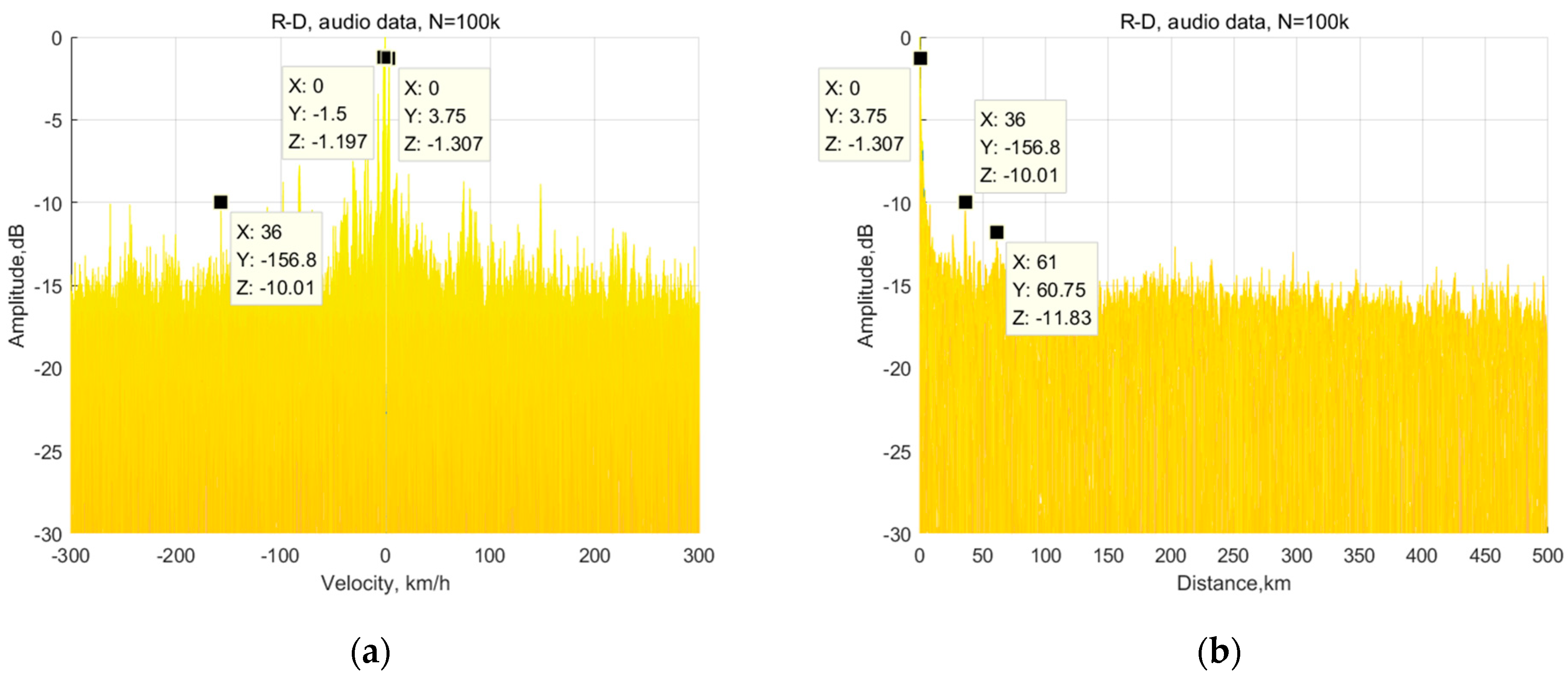
3.2.1. Measured Results and Analysis of the Audio Signal
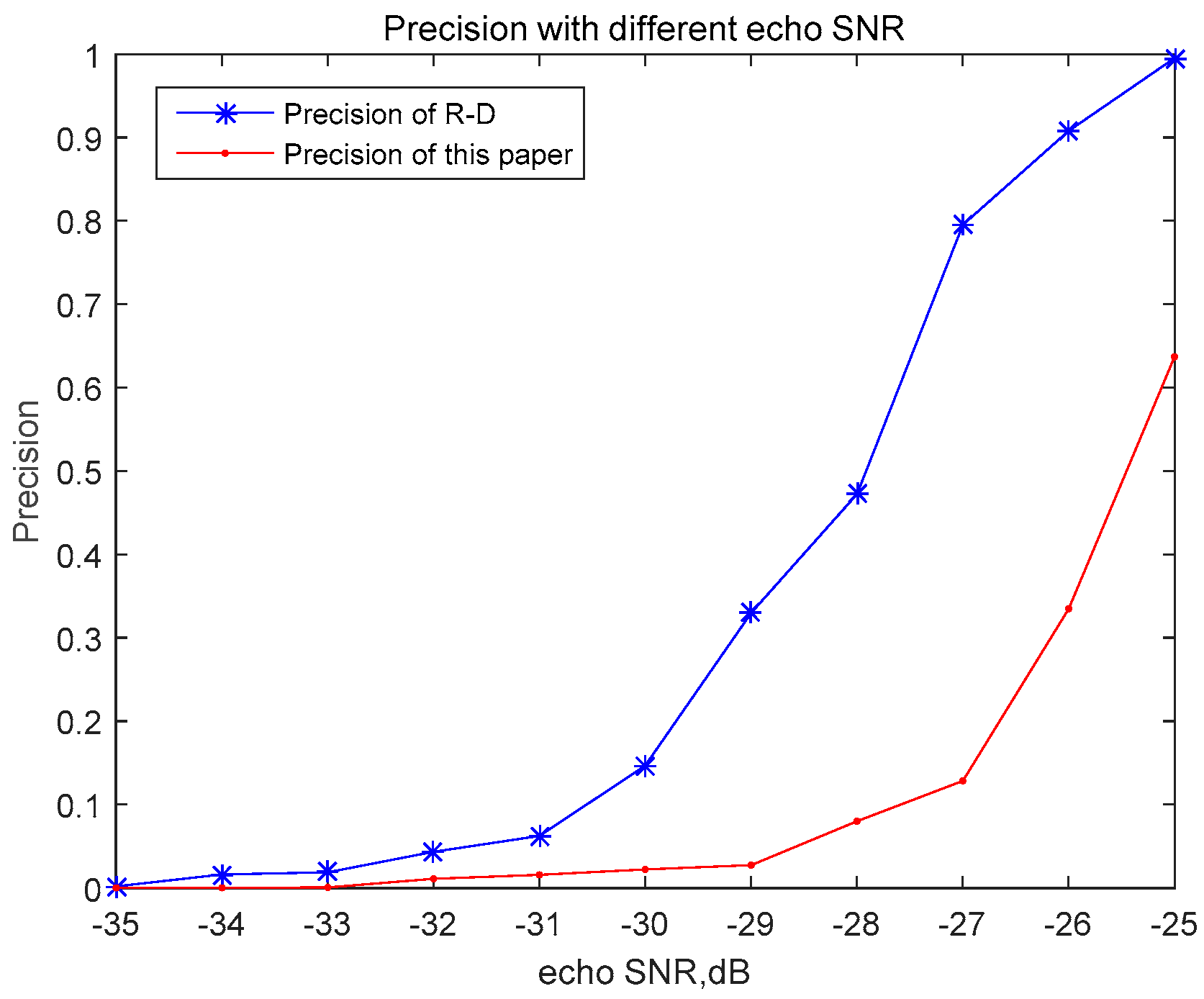
3.2.2. Measured Results and Analysis of the FM Signal
4. Discussion
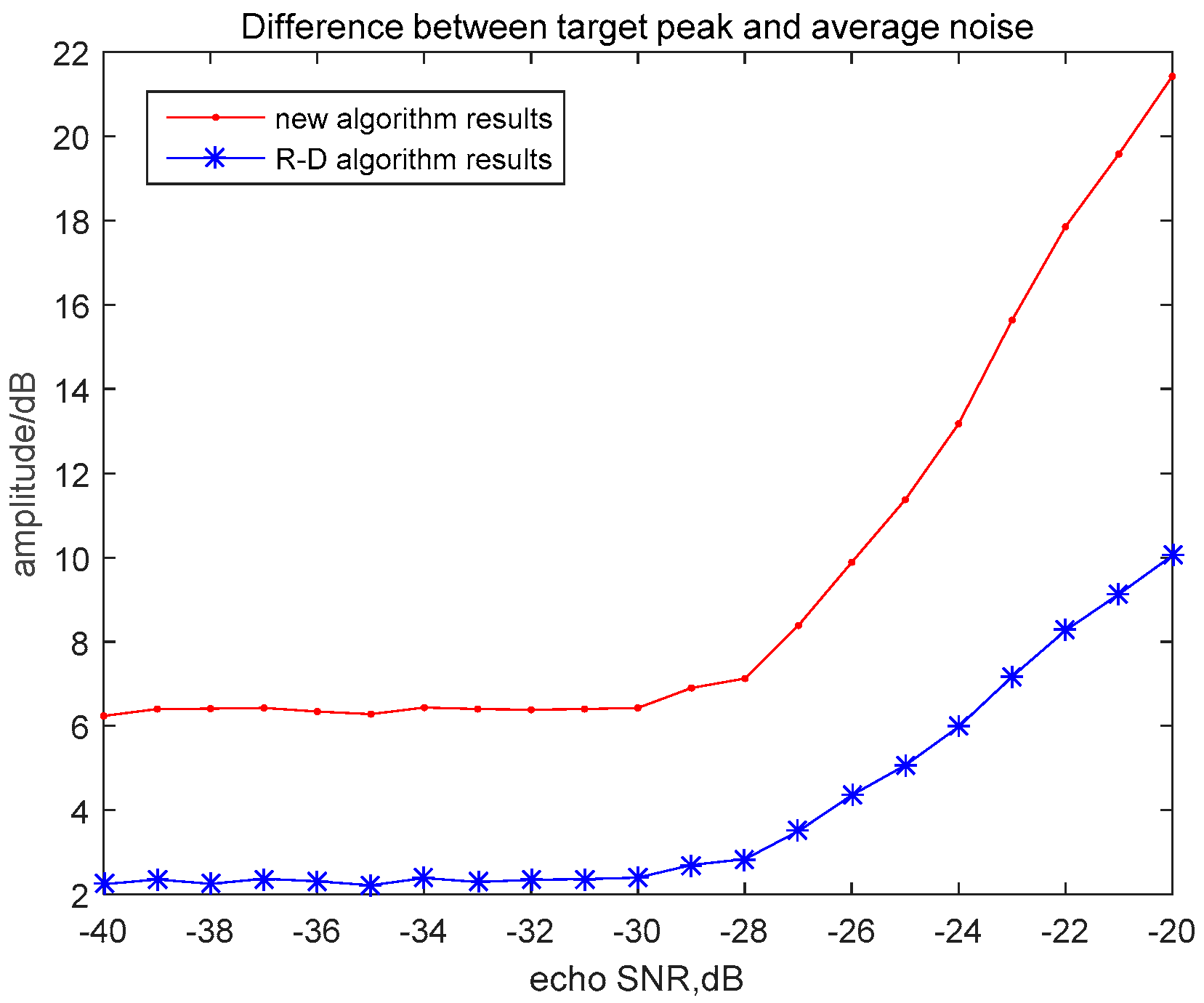
4.1. Reference Signal without Noise
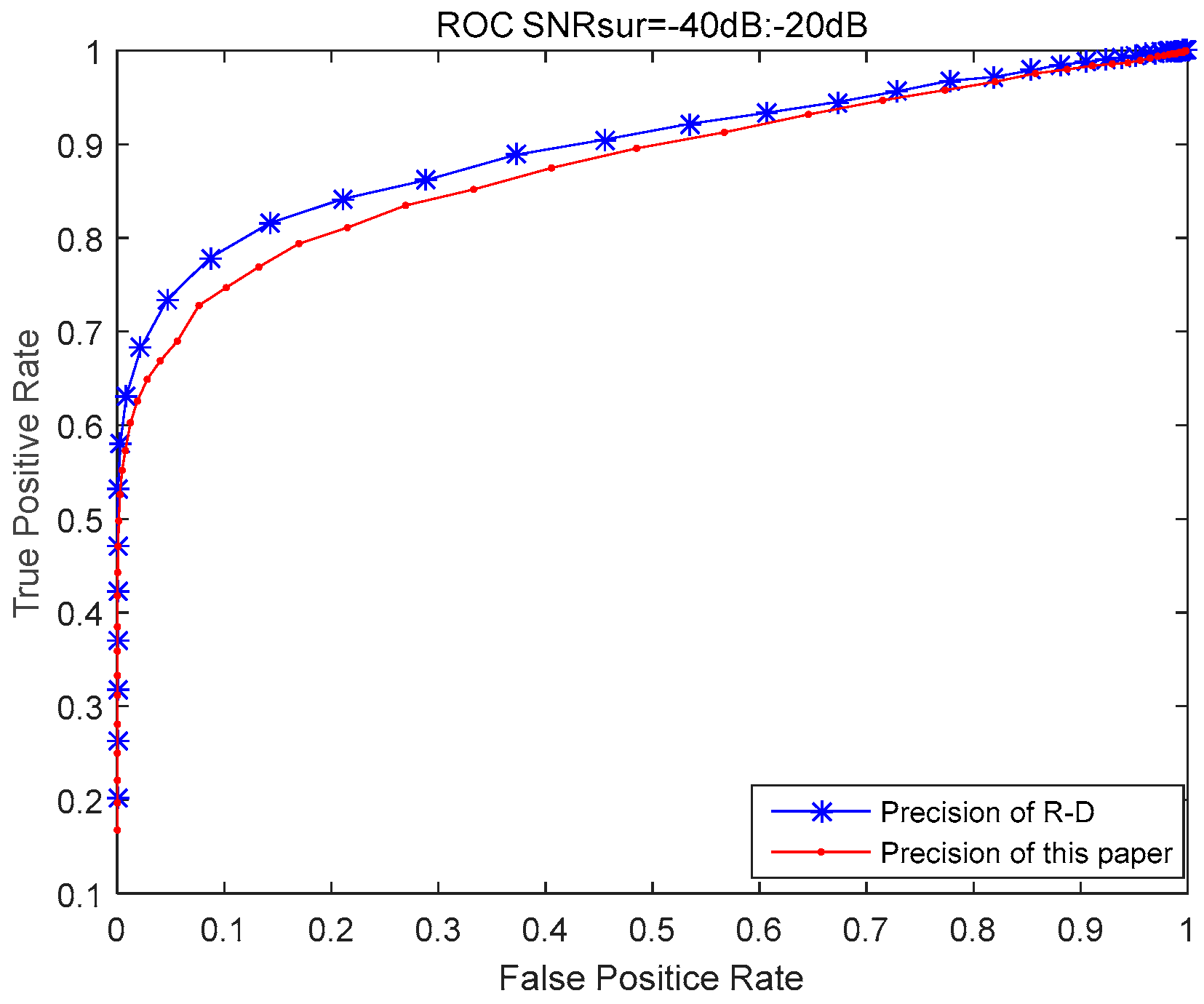
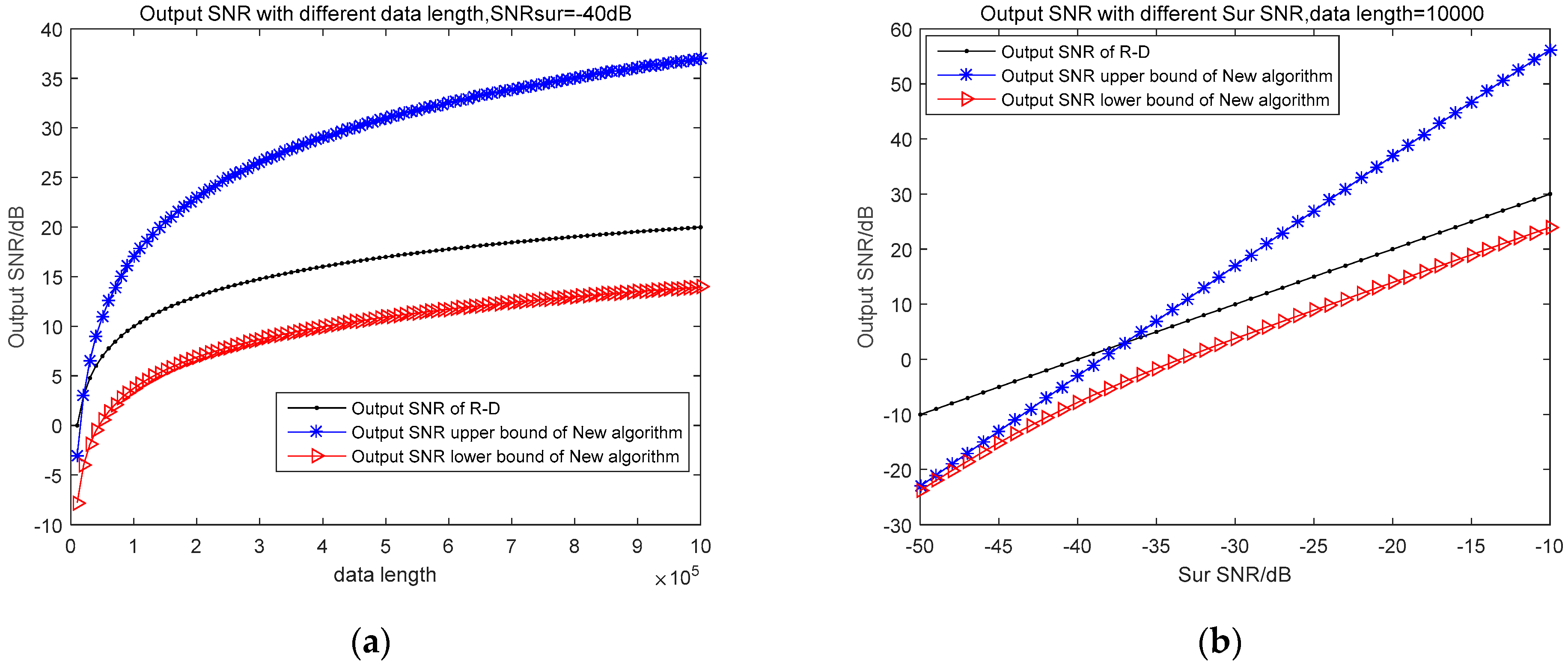
4.2. The Influence of the Reference Channel SNR on the Performance of the Algorithms
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, Y.; Liang, S.; Gong, M.; Yan, J. Decomposed POMDP Optimization-Based Sensor Management for Multi-Target Tracking in Passive Multi-Sensor Systems. IEEE Sens. J. 2022, 22, 3565–3578. [Google Scholar] [CrossRef]
- You, H.; Jian, G.; Meng, X. Radar Target Detection and CFAR Processing; Tsinghua University Press: Beijing, China, 2011. [Google Scholar]
- Xiong, J.; Hong, H.; Zhang, H.; Wang, N.; Chu, H.; Zhu, X. Multitarget Respiration Detection With Adaptive Digital Beamforming Technique Based on SIMO Radar. IEEE Trans. Microw. Theory Tech. 2020, 68, 4814–4824. [Google Scholar] [CrossRef]
- Yuan, S.; Fan, W.; Xu, L. Tow-Ship Interference Suppression Based on Blind Source Separation for Passive Sonar. In Proceedings of the Third International Symposium on Parallel Architectures, Liaoning, China, 18–20 December 2010. [Google Scholar]
- Melvin, W.L. Space-Time Adaptive Processing for Radar. Acad. Press Libr. Signal Process. 2014, 2, 595–665. [Google Scholar]
- Colone, F.; O’Hagan, D.W.; Lombardo, P.; Baker, C.J. A Multistage Processing Algorithm for Disturbance Removal and Target Detection in Passive Bistatic Radar. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 698–722. [Google Scholar] [CrossRef]
- Griffin, D.W.; Lim, J.S. Multiband excitation vocoder. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1223–1235. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Yuan, J. Simulation Analysis for MTD Detectability Improvement Using the Discrete Wavelet Transform (DWT). J. Signal Process. 2001, 17, 148–151. [Google Scholar]
- Howland, P.E.; Maksimiuk, D.; Reitsma, G. FM radio based bistatic radar. IEE Proc.—Radar Sonar Navig. 2005, 152, 107–115. [Google Scholar] [CrossRef] [Green Version]
- Coleman, C.; Yardley, H. Passive bistatic radar based on target illuminations by digital audio broadcasting. IET Radar Sonar Navig. 2008, 2, 366–375. [Google Scholar] [CrossRef]
- Park, G.H.; Seo, Y.K.; Kim, H.N. Range-Doppler Domain-Based DOA Estimation Method for FM-Band Passive Bistatic Radar. IEEE Access 2020, 8, 56880–56891. [Google Scholar] [CrossRef]
- Park, G.H.; Kim, H.N. Convolutional Neural Network-based Target Detection Method for Passive Bistatic Radar using FM Broadcasting Signals. J. Inst. Electron. Inf. Eng. 2020, 57, 70–78. [Google Scholar]
- Griffiths, H.D.; Long, N.R. Television-based bistatic radar. IEE Proc. F Commun. Radar Signal Process. 1986, 133, 649–657. [Google Scholar] [CrossRef]
- Poullin, D. Passive detection using digital broadcasters (DAB, DVB) with COFDM modulation. IEE Proc.—Radar Sonar Navig. 2005, 152, 143–152. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Zhong, L. Mismatched filter for analogue TV-based passive bistatic radar. IET Radar Sonar Navig. 2011, 5, 573–581. [Google Scholar] [CrossRef]
- Tao, R.; Wu, H.; Shan, T. Direct-path suppression by spatial filtering in digital television terrestrial broadcasting-based passive radar. IET Radar Sonar Navig. 2010, 4, 791–805. [Google Scholar] [CrossRef]
- Tan, D.; Sun, H.; Lu, Y.; Lesturgie, M.; Chan, H. Passive radar using Global System for Mobile communication signal: Theory, implementation and measurements. IEE Proc.—Radar Sonar Navig. 2005, 152, 116–123. [Google Scholar] [CrossRef]
- Guo, H.; Woodbridge, K.; Baker, C.J. Evaluation of WIFI beacon transmissions for wireless based passive radar. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Wang, H.; Wang, J.; Li, H. Target detection using CDMA based passive bistatic radar. Syst. Eng. Electron. Technol. (Engl. Version) 2012, 23, 858–865. [Google Scholar] [CrossRef]
- Salah, A.A.; Raja Abdullah, R.S.; Ismail, A.; Hashim, F.; Abdul Aziz, N.H. Experimental study of LTE signals as illuminators of opportunity for passive bistatic radar applications. Electron. Lett. 2014, 50, 545–547. [Google Scholar] [CrossRef]
- Maussang, F.; Garello, R.; Soulat, F.; Desjonqueres, J.D.; Pourthie, N. GPS passive bistatic radar system in oceanic environment: Detection performance estimation. In Proceedings of the OCEANS 2011 IEEE-Spain, Santander, Spain, 6–9 June 2011. [Google Scholar]
- Chow, Y.P.; Trinkle, M. Experimental Results Investigating the Feasibility of GPS Bistatic Radar for Target Detection and Estimation. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011. [Google Scholar]
- Huang, P.; Liao, G.; Yang, Z.; Shu, Y.; Du, W. Approach for space-based radar manoeuvring target detection and high-order motion parameter estimation. IET Radar Sonar Navig. 2015, 9, 732–741. [Google Scholar] [CrossRef]
- Carlson, B.D.; Evans, E.D.; Wilson, S.L. Errata: Search radar detection and track with the Hough transform. IEEE Trans. Aerosp. Electron. Syst. 2003, 30, 109–115. [Google Scholar] [CrossRef]
- Boers, Y.; Mandal, P.K. Optimal Particle-Filter-Based Detector. IEEE Signal Process. Lett. 2019, 26, 435–439. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.Y.; Ristic, B.; Guan, R.; Rosenberg, L. A Bernoulli Track-Before-Detect Filter for Interacting Targets in Maritime Radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1981–1991. [Google Scholar] [CrossRef]
- Quan, N.V.; Markelov, O.A.; Veremyev, V.I. Passive Bistatic Radar Monitoring with GPS Satellites as Transmitters of Opportunity. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg, Moscow, Russia, 26–29 January 2021. [Google Scholar]
- Chen, X.; Guan, J.; Liu, N.; He, Y. Maneuvering Target Detection via Radon-Fractional Fourier Transform-Based Long-Time Coherent Integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Hou, L.; Song, H.; Zheng, M.; Wang, W. Fast moving target imaging and motion parameters estimation based on Radon transform and bi-directional approach. IET Radar Sonar Navig. 2016, 10, 1013–1023. [Google Scholar] [CrossRef]
- Gao, Z.; Tao, R. Calculation and performance analysis of coherent integration gain of passive radar. J. Electron. 2008, 36, 1227–1230. [Google Scholar]






| Range Unit | Doppler Unit | SNR | |
|---|---|---|---|
| Tar 1 | 300 | 50 | −25 dB |
| Tar 2 | 100 | 300 | −30 dB |
| Correlation Coefficient | |
|---|---|
| First item | 0.2636 |
| Second item | 0.2686 |
| Third item | 0.0118 |
| Gaussian white | 0.0188 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Wang, J.; Zuo, L.; Wang, J. A Novel Cross-Correlation Algorithm Based on the Differential for Target Detection of Passive Radar. Remote Sens. 2023, 15, 224. https://doi.org/10.3390/rs15010224
Zhao D, Wang J, Zuo L, Wang J. A Novel Cross-Correlation Algorithm Based on the Differential for Target Detection of Passive Radar. Remote Sensing. 2023; 15(1):224. https://doi.org/10.3390/rs15010224
Chicago/Turabian StyleZhao, Dawei, Jun Wang, Luo Zuo, and Jipeng Wang. 2023. "A Novel Cross-Correlation Algorithm Based on the Differential for Target Detection of Passive Radar" Remote Sensing 15, no. 1: 224. https://doi.org/10.3390/rs15010224
APA StyleZhao, D., Wang, J., Zuo, L., & Wang, J. (2023). A Novel Cross-Correlation Algorithm Based on the Differential for Target Detection of Passive Radar. Remote Sensing, 15(1), 224. https://doi.org/10.3390/rs15010224







