Research on Glacier Elevation Variability in the Qilian Mountains of the Qinghai-Tibet Plateau Based on Topographic Correction by Pyramid Registration
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
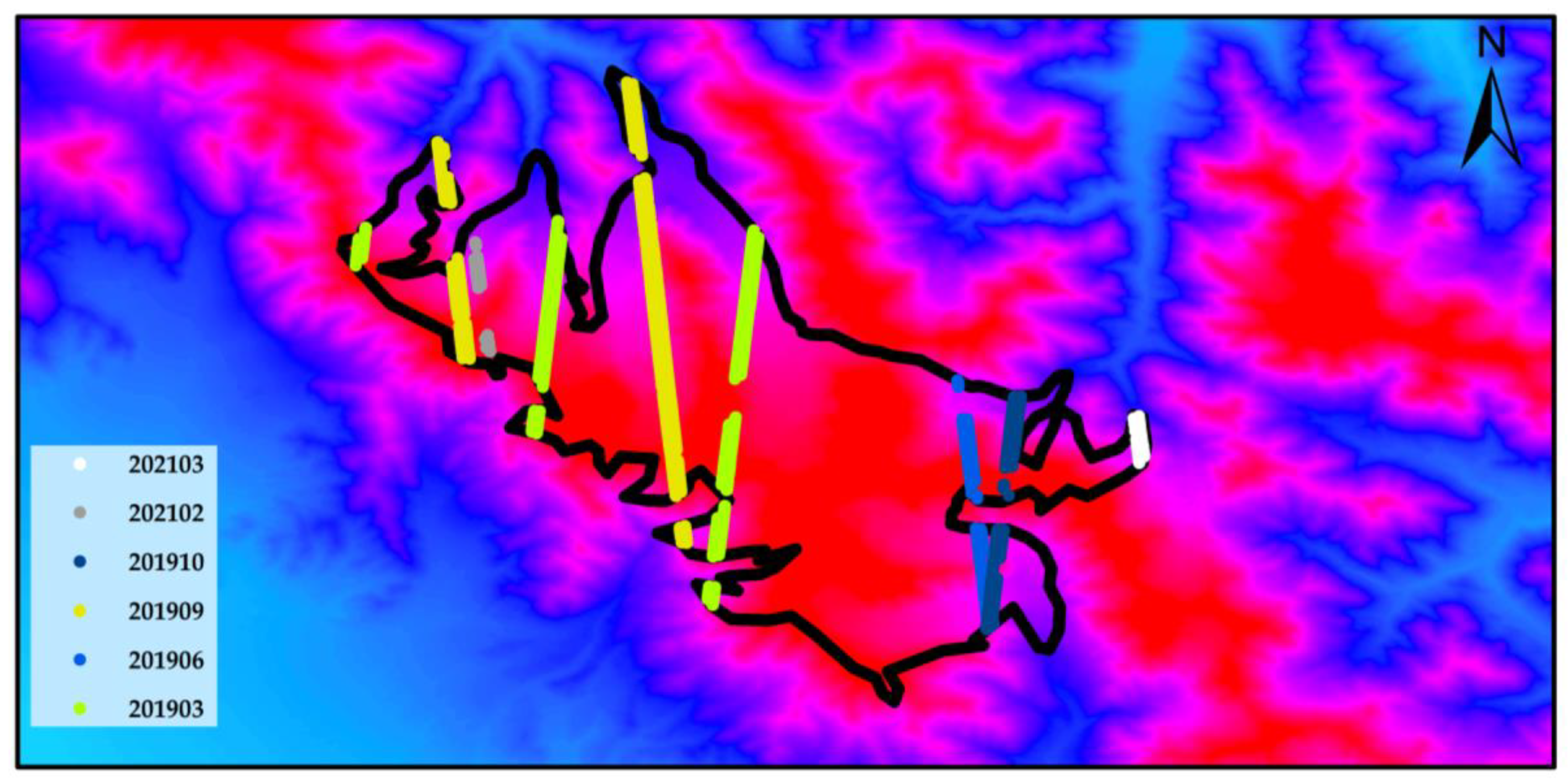
2.2.1. ICESat-2 Data
2.2.2. ALOS DEM
2.2.3. Auxiliary Data
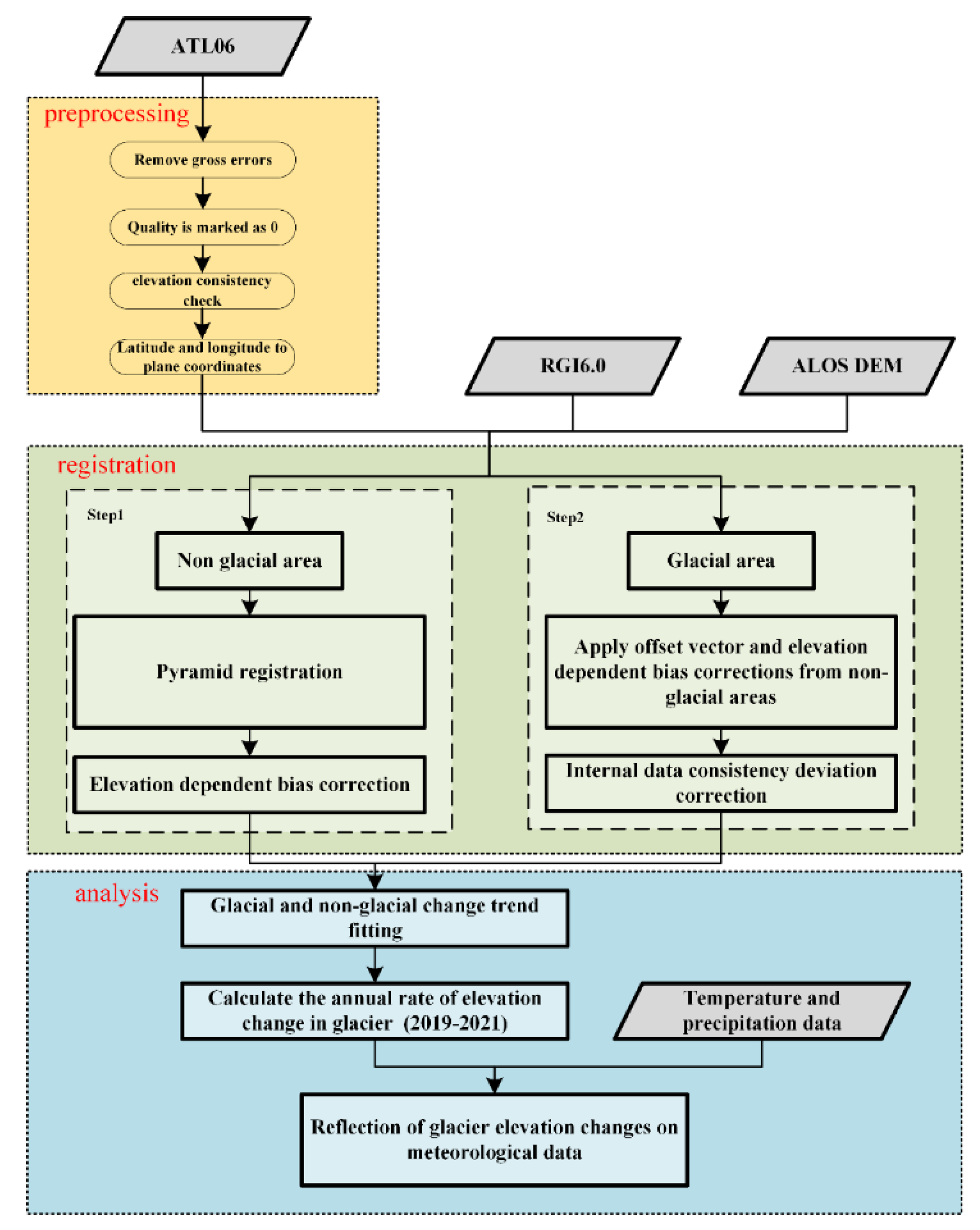
3. Methodology
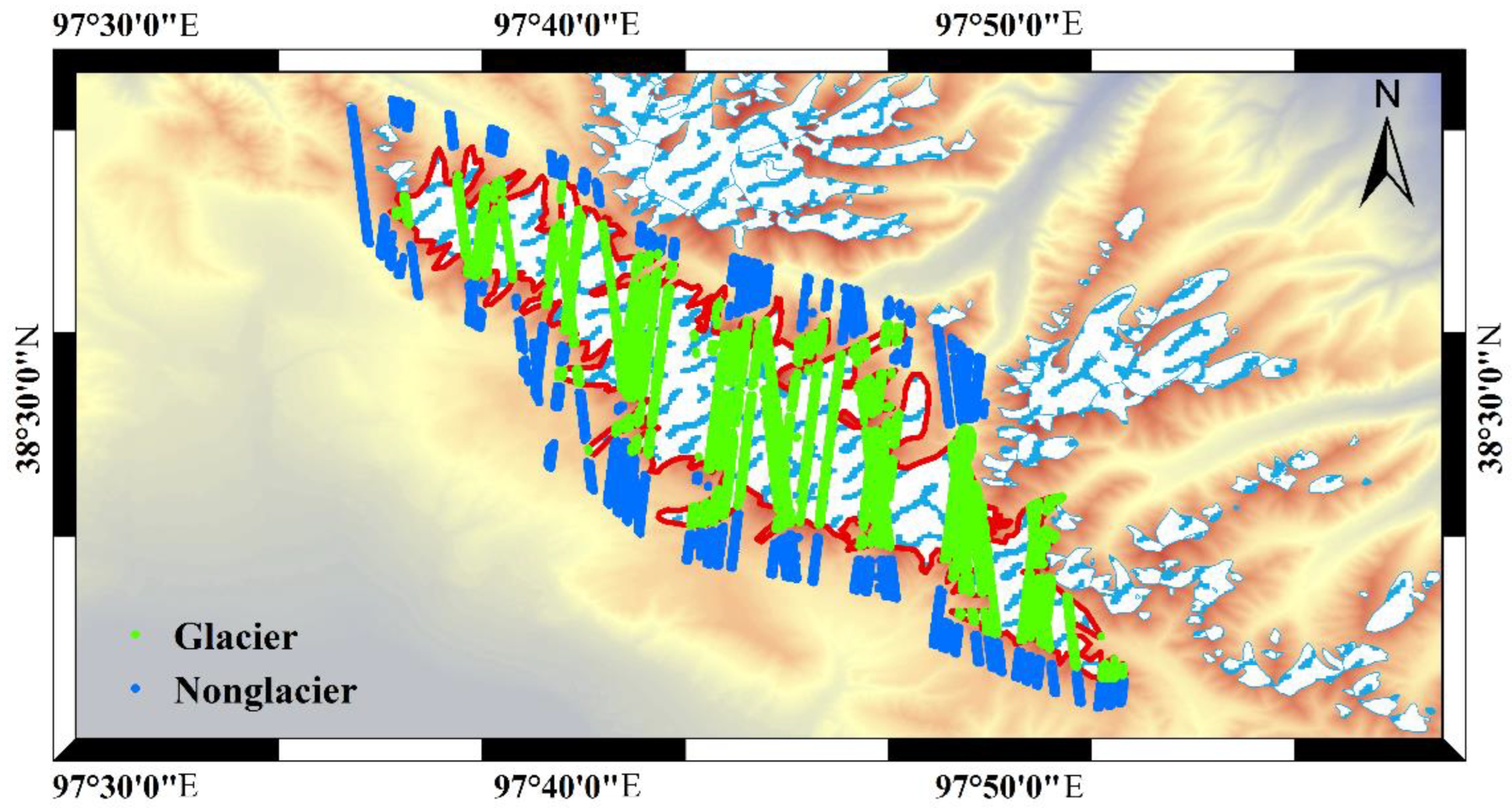
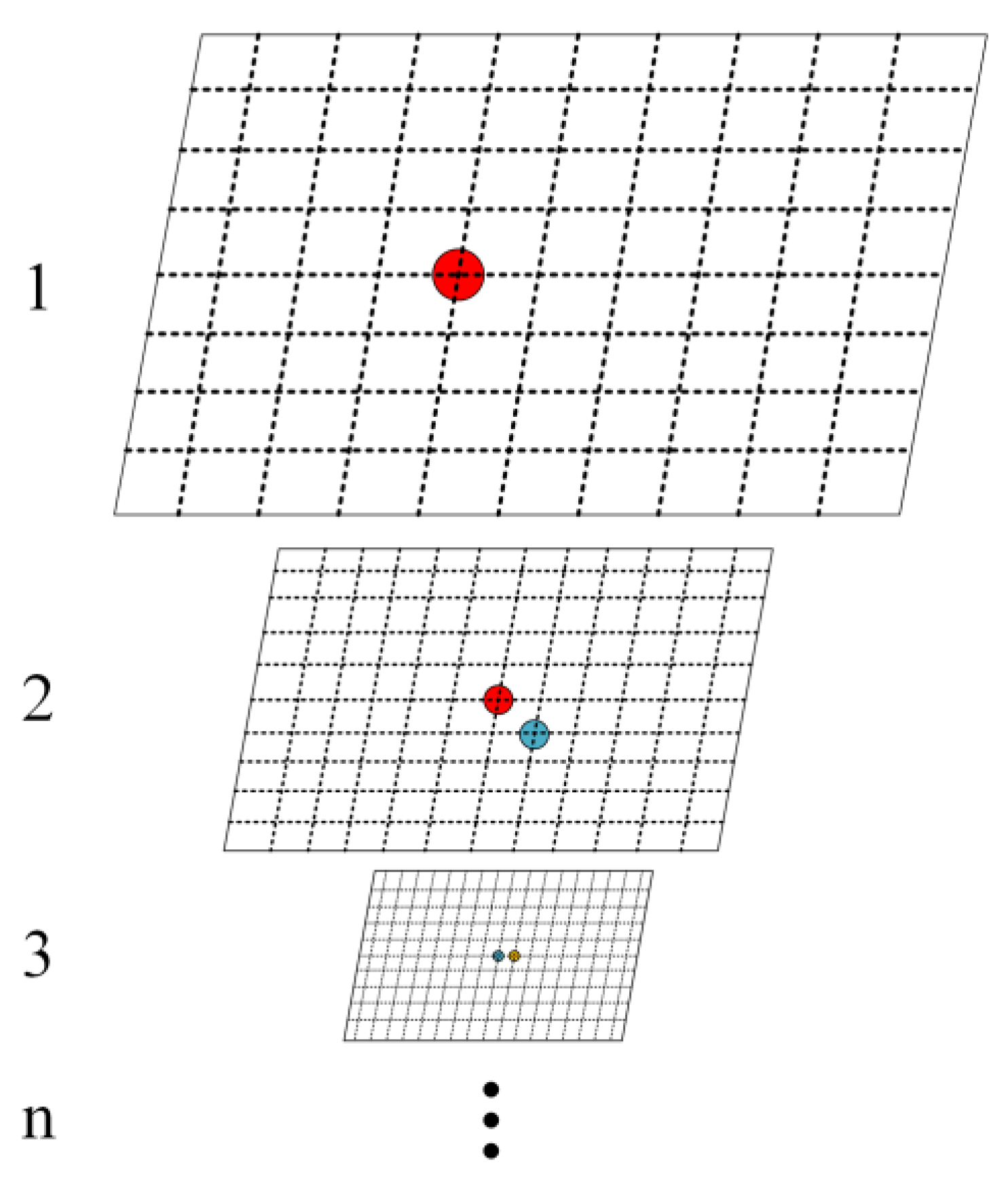
3.1. Registration of ICESat-2 Data and the ALOS DEM
- Geographical bias (x, y, and z directions)
- Elevation-dependent bias
3.2. Elevation Difference Calculation and Internal Consistency
3.3. Elevation Variation Trend Estimation and Uncertainty Analysis
4. Result
4.1. Registration Results
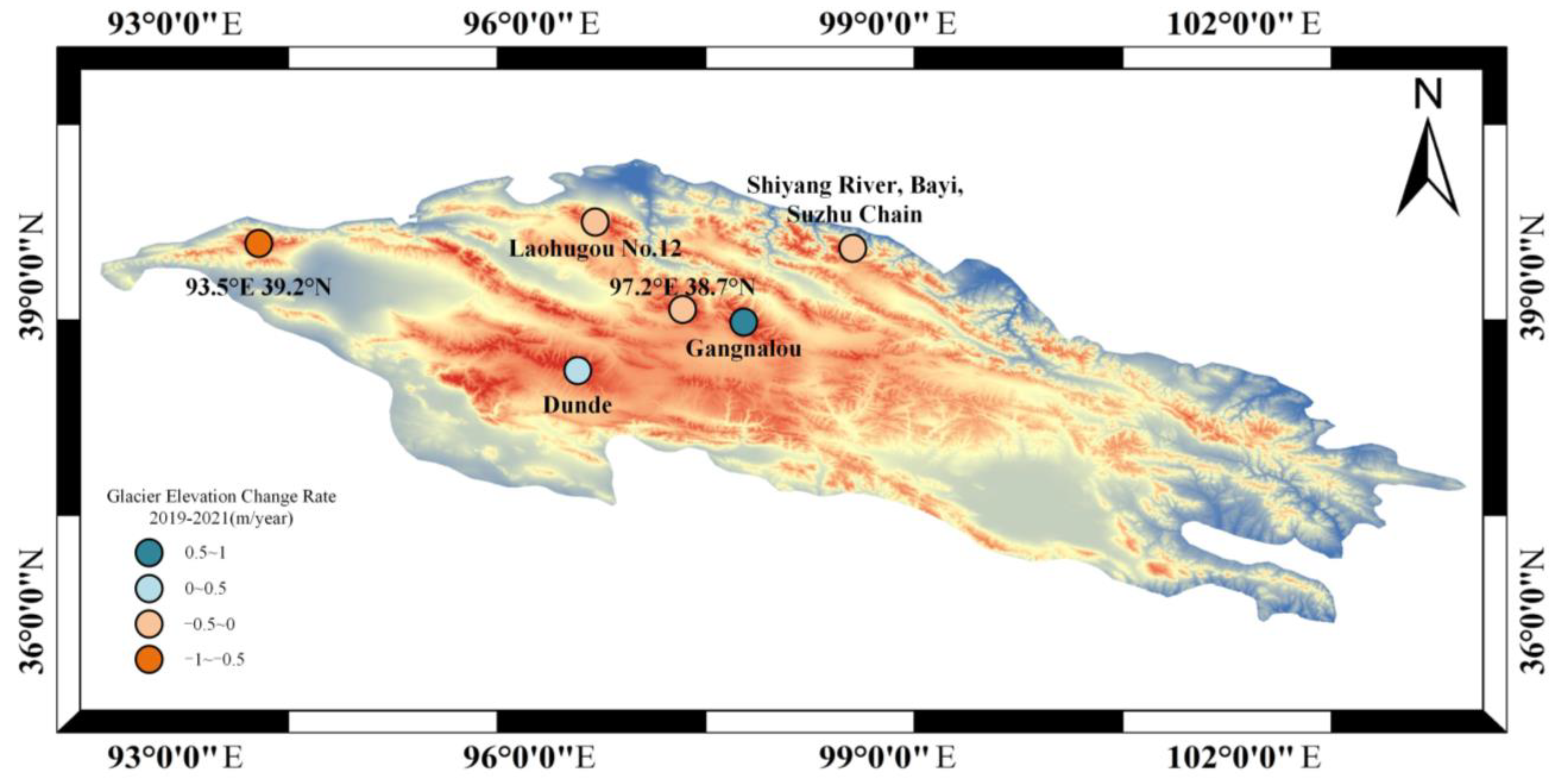
4.2. Annual Change Rate of Glacier Elevation
4.3. Interannual Variation in Glacier Elevation
5. Discussion
5.1. Factors Affecting the Change in Glacier Elevation
5.2. Comparison with Existing Research Results
5.3. Advantages and Disadvantages of Using the ALOS DEM with ICESat-2 Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clarke, G.K.C. The Mass Balance of the Cryosphere: Observations and Modelling of Contemporary and Future Changes. EOS Trans. Am. Geophys. Union 2004, 85, 230. [Google Scholar] [CrossRef]
- Mernild, S.H.; Lipscomb, W.H.; Bahr, D.B.; Radić, V.; Zemp, M. Global glacier changes: A revised assessment of committed mass losses and sampling uncertainties. Cryosphere 2013, 7, 1565–1577. [Google Scholar] [CrossRef] [Green Version]
- Hugonnet, R.; McNabb, R.; Berthier, E.; Menounos, B.; Nuth, C.; Girod, L.; Farinotti, D.; Huss, M.; Dussaillant, I.; Brun, F.; et al. Accelerated global glacier mass loss in the early twenty-first century. Nature 2021, 592, 726–731. [Google Scholar] [CrossRef] [PubMed]
- Oerlemans, J.; Knap, W.H. A 1 year record of global radiation and albedo in the ablation zone of Morteratschgletscher, Switzerland. J. Glaciol. 2017, 44, 231–238. [Google Scholar] [CrossRef] [Green Version]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A reconciled estimate of glacier contributions to sea level rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Jiang, L.; Liu, L.; Sun, Q.; Wang, H.; Hsu, H. Mapping Glacier Elevations and Their Changes in the Western Qilian Mountains, Northern Tibetan Plateau, by Bistatic InSAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 68–78. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, D.; Li, Y.; Qin, X.; Li, Z.; Wang, J.; Jin, Z.; Wang, L. Changes in the Surface Elevation of the Laohugou Glacier No. 12 in Western Qilian Mountains. Front. Earth Sci. 2022, 10, 832701. [Google Scholar] [CrossRef]
- Zhao, P.; He, Z. A First Evaluation of ERA5-Land Reanalysis Temperature Product Over the Chinese Qilian Mountains. Front. Earth Sci. 2022, 10, 907730. [Google Scholar] [CrossRef]
- Finkelnburg, R.; Curio, J.; Collier, E.; Mölg, T.; Scherer, D.; Maussion, F. Precipitation Seasonality and Variability over the Tibetan Plateau as Resolved by the High Asia Reanalysis. J. Clim. 2014, 27, 1910–1927. [Google Scholar]
- Wang, Q.; Yi, S.; Chang, L.; Sun, W. Large-Scale Seasonal Changes in Glacier Thickness Across High Mountain Asia. Geophys. Res. Lett. 2017, 44, 10427–10435. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Shum, C.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Yi, S.; Sun, W. Precipitation-driven glacier changes in the Pamir and Hindu Kush mountains. Geophys. Res. Lett. 2017, 44, 2817–2824. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Li, Z.; Wang, F.; Li, H.; Li, Y.; Huang, X. Glacier area variation and climate change in the Chinese Tianshan Mountains since 1960. J. Geogr. Sci. 2011, 21, 263–273. [Google Scholar] [CrossRef]
- Muskett, R.R.; Lingle, C.S.; Sauber, J.M.; Post, A.S.; Tangborn, W.V.; Rabus, B.T.; Echelmeyer, K.A. Airborne and spaceborne DEM- and laser altimetry-derived surface elevation and volume changes of the Bering Glacier system, Alaska, USA, and Yukon, Canada, 1972–2006. J. Glaciol. 2009, 55, 316–326. [Google Scholar] [CrossRef] [Green Version]
- Rignot, E.; Rivera, A.; Casassa, G. Contribution of the Patagonia Icefields of South America to Sea Level Rise. Science 2003, 302, 434–437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sund, M.; Eiken, T.; Hagen, J.O.; Kaab, A. Svalbard surge dynamics derived from geometric changes. Ann. Glaciol. 2009, 50, 50–60. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liu, S.; Shangguan, D.; Li, J.; Zhao, J. Thinning and shrinkage of Laohugou No. 12 glacier in the Western Qilian Mountains, China, from 1957 to 2007. J. Mt. Sci. 2012, 9, 343–350. [Google Scholar] [CrossRef]
- Ren, S.; Li, X.; Wang, Y.; Zheng, D.; Jiang, D.; Nian, Y.; Zhou, Y. Multitemporal Glacier Mass Balance and Area Changes in the Puruogangri Ice Field during 1975–2021 Based on Multisource Satellite Observations. Remote Sens. 2022, 14, 4078. [Google Scholar] [CrossRef]
- Fujisada, H.; Bailey, G.B.; Kelly, G.G.; Hara, S.; Abrams, M.J. ASTER DEM performance. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2707–2714. [Google Scholar] [CrossRef]
- Toutin, T. Three-dimensional topographic mapping with ASTER stereo data in rugged topography. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2241–2247. [Google Scholar] [CrossRef]
- Kacimi, S.; Kwok, R. Arctic Snow Depth, Ice Thickness, and Volume From ICESat-2 and CryoSat-2: 2018–2021. Geophys. Res. Lett. 2022, 49, e2021GL097448. [Google Scholar] [CrossRef]
- Lai, Y.-R.; Wang, L. Monthly Surface Elevation Changes of the Greenland Ice Sheet From ICESat-1, CryoSat-2, and ICESat-2 Altimetry Missions. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Michaelides, R.J.; Bryant, M.B.; Siegfried, M.R.; Borsa, A.A. Quantifying Surface-Height Change Over a Periglacial Environment With ICESat-2 Laser Altimetry. Earth Space Sci. 2021, 8, e2020EA001538. [Google Scholar] [CrossRef] [PubMed]
- Yue, L.; Shen, H.; Zhang, L.; Zheng, X.; Zhang, F.; Yuan, Q. High-quality seamless DEM generation blending SRTM-1, ASTER GDEM v2 and ICESat/GLAS observations. ISPRS J. Photogramm. Remote Sens. 2017, 123, 20–34. [Google Scholar] [CrossRef] [Green Version]
- Nuimura, T.; Fujita, K.; Yamaguchi, S.; Sharma, R.R. Elevation changes of glaciers revealed by multitemporal digital elevation models calibrated by GPS survey in the Khumbu region, Nepal Himalaya, 1992–2008. J. Glaciol. 2017, 58, 648–656. [Google Scholar] [CrossRef] [Green Version]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Slight mass gain of Karakoram glaciers in the early twenty-first century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
- Kaab, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef]
- Moholdt, G.; Nuth, C.; Hagen, J.O.; Kohler, J. Recent elevation changes of Svalbard glaciers derived from ICESat laser altimetry. Remote Sens. Environ. 2010, 114, 2756–2767. [Google Scholar] [CrossRef]
- Sun, M.; Ma, W.; Yao, X.; Zhao, L.; Li, Z.; Qin, D. Evaluation and spatiotemporal characteristics of glacier service value in the Qilian Mountains. J. Geogr. Sci. 2020, 30, 1233–1248. [Google Scholar] [CrossRef]
- Cai, X.; Li, Z.; Xu, C. Glacier wastage and its vulnerability in the Qilian Mountains. J. Geogr. Sci. 2022, 32, 117–140. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, C.; Feng, Z.; Zhang, F.; Sher, H.; Wang, C.; Peng, H.; Wang, Y.; Zhao, Y.; Wang, Y. Estimating realized and potential carbon storage benefits from reforestation and afforestation under climate change: A case study of the Qinghai spruce forests in the Qilian Mountains, northwestern China. Mitig. Adapt. Strateg. Glob. Chang. 2013, 18, 1257–1268. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.; Bierkens, M.; Lutz, A.; Immerzeel, W. Impact of a global temperature rise of 1.5 degrees Celsius on Asia’s glaciers. Nature 2017, 549, 257–260. [Google Scholar] [CrossRef] [PubMed]
- Webster, P.J.; Magaña, V.O.; Palmer, T.N.; Shukla, J.; Tomas, R.A.; Yanai, M.; Yasunari, T. Monsoons: Processes, predictability, and the prospects for prediction. J. Geophys. Res. Ocean. 1998, 103, 14451–14510. [Google Scholar] [CrossRef]
- Guo, S.; Chen, R.; Li, H. Surface Sublimation/Evaporation and Condensation/Deposition and Their Links to Westerlies During 2020 on the August-One Glacier, the Semi-Arid Qilian Mountains of Northeast Tibetan Plateau. J. Geophys. Res. Atmos. 2022, 127, e2022JD036494. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W. The Ice, Cloud, and Land Elevation Satellite-2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Pang, Y.; Cui, D.; Ma, Y.; Chen, L. Accuracy Assessment of the ICESat-2/ATL06 Product in the Qilian Mountains Based on CORS and UAV Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1558–1571. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Hao, T.; Qiao, G.; Cui, H.; He, Y.; Hai, G.; Xie, H.; Cheng, Y.; Li, B. Assessment of ICESat-2 ice surface elevations over the Chinese Antarctic Research Expedition (CHINARE) route, East Antarctica, based on coordinated multi-sensor observations. Cryosphere 2021, 15, 3083–3099. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Smith, B.E. Assessment of ICESat-2 Ice Sheet Surface Heights, Based on Comparisons Over the Interior of the Antarctic Ice Sheet. Geophys. Res. Lett. 2019, 46, 13072–13078. [Google Scholar] [CrossRef] [Green Version]
- Kawata, Y.; Funatsu, Y.; Yoshii, S.; Takemata, K. Accuracy analysis of DEM extraction over Japan using ALOS PRISM stereo images. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications II, Prague, Czech Republic, 20–22 September 2011; pp. 13–21. [Google Scholar]
- Yan, S.; Guo, H.; Liu, G.; Ruan, Z. Mountain glacier displacement estimation using a DEM-assisted offset tracking method with ALOS/PALSAR data. Remote Sens. Lett. 2013, 4, 494–503. [Google Scholar] [CrossRef]
- Yang, S.; Li, R.; Wu, T.; Hu, G.; Xiao, Y.; Du, Y.; Zhu, X.; Ni, J.; Ma, J.; Zhang, Y. Evaluation of reanalysis soil temperature and soil moisture products in permafrost regions on the Qinghai-Tibetan Plateau. Geoderma 2020, 377, 114583. [Google Scholar] [CrossRef]
- Li, T.; Dawson, G.J.; Chuter, S.J.; Bamber, J.L. A high-resolution Antarctic grounding zone product from ICESat-2 laser altimetry. Earth Syst. Sci. Data 2022, 14, 535–557. [Google Scholar] [CrossRef]
- Fisher, P. Improved modeling of elevation error with geostatistics. Geoinformatica 1998, 2, 215–233. [Google Scholar] [CrossRef]
- Li, Z. On the measure of digital terrain model accuracy. Photogramm. Rec. 1988, 12, 873–877. [Google Scholar] [CrossRef]
- Berthier, E.; Arnaud, Y.; Vincent, C.; Rémy, F. Biases of SRTM in high-mountain areas: Implications for the monitoring of glacier volume changes. Geophys. Res. Lett. 2006, 33, 8502-1–8502-5. [Google Scholar] [CrossRef]
- Surazakov, A.B.; Aizen, V.B. Estimating volume change of mountain glaciers using SRTM and map-based topographic data. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2991–2995. [Google Scholar] [CrossRef]
- Guo, X.; Feng, Q.; Si, J.; Zhang, X. Considerable influences of recycled moistures and summer monsoons to local precipitation on the northeastern Tibetan Plateau. J. Hydrol. 2022, 605, 127343. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, S.; Sun, W. Continuous estimates of glacier mass balance in high mountain Asia based on ICESat-1, 2 and GRACE/GRACE follow-on data. Geophys. Res. Lett. 2021, 48, e2020GL090954. [Google Scholar] [CrossRef]
- Zhang, Q.; Kang, S. Glacier elevation change in the Western Qilian mountains as observed by TerraSAR-X/TanDEM-X images. Geocarto Int. 2021, 36, 1365–1377. [Google Scholar] [CrossRef]
- Shen, C.; Jia, L.; Ren, S. Inter- and Intra-Annual Glacier Elevation Change in High Mountain Asia Region Based on ICESat-1&2 Data Using Elevation-Aspect Bin Analysis Method. Remote Sens. 2022, 14, 1630. [Google Scholar]
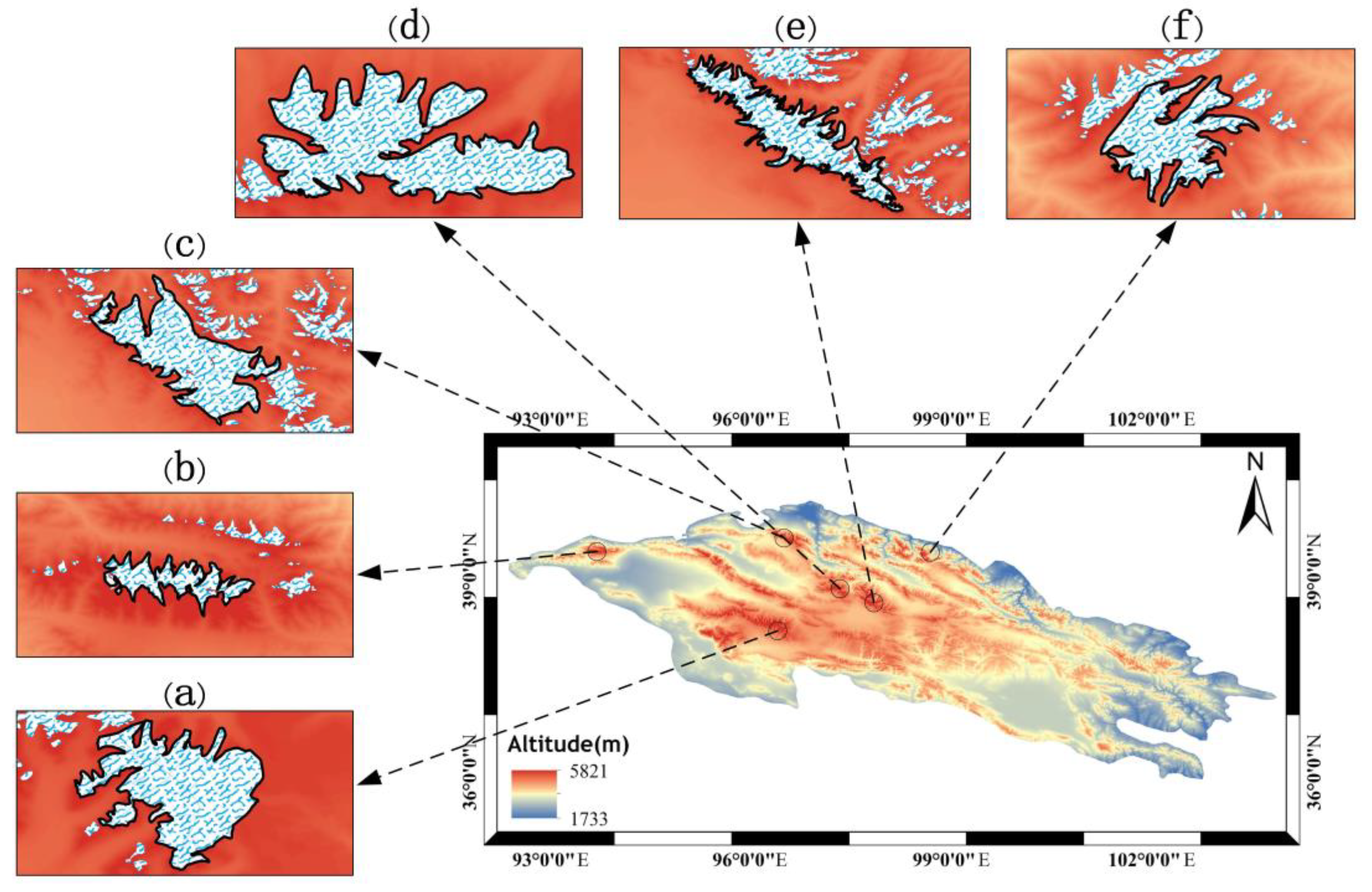

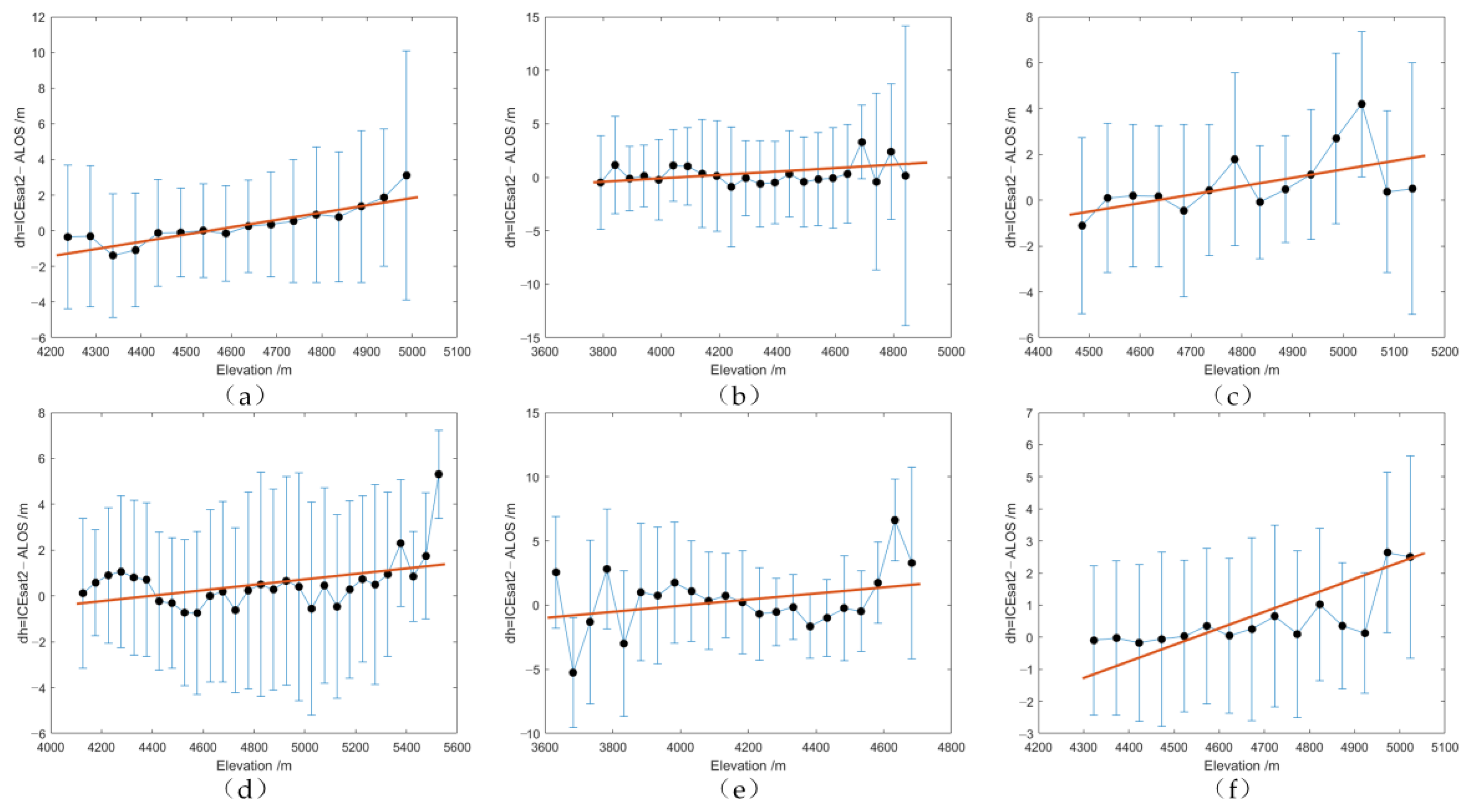


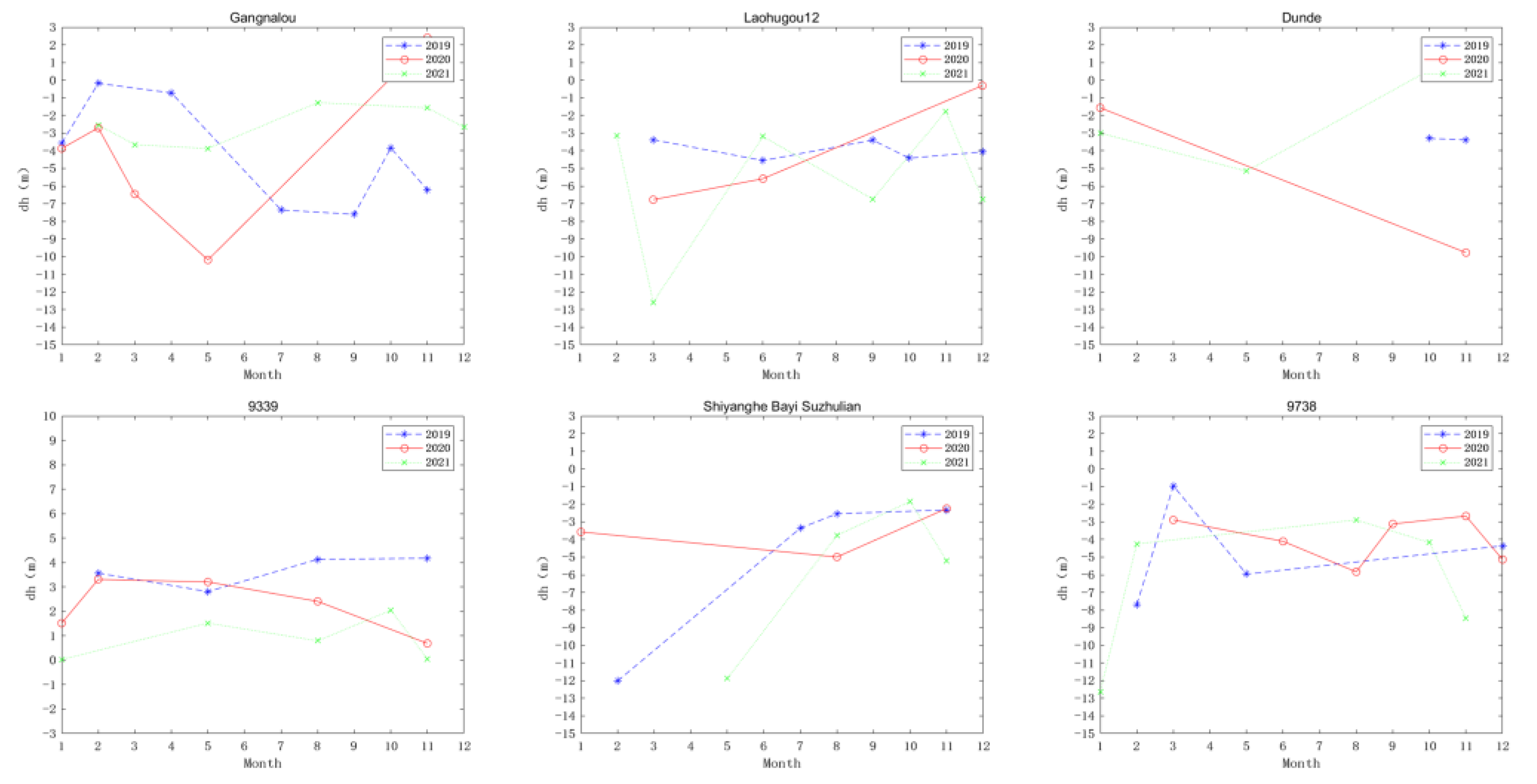

| Region | Before Registration | Pyramid Method | Method of Nuth et al. [12] | Number of Foot Points | |||
|---|---|---|---|---|---|---|---|
| Mean (m) | RMSE (m) | Mean (m) | RMSE (m) | Mean (m) | RMSE (m) | ||
| Gangnalou | −0.38 | 3.63 | 0.035 | 2.88 | −0.04 | 2.94 | 15,178 |
| Laohugou No. 12 | −0.79 | 4.65 | −0.18 | 4.14 | −0.18 | 4.09 | 8861 |
| Dunde | −0.26 | 3.63 | −0.08 | 3.21 | 0.06 | 3.18 | 5155 |
| 93.5°E 39.2°N | −1.32 | 4.43 | −0.18 | 3.69 | 0.14 | 3.72 | 9986 |
| Shiyang River, Bayi, Suzhulian | −1.14 | 4.62 | −0.16 | 3.91 | 0.09 | 3.94 | 5965 |
| 97.2°E 38.7°N | −1.99 | 3.56 | −0.06 | 2.51 | 0.06 | 2.51 | 10,883 |
| Glacier Area | X Direction | Y Direction | Z Direction |
|---|---|---|---|
| Gangnalou | −6.2 m | −0.1 m | −0.76 m |
| Laohugou No. 12 | −2.45 m | 0.2 m | −1.01 m |
| Dunde | −3.45 m | 1.25 m | −0.35 m |
| 93.5°E 39.2°N | −6.5 m | −2 m | −1.72 m |
| Shiyang River, Bayi, Suzhulian | −4.45 m | 1.35 m | −1.16 m |
| 97.2°E 38.7°N | −7.7 m | −1.1 m | −1.85 m |
| Glacier Name | Change Rate of Elevation per Year |
|---|---|
| Gangnalou | 0.74 ± 0.84 m |
| Laohugou No. 12 | −0.08 ± 0.79 m |
| Dunde | 0.09 ± 0.94 m |
| 93.5°E 39.2°N | −0.99 ± 0.34 m |
| Shiyang River, Bayi, Suzhulian | −0.27 ± 0.77 m |
| 97.2°E 38.7°N | −0.16 ± 0.85 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Xie, J.; Liu, R.; Mo, F.; Yang, X. Research on Glacier Elevation Variability in the Qilian Mountains of the Qinghai-Tibet Plateau Based on Topographic Correction by Pyramid Registration. Remote Sens. 2023, 15, 62. https://doi.org/10.3390/rs15010062
Zeng J, Xie J, Liu R, Mo F, Yang X. Research on Glacier Elevation Variability in the Qilian Mountains of the Qinghai-Tibet Plateau Based on Topographic Correction by Pyramid Registration. Remote Sensing. 2023; 15(1):62. https://doi.org/10.3390/rs15010062
Chicago/Turabian StyleZeng, Junze, Junfeng Xie, Ren Liu, Fan Mo, and Xiaomeng Yang. 2023. "Research on Glacier Elevation Variability in the Qilian Mountains of the Qinghai-Tibet Plateau Based on Topographic Correction by Pyramid Registration" Remote Sensing 15, no. 1: 62. https://doi.org/10.3390/rs15010062
APA StyleZeng, J., Xie, J., Liu, R., Mo, F., & Yang, X. (2023). Research on Glacier Elevation Variability in the Qilian Mountains of the Qinghai-Tibet Plateau Based on Topographic Correction by Pyramid Registration. Remote Sensing, 15(1), 62. https://doi.org/10.3390/rs15010062









