Non-Uniform MIMO Array Design for Radar Systems Using Multi-Channel Transceivers

Abstract

Multiple-input multiple-output (MIMO) technology has recently attracted attention with regard to improving the angular resolution of small antennas such as automotive radars. If appropriately placed, the co-located transmit and receive arrays can make a large virtual aperture. This paper proposes a new method for designing arrays by adopting a structure with minimum redundancy. The proposed structure can significantly increase the virtual array aperture while keeping the transmit and receive antennas at the same size. We describe the application of the proposed method to subarray-type antennas using multi-channel transceivers, which is essential for arranging RF hardware in a small antenna operating at high frequency. Further, we present an analysis of the final beam pattern and discuss its benefits and limitations.

1. Introduction

An essential requirement for a radar system is its angular resolution. As the angular resolution depends on the aperture size, a small antenna system, such as an automotive radar, is challenging to achieve. Subspace-based algorithms, such as multiple signal classification (MUSIC) and estimation of signal parameters via rational invariance techniques (ESPRIT), and parameter estimation algorithms based on the maximum likelihood (ML) function have been used to achieve the high-resolution angle estimation [1,2]. However, the multiple-input multiple-output (MIMO) technology has recently attracted the most attention.

A MIMO radar, which synthesizes a virtual antenna array (VAA) using co-located transmit and receive antennas, is typically used in automotive systems [3,4,5,6]. If appropriately placed, co-located transmit and receive arrays can create a large virtual aperture with a small number of arrays. The arrangement of the VAA is determined by the spatial convolution of the transmit and receive array positions, and its aperture is the sum of each antenna aperture [7]. In the case of a uniform linear array (ULA), if the receive array has $M_r$ elements and the transmit array has $M_t$ elements, the VAA can become a filled ULA with $M_t\times M_r$ elements when the interelement spacing is d and $M_r\times d$, respectively. Furthermore, if the total number of arrays is 2K, the maximum aperture is obtained when $M_r=M_t=K$. However, in this case, the sizes of the receive and transmit arrays are considerably different, i.e., $M_r\times d$ and $\left(M_t-1\right)\times M_r\times d$. For example, if $K=8$, the maximum VAA aperture can be 16d when $M_r=M_t=4$. The apertures of receive and transmit arrays are 4d and 12d, respectively. Thus, the two antennas have a three-fold size difference, and the long antenna will ultimately determine the physical dimensions of the entire antenna. Therefore, this arrangement is insufficient for the miniaturization of the antenna when considering the physical dimensions and the VAA aperture. A simple design to make the size of the transmit and receive arrays the same is to use $M_t=2$. Then, although the aperture of the VAA is reduced to 12d in this example, the physical size becomes half.

Most automotive radars employ this type of transmit-and-receive array spacing, and it is difficult to find other arrangements. This paper suggests a new spacing method for VAA that provides the largest VAA aperture and makes the physical size of the transmit and receive array antennas the same by employing the co-array property of the non-uniform, minimum redundancy array.

Another trend driving module size reduction is to move to higher operating frequencies. A higher operating frequency in radar systems is preferred because of its increased bandwidth, high range resolution, and accuracy. The unlicensed industrial, scientific, and medical (ISM) frequency above 100 GHz is particularly interesting for mass-volume commercial radar-sensor applications [8]. However, when the frequency increases, arranging the RF hardware becomes challenging due to the compact antenna. Research on integrating antennas into packages or chips is ongoing to find a cost-effective solution without requiring RF signals on the printed circuit board (PCB) [9]. Several studies on D band (110~170 GHz) transceivers have been published [10,11,12,13]. The multi-channel transceiver is a single-chip solution that integrates multiple transmit and receive channels. It includes amplifiers and a phase shifter in each channel supporting analog beamforming in both transmit and receive directions. Transmission beamforming can increase the power and extend the detection range. Receive beamforming decreases the number of analog-to-digital converters (ADCs) and all subsequent digital hardware, effectively reducing size and cost of the system. However, this front-end beamforming, or subarray structure, is disadvantageous for adaptive beamforming or multiple beamforming compared with full digital arrays and affects the MIMO VAA configuration as well [14].

In this paper, we propose a design approach for MIMO VAA considering the transmit and receive subarray structure using multi-channel transceivers. We herein present an analysis of the final beam pattern using subarray structure and MIMO VAA and the application of the proposed MIMO arrangement method. The benefits and limitations are discussed.

The remainder of this paper is organized as follows. The next section derives the fundamental formula of a MIMO antenna with subarrays. Section 3 describes the non-uniform arrays, including the non-redundant array and minimum redundancy array (MRA), and proposes a new MIMO configuration. Section 4 suggests a subarray-type MIMO antenna using non-uniform spacing and, finally, Section 5 presents the conclusion.

2. MIMO with Subarrays

2.1. Basic Principle

A MIMO, in which the transmit arrays are configured using subarrays, is called phased MIMO, and the beam pattern, SNR, and SINR are discussed in [15,16,17]. Based on this, the following formula is derived for M transmission subarrays with L arrays shown in Figure 1.

We assume that each subarray transmits a different waveform ${\varphi }_m\left(t\right)$, and the waveforms are orthogonal to one another.

$$\mathit{\varphi }\left(t\right)={\left[\begin{array}{ccc}{\varphi }_1\left(t\right)& {\varphi }_2\left(t\right)& \dots {\varphi }_M\left(t\right)\end{array}\right]}^T$$

(1)

$${{\displaystyle \int }}_{T_0}\mathit{\varphi }\left(t\right){\mathit{\varphi }}^H\left(t\right)dt=I_M$$

(2)

where $I_M$ is the $M\times M$ identity matrix. If the beamforming weight of each subarray is ${\mathrm{w}}_{ml}$, the transmission signal in the $\theta$ direction by the m-th subarray can be expressed as follows:

$$\begin{gathered} s_m\left(t,\theta \right)=\left[{\mathrm{w}}_{m1}^{*}{ \mathrm{w}}_{m2}^{*},\cdots {\mathrm{w}}_{mL}^{*}\right]{\left[1 e^{-jk{d}_{t1}\sin \theta }\cdots e^{-jk{d}_{t\left(L-1\right)}\sin \theta }\right]}^T{e}^{-jk{D}_{t\left(m-1\right)}\sin \theta }{\varphi }_m\left(t\right) \\ =w_m^H a\left(\theta \right)e^{-jk{D}_{t\left(m-1\right)}\sin \theta }{\varphi }_m\left(t\right) \left(m=1,2,\dots M\right) \end{gathered}$$

(3)

where $w_m={\left[{\mathrm{w}}_{m1}{ \mathrm{w}}_{m2},\cdots {\mathrm{w}}_{mL}\right]}^T\in C^{L\times 1}, a\left(\theta \right)={\left[1 e^{-jk{d}_{t1}\sin \theta }\cdots e^{-jk{d}_{t\left(L-1\right)}\sin \theta }\right]}^T,$ k is the wave number, $2\pi /\lambda \left(\lambda : wavelength\right)$, and * and H stand for the complex conjugate and conjugate transpose, respectively.

Then, the transmit signal becomes the sum of them.

$$\begin{array}{l}s\left(t,\theta \right)={\displaystyle {\displaystyle \sum }_{m=1}^M}{s}_m\left(t,\theta \right)={\displaystyle {\displaystyle \sum }_{m=1}^M}{w}_m^H a\left(\theta \right)e^{-jk{D}_{t\left(m-1\right)}\sin \theta }{\varphi }_m\left(t\right)\\ =\left[w_1^H a\left(\theta \right)w_2^H a\left(\theta \right)\cdots w_M^H a\left(\theta \right)\right]\odot \left[1e^{\left(-jk{D}_{t1}\sin \theta \right)}\cdots e^{-jk{D}_{t\left(M-1\right)}\sin \theta }\right]\left[\begin{array}{c}{\varphi }_1\left(t\right)\\ {\varphi }_2\left(t\right)\\ \\ ⋮\\ {\varphi }_M\left(t\right)\end{array}\right]\\ ={\overline{a}}^T\left(\theta \right)\odot d^T\left(\theta \right)\mathit{\varphi }\left(t\right)\end{array}$$

(4)

where $\overline{a} \left(\theta \right)={\left[w_1^H a\left(\theta \right)\cdots w_M^H a\left(\theta \right)\right]}^T\in C^{M\times 1},$ $d\left(\theta \right)={\left[1 e^{-jk{D}_{t1}\sin \theta }\cdots e^{-jk{D}_{t\left(M-1\right)}\sin \theta }\right]}^T$, and $\odot$ stands for the Hadamard product. Moreover, if the weights for the subarrays are identical, i.e., $w_1=w_2=\cdots =w_M=w$, it is simplified to

$$s\left(t,\theta \right)=w^{T}a\left(\theta \right)d^T\left(\theta \right)\mathit{\varphi }\left(t\right)=g_t\left(\theta \right)d^T\left(\theta \right)\mathit{\varphi }\left(t\right),$$

(5)

where $g_t\left(\theta \right)=w^{T}a\left(\theta \right)$.

The target reflection signal in the $\theta$ direction can be expressed by

$$r\left(t,\theta \right)=\beta {\overline{a}}^T\left(\theta \right)\odot d^T\left(\theta \right)\mathit{\varphi }\left(t-\tau \right)+n\left(t\right)=\beta g_t\left(\theta \right)d^T\left(\theta \right)\mathit{\varphi }\left(t-\tau \right)+n\left(t\right)$$

(6)

where $\beta$ is the complex reflection coefficient, $\tau$ is the delay by the target distance, and $n\left(t\right)$ is the white Gaussian noise.

Suppose the receiver, like the transmit arrays, has a structure that performs analog beamforming in subarray units and then performs digital beamforming, as shown in Figure 2. Then the output of the nth subarray can be written as follows:

$$r_n\left(t,\theta \right)=c_n^{H}b\left(\theta \right)e^{-jk{D}_{r\left(n-1\right)}\sin \theta } r\left(t,\theta \right) \left(n=1,\dots N\right)$$

(7)

where $c_n={\left[c_{n1} c_{n2} \dots c_{nP}\right]}^T$ are the analog beamforming weights within each subarray, and $b\left(\theta \right)={\left[1 e^{-jk{d}_{r1}\sin \theta } \dots e^{-jk{d}_{r\left(P-1\right)}\sin \theta }\right]}^T$ is the phase difference in the $\theta$ direction. Again, if $c_1=c_2=\cdots =c_N=c,$ then we can simplify to $c_1^{H}b\left(\theta \right)=c_2^{H}b\left(\theta \right)=\cdots c_N^{H}b\left(\theta \right)=g_r\left(\theta \right)$ and the receive signal vector from all subarray is expressed by

$$\begin{array}{l}r\left(r,\theta \right)={\left[r_1\left(t,\theta \right) r_2\left(t,\theta \right)\dots r_N\left(t,\theta \right)\right]}^T\\ \hspace{1em}\hspace{1em}=g_r\left(\theta \right){\left[1 e^{-jk{D}_{r1}\sin \theta }\dots e^{-jk{D}_{r\left(N-1\right)}\sin \theta }\right]}^{T}r\left(t,\theta \right)=g_r\left(\theta \right)h\left(\theta \right)r\left(t,\theta \right)\end{array}$$

(8)

where $h\left(\theta \right)={\left[1 e^{-jk{D}_{r1}\sin \theta }\dots e^{-jk{D}_{r\left(N-1\right)}\sin \theta }\right]}^T$.

Each transmit waveform is recovered by matched filtering with ${\left\{\varphi \left(t\right)\right\}}_{m=1}^M$. The m-th signal after matched filtering is

$$x_m\left(\theta \right)={{\displaystyle \int }}_{T_0}r\left(t,\theta \right){\varphi }_m^{*}\left(t\right)dt=\beta g_t\left(\theta \right)g_r\left(\theta \right)d_{m}h\left(\theta \right)+{\tilde{n}}_m\left(t\right), \mathrm{m}=1\dots ,M$$

(9)

where $d_m$ is the m-th element of the vector $d\left(\theta \right)$ in (4). Thus, the final MIMO received signal of $NM\times 1$ is represented as follows:

$$y={\left[x_1^T\left(\theta \right) x_2^T\left(\theta \right) \dots x_M^T\left(\theta \right)\right]}^T=\beta g_t\left(\theta \right)g_r\left(\theta \right) d\left(\theta \right)\otimes h\left(\theta \right)+\tilde{N}$$

(10)

The above equation is the same as the typical MIMO formula except for the subarray gains of $g_t\left(\theta \right)$ and $g_r\left(\theta \right)$. After MIMO VAA beamforming with the weight vector $w_{\mathrm{MIMO}}\in C^{NM\times 1}$, the final beam pattern is expressed by

$$G\left(\theta \right)={\left|w^{H}a\left(\theta \right)\right|}^2{\left|c^{H}b\left(\theta \right)\right|}^2{\left|w_{\mathrm{MIMO}}^H\left[d\left(\theta \right)\otimes h\left(\theta \right)\right]\right|}^2={\left|g_t\left(\theta \right)\right|}^2{\left|g_r\left(\theta \right)\right|}^2{\left|g_{\mathrm{MIMO}}\left(\theta \right)\right|}^2$$

(11)

The final pattern revealed is the multiplication of the transmitter subarray pattern, the receiver subarray pattern, and the MIMO VAA beampattern.

Here, we can summarize three design factors of the subarray MIMO antenna:

• the orthogonal waveforms $\left\{{\varphi }_m\right\}$, which are not a subject of this manuscript, but are an important issue. Conventionally, the orthogonality is obtained by time-domain multiplexing (TDM), frequency domain multiplexing (FDM), or code domain multiplexing (CDM) [18,19,20,21]. Beat-frequency multiplexing or Doppler-domain multiplexing (DDM) is also proposed in automotive radars [3,5];
• the antenna structure, including the subarrays and MIMO configuration; and
• the beamforming weights.

The antenna structure is represented by $a(\theta )$, $b\left(\theta \right)$, and d$\left(\theta \right)$, while h$\left(\theta \right).$ $a(\theta$) and $b\left(\theta \right)$ are the subarray configuration, and d$\left(\theta \right)$ and h$\left(\theta \right)$ are the MIMO configuration which results from the structure among subarrays. The beamforming weights are $w \mathrm{and} c$, and $w_{\mathrm{MIMO}}$. w and c are the transmit and receive subarray weights, respectively, designed for suppressing the sidelobe level as well as steering the subarray beam direction. ${\mathrm{w}}_{\mathrm{MIMO}}$ is the beamforming weight of MIMO VAA for multiple beamforming, adaptive beamforming, or any purpose.

2.2. MIMO Configuration

A MIMO antenna is typically defined as having transmit arrays with L = 1 in Figure 1 and receive arrays with p = 1 in Figure 2, implying that it does not have subarrays. The VAA beam pattern is determined in this case by the array spacing $D_t, D_r$ and the MIMO beamforming weight. From Equation (10), the input is written as follows:

$$y={\left[x_1^T\left(\theta \right) x_1^T\left(\theta \right) \dots x_1^T\left(\theta \right)\right]}^T=\beta d\left(\theta \right)\otimes h\left(\theta \right)+\tilde{N}=\beta v\left(\theta \right)+\tilde{N}$$

(12)

where $v\left(\theta \right)=d\left(\theta \right)\otimes h\left(\theta \right)={\left[{\mathrm{v}}_1\left(\theta \right),{\mathrm{v}}_2\left(\theta \right),\cdots ,{\mathrm{v}}_{NM}\left(\theta \right)\right]}^T$ and the element is

$${\mathrm{v}}_{\left[n+\left(m-1\right)N\right]}\left(\theta \right)=e^{-jk\sin \theta \left[D_{t\left(m-1\right)}+D_{r\left(n-1\right)}\right]}, m=1,\dots M \mathrm{and} n=1,\dots ,N$$

(13)

This equation is more commonly referred to as the spatial convolution of transmit and receive array positions. If the transmit and receive antenna has a uniform interval, then we can write that $D_{t\left(m-1\right)}=\left(m-1\right)D_t$ and $D_{r\left(n-1\right)}=\left(n-1\right)D_r$. The maximum length of the VAA that can be implemented with $\left(M+N\right)$ arrays is $MN\times D_r,$ when $D_t=N{D}_r$ (or $D_r=M{D}_t$). In addition, the maximum length is achieved when the number of transmit arrays is the same as the number of receive arrays, i.e., $M=N=K$ if $M+N=2K$. However, in this case, the physical lengths of the antennas are $\left(M-1\right)\times N{D}_r$, and $N{D}_r$, respectively, so the transmit antenna is $\left(M-1\right)$ times longer than the receive antenna. For example, if $M+N=8$, the maximum length of the VAA is $16D_r$ when $M=N=4$. The length of the transmit antenna is $12D_r$, which is three times longer than that of the receive antenna, $4D_r$. A similar physical size of the two antennas can be obtained using two transmit arrays and six receive arrays, but the length of the virtual antenna is reduced to $12D_r$. Figure 3 shows VAAs for two cases.

Although the beam pattern of the VAA varies depending on the selection of weights, if we choose $w_{MIMO}=d\left({\theta }_s\right)\otimes h\left({\theta }_s\right)$, which is the conventional beamforming weight for a uniform array, the resulting beam pattern becomes the product of the transmit pattern and the receive pattern is as follows:

$$\begin{array}{ll}\left(\theta \right)& ={\left|w_{\mathrm{MIMO}}^H\left[d\left(\theta \right)\otimes h\left(\theta \right)\right]\right|}^2={\left|{\left[d\left({\theta }_s\right)\otimes h\left({\theta }_s\right)\right]}^H\left[d\left(\theta \right)\otimes h\left(\theta \right)\right]\right|}^2\\ & ={\left|d^H\left({\theta }_s\right)d\left(\theta \right)\right|}^2{\left|h^H\left({\theta }_s\right)h\left(\theta \right)\right|}^2={\left|g_{tx}\left(\theta \right)\right|}^2{\left|g_{rx}\left(\theta \right)\right|}^2\end{array}$$

(14)

where ${\theta }_s$ is the steering direction. If the beam direction is fixed to only one angle, it is theoretically the same pattern as performing transmit beamforming by d(θ) and receive beamforming by h(θ) separately. However, in the MIMO approach, the beamforming is performed only in the receiver, and the number of weights increases MN. Thus, it has more degree of freedom to make multiple beams simultaneously in several directions or perform adaptive beamforming, which is usually performed digitally.

2.3. Transmit and Receive Subarray

In the case of a MIMO antenna with transmit and receive subarrays, the final pattern is the product of the subarray pattern and the MIMO pattern, as written in Equation (11). If w or c steers the subarray pattern at a specific angle, MIMO beamforming to a different angle is bound by the subarray pattern and suffers a loss. The loss increases as the beamwidth of the subarray gets smaller, i.e., as the size of the subarray becomes larger. The idea is the same as how a single array pattern constrains the array antenna pattern.

Figure 4 shows a case where each transmit array of Figure 3b is replaced by subarrays with four arrays. The space of all the arrays is set to 0.5 wavelengths. The resulting beam patterns are shown in Figure 5. The MIMO pattern is obtained by the Figure 3b configuration, and four arrays make the subarray pattern. The final pattern becomes a product of these two patterns, which has the good effect of suppressing the sidelobe but shows a loss of gain when steering at 10° compared with the gain at 0°.

The adoption of the transmit subarray can improve the SNR by increasing the output power and has the effect of suppressing the sidelobe. However, because it restricts the angle of multi-beams, it is recommended to use a window to increase the beamwidth. Figure 6 shows the beampattern created by applying a Taylor window to the transmit subarray. It demonstrates that the sidelobe is still suppressed while the loss in the 10° beam is decreased.

On the other hand, when the receive array is composed of an analog beamforming subarray without overlap, another consequence appears in addition to the pattern constraint. Figure 7 shows the receive antenna configured in the form of a subarray. In this case, the spacing of the MIMO receiver is no longer half a wavelength and thus results in the grating lobe of the MIMO pattern, as shown in Figure 8. The final pattern is the same as the uniform array pattern if both the subarray beamforming on an analog receiver and the MIMO beamforming are performed in the same direction. However, if the angle of the MIMO beamforming is changed in a different direction, the grating lobe and the subarray pattern modify the final pattern at the same time.

Although the receiver subarray is unavoidable due to the space constraint of hardware as frequency increases, the performance is somewhat limited compared with the full digital array.

3. Design of MIMO Array

3.1. Minimum Redundancy Array

The MRA is a class of non-uniform linear array designed to minimize the number of sensor pairs with the same spatial correlation lag. If this number of sensor pairs is 1, it is called a perfect array. If we assume that the arrays are located on an underlying grid with unit spacing and that w is a vector having 1 at the array position and 0 at the other location, then the number of times each spatial correlation lag is computed by the autocorrelation of the position vector with itself, which is called the co-array [22].

$$c\left(\gamma \right)={\displaystyle \sum }_{\mathrm{k}=1}^{N_e}\mathrm{w}\left(k\right)\mathrm{w}\left(k-\gamma \right)$$

(15)

where $N_e$ is the size of w, w(k) is k-th element of w, and w(k) = 0 if $k<1$ or $k>N_e$. For example, a vector w = [1 1 0 0 1 0 1] has 4 arrays (N) and the size ($N_e$) is 7. As illustrated in Figure 9, in this case, all co-arrays have one except when $\gamma =0$, indicating that the sensor pair with the same spatial correlation lag is 1. This type of co-array is called a perfect array. However, because there is no perfect array for $N>4$, it should be chosen between non-redundant arrays that partially permit holes and MRA with no holes. A hole is a position where the co-array value is 0, and redundancy is a position where the co-array value is greater than 1, where $\gamma$ is not 0. The following equation determines the final size:

$$N_e=\frac{N\left(N-1\right)}{2}-N_R+N_H+1$$

(16)

where $N_R$ is the number of redundancies and $N_H$ is the number of holes.

The MRA is designed to make the largest possible aperture without holes. There has been a significant amount of research on element spacing to achieve as low a redundancy as possible for arrays of up to 30 elements [23,24,25].

3.2. Non-Uniform MIMO Array Configuration

The co-array property is applied to a bistatic MIMO VAA. Because the location of the MIMO virtual arrays consists of the spatial convolution of the transmit and receive arrays, if we choose the receive array as the reverse of the transmit arrays, the resulting VAA is the co-array structure with a length approximately twice that of the transmit array. When the size of a single antenna is $N_e$, the size of the resulting VAA is as follows:

$$N_{VAA}=2N_e-1$$

(17)

In other words, a VAA composed of an MRA generates uniform arrays, and one made up of non-redundant arrays results in sparse arrays. For example, suppose the transmit arrays and receive arrays are configured with a perfect array of $N=4$ and $N_e=7$ in the previous section. In that case, the VAA can have the same beam pattern as that of uniform arrays with 13 elements, as shown in Figure 10.

For each N, the size of non-redundant arrays, $N_{e,nr}$, and the size of the MRA, $N_{e,mr}$, are summarized in

Table 1. List of VAA sizes for the non-uniform array configurations and number.

N	Non-Redundant Array		Minimum Redundancy Array		2-Transmit Arrays
	${\mathit{N}}_{\mathit{e}\mathbf{,}\mathit{n}\mathit{r}}$	${\mathit{N}}_{\mathit{V}\mathit{A}\mathit{A}}$	${\mathit{N}}_{\mathit{e}\mathbf{,}\mathit{m}\mathit{r}}$	${\mathit{N}}_{\mathit{V}\mathit{A}\mathit{A}}$	${\mathit{N}}_{\mathit{r}\mathit{x}}$	${\mathit{N}}_{\mathit{V}\mathit{A}\mathit{A}}$
3	4	7	4	7	6	4
4	7	13	7	13	6	12
5	12	23	10	19	8	16
6	18	35	14	27	10	20
7	26	51	18	35	12	24
8	35	69	24	47	14	28

. The size of the MIMO VAA for each is also listed. In addition, the VAA size for the case of using two transmit arrays and ($2N-2$) receive arrays is written, in which the transmit antenna and the receive antenna have the same size. Table 1 shows that when N is greater than 3, VAA apertures using non-uniform arrays are longer than the aperture using conventional two-transmit array structures. The VAA aperture ratio increases with N; when N = 8, the ratio is up to 2.46 and 1.68, respectively.

When using five transmit and receive arrays, it is possible to make a VAA with 23 sizes using non-redundant arrays with an interval of (1,3,5,2) and a VAA with 19 sizes using an MRA with an interval of (1,3,3,2). Both are larger than a VAA with 16 sizes, which is composed of 10 arrays of two transmit arrays and eight receive arrays as shown in Figure 11.

Figure 12 shows the beampattern for each case. The beamforming is performed by adjusting the weight to make it the same as for uniform arrays, although the hole cannot be filled out. The non-redundant array has less beamwidth than the MRA because of the larger aperture size. However, due to the two holes, it has different positions and higher sidelobe than 23 uniform arrays. Both the MRA and non-redundant arrays have small beamwidth compared with 16 uniform arrays with two transmit arrays.

4. Proposed MRA MIMO with Subarrays

The minimum redundancy configuration can be applied to $D_t$ in Figure 1 and $D_r$ in Figure 2 to build a subarray MIMO structure using a multi-channel transceiver. The number of arrays that comprise the subarray, L and P, depends on the hardware structure of the transceiver, which are four in this paper.

Assume five transmission waveforms and five receive antennas, as shown in Figure 13. The spacing of the arrays is 0.5 wavelength and the minimum spacing of the subarrays is 2 wavelengths. The ratio of the spacing between subarrays is 1:3:3:2. The aperture of the transmit and the receive antenna is 20 wavelengths, and the final aperture is doubled to 40 wavelengths.

According to Equation (11), the final beam pattern is the product of the transmit subarray beampattern, the receive subarray beampattern, and the MIMO beampattern. Again, MIMO beamforming is performed by adjusting the weight to make it the same as for uniform arrays.

When the transmit subarray beamforming, the receive subarray beamforming, and the MIMO beamforming are performed at the same boresight angle, say 0°, we can get the same result as the uniform array, as shown in the upper graph of Figure 14. However, if we control the MIMO digital beam at 5°, it suffers a loss by the subarray beampattern, and the grating lobe also occurs, as shown in the lower graph of Figure 14. In other words, the subarray beamwidth limits the MIMO beamforming angle. The transmit subarray pattern in the figure employs the Taylor window to broaden the beamwidth, whereas the receive subarray pattern does not.

Next, Figure 15 shows the configuration in which the non-redundant structure is applied to MIMO. Likewise, the spacing of the arrays is 0.5 wavelengths, the spacing of the subarrays has two wavelengths as the minimum spacing, and the spacing ratio is 1:3:5:2. The total aperture is 48 wavelengths longer than the minimum redundancy configuration, so the beam width is improved. However, the sidelobe characteristics deteriorate due to holes in the MIMO structure. The upper graph in Figure 16 shows the beampattern formed when the steering angle of the subarrays and the steering angle of the MIMO beam are equal to 0°, and the lower graph shows the beampattern when only the MIMO steering angle is changed to 5°.

Finally, if two transmitters and eight receivers with about 18 wavelengths are configured as shown in Figure 17, the final aperture becomes a uniform array of 36 wavelengths.

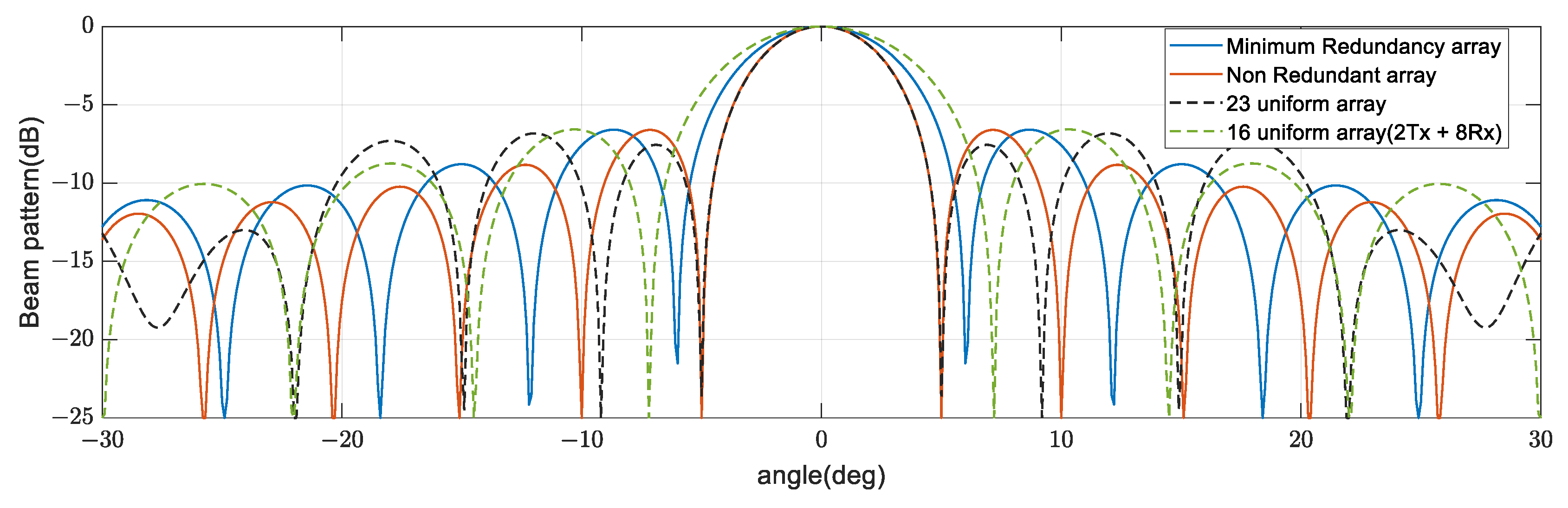
Figure 18 compares beampatterns for three configurations steered to 5°. As expected from the aperture length, the non-redundant array has the smallest beamwidth and the worst sidelobe characteristic. Grating lobes due to the minimum interval of the subarray are common.

5. Conclusions

We devised a new method for placing transmit and receive arrays for MIMO VAA with non-redundant or minimum redundant structures. In contrast to the conventional arrangement, wherein one of the antennas has a relatively long physical size, the proposed design can increase the VAA aperture while keeping the transmit and receive antennas at the same size.

In addition, we applied the proposed method to the MIMO antenna with subarrays and analyzed the beampatterns. Subarrays restrict the direction of multiple beamforming, and produce grating lobes if the subarrays do not overlap and the interval is substantially greater than a half waveform. However, the subarray structure is expected to be essential for small antennas with multi-channel transceivers, which are necessary for moving to a high operating frequency to improve the range resolution and miniaturize antennas. The goal of this study was to develop a D-band radar; the results will be implemented using multi-channel transceivers currently under development.