1. Introduction
Precise Global Navigation Satellite Systems (GNSS) satellite orbits and clock offset are prerequisites for precision positioning and other related scientific applications. Despite the fact that the International GNSS Service (IGS) has a unified processing strategy for reprocessing, the concrete processing strategy during routine processing still differs slightly. Numerous scholars have analyzed the precision products and the consistency of products from various institutions, revealing that the GPS orbit consistency [
1], clock offset consistency [
2], and user equivalent distance comparison [
3] between different analysis centers are at the centimeter (cm) level [
4,
5,
6,
7], which can serve as a foundation for further scientific research. In addition to the evaluation method of obtaining the relative accuracy of the orbit by comparing it with other precision products or satellite laser ranging (SLR), the internal conforming accuracy of the precision orbit products cannot be ignored when evaluating the stability of the products. The internal stability is also an essential evaluation index [
8,
9]. However, when evaluating the internal stability of the products of different analysis centers (AC) and their performance near the daily boundary, significant jumps and differences remain [
10]. Whether it be the overlap [
11] or the boundary point comparison [
12], the 1D mean daily boundary discontinuity (DBD) of final GPS orbit products is reported to be a dozen millimeters (mm) or even tens of millimeters, and the performance of analysis center (Ac) products varies [
13].
The post-processing Precise Point Positioning (PPP) technology is mature, and the static and kinematic accuracy can reach mm and cm-levels, respectively, when DBD is ignored [
14,
15]. Three precision orbiting methods for LEO satellites—dynamic, reduced-dynamic, and kinematic methodologies—all provide cm-level orbit positions that meet the accuracy requirement for major LEO missions [
16,
17,
18,
19,
20]. Among them, the reduced dynamic method has gradually replaced the dynamic-only method and is used as the main method for determining the orbits of various LEO missions [
21] due to its ability to produce more accurate and smooth orbits by incorporating process noise to absorb force model errors. In contrast, the kinematic methodology utilizes only GNSS observations and lacks a priori information on the gravity field and dynamical parameters, making it more appropriate for LEO satellites performing gravity field recovery missions [
22,
23]. The major of LEO satellite orbits are derived from various GNSS precise orbit and clock products. Consequently, the factors affecting the accuracy of LEO satellite orbits include not only the LEO satellite orbit processing methods and models but also the quality of the GNSS products employed [
24].
Unfortunately, jumps near the end of the day in precise products can directly lead to decreased positioning accuracy and erratic LEO satellite orbits. For long-term GNSS point displacement monitoring activities, deformation is more likely to be concealed or falsely detected [
25,
26,
27]. For two-step gravity field recovery based on precise gravity satellite orbits, the recovery of the gravity field is also affected by unwarranted gravity satellite orbits [
28,
29]. In summary, the PPP and LEO precise orbit determination (POD) processes transmit the quality of GPS products and the inevitable DBD.
The primary methods to reduce the impact of DBD are currently centered on the orbit determination process by enhancing the precision or increasing the length of solution arcs [
30,
31,
32], including improving the dynamical model and error model [
33,
34,
35], multi-system joint solution [
36,
37], and multi-technology integration with SLR and LEO satellites [
38,
39,
40,
41]. Song et al. absorbed the precision product orbital jumps by enhancing the orbital interpolation method, effectively reducing the interpolation accuracy loss at the orbit boundary and enhancing the performance of static PPP close to the boundary [
42]. However, the first method necessitates reprocessing the GNSS precise orbit determination project, which is cumbersome and even using multi-day data or improved processing strategies, DBD still exists and may still affect the positioning result. The other approach does not alter the precision of the GNSS precise products but rather adopts a novel method to account for their deviations, which is not universally applicable.
This study focuses on the phenomenon of precision products jumping on consecutive days and aims to mitigate the DBD effect on the user side through a simple and straightforward method of calibrating adjacent orbits and correcting clock offset. Following this introduction,
Section 2 describes the orbit calibration and clock offset correction procedures. The performance of GPS DBD and its effect on user-side applications are covered in
Section 3. Using the calibration method described in
Section 4, the experiments for validation compare the precision at the boundary with that at the non-boundary.
Section 5 summarizes the principal findings.
2. Processing Procedure
The orbit calibration method used in this study is calibrated with reference to the JPL time-weighted smoothing GRACE scientific orbit method and adds an equal-weighted correction scheme (
ftp://rz-vm152.gfz-potsdam.de/grace/DOCUMENTS/Level-1/Algorithm_Theoretical_Basis_Document_for_GRACE_Level-1B_Data_Processing_V1.2, accessed on 11 July 2022). The 9th-order Lagrange interpolation polynomial is used to interpolate the orbit of the middle point, and the data of four epochs of the adjacent day orbit are required at the daily boundary. Consequently, the orbit correction time period chosen in this paper consists of a total of eight epoch interval lengths before and after the boundary.
Figure 1 illustrates the complete processing flow and calibrated orbit results for GPS orbit and clock offset products. Notably, the orbit calibration method in this instance requires the orbits of adjacent days that contain overlapping arc data, so the orbit prediction of the original data is required first.
For overlapping orbit arcs, a brief orbit calibration can be expressed as
where
and
denote the calibrated orbits around the start and end of the current day.
,
and
represent the previous day, the current day and the next day’s orbit data, respectively.
and
are the weights of the orbit data around the start and end of the current day. Assuming both weights are set to 0.5, there is no difference between Equations (1) and (2), and the other is to create a smoothing window based on time as shown in Equations (3) and (4).
where
is defined as:
Furthermore, in Equations (3) and (4), and signify the start and end moments of orbit calibration, respectively. represents the length of the orbit calibration time, i.e., the length of the smooth window.
GNSS satellite orbits are highly correlated with satellite clock offset, so orbital modifications must account for the relative clock offset [
43,
44]. The satellite clock offset can absorb up to 97% of the orbit error in the radial direction for the GPS constellation [
45]. Consequently, only the radial modification is corrected for the clock offset in this paper. Following the completion of the aforementioned orbit calibration procedure, the obtained orbit is compared to the initial orbit to determine the amount of orbit modification. The original clock offset is then corrected further. This is illustrated by Equation (6).
where
denotes the original satellite clock offset.
signifies the orbit modification in the radial direction, and
represents the speed of light in the vacuum, which is a constant as
c = 299,792,458 m/s adopted by the GPS constellation.
Now, the precise orbit and clock offset products supplied by different ACs have been calibrated and the correlation has been effectively assured.
Figure 2 illustrates the effect of adjacent orbits in which the satellite clock offset has been synchronized with the respective orbits. Compared to the initial orbit, the calibrated orbit has a smoother presentation near the daily boundary, and there is no abrupt jump over a short time period.
3. Influence of Orbit Discontinuities
This section describes several ACs orbit product DBDs and illustrates their impact by contrasting the post-processing kinematic PPP positioning accuracy near the daily boundary with that near the non-boundary. An additional DBD evaluation experiment for GPS orbital products from 2010 to 2022 was also performed, and the results showed no significant improvement. Therefore, all the experimental data in this study were selected from day 063 to day 100 data in 2010. Products were chosen from 6 ACs: The Center for Orbit Determination in Europe (COD), the Jet Propulsion Laboratory (JPL), the International GNSS Service (IGS), the Natural Resources Canada (EMR), the European Space Agency (ESA), and the German Research Centre for Geosciences (GFZ).
Each of these orbit products has a sampling rate of 15 min and a time span of 23 h and 45 min. The COD and JPL orbit products are both inter-day solutions with processing durations of 72 h and 30 h, respectively. The IGS orbit is an integrated solution with a processing duration of 27 h (Solution strategies in 2010 obtained from
ftp://igs.ign.fr/pub/igs/igscb/center/analysis/archive/, accessed on 11 July 2022) while the remaining EMR, ESA, and GFZ products are single-day solutions with a processing duration of 24 h. The satellite clock products have a sampling rate of 30 s for all ACs besides JPL and GFZ with a time interval of 5 min. To prevent the loss of accuracy caused by the interpolation of satellite clocks, the sampling interval for all subsequent validation was set to 5 min.
3.1. GPS Day Boundary Discontinuities
Additional residual error absorption is achieved by inserting random pulses every 2 h when fitting the original final orbital product [
42,
46]. During this step, the initial daily orbit products were used as virtual observations to correct the initial state parameters, SRP model parameters, and random pulse parameters for each satellite. Afterwards, these products were densified and predicted using numerical integration.
In order to verify the quality of the extended orbit, the records from 00:00 to 23:00 of each day were used to perform the orbit fitting and prediction steps, while the final one-hour records were used to examine the prediction error. However, all records from 00:00 to 23:45 each day were used to construct the actual orbit.
Table 1 presents the one-dimensional (1D) root mean square (RMS) values corresponding to the orbit fitting residual and prediction error. FIT_24h is the fitting time of 24-h, FIT_23h is the fitting time of 23-h, and EXP_1h is the prediction time of 1 h for a 23-h orbit fit.
As shown in
Table 1, the residuals of the orbit fitting using 23-h data are consistent with those using 24-h data with a maximum deviation of less than 2 mm. Consequently, the 1-h prediction accuracy after using the 24-h orbit fitting can also be considered the accuracy after using the 23-h orbit fitting. Therefore, the 1-h accuracy of this study’s forecast is estimated to be approximately 2 mm, which is in good agreement with the original orbit.
Using the above strategy for orbit fitting and prediction, the difference between the 00:00 moments of adjacent days is taken as the DBD of GPS, and the results of each orbit product are shown in
Figure 3. Each orbit product has a non-negligible increase at the daily boundary, with a minimum of nearly 2 cm and a maximum of 3 cm, as depicted in the graph. Considering the high consistency of the products of each AC, the DBD of the orbit products is related to the arc length determined by different ACs. The single-day 24-h solutions are greater than 27 mm, the inter-day solutions are all less than 22 mm, and the DBD of the COD orbit products with the longest arc length 72-h solution is reduced to less than 20 mm.
3.2. Products DBD Performance
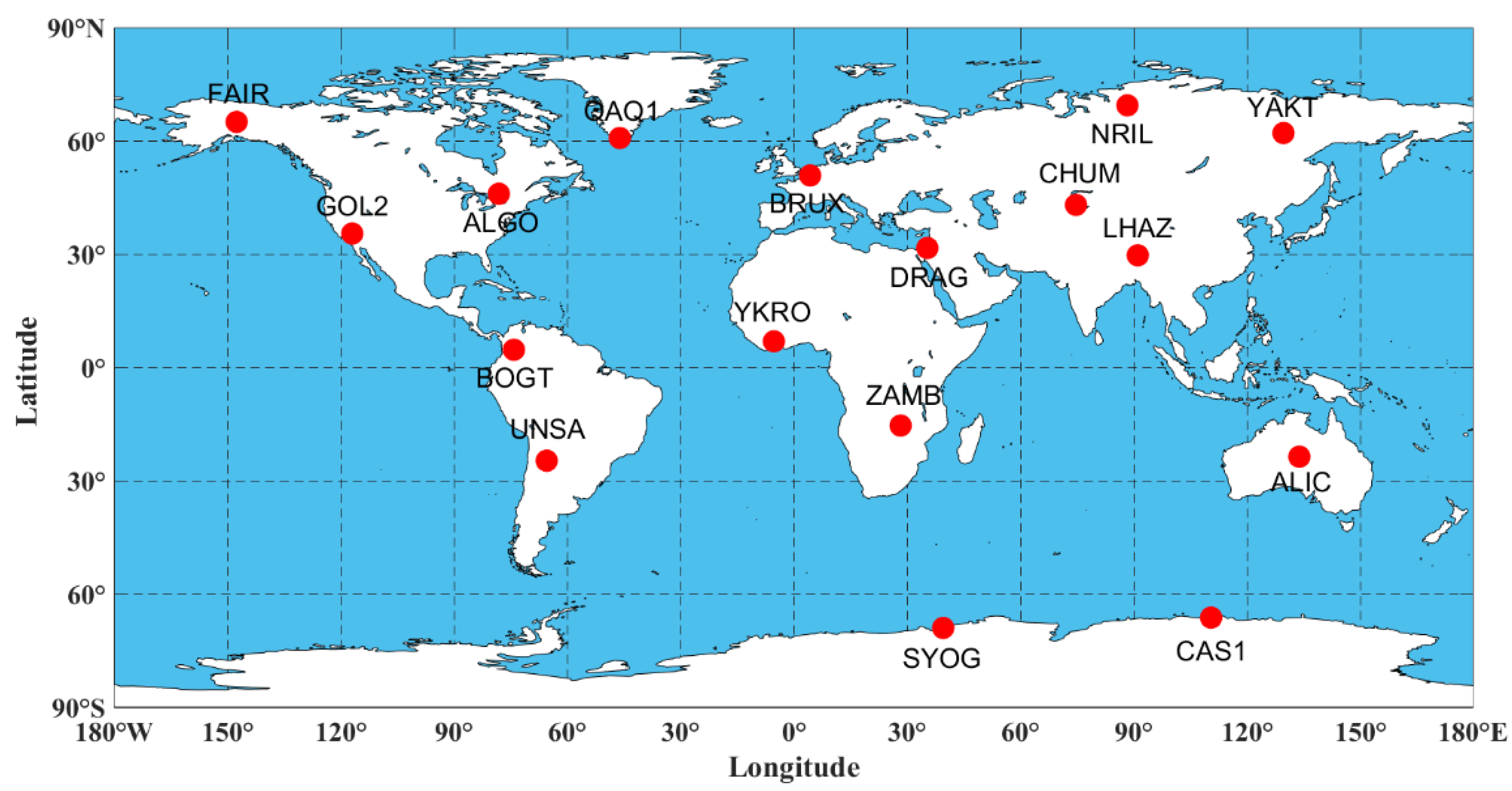
This subsection selects 17 globally distributed IGS stations (illustrated in
Figure 4) to solve the post-processing kinematic PPP results with a 7-day arc length to verify the effect of DBD existing in the original precise product on the PPP. Phase center offset/phase center variation (PCO/PCV) corrections for both satellites and receivers were applied according to the IGS conversions. Tide effects involving solid earth tides, ocean loading, and polar motion were corrected based on the International Earth Rotation and Reference Systems Service (IERS) conversions (2010). The effects of phase wind-up, earth’s rotation, and relativity were also corrected during PPP processing. More details of the PPP configurations are summarized in
Table 2.
Boundary and non-boundary positioning performance is statistically used to analyze the impact of product DBD. The definitions for the boundary are divided into three types: 5, 15, and 60 min between days. 5 min represents the midnight 00:00 epoch, 15 min is aligned with the missing part of the last 15 min of the daily orbit product, and 60 min is aligned with the time period for which concerned by the orbit interpolation method is concerned.
Figure 5 depicts the accuracy performance at the boundary and non-boundary after PPP solving with six ACs’ products, while
Table 3 provides statistics on the PPP 1D-RMS accuracy.
Figure 5 and
Table 3 show that PPP positioning in non-boundary time has better accuracy performance, regardless of the defined range at the boundary. Corresponding to the DBD of each AC orbit product in the previous section, the accuracy loss near the boundary is slightly smaller using inter-day solved products than using EMR, ESA, GFZ single-day solved products. The results show that the precise products do suffer from non-negligible jumps near the boundary, which can reduce the positioning accuracy for subsequent applications.
4. Orbit Discontinuities Calibration and Validation
In this section, calibrated GPS precise products were used to perform post-processing kinematic PPP and dynamic and kinematic LEO POD results near the day boundary. The weekly solution files provided by IGS are used as reference coordinates for the PPP results, and the precision scientific orbits provided by JPL are used as reference coordinates for the LEO POD. Three types of GPS precise products were utilized as inputs, and their accuracy and smoothness were compared to determine whether the proposed calibration method can mitigate the DBD effect. These inputs are described as follows:
Input I: Original orbit and clock offset products without any change.
Input II: Equal-weighted calibrated orbit and clock offset after modifying the orbital radial direction.
Input III: Time-weighted calibrated orbit and clock offset after modifying the orbital radial direction.
4.1. Post-Processing Kinematic PPP
Figure 6 uses the first day of YAKT as an illustration of the time series variation near its daily boundary. Subplot (a) depicts the time series within 15 min before and after the boundary point, while subplot (b) depicts the time series before and after the boundary point.
It can be seen from the figures that the uncalibrated products have obvious accuracy loss near the boundary, while the calibrated products can all effectively reduce the jump phenomenon near the boundary so that the accuracy at the boundary is compared to that at the non-boundary location, which is particularly evident in subplot (b). The time-weighted calibrated method has a more gradual effect than the equal-weighted calibration, and there is no significant change in positioning accuracy. In addition, the method does not have the issue where the calibration is too extreme at both ends of the daily boundary range and results in excessive errors.
In
Table 4, the 1D-RMS differences of the kinematic PPP of the three schemes are counted near the boundary with the non-boundary, and the boundary range is defined as 15 min preceding and following each boundary point. It is evident that the application of both calibration techniques can effectively reduce the effect of DBD. For COD, JPL inter-day orbit solutions, the maximum improvement is only 2 mm, whereas for EMR, ESA, and GFZ single-day solution precision orbits with larger DBD, the maximum improvement can reach 9 mm, and the maximum reduction rate of the difference in accuracy between boundary and non-boundary is 41%.
4.2. Dynamic LEO POD
The LEO POD is solved by the least squares method for the non-differential ionospheric-free combined GPS observations. The Macro solar pressure model [
49] and the DTM9 atmospheric drag model [
50] were adopted. The phase center offset correction for LEO satellite receivers is referred to in the GRACE manual [
51]. More details of the force models, observation models, and parameters to be estimated in dynamic and kinematic LEO POD are shown in
Table 5. The force model in
Table 5 is useless for kinematic LEO POD.
Analysis of the dynamic GRACE-A orbit is performed here.
Figure 7 depicts the LEO orbit 1D-RMS time series obtained using precise GPS products as inputs. Subplot (a) depicts the time series within 15 min preceding and following the boundary point, and subplot (b) depicts the time series within 5 min preceding and following the boundary point.
Figure 8 depicts the 1D-RMS statistics for 15 min surrounding daily boundary points, which were solved for multiple days.
Table 6 depicts their values and enhancement rates.
The calibration of the GPS precise orbit and the clock offset product causes a slight change in the accuracy of the LEO precise orbit. However, the time series oscillation of the 1D-RMS is reduced within 15 min or 5 min preceding and following the boundary point. Specifically, as illustrated in subfigure (b), the precision of the boundary point can be roughly consistent with 5 min before and after. The violent jump at the boundary has been drastically reduced.
In
Figure 8 and
Table 6, despite the fact that the GPS product DBD improvement exceeds 2 cm, the softening effect of the force parameters in the LEO dynamic orbit determination process has a certain weakening effect on the GPS DBD, causing the maximum dynamic orbit DBD improvement to reach only 3 mm, with a maximum average improvement rate of 9.4%. The method of equal-weighted calibration of GPS products is more effective, whereas the effect of time-weighted calibration is more gradual, particularly at the two ends of the period, which are closer to the original orbit.
4.3. Kinematic LEO POD
The LEO kinematic orbit analysis method is identical to that described for the dynamic orbit, and the same day time series is chosen for comparison and analysis.
Figure 9 depicts the time series of kinematic orbit errors.
LEO DBD is not only associated with the GPS product DBD, but also with the LEO orbit-solving precision.
Figure 9 shows that the improvement is more evident due to the lower accuracy of the kinematic orbit compared to the dynamic orbit. When using the single-day solution product such as ESA in subplot (b), the noticeable inconsistency in accuracy that occurs when utilizing the original product is significantly reduced.
Figure 10 depicts the 1D-RMS statistics for 15 min surrounding the daily boundary point, which were solved for multiple days.
Table 7 displays their values and enhancement rates. This study’s proposed calibration method also performs better in the kinematic LEO orbit, with a maximum reduction of 13 mm in DBD and a 20% improvement in accuracy variation at the boundary.
5. Conclusions
In this study, we first evaluate the DBD of GPS orbit products from various analysis centers and then evaluate the impact of GPS orbit DBD by comparing the accuracy results of post-processing kinematic PPP at both the boundary and non-boundary. Then, the orbit products are calibrated using both equal-weighted and time-weighted methods, and the orbit variation is corrected to the clock offset synchronously to ensure consistency. Finally, post-processing kinematic PPP, dynamitic LEO POD, kinematic LEO POD experiments are conducted to verify the efficacy of the method proposed in this paper.
There is a high level of consistency across analysis centers, but product DBDs vary. In addition to the effect of different force models and the error correction method, the DBD of products with inter-day solutions is less than that of products with single-day solutions. Products from the COD showed the best continuity, while those from the EMR performed the worst. During the verification of the effect of the GPS product’s DBD, it was determined that the user side’s accuracy performance at the boundary is consistent with the difference in the product’s DBD. The accuracy difference between products using inter-day solutions near the day boundary and non-boundary is significantly smaller than that of using single-day solutions.
Experiments on verification demonstrate that the correction method described in this paper can effectively mitigate the problem of accuracy degradation at the application boundary. For kinematic PPP, dynamic LEO POD and kinematic LEO POD, the maximum difference between boundary and non-boundary accuracy can be reduced by 9, 3, and 13 mm, respectively, with the improvement of 41.5%, 9.4%, and 20.5%. The rate of improvement is primarily dependent on the precision of the experiment and is unrelated to the accuracy difference reduction, as in the case of the kinematic LEO POD, which has an accuracy difference reduction of 13 mm despite the improvement being only 20.5%. The reason why the improvement for dynamitic is significantly less than for the other two validation schemes is that dynamitic LEO POD processing has a smoothing effect, so the minor improvements to the GPS products described in this paper will be diminished.
Although we have high-quality GPS products, the effects of DBD are still unavoidable and visible from the user’s perspective. Therefore, they must also be corrected [
17]. The method presented in this paper, which is implemented on GPS products, is capable of achieving significant enhancements and has wide applicability without requiring complicated operations.