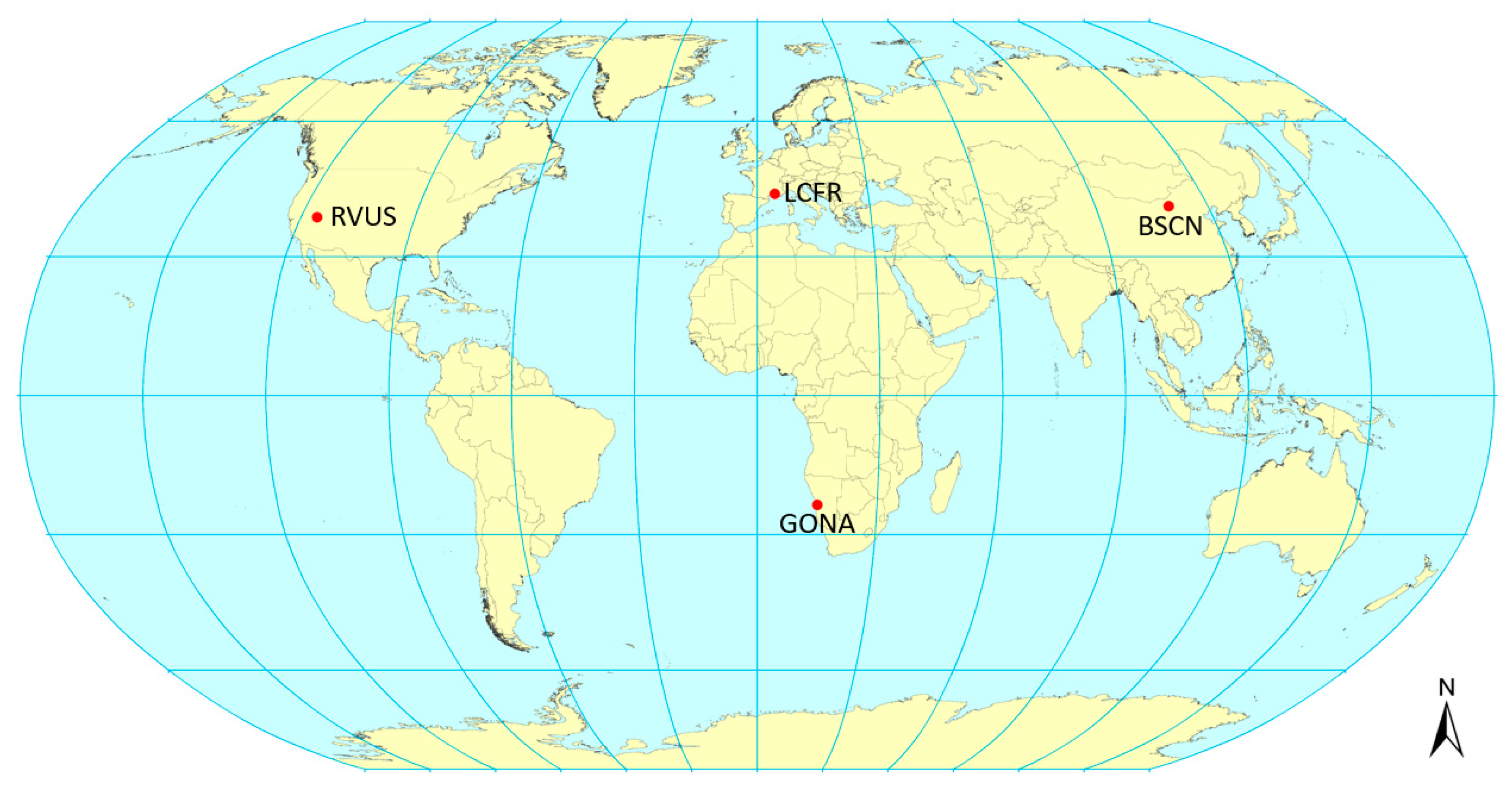
Figure 1.
Global distribution for four sites of RadCalNet.
Figure 1.
Global distribution for four sites of RadCalNet.
Figure 2.
Remote sensing images for four sites of RadCalNet with the ground core region indicated by the red square.
Figure 2.
Remote sensing images for four sites of RadCalNet with the ground core region indicated by the red square.
Figure 3.
Spectral response function for each band of ETM+, OLI, and MSI sensors (For the purpose of this article, only VNIR, SWIR1, and SWIR2 bands are displayed).
Figure 3.
Spectral response function for each band of ETM+, OLI, and MSI sensors (For the purpose of this article, only VNIR, SWIR1, and SWIR2 bands are displayed).
Figure 4.
TOA reflectance before SAF adjustment of the combined data.
Figure 4.
TOA reflectance before SAF adjustment of the combined data.
Figure 5.
TOA reflectance after SAF adjustment of the combined data.
Figure 5.
TOA reflectance after SAF adjustment of the combined data.
Figure 6.
TOA reflectance after BRDF correction of GONA.
Figure 6.
TOA reflectance after BRDF correction of GONA.
Figure 7.
TOA reflectance after weight adjustment of the combined data of GONA.
Figure 7.
TOA reflectance after weight adjustment of the combined data of GONA.
Figure 8.
Test of abrupt change points for the combined TOA data of GONA.
Figure 8.
Test of abrupt change points for the combined TOA data of GONA.
Figure 9.
Test of abrupt change points for the combined BOA data of GONA.
Figure 9.
Test of abrupt change points for the combined BOA data of GONA.
Figure 10.
Test of abrupt change points for the combined TOA data of BSCN.
Figure 10.
Test of abrupt change points for the combined TOA data of BSCN.
Figure 11.
Test of abrupt change points for the combined BOA data of BSCN.
Figure 11.
Test of abrupt change points for the combined BOA data of BSCN.
Figure 12.
Test of abrupt change points for the combined TOA data of RVUS.
Figure 12.
Test of abrupt change points for the combined TOA data of RVUS.
Figure 13.
Test of abrupt change points for the combined BOA data of RVUS.
Figure 13.
Test of abrupt change points for the combined BOA data of RVUS.
Figure 14.
Test of abrupt change points for the combined TOA data of LCFR (winter and spring).
Figure 14.
Test of abrupt change points for the combined TOA data of LCFR (winter and spring).
Figure 15.
Test of abrupt change points for the combined BOA data of LCFR (winter and spring).
Figure 15.
Test of abrupt change points for the combined BOA data of LCFR (winter and spring).
Figure 16.
Test of abrupt change points for the combined TOA data of LCFR (summer and autumn).
Figure 16.
Test of abrupt change points for the combined TOA data of LCFR (summer and autumn).
Figure 17.
Test of abrupt change points for the combined BOA data of LCFR (summer and autumn).
Figure 17.
Test of abrupt change points for the combined BOA data of LCFR (summer and autumn).
Table 1.
Time series range of BOA and TOA of RadCalNet.
Table 1.
Time series range of BOA and TOA of RadCalNet.
| Region | Time Series Range of BOA
(yyyy.mm.dd) | Time Series Range of TOA
(yyyy.mm.dd) |
|---|
| BSCN | 2017.06.01–2023.01.01 | 2017.01.01–2023.01.01 |
| LCFR | 2015.01.01–2023.01.01 | 2015.01.01–2023.01.01 |
| RVUS | 2013.04.01–2023.01.01 | 2013.01.01–2023.01.01 |
| GONA | 2017.07.01–2023.01.01 | 2017.01.01–2023.01.01 |
Table 2.
Total average uncertainty of RadCalNet.
Table 2.
Total average uncertainty of RadCalNet.
| Bands | BSCN | GONA | LCFR
(Winter and Spring) | LCFR
(Summer and Autumn) | RVUS |
|---|
| Blue | 6.04 | 2.62 | 6.34 | 4.64 | 6.14 |
| Green | 5.56 | 2.88 | 6.00 | 6.32 | 5.35 |
| Red | 5.39 | 2.96 | 6.26 | 5.62 | 5.36 |
| NIR | 4.56 | 3.25 | 5.96 | 5.55 | 5.60 |
| SWIR1 | 4.94 | 2.67 | 6.55 | 4.85 | 5.39 |
| SWIR2 | 5.02 | 3.13 | 7.20 | 5.35 | 5.88 |
Table 3.
Change point detection using sequential MK test for TOA data of GONA (* p ≤ 0.05).
Table 3.
Change point detection using sequential MK test for TOA data of GONA (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | - | - | 2021 | - | |
| Green | - | - | 2021 | - | |
| Red | - | - | 2021 | - | |
| NIR | 2017 | 2018 * | - | 2022 * | Significant |
| SWIR1 | 2017 | 2018 * | 2021 * | 2022 | Significant |
| SWIR2 | - | - | - | 2022 | |
Table 4.
Change point detection using the sequential MK test for BOA data of GONA (* p ≤ 0.05).
Table 4.
Change point detection using the sequential MK test for BOA data of GONA (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | 2021 * | - | Significant |
| Green | 2021 * | - | Significant |
| Red | 2021 * | - | Significant |
| NIR | - | 2022 * | Significant |
| SWIR1 | 2021 * | - | Significant |
Table 5.
MK trend test and Sen’s slope for TOA and BOA data of GONA (at 0.05 significance level).
Table 5.
MK trend test and Sen’s slope for TOA and BOA data of GONA (at 0.05 significance level).
| Band | p Value | Decision | Slope | p Value | Decision | Slope |
|---|
| TOA | BOA |
|---|
| Blue | 2.50 × 10−5 | Upward trend | 4.926 × 10−6 | 0 | Upward trend | 9.414 × 10−6 |
| Green | 4.50 × 10−6 | Upward trend | 9.578 × 10−6 | 0 | Upward trend | 2.196 × 10−5 |
| Red | 9.50 × 10−7 | Upward trend | 1.523 × 10−5 | 0 | Upward trend | 2.889 × 10−5 |
| NIR | 0.579 | No trend | 1.998 × 10−6 | 0 | Upward trend | 1.733 × 10−5 |
| SWIR1 | 0.553 | No trend | 1.938 × 10−6 | 0 | Upward trend | 1.680 × 10−5 |
| SWIR2 | 0.069 | No trend | 7.544 × 10−6 | | | |
Table 6.
MK trend test and Sen’s slope for each change point for TOA and BOA data of GONA (at 0.05 significance level).
Table 6.
MK trend test and Sen’s slope for each change point for TOA and BOA data of GONA (at 0.05 significance level).
| Band | Period | p Value | Decision | Slope |
|---|
| TOA |
|---|
| NIR | 2017–2018 | 4.528 × 10−8 | Upward trend | 2.296 × 10−4 |
| 2018–2022 | 0.003 | Upward trend | 1.747 × 10−5 |
| SWIR1 | 2017–2018 | 1.676 × 10−5 | Upward trend | 2.628 × 10−4 |
| 2018–2021 | 0.129 | No trend | 1.339 × 10−5 |
| 2021–2022 | 0.006 | Downward trend | –5.694 × 10−5 |
| BOA |
| Blue | 2017–2021 | 4.074 × 10−8 | Upward trend | 7.396 × 10−6 |
| 2021–2022 | 4.883 × 10−8 | Upward trend | 3.062 × 10−5 |
| Green | 2017–2021 | 1.443 × 10−7 | Upward trend | 1.805 × 10−5 |
| 2021–2022 | 1.786 × 10−7 | Upward trend | 2.727 × 10−5 |
| Red | 2017–2021 | 1.175 × 10−6 | Upward trend | 2.118 × 10−5 |
| 2021–2022 | 8.981 × 10−7 | Upward trend | 2.933 × 10−5 |
| NIR | 2017–2021 | 1.430 × 10−8 | Upward trend | 1.256 × 10−5 |
| 2021–2022 | 1.784 × 10−8 | Upward trend | 2.429 × 10−4 |
| SWIR1 | 2017–2021 | 6.428 × 10−3 | Downward trend | –9.085 × 10−6 |
| 2021–2022 | 7.608 × 10−3 | Downward trend | –1.269 × 10−5 |
Table 7.
Change points detected using the sequential MK test for TOA data of BSCN (* p ≤ 0.05).
Table 7.
Change points detected using the sequential MK test for TOA data of BSCN (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | 2017 | - | - | 2020 * | 2022 | Significant |
| Green | 2017 | - | 2019 * | - | 2022 | Significant |
| Red | - | - | 2019 * | 2021 * | 2022 | Significant |
| NIR | 2017 | 2018 * | 2019 * | - | 2022 | Significant |
| SWIR1 | - | - | 2019 * | - | - | Significant |
| SWIR2 | 2017 | 2018 | - | 2021 * | 2022 | Significant |
Table 8.
Change points detected using the sequential MK test for BOA data of BSCN (* p ≤ 0.05).
Table 8.
Change points detected using the sequential MK test for BOA data of BSCN (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | - | 2020 * | - | 2022 | Significant |
| Green | 2018 | 2020 * | - | 2022 | Significant |
| Red | 2018 | - | 2021 | 2022 | |
| NIR | 2018 | - | 2021 | 2022 | |
Table 9.
MK trend test and Sen’s slope of each change point for TOA and BOA data of BSCN (at 0.05 significance level).
Table 9.
MK trend test and Sen’s slope of each change point for TOA and BOA data of BSCN (at 0.05 significance level).
| Band | Period | p Value | Decision | Slope |
|---|
| TOA |
|---|
| Blue | 2017–2020 | 0.005 | Upward trend | 2.511 × 10−5 |
| 2020–2022 | 0.008 | Upward trend | 1.390 × 10−5 |
| Green | 2017–2019 | 0.001 | Upward trend | 3.733 × 10−5 |
| 2019–2022 | 0.001 | Upward trend | 1.331 × 10−5 |
| Red | 2017–2019 | 9.919 × 10−4 | Upward trend | 4.385 × 10−5 |
| 2019–2021 | 0.007 | Upward trend | 4.626 × 10−5 |
| 2021–2022 | 0.008 | Downward trend | −3.361 × 10−5 |
| NIR | 2017–2018 | 0.016 | Upward trend | 3.367 × 10−5 |
| 2018–2022 | 0.008 | Upward trend | 1.180 × 10−5 |
| SWIR1 | 2017–2019 | 9.970 × 10−4 | Upward trend | 4.676 × 10−5 |
| 2019–2022 | 5.154 × 10−4 | Upward trend | 2.508 × 10−5 |
| SWIR2 | 2017–2021 | 2.127 × 10−4 | Downward trend | −3.207 × 10−5 |
| 2021–2022 | 2.890 × 10−4 | Downward trend | −9.895 × 10−5 |
| BOA |
| Blue | 2018–2020 | 0.020 | Downward trend | −4.910 × 10−4 |
| 2020–2022 | 0.004 | Downward trend | −1.812 × 10−4 |
| Green | 2018–2020 | 0.032 | Downward trend | −4.693 × 10−4 |
| 2020–2022 | 0.019 | Downward trend | −1.826 × 10−4 |
Table 10.
Change points detected using the sequential MK test for TOA data of RVUS (* p ≤ 0.05).
Table 10.
Change points detected using the sequential MK test for TOA data of RVUS (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | 2022 * | Significant |
| Green | 2022 * | Significant |
| Red | 2022 * | Significant |
| NIR | 2022 * | Significant |
| SWIR1 | 2022 * | Significant |
| SWIR2 | 2022 * | Significant |
Table 11.
Change points detected using the sequential MK test for BOA data of RVUS (* p ≤ 0.05).
Table 11.
Change points detected using the sequential MK test for BOA data of RVUS (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | 2020 * | - | 2022 * | Significant |
| Green | 2020 * | - | 2022 * | Significant |
| Red | 2020 * | - | 2022 * | Significant |
| NIR | 2020 * | 2021 * | 2022 * | Significant |
| SWIR1 | 2020 * | 2021 * | 2022 * | Significant |
Table 12.
MK trend test and Sen’s slope of each change point for TOA data of RVUS (at 0.05 significance level).
Table 12.
MK trend test and Sen’s slope of each change point for TOA data of RVUS (at 0.05 significance level).
| Band | Period | p Value | Decision | Slope |
|---|
| TOA |
|---|
| Blue | 2013–2022 | 1.701 × 10−11 | Upward trend | 6.332 × 10−5 |
| 2022–2022 | 1.485 × 10−11 | Upward trend | 5.777 × 10−4 |
| Green | 2013–2022 | 4.014 × 10−10 | Upward trend | 6.957 × 10−5 |
| 2022–2022 | 3.963 × 10−9 | Upward trend | 4.323 × 10−4 |
| Red | 2013–2022 | 1.580 × 10−9 | Upward trend | 7.191 × 10−5 |
| 2022–2022 | 1.568 × 10−8 | Upward trend | 4.361 × 10−4 |
| NIR | 2013–2022 | 2.541 × 10−7 | Upward trend | 7.118 × 10−5 |
| 2022–2022 | 1.937 × 10−7 | Upward trend | 4.073 × 10−4 |
| SWIR1 | 2013–2022 | 4.691 × 10−11 | Upward trend | 7.791 × 10−5 |
| 2022–2022 | 3.053 × 10−11 | Upward trend | 6.179 × 10−4 |
| SWIR2 | 2013–2022 | 1.089 × 10−7 | Upward trend | 6.393 × 10−5 |
| 2022–2022 | 6.485 × 10−8 | Upward trend | 1.458 × 10−3 |
| BOA |
| Blue | 2013–2020 | 0 | Downward trend | –3.162 × 10−5 |
| 2020–2022 | 0 | Downward trend | –1.966 × 10−4 |
| Green | 2013–2020 | 0 | Downward trend | –3.587 × 10−5 |
| 2020–2022 | 0 | Downward trend | –2.224 × 10−4 |
| Red | 2013–2020 | 0 | Downward trend | –3.109 × 10−5 |
| 2020–2022 | 0 | Downward trend | –2.536 × 10−4 |
| NIR | 2013–2020 | 0 | Downward trend | –3.340 × 10−5 |
| 2020–2021 | 0.896 | No trend | 6.067 × 10−6 |
| 2021–2022 | 0 | Downward trend | –2.227 × 10−4 |
| SWIR1 | 2013–2020 | 0 | Downward trend | –3.284 × 10−5 |
| 2020–2021 | 2.678 × 10−5 | Upward trend | 3.181 × 10−4 |
| 2021–2022 | 3.427 × 10−4 | Downward trend | –6.497 × 10−5 |
Table 13.
Change points detected using the sequential MK test for TOA data of LCFR (winter and spring) (* p ≤ 0.05).
Table 13.
Change points detected using the sequential MK test for TOA data of LCFR (winter and spring) (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | - | - | 2020 * | - | - | Significant |
| Green | - | 2019 | - | - | - | |
| Red | - | 2019 * | - | - | - | Significant |
| NIR | - | - | - | 2021 | - | |
| SWIR1 | 2016 | 2019 | - | - | 2022 | |
| SWIR2 | 2016 | 2019 | - | - | 2022 | |
Table 14.
Change points detected using the sequential MK test for BOA data of LCFR (winter and spring) (* p ≤ 0.05).
Table 14.
Change points detected using the sequential MK test for BOA data of LCFR (winter and spring) (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | 2015 | 2016 | 2017 * | 2018 * | 2019 * | 2020 | 2021 | 2022 | Significant |
| Green | 2015 * | - | - | - | 2019 | 2020 * | - | - | Significant |
| Red | - | - | 2017 * | - | - | 2020 * | 2021 | - | Significant |
| NIR | 2015 | - | 2017 | - | 2019 * | 2020 * | 2021 | - | Significant |
| SWIR1 | - | - | 2017 | - | - | - | - | - | |
| SWIR2 | - | - | 2017 | - | - | - | - | - | |
Table 15.
MK trend test and Sen’s slope of each change point for TOA and BOA data of LCFR (winter and spring) (at 0.05 significance level).
Table 15.
MK trend test and Sen’s slope of each change point for TOA and BOA data of LCFR (winter and spring) (at 0.05 significance level).
| Band | Period | p Value | Decision | Slope |
|---|
| TOA |
|---|
| Blue | 2015–2020 | 0.047 | Upward trend | 5.199 × 10−5 |
| 2020–2022 | 0.022 | Upward trend | 6.381 × 10−5 |
| Red | 2015–2019 | 0.019 | Upward trend | 1.118 × 10−4 |
| 2019–2022 | 0.047 | Upward trend | 1.200 × 10−4 |
| BOA |
| Blue | 2015–2017 | 0.051 | No trend | 7.253 × 10−5 |
| 2017–2018 | 4.485 × 10−14 | Upward trend | 4.846 × 10−4 |
| 2018–2019 | 0.042 | Upward trend | 8.249 × 10−5 |
| 2019–2022 | 0.007 | Downward trend | –3.735 × 10−5 |
| Green | 2015–2020 | 2.357 × 10−6 | Upward trend | 5.339 × 10−5 |
| 2020–2022 | 0.003 | Upward trend | 2.438 × 10−4 |
| Red | 2015–2017 | 7.52 × 10−4 | Upward trend | 3.879 × 10−4 |
| 2017–2020 | 6.974 × 10−9 | Upward trend | 1.519 × 10−4 |
| 2020–2022 | 7.761 × 10−4 | Upward trend | 2.123 × 10−4 |
| NIR | 2015–2019 | 0.011 | Downward trend | –4.408 × 10−5 |
| 2019–2020 | 0.023 | Upward trend | 3.501 × 10−4 |
| 2020–2022 | 0.037 | Upward trend | 2.837 × 10−4 |
Table 16.
Change points detected using the sequential MK test for TOA data of LCFR (summer and autumn) (* p ≤ 0.05).
Table 16.
Change points detected using the sequential MK test for TOA data of LCFR (summer and autumn) (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | 2015 | 2016 * | 2019 * | - | - | Significant |
| Green | - | - | - | 2020 | 2022 * | Significant |
| Red | - | - | - | 2020 | - | |
| NIR | - | - | - | 2020 * | - | Significant |
| SWIR1 | - | - | - | 2020 | - | |
| SWIR2 | - | - | 2019 | - | 2022 * | Significant |
Table 17.
Change points detected using the sequential MK test for BOA data of LCFR (summer and autumn) (* p ≤ 0.05).
Table 17.
Change points detected using the sequential MK test for BOA data of LCFR (summer and autumn) (* p ≤ 0.05).
| Band | Detected Change Points (Year) | Remarks |
|---|
| Blue | - | - | 2019 | - | - | |
| Green | 2015 * | - | - | 2020 | - | Significant |
| Red | 2015 * | - | 2019 * | 2020 | - | Significant |
| NIR | - | 2016 * | - | 2020 | - | Significant |
| SWIR1 | 2015 | 2016 * | 2019 * | 2020 * | 2021 | Significant |
| SWIR2 | 2015 | 2016 * | 2019 * | 2020 * | 2021 | Significant |
Table 18.
MK trend test and Sen’s slope of each change point for TOA and BOA data of LCFR (summer and autumn) (at 0.05 significance level).
Table 18.
MK trend test and Sen’s slope of each change point for TOA and BOA data of LCFR (summer and autumn) (at 0.05 significance level).
| Band | Period | p Value | Decision | Slope |
|---|
| TOA |
|---|
| Blue | 2015–2016 | 0.029 | Downward trend | –1.516 × 10−4 |
| 2016–2019 | 9.257 × 10−4 | Upward trend | 7.877 × 10−4 |
| 2019–2022 | 1.253 × 10−6 | Upward trend | 6.736 × 10−5 |
| Green | 2015–2022 | 6.880 × 10−6 | Downward trend | –5.628 × 10−5 |
| NIR | 2015–2020 | 2.258 × 10−4 | Upward trend | 1.401 × 10−4 |
| 2020–2022 | 3.525 × 10−3 | Upward trend | 9.900 × 10−5 |
| SWIR2 | 2015–2022 | 1.297 × 10−3 | Downward trend | –9.159 × 10−5 |
| BOA |
| Green | 2015–2022 | 2.500 × 10−7 | Downward trend | –6.184 × 10−5 |
| Red | 2015–2019 | 0.950 | No trend | –2.585 × 10−6 |
| 2019–2022 | 0.007 | Upward trend | 1.756 × 10−4 |
| NIR | 2015–2016 | 4.853 × 10−4 | Downward trend | –2.316 × 10−4 |
| 2016–2022 | 4.198 × 10−4 | Downward trend | –5.463 × 10−5 |
| SWIR1 | 2015–2016 | 0.078 | No trend | –3.518 × 10−4 |
| 2016–2019 | 0.516 | No trend | 2.541 × 10−5 |
| 2019–2020 | 0.620 | No trend | –3.677 × 10−4 |
| 2020–2022 | 0.016 | Upward trend | 2.346 × 10−4 |
| SWIR2 | 2015–2016 | 0.046 | Downward trend | –4.589 × 10−4 |
| 2016–2019 | 0.511 | No trend | 2.515 × 10−5 |
| 2019–2020 | 0.448 | No trend | 7.171 × 10−4 |
| 2020–2022 | 0.034 | Upward trend | 2.299 × 10−4 |
Table 19.
MK trend test and Sen’s slope for TOA and BOA data of BSCN, RVUS, and LCFR (at 0.05 significance level, * indicates instances where the reflectance of the corresponding wavelength was not provided).
Table 19.
MK trend test and Sen’s slope for TOA and BOA data of BSCN, RVUS, and LCFR (at 0.05 significance level, * indicates instances where the reflectance of the corresponding wavelength was not provided).
| Band | p Value | Decision | Slope | p Value | Decision | Slope |
|---|
| TOA | BOA |
|---|
| BSCN |
|---|
| Blue | 0.477 | No trend | –1.770 × 10−6 | 0.114 | No trend | 8.818 × 10−5 |
| Green | 0.500 | No trend | –1.089 × 10−6 | 0.803 | No trend | 1.762 × 10−5 |
| Red | 0.037 | Downward trend | –6.036 × 10−6 | 0.543 | No trend | –3.514 × 10−5 |
| NIR | 0.622 | No trend | 9.716 × 10−7 | 0.789 | No trend | 1.351 × 10−5 |
| SWIR1 | 0.003 | Downward trend | –9.509 × 10−6 | * | * | * |
| SWIR2 | 0.064 | No trend | –9.374 × 10−6 | * | * | * |
| RVUS |
| Blue | 0 | Upward trend | 9.543 × 10−5 | 4.755 × 10−9 | Upward trend | 1.574 × 10−5 |
| Green | 0 | Upward trend | 1.082 × 10−4 | 1.711 × 10−9 | Upward trend | 1.712 × 10−5 |
| Red | 0 | Upward trend | 1.136 × 10−4 | 2.727 × 10−9 | Upward trend | 1.611 × 10−5 |
| NIR | 0 | Upward trend | 1.286 × 10−4 | 9.523 × 10−8 | Upward trend | 1.504 × 10−5 |
| SWIR1 | 0 | Upward trend | 1.039 × 10−4 | 2.975 × 10−4 | Upward trend | 9.031 × 10−6 |
| SWIR2 | 4.440 × 10−16 | Upward trend | 8.553 × 10−5 | * | * | * |
| LCFR (winter and spring) |
| Blue | 0.078 | No trend | –1.947 × 10−5 | 0.870 | No trend | 1.131 × 10−6 |
| Green | 3.801 × 10−4 | Downward trend | –4.333 × 10−5 | 0.162 | No trend | 9.721 × 10−6 |
| Red | 2.192 × 10−4 | Downward trend | –7.812 × 10−5 | 0.051 | No trend | 2.391 × 10−5 |
| NIR | 0.010 | Downward trend | –7.211 × 10−5 | 0.836 | No trend | –2.707 × 10−6 |
| SWIR1 | 0.249 | No trend | –5.912 × 10−5 | 4.330 × 10−9 | Upward trend | 1.119 × 10−4 |
| SWIR2 | 0.311 | No trend | –3.248 × 10−5 | 2.648 × 10−9 | Upward trend | 1.126 × 10−4 |
| LCFR (summer and autumn) |
| Blue | 0.164 | No trend | –7.678 × 10−6 | 6.797 × 10−5 | Downward trend | –3.194 × 10−5 |
| Green | 3.801 × 10−4 | Downward trend | –3.552 × 10−5 | 4.415 × 10−3 | Downward trend | –3.076 × 10−5 |
| Red | 1.424 × 10−5 | Downward trend | –9.603 × 10−5 | 0.053 | No trend | –3.233 × 10−5 |
| NIR | 0.008 | Downward trend | –4.468 × 10−5 | 5.281 × 10−8 | Downward trend | –5.380 × 10−5 |
| SWIR1 | 2.174 × 10−5 | Downward trend | –8.992 × 10−5 | 0.279 | No trend | 1.781 × 10−5 |
| SWIR2 | 0.007 | Downward trend | –6.249 × 10−5 | 0.231 | No trend | 2.013 × 10−5 |
Table 20.
Annual percentage change in TOA and BOA data over the study period (- represents insufficient evidence to support monotonous trends. * indicates instances where the reflectance of the corresponding wavelength range was not provided by the site instrument).
Table 20.
Annual percentage change in TOA and BOA data over the study period (- represents insufficient evidence to support monotonous trends. * indicates instances where the reflectance of the corresponding wavelength range was not provided by the site instrument).
| Band | GONA | BSCN | RVUS | LCFR
(Winter and Spring) | LCFR
(Summer and Autumn) |
|---|
| TOA |
|---|
| Blue | 0.172 | - | 1.788 | - | - |
| Green | 0.283 | - | 1.702 | –0.615 | –0.580 |
| Red | 0.323 | –0.153 | 1.566 | –0.978 | –1.133 |
| NIR | - | - | 1.567 | –0.416 | –0.425 |
| SWIR1 | - | –0.149 | 1.142 | - | –0.614 |
| SWIR2 | - | - | 1.126 | - | –0.589 |
| BOA |
| Blue | 0.914 | - | 0.801 | - | –1.324 |
| Green | 1.293 | - | 0.676 | - | –0.858 |
| Red | 0.957 | - | 0.579 | - | - |
| NIR | 0.731 | - | 0.498 | - | –0.682 |
| SWIR1 | 0.569 | * | 0.282 | 1.144 | - |
| SWIR2 | * | * | * | 1.803 | - |
Table 21.
Ratio of CV and Gi meeting conditions at each site of RadCalNet during the operation (The condition of CV is less than 3%, and of Gi* greater than 0).
Table 21.
Ratio of CV and Gi meeting conditions at each site of RadCalNet during the operation (The condition of CV is less than 3%, and of Gi* greater than 0).
| Site | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|
| CV ratio |
|---|
| GONA | 1.000 | 1.000 | 0.998 | 0.998 | 0.988 | 0.988 |
| BSCN | 0.948 | 0.939 | 0.911 | 0.943 | 0.916 | 0.886 |
| RVUS | 0.998 | 0.997 | 0.997 | 0.995 | 0.971 | 0.969 |
| LCFR | 0.981 | 0.960 | 0.799 | 0.925 | 0.939 | 0.813 |
| Gi* ratio |
| GONA | 0.998 | 0.998 | 0.998 | 0.996 | 0.996 | 0.979 |
| BSCN | 0.916 | 0.939 | 0.946 | 0.911 | 0.986 | 0.988 |
| RVUS | 0.920 | 0.957 | 0.965 | 0.922 | 0.915 | 0.674 |
| LCFR | 0.962 | 0.976 | 0.986 | 0.582 | 0.995 | 0.991 |