Estimation of Instantaneous Air Temperature under All-Weather Conditions Based on MODIS Products in North and Southwest China
Abstract
:1. Introduction
2. Study Area and Materials
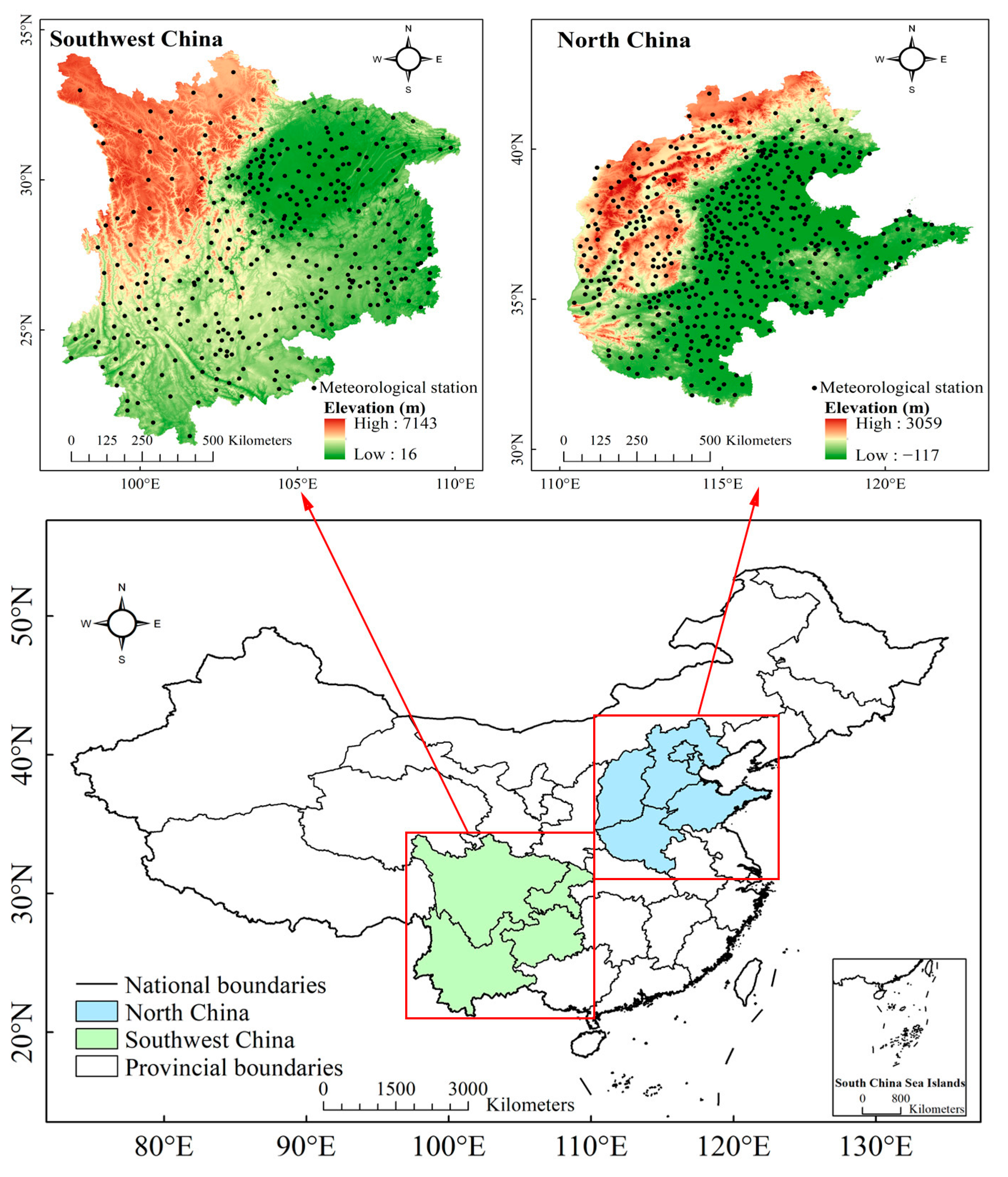
2.1. Study Area
2.1.1. North China
2.1.2. Southwest China
2.2. Datasets
2.2.1. MODIS Datasets
2.2.2. Meteorological and Digital Elevation Model Datasets
3. Methodology
3.1. Estimation of Instantaneous under Clear Sky Conditions
3.1.1. Atmospheric Profile Extrapolation
3.1.2. Average Method
3.1.3. Multiple Linear Regression Model
3.2. Estimation of Instantaneous under Cloudy Sky Conditions
3.2.1. Simple Linear Regression Model
3.2.2. Multiple Linear Regression Model
3.3. Statistical Metrics
4. Results
4.1. Accuracy of Instantaneous Estimation under Clear Sky Conditions
4.1.1. Atmospheric Profile Extrapolation and Average Method
4.1.2. Multiple Linear Regression Model
4.2. Accuracy of Instantaneous Estimation under Cloudy Sky Conditions
4.2.1. Simple Linear Regression Model
4.2.2. Multiple Linear Regression Model
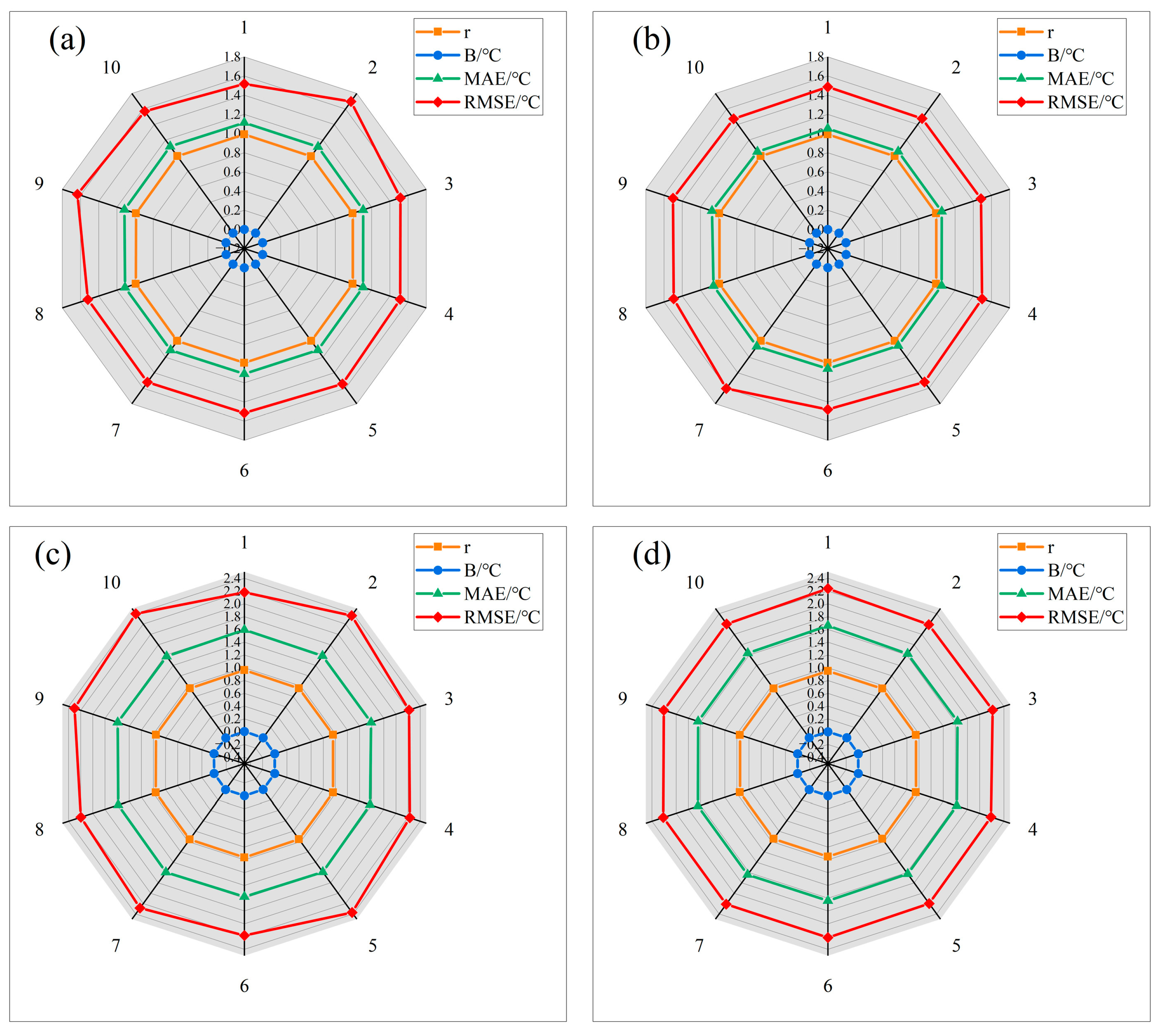
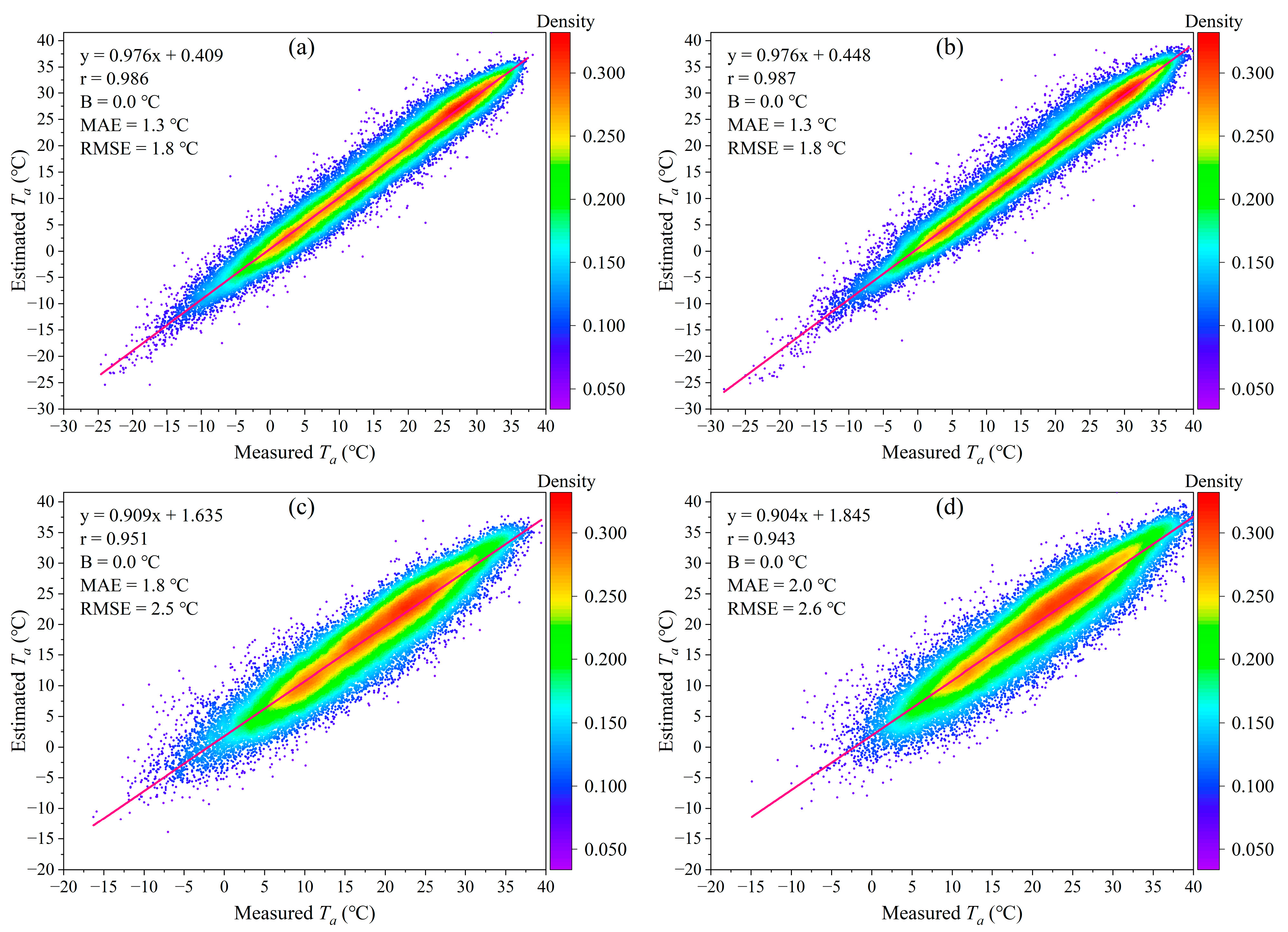
4.3. Accuracy of Instantaneous Estimation under All-Weather Conditions
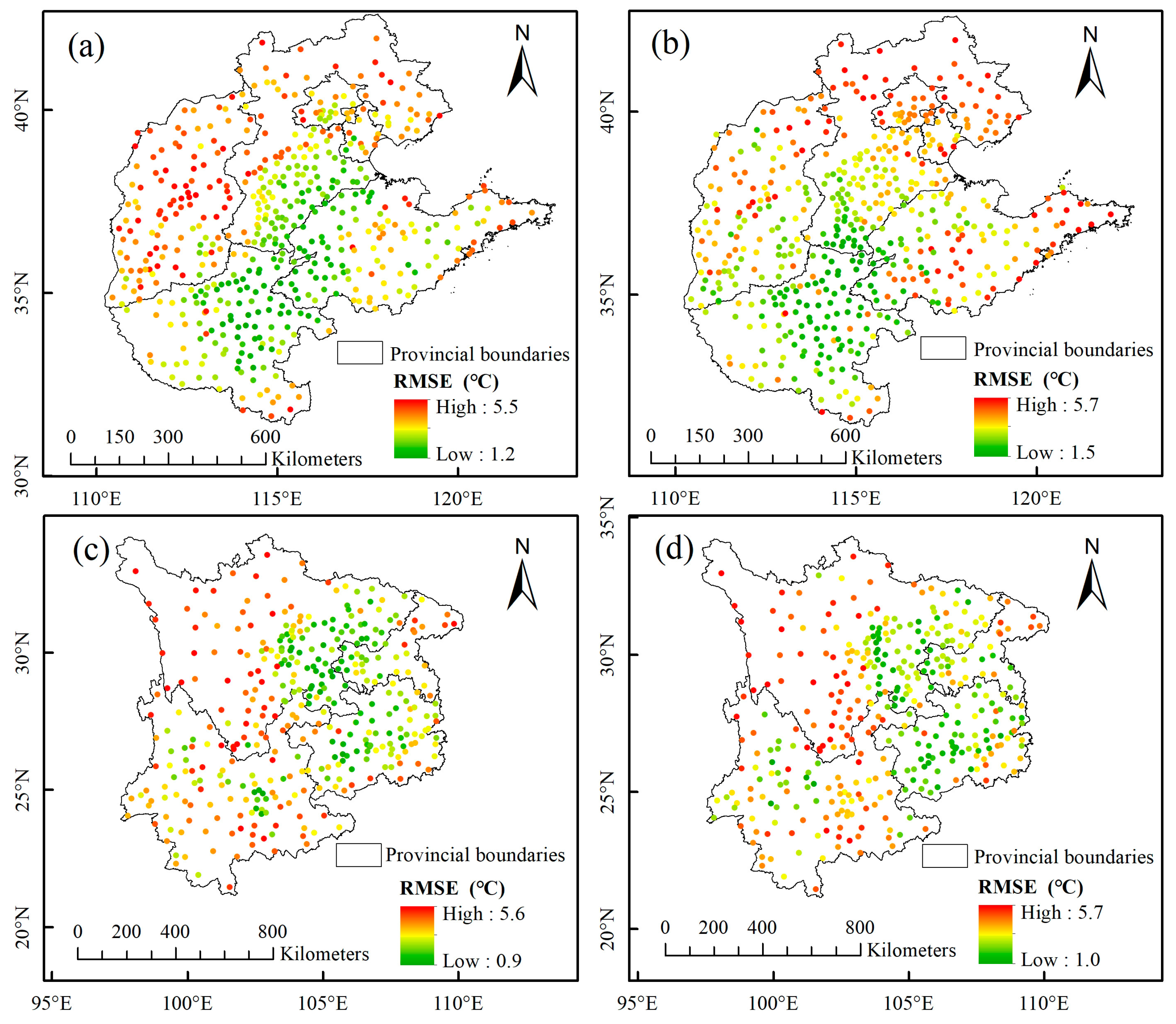
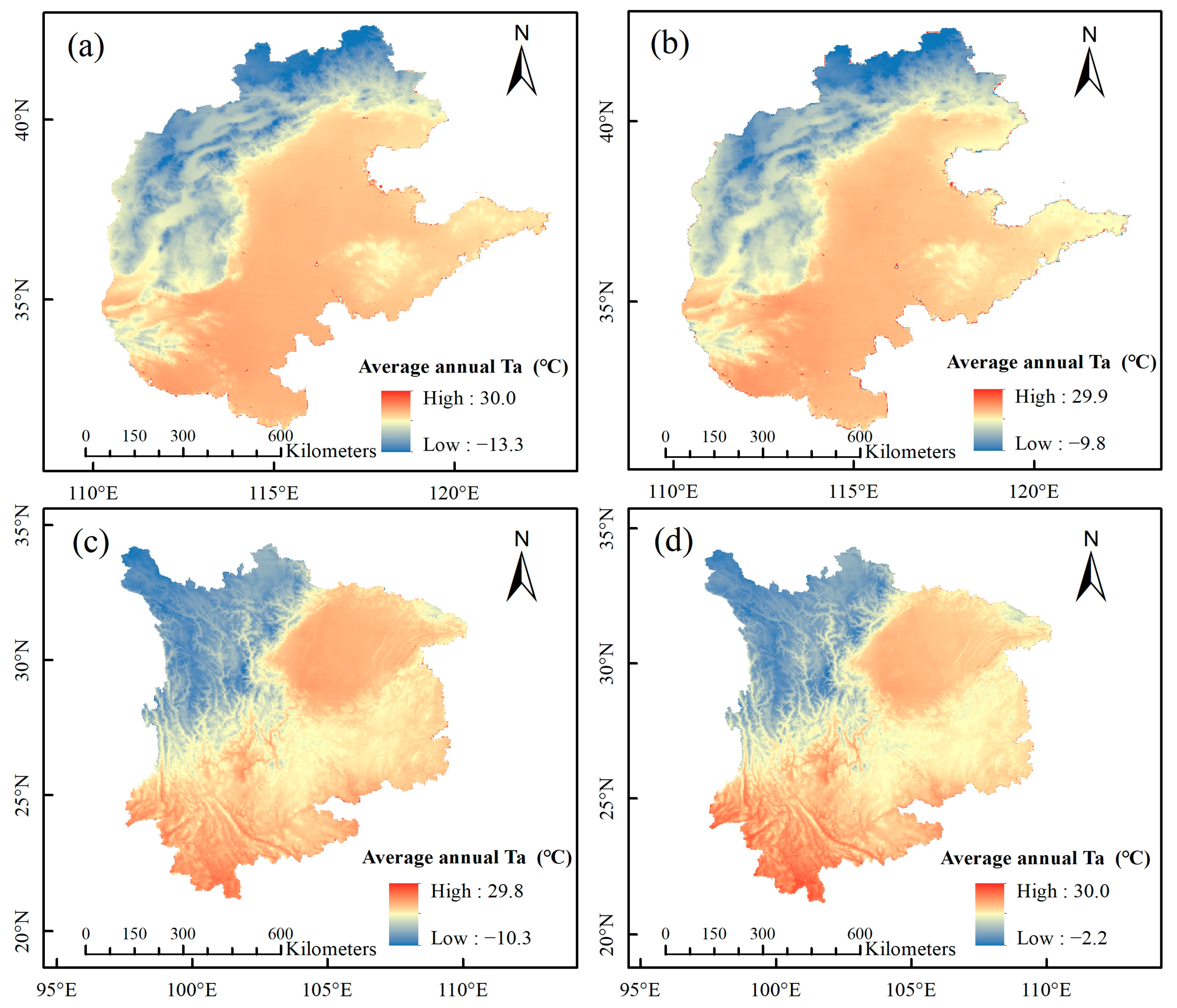
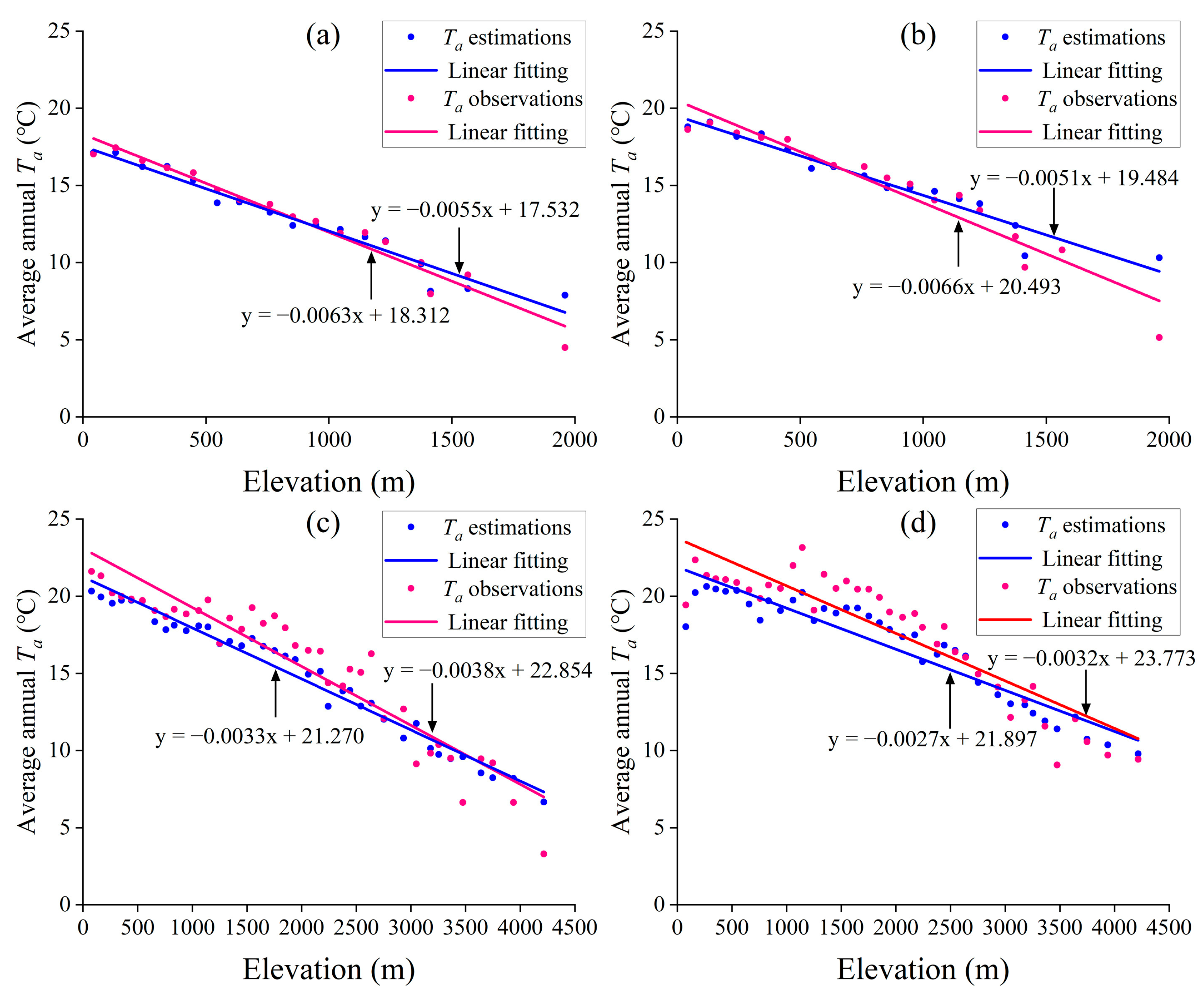
4.4. Spatial Distribution of in North and Southwest China
5. Discussion
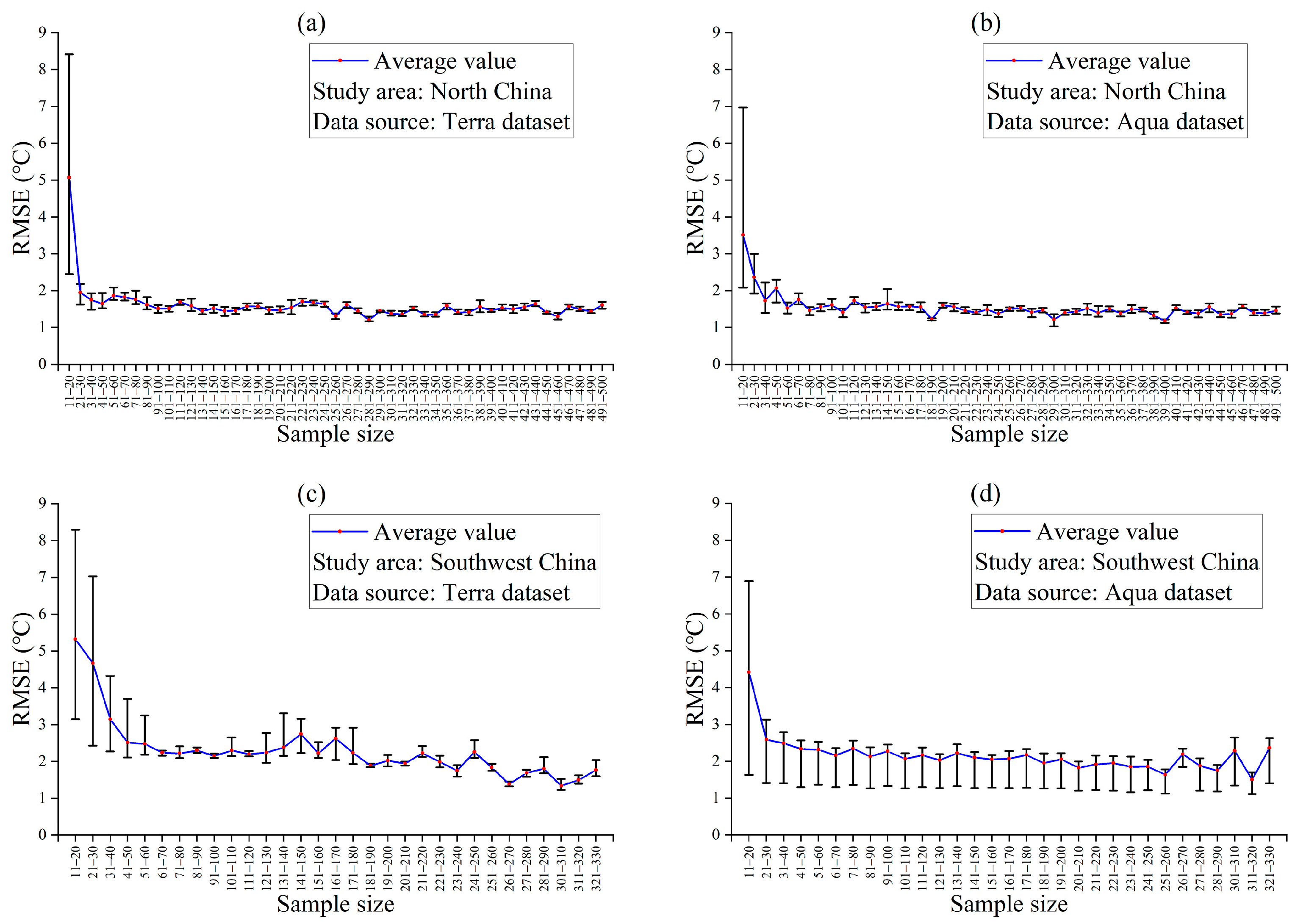
5.1. Effect of Sample Size on the Multiple Linear Regression Model
5.2. The Correlation of Variables and Relative Importance of Each Independent Variable
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Bi, X.; Luan, Q.; Li, Z. Estimation of Daily and Instantaneous Near-Surface Air Temperature from MODIS Data Using Machine Learning Methods in the Jingjinji Area of China. Remote Sens. 2022, 14, 1916. [Google Scholar] [CrossRef]
- Nieto, H.; Sandholt, I.; Aguado, I.; Chuvieco, E.; Stisen, S. Air temperature estimation with MSG-SEVIRI data: Calibration and validation of the TVX algorithm for the Iberian Peninsula. Remote Sens. Environ. 2011, 115, 107–116. [Google Scholar] [CrossRef]
- Lofgren, B.M.; Hunter, T.S.; Wilbarger, J. Effects of using air temperature as a proxy for potential evapotranspiration in climate change scenarios of Great Lakes basin hydrology. Great Lakes Res. 2011, 37, 744–752. [Google Scholar] [CrossRef]
- Harvell, C.D.; Mitchell, C.E.; Ward, J.R.; Altizer, S.; Dobson, A.P.; Ostfeld, R.S.; Samuel, M.D. Climate warming and disease risks for terrestrial and marine biota (Review). Science 2002, 296, 2158–2162. [Google Scholar] [CrossRef]
- Westerling, A.L.; Hidalgo, H.G.; Cayan, D.R.; Swetnam, T.W. Warming and Earlier Spring Increase Western U.S. Forest Wildfire Activity. Science 2006, 313, 940–943. [Google Scholar] [CrossRef]
- Yoo, C.; Im, J.; Park, S.; Quackenbush, L.J. Estimation of daily maximum and minimum air temperatures in urban landscapes using MODIS time series satellite data. ISPRS-J. Photogramm. Remote Sens. 2018, 137, 149–162. [Google Scholar] [CrossRef]
- Shamir, E.; Georgakakos, K.P. MODIS Land Surface Temperature as an Index of Surface Air Temperature for Operational Snowpack Estimation. Remote Sens. Environ. 2014, 152, 83–98. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Asplin, M.G.; Floyer, J.A.; McKendry, I.G.; Moore, R.D.; Stahl, K. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar]
- Wloczyk, C.; Borg, E.; Richter, R.; Miegel, K. Estimation of instantaneous air temperature above vegetation and soil surfaces from Landsat 7 ETM+ data in northern Germany. Int. J. Remote Sens. 2011, 32, 9119–9136. [Google Scholar] [CrossRef]
- Williamson, S.N.; Hik, D.S.; Gamon, J.A.; Kavanaugh, J.L.; Flowers, G.E. Estimating Temperature Fields from MODIS Land Surface Temperature and Air Temperature Observations in a Sub-Arctic Alpine Environment. Remote Sens. 2014, 6, 946–963. [Google Scholar] [CrossRef]
- Kloog, I.; Chudnovsky, A.; Koutrakis, P.; Schwartz, J. Temporal and spatial assessments of minimum air temperature using satellite surface temperature measurements in Massachusetts, USA. Remote Sens. Environ. 2012, 432, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Czakowski, K.P.; Goward, S.N. Thermal Remote Sensing of Near Surface Environmental Variables: Application Over the Oklahoma. Prof. Geogr. 2000, 52, 345. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Zhu, W.; Lu, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Sun, L.; Sun, R.; Li, X.; Liang, S.; Zhang, R. Monitoring surface soil moisture status based on remotely sensed surface temperature and vegetation index information. Agric. For. Meteorol. 2012, 166–167, 175–187. [Google Scholar] [CrossRef]
- Zhang, R.; Rong, Y.; Tian, J.; Su, H.; Li, Z.; Liu, S. A Remote Sensing Method for Estimating Surface Air Temperature and Surface Vapor Pressure on a Regional Scale. Remote Sens. 2015, 7, 6005–6025. [Google Scholar] [CrossRef]
- Pape, R.; Lffler, J. Modelling spatio-temporal near-surface temperature variation in high mountain landscapes. Ecol. Model. 2004, 178, 483–501. [Google Scholar] [CrossRef]
- Bhati, S.; Mohan, M. WRF model evaluation for the urban heat island assessment under varying land use/land cover and reference site conditions. Theor. Appl. Climatol. 2016, 126, 385–400. [Google Scholar] [CrossRef]
- Chen, F.; Yang, X.; Zhu, W. WRF simulations of urban heat island under hot-weather synoptic conditions: The case study of Hangzhou City, China. Atmos. Res. 2014, 138, 364–377. [Google Scholar] [CrossRef]
- Noi, P.T.; Kappas, M.; Degener, J. Estimating Daily Maximum and Minimum Land Air Surface Temperature Using MODIS Land Surface Temperature Data and Ground Truth Data in Northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating Air Surface Temperature in Portugal Using MODIS Lst Data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2017, 37, 1181–1194. [Google Scholar] [CrossRef]
- Hrisko, J.; Ramamurthy, P.; Yu, Y.Y.; Yu, P.; Melecio-Vazquez, D. Urban air temperature model using GOES-16 LST and a diurnal regressive neural network algorithm. Remote Sens. Environ. 2020, 237, 111495. [Google Scholar] [CrossRef]
- Ruiz-Álvarez, M.; Alonso-Sarria, F.; Gomariz-Castillo, F. Interpolation of instantaneous air temperature using geographical and MODIS derived variables with machine learning techniques. ISPRS Int. J. Geo Inf. 2019, 8, 382. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.C.; Huang, X.; Li, L.; Sun, J.; Wu, X.J.; Jiang, W.X. Developing a temporally accurate air temperature dataset for Mainland China. Sci. Total Environ. 2020, 706, 136037. [Google Scholar] [CrossRef]
- Peón, J.; Recondo, C.; Calleja, J.F. Improvements in the estimation of daily minimum air temperature in peninsular Spain using MODIS land surface temperature. Int. J. Remote Sens. 2014, 35, 5148–5166. [Google Scholar] [CrossRef]
- Recondo, C.; Corbea-Pérez, A.; Peón, J.; Pendás, E.; Ramos, M.; Calleja, J.F.; Pablo, M.Á.d.; Fernández, S.; Corrales, J.A. Empirical Models for Estimating Air Temperature Using MODIS Land Surface Temperature (and Spatiotemporal Variables) in the Hurd Peninsula of Livingston Island, Antarctica, between 2000 and 2016. Remote Sens. 2022, 14, 3206. [Google Scholar] [CrossRef]
- Bisht, G.; Bras, R.L. Estimation of net radiation from the MODIS data under all sky conditions: Southern Great Plains case study. Remote Sens. Environ. 2010, 114, 1522–1534. [Google Scholar] [CrossRef]
- Jocik, A.M. Estimate Ambient Air Temperature at Regional Level Using Remote Sensing Techniques. Master’s Thesis, International Institute for Geo-Information Science and Earth Observation (ITC), Enschede, The Netherlands, 2004. [Google Scholar]
- Zhu, W.; Lu, A.; Jia, S.; Yan, J.; Mahmood, R. Retrievals of all-weather daytime air temperature from MODIS products. Remote Sens. Environ. 2017, 189, 152–163. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, B.; Zhu, W.; Tang, X.; Li, F.; Liu, X.; Yu, Q. Comprehensive assessment of MODIS-derived near-surface air temperature using wide elevation-spanned measurements in China. Sci. Total Environ. 2021, 800, 149535. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Liu, P.; Kloog, I.; Lee, M.; Kosheleva, A.; Schwartz, J. Estimating daily air temperature across the Southeastern United States using high-resolution satellite data: A statistical modeling study. Environ Res. 2016, 146, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Leptoukh, G.G. Estimation of surface air temperature over central and eastern Eurasia from MODIS land surface temperature. Environ. Res. Lett. 2011, 6, 045206. [Google Scholar] [CrossRef]
- Xu, Y.; Knudby, A.; Ho, H. Estimating daily maximum air temperature from MODIS in British Columbia, Canada. Int. J. Remote Sens. 2014, 35, 8108–8121. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Müller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping Daily Air Temperature for Antarctica Based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef]
- Garcia, M.; Fernández, N.; Villagarcía, L.; Domingo, F.; Puigdefábregas, J.; Sandholt, I. Accuracy of the Temperature–Vegetation Dryness Index using MODIS under water-limited vs. energy-limited evapotranspiration conditions. Remote Sens. Environ. 2014, 149, 100–117. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS (Moderate Resolution Imaging Spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, Y.; Qiu, G.; Qin, Q.; Yao, Y.; Xiong, Y.; Li, C. Remote detection of bare soil moisture using a surface-temperature-based soil evaporation transfer coefficient. Int. J. Appl. Earth Obs. 2010, 12, 351–358. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, W.; Yang, J. Evaluation of MODIS Land Surface Temperature Data to Estimate Near-Surface Air Temperature in Northeast China. Remote Sens. 2017, 9, 410. [Google Scholar] [CrossRef]
- Bai, H.; Gong, Z.; Sun, G.; Li, L.; Zhou, L. Influence of Meteorological Elements on Summer Vegetation Coverage in North China. Chin. J. Atmos. Sci. 2022, 46, 27–39. (In Chinese) [Google Scholar]
- Huang, Y.; Wang, H. Is the Regional Precipitation Predictable in Decadal Scale? A Possible Approach for the Decadal Prediction of the Summer Precipitation Over North China. Earth. Space Sci. 2020, 7, e2019EA000986. [Google Scholar] [CrossRef]
- Song, C.; Huang, X.; Les, O.; Ma, H.; Liu, R. The Economic Impact of Climate Change on Wheat and Maize Yields in the North China Plain. Int. J. Environ. Res. Public Health 2022, 19, 5707. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Cheng, G.; Wang, N.; Shen, H.; Ma, X. Spatiotemporal Patterns of Multiscale Drought and Its Impact on Winter Wheat Yield over North China Plain. Agronomy 2022, 12, 1209. [Google Scholar] [CrossRef]
- Zheng, G.; Li, Y.; Chen, Q.; Zhou, X.; Gao, G.; Li, M.; Duan, T. The increasing predominance of extreme precipitation in Southwest China since the late 1970s. Atmos. Ocean. Sci. Lett. 2022, 15, 45–50. [Google Scholar] [CrossRef]
- Sun, H.; Wang, X.; Fan, D.; Sun, O.J. Contrasting vegetation response to climate change between two monsoon regions in Southwest China: The roles of climate condition and vegetation height. Sci. Total Environ. 2022, 802, 149643. [Google Scholar] [CrossRef]
- Pei, J.; Niu, Z.; Wang, L.; Huang, N.; Cao, J. Quantifying the spatio-temporal variations and impact factors for vegetation coverage in the karst regions of Southwest China using Landsat data and Google Earth engine. Proc. SPIE 2018, 10780, 107800E. [Google Scholar]
- Huang, F.; Zhan, W.; Wang, Z.-H.; Voogt, J.; Hu, L.; Quan, J.; Liu, C.; Zhang, N.; Lai, J. Satellite identification of atmospheric-surface-subsurface urban heat islands under clear sky. Remote Sens. Environ. 2020, 250, 112039. [Google Scholar] [CrossRef]
- Seddon, A.W.R.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef]
- Orellana-Samaniego, M.L.; Ballari, D.; Guzman, P.; Ospina, J.E. Estimating monthly air temperature using remote sensing on a region with highly variable topography and scarce monitoring in the southern Ecuadorian Andes. Theor. Appl. Climatol. 2021, 144, 949–966. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, C.; Huang, J.; Zhu, D.; Wang, L.; Liu, J. Mapping of Daily Mean Air Temperature in Agricultural Regions Using Daytime and Nighttime Land Surface Temperatures Derived from TERRA and AQUA MODIS Data. Remote Sens. Environ. 2015, 7, 8728–8756. [Google Scholar] [CrossRef]
- Noi, P.T.; Degener, J.; Kappas, M. Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data. Remote Sens. 2017, 9, 398. [Google Scholar] [CrossRef]
- Bappa, S.A.; Malaker, T.; Mia, M.R.; Islam, M.D. Spatio-temporal variation of land use and land cover changes and their impact on land surface temperature: A case of Kutupalong Refugee Camp, Bangladesh. Heliyon 2022, 8, e10449. [Google Scholar] [CrossRef] [PubMed]
- Zakšek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS-J. Photogramm. Remote Sens. 2009, 64, 414–421. [Google Scholar] [CrossRef]
- Kankeo, D.; Hind, M. Relation between NDVI and Maximum Air Temperature on Clear DaysCertification of the Estimation Method using NDVI for Vegetation Mitigation Effects on Air Temperature. J. Jpn. Soc. Hydrol. Water Resour. 1996, 9, 271–279. [Google Scholar] [CrossRef]
- Cresswell, M.P.; Morse, A.P.; Thomson, M.C.; Connor, S.J. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle model. Int. J. Remote Sens. 1999, 20, 1125–1132. [Google Scholar] [CrossRef]
- Wang, R.; Yao, X.; Shi, Y.; Wu, C.; Liu, B. Study on air temperature estimation and its influencing factors in a complex mountainous area. PLoS ONE 2022, 17, e0272946. [Google Scholar]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lu, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Xu, W.; Sun, R.; Jin, Z.; Hu, B. Estimation of near surface air temperature based on MODIS data. Meteorol. Environ. Sci. 2015, 38, 1–6. (In Chinese) [Google Scholar]
- Xu, Y.; Qin, Z.; Shen, Y. Study on the estimation of near-surface air temperature from MODIS data by statistical methods. Int. J. Remote Sens. 2012, 33, 7629–7643. [Google Scholar] [CrossRef]
- Hanley, J.A. Simple and multiple linear regression: Sample size considerations (Article). J. Clin. Epid. 2016, 79, 112–119. [Google Scholar] [CrossRef] [PubMed]
- Jan, S.-L.; Shieh, G. Sample size calculations for model validation in linear regression analysis. BMC Med. Res. Method 2019, 19, 54. [Google Scholar] [CrossRef] [PubMed]
- Kovács, D.; Király, P.; Tóth, G. Sample-size dependence of validation parameters in linear regression models and in QSAR. SAR QSAR Environ. Res. 2021, 32, 247–268. [Google Scholar] [CrossRef]
- Mayer, L.; Younger, M. Estimation of Standardized Regression Coefficients. J. Amer. Stat. Assoc. 1976, 71, 154. [Google Scholar] [CrossRef]
- Liu, S. The Contributory Big or Small of Every Variability to Regression Analyse and Realize in Multivariable Regression. J. Math. Med. 2005, 18, 524–525. (In Chinese) [Google Scholar]
- Barry, R.G. Mountain Weather and Climate; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]


| Clear Sky Conditions | Cloudy Sky Conditions | Data Source |
|---|---|---|
| LST | LST | MOD06_L2 and MYD06_L2 |
| NDVI | NDVI | MOD13A2 |
| SZA | SZA | MOD03 and MYD03 |
| Elevation | Elevation | SRTM DEM |
| - | The clear sky from atmospheric profile extrapolation method |
| Study Area | Variable | Data Source | r | B/°C | MAE/°C | RMSE/°C |
|---|---|---|---|---|---|---|
| North China | Terra | 0.949 | −0.2 | 4.3 | 5.2 | |
| Aqua | 0.951 | 0.1 | 2.9 | 4.0 | ||
| Terra | 0.951 | 0.0 | 2.8 | 3.5 | ||
| Aqua | 0.969 | 0.2 | 3.5 | 4.2 | ||
| Southwest China | Terra | 0.762 | −0.3 | 5.8 | 7.7 | |
| Aqua | 0.758 | −0.2 | 4.6 | 6.7 | ||
| Terra | 0.868 | 0.0 | 2.8 | 4.0 | ||
| Aqua | 0.844 | −0.1 | 3.1 | 4.4 |
| Study Area | Data Source | r | B/°C | MAE/°C | RMSE/°C |
|---|---|---|---|---|---|
| North China | Terra | 0.991 | 0.0 | 1.1 | 1.6 |
| Aqua | 0.991 | 0.0 | 1.1 | 1.5 | |
| Southwest China | Terra | 0.959 | 0.0 | 1.6 | 2.2 |
| Aqua | 0.950 | 0.0 | 1.6 | 2.3 |
| Study Area | Data Source | r | B/°C | MAE/°C | RMSE/°C |
|---|---|---|---|---|---|
| North China | Terra | 0.890 | −0.2 | 3.8 | 4.6 |
| Aqua | 0.945 | 0.7 | 3.1 | 3.9 | |
| Southwest China | Terra | 0.813 | −0.3 | 3.5 | 4.5 |
| Aqua | 0.823 | −0.1 | 3.4 | 4.4 |
| Study Area | Data Source | r | B/°C | MAE/°C | RMSE/°C |
|---|---|---|---|---|---|
| North China | Terra | 0.895 | 0.0 | 3.6 | 4.5 |
| Aqua | 0.948 | 0.0 | 2.5 | 3.3 | |
| Southwest China | Terra | 0.848 | −0.1 | 3.4 | 4.3 |
| Aqua | 0.901 | 0.0 | 2.6 | 3.4 |
| Study Area | Data Source | r | B/°C | MAE/°C | RMSE/°C |
|---|---|---|---|---|---|
| North China | Terra | 0.916 | 0.0 | 3.5 | 4.3 |
| Aqua | 0.961 | 0.0 | 2.5 | 3.0 | |
| Southwest China | Terra | 0.917 | −0.2 | 3.4 | 4.0 |
| Aqua | 0.946 | −0.1 | 2.4 | 2.9 |
| Study Area | Data Source | Cultivated Land | Woodland | Grassland | Constructive Land |
|---|---|---|---|---|---|
| North China | Terra | 2.0 | 3.0 | 3.0 | 2.0 |
| Aqua | 2.6 | 3.6 | 3.2 | 2.7 | |
| Southwest China | Terra | 2.5 | 2.5 | 2.8 | 2.4 |
| Aqua | 2.7 | 2.8 | 2.9 | 2.7 |
| Weather Conditions | Study Area | Data Source | LST | SZA | NDVI | Elevation | |
|---|---|---|---|---|---|---|---|
| Clear sky conditions | NorthChina | Terra | 0.296 | 0.232 | 0.200 | 0.044 | 0.551 |
| Aqua | 0.304 | 0.172 | 0.242 | 0.068 | 0.617 | ||
| Southwest China | Terra | 0.339 | 0.149 | 0.155 | 0.066 | 0.656 | |
| Aqua | 0.321 | 0.160 | 0.257 | 0.087 | 0.694 | ||
| Cloudy sky conditions | NorthChina | Terra | - | 0.438 | 0.193 | 0.067 | 0.492 |
| Aqua | - | 0.512 | 0.189 | 0.066 | 0.427 | ||
| Southwest China | Terra | - | 0.361 | 0.248 | 0.105 | 0.536 | |
| Aqua | - | 0.517 | 0.320 | 0.079 | 0.484 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, J.; Zhu, W. Estimation of Instantaneous Air Temperature under All-Weather Conditions Based on MODIS Products in North and Southwest China. Remote Sens. 2023, 15, 2701. https://doi.org/10.3390/rs15112701
Wang Y, Liu J, Zhu W. Estimation of Instantaneous Air Temperature under All-Weather Conditions Based on MODIS Products in North and Southwest China. Remote Sensing. 2023; 15(11):2701. https://doi.org/10.3390/rs15112701
Chicago/Turabian StyleWang, Yuanxin, Jinxiu Liu, and Wenbin Zhu. 2023. "Estimation of Instantaneous Air Temperature under All-Weather Conditions Based on MODIS Products in North and Southwest China" Remote Sensing 15, no. 11: 2701. https://doi.org/10.3390/rs15112701
APA StyleWang, Y., Liu, J., & Zhu, W. (2023). Estimation of Instantaneous Air Temperature under All-Weather Conditions Based on MODIS Products in North and Southwest China. Remote Sensing, 15(11), 2701. https://doi.org/10.3390/rs15112701







