Spatial-Temporal Changes of Abarkuh Playa Landform from Sentinel-1 Time Series Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. Satellite Data
2.2.2. Geological and Meteorological Data
2.3. Methods
2.3.1. Radiometric Terrain Correction
- Shadow: When the back slope’s angle is such that the sensor cannot image it entirely, it receives no information for a steep back slope;
- Foreshortening: In this case, the backscatter from the front side of the mountain will be compressed altogether with returns from a large area arriving back to the sensor, which results in the front slope being shown as narrow;
- Layover: In this case, returns from the back slope, the front slope, and part of the area before the slope arrived back to the sensor simultaneously. Thus, an area in the front of the slopes is projected onto the back side in the slant range direction of the image, and the data from the front slope is missed.
2.3.2. Independent Component Analysis
3. Results and Analysis
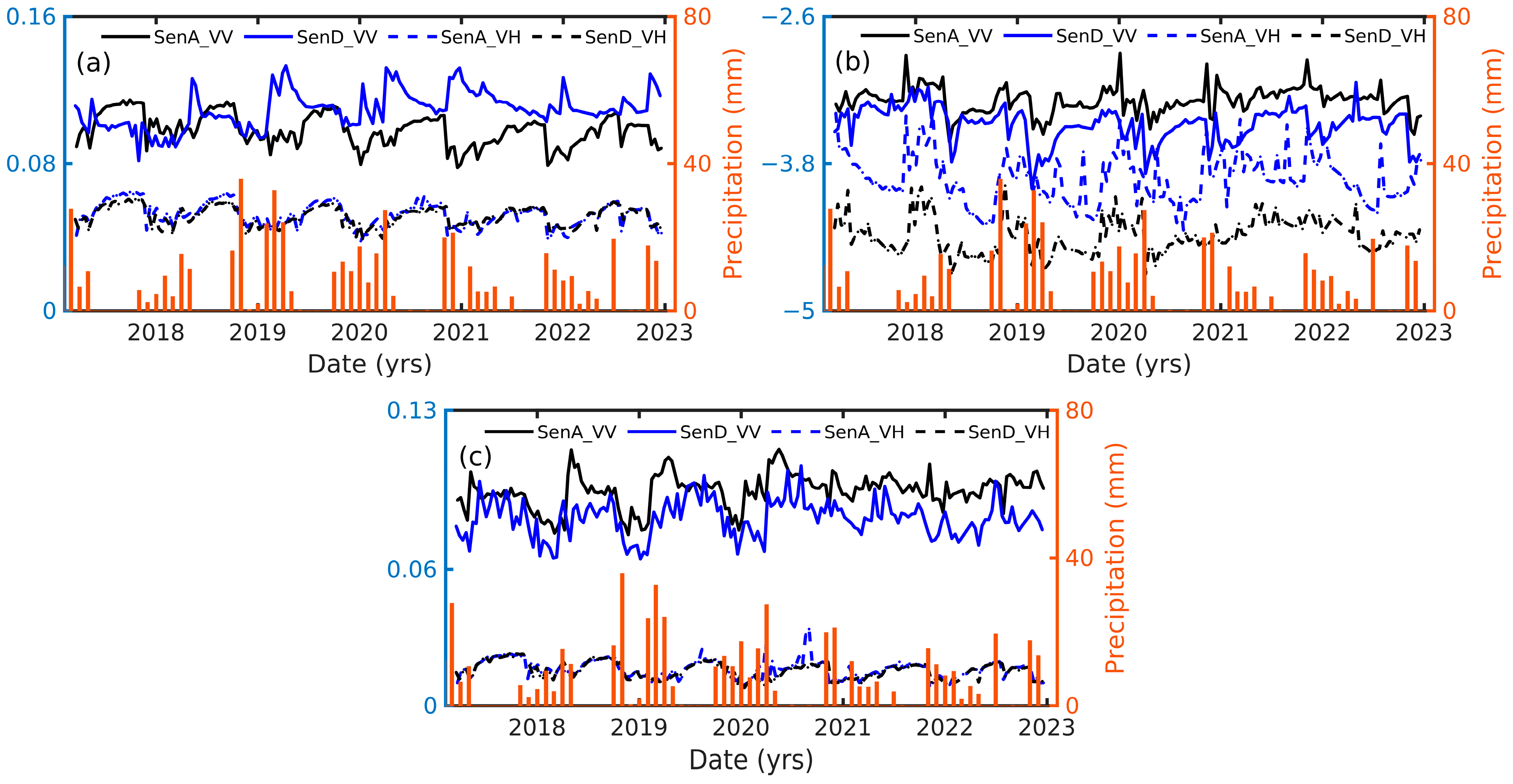
3.1. Variations of Precipitation and LST
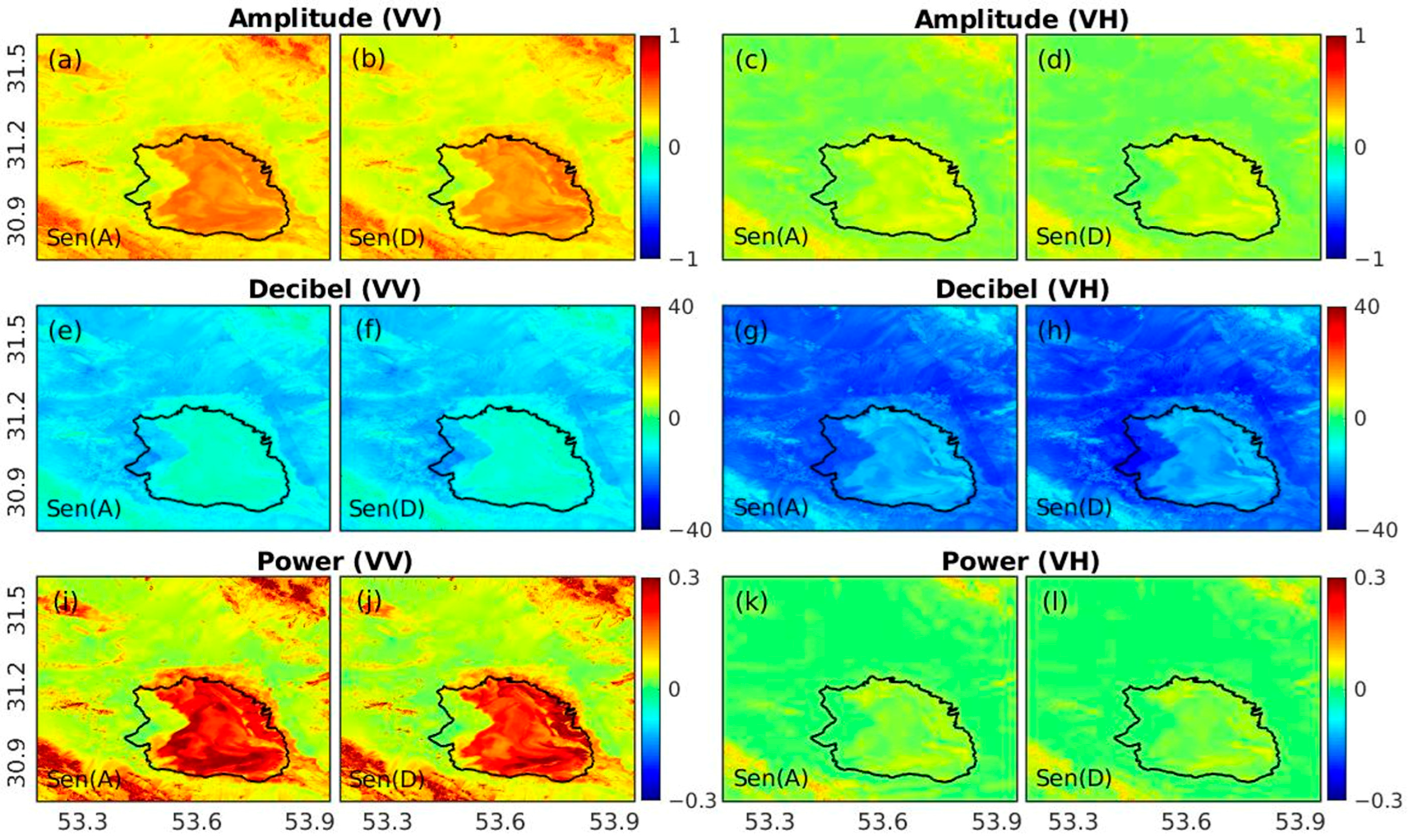
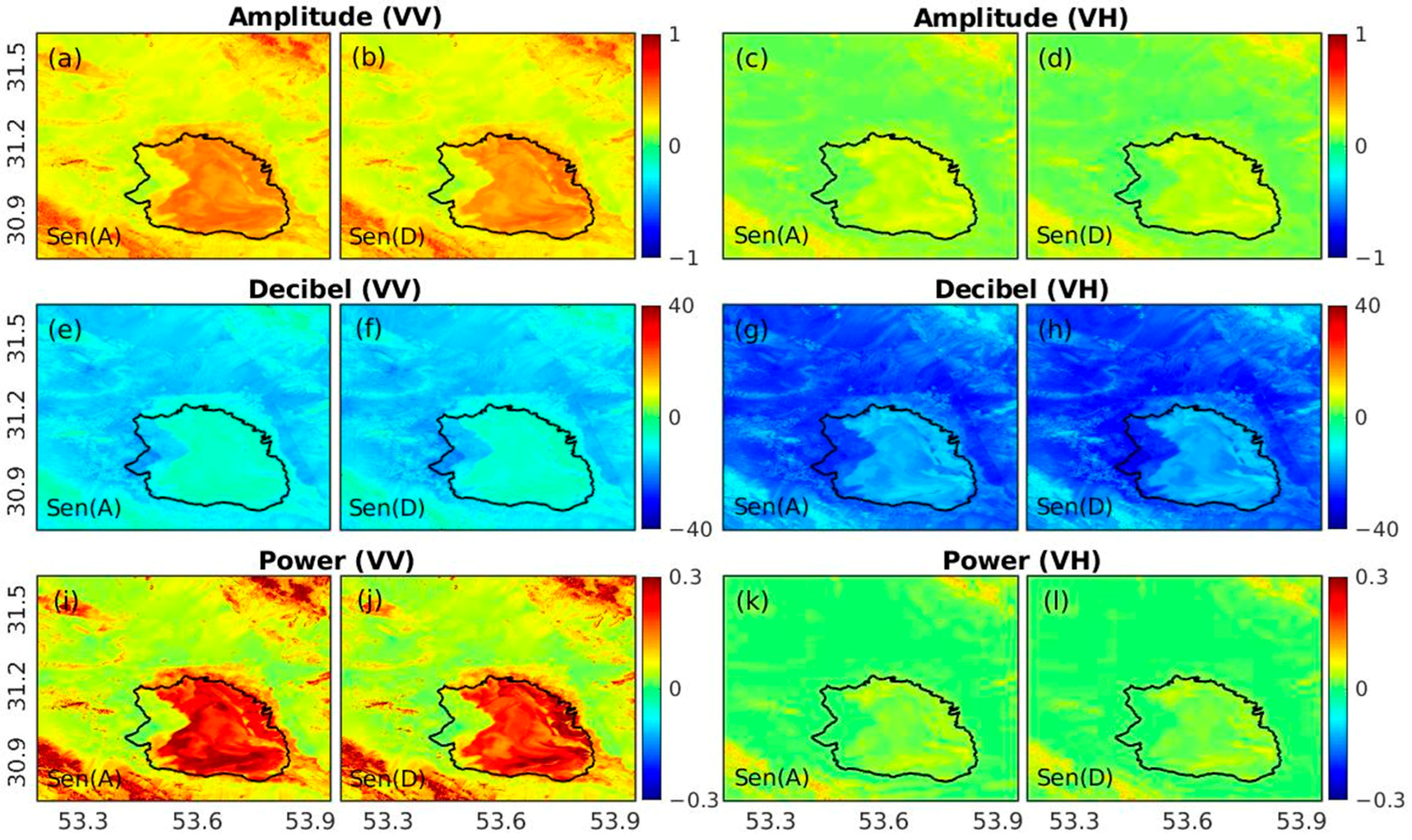
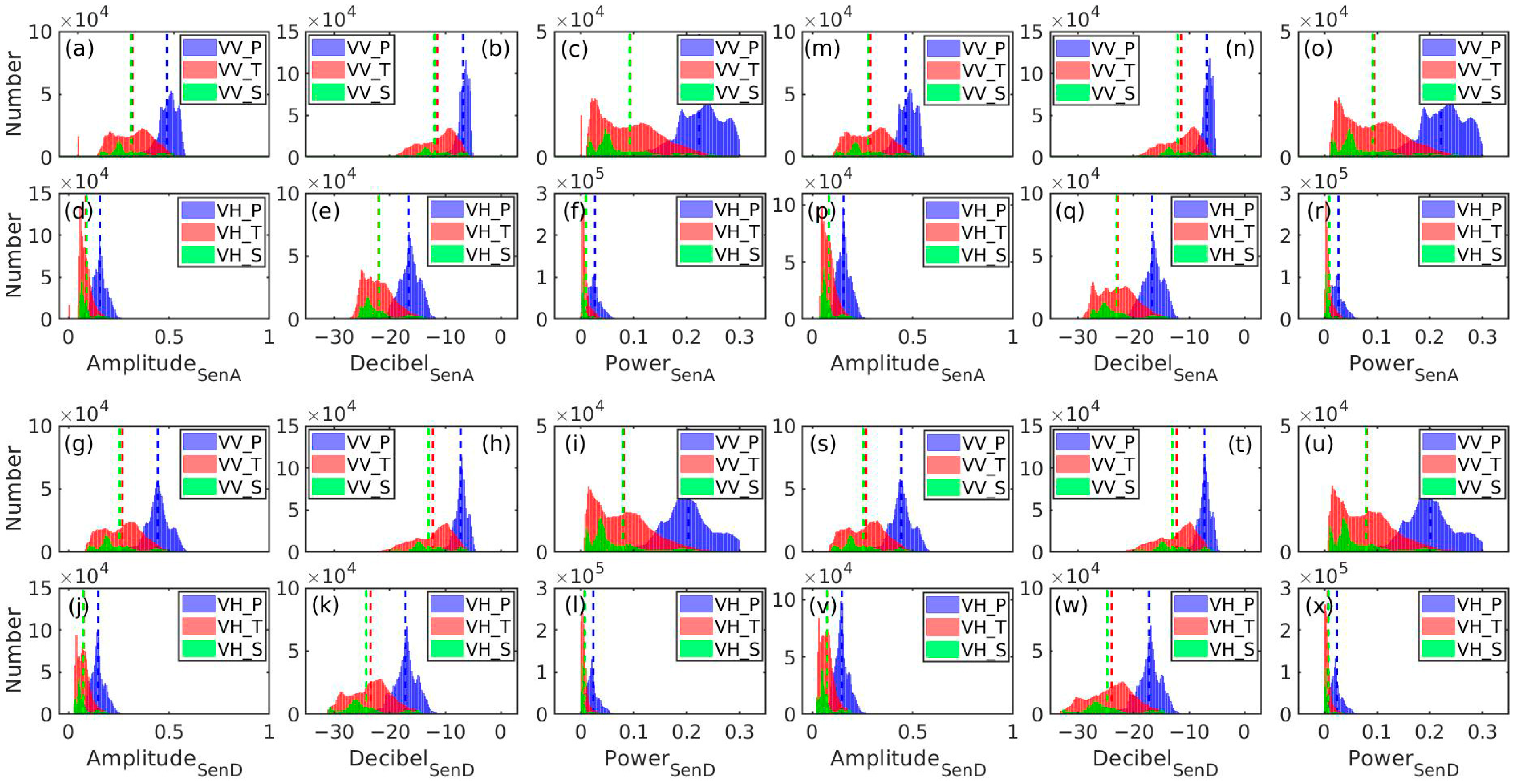
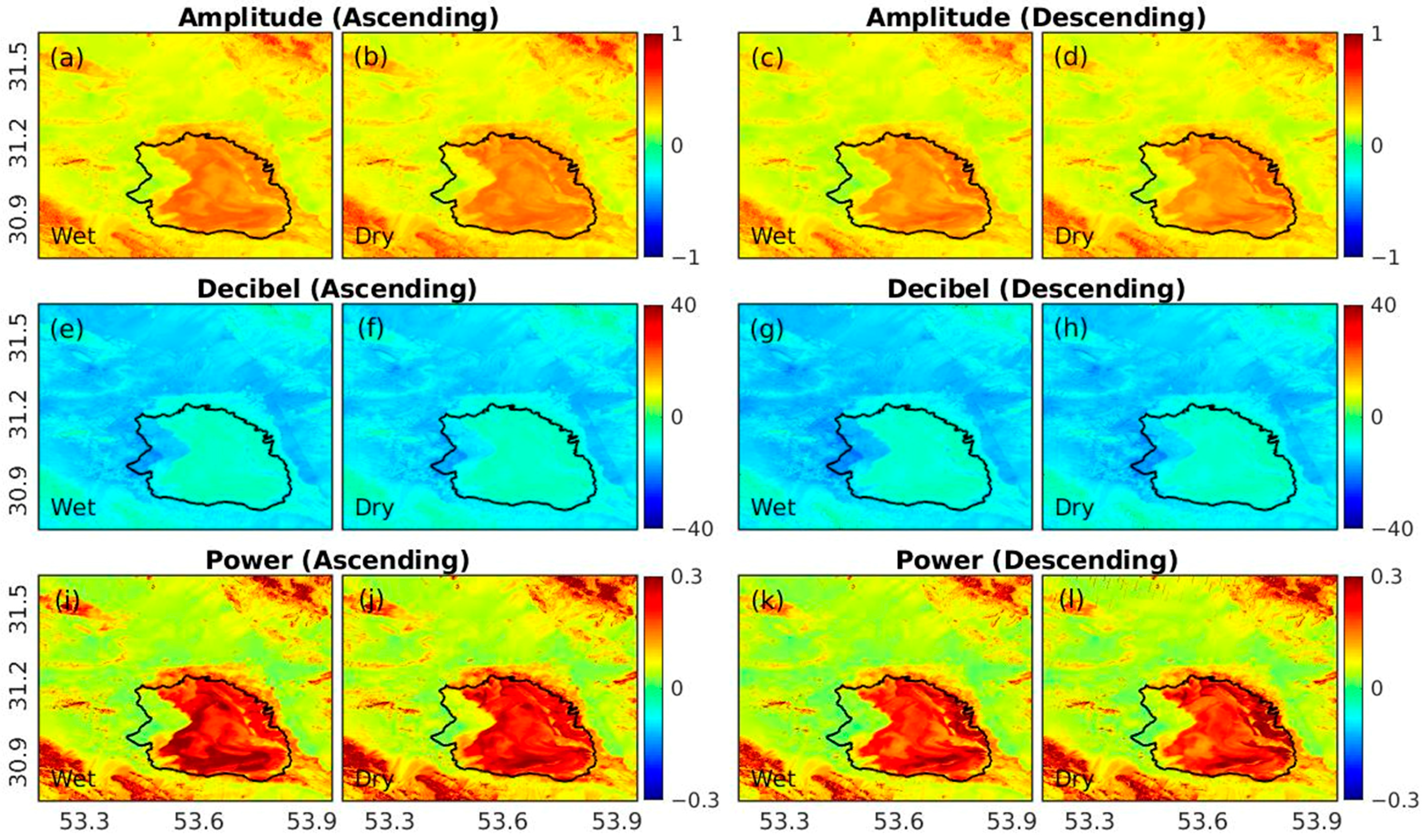
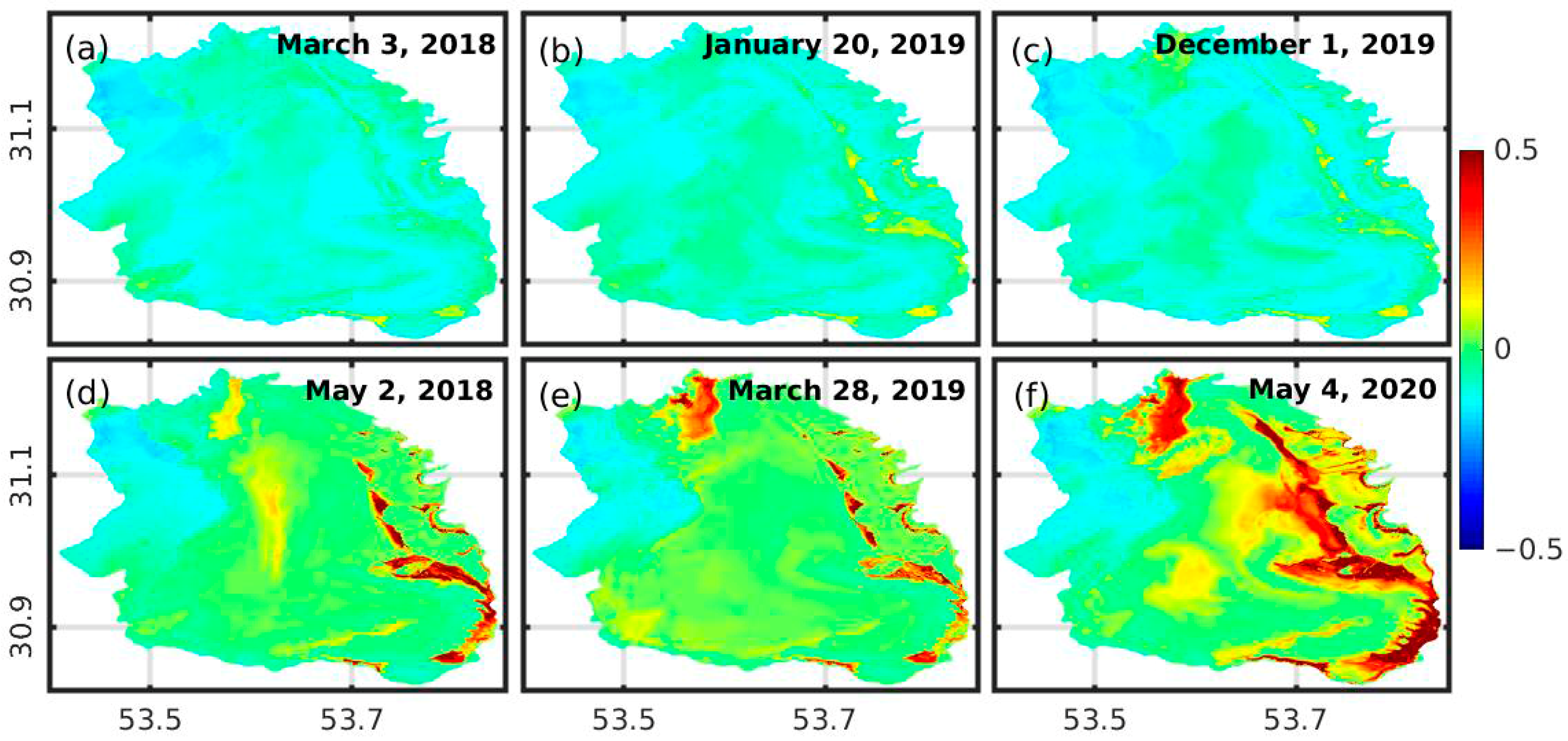
3.2. Spatial Patterns of Backscatter
3.3. Seasonal Backscatter Changes
3.4. Controls on Spatial-Temporal Variations of Backscatter
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neal, J.T. Playas and Dried Lakes; Dowden, Hutchinson & Ross: Stroudsburg, PA, USA, 1975. [Google Scholar]
- Sharp, R.P.; Glazner, A.F. Geology Underfoot in Death Valley and Owens Valley; Mountain Press Publishing: Missoula, MT, USA, 1997. [Google Scholar]
- Turk, L. Evaporation of brine: A field study on the Bonneville Salt Flats, Utah. Water Resour. Res. 1970, 6, 1209–1215. [Google Scholar] [CrossRef]
- Middleton, N.J. Desert dust hazards: A global review. Aeolian Res. 2017, 24, 53–63. [Google Scholar] [CrossRef]
- Gill, T.E. Dust Generation Resulting from Desiccation of Playa Systems: Studies on Mono and Owens Lakes, California; University of California: Davis, CA, USA, 1995. [Google Scholar]
- Hamzehpour, N.; Marcolli, C.; Klumpp, K.; Thöny, D.; Peter, T. The Urmia playa as a source of airborne dust and ice-nucleating particles–Part 2: Unraveling the relationship between soil dust composition and ice nucleation activity. Atmos. Chem. Phys. 2022, 22, 14931–14956. [Google Scholar] [CrossRef]
- Hamzehpour, N.; Marcolli, C.; Pashai, S.; Klumpp, K.; Peter, T. Measurement report: The Urmia playa as a source of airborne dust and ice-nucleating particles–Part 1: Correlation between soils and airborne samples. Atmos. Chem. Phys. 2022, 22, 14905–14930. [Google Scholar] [CrossRef]
- Ge, Y.; Abuduwaili, J.; Ma, L.; Wu, N.; Liu, D. Potential transport pathways of dust emanating from the playa of Ebinur Lake, Xinjiang, in arid northwest China. Atmos. Res. 2016, 178, 196–206. [Google Scholar] [CrossRef]
- Rosen, M.R. The importance of groundwater in playas: A review of playa classifications and the sedimentology and hydrology of playas. Geol. Soc. Am. 1994, 289. [Google Scholar] [CrossRef]
- Embabi, N.S.; Moawad, M.B. A semi-automated approach for mapping geomorphology of El Bardawil Lake, Northern Sinai, Egypt, using integrated remote sensing and GIS techniques. Egypt. J. Remote Sens. Space Sci. 2014, 17, 41–60. [Google Scholar] [CrossRef]
- Verstappen, H.T. Old and new trends in geomorphological and landform mapping. Dev. Earth Surf. Process. 2011, 15, 13–38. [Google Scholar]
- Dixon, L. Analytical photogrammetry for geomorphological research. Landf. Monit. Model. Anal. 1998, 63–91. Available online: https://cir.nii.ac.jp/crid/1571417124526752384 (accessed on 4 January 2023).
- Slaymaker, O. The role of remote sensing in geomorphology and terrain analysis in the Canadian Cordillera. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 11–17. [Google Scholar] [CrossRef]
- Smith, M.; Pain, C. Applications of remote sensing in geomorphology. Prog. Phys. Geogr. 2009, 33, 568–582. [Google Scholar] [CrossRef]
- Hammond, E.H. Small-scale continental landform maps. Ann. Assoc. Am. Geogr. 1954, 44, 33–42. [Google Scholar] [CrossRef]
- Hammond, E.H. Analysis of properties in land form geography: An application to broad-scale land form mapping. Ann. Assoc. Am. Geogr. 1964, 54, 11–19. [Google Scholar] [CrossRef]
- Papp, E.; Cudahy, T. Hyperspectral remote sensing. Geophys. Remote Sens. Methods Regolith Explor. 2002, 144, 13–21. [Google Scholar]
- Higgitt, D.L.; Warburton, J. Applications of differential GPS in upland fluvial geomorphology. Geomorphology 1999, 29, 121–134. [Google Scholar] [CrossRef]
- Mullen, I.; Kellett, J. Groundwater salinity mapping using airborne electromagnetics and borehole data within the lower Balonne catchment, Queensland, Australia. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 116–123. [Google Scholar] [CrossRef]
- Hodge, R.; Brasington, J.; Richards, K. In situ characterization of grain-scale fluvial morphology using Terrestrial Laser Scanning. Earth Surf. Process. Landf. 2009, 34, 954–968. [Google Scholar]
- Hynek, B.M.; Phillips, R.J. New data reveal mature, integrated drainage systems on Mars indicative of past precipitation. Geology 2003, 31, 757–760. [Google Scholar] [CrossRef]
- Chandler, J.H.; Fryer, J.G.; Jack, A. Metric capabilities of low-cost digital cameras for close range surface measurement. Photogramm. Rec. 2005, 20, 12–26. [Google Scholar] [CrossRef]
- Hättestrand, C.; Clark, C.D. The glacial geomorphology of Kola Peninsula and adjacent areas in the Murmansk Region, Russia. J. Maps 2006, 2, 30–42. [Google Scholar] [CrossRef]
- Wilford, J. Using airborne geophysics to define the 3D distribution and landscape evolution of Quaternary valley-fill deposits around the Jamestown area, South Australia. Aust. J. Earth Sci. 2009, 56, S67–S88. [Google Scholar] [CrossRef]
- Vencataswamy, C. Landform and lineament mapping using radar remote sensing. Landf. Monit. Model. Anal. 1998, 165–194. Available online: https://cir.nii.ac.jp/crid/1570854174587933824 (accessed on 4 January 2023).
- Buchroithner, M. Creating the virtual Eiger North Face. ISPRS J. Photogramm. Remote Sens. 2002, 57, 114–125. [Google Scholar] [CrossRef]
- Gazioğlu, C.; Yücel, Z.; Kaya, H.; Doğan, E. Geomorphological features of Mt. Erciyes using by DTM and remote sensing technologies. In Proceedings of the XXth International Society for Photogrammetry and Remote Sensing Conference Proceedings, Istanbul, Turkey, 15–23 July 2004. [Google Scholar]
- Schneevoigt, N.; Schrott, L. Linking geomorphic systems theory and remote sensing: A conceptual approach to Alpine landform detection (Reintal, Bavarian Alps, Germany). Geogr. Helv. 2006, 61, 181–190. [Google Scholar] [CrossRef]
- Smith, M.J.; Clark, C.D. Methods for the visualization of digital elevation models for landform mapping. Earth Surf. Process. Landf. 2005, 30, 885–900. [Google Scholar] [CrossRef]
- Burberry, C.M.; Cosgrove, J.W.; Liu, J.G. Spatial arrangement of fold types in the Zagros Simply Folded Belt, Iran, indicated by landform morphology and drainage pattern characteristics. J. Maps 2008, 4, 417–430. [Google Scholar] [CrossRef]
- Potts, L.; Akyilmaz, O.; Braun, A.; Shum, C. Multi-resolution dune morphology using Shuttle Radar Topography Mission (SRTM) and dune mobility from fuzzy inference systems using SRTM and altimetric data. Int. J. Remote Sens. 2008, 29, 2879–2901. [Google Scholar] [CrossRef]
- Bubenzer, O.; Bolten, A. The use of new elevation data (SRTM/ASTER) for the detection and morphometric quantification of Pleistocene megadunes (draa) in the eastern Sahara and the southern Namib. Geomorphology 2008, 102, 221–231. [Google Scholar] [CrossRef]
- Clauss, K.; Ottinger, M.; Künzer, C. Mapping rice areas with Sentinel-1 time series and superpixel segmentation. Int. J. Remote Sens. 2018, 39, 1399–1420. [Google Scholar] [CrossRef]
- Nguyen, D.B.; Gruber, A.; Wagner, W. Mapping rice extent and cropping scheme in the Mekong Delta using Sentinel-1A data. Remote Sens. Lett. 2016, 7, 1209–1218. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Askar, A.; Stratoulias, D.; Wicaksono, P. Combined use of Sentinel-1 and Sentinel-2 data for improving above-ground biomass estimation. Geocarto Int. 2022, 37, 366–376. [Google Scholar] [CrossRef]
- Amani, M.; Kakooei, M.; Moghimi, A.; Ghorbanian, A.; Ranjgar, B.; Mahdavi, S.; Davidson, A.; Fisette, T.; Rollin, P.; Brisco, B. Application of google earth engine cloud computing platform, sentinel imagery, and neural networks for crop mapping in Canada. Remote Sens. 2020, 12, 3561. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Sentinel-1 and Sentinel-2 data fusion for wetlands mapping: Balikdami, Turkey. Int. Soc. Photogramm. Remote Sens. 2018, 42. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Homayouni, S.; Gill, E. The first wetland inventory map of newfoundland at a spatial resolution of 10 m using sentinel-1 and sentinel-2 data on the google earth engine cloud computing platform. Remote Sens. 2018, 11, 43. [Google Scholar] [CrossRef]
- Amani, M.; Mahdavi, S.; Berard, O. Supervised wetland classification using high spatial resolution optical, SAR, and LiDAR imagery. J. Appl. Remote Sens. 2020, 14, 024502. [Google Scholar] [CrossRef]
- Muro, J.; Canty, M.; Conradsen, K.; Hüttich, C.; Nielsen, A.A.; Skriver, H.; Remy, F.; Strauch, A.; Thonfeld, F.; Menz, G. Short-term change detection in wetlands using Sentinel-1 time series. Remote Sens. 2016, 8, 795. [Google Scholar] [CrossRef]
- Rüetschi, M.; Schaepman, M.E.; Small, D. Using multitemporal sentinel-1 c-band backscatter to monitor phenology and classify deciduous and coniferous forests in northern switzerland. Remote Sens. 2017, 10, 55. [Google Scholar] [CrossRef]
- Mirmazloumi, S.M.; Kakooei, M.; Mohseni, F.; Ghorbanian, A.; Amani, M.; Crosetto, M.; Monserrat, O. ELULC-10, a 10 m European land use and land cover map using sentinel and landsat data in google earth engine. Remote Sens. 2022, 14, 3041. [Google Scholar] [CrossRef]
- Markert, K.N.; Chishtie, F.; Anderson, E.R.; Saah, D.; Griffin, R.E. On the merging of optical and SAR satellite imagery for surface water mapping applications. Results Phys. 2018, 9, 275–277. [Google Scholar] [CrossRef]
- Markert, K.N.; Markert, A.M.; Mayer, T.; Nauman, C.; Haag, A.; Poortinga, A.; Bhandari, B.; Thwal, N.S.; Kunlamai, T.; Chishtie, F. Comparing sentinel-1 surface water mapping algorithms and radiometric terrain correction processing in southeast asia utilizing google earth engine. Remote Sens. 2020, 12, 2469. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Kiran, K.S.; Manjusree, P.; Viswanadham, M. Sentinel-1 SAR data preparation for extraction of flood footprints—A case study. Disaster Adv. 2019, 12, 10–20. [Google Scholar]
- Mahdavi, S.; Salehi, B.; Huang, W.; Amani, M.; Brisco, B. A PolSAR change detection index based on neighborhood information for flood mapping. Remote Sens. 2019, 11, 1854. [Google Scholar] [CrossRef]
- Rüetschi, M.; Small, D.; Waser, L.T. Rapid detection of windthrows using Sentinel-1 C-band SAR data. Remote Sens. 2019, 11, 115. [Google Scholar] [CrossRef]
- Small, D. Flattening gamma: Radiometric terrain correction for SAR imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Ullmann, T.; Büdel, C.; Baumhauer, R.; Padashi, M. Sentinel-1 SAR data revealing fluvial morphodynamics in damghan (Iran): Amplitude and coherence change detection. Int. J. Earth Sci. Geophys. 2016, 2, 7. [Google Scholar]
- Eibedingil, I.G.; Gill, T.E.; Van Pelt, R.S.; Tong, D.Q. Combining optical and radar satellite imagery to investigate the surface properties and evolution of the Lordsburg Playa, New Mexico, USA. Remote Sens. 2021, 13, 3402. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Ling, F.; Wang, Q.; Li, W.; Li, X. Water bodies’ mapping from Sentinel-2 imagery with modified normalized difference water index at 10-m spatial resolution produced by sharpening the SWIR band. Remote Sens. 2016, 8, 354. [Google Scholar] [CrossRef]
- Jiang, W.; Ni, Y.; Pang, Z.; He, G.; Fu, J.; Lu, J.; Yang, K.; Long, T.; Lei, T. A new index for identifying water body from sentinel-2 satellite remote sensing imagery. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-3-2020, 33–38. [Google Scholar] [CrossRef]
- Geological Survey of Iran. GSI 1997. Available online: https://gsi.ir/en (accessed on 15 November 2019).
- Muñoz Sabater, J. ERA5-Land hourly data from 1981 to present. Copernic. Clim. Change Serv. (C3S) Clim. Data Store (CDS) 2019, 10, 10.24381. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A2 MODIS/Terra land surface temperature/emissivity 8-day L3 global 1km SIN grid V006. Nasa Eosdis Land Process. Daac 2015, 10. [Google Scholar] [CrossRef]
- Meyer, F. Spaceborne Synthetic Aperture Radar: Principles, data access, and basic processing techniques. Synth. Aperture Radar (SAR) Handb. Compr. Methodol. For. Monit. Biomass Estim. 2019, 21–64. [Google Scholar] [CrossRef]
- Hogenson, K.; Arko, S.A.; Logan, T.A.; Gens, R.; Arnoult, K., Jr.; Nicoll, J.B. Hybrid Pluggable Processing Pipeline (HyP3): A cloud-based infrastructure for generic processing of SAR data. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 1 August 2018; p. G32A-03. [Google Scholar]
- Lopes, A.; Touzi, R.; Nezry, E. Adaptive speckle filters and scene heterogeneity. IEEE Trans. Geosci. Remote Sens. 1990, 28, 992–1000. [Google Scholar] [CrossRef]
- Lee, J.-S. Digital image smoothing and the sigma filter. Comput. Vis. Graph. Image Process. 1983, 24, 255–269. [Google Scholar] [CrossRef]
- Lee, J.-S. A simple speckle smoothing algorithm for synthetic aperture radar images. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 85–89. [Google Scholar] [CrossRef]
- Gualandi, A.; Avouac, J.-P.; Galetzka, J.; Genrich, J.F.; Blewitt, G.; Adhikari, L.B.; Koirala, B.P.; Gupta, R.; Upreti, B.N.; Pratt-Sitaula, B. Pre-and post-seismic deformation related to the 2015, Mw7. 8 Gorkha earthquake, Nepal. Tectonophysics 2017, 714, 90–106. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. A fast fixed-point algorithm for independent component analysis. Neural Comput. 1997, 9, 1483–1492. [Google Scholar] [CrossRef]
- Chaussard, E.; Farr, T.G. A new method for isolating elastic from inelastic deformation in aquifer systems: Application to the San Joaquin Valley, CA. Geophys. Res. Lett. 2019, 46, 10800–10809. [Google Scholar] [CrossRef]
- Wuebbles, D.; Fahey, D.; Takle, E.; Hibbard, K.; Arnold, J.; DeAngelo, B.; Doherty, S.; Easterling, D.; Edmonds, J.; Edmonds, T. Climate Science Special Report: Fourth National Climate Assessment (NCA4), Volume I; CSSR: Rome, Italy, 2017. [Google Scholar]
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Rezaei, A. Ocean-atmosphere circulation controls on integrated meteorological and agricultural drought over Iran. J. Hydrol. 2021, 603, 126928. [Google Scholar] [CrossRef]
- Tollerud, H.J.; Fantle, M.S. The temporal variability of centimeter-scale surface roughness in a playa dust source: Synthetic aperture radar investigation of playa surface dynamics. Remote Sens. Environ. 2014, 154, 285–297. [Google Scholar] [CrossRef]
- Guo, Y.-Q.; Zhou, F.; Tao, M.; Sheng, M. A new method for SAR radio frequency interference mitigation based on maximum a posterior estimation. In Proceedings of the 2017 XXXIInd General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Montreal, Canada, 19–26 August 2017; pp. 1–4. [Google Scholar]


| Name | Resolution | Units | Description |
|---|---|---|---|
| precipitation | 0.05 degree | mm | Precipitation |
| LST_Day_1 km | 1000 m | Kelvin | Daytime Land Surface Temperature |
| Parameters | Options | |||
|---|---|---|---|---|
| Radiometry | Gamma0 () | Sigma0 () | ||
| Scale | Power | Decibel | Amplitude | |
| Pixel Spacing | 30 m | 10 m | ||
| DEM | Copernicus | NED 1/SRTM 2 | ||
| Co-registration | Dead Reckoning | DEM Matching | ||
| Filtering | Do Not Apply | Enhanced Lee Speckle Filter | ||
| Dataset | Epochs | |||||
|---|---|---|---|---|---|---|
| Dry Period | Wet Period | |||||
| Sentinel-1 | 2018.03.03 | 2019.01.21 | 2019.11.29 | 2018.05.02 | 2019.04.03 | 2020.05.03 |
| Sentinel-2 | 2018.03.03 | 2019.01.20 | 2019.12.01 | 2018.05.02 | 2019.03.28 | 2020.05.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirzadeh, S.M.J.; Jin, S.; Amani, M. Spatial-Temporal Changes of Abarkuh Playa Landform from Sentinel-1 Time Series Data. Remote Sens. 2023, 15, 2774. https://doi.org/10.3390/rs15112774
Mirzadeh SMJ, Jin S, Amani M. Spatial-Temporal Changes of Abarkuh Playa Landform from Sentinel-1 Time Series Data. Remote Sensing. 2023; 15(11):2774. https://doi.org/10.3390/rs15112774
Chicago/Turabian StyleMirzadeh, Sayyed Mohammad Javad, Shuanggen Jin, and Meisam Amani. 2023. "Spatial-Temporal Changes of Abarkuh Playa Landform from Sentinel-1 Time Series Data" Remote Sensing 15, no. 11: 2774. https://doi.org/10.3390/rs15112774
APA StyleMirzadeh, S. M. J., Jin, S., & Amani, M. (2023). Spatial-Temporal Changes of Abarkuh Playa Landform from Sentinel-1 Time Series Data. Remote Sensing, 15(11), 2774. https://doi.org/10.3390/rs15112774








