Geometric Configuration Design and Fast Imaging for Multistatic Forward-Looking SAR Based on Wavenumber Spectrum Formation Approach
Abstract
:1. Introduction
2. Echo Model and Related Work of Mu-FLSAR
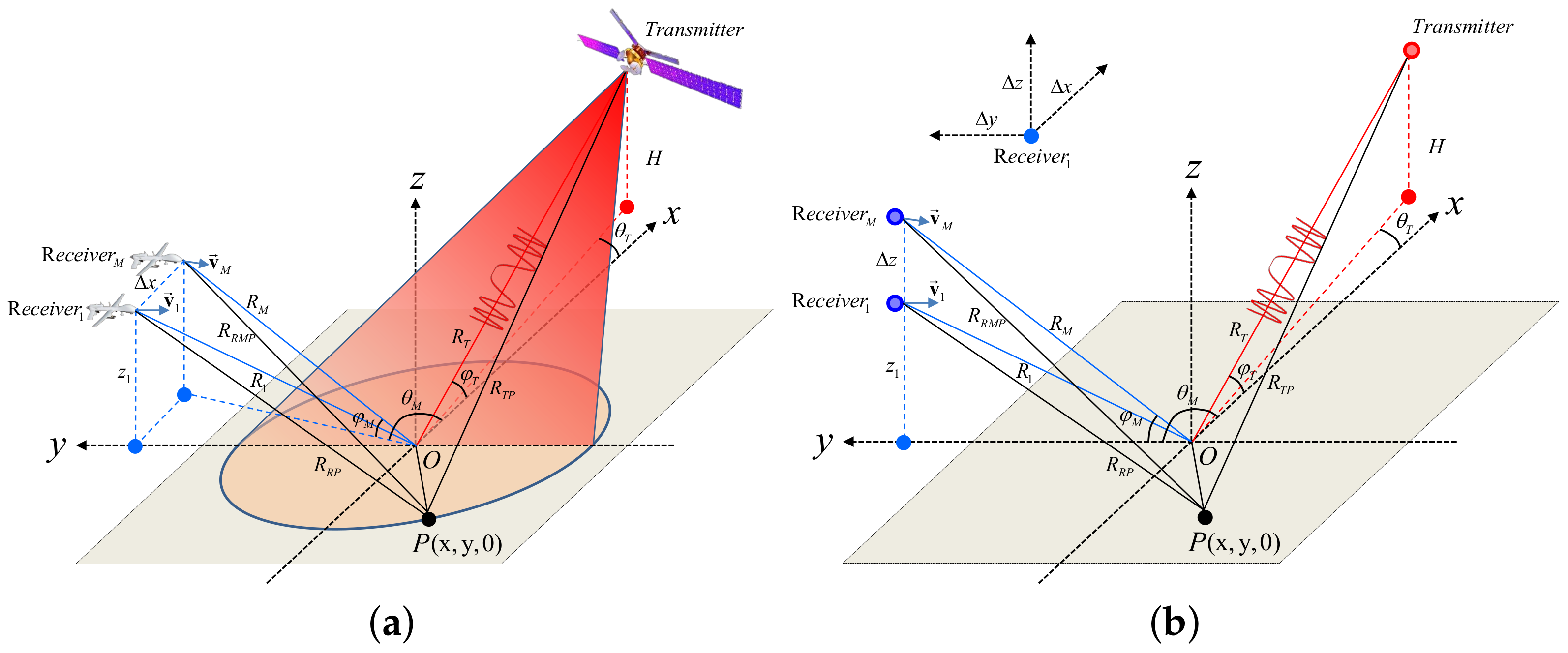
2.1. Echo Model
2.2. Spatial Resolution Analysis
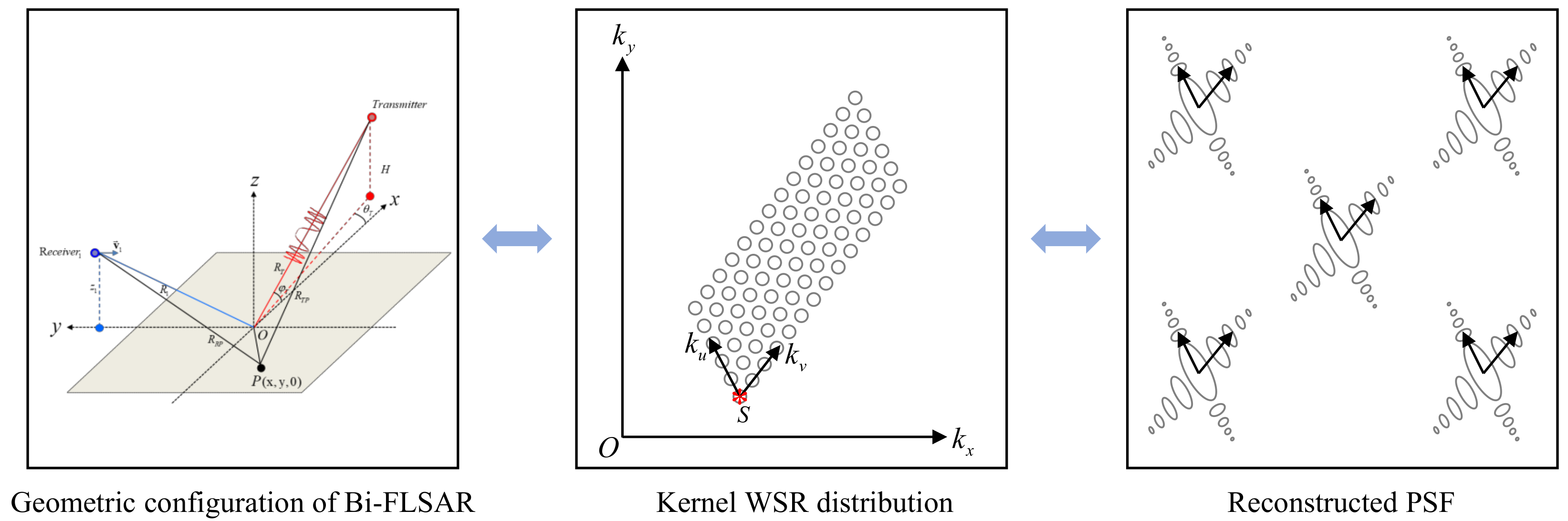
2.2.1. Relationship among Geometric Configuration, Kernel WSR and Spatial Resolution of the Master Bi-FLSAR Pair
2.2.2. Influences of Horizontal and Vertical Spacings on Mu-FLSAR
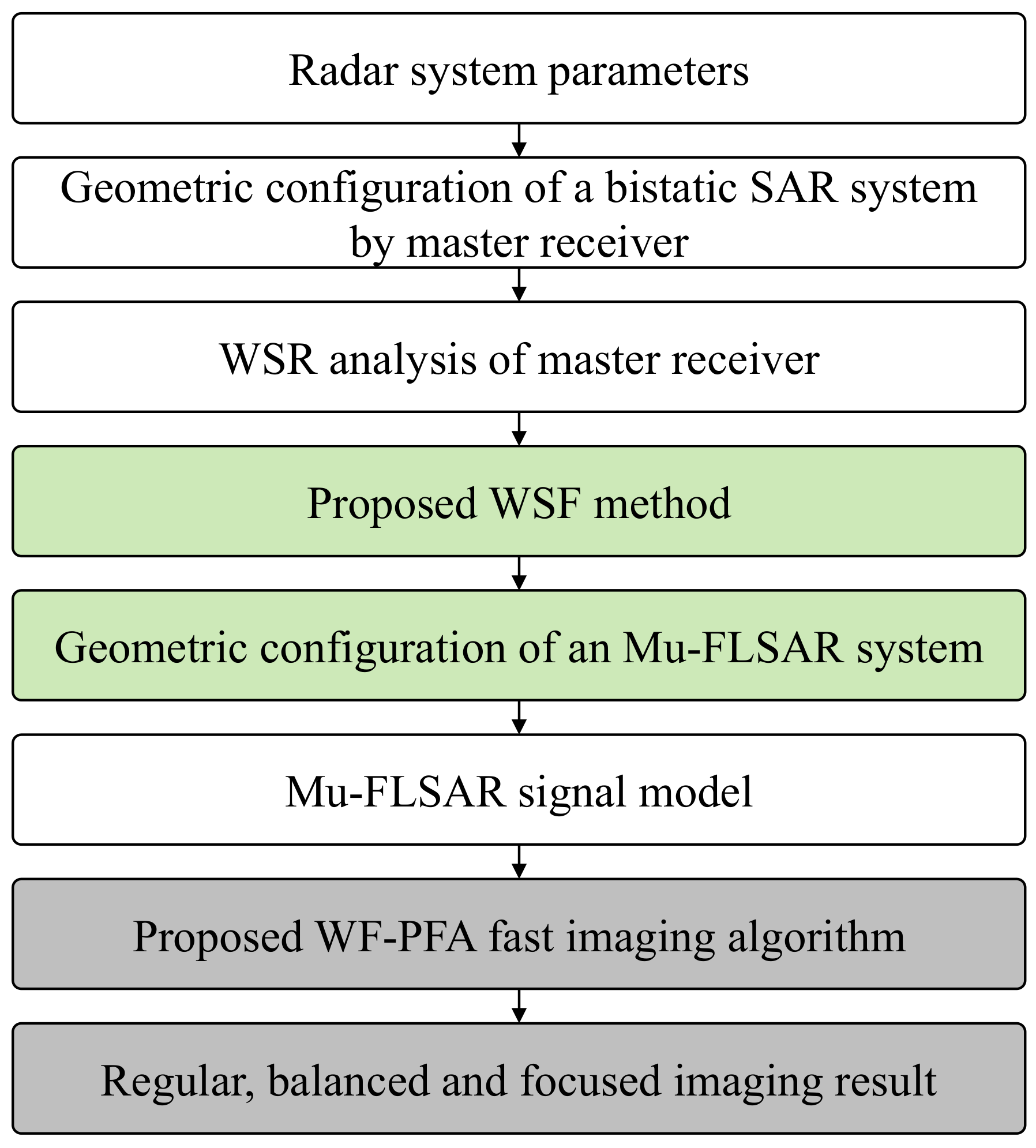
3. Proposed WSF-WFPFA Method
3.1. Proposed WSF Method
3.2. Fast Imaging Based on WF-PFA Method
3.2.1. Coherent Data Combination of Multiple Receivers
3.2.2. Computational Complexity Analysis
4. Simulations and Challenges Discussion
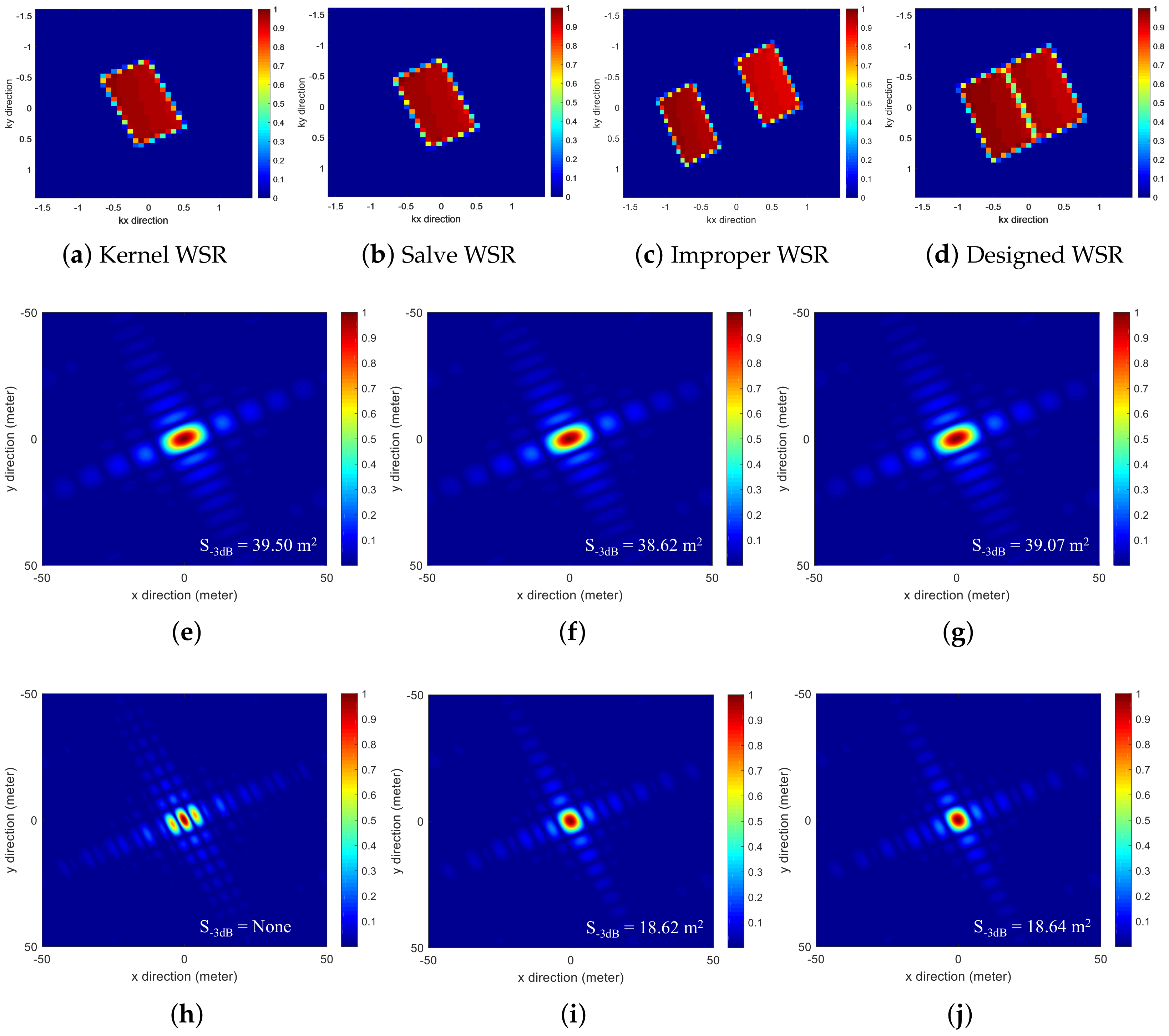
4.1. An Mu-FLSAR System with Two Receivers
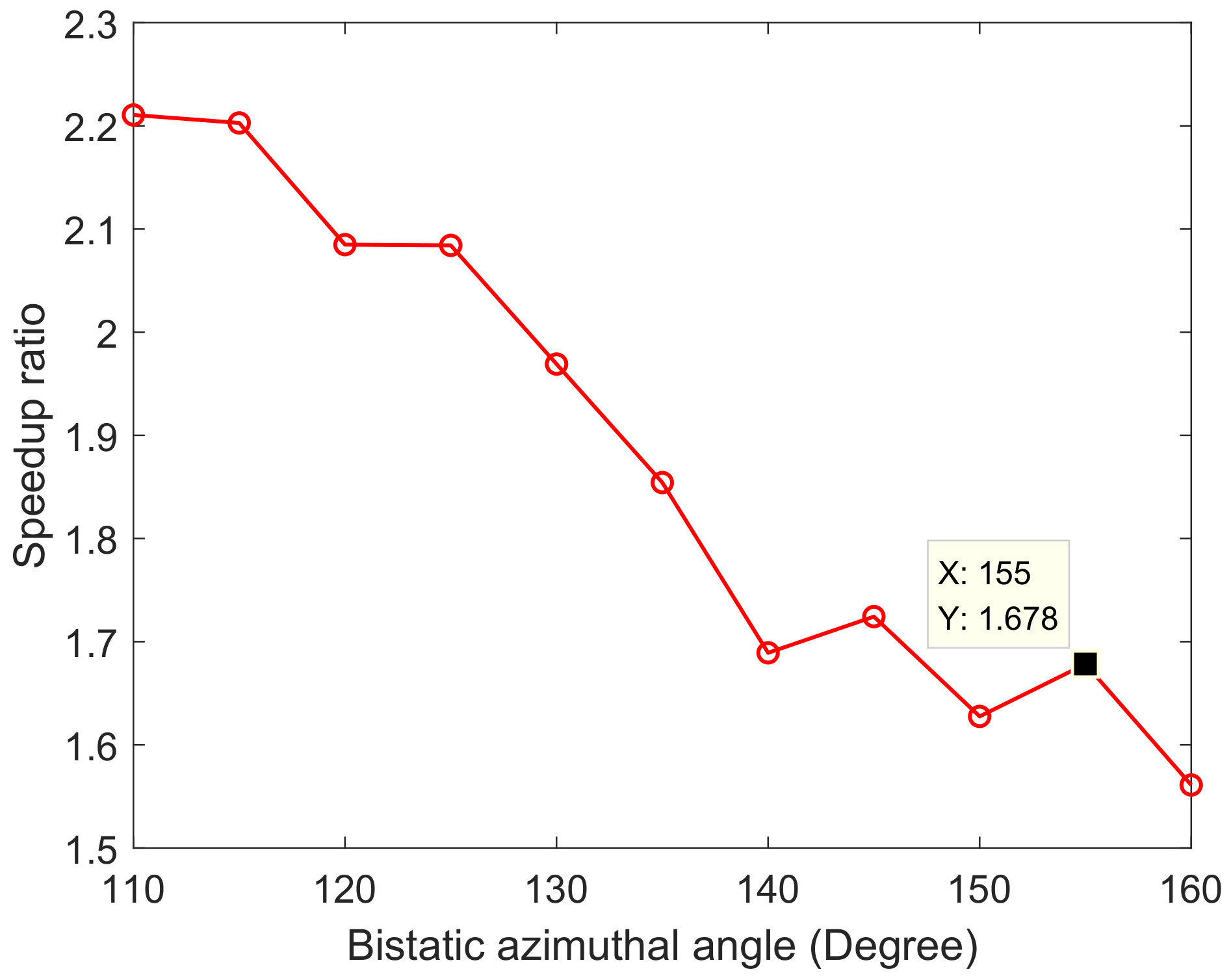
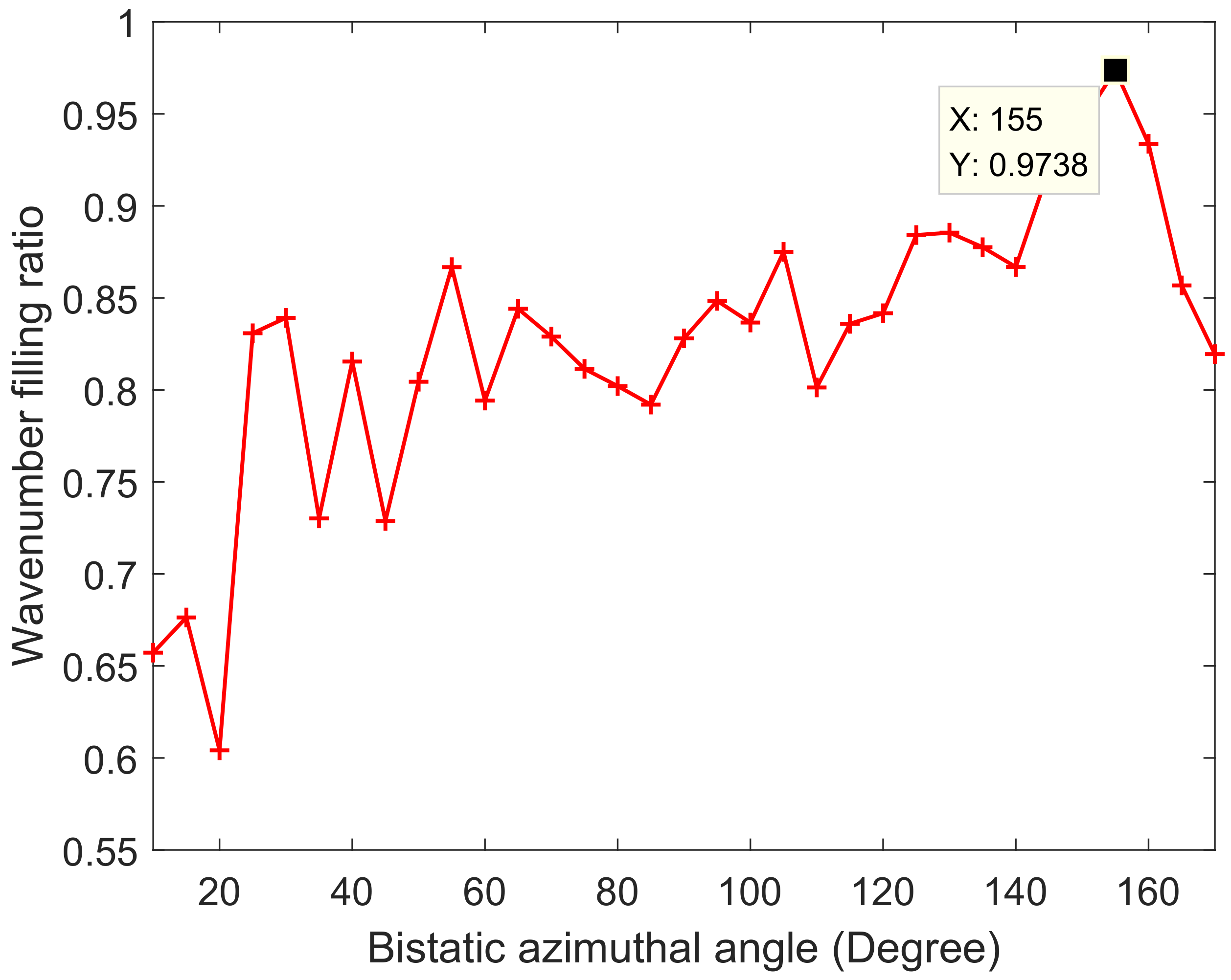
4.1.1. Geometric Configuration Design
4.1.2. Point Target Simulation
4.1.3. Distributed Targets Simulation
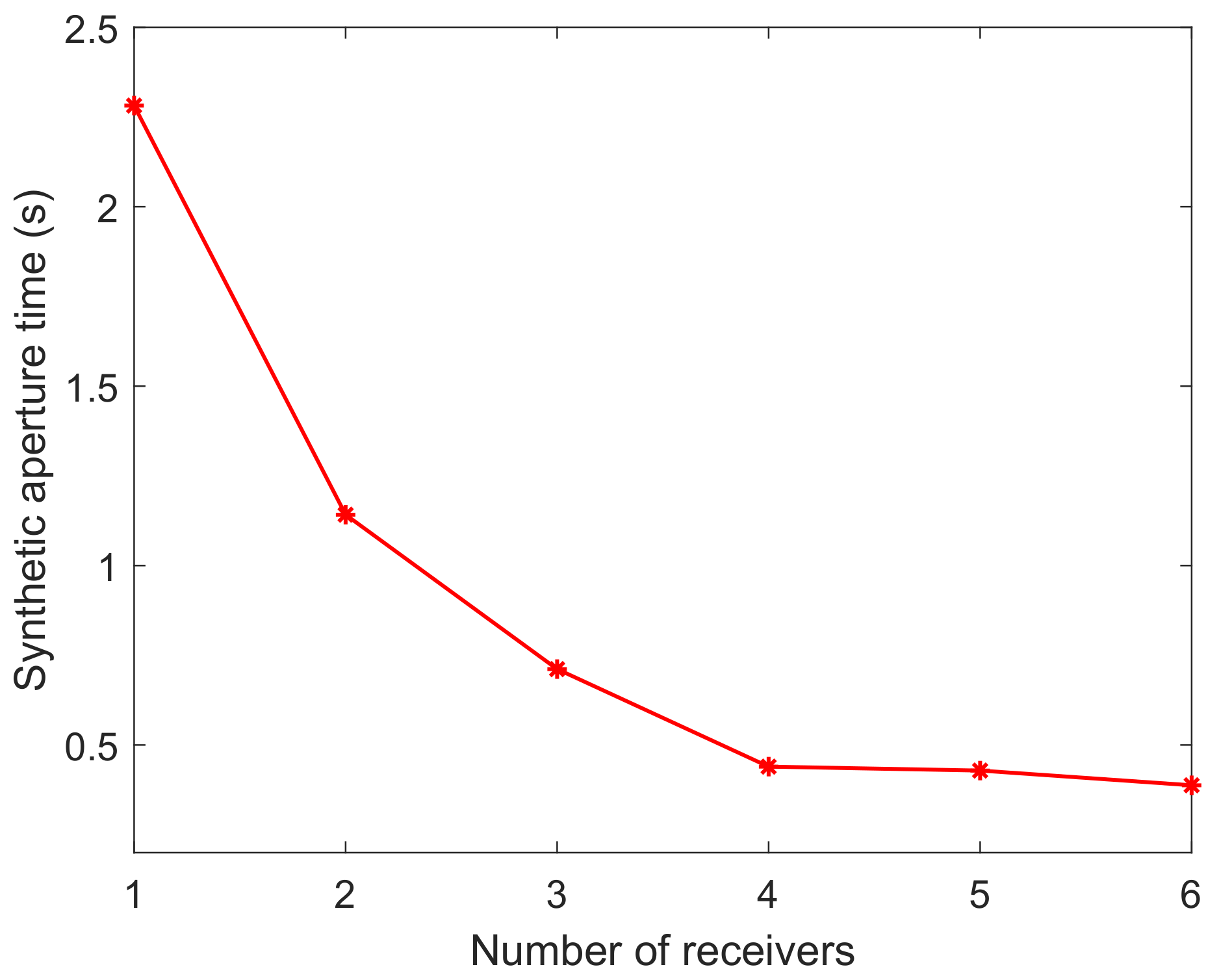
4.2. An Mu-FLSAR System with Multiple Receivers
4.3. Operational Complexity Comparison
4.4. Challenges and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.; Yuan, Y.; Zhang, S.; Zhao, H.; Chen, Y. A new imaging algorithm for forward-looking missile-borne bistatic SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1543–1552. [Google Scholar] [CrossRef]
- Li, Y.; Meng, Z.; Xing, M.; Bao, Z. Configuration study of missile-borne bistatic forward-looking SAR. In Proceedings of the 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014; IEEE: New York, NY, USA, 2014; pp. 184–188. [Google Scholar]
- Yates, G.; Horne, A.; Blake, A.; Middleton, R. Bistatic SAR image formation. IEEE Proc. Radar Sonar Navig. 2006, 153, 208–213. [Google Scholar] [CrossRef]
- Mao, D.; Yang, J.; Zhang, Y.; Huo, W.; Xu, F.; Pei, J.; Zhang, Y.; Huang, Y. Angular superresolution of real aperture radar with high-dimensional data: Normalized projection array model and adaptive reconstruction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Multistatic SAR satellite formations: Potentials and challenges. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005; IEEE: New York, NY, USA, 2005; Volume 4, pp. 2680–2684. [Google Scholar]
- D’Errico, M. Distributed Space Missions for Earth System Monitoring; Springer Science and Business Media: New York, NY, USA, 2012; Volume 31. [Google Scholar]
- Cherniakov, M. Bistatic Radar: Emerging Technology; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Massonnet, D. The interferometric cartwheel: A constellation of passive satellites to produce radar images to be coherently combined. Int. J. Remote Sensing 2001, 22, 2413–2430. [Google Scholar] [CrossRef]
- Daout, F.; Schmitt, F.; Ginolhac, G.; Fargette, P. Multistatic and multiple frequency imaging resolution analysis-application to GPS-based multistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3042–3057. [Google Scholar] [CrossRef]
- Mao, D.; Zhang, Y.; Pei, J.; Huo, W.; Zhang, Y.; Huang, Y.; Yang, J. Forward-looking geometric configuration optimization design for spaceborne-airborne multistatic synthetic aperture radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8033–8047. [Google Scholar] [CrossRef]
- Moccia, A.; Renga, A. Spatial resolution of bistatic synthetic aperture radar: Impact of acquisition geometry on imaging performance. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3487–3503. [Google Scholar] [CrossRef]
- Martin, M.; Stallard, M. Distributed satellite missions and technologies—The TechSat 21 program. In Proceedings of the Space Technology Conference and Exposition, Albuquerque, NM, USA, 28–30 September 1999; p. 4479. [Google Scholar]
- Burns, R.; McLaughlin, C.A.; Leitner, J.; Martin, M. TechSat 21: Formation design, control, and simulation. In Proceedings of the 2000 IEEE Aerospace Conference. Proceedings (Cat. No. 00TH8484), Big Sky, MT, USA, 25 March 2000; IEEE: New York, NY, USA, 2000; Volume 7, pp. 19–25. [Google Scholar]
- López-Dekker, P.; Biggs, J.; Chapron, B.; Hooper, A.; Kääb, A.; Masina, S.; Mouginot, J.; Nardelli, B.B.; Pasquero, C.; Prats-Iraola, P.; et al. The Harmony Mission: End of Phase-0 Science Overview. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2021; pp. 7752–7755. [Google Scholar]
- Lopez-Dekker, P.; Chapron, B.; Johnsen, H. Observations of Sea Surface Winds and Sea Surface Deformation with the Harmony mission. In Proceedings of the EUSAR 2021; 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021; VDE: Frankfurt, Germany, 2021; pp. 1–4. [Google Scholar]
- Stojanovic, I.; Karl, W.C. Imaging of moving targets with multi-static SAR using an overcomplete dictionary. IEEE J. Sel. Top. Signal Process. 2010, 4, 164–176. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.; Dong, X.; Cui, C.; Long, T. Impacts of temporal-spatial variant background ionosphere on repeat-track GEO D-InSAR system. Remote Sens. 2016, 8, 916. [Google Scholar] [CrossRef]
- Lazarov, A. InSAR Geometry and Basic Operations; Burgas Free University: Burgas, Bulgaria, 2010. [Google Scholar]
- Zhang, Y.; Zhang, H.; Hou, S.; Deng, Y.; Yu, W.; Wang, R. An Innovative Superpolyhedron (SP) Formation for Multistatic SAR (M-SAR) Interferometry. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10136–10150. [Google Scholar] [CrossRef]
- Rigling, B.D.; Moses, R.L. Three-dimensional surface reconstruction from multistatic SAR images. IEEE Trans. Image Process. 2005, 14, 1159–1171. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wu, J.; Pei, J.; Sun, Z.; Yang, J.; Yi, Q. Antirange-Deception Jamming From Multijammer for Multistatic SAR. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5212512. [Google Scholar] [CrossRef]
- Massonnet, D. Capabilities and limitations of the interferometric cartwheel. IEEE Trans. Geosci. Remote Sens. 2001, 39, 506–520. [Google Scholar] [CrossRef]
- Sakar, N.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Moreira, A. Azimuth reconstruction algorithm for multistatic SAR formations with large along-track baselines. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1931–1940. [Google Scholar] [CrossRef]
- Sakar, N.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Moreira, A. Doppler Based Azimuth Reconstruction Algorithm for Multistatic SAR Formations in High Resolution Wide Swath Mode. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: New York, NY, USA, 2019; pp. 1124–1127. [Google Scholar]
- Xu, F.; Zhang, Y.; Wang, R.; Mi, C.; Zhang, Y.; Huang, Y.; Yang, J. Heuristic Path Planning Method for Multistatic UAV-Borne SAR Imaging System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8522–8536. [Google Scholar] [CrossRef]
- Zhu, J.; Mao, D.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, H. A Topology Design Method Based on Wavenumber Spectrum Generation for Multistatic Synthetic Aperture Radar. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Krieger, G. Advanced bistatic and multistatic SAR concepts and applications. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), Dresden, Germany, 16–18 May 2006; VDE: Frankfurt, Germany, 2006; pp. 1–101. [Google Scholar]
- Miao, Y.; Wu, J.; Yang, J.; Gao, H. Comparison between resolution features of BPA and PFA through wavenumber domain analysis for general spotlight SAR. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: New York, NY, USA, 2019; pp. 2969–2972. [Google Scholar]
- Zeng, T.; Cherniakov, M.; Long, T. Generalized approach to resolution analysis in BSAR. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 461–474. [Google Scholar] [CrossRef]
- Yarman, C.E.; Yazici, B.; Cheney, M. Bistatic synthetic aperture radar imaging for arbitrary flight trajectories. IEEE Trans. Image Process. 2007, 17, 84–93. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Ding, C. Some reflections on bistatic SAR of forward-looking configuration. IEEE Geosci. Remote Sens. Lett. 2008, 5, 735–739. [Google Scholar] [CrossRef]
- Wu, J.; Yang, J.; Yang, H.; Huang, Y. Optimal geometry configuration of bistatic forward-looking SAR. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; IEEE: New York, NY, USA, 2009; pp. 1117–1120. [Google Scholar]
- Dogaru, T. Polar Format Algorithm for 3-D Imaging with Forward-Looking Synthetic Aperture Radar; Technical Report; Combat Capabilities Development Command Army Research Laboratory: Adelphi, MD, USA, 2020. [Google Scholar]
- Walterscheid, I.; Espeter, T.; Klare, J.; Brenner, A.R.; Ender, J.H. Potential and limitations of forward-looking bistatic SAR. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; IEEE: New York, NY, USA, 2010; pp. 216–219. [Google Scholar]
- Dower, W.; Yeary, M. Bistatic SAR: Forecasting spatial resolution. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1584–1595. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.J.; Ender, J.H. An approach to multistatic spaceborne SAR/MTI processing and performance analysis. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; IEEE: New York, NY, USA, 2003; Volume 7, pp. 4446–4449. [Google Scholar]
- Rosu, F.; Anghel, A.; Cacoveanu, R.; Rommen, B.; Datcu, M. Multiaperture Focusing for Spaceborne Transmitter/Ground-Based Receiver Bistatic SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5823–5832. [Google Scholar] [CrossRef]
- Krieger, G.; Younis, M. Impact of oscillator noise in bistatic and multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2006, 3, 424–428. [Google Scholar] [CrossRef]
- Miao, Y.; Wu, J.; Li, Z.; Yang, J. A Generalized Wavefront-Curvature-Corrected Polar Format Algorithm to Focus Bistatic SAR Under Complicated Flight Paths. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3757–3771. [Google Scholar] [CrossRef]
- Rigling, B.D.; Moses, R.L. Polar format algorithm for bistatic SAR. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1147–1159. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, L.; Zhao, L.; Bi, G. Quasi-polar-based FFBP algorithm for miniature UAV SAR imaging without navigational data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7053–7065. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, G.C.; Yang, Z.; Guo, L.; Xing, M. Cartesian factorized backprojection algorithm for high-resolution spotlight SAR imaging. IEEE Sensors J. 2017, 18, 1160–1168. [Google Scholar] [CrossRef]
- Chen, X.; Sun, G.C.; Xing, M.; Li, B.; Yang, J.; Bao, Z. Ground Cartesian Back-Projection Algorithm for High Squint Diving TOPS SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5812–5827. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, Z.; Li, J.; Li, C. Focusing Multistatic GEO SAR With Two Stationary Receivers Using Spectrum Alignment and Extrapolation. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4018805. [Google Scholar] [CrossRef]
- An, H.; Wu, J.; Sun, Z.; Yang, J.; Huang, Y.; Yang, H. Topology design for geosynchronous spaceborne–airborne multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1715–1719. [Google Scholar] [CrossRef]
- Shin, H.S.; Lim, J.T. Omega-k algorithm for airborne forward-looking bistatic spotlight SAR imaging. IEEE Geosci. Remote Sens. Lett. 2009, 6, 312–316. [Google Scholar] [CrossRef]
- Espeter, T.; Walterscheid, I.; Klare, J.; Brenner, A.R.; Ender, J.H. Bistatic forward-looking SAR: Results of a spaceborne–airborne experiment. IEEE Geosci. Remote Sens. Lett. 2011, 8, 765–768. [Google Scholar] [CrossRef]
- Pu, W.; Wu, J.; Huang, Y.; Li, W.; Sun, Z.; Yang, J.; Yang, H. Motion errors and compensation for bistatic forward-looking SAR with cubic-order processing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6940–6957. [Google Scholar] [CrossRef]
- Sakamoto, T.; Sato, T.; Aubry, P.; Yarovoy, A. Auto-focusing UWB radar imaging for moving human target using revised range point migration. In Proceedings of the The 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014; IEEE: New York, NY, USA, 2014; pp. 3600–3604. [Google Scholar]


| System Parameters | Geometric Configuration Parameters | ||
|---|---|---|---|
| Carrier frequency | 9.6 Hz | Location of transmitter | (514, 0, 100) km |
| Bandwidth | 120 MHz | Location of leader receiver | |
| Sampling frequency | 180 MHz | Location of the following receiver | |
| Time width | 10 us | Pulse repetition frequency | 800 Hz |
| Range of the leader receiver | 20 km | Magnitude of receiver speed | 340 m/s |
| Designed geometric configuration parameters | |||
| Synthetic aperture time | |||
| Azimuthal angle | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhao, Y.; Ding, Y. Geometric Configuration Design and Fast Imaging for Multistatic Forward-Looking SAR Based on Wavenumber Spectrum Formation Approach. Remote Sens. 2023, 15, 2783. https://doi.org/10.3390/rs15112783
Liu Y, Zhao Y, Ding Y. Geometric Configuration Design and Fast Imaging for Multistatic Forward-Looking SAR Based on Wavenumber Spectrum Formation Approach. Remote Sensing. 2023; 15(11):2783. https://doi.org/10.3390/rs15112783
Chicago/Turabian StyleLiu, Yumeng, Yijing Zhao, and Yi Ding. 2023. "Geometric Configuration Design and Fast Imaging for Multistatic Forward-Looking SAR Based on Wavenumber Spectrum Formation Approach" Remote Sensing 15, no. 11: 2783. https://doi.org/10.3390/rs15112783
APA StyleLiu, Y., Zhao, Y., & Ding, Y. (2023). Geometric Configuration Design and Fast Imaging for Multistatic Forward-Looking SAR Based on Wavenumber Spectrum Formation Approach. Remote Sensing, 15(11), 2783. https://doi.org/10.3390/rs15112783








