Large-Scale Land Subsidence Monitoring and Prediction Based on SBAS-InSAR Technology with Time-Series Sentinel-1A Satellite Data
Abstract
:1. Introduction
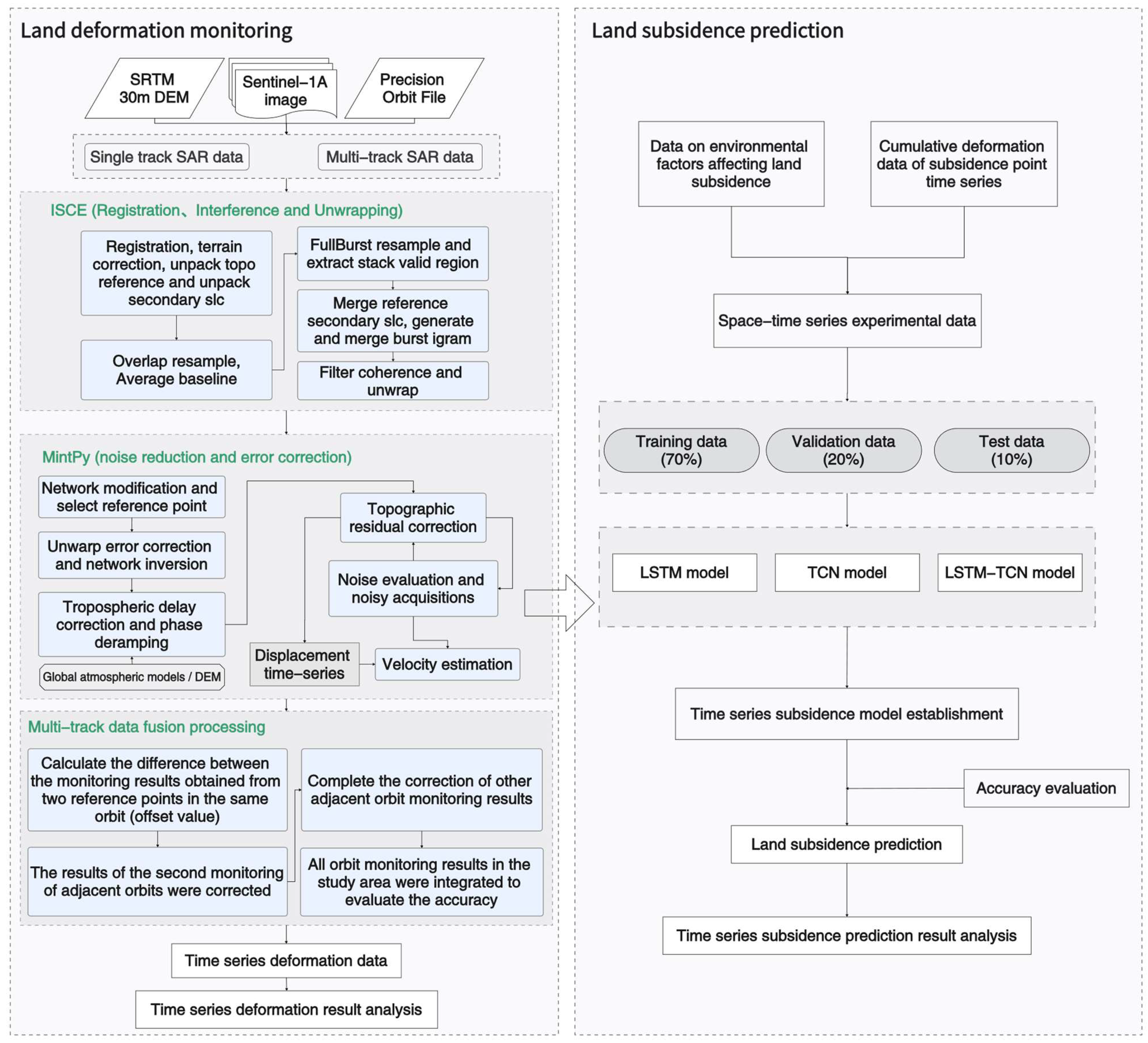
2. Materials and Process
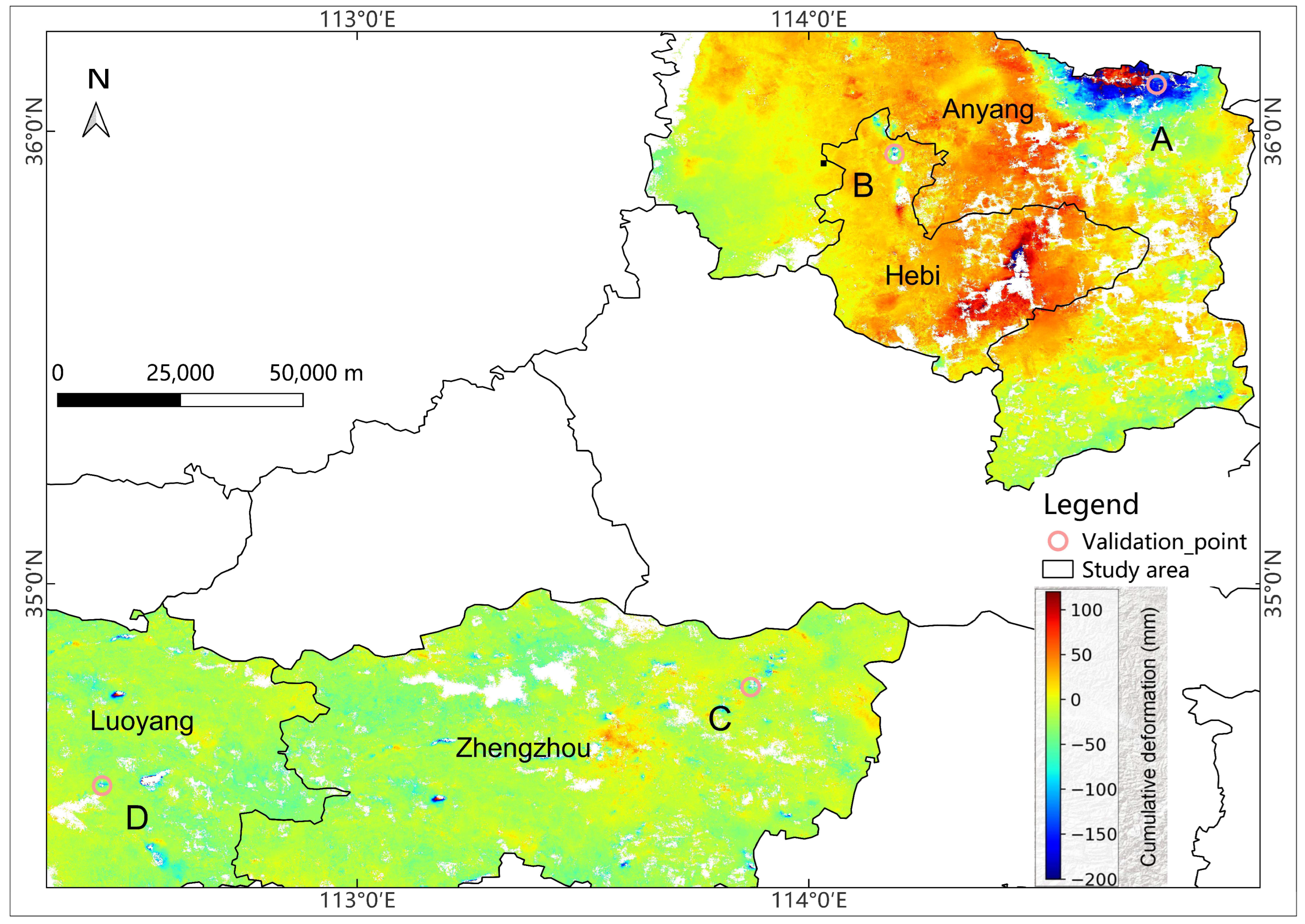
2.1. Study Area
2.2. Sentinel-1A SAR Data
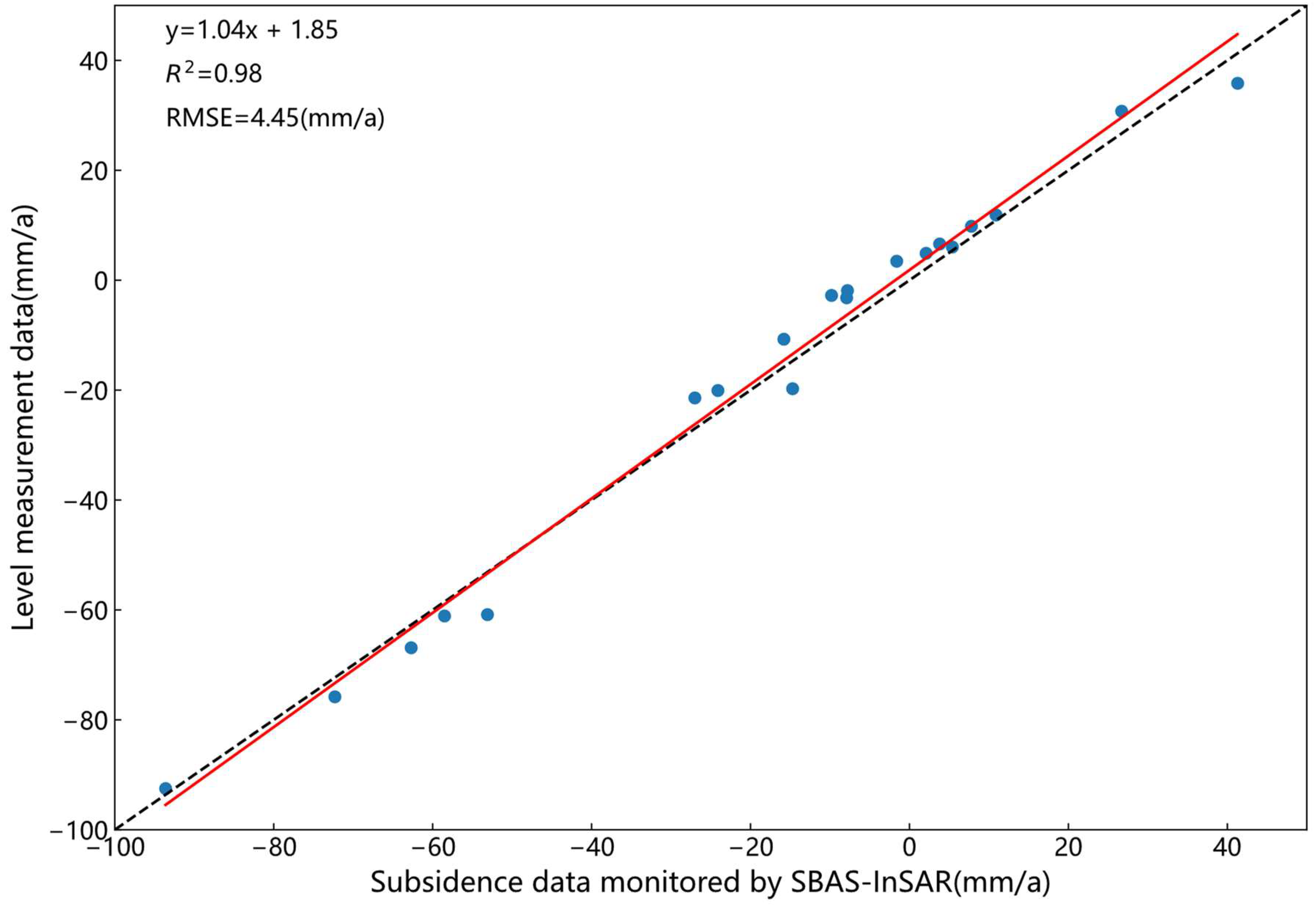
2.3. Level Measurement Data
2.4. Environmental Influencing Factor Data
3. Methods
3.1. SBAS-InSAR
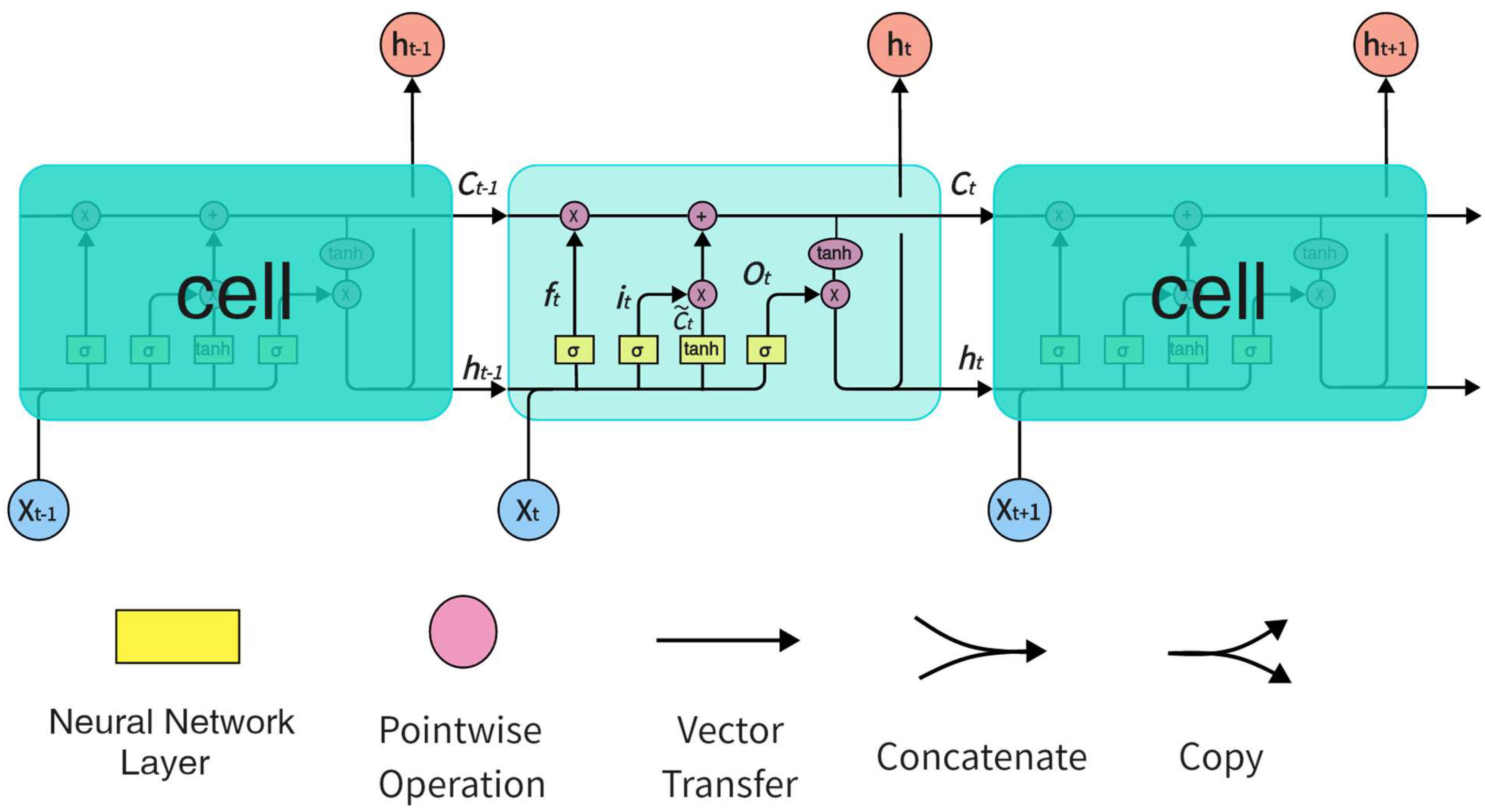
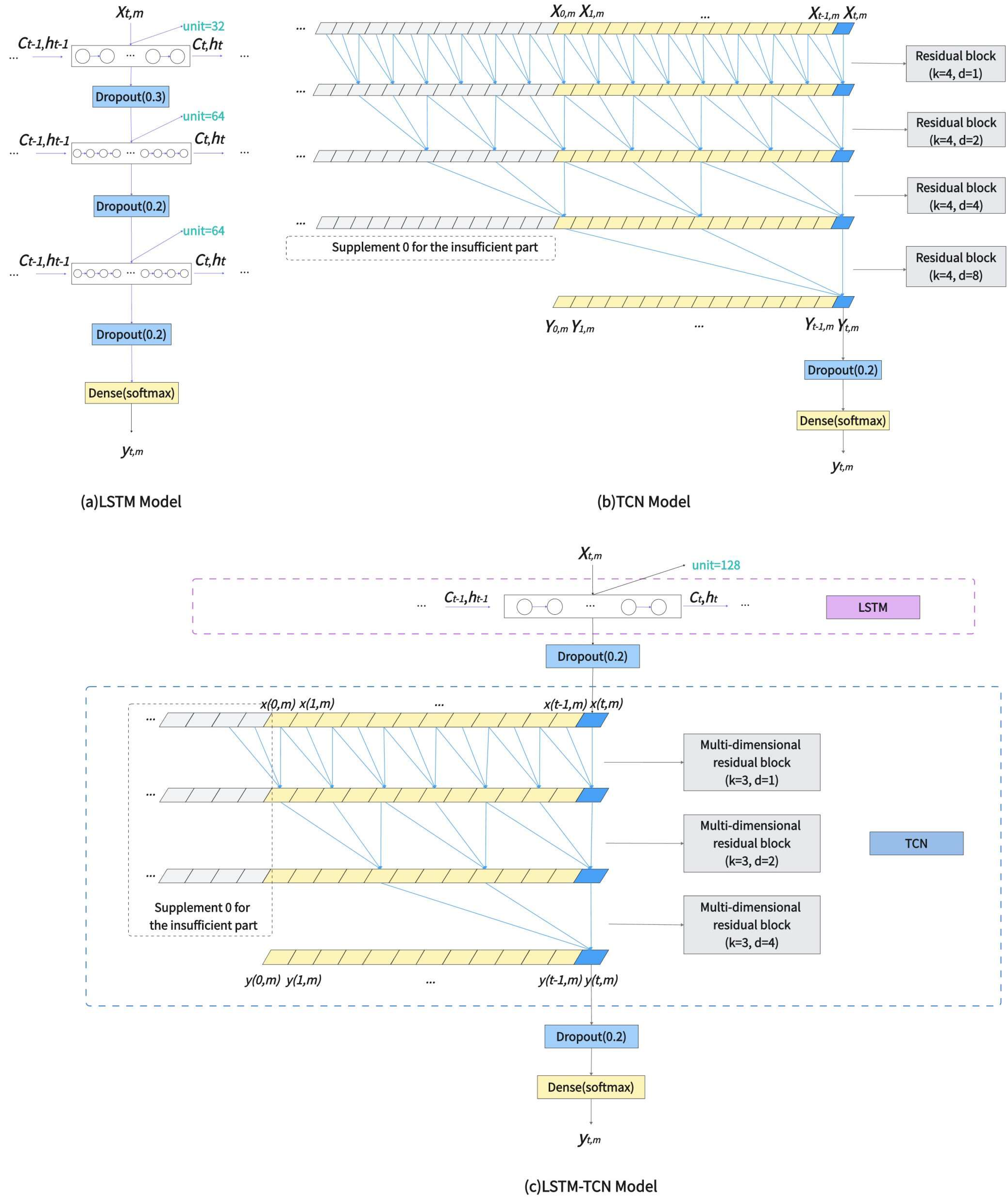
3.2. LSTM-TCN Model
4. Results
4.1. Seasonal Characteristics of Land Subsidence and Its Causal Analysis
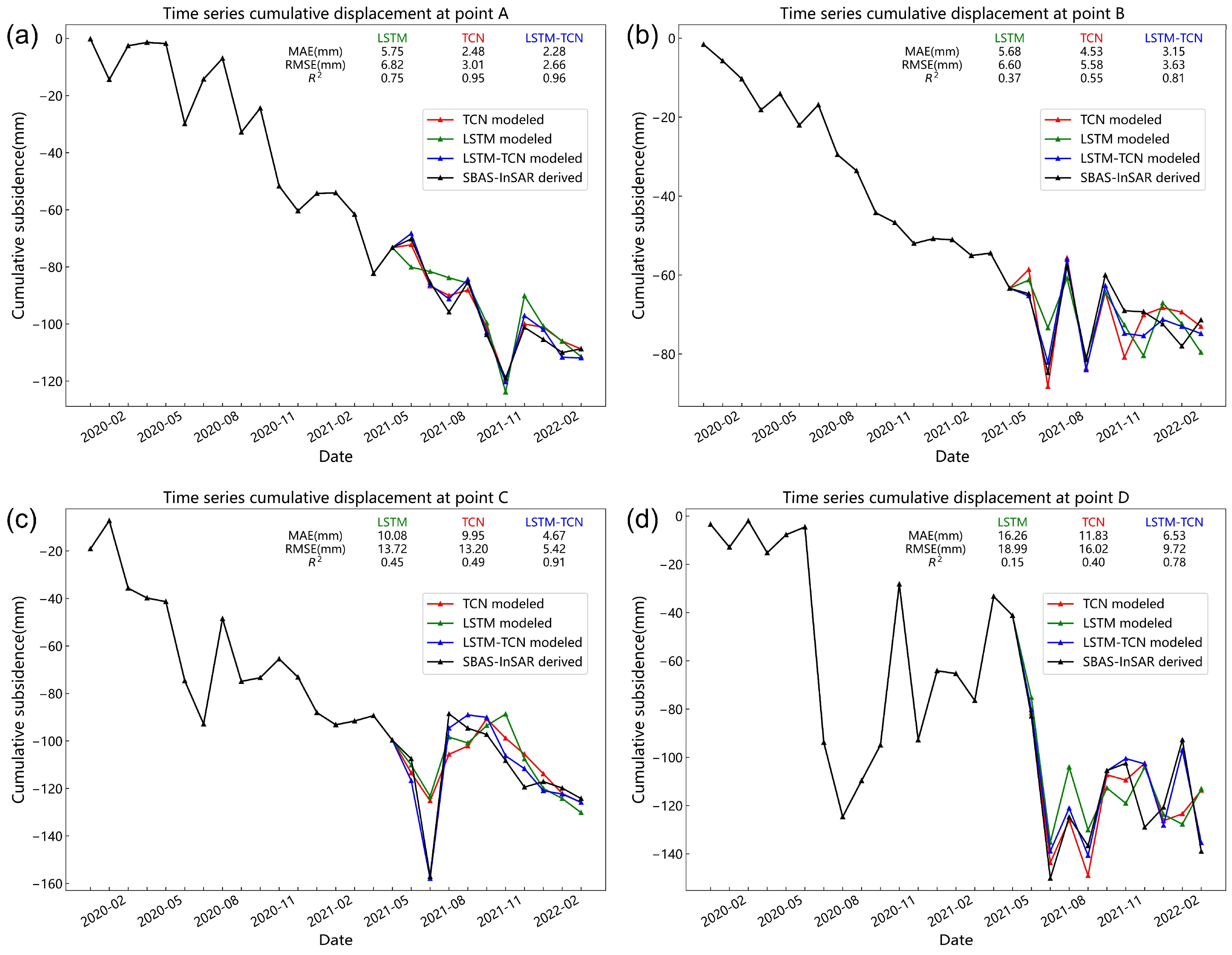
4.2. Land Subsidence Monitoring Results
4.3. Land Subsidence Model Prediction Results
5. Discussion
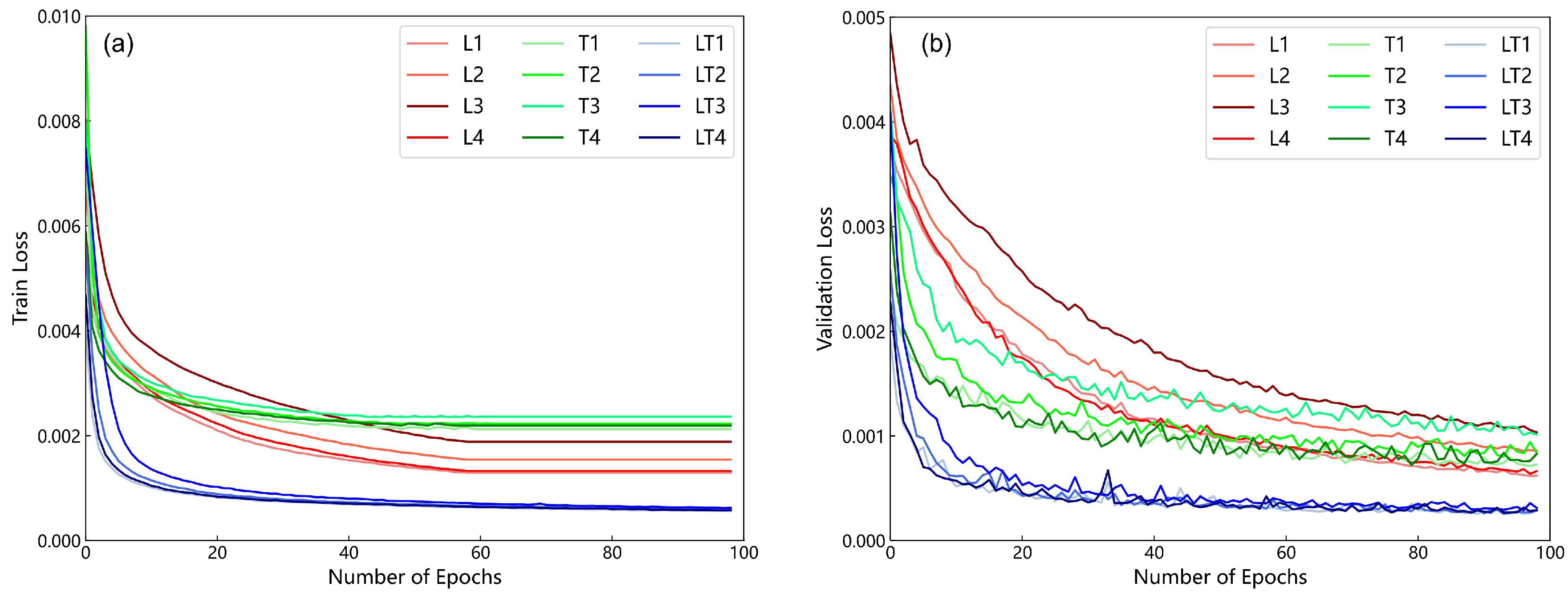
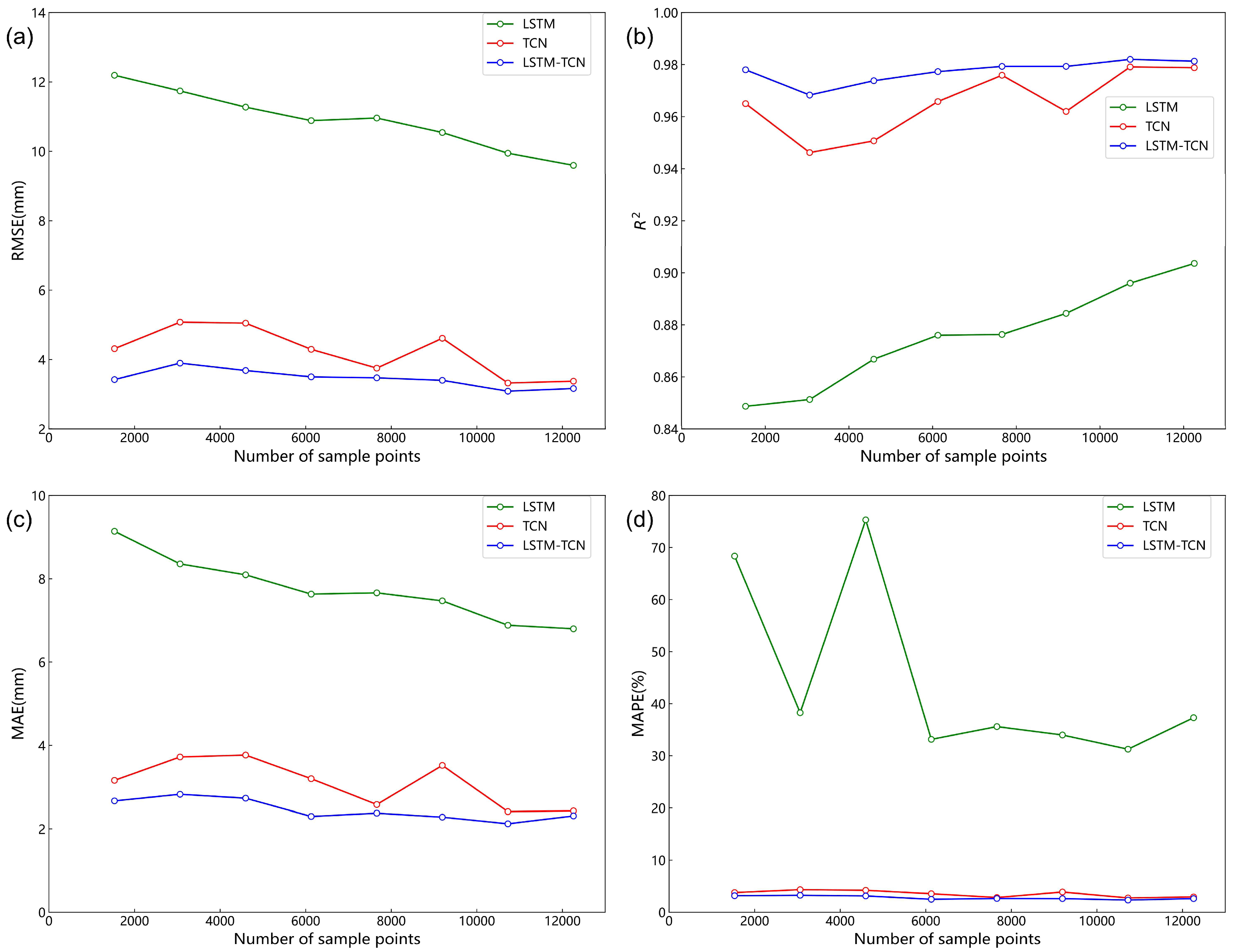
5.1. Influence of the Sample Division Ratio and Quantity on the Prediction Results
5.2. Advantages of Adding Environmental Factors
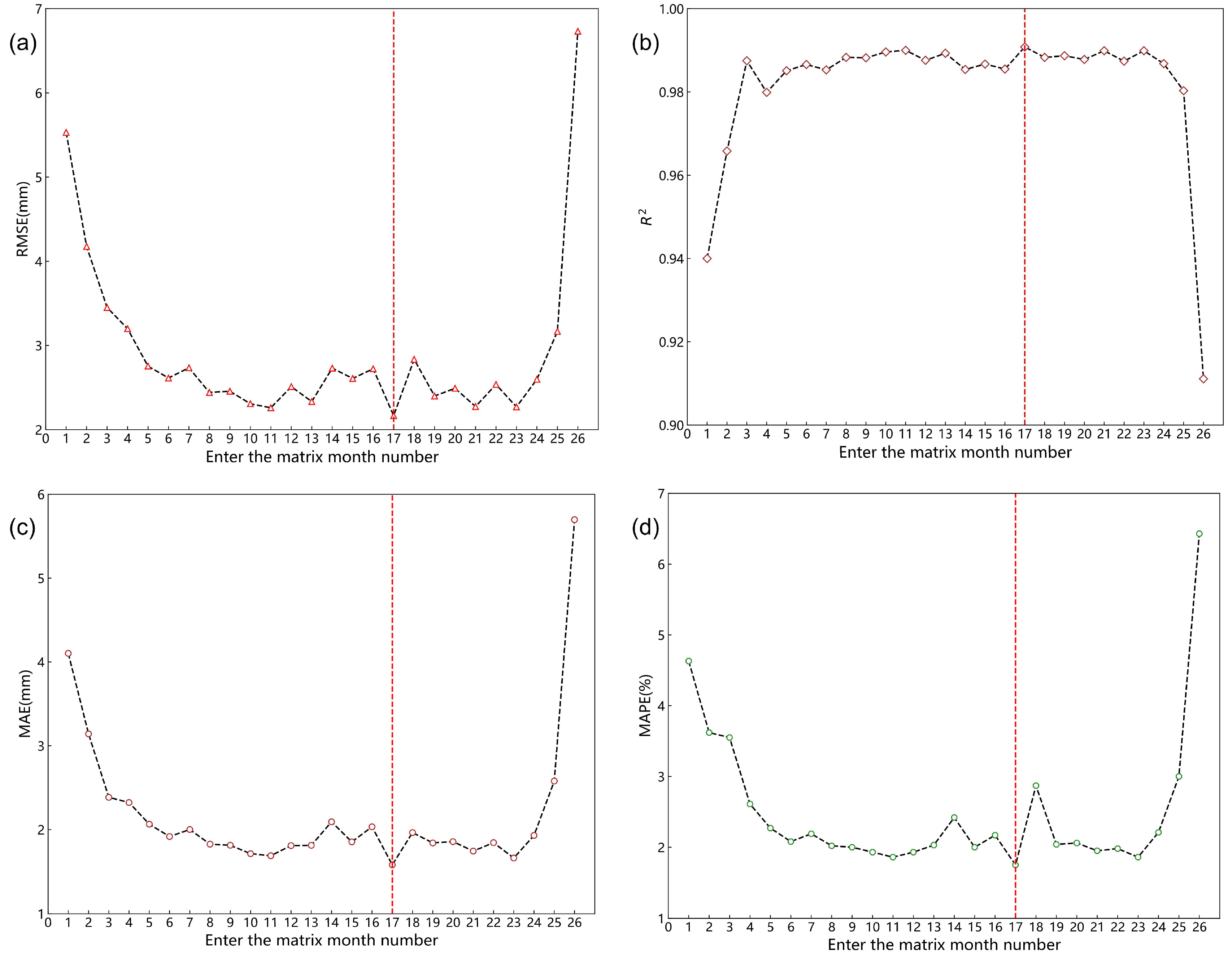
5.3. Influence of the Different Lengths on the Prediction Results
5.4. Exploration of the LSTM-TCN-Based Model in Time-Series Land Subsidence Prediction
5.5. Effect of Input Environmental Factors
6. Conclusions
- (1)
- Henan Province has undergone significant deformation in the past two years. From November 2019 to February 2022, the maximum and minimum land deformation rates in Henan Province were −94.54 mm/a and 41.23 mm/a, respectively. The most severe land subsidence occurred in Shangqiu city, and the maximum cumulative subsidence was −194.78 mm.
- (2)
- Land subsidence in the study area has obvious seasonal characteristics. The semiannual average rate of land subsidence in the study area is greater in spring and summer than in autumn and winter. The effect of precipitation on land subsidence has a certain hysteresis, and abundant precipitation in spring and summer can replenish the lower groundwater and delay land subsidence in autumn and winter. The volumetric soil layer water content shows the same trend as land subsidence.
- (3)
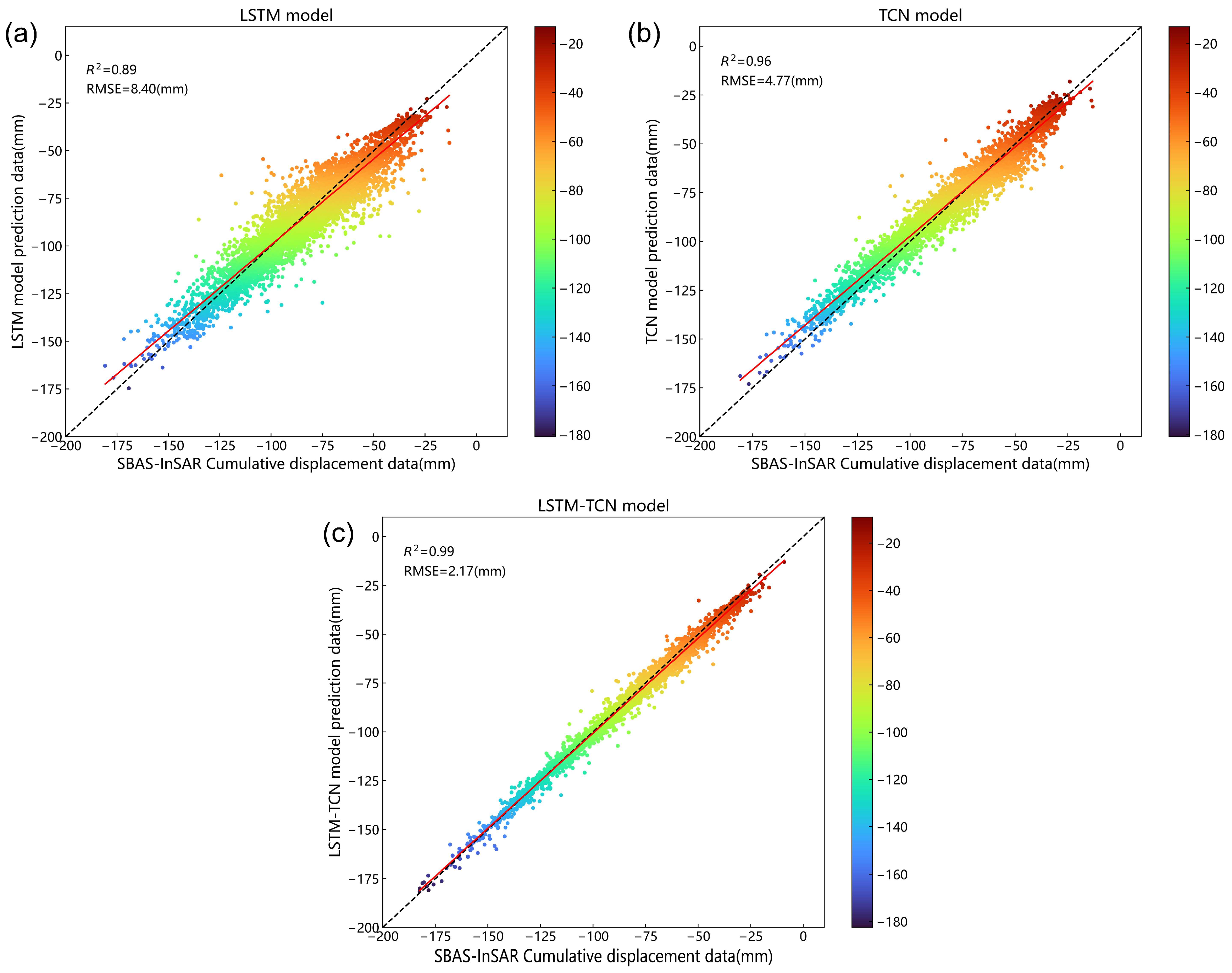
- The LSTM-TCN model can combine the advantages of the LSTM and TCN models, which is better for exploring the nonlinear characteristics of land subsidence. Specifically, the LSTM-TCN model could effectively predict the cumulative land subsidence in Henan Province, and its prediction accuracy was better than that of the LSTM and TCN models in areas with obvious subsidence. When predicting the area with subsidence exceeding 100 mm, the MAE of the LSTM-TCN model was 1.97 mm, which was 68.35% and 63.98% higher than the 6.23 mm value of the LSTM model and the 5.48 mm value of the TCN model, respectively.
- (4)
- After introducing the environmental impact factors in the prediction model, the determination coefficient of the LSTM-TCN model increased from 0.95 to 0.99, indicating that environmental factors and geological characteristics are indispensable in exploring land subsidence.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carlson, G.; Shirzaei, M.; Werth, S.; Zhai, G.; Ojha, C. Seasonal and Long-Term Groundwater Unloading in the Central Valley Modifies Crustal Stress. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018490. [Google Scholar] [CrossRef] [PubMed]
- Cianflone, G.; Vespasiano, G.; Tolomei, C.; De Rosa, R.; Dominici, R.; Apollaro, C.; Walraevens, K.; Polemio, M. Different Ground Subsidence Contributions Revealed by Integrated Discussion of Sentinel-1 Datasets, Well Discharge, Stratigraphical, and Geomorphological Data: The Case of the Gioia Tauro Coastal Plain (Southern Italy). Sustainability 2022, 14, 2926. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Satellite InSAR survey of structurally-controlled land subsidence due to groundwater exploitation in the Aguascalientes Valley, Mexico. Remote Sens. Environ. 2021, 254, 112254. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Urban growth and land subsidence: Multi-decadal investigation using human settlement data and satellite InSAR in Morelia, Mexico. Sci. Total Environ. 2022, 811, 152211. [Google Scholar] [CrossRef] [PubMed]
- Kamali Maskooni, E.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R. Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data. Remote Sens. 2020, 12, 42. [Google Scholar] [CrossRef]
- Nguyen, M.; Lin, Y.N.; Tran, Q.C.; Ni, C.-F.; Chan, Y.-C.; Tseng, K.-H.; Chang, C.-P. Assessment of long-term ground subsidence and groundwater depletion in Hanoi, Vietnam. Eng. Geol. 2022, 299, 106555. [Google Scholar] [CrossRef]
- Guzy, A.; Malinowska, A. State of the Art and Recent Advancements in the Modelling of Land Subsidence Induced by Groundwater Withdrawal. Water 2020, 12, 2051. [Google Scholar] [CrossRef]
- van Natijne, A.L.; Bogaard, T.A.; van Leijen, F.J.; Hanssen, R.F.; Lindenbergh, R.C. World-wide InSAR sensitivity index for landslide deformation tracking. Int. J. Appl. Earth Obs. Geoinf. 2022, 111, 102829. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Present-day land subsidence rates, surface faulting hazard and risk in Mexico City with 2014–2020 Sentinel-1 IW InSAR. Remote Sens. Environ. 2021, 253, 112161. [Google Scholar] [CrossRef]
- Peng, M.; Lu, Z.; Zhao, C.; Motagh, M.; Bai, L.; Conway, B.D.; Chen, H. Mapping land subsidence and aquifer system properties of the Willcox Basin, Arizona, from InSAR observations and independent component analysis. Remote Sens. Environ. 2022, 271, 112894. [Google Scholar] [CrossRef]
- Rezaei, A.; Mousavi, Z. Characterization of land deformation, hydraulic head, and aquifer properties of the Gorgan confined aquifer, Iran, from InSAR observations. J. Hydrol. 2019, 579, 124196. [Google Scholar] [CrossRef]
- Hu, L.; Navarro-Hernández, M.I.; Liu, X.; Tomás, R.; Tang, X.; Bru, G.; Ezquerro, P.; Zhang, Q. Analysis of regional large-gradient land subsidence in the Alto Guadalentín Basin (Spain) using open-access aerial LiDAR datasets. Remote Sens. Environ. 2022, 280, 113218. [Google Scholar] [CrossRef]
- Kumar Maurya, V.; Dwivedi, R.; Ranjan Martha, T. Site scale landslide deformation and strain analysis using MT-InSAR and GNSS approach–A case study. Adv. Space Res. 2022, 70, 3932–3947. [Google Scholar] [CrossRef]
- Shahbazi, S.; Mousavi, Z.; Rezaei, A. Constraints on the hydrogeological properties and land subsidence through GNSS and InSAR measurements and well data in Salmas plain, northwest of Urmia Lake, Iran. Hydrogeol. J. 2022, 30, 533–555. [Google Scholar] [CrossRef]
- Dong, J.; Lai, S.; Wang, N.; Wang, Y.; Zhang, L.; Liao, M. Multi-scale deformation monitoring with Sentinel-1 InSAR analyses along the Middle Route of the South-North Water Diversion Project in China. Int. J. Applied Earth Obs. Geoinf. 2021, 100, 102324. [Google Scholar] [CrossRef]
- Xie, X.; Xu, C.; Wen, Y.; Li, W. Monitoring Groundwater Storage Changes in the Loess Plateau Using GRACE Satellite Gravity Data, Hydrological Models and Coal Mining Data. Remote Sens. 2018, 10, 605. [Google Scholar] [CrossRef]
- Ojha, C.; Werth, S.; Shirzaei, M. Recovery of aquifer-systems in Southwest US following 2012–2015 drought: Evidence from InSAR, GRACE and groundwater level data. J. Hydrol. 2020, 587, 124943. [Google Scholar] [CrossRef]
- Vasco, D.W.; Kim, K.H.; Farr, T.G.; Reager, J.T.; Bekaert, D.; Sangha, S.S.; Rutqvist, J.; Beaudoing, H.K. Using Sentinel-1 and GRACE satellite data to monitor the hydrological variations within the Tulare Basin, California. Sci. Rep. 2022, 12, 3867. [Google Scholar] [CrossRef]
- Hou, J.; Xu, B.; Li, Z.; Zhu, Y.; Feng, G. Block PS-InSAR ground deformation estimation for large-scale areas based on network adjustment. J. Geod. 2021, 95, 111. [Google Scholar] [CrossRef]
- Lyu, M.; Ke, Y.; Guo, L.; Li, X.; Zhu, L.; Gong, H.; Constantinos, C. Change in regional land subsidence in Beijing after south-to-north water diversion project observed using satellite radar interferometry. GIScience Remote Sens. 2019, 57, 140–156. [Google Scholar] [CrossRef]
- Shi, X.; Yang, C.; Zhang, L.; Jiang, H.; Liao, M.; Zhang, L.; Liu, X. Mapping and characterizing displacements of active loess slopes along the upstream Yellow River with multi-temporal InSAR datasets. Sci. Total Environ. 2019, 674, 200–210. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Yang, Z.; Ding, X.; Zhang, B.; Zhang, L.; Lu, Z. Two decades of settlement of Hong Kong International Airport measured with multi-temporal InSAR. Remote Sens. Environ. 2020, 248, 111976. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, X.M.; Dijkstra, T.A.; Jordan, C.J.; Chen, G.; Zeng, R.Q.; Novellino, A. Forecasting the magnitude of potential landslides based on InSAR techniques. Remote Sens. Environ. 2020, 241, 111738. [Google Scholar] [CrossRef]
- Goorabi, A.; Karimi, M.; Yamani, M.; Perissin, D. Land subsidence in Isfahan metropolitan and its relationship with geological and geomorphological settings revealed by Sentinel-1A InSAR observations. J. Arid. Environ. 2020, 181, 104238. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Michel, C.; Russell, H.A.J. Surface deformation observed by InSAR shows connections with water storage change in Southern Ontario. J. Hydrol. Reg. Stud. 2020, 27, 100661. [Google Scholar] [CrossRef]
- Saowiang, K.; Giao, P.H. Numerical analysis of subsurface deformation induced by groundwater level changes in the Bangkok aquifer system. Acta Geotech. 2020, 16, 1265–1279. [Google Scholar] [CrossRef]
- Sharma, U.; Khan, A.; Dutta, V. Long-term sustainability of groundwater resources in the central Ganga Alluvial Plain, India: Study from Gomti River Basin. Environ. Dev. Sustain. 2021, 23, 16015–16037. [Google Scholar] [CrossRef]
- Wang, L.; Deng, K.; Zheng, M. Research on ground deformation monitoring method in mining areas using the probability integral model fusion D-InSAR, sub-band InSAR and offset-tracking. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101981. [Google Scholar] [CrossRef]
- Fiorentini, N.; Maboudi, M.; Leandri, P.; Losa, M.; Gerke, M. Surface Motion Prediction and Mapping for Road Infrastructures Management by PS-InSAR Measurements and Machine Learning Algorithms. Remote Sens. 2020, 12, 3976. [Google Scholar] [CrossRef]
- Hussain, M.A.; Chen, Z.; Shoaib, M.; Shah, S.U.; Khan, J.; Ying, Z. Sentinel-1A for monitoring land subsidence of coastal city of Pakistan using Persistent Scatterers In-SAR technique. Sci. Rep. 2022, 12, 5294. [Google Scholar] [CrossRef]
- Zhang, Z.; Zeng, Q.; Jiao, J. Deformations monitoring in complicated-surface areas by adaptive distributed Scatterer InSAR combined with land cover: Taking the Jiaju landslide in Danba, China as an example. ISPRS J. Photogramm. Remote Sens. 2022, 186, 102–122. [Google Scholar] [CrossRef]
- Chang, F.; Dong, S.; Yin, H.; Wu, Z. Using the SBAS InSAR technique to monitor surface deformation in the Kuqa fold-thrust belt, Tarim Basin, NW China. J. Asian Earth Sci. 2022, 231, 105212. [Google Scholar] [CrossRef]
- Li, S.; Xu, W.; Li, Z. Review of the SBAS InSAR Time-series algorithms, applications, and challenges. Geod. Geodyn. 2022, 13, 114–126. [Google Scholar] [CrossRef]
- Li, X.; Yan, L.; Lu, L.; Huang, G.; Zhao, Z.; Lu, Z. Adjacent-Track InSAR Processing for Large-Scale Land Subsidence Monitoring in the Hebei Plain. Remote Sens. 2021, 13, 795. [Google Scholar] [CrossRef]
- Sabrian, P.G.; Saepuloh, A.; Kashiwaya, K.; Koike, K. Combined SBAS-InSAR and geostatistics to detect topographic change and fluid paths in geothermal areas. J. Volcanol. Geotherm. Res. 2021, 416, 107272. [Google Scholar] [CrossRef]
- Chen, M.; Tomás, R.; Li, Z.; Motagh, M.; Li, T.; Hu, L.; Gong, H.; Li, X.; Yu, J.; Gong, X. Imaging Land Subsidence Induced by Groundwater Extraction in Beijing (China) Using Satellite Radar Interferometry. Remote Sens. 2016, 8, 486. [Google Scholar] [CrossRef]
- Chitsazan, M.; Rahmani, G.; Ghafoury, H. Land subsidence susceptibility mapping using PWRSTFAL framework and analytic hierarchy process: Fuzzy method (case study: Damaneh-Daran Plain in the west of Isfahan Province, Iran). Environ. Monit. Assess. 2022, 194, 192. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Tiefenbacher, J.P.; Cerda, A.; Biggs, T.; Pradhan, B.; Ngo, P.T.T.; Collins, A.L. A novel ensemble computational intelligence approach for the spatial prediction of land subsidence susceptibility. Sci. Total Environ. 2020, 726, 138595. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Chen, Y.; Lei, K.; Zhou, C.; Si, Y.; Li, X.; Pan, Y.; Gao, M. Investigating land subsidence and its causes along Beijing high-speed railway using multi-platform InSAR and a maximum entropy model. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102284. [Google Scholar] [CrossRef]
- Hakim, W.; Achmad, A.; Lee, C.-W. Land Subsidence Susceptibility Mapping in Jakarta Using Functional and Meta-Ensemble Machine Learning Algorithm Based on Time-Series InSAR Data. Remote Sens. 2020, 12, 3627. [Google Scholar] [CrossRef]
- Li, H.; Zhu, L.; Dai, Z.; Gong, H.; Guo, T.; Guo, G.; Wang, J.; Teatini, P. Spatiotemporal modeling of land subsidence using a geographically weighted deep learning method based on PS-InSAR. Sci. Total Environ. 2021, 799, 149244. [Google Scholar] [CrossRef]
- Mohammady, M.; Pourghasemi, H.R.; Amiri, M.; Tiefenbacher, J.P. Spatial modeling of susceptibility to subsidence using machine learning techniques. Stoch. Environ. Res. Risk Assess. 2021, 35, 1689–1700. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Deng, M.; Wu, H.; Kang, Y.; Wei, J. Time series prediction method of large-scale surface subsidence based on deep learning. Acta Geod. Cartogr. Sin. 2021, 50, 396–404. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, G. Prediction of Composite Foundation Settlement Based on Multi-Variable Gray Model. Appl. Mech. Mater. 2014, 580–583, 669–673. [Google Scholar] [CrossRef]
- Zhou, D.; Zuo, X.; Zhao, Z. Constructing a Large-Scale Urban Land Subsidence Prediction Method Based on Neural Network Algorithm from the Perspective of Multiple Factors. Remote Sens. 2022, 14, 1803. [Google Scholar] [CrossRef]
- Hill, P.; Biggs, J.; Ponce-López, V.; Bull, D. Time-Series Prediction Approaches to Forecasting Deformation in Sentinel-1 InSAR Data. J. Geophys. Research. Solid Earth: JGR 2021, 126, e2020JB020176. [Google Scholar] [CrossRef]
- Ding, Q.; Shao, Z.; Huang, X.; Altan, O.; Zhuang, Q.; Hu, B. Monitoring, analyzing and predicting urban surface subsidence: A case study of Wuhan City, China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102422. [Google Scholar] [CrossRef]
- Bai, S.; Zico Kolter, J.; Koltun, V.J.a.e.-p. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. Available online: https://ui.adsabs.harvard.edu/abs/2018arXiv180301271B (accessed on 20 March 2022).
- Jiang, Y.; Yang, K.; Shao, C.; Zhou, X.; Zhao, L.; Chen, Y.; Wu, H. A downscaling approach for constructing high-resolution precipitation dataset over the Tibetan Plateau from ERA5 reanalysis. Atmos. Res. 2021, 256, 105574. [Google Scholar] [CrossRef]
- Rosen, P.A.; Gurrola, E.M.; Agram, P.; Cohen, J.; Lavalle, M.; Riel, B.V.; Fattahi, H.; Aivazis, M.A.G.; Simons, M.; Buckley, S.M. The InSAR Scientific Computing Environment 3.0: A Flexible Framework for NISAR Operational and User-Led Science Processing. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4897–4900. [Google Scholar] [CrossRef]
- Zhang, Y.; Heresh, F.; Falk, A. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef]
- Li, H.; Zhu, L.; Gong, H.; Sun, H.; Yu, J. Land subsidence modelling using a long short-term memory algorithm based on time-series datasets. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 505–510. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Naghibi, S.A.; Khodaei, B.; Hashemi, H. An integrated InSAR-machine learning approach for ground deformation rate modeling in arid areas. J. Hydrol. 2022, 608, 127627. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Y.; Xu, S.; He, Y.; Li, Z.; Yu, X.; Liang, Y.; Wu, W.; Wang, Y. Combining a class-weighted algorithm and machine learning models in landslide susceptibility mapping: A case study of Wanzhou section of the Three Gorges Reservoir, China. Comput. Geosci. 2022, 158, 104966. [Google Scholar] [CrossRef]
- Chen, Y.; He, Y.; Zhang, L.; Chen, Y.; Pu, H.; Chen, B.; Gao, L. Prediction of InSAR deformation time-series using a long short-term memory neural network. Int. J. Remote Sens. 2021, 42, 6919–6942. [Google Scholar] [CrossRef]
- He, Y.; Yao, H.; Yang, W.; Yao, S.; Zhang, L.; Chen, Y.; Liu, T. Time-Series Analysis and Prediction of Surface Deformation in the Jinchuan Mining Area, Gansu Province, by Using InSAR and CNN–PhLSTM Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6732–6751. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Wei, J.; Wu, H. and Deng, M. HLSTM: Heterogeneous Long Short-Term Memory Network for Large-Scale InSAR Ground Subsidence Prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8679–8688. [Google Scholar] [CrossRef]
- Li, R.; Sun, J. Monitoring and prediction of tailings pond settlement based on integration of SBAS-InSAR and GS-LSTM. Met. Mine 2023, 1, 102–109. [Google Scholar] [CrossRef]
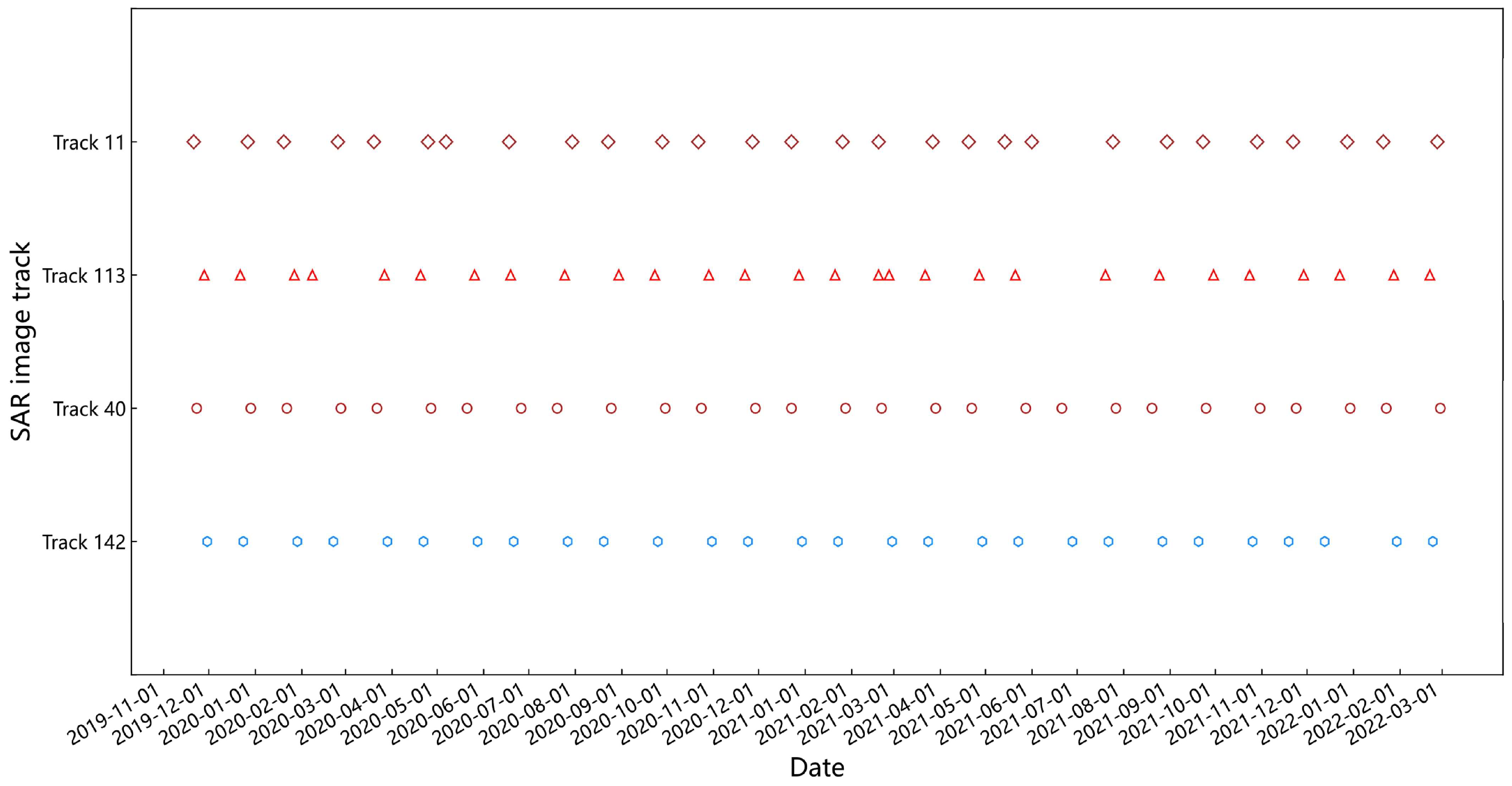



| Orbital Number | Quantity | Polarizations |
|---|---|---|
| Track 11 | 84 | VV + VH |
| Track 113 | 112 | VV + VH |
| Track 40 | 112 | VV + VH |
| Track 142 | 56 | VV + VH |
| Name | Depth | Range of Elevation | Soil Type |
|---|---|---|---|
| Volume soil layer 1 | 0~7 cm | 23.2~2413.8 m | Silty clay, soft soil |
| Volume soil layer 2 | 7~28 cm | 23.1~2414.5 m | Silty clay, soft soil |
| Volume soil layer 3 | 28~100 cm | 22.9~2412.8 m | Silty clay, soft soil |
| Volume soil layer 4 | 100~289 cm | 22.3~2410.8 m | Silty clay, soft soil |
| Indicators | The Semiannual Average in Spring and Summer | The Semiannual Average in Autumn and Winter |
|---|---|---|
| Accumulated subsidence | −17.61 mm/semiannual | −16.42 mm/semiannual |
| Precipitation | 619.29 mm/semiannual | 229.61 mm/semiannual |
| Volumetric soil layer water content (first layer) | 1.33 m3m−3/semiannual | 1.62 m3m−3/semiannual |
| Volumetric soil layer water content (second layer) | 1.29 m3m−3/semiannual | 1.64 m3m−3/semiannual |
| Volumetric soil layer water content (third layer) | 1.24 m3m−3/semiannual | 1.78 m3m−3/semiannual |
| Volumetric soil layer water content (fourth layer) | 1.20 m3m−3/semiannual | 1.65 m3m−3/semiannual |
| Methods | lr | Batch Size | Epochs | LSTM Layer | Atrous Convolution Layers | |
|---|---|---|---|---|---|---|
| LSTM | L1 | 0.0002 | 32 | 100 | 2 | 0 |
| L2 | 0.0002 | 64 | 100 | 3 | 0 | |
| L3 | 0.0002 | 128 | 100 | 3 | 0 | |
| L4 | 0.0003 | 64 | 100 | 3 | 0 | |
| TCN | T1 | 0.0002 | 32 | 100 | 0 | 3 |
| T2 | 0.0002 | 64 | 100 | 0 | 4 | |
| T3 | 0.0002 | 128 | 100 | 0 | 5 | |
| T4 | 0.0003 | 64 | 100 | 0 | 4 | |
| LSTM-TCN | LT1 | 0.0002 | 32 | 100 | 1 | 3 |
| LT2 | 0.0002 | 64 | 100 | 1 | 4 | |
| LT3 | 0.0002 | 128 | 100 | 1 | 5 | |
| LT4 | 0.0003 | 64 | 100 | 1 | 3 | |
| Methods | LSTM | TCN | LSTM-TCN |
|---|---|---|---|
| MAE (mm) | 6.16 | 3.51 | 1.58 |
| MAPE (%) | 8.79 | 4.69 | 1.75 |
| The prediction error is less than 3 mm (%) | 34.71 | 55.41 | 87.70 |
| 0~100 mm mean absolute error (mm) | 5.81 | 3.12 | 1.44 |
| 100~200 mm mean absolute error (mm) | 6.23 | 5.48 | 1.97 |
| Methods | RMSE (mm) | MAE (mm) | MAPE (%) | Prediction Error Is Less than 3 mm (%) | |
|---|---|---|---|---|---|
| LSTM (Univariate) | 9.88 | 0.84 | 7.03 | 9.72 | 29.35 |
| LSTM | 8.40 | 0.89 | 6.16 | 8.79 | 34.71 |
| TCN (Univariate) | 6.27 | 0.94 | 4.54 | 6.42 | 46.06 |
| TCN | 4.77 | 0.96 | 3.51 | 4.69 | 55.41 |
| LSTM-TCN (Univariate) | 5.43 | 0.95 | 4.17 | 5.19 | 50.52 |
| LSTM-TCN | 2.17 | 0.99 | 1.58 | 1.75 | 87.70 |
| Soil Type | Underground Depth | Soil Properties |
|---|---|---|
| Powdery clay | 8~13.2 m | Yellowish-brown, high dry strength, high toughness. |
| Powdered clay | 5.4~8 m | Yellowish-brown, low dry strength, low toughness. |
| Powdered sand | 13.2~14.5 m | Brownish-yellow, mainly chalky sand interspersed with a lot of chalky soil. |
| Fine Sand | 14.5~26.7 m | Brownish-yellow, with a few mica fragments, and average grain gradation. |
| Study Area | Input Factor | Number of Subsidence Points | RMSE (mm) | MAE (mm) |
|---|---|---|---|---|
| Zhengzhou City | Volumetric soil water content (1,2,3,4), precipitation. | 201 | 1.92 | 1.21 |
| Zhengzhou City | Monthly stabilization of groundwater level, precipitation. | 201 | 1.48 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Yuan, Y.; Wang, J.; Cui, J.; Zhang, D.; Zhang, R.; Cao, Q.; Li, J.; Dai, W.; Bao, H.; et al. Large-Scale Land Subsidence Monitoring and Prediction Based on SBAS-InSAR Technology with Time-Series Sentinel-1A Satellite Data. Remote Sens. 2023, 15, 2843. https://doi.org/10.3390/rs15112843
Guo H, Yuan Y, Wang J, Cui J, Zhang D, Zhang R, Cao Q, Li J, Dai W, Bao H, et al. Large-Scale Land Subsidence Monitoring and Prediction Based on SBAS-InSAR Technology with Time-Series Sentinel-1A Satellite Data. Remote Sensing. 2023; 15(11):2843. https://doi.org/10.3390/rs15112843
Chicago/Turabian StyleGuo, Hengliang, Yonghao Yuan, Jinyang Wang, Jian Cui, Dujuan Zhang, Rongrong Zhang, Qiaozhuoran Cao, Jin Li, Wenhao Dai, Haoming Bao, and et al. 2023. "Large-Scale Land Subsidence Monitoring and Prediction Based on SBAS-InSAR Technology with Time-Series Sentinel-1A Satellite Data" Remote Sensing 15, no. 11: 2843. https://doi.org/10.3390/rs15112843
APA StyleGuo, H., Yuan, Y., Wang, J., Cui, J., Zhang, D., Zhang, R., Cao, Q., Li, J., Dai, W., Bao, H., Qiao, B., & Zhao, S. (2023). Large-Scale Land Subsidence Monitoring and Prediction Based on SBAS-InSAR Technology with Time-Series Sentinel-1A Satellite Data. Remote Sensing, 15(11), 2843. https://doi.org/10.3390/rs15112843






