Hyperspectral Unmixing Using Robust Deep Nonnegative Matrix Factorization
Abstract
1. Introduction
2. Methodology
2.1. Linear Mixing Model
2.2. DNMF
2.3. Proposed -RDNMF
| Algorithm 1 Proposed -RDNMF |
| Input: HSI data ; number of layers L; inner ranks . |
| Output: Endmembers ; abundances . |
| Pretraining stage: |
| 1: for do |
| 2: Obtain initial and by VCA-FCLS. |
| 3: repeat |
| 4: Compute using Equation (21). |
| 5: Update by Equation (22). |
| 6: Update by Equation (23). |
| 7: until convergence |
| 8: end for |
| Fine-tuning stage: |
| 9: repeat |
| 10: for do |
| 11: Compute using Equation (8). |
| 12: Compute using Equation (9). |
| 13: Compute using Equation (26). |
| 14: Update by Equation (28). |
| 15: end for |
| 16: Update by Equation (29). |
| 17: until the stopping criterion is satisfied. |
| 18: Compute using Equation (14). |
| 19: Compute using Equation (15). |
| 20: return and |
2.4. Implementation Issues
3. Experiments
3.1. Experiments on Synthetic Data
3.1.1. Experiment 1 (Investigation of the Number of Layers)
3.1.2. Experiment 2 (Investigation of Noise Intensities)
3.1.3. Experiment 3 (Investigation of Noise Types)
3.2. Experiments on Real Data
3.2.1. Samson Dataset
3.2.2. Cuprite Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, X.R.; Li, H.C.; Wang, R.; Du, Q.; Jia, X.; Plaza, A.J. Hyperspectral unmixing based on nonnegative matrix factorization: A comprehensive review. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2022, 15, 4414–4436. [Google Scholar] [CrossRef]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. Hyperspectral unmixing via L1/2 sparsity-constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4282–4297. [Google Scholar] [CrossRef]
- Huck, A.; Guillaume, M.; Blanc-Talon, J. Minimum dispersion constrained nonnegative matrix factorization to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2590–2602. [Google Scholar] [CrossRef]
- Lu, X.; Wu, H.; Yuan, Y.; Yan, P.; Li, X. Manifold regularized sparse NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2815–2826. [Google Scholar] [CrossRef]
- Wang, N.; Du, B.; Zhang, L. An endmember dissimilarity constrained non-negative matrix factorization method for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 554–569. [Google Scholar] [CrossRef]
- Lei, T.; Zhou, J.; Qian, Y.; Xiao, B.; Gao, Y. Nonnegative-matrix-factorization-based hyperspectral unmixing with partially known endmembers. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6531–6544. [Google Scholar]
- Févotte, C.; Dobigeon, N. Nonlinear hyperspectral unmixing with robust nonnegative matrix factorization. IEEE Trans. Image Process. 2015, 24, 4810–4819. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral unmixing with robust collaborative sparse regression. Remote Sens. 2016, 8, 588. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L. Sparsity-regularized robust non-negative matrix factorization for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4267–4279. [Google Scholar] [CrossRef]
- Ding, C.; Zhou, D.; He, X.; Zha, H. R1-PCA: Rotational invariant L1-norm principal component analysis for robust subspace factorization. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 281–288. [Google Scholar]
- Nie, F.; Huang, H.; Cai, X.; Ding, C.H. Efficient and robust feature selection via joint ℓ2,1-norms minimization. In Advances in Neural Information Processing Systems 23 (NIPS 2010); Morgan Kaufmann: Vancouver, BC, Canada, 2010; pp. 1813–1821. [Google Scholar]
- Huang, H.; Ding, C. Robust tensor factorization using R1 norm. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–8. [Google Scholar]
- Ren, C.X.; Dai, D.Q.; Yan, H. Robust classification using ℓ2,1-norm based regression model. Pattern Recognit. 2012, 45, 2708–2718. [Google Scholar] [CrossRef]
- Yang, S.; Hou, C.; Zhang, C.; Wu, Y. Robust non-negative matrix factorization via joint sparse and graph regularization for transfer learning. Neur. Comput. Appl. 2013, 23, 541–559. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C.; Mei, X.; Liu, C.; Ma, J. Robust sparse hyperspectral unmixing with ℓ2,1 norm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1227–1239. [Google Scholar] [CrossRef]
- Kong, D.; Ding, C.; Huang, H. Robust nonnegative matrix factorization using L21-norm. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; ACM: New York, NY, USA, 2011; pp. 673–682. [Google Scholar]
- Wang, Y.; Pan, C.; Xiang, S.; Zhu, F. Robust hyperspectral unmixing with correntropy-based metric. IEEE Trans. Image Process. 2015, 24, 4027–4040. [Google Scholar] [PubMed]
- Li, X.; Huang, R.; Zhao, L. Correntropy-based spatial-spectral robust sparsity-regularized hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1453–1471. [Google Scholar] [CrossRef]
- Wang, H.; Yang, W.; Guan, N. Cauchy sparse NMF with manifold regularization: A robust method for hyperspectral unmixing. Knowl.-Based Syst. 2019, 184, 104898. [Google Scholar] [CrossRef]
- Huang, R.; Li, X.; Zhao, L. Spectral-spatial robust nonnegative matrix factorization for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8235–8254. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, Y.; Sun, W.; Du, Q.; Xia, L. Self-paced nonnegative matrix factorization for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1501–1515. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, P.; Li, Y.; Wang, H.; Yang, Y. Spectrum interference-based two-level data augmentation method in deep learning for automatic modulation classification. Neur. Comput. Appl. 2021, 33, 7723–7745. [Google Scholar]
- Zhao, M.; Liu, Q.; Jha, A.; Deng, R.; Yao, T.; Mahadevan-Jansen, A.; Tyska, M.J.; Millis, B.A.; Huo, Y. VoxelEmbed: 3D instance segmentation and tracking with voxel embedding based deep learning. In Proceedings of the Machine Learning in Medical Imaging: 12th International Workshop, MLMI 2021, Held in Conjunction with MICCAI 2021, Strasbourg, France, 27 September 2021, Proceedings 12; Springer: Berlin/Heidelberg, Germany, 2021; pp. 437–446. [Google Scholar]
- Rajabi, R.; Ghassemian, H. Spectral unmixing of hyperspectral imagery using multilayer NMF. IEEE Geosci. Remote Sens. Lett. 2014, 12, 38–42. [Google Scholar]
- Cichocki, A.; Zdunek, R. Multilayer nonnegative matrix factorisation. Electron. Lett. 2006, 42, 947–948. [Google Scholar] [CrossRef]
- De Handschutter, P.; Gillis, N.; Siebert, X. A survey on deep matrix factorizations. Comput. Sci. Rev. 2021, 42, 100423. [Google Scholar] [CrossRef]
- Trigeorgis, G.; Bousmalis, K.; Zafeiriou, S.; Schuller, B.W. A deep matrix factorization method for learning attribute representations. IEEE Trans. Patt. Anal. Mach. Intell. 2016, 39, 417–429. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.S.; Zeng, Q.; Pan, B. A survey of deep nonnegative matrix factorization. Neurocomputing 2022, 491, 305–320. [Google Scholar] [CrossRef]
- Sun, J.; Kong, Q.; Xu, Z. Deep alternating non-negative matrix factorisation. Knowl.-Based Syst. 2022, 251, 109210. [Google Scholar] [CrossRef]
- Fang, H.; Li, A.; Xu, H.; Wang, T. Sparsity-constrained deep nonnegative matrix factorization for hyperspectral unmixing. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1105–1109. [Google Scholar] [CrossRef]
- Feng, X.R.; Li, H.C.; Li, J.; Du, Q.; Plaza, A.; Emery, W.J. Hyperspectral unmixing using sparsity-constrained deep nonnegative matrix factorization with total variation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6245–6257. [Google Scholar] [CrossRef]
- Huang, R.; Li, X.; Fang, Y.; Cao, Z.; Xia, C. Robust Hyperspectral Unmixing with Practical Learning-Based Hyperspectral Image Denoising. Remote Sens. 2023, 15, 1058. [Google Scholar] [CrossRef]
- Feng, X.R.; Li, H.C.; Liu, S.; Zhang, H. Correntropy-based autoencoder-like NMF with total variation for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2022, 19, 1–5. [Google Scholar]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems 13 (NIPS 2000); Morgan Kaufmann: Denver, CO, USA, 2001; pp. 556–562. [Google Scholar]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Heinz, D.C.; Chang, C.I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Clark, R.N.; Swayze, G.A.; Gallagher, A.J.; King, T.V.; Calvin, W.M. The US Geological Survey, Digital Spectral Library: Version 1 (0.2 to 3.0 um); U.S. Geological Survey Open-File ReportThe US Geological Survey: Denver, CO, USA, 1993. [Google Scholar]
- Zhu, F. Hyperspectral Unmixing Datasets & Ground Truths. 2014. Available online: http://www.escience.cn/people/feiyunZHU/Dataset_GT.html (accessed on 10 March 2019).
- Zhu, F.; Wang, Y.; Fan, B.; Xiang, S.; Meng, G.; Pan, C. Spectral unmixing via data-guided sparsity. IEEE Trans. Image Process. 2014, 23, 5412–5427. [Google Scholar] [CrossRef] [PubMed]



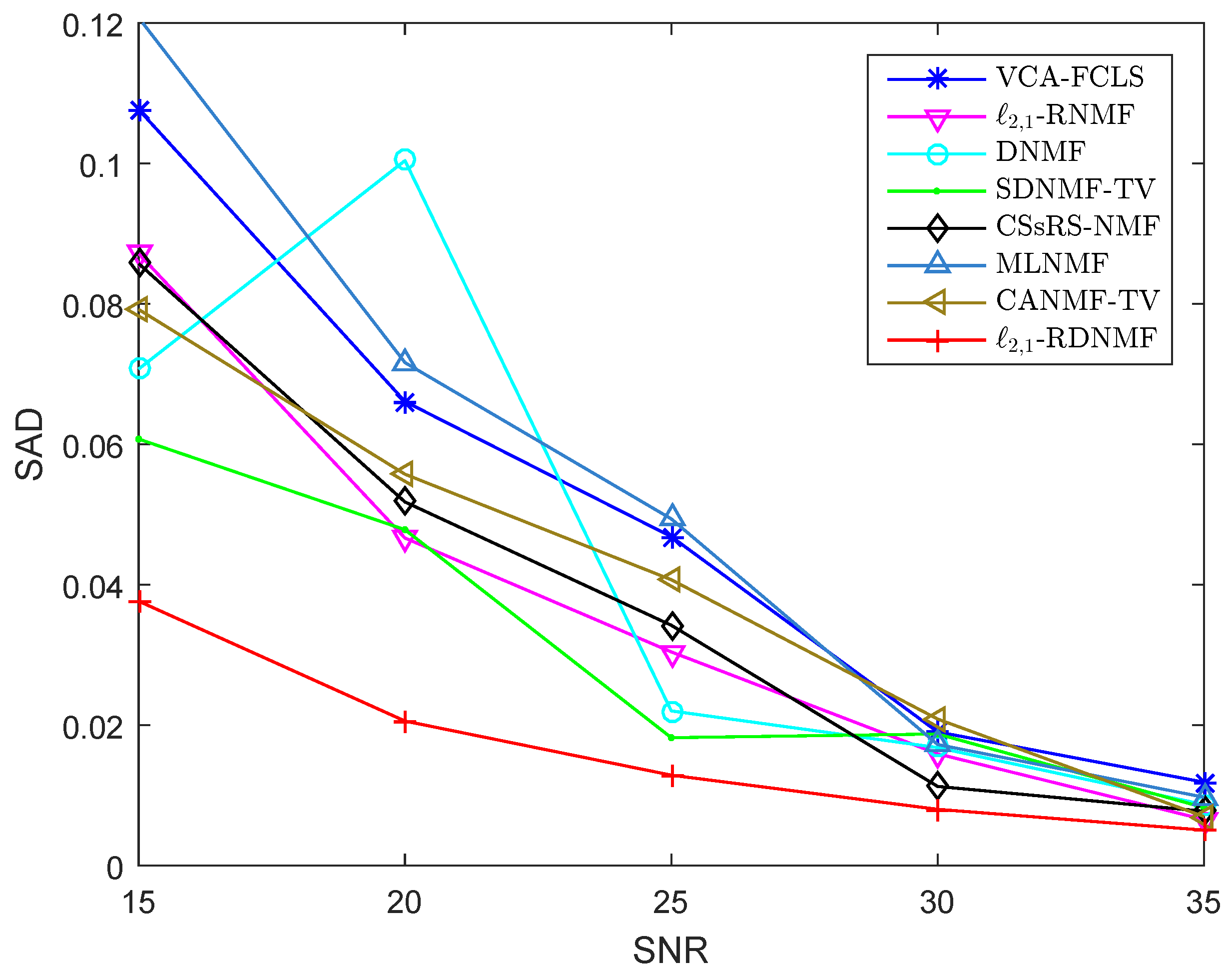






| VCA-FCLS | -NMF | DNMF | SDNMF-TV | CSsRS-NMF | MLNMF | CANMF-TV | -RDNMF |
|---|---|---|---|---|---|---|---|
| 1.30 s | 9.51 s | 20.72 s | 141.60 s | 123.80 s | 21.82 s | 149.63 s | 57.06 s |
| Noise Type | Methods | |||||||
|---|---|---|---|---|---|---|---|---|
| VCA-FCLS | -NMF | DNMF | SDNMF-TV | CSsRS-NMF | MLNMF | CANMF-TV | -RDNMF | |
| Gaussian noise | 0.0190 | 0.0159 | 0.0168 | 0.0187 | 0.0113 | 0.0172 | 0.0209 | 0.0080 |
| Gaussian noise and Impulse noise | 0.2006 | 0.2348 | 0.1635 | 0.1919 | 0.1466 | 0.3062 | 0.2078 | 0.0190 |
| Gaussian noise and Dead pixels | 0.2017 | 0.3170 | 0.2810 | 0.4668 | 0.5244 | 0.4296 | 0.5716 | 0.0233 |
| Gaussian noise, Impulse noise, and Dead pixels | 0.4721 | 0.5641 | 0.2865 | 0.4507 | 0.3660 | 0.5692 | 0.6282 | 0.0617 |
| Noise Type | Methods | |||||||
|---|---|---|---|---|---|---|---|---|
| VCA-FCLS | -NMF | DNMF | SDNMF-TV | CSsRS-NMF | MLNMF | CANMF-TV | -RDNMF | |
| Gaussian noise | 0.0251 | 0.0298 | 0.0371 | 0.0307 | 0.0265 | 0.0319 | 0.0345 | 0.0225 |
| Gaussian noise and Impulse noise | 0.1719 | 0.1401 | 0.1060 | 0.1332 | 0.1780 | 0.1793 | 0.1256 | 0.0339 |
| Gaussian noise and Dead pixels | 0.3326 | 0.3330 | 0.2338 | 0.3165 | 0.4166 | 0.3804 | 0.3164 | 0.0441 |
| Gaussian noise and Impulse noise and Dead pixels | 0.4216 | 0.3737 | 0.2740 | 0.3411 | 0.4680 | 0.3222 | 0.3801 | 0.0522 |
| Endmember | Methods | |||||||
|---|---|---|---|---|---|---|---|---|
| VCA-FCLS | -NMF | DNMF | SDNMF-TV | CSsRS-NMF | MLNMF | CANMF-TV | -RDNMF | |
| Soil | 0.2680 | 0.1817 | 0.0568 | 0.1584 | 0.1675 | 0.1250 | 0.0903 | 0.0274 |
| Tree | 0.0518 | 0.0868 | 0.0524 | 0.1284 | 0.0870 | 0.0811 | 0.0625 | 0.0505 |
| Water | 0.1281 | 0.1235 | 0.1373 | 0.2076 | 0.2635 | 0.2492 | 0.1440 | 0.1467 |
| Mean | 0.1493 | 0.1307 | 0.0822 | 0.1648 | 0.1726 | 0.1518 | 0.0989 | 0.0748 |
| Endmember | Methods | |||||||
|---|---|---|---|---|---|---|---|---|
| VCA-FCLS | -NMF | DNMF | SDNMF-TV | CSsRS-NMF | MLNMF | CANMF-TV | -RDNMF | |
| Alunite | 0.0847 | 0.0968 | 0.0914 | 0.0917 | 0.0946 | 0.1567 | 0.1351 | 0.2765 |
| Andradite | 0.0778 | 0.0826 | 0.1084 | 0.0897 | 0.0831 | 0.1146 | 0.0781 | 0.0731 |
| Buddingtonite | 0.1215 | 0.1430 | 0.1115 | 0.1264 | 0.1224 | 0.1142 | 0.0601 | 0.1132 |
| Dumortierite | 0.1000 | 0.1329 | 0.1172 | 0.1323 | 0.1046 | 0.1648 | 0.1095 | 0.0821 |
| Kaolinite #1 | 0.0855 | 0.0688 | 0.0629 | 0.0652 | 0.0738 | 0.0846 | 0.1504 | 0.0785 |
| Kaolinite #2 | 0.1133 | 0.0888 | 0.0640 | 0.0613 | 0.0859 | 0.0941 | 0.1225 | 0.0599 |
| Muscovite | 0.1976 | 0.1349 | 0.2191 | 0.1532 | 0.1924 | 0.4113 | 0.1662 | 0.1216 |
| Montmorillonite | 0.1110 | 0.0632 | 0.0619 | 0.1276 | 0.0634 | 0.0665 | 0.0620 | 0.0637 |
| Nontronite | 0.0996 | 0.0982 | 0.1135 | 0.1227 | 0.0934 | 0.1382 | 0.1007 | 0.0833 |
| Pyrope | 0.1118 | 0.0583 | 0.1908 | 0.0573 | 0.0567 | 0.0787 | 0.0574 | 0.0524 |
| Sphene | 0.0544 | 0.2495 | 0.0545 | 0.2320 | 0.2506 | 0.0960 | 0.0898 | 0.0703 |
| Chalcedony | 0.1902 | 0.1242 | 0.1288 | 0.1283 | 0.1154 | 0.1525 | 0.1326 | 0.1464 |
| Mean | 0.1123 | 0.1118 | 0.1103 | 0.1156 | 0.1114 | 0.1393 | 0.1054 | 0.1017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, R.; Jiao, H.; Li, X.; Chen, S.; Xia, C. Hyperspectral Unmixing Using Robust Deep Nonnegative Matrix Factorization. Remote Sens. 2023, 15, 2900. https://doi.org/10.3390/rs15112900
Huang R, Jiao H, Li X, Chen S, Xia C. Hyperspectral Unmixing Using Robust Deep Nonnegative Matrix Factorization. Remote Sensing. 2023; 15(11):2900. https://doi.org/10.3390/rs15112900
Chicago/Turabian StyleHuang, Risheng, Huiyun Jiao, Xiaorun Li, Shuhan Chen, and Chaoqun Xia. 2023. "Hyperspectral Unmixing Using Robust Deep Nonnegative Matrix Factorization" Remote Sensing 15, no. 11: 2900. https://doi.org/10.3390/rs15112900
APA StyleHuang, R., Jiao, H., Li, X., Chen, S., & Xia, C. (2023). Hyperspectral Unmixing Using Robust Deep Nonnegative Matrix Factorization. Remote Sensing, 15(11), 2900. https://doi.org/10.3390/rs15112900







