Landsat 8 and Sentinel-2 Fused Dataset for High Spatial-Temporal Resolution Monitoring of Farmland in China’s Diverse Latitudes
Abstract
:1. Introduction
- Enhance the cross-sensor band consistency by effectively eliminating anomalous pixel information.
- Investigate the variability of complementary spectral measurements between L8 OLI and S-2 MSI in crop-growing areas situated at different latitudes in China.
- Develop a high-resolution product that is universally applicable to crop-growing areas at various latitudes, enabling the capture of detailed information on crop growth under varying latitudinal conditions.
2. Materials and Methods
2.1. Study Area
2.2. Satellite Imagery and Its Characteristics
2.2.1. Landsat 8 OLI Satellite Imagery
2.2.2. Sentinel-2 MSI Satellite Imagery
2.2.3. Comparison of Spectral Band Information and Spectral Response Functions
2.3. Selection of Image Pairs
2.4. Flow of Harmonized Consistency Analysis
2.5. C-Factor BRDF Correction
2.6. Isolation Forest Algorithm
2.7. Statistical Analysis
2.7.1. Qualitative Analysis
2.7.2. Quantitative Analysis
3. Results
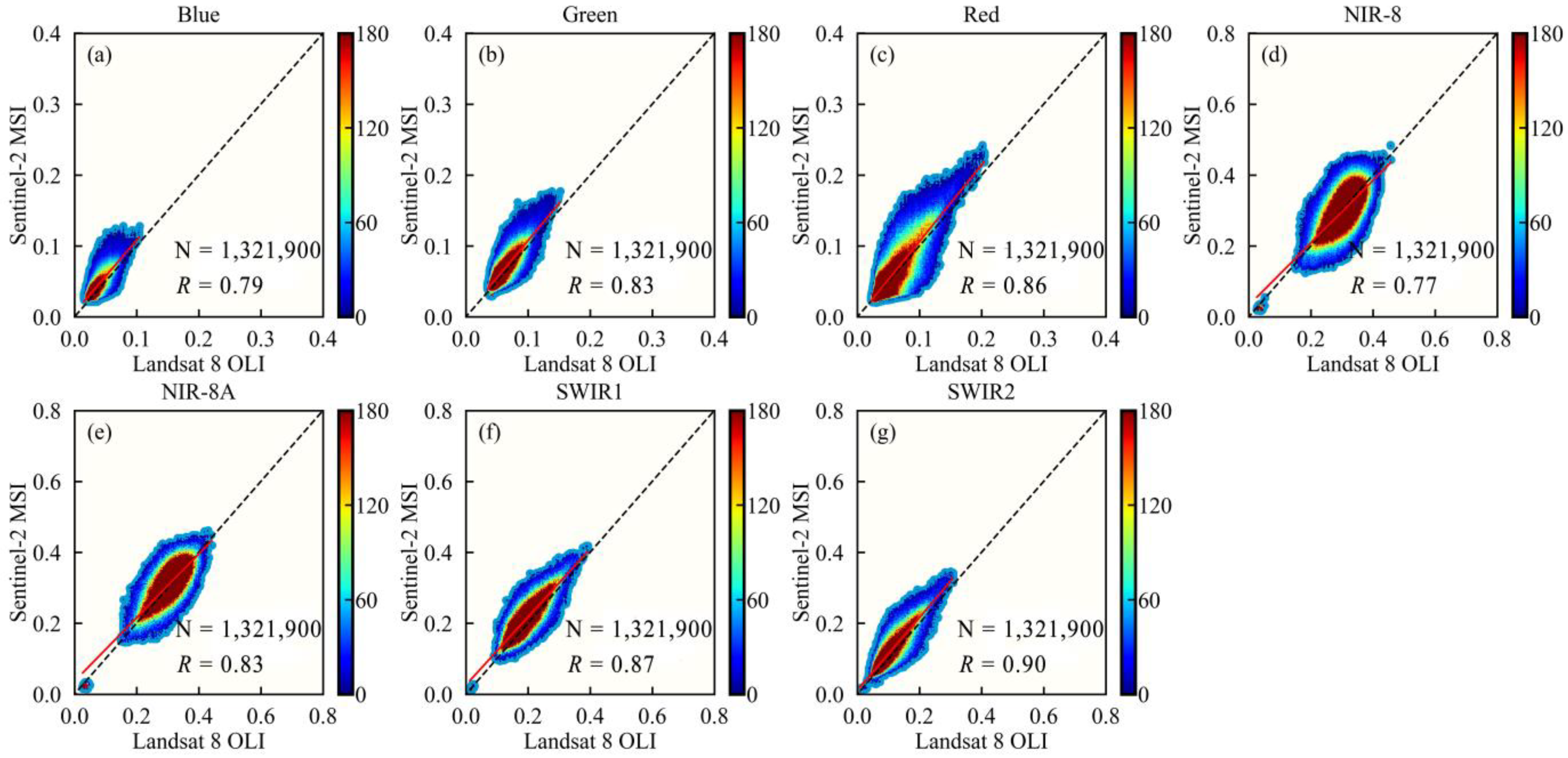
3.1. Quantitative Spectral Conversion Relationships for Different Latitudinal Farming Regions
3.2. Adjustment Coefficients Derived for Integrated L8 and S-2 Data with High-Spatial Resolution at Mixed Latitudes
3.3. Application Examples of Adjustment Coefficients Derived for Integrated L8 and S-2 Data with High-Spatial Resolution at Mixed Latitudes
4. Discussion
4.1. Comparison with Results without Outlier Processing
4.2. Strengths and Weaknesses of Adjustment Coefficients Derived for Integrated L8 and S-2 Data with High-Spatial Resolution at Mixed Latitudes
5. Conclusions
- (1)
- The implementation of the isolation forest algorithm proved effective in removing abnormal pixels from remote sensing images. This resulted in improved correlation between corresponding bands of Landsat 8 OLI and Sentinel-2 MSI sensors while reducing variations across farming areas at different latitudes. Notably, when both satellite images were resampled to a spatial resolution of 10 m, the correlation coefficients between corresponding bands consistently exceeded 0.88, indicating high radiometric consistency.
- (2)
- We employed a linear regression technique to linearly transform the six image pairs, encompassing high, middle, and low latitudes, thereby obtaining adjustment coefficients for integrating Landsat 8 OLI and Sentinel-2 data with high-spatial resolution at mixed latitudes. Through rigorous qualitative and quantitative analyses and a thorough examination of spatial heterogeneity, we have successfully verified the overall applicability of these adjustment factors, yielding highly satisfactory results.
- (3)
- The application of the derived adjustment coefficients significantly improved monitoring density and accuracy in crop growth and development monitoring. Furthermore, the resulting NDVI time series accurately captured the intensity changes in crop growth status.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A











References
- Soriano-González, J.; Angelats, E.; Martínez-Eixarch, M.; Alcaraz, C. Monitoring Rice Crop and Yield Estimation with Sentinel-2 Data. Field. Crop. Res. 2022, 281, 108507. [Google Scholar] [CrossRef]
- Elmendorf, S.C.; Henry, G.H.; Hollister, R.D.; Björk, R.G.; Bjorkman, A.D.; Callaghan, T.V.; Collier, L.S.; Cooper, E.J.; Cornelissen, J.H.; Day, T.A. Global Assessment of Experimental Climate Warming on Tundra Vegetation: Heterogeneity over Space and Time. Ecol. Lett. 2012, 15, 164–175. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 Reflective Wavelength and Normalized Difference Vegetation Index Continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Z.; Hao, P.; Liu, J.; An, M.; Han, B. Technical Demands of Agricultural Remote Sensing Satellites in China. Smart Agric. 2019, 1, 32–42. [Google Scholar]
- Shen, H.; Wu, J.; Cheng, Q.; Aihemaiti, M.; Zhang, C.; Li, Z. A Spatiotemporal Fusion Based Cloud Removal Method for Remote Sensing Images with Land Cover Changes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 862–874. [Google Scholar] [CrossRef]
- Shao, Z.; Pan, Y.; Diao, C.; Cai, J. Cloud Detection in Remote Sensing Images Based on Multiscale Features-Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4062–4076. [Google Scholar] [CrossRef]
- Poortinga, A.; Tenneson, K.; Shapiro, A.; Nguyen, Q.; San Aung, K.; Chishtie, F.; Saah, D. Mapping Plantations in Myanmar by Fusing Landsat-8, Sentinel-2 and Sentinel-1 Data along with Systematic Error Quantification. Remote Sens. 2019, 11, 831. [Google Scholar] [CrossRef] [Green Version]
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current Status of Landsat Program, Science, and Applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary Analysis of the Performance of the Landsat 8/OLI Land Surface Reflectance Product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Sicre, C.M.; Le Dantec, V.; Demarez, V. Estimating Maize Biomass and Yield over Large Areas Using High Spatial and Temporal Resolution Sentinel-2 like Remote Sensing Data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Rahman, M.M.; Robson, A. Integrating Landsat-8 and Sentinel-2 Time Series Data for Yield Prediction of Sugarcane Crops at the Block Level. Remote Sens. 2020, 12, 1313. [Google Scholar] [CrossRef] [Green Version]
- Bolton, D.K.; Gray, J.M.; Melaas, E.K.; Moon, M.; Eklundh, L.; Friedl, M.A. Continental-Scale Land Surface Phenology from Harmonized Landsat 8 and Sentinel-2 Imagery. Remote Sens. Environ. 2020, 240, 111685. [Google Scholar] [CrossRef]
- Flood, N. Comparing Sentinel-2A and Landsat 7 and 8 Using Surface Reflectance over Australia. Remote Sens. 2017, 9, 659. [Google Scholar] [CrossRef] [Green Version]
- Barsi, J.A.; Alhammoud, B.; Czapla-Myers, J.; Gascon, F.; Haque, M.O.; Kaewmanee, M.; Leigh, L.; Markham, B.L. Sentinel-2A MSI and Landsat-8 OLI Radiometric Cross Comparison over Desert Sites. Eur. J. Remote Sens. 2018, 51, 822–837. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 Surface Reflectance Data Set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Mandanici, E.; Bitelli, G. Preliminary Comparison of Sentinel-2 and Landsat 8 Imagery for a Combined Use. Remote Sens. 2016, 8, 1014. [Google Scholar] [CrossRef] [Green Version]
- Chastain, R.; Housman, I.; Goldstein, J.; Finco, M.; Tenneson, K. Empirical Cross Sensor Comparison of Sentinel-2A and 2B MSI, Landsat-8 OLI, and Landsat-7 ETM + Top of Atmosphere Spectral Characteristics over the Conterminous United States. Remote Sens. Environ. 2019, 221, 274–285. [Google Scholar] [CrossRef]
- Zhang, H.K.; Roy, D.P.; Yan, L.; Li, Z.; Huang, H.; Vermote, E.; Skakun, S.; Roger, J.-C. Characterization of Sentinel-2A and Landsat-8 Top of Atmosphere, Surface, and Nadir BRDF Adjusted Reflectance and NDVI Differences. Remote Sens. Environ. 2018, 215, 482–494. [Google Scholar] [CrossRef]
- Cao, H.; Han, L.; Li, L. Harmonizing surface reflectance between Landsat-7 ETM +, Landsat-8 OLI, and Sentinel-2 MSI over China. Environ. Sci. Pollut. Res. 2022, 29, 70882–70898. [Google Scholar] [CrossRef]
- Arekhi, M.; Goksel, C.; Sanli, F.B.; Senel, G. Comparative Evaluation of the Spectral and Spatial Consistency of Sentinel-2 and Landsat-8 OLI Data for Igneada Longos Forest. ISPRS. Int. J. Geo-Inf. 2019, 8, 56. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhu, W. Comparing Landsat-8 and Sentinel-2 Top of Atmosphere and Surface Reflectance in High Latitude Regions: Case Study in Alaska. Geocarto. Int. 2022, 37, 6052–6071. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in Remote Sensing of Agriculture: Context Description, Existing Operational Monitoring Systems and Major Information Needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Jia, K.; Wei, X.; Xia, M.; Yao, Y.; Zhang, X.; Liu, D.; Tao, G. Generating Spatiotemporally Consistent Fractional Vegetation Cover at Different Scales Using Spatiotemporal Fusion and Multiresolution Tree Methods. ISPRS J. Photogramm. 2020, 167, 214–229. [Google Scholar] [CrossRef]
- Guo, J.; Hu, Y. Spatiotemporal Variations in Satellite-Derived Vegetation Phenological Parameters in Northeast China. Remote Sens. 2022, 14, 705. [Google Scholar] [CrossRef]
- Meraner, A.; Ebel, P.; Zhu, X.X.; Schmitt, M. Cloud Removal in Sentinel-2 Imagery Using a Deep Residual Neural Network and SAR-Optical Data Fusion. ISPRS J. Photogramm. 2020, 166, 333–346. [Google Scholar] [CrossRef]
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using Low Resolution Satellite Imagery for Yield Prediction and Yield Anomaly Detection. Remote Sens. 2013, 5, 1704–1733. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and Product Vision for Terrestrial Global Change Research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef] [Green Version]
- Barsi, J.A.; Lee, K.; Kvaran, G.; Markham, B.L.; Pedelty, J.A. The Spectral Response of the Landsat-8 Operational Land Imager. Remote Sens. 2014, 6, 10232–10251. [Google Scholar] [CrossRef] [Green Version]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Veloso, A.; Mermoz, S.; Bouvet, A.; Thuy Le, T.; Planells, M.; Dejoux, J.-F.; Ceschia, E. Understanding the Temporal Behavior of Crops Using Sentinel-1 and Sentinel-2-Like Data for Agricultural Applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
- Zheng, H.; Du, P.; Chen, J.; Xia, J.; Li, E.; Xu, Z.; Li, X.; Yokoya, N. Performance Evaluation of Downscaling Sentinel-2 Imagery for Land Use and Land Cover Classification by Spectral-Spatial Features. Remote Sens. 2017, 9, 1274. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A General Method to Normalize Landsat Reflectance Data to Nadir BRDF Adjusted Reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation Forest. In Proceedings of the 8th IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar]
- Li, S.; Zhang, K.; Duan, P.; Kang, X. Hyperspectral Anomaly Detection with Kernel Isolation Forest. IEEE Trans. Geosci. Remote Sens. 2020, 58, 319–329. [Google Scholar] [CrossRef]
- Liu, D.; Zhen, H.; Kong, D.; Chen, X.; Zhang, L.; Yuan, M.; Wang, H. Sensors Anomaly Detection of Industrial Internet of Things Based on Isolated Forest Algorithm and Data Compression. Sci. Program. 2021, 2021, 6699313. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Y.; Wu, K.; Chen, T. Hyperspectral Anomaly Detection with Otsu-Based Isolation Forest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9079–9088. [Google Scholar] [CrossRef]
- Rzhetsky, A.; Nei, M. Statistical Properties of the Ordinary Least-Squares, Generalized Least-Squares, and Minimum-Evolution Methods of Phylogenetic Inference. J. Mol. Evol. 1992, 35, 367–375. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Q.; Xu, Y.; Qin, S.; Zhang, H.; Qiao, B.; Dang, Y.; Yang, X.; Cheng, Q.; Chintalapati, M. Cross-dataset Time Series Anomaly Detection for Cloud Systems. In Proceedings of the USENIX Annual Technical Conference, Renton, WA, USA, 30 September–2 October 2019; pp. 1063–1076. [Google Scholar]
- Landsat 8 Collection 1 Land Surface Reflectance Code Product Guide. Available online: https://www.usgs.gov/media/files/landsat-8-collection-1-land-surface-reflectance-code-product-guide (accessed on 21 October 2022).
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.-P.; Xu, X. DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. Acm. T. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Paulauskas, N.; Bagdonas, A.F. Local Outlier Factor Use for the Network Flow Anomaly Detection. Secur. Commun. Netw. 2015, 8, 4203–4212. [Google Scholar] [CrossRef] [Green Version]
- Claverie, M.; Masek, J.G.; Ju, J.; Dungan, J.L. Harmonized Landsat-8 Sentinel-2 (HLS) Product User’s Guide; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2017.














| Sensor | Measure | Blue | Green | Red | NIR-8 | NIR-8A | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|---|
| S-2A MSI | Spatial resolution (m) | 10 | 10 | 10 | 10 | 20 | 20 | 20 |
| Central wavelength (nm) | 492.7 | 559.8 | 664.6 | 832.8 | 864.7 | 1613.7 | 2202.4 | |
| Bandwidth (nm) | 65 | 35 | 30 | 105 | 21 | 90 | 174 | |
| S-2B MSI | Spatial resolution (m) | 10 | 10 | 10 | 10 | 20 | 20 | 20 |
| Central wavelength (nm) | 492.3 | 558.9 | 664.9 | 832.9 | 864.0 | 1610.4 | 2185.7 | |
| Bandwidth (nm) | 65 | 36 | 31 | 104 | 21 | 94 | 184 | |
| L8 OLI | Spatial resolution (m) | 30 | 30 | 30 | - | 30 | 30 | 30 |
| Central wavelength (nm) | 482 | 561 | 655 | - | 865 | 1609 | 2201 | |
| Bandwidth (nm) | 65 | 60 | 40 | - | 30 | 85 | 190 |
| Study Area | Date (Day-Month-Year) | Satellite Sensors | Time (UTC) | Solar Zenith Angle (°) | Solar Azimuth Angle (°) |
|---|---|---|---|---|---|
| SA1 | 10 June 2020 | S-2A MSI | 01:56:59 | 26.91 | 149.71 |
| L8 OLI | 01:49:19 | 28.29 | 143.44 | ||
| 26 April 2021 | S-2A MSI | 02:00:15 | 35.78 | 156.29 | |
| L8 OLI | 01:49:19 | 36.92 | 150.86 | ||
| SA2 | 4 September 2020 | S-2B MSI | 03:17:47 | 31.29 | 148.58 |
| L8 OLI | 02:55:17 | 33.63 | 140.22 | ||
| 2 May 2021 | S-2B MSI | 03:17:47 | 23.72 | 140.60 | |
| L8 OLI | 02:54:38 | 26.68 | 130.86 | ||
| SA3 | 10 August 2020 | S-2A MSI | 03:20:21 | 20.43 | 97.84 |
| L8 OLI | 03:05:15 | 24.43 | 97.17 | ||
| 3 December 2021 | S-2A MSI | 03:11:09 | 44.77 | 157.18 | |
| L8 OLI | 03:05:38 | 47.14 | 152.79 | ||
| SA4 | 26 April 2021 | S-2A MSI | 03:38:50 | 22.62 | 127.25 |
| L8 OLI | 03:33:23 | 25.47 | 122.32 |
| Coefficient | Blue | Green | Red | NIR-8 | NIR-8A | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|
| Slope | 0.7802 | 1.0293 | 1.0912 | 0.9198 | 0.9539 | 1.0555 | 1.0810 |
| Intercept | 0.0204 | 0.0061 | 0.0001 | 0.0186 | 0.0155 | 0.0052 | 0.0049 |
| Study Area | Index | Bands | ||||||
|---|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR-8 | NIR-8A | SWIR1 | SWIR2 | ||
| SA1 | RMSE | 0.012 | 0.008 | 0.011 | 0.018 | 0.014 | 0.023 | 0.019 |
| MAE | 0.009 | 0.006 | 0.008 | 0.013 | 0.010 | 0.014 | 0.011 | |
| SA2 | RMSE | 0.014 | 0.016 | 0.021 | 0.019 | 0.017 | 0.013 | 0.015 |
| MAE | 0.010 | 0.013 | 0.017 | 0.014 | 0.013 | 0.010 | 0.010 | |
| SA3 | RMSE | 0.017 | 0.019 | 0.025 | 0.066 | 0.067 | 0.047 | 0.024 |
| MAE | 0.011 | 0.011 | 0.015 | 0.044 | 0.048 | 0.029 | 0.013 | |
| Index | Bands | ||||||
|---|---|---|---|---|---|---|---|
| Blue | Green | Red | NIR-8 | NIR-8A | SWIR1 | SWIR2 | |
| RMSE | 0.018 | 0.017 | 0.023 | 0.046 | 0.042 | 0.022 | 0.020 |
| MAE | 0.012 | 0.012 | 0.016 | 0.032 | 0.029 | 0.013 | 0.011 |
| Product | Direction of Adjustment | Spatial Resolution | Coefficient | Blue | Green | Red | NIR-8 | NIR-8A | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|---|---|---|
| HLS | L8 OLI from S-2 MSI | 30 m | Slope | 1.005 | 1.020 | 0.994 | 1.017 | 0.999 | 0.999 | 1.003 |
| Intercept | 2.09 × 10−4 | 4.47× 10−³ | 1.09 × 10−³ | −1.04 × 10−³ | 2.50 × 10−4 | 1.24 × 10−4 | 1.19 × 10−³ | |||
| This article | S-2 MSI from L8 OLI | 10 m | Slope | 0.8527 | 1.0733 | 1.1404 | 0.9024 | 0.9311 | 1.0416 | 1.1116 |
| Intercept | 0.0186 | 0.0027 | −0.0025 | 0.0199 | 0.0163 | 0.0032 | 0.0013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, Y.; Gao, T.; Lan, S.; Tong, F.; Li, M. Landsat 8 and Sentinel-2 Fused Dataset for High Spatial-Temporal Resolution Monitoring of Farmland in China’s Diverse Latitudes. Remote Sens. 2023, 15, 2951. https://doi.org/10.3390/rs15112951
Zhang H, Zhang Y, Gao T, Lan S, Tong F, Li M. Landsat 8 and Sentinel-2 Fused Dataset for High Spatial-Temporal Resolution Monitoring of Farmland in China’s Diverse Latitudes. Remote Sensing. 2023; 15(11):2951. https://doi.org/10.3390/rs15112951
Chicago/Turabian StyleZhang, Haiyang, Yao Zhang, Tingyao Gao, Shu Lan, Fanghui Tong, and Minzan Li. 2023. "Landsat 8 and Sentinel-2 Fused Dataset for High Spatial-Temporal Resolution Monitoring of Farmland in China’s Diverse Latitudes" Remote Sensing 15, no. 11: 2951. https://doi.org/10.3390/rs15112951
APA StyleZhang, H., Zhang, Y., Gao, T., Lan, S., Tong, F., & Li, M. (2023). Landsat 8 and Sentinel-2 Fused Dataset for High Spatial-Temporal Resolution Monitoring of Farmland in China’s Diverse Latitudes. Remote Sensing, 15(11), 2951. https://doi.org/10.3390/rs15112951






