Remote Sensing and Data Analyses on Planetary Topography
Abstract
:1. Introduction
2. Review of Planetary Topography Mapping
2.1. Moon
2.2. Mars
2.3. Venus/Mercury—Inner Planets
2.4. Asteroids and Comets
2.5. Satellites of Giant Planets
2.6. Trans-Neptunian Object (TNO)
3. Technical Point of Review
3.1. Optical Image and Stereo/Mono Analysis

3.2. LIDAR Altimetry
3.3. SAR and Radar Altimetry
3.4. Geodetic Point of View
4. Compile/Applications
4.1. Co-Registration
- (1)
- Co-registration between different data frames generated by the same sensor (e.g., stereo DEM extraction, orthogonal image alignment of an along-track sensor, and laser profile cross-over analysis/self-registration);
- (2)
- Co-registration between data frames of hybrid sensors with the same operating mechanism (e.g., co-registration between orthoimages and DEMs from different optical sensors);
- (3)
- Co-registration of data sets from sensors that operate in different mechanisms, such as between optical images and altimetry profiles.
4.2. Scientific Applications
4.3. Visualization, Public Interaction, and Data Distributions
- (1)
- More planetary missions to maintain sufficient data sets and ultimately aim to cover extensive planetary surfaces;
- (2)
- Sufficient co-registration accuracy to create seamless datasets with hybrid data sources;
- (3)
- A data distribution and exchange mechanism that ensures multi-peer data access.
5. Future Perspective and Suggestions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pigatto, L.; Zanini, V. Lunar maps of the 17th and 18th centuries. Tobias Mayer’s map and its 19th-century edition. In Earth-Moon Relationships; Springer Dordrecht: Berlin/Heidelberg, Germany, 2001; pp. 365–377. [Google Scholar]
- Greeley, R.; Batson, R.M. Planetary Mapping; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Carder, R.W. Lunar Mapping on a Scale of 1: 1000000. In The Moon; 1962; pp. 117–129. Available online: https://adsabs.harvard.edu/full/1962IAUS...14..117C (accessed on 28 March 2023).
- Kopal, Z.; Carder, R.W. USSR Lunar Mapping. In Mapping of the Moon; Springer: Berlin/Heidelberg, Germany, 1974; pp. 213–228. [Google Scholar]
- Greenwood, W.; Jones, R.; Heiken, G.; Bender, M.; Hill, R.O. Lunar-Surface Closeup Stereoscopic Photography on the Sea of Tranquility (Apollo 11 Landing Site); National Aeronautics and Space Administration (NASA) Manned Spacecraft Center: Houston, TX, USA, 1971. [Google Scholar]
- Pettengill, G.H.; Eliason, E.; Ford, P.G.; Loriot, G.B.; Masursky, H.; McGill, G.E. Pioneer Venus radar results altimetry and surface properties. J. Geophys. Res. Space Phys. 1980, 85, 8261–8270. [Google Scholar] [CrossRef]
- Pettengill, G.H.; Ford, P.G.; Johnson, W.T.; Raney, R.K.; Soderblom, L.A. Magellan: Radar performance and data products. Science 1991, 252, 260–265. [Google Scholar] [CrossRef] [PubMed]
- McEwen, A.; Eliason, E.; Isbell, C.; Lee, E.; Becker, T.; Robinson, M. The Clementine basemap mosaic. Clementine UVVIS 1997, 750. [Google Scholar]
- Malin, M.; Carr, M.; Danielson, G.; Davies, M.; Hartmann, W.; Ingersoll, A.; James, P.; Masursky, H.; McEwen, A.; Soderblom, L. Early views of the martian surface from the Mars Orbiter Camera of Mars Global Surveyor. Science 1998, 279, 1681–1685. [Google Scholar] [CrossRef] [Green Version]
- Saunders, R.; Pettengill, G.; Arvidson, R.; Sjogren, W.; Johnson, W.; Pieri, L. The Magellan Venus radar mapping mission. J. Geophys. Res. Solid Earth 1990, 95, 8339–8355. [Google Scholar] [CrossRef]
- Brown, R.H.; Baines, K.H.; Bellucci, G.; Bibring, J.-P.; Buratti, B.J.; Capaccioni, F.; Cerroni, P.; Clark, R.N.; Coradini, A.; Cruikshank, D.P. The Cassini visual and infrared mapping spectrometer (VIMS) investigation. Space Sci. Rev. 2004, 115, 111–168. [Google Scholar] [CrossRef]
- Elachi, C.; Allison, M.; Borgarelli, L.; Encrenaz, P.; Im, E.; Janssen, M.; Johnson, W.; Kirk, R.L.; Lorenz, R.; Lunine, J. Radar: The Cassini Titan radar mapper. Cassini-Huygens Mission 2004, 115, 71–110. [Google Scholar]
- Chicarro, A.; Martin, P.; Trautner, R. The Mars Express mission: An overview. Mars Express Sci. Payload 2004, 1240, 3–13. [Google Scholar]
- Stern, S.A.; Grundy, W.M.; McKinnon, W.B.; Weaver, H.A.; Young, L.A. The Pluto system after new horizons. Annu. Rev. Astron. Astrophys. 2018, 56, 357–392. [Google Scholar] [CrossRef] [Green Version]
- Sundararajan, V. Overview and technical architecture of India’s Chandrayaan-2 mission to the Moon. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 2178. [Google Scholar]
- Bhandari, N. Chandrayaan-1: Science goals. J. Earth Syst. Sci. 2005, 114, 701–709. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Liu, J.; Ren, X.; Zuo, W.; Tan, X.; Wen, W.; Li, H.; Mu, L.; Su, Y.; Zhang, H. The Chang’e 3 mission overview. Space Sci. Rev. 2015, 190, 85–101. [Google Scholar] [CrossRef]
- Jia, Y.; Zou, Y.; Ping, J.; Xue, C.; Yan, J.; Ning, Y. The scientific objectives and payloads of Chang’E− 4 mission. Planet. Space Sci. 2018, 162, 207–215. [Google Scholar] [CrossRef]
- Huixian, S.; Shuwu, D.; Jianfeng, Y.; Ji, W.; Jingshan, J. Scientific objectives and payloads of Chang’E-1 lunar satellite. J. Earth Syst. Sci. 2005, 114, 789–794. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, Y.; Bai, Y.; Wang, L.; Jia, Y.; Shen, W.; Fan, Y.; Liu, Y.; Wang, C.; Zhang, A. Scientific objectives and payloads of Tianwen-1, China’s first Mars exploration mission. Adv. Space Res. 2021, 67, 812–823. [Google Scholar] [CrossRef]
- Amiri, H.; Brain, D.; Sharaf, O.; Withnell, P.; McGrath, M.; Alloghani, M.; Al Awadhi, M.; Al Dhafri, S.; Al Hamadi, O.; Al Matroushi, H. The emirates Mars mission. Space Sci. Rev. 2022, 218, 4. [Google Scholar] [CrossRef]
- Kirk, R.L.; Archinal, B.A.; Gaddis, L.R.; Rosiek, M.R. Cartography for lunar exploration: 2008 status and mission plans. In Proceedings of the European Planetary Science Congress, Beijing, China, 3–11 July 2008. [Google Scholar]
- Regeon, P.; Chapman, R.; Baugh, R. CLEMENTINE:“The Deep Space Program Science Experiment”. Acta Astronaut. 1995, 35, 307–321. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G. Topography of the Moon from the Clementine lidar. J. Geophys. Res. Planets 1997, 102, 1591–1611. [Google Scholar] [CrossRef] [Green Version]
- McEwen, A.; Robinson, M. Mapping of the Moon by Clementine. Adv. Space Res. 1997, 19, 1523–1533. [Google Scholar] [CrossRef]
- Robinson, M.; McEwen, A.; Eliason, E.; Lee, E.; Malaret, E.; Lucey, P. Clementine UVVIS global mosaic: A new tool for understanding the lunar crust. In Proceedings of the 30th Annual Lunar and Planetary Science Conference, Houston, TX, USA, 15–29 March 1999; p. 1931. [Google Scholar]
- Foing, B.; Racca, G.; Marini, A.; Heather, D.; Koschny, D.; Grande, M.; Huovelin, J.; Keller, H.; Nathues, A.; Josset, J. SMART-1 mission to the moon: Technology and science goals. Adv. Space Res. 2003, 31, 2323–2333. [Google Scholar] [CrossRef]
- Basilevsky, A.; Keller, H.U.; Nathues, A.; Mall, U.; Hiesinger, H.; Rosiek, M. Scientific objectives and selection of targets for the SMART-1 Infrared Spectrometer (SIR). Planet. Space Sci. 2004, 52, 1261–1285. [Google Scholar] [CrossRef]
- Foing, B.; Racca, G.D.; Marini, A.; Evrard, E.; Stagnaro, L.; Almeida, M.; Koschny, D.; Frew, D.; Zender, J.; Heather, J. SMART-1 mission to the Moon: Status, first results and goals. Adv. Space Res. 2006, 37, 6–13. [Google Scholar] [CrossRef]
- Grieger, B.; Foing, B.; Koschny, D.; Josset, J.; Beauvivre, S.; Frew, D.; Almeida, M.; Sarkarati, M.; Volp, J.; Pinet, P. Coverage and pointing accuracy of SMART-1/AMIE images. In Proceedings of the 39th Lunar and Planetary Science Conference, (Lunar and Planetary Science XXXIX), League City, TX, USA, 10–14 March 2008. [Google Scholar]
- Spudis, P.D.; Bussey, B.; Plescia, J.; Josset, J.L.; Beauvivre, S. Geology of Shackleton Crater and the south pole of the Moon. Geophys. Res. Lett. 2008, 35, 5. [Google Scholar] [CrossRef] [Green Version]
- Brost, A.R.; Jordan, A.-M.S. Punishment that does not fit the crime: The unconstitutional practice of placing youth on sex offender registries. SDL Rev. 2017, 62, 806. [Google Scholar]
- Kato, M.; Sasaki, S.; Tanaka, K.; Iijima, Y.; Takizawa, Y. The Japanese lunar mission SELENE: Science goals and present status. Adv. Space Res. 2008, 42, 294–300. [Google Scholar] [CrossRef]
- Goswami, J.; Annadurai, M. Chandrayaan-1: India’s first planetary science mission to the Moon. Curr. Sci. 2009, 96, 486–491. [Google Scholar]
- Zheng, Y.; Ouyang, Z.; Li, C.; Liu, J.; Zou, Y. China’s lunar exploration program: Present and future. Planet. Space Sci. 2008, 56, 881–886. [Google Scholar] [CrossRef]
- Haruyama, J.i.; Ohtake, M.; Matsunaga, T.; GROUP, L.W. Global high-resolution stereo mapping of the Moon with the SELENE Terrain Camera. In Advances in Geosciences: Volume 3: Planetary Science (PS); World Scientific: Singapore, 2006; pp. 101–108. [Google Scholar]
- Araki, H.; Tazawa, S.; Noda, H.; Ishihara, Y.; Goossens, S.; Sasaki, S.; Kawano, N.; Kamiya, I.; Otake, H.; Oberst, J. Lunar global shape and polar topography derived from Kaguya-LALT laser altimetry. Science 2009, 323, 897–900. [Google Scholar] [CrossRef]
- Huang, Q.; Ping, J.; Su, X.; Shu, R.; Tang, G. New features of the Moon revealed and identified by CLTM-s01. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 1815–1823. [Google Scholar] [CrossRef]
- Kumar, A.; Chowdhury, A.R.; Banerjee, A.; Dave, A.; Sharma, B.; Shah, K.; Murali, K.; Joshi, S.; Sarkar, S.; Patel, V. Terrain Mapping Camera: A stereoscopic high-resolution instrument on Chandrayaan-1. Curr. Sci. 2009, 96, 492–495. [Google Scholar]
- Kamalakar, J.; Bhaskar, K.; Laxmi Prasad, A.; Ranjith, R.; Lohar, K.; Venketeswaran, R.; Alex, T. Lunar ranging instrument for Chandrayaan-1. J. Earth Syst. Sci. 2005, 114, 725–731. [Google Scholar] [CrossRef]
- Robinson, M.; Brylow, S.; Tschimmel, M.; Humm, D.; Lawrence, S.; Thomas, P.; Denevi, B.; Bowman-Cisneros, E.; Zerr, J.; Ravine, M. Lunar reconnaissance orbiter camera (LROC) instrument overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W., III; Duxbury, T.H. Initial observations from the lunar orbiter laser altimeter (LOLA). Geophys. Res. Lett. 2010, 37, 6. [Google Scholar] [CrossRef]
- Ping, J.; Huang, Q.; Yan, J.; Cao, J.; Tang, G.; Shu, R. Lunar topographic model CLTM-s01 from Chang’E-1 laser altimeter. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 1105–1114. [Google Scholar] [CrossRef]
- Noda, H.; Araki, H.; Goossens, S.; Ishihara, Y.; Matsumoto, K.; Tazawa, S.; Kawano, N.; Sasaki, S. Illumination conditions at the lunar polar regions by KAGUYA (SELENE) laser altimeter. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Teodoro, L.; Eke, V.; Elphic, R. Spatial distribution of lunar polar hydrogen deposits after KAGUYA (SELENE). Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Bhaskar, K.; Kamalakar, J.; Laxmiprasad, A.; Sridhar Raja, V.; Goswami, A.; Kumar, K.R.; Kalyani, K. Lunar Topography by Laser Ranging Instrument Onboard CHANDRAYAAN-1. In Advances in Geosciences: Volume 25: Planetary Science (PS); World Scientific: Singapore, 2011; pp. 73–85. [Google Scholar]
- Vondrak, R.; Keller, J.; Chin, G.; Garvin, J. Lunar Reconnaissance Orbiter (LRO): Observations for lunar exploration and science. Space Sci. Rev. 2010, 150, 7–22. [Google Scholar] [CrossRef]
- Wu, B.; Liu, W.C.; Grumpe, A.; Wöhler, C. Construction of pixel-level resolution DEMs from monocular images by shape and albedo from shading constrained with low-resolution DEM. ISPRS J. Photogramm. Remote Sens. 2018, 140, 3–19. [Google Scholar] [CrossRef]
- Karachevtseva, I.; Oberst, J.; Scholten, F.; Konopikhin, A.; Shingareva, K.; Cherepanova, E.; Gusakova, E.; Haase, I.; Peters, O.; Plescia, J. Cartography of the Lunokhod-1 landing site and traverse from LRO image and stereo-topographic data. Planet. Space Sci. 2013, 85, 175–187. [Google Scholar] [CrossRef]
- Bray, V.J.; Tornabene, L.L.; Keszthelyi, L.P.; McEwen, A.S.; Hawke, B.R.; Giguere, T.A.; Kattenhorn, S.A.; Garry, W.B.; Rizk, B.; Caudill, C. New insight into lunar impact melt mobility from the LRO camera. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Shkuratov, Y.; Kaydash, V.; Videen, G. The lunar crater Giordano Bruno as seen with optical roughness imagery. Icarus 2012, 218, 525–533. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Jackson, G.B.; Cavanaugh, J.F.; Neumann, G.A.; Riris, H.; Sun, X.; Zellar, R.S.; Coltharp, C.; Connelly, J. The lunar orbiter laser altimeter investigation on the lunar reconnaissance orbiter mission. Space Sci. Rev. 2010, 150, 209–241. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E.; Lemoine, F.G.; Head, J.W., III; Lucey, P.G.; Aharonson, O.; Robinson, M.S.; Sun, X. Summary of the results from the lunar orbiter laser altimeter after seven years in lunar orbit. Icarus 2017, 283, 70–91. [Google Scholar] [CrossRef] [Green Version]
- Mazarico, E.; Rowlands, D.; Neumann, G.; Smith, D.; Torrence, M.; Lemoine, F.; Zuber, M. Orbit determination of the lunar reconnaissance orbiter. J. Geod. 2012, 86, 193–207. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, J.; Wen, D.; Gao, W.; Chang, L.; Song, Z.; Xue, B.; Zhao, W. Overall scheme and on-orbit images of Chang’E-2 lunar satellite CCD stereo camera. Sci. China Technol. Sci. 2011, 54, 2237–2242. [Google Scholar] [CrossRef]
- Li, C.; Hu, H.; Yang, M.-F.; Pei, Z.-Y.; Zhou, Q.; Ren, X.; Liu, B.; Liu, D.; Zeng, X.; Zhang, G. Characteristics of the lunar samples returned by the Chang’E-5 mission. Natl. Sci. Rev. 2022, 9, nwab188. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Guo, J.; Hu, H.; Li, Z.; Chen, Y. Co-registration of lunar topographic models derived from Chang’E-1, SELENE, and LRO laser altimeter data based on a novel surface matchingmethod. Earth Planet. Sci. Lett. 2013, 364, 68–84. [Google Scholar] [CrossRef]
- Wu, B.; Guo, J.; Zhang, Y.; King, B.A.; Li, Z.; Chen, Y. Integration of Chang’E-1 imagery and laser altimeter data for precision lunar topographic modeling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4889–4903. [Google Scholar]
- Barker, M.; Mazarico, E.; Neumann, G.; Zuber, M.; Haruyama, J.; Smith, D. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef] [Green Version]
- Karachevtseva, I.; Kozlova, N.; Kokhanov, A.; Zubarev, A.; Nadezhdina, I.; Patratiy, V.; Konopikhin, A.; Basilevsky, A.; Abdrakhimov, A.; Oberst, J. Cartography of the Luna-21 landing site and Lunokhod-2 traverse area based on Lunar Reconnaissance Orbiter Camera images and surface archive TV-panoramas. Icarus 2017, 283, 104–121. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.; Mahanti, P.; Carter, L.; Denevi, B.; Estes, N.; Ravine, M.; Speyerer, E.; Wagner, R. ShadowCam—Seeing in the dark. In Proceedings of the European Planetary Science Congress, Riga, Latvia, 17–22 September 2017; p. 506. [Google Scholar]
- Carr, M. Astronomy: Martian illusions. Nature 2011, 470, 172–173. [Google Scholar] [CrossRef] [Green Version]
- Assembly, I.A.U.G. Transactions of the International Astronomical Union, Vol X: Tenth General Assembly Held at Moscow, 12–20 August 1958; Cambridge University Press: Cambridge, UK, 1960. [Google Scholar]
- Chapman, C.R.; Pollack, J.B.; Sagan, C. An Analysis of the Mariner 4 Photography of Mars; NASA: Washington, DC, USA, 1968.
- Rindfleisch, T.; Dunne, J.; Frieden, H.; Stromberg, W.; Ruiz, R. Digital processing of the Mariner 6 and 7 pictures. J. Geophys. Res. 1971, 76, 394–417. [Google Scholar] [CrossRef]
- Leighton, R.; Horowitz, N.; Murray, B.; Sharp, R.; Herriman, A.; Young, A.; Smith, B.; Davies, M.; Leovy, C. Mariner 6 and 7 television pictures: Preliminary analysis. Science 1969, 166, 49–67. [Google Scholar] [CrossRef] [PubMed]
- Batson, R.M. Cartographic products from the Mariner 9 mission. J. Geophys. Res. 1973, 78, 4424–4435. [Google Scholar] [CrossRef]
- Carr, M.; Baum, W.; Briggs, G.; Masursky, H.; Wise, D.; Montgomery, D. Imaging experiment: The viking Mars orbiter. Icarus 1972, 16, 17–33. [Google Scholar] [CrossRef]
- Carr, M.H.; Masursky, H.; Baum, W.A.; Blasius, K.R.; Briggs, G.A.; Cutts, J.A.; Duxbury, T.; Greeley, R.; Guest, J.E.; Smith, B.A. Preliminary results from the Viking orbiter imaging experiment. Science 1976, 193, 766–776. [Google Scholar] [CrossRef] [PubMed]
- Davies, M.E.; Katayama, F.Y. The 1982 control network of Mars. J. Geophys. Res. Solid Earth 1983, 88, 7503–7504. [Google Scholar] [CrossRef]
- Wellman, J.B.; Landauer, F.P.; Norris, D.D.; Thorpe, T.E. The Viking orbiter visual imaging subsystem. J. Spacecr. Rocket. 1976, 13, 660–666. [Google Scholar] [CrossRef]
- Duxbury, T.; Kirk, R.L.; Archinal, B.A.; Neumann, G. Mars Geodesy/Cartography Working Group recommendations on Mars cartographic constants and coordinate systems. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 743–748. [Google Scholar]
- Archinal, B.A.; Kirk, R.L.; Duxbury, T.; Lee, E.M.; Sucharski, R.M.; Cook, D. Mars Digital Image Model (MDIM) 2.1 Control Network. In Proceedings of the ISPRS Working Group IV/9 Workshop, Houston, TX, USA, 22 March 2003. [Google Scholar]
- Smith, D.E.; Zuber, M.T.; Frey, H.V.; Garvin, J.B.; Head, J.W.; Muhleman, D.O.; Pettengill, G.H.; Phillips, R.J.; Solomon, S.C.; Zwally, H.J. Mars Orbiter Laser Altimeter: Experiment summary after the first year of global mapping of Mars. J. Geophys. Res. Planets 2001, 106, 23689–23722. [Google Scholar] [CrossRef]
- Abshire, J.B.; Sun, X.; Afzal, R.S. Mars Orbiter Laser Altimeter: Receiver model and performance analysis. Appl. Opt. 2000, 39, 2449–2460. [Google Scholar] [CrossRef] [Green Version]
- Zuber, M.T.; Smith, D.E.; Solomon, S.; Muhleman, D.; Head, J.; Garvin, J.; Abshire, J.; Bufton, J. The Mars Observer laser altimeter investigation. J. Geophys. Res. Planets 1992, 97, 7781–7797. [Google Scholar] [CrossRef]
- Smith, D.; Zuber, M.; Frey, H.; Garvin, J.; Head, J.; Muhleman, D.; Pettengill, G.; Phillips, R.; Solomon, S.; Zwally, H. Topography of the northern hemisphere of Mars from the Mars Orbiter Laser Altimeter. Science 1998, 279, 1686–1692. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malin, M.C.; Edgett, K.S. Mars global surveyor Mars orbiter camera: Interplanetary cruise through primary mission. J. Geophys. Res. Planets 2001, 106, 23429–23570. [Google Scholar] [CrossRef]
- Kirk, R.; Becker, T.; Eliason, E.; Anderson, J.; Soderblom, L. Geometric calibration of the Mars Orbiter Cameras and coalignment with the Mars Orbiter Laser Altimeter. In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 12–16 March 2001; p. 1863. [Google Scholar]
- Kirk, R.; Soderblom, L.; Howington-Kraus, E.; Archinal, B.; Team, A. USGS High Resolution Topo-Mapping of Mars with Mars Orbiter Camera Narrow-Angle Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 713–722. [Google Scholar]
- Kirk, R.L.; Howington-Kraus, E.; Redding, B.; Galuszka, D.; Hare, T.M.; Archinal, B.A.; Soderblom, L.A.; Barrett, J.M. High-resolution topomapping of candidate MER landing sites with Mars Orbiter Camera narrow-angle images. J. Geophys. Res. Planets 2003, 108. [Google Scholar] [CrossRef]
- Archinal, B.; Kirk, R.; Duxbury, T.; Lee, E.; Sucharski, R.; Cook, D. Mars digital image model 2.1 control network. In Proceedings of the Lunar and Planetary Science Conference, League, TX, USA, 17–21 March 2003; p. 1485. [Google Scholar]
- Neukum, G.; Jaumann, R. HRSC: The high resolution stereo camera of Mars Express. Mars Express Sci. Payload 2004, 1240, 17–35. [Google Scholar]
- Scholten, F.; Gwinner, K.; Roatsch, T.; Matz, K.-D.; Wählisch, M.; Giese, B.; Oberst, J.; Jaumann, R.; Neukum, G. Mars Express HRSC data processing–Methods and operational aspects. Photogramm. Eng. Remote Sens. 2005, 71, 1143–1152. [Google Scholar] [CrossRef] [Green Version]
- Gwinner, K.; Scholten, F.; Spiegel, M.; Schmidt, R.; Giese, B.; Oberst, J.; Heipke, C.; Jaumann, R.; Neukum, G. Derivation and validation of high-resolution digital terrain models from Mars Express HRSC data. Photogramm. Eng. Remote Sens. 2009, 75, 1127–1142. [Google Scholar] [CrossRef] [Green Version]
- Jaumann, R.; Tirsch, D.; Hauber, E.; Ansan, V.; Di Achille, G.; Erkeling, G.; Fueten, F.; Head, J.; Kleinhans, M.; Mangold, N. Quantifying geological processes on Mars—Results of the high resolution stereo camera (HRSC) on Mars express. Planet. Space Sci. 2015, 112, 53–97. [Google Scholar] [CrossRef] [Green Version]
- McEwen, A.S.; Eliason, E.M.; Bergstrom, J.W.; Bridges, N.T.; Hansen, C.J.; Delamere, W.A.; Grant, J.A.; Gulick, V.C.; Herkenhoff, K.E.; Keszthelyi, L. Mars reconnaissance orbiter’s high resolution imaging science experiment (HiRISE). J. Geophys. Res. Planets 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Malin, M.C.; Bell, J.F., III; Cantor, B.A.; Caplinger, M.A.; Calvin, W.M.; Clancy, R.T.; Edgett, K.S.; Edwards, L.; Haberle, R.M.; James, P.B. Context camera investigation on board the Mars Reconnaissance Orbiter. J. Geophys. Res. Planets 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Muller, J. Very high resolution stereo DTM extraction and its application to surface roughness estimation over Martian surface. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 993–998. [Google Scholar]
- Kirk, R.L.; Howington-Kraus, E.; Rosiek, M.R.; Anderson, J.A.; Archinal, B.A.; Becker, K.J.; Cook, D.; Galuszka, D.M.; Geissler, P.E.; Hare, T.M. Ultrahigh resolution topographic mapping of Mars with MRO HiRISE stereo images: Meter-scale slopes of candidate Phoenix landing sites. J. Geophys. Res. Planets 2008, 113. [Google Scholar] [CrossRef]
- Thomas, N.; Cremonese, G.; Ziethe, R.; Gerber, M.; Brändli, M.; Bruno, G.; Erismann, M.; Gambicorti, L.; Gerber, T.; Ghose, K. The colour and stereo surface imaging system (CaSSIS) for the ExoMars trace gas orbiter. Space Sci. Rev. 2017, 212, 1897–1944. [Google Scholar] [CrossRef] [Green Version]
- Misra, I.; Rohil, M.K.; Manthira Moorthi, S.; Dhar, D. Mars Surface Multi-decadal Change Detection Using ISRO’s Mars Color Camera (MCC) and Viking Orbiter Images. In Proceedings of the 8th International Conference on Computer Vision and Image Processing, Jammu, India, 3–5 November 2023; pp. 25–33. [Google Scholar]
- Zeng, X.; Liu, J.; Ren, X.; Yan, W.; Fu, Q.; Gao, X.; Chen, W.; Zuo, W.; Li, C. Pan-location mapping and localization for the in-situ science exploration of Zhurong Mars rover. Sci. China Inf. Sci. 2022, 65, 172201. [Google Scholar] [CrossRef]
- Colin, L. The pioneer Venus program. J. Geophys. Res. Space Phys. 1980, 85, 7575–7598. [Google Scholar] [CrossRef]
- Ford, P.G.; Pettengill, G.H. Venus topography and kilometer-scale slopes. J. Geophys. Res. Planets 1992, 97, 13103–13114. [Google Scholar] [CrossRef]
- Pettengill, G.; Ford, P.; Nozette, S. Venus: Global surface radar reflectivity. Science 1982, 217, 640–642. [Google Scholar] [CrossRef]
- Masursky, H.; Eliason, E.; Ford, P.G.; McGill, G.E.; Pettengill, G.H.; Schaber, G.G.; Schubert, G. Pioneer Venus radar results: Geology from images and altimetry. J. Geophys. Res. Space Phys. 1980, 85, 8232–8260. [Google Scholar] [CrossRef]
- Senske, D. Geology of the Venus equatorial region from Pioneer Venus radar imaging. Earth Moon Planets 1990, 50, 305–327. [Google Scholar] [CrossRef] [Green Version]
- Radiotelescope, R.S.N. Mapping Venus. Phys. Bull. 1976, 27, 535. [Google Scholar]
- Johnson, W.T. Magellan imaging radar mission to Venus. Proc. IEEE 1991, 79, 777–790. [Google Scholar] [CrossRef]
- Batson, R.; Kirk, R.L.; Edwards, K.; Morgan, H. Venus cartography. J. Geophys. Res. Planets 1994, 99, 21173–21181. [Google Scholar]
- Solomon, S.C.; Smrekar, S.E.; Bindschadler, D.L.; Grimm, R.E.; Kaula, W.M.; McGill, G.E.; Phillips, R.J.; Saunders, R.S.; Schubert, G.; Squyres, S.W. Venus tectonics: An overview of Magellan observations. J. Geophys. Res. Planets 1992, 97, 13199–13255. [Google Scholar] [CrossRef] [Green Version]
- Head, J.W.; Crumpler, L.; Aubele, J.C.; Guest, J.E.; Saunders, R.S. Venus volcanism: Classification of volcanic features and structures, associations, and global distribution from Magellan data. J. Geophys. Res. Planets 1992, 97, 13153–13197. [Google Scholar] [CrossRef] [Green Version]
- Campbell, D.; Stacy, N.; Newman, W.; Arvidson, R.; Jones, E.; Musser, G.; Roper, A.; Schaller, C. Magellan observations of extended impact crater related features on the surface of Venus. J. Geophys. Res. Planets 1992, 97, 16249–16277. [Google Scholar] [CrossRef]
- Baker, V.; Komatsu, G.; Parker, T.; Gulick, V.; Kargel, J.; Lewis, J. Channels and valleys on Venus: Preliminary analysis of Magellan data. J. Geophys. Res. Planets 1992, 97, 13421–13444. [Google Scholar] [CrossRef]
- Hensley, S.; Shaffer, S. Automatic DEM generation using Magellan stereo data. In Proceedings of the Proceedings of IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; pp. 1470–1472. [Google Scholar]
- Howington-Kraus, E.; Kirk, R.L.; Galuszka, D.; Redding, B. USGS Magellan stereomapping of Venus. In Proceedings of the European Planetary Science Congress, Berlin, Germany, 18–22 September 2006; p. 490. [Google Scholar]
- Kirk, R.L.; Howington-Kraus, E. Radargrammetry on three planets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. XXXVII Part 2008, 4, 973–980. [Google Scholar]
- Shirley, D.L. The mariner 10 mission to venus and mercury. Acta Astronaut. 2003, 53, 375–385. [Google Scholar] [CrossRef]
- Cook, A.; Robinson, M.S. Mariner 10 stereo image coverage of Mercury. J. Geophys. Res. Planets 2000, 105, 9429–9443. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B.; Danielson, G.E., Jr.; Klaasen, K.; Wilson, L. Photometric observations of Mercury from Mariner 10. J. Geophys. Res. 1975, 80, 2431–2443. [Google Scholar] [CrossRef]
- Solomon, S.C.; McNutt, R.L., Jr.; Gold, R.E.; Acuña, M.H.; Baker, D.N.; Boynton, W.V.; Chapman, C.R.; Cheng, A.F.; Gloeckler, G.; Head, J.W., III. The MESSENGER mission to Mercury: Scientific objectives and implementation. Planet. Space Sci. 2001, 49, 1445–1465. [Google Scholar] [CrossRef]
- Solomon, S.C.; Nittler, L.R.; Anderson, B.J. Mercury: The View after MESSENGER; Cambridge University Press: Cambridge, UK, 2018; Volume 21. [Google Scholar]
- Cavanaugh, J.F.; Smith, J.C.; Sun, X.; Bartels, A.E.; Ramos-Izquierdo, L.; Krebs, D.J.; McGarry, J.F.; Trunzo, R.; Novo-Gradac, A.M.; Britt, J.L. The Mercury Laser Altimeter instrument for the MESSENGER mission. Space Sci. Rev. 2007, 131, 451–479. [Google Scholar] [CrossRef] [Green Version]
- Oberst, J.; Preusker, F.; Phillips, R.J.; Watters, T.R.; Head, J.W.; Zuber, M.T.; Solomon, S.C. The morphology of Mercury’s Caloris basin as seen in MESSENGER stereo topographic models. Icarus 2010, 209, 230–238. [Google Scholar] [CrossRef]
- Preusker, F.; Oberst, J.; Head, J.W.; Watters, T.R.; Robinson, M.S.; Zuber, M.T.; Solomon, S.C. Stereo topographic models of Mercury after three MESSENGER flybys. Planet. Space Sci. 2011, 59, 1910–1917. [Google Scholar] [CrossRef]
- Preusker, F.; Stark, A.; Oberst, J.; Matz, K.-D.; Gwinner, K.; Roatsch, T.; Watters, T.R. Toward high-resolution global topography of Mercury from MESSENGER orbital stereo imaging: A prototype model for the H6 (Kuiper) quadrangle. Planet. Space Sci. 2017, 142, 26–37. [Google Scholar]
- Becker, K.J.; Robinson, M.S.; Becker, T.L.; Weller, L.A.; Edmundson, K.L.; Neumann, G.A.; Perry, M.E.; Solomon, S.C. First global digital elevation model of Mercury. In Proceedings of the 47th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 21–25 March 2016; p. 2959. [Google Scholar]
- Stark, A.; Oberst, J.; Preusker, F.; Gwinner, K.; Peale, S.J.; Margot, J.-L.; Phillips, R.J.; Zuber, M.T.; Solomon, S.C. Mercury’s rotational parameters from MESSENGER image and laser altimeter data: A feasibility study. Planet. Space Sci. 2015, 117, 64–72. [Google Scholar] [CrossRef] [Green Version]
- Watters, T.R.; Solomon, S.C.; Robinson, M.S.; Head, J.W.; André, S.L.; Hauck, S.A., II; Murchie, S.L. The tectonics of Mercury: The view after MESSENGER’s first flyby. Earth Planet. Sci. Lett. 2009, 285, 283–296. [Google Scholar] [CrossRef]
- Bergquist, B.A. Mercury, volcanism, and mass extinctions. Proc. Natl. Acad. Sci. USA 2017, 114, 8675–8677. [Google Scholar] [CrossRef] [Green Version]
- Benkhoff, J.; Van Casteren, J.; Hayakawa, H.; Fujimoto, M.; Laakso, H.; Novara, M.; Ferri, P.; Middleton, H.R.; Ziethe, R. BepiColombo—Comprehensive exploration of Mercury: Mission overview and science goals. Planet. Space Sci. 2010, 58, 2–20. [Google Scholar] [CrossRef]
- Cremonese, G.; Capaccioni, F.; Capria, M.; Doressoundiram, A.; Palumbo, P.; Vincendon, M.; Massironi, M.; Debei, S.; Zusi, M.; Altieri, F. SIMBIO-SYS: Scientific cameras and spectrometer for the BepiColombo mission. Space Sci. Rev. 2020, 216, 1–78. [Google Scholar] [CrossRef]
- Thomas, N.; Hussmann, H.; Spohn, T.; Lara, L.; Christensen, U.; Affolter, M.; Bandy, T.; Beck, T.; Chakraborty, S.; Geissbühler, U. The BepiColombo laser altimeter. Space Sci. Rev. 2021, 217, 1–62. [Google Scholar] [CrossRef]
- Pollack, J.B.; Veverka, J.; Noland, M.; Sagan, C.; Hartmann, W.; Duxbury, T.; Born, G.; Milton, D.; Smith, B. Mariner 9 television observations of Phobos and Deimos. Icarus 1972, 17, 394–407. [Google Scholar] [CrossRef]
- Duxbury, T.; Callahan, J. Phobos and Deimos astrometric observations from Mariner 9. Astron. Astrophys. 1989, 216, 284–293. [Google Scholar]
- Duxbury, T.; Veverka, J. Viking imaging of Phobos and Deimos: An overview of the primary mission. J. Geophys. Res. 1977, 82, 4203–4211. [Google Scholar] [CrossRef]
- Oberst, J.; Matz, K.; Roatsch, T.; Giese, B.; Hoffmann, H.; Duxbury, T.; Neukum, G. Astrometric observations of Phobos and Deimos with the SRC on Mars Express. Astron. Astrophys. 2006, 447, 1145–1151. [Google Scholar] [CrossRef] [Green Version]
- Oberst, J.; Matz, K.-D.; Roatsch, T.; Giese, B.; Hoffmann, H.; Neukum, G. New Observations of Phobos, Deimos, and Their Shadows with the HRSC/SRC on Mars Express. In Proceedings of the AEF Frühjahrstagung 2006, Heidelberg, Germany, 13–16 March 2006. [Google Scholar]
- Witasse, O.; Duxbury, T.; Chicarro, A.; Altobelli, N.; Andert, T.; Aronica, A.; Barabash, S.; Bertaux, J.-L.; Bibring, J.-P.; Cardesin-Moinelo, A. Mars express investigations of Phobos and Deimos. Planet. Space Sci. 2014, 102, 18–34. [Google Scholar] [CrossRef]
- Thomas, N.; Ivanov, A. HiRISE and Mars Pathfinder observations of Phobos and Deimos. In Proceedings of the European Planetary Science Congress, Potsdam, Germany, 13–18 September 2009; p. 494. [Google Scholar]
- Wählisch, M.; Willner, K.; Oberst, J.; Matz, K.-D.; Scholten, F.; Roatsch, T.; Hoffmann, H.; Semm, S.; Neukum, G. A new topographic image atlas of Phobos. Earth Planet. Sci. Lett. 2010, 294, 547–553. [Google Scholar] [CrossRef]
- Willner, K.; Shi, X.; Oberst, J. Phobos’ shape and topography models. Planet. Space Sci. 2014, 102, 51–59. [Google Scholar] [CrossRef] [Green Version]
- Belton, M.J.; Chapman, C.R.; Klaasen, K.P.; Harch, A.P.; Thomas, P.C.; Veverka, J.; McEwen, A.S.; Pappalardo, R.T. Galileo’s encounter with 243 Ida: An overview of the imaging experiment. Icarus 1996, 120, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Thomas, P.; Belton, M.; Carcich, B.; Chapman, C.; Davies, M.; Sullivan, R.; Veverka, J. The shape of Ida. Icarus 1996, 120, 20–32. [Google Scholar]
- Stooke, P.J. The surface of asteroid 951 Gaspra. Earth Moon Planets 1996, 75, 53–75. [Google Scholar] [CrossRef]
- Belton, M.; Veverka, J.; Thomas, P.; Helfenstein, P.; Simonelli, D.; Chapman, C.; Davies, M.; Greeley, R.; Greenberg, R.; Head, J. Galileo encounter with 951 Gaspra: First pictures of an asteroid. Science 1992, 257, 1647–1652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veverka, J.; Belton, M.; Klaasen, K.; Chapman, C. Galileo’s encounter with 951 Gaspra: Overview. Icarus 1994, 107, 2–17. [Google Scholar] [CrossRef]
- McCurdy, H.E. Low-Cost Innovation in Spaceflight: The Near Earth Asteroid Rendezvous (NEAR) Shoemaker Mission; National Aeronautics and Space Administration, Office of External Relations: Washington, DC, USA, 2005. [Google Scholar]
- Zuber, M.T.; Smith, D.E.; Cheng, A.F.; Garvin, J.B.; Aharonson, O.; Cole, T.D.; Dunn, P.J.; Guo, Y.; Lemoine, F.G.; Neumann, G.A. The shape of 433 Eros from the NEAR-Shoemaker laser rangefinder. Science 2000, 289, 2097–2101. [Google Scholar] [CrossRef] [Green Version]
- Veverka, J.; Thomas, P.; Harch, A.; Clark, B.; Bell, J., III; Carcich, B.; Joseph, J.; Murchie, S.; Izenberg, N.; Chapman, C. NEAR encounter with asteroid 253 Mathilde: Overview. Icarus 1999, 140, 3–16. [Google Scholar] [CrossRef]
- Becker, K.J.; Gaskell, R.W.; LeCorre, L.; Reddy, V. Hayabusa and Dawn image control from generation of digital elevation models for mapping and analysis. In Proceedings of the 46th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 16–20 March 2015. [Google Scholar]
- Ishiguro, M.; Hiroi, T.; Tholen, D.J.; Sasaki, S.; Ueda, Y.; Nimura, T.; Abe, M.; Clark, B.E.; Yamamoto, A.; Yoshida, F. Global mapping of the degree of space weathering on asteroid 25143 Itokawa by Hayabusa/AMICA observations. Meteorit. Planet. Sci. 2007, 42, 1791–1800. [Google Scholar] [CrossRef]
- Nardi, L.; Palomba, E.; Longobardo, A.; Galiano, A.; Dirri, F. Mapping olivine abundance on asteroid (25143) Itokawa from Hayabusa/NIRS data. Icarus 2019, 321, 14–28. [Google Scholar] [CrossRef]
- Jorda, L.; Gaskell, R.; Capanna, C.; Hviid, S.; Lamy, P.; Ďurech, J.; Faury, G.; Groussin, O.; Gutiérrez, P.; Jackman, C. The global shape, density and rotation of Comet 67P/Churyumov-Gerasimenko from preperihelion Rosetta/OSIRIS observations. Icarus 2016, 277, 257–278. [Google Scholar] [CrossRef]
- Preusker, F.; Scholten, F.; Knollenberg, J.; Kührt, E.; Matz, K.-D.; Mottola, S.; Roatsch, T.; Thomas, N. The northern hemisphere of asteroid (21) Lutetia—Topography and orthoimages from Rosetta OSIRIS NAC image data. Planet. Space Sci. 2012, 66, 54–63. [Google Scholar] [CrossRef]
- Preusker, F.; Scholten, F.; Matz, K.-D.; Roatsch, T.; Willner, K.; Hviid, S.; Knollenberg, J.; Jorda, L.; Gutiérrez, P.J.; Kührt, E. Shape model, reference system definition, and cartographic mapping standards for comet 67P/Churyumov-Gerasimenko–Stereo-photogrammetric analysis of Rosetta/OSIRIS image data. Astron. Astrophys. 2015, 583, A33. [Google Scholar]
- Zheng, C.; Ping, J.; Wang, M. Hierarchical classification for the topography analysis of Asteroid (4179) Toutatis from the Chang’E-2 images. Icarus 2016, 278, 119–127. [Google Scholar] [CrossRef]
- Tsuda, Y.; Yoshikawa, M.; Saiki, T.; Nakazawa, S.; Watanabe, S.-i. Hayabusa2–Sample return and kinetic impact mission to near-earth asteroid Ryugu. Acta Astronaut. 2019, 156, 387–393. [Google Scholar] [CrossRef]
- Roatsch, T.; Kersten, E.; Matz, K.-D.; Preusker, F.; Scholten, F.; Jaumann, R.; Raymond, C.A.; Russell, C.T. High resolution Vesta high altitude mapping orbit (HAMO) atlas derived from Dawn Framing Camera images. Planet. Space Sci. 2012, 73, 283–286. [Google Scholar] [CrossRef]
- Roatsch, T.; Kersten, E.; Matz, K.-D.; Preusker, F.; Scholten, F.; Jaumann, R.; Raymond, C.; Russell, C. High-resolution Ceres high altitude mapping orbit atlas derived from Dawn framing camera images. Planet. Space Sci. 2016, 129, 103–107. [Google Scholar] [CrossRef]
- Reuter, D.; Simon, A.; Hair, J.; Lunsford, A.; Manthripragada, S.; Bly, V.; Bos, B.; Brambora, C.; Caldwell, E.; Casto, G. The OSIRIS-REx Visible and InfraRed Spectrometer (OVIRS): Spectral maps of the asteroid Bennu. Space Sci. Rev. 2018, 214, 54. [Google Scholar] [CrossRef] [Green Version]
- Daly, M.; Barnouin, O.; Dickinson, C.; Seabrook, J.; Johnson, C.; Cunningham, G.; Haltigin, T.; Gaudreau, D.; Brunet, C.; Aslam, I. The OSIRIS-REx laser altimeter (OLA) investigation and instrument. Space Sci. Rev. 2017, 212, 899–924. [Google Scholar] [CrossRef]
- Levison, H.F.; Olkin, C.B.; Noll, K.S.; Marchi, S.; Bell, J.F., III; Bierhaus, E.; Binzel, R.; Bottke, W.; Britt, D.; Brown, M. Lucy mission to the Trojan asteroids: Science goals. Planet. Sci. J. 2021, 2, 171. [Google Scholar] [CrossRef]
- Olkin, C.B.; Levison, H.F.; Vincent, M.; Noll, K.S.; Andrews, J.; Gray, S.; Good, P.; Marchi, S.; Christensen, P.; Reuter, D. Lucy mission to the trojan asteroids: Instrumentation and encounter concept of operations. Planet. Sci. J. 2021, 2, 172. [Google Scholar] [CrossRef]
- Okada, T.; Kebukawa, Y.; Aoki, J.; Matsumoto, J.; Yano, H.; Iwata, T.; Mori, O.; Bibring, J.-P.; Ulamec, S.; Jaumann, R. Science exploration and instrumentation of the OKEANOS mission to a Jupiter Trojan asteroid using the solar power sail. Planet. Space Sci. 2018, 161, 99–106. [Google Scholar] [CrossRef]
- Swindell, W.; Doose, L.R. The imaging experiment on Pioneer 10. J. Geophys. Res. 1974, 79, 3634–3644. [Google Scholar] [CrossRef]
- Van Allen, J.A. Findings on rings and inner satellites of Saturn by Pioneer 11. Icarus 1982, 51, 509–527. [Google Scholar] [CrossRef]
- Smith, B.A.; Soderblom, L.; Beebe, R.; Boyce, J.; Briggs, G.; Bunker, A.; Collins, S.A.; Hansen, C.J.; Johnson, T.V.; Mitchell, J.L. Encounter with Saturn: Voyager 1 imaging science results. Science 1981, 212, 163–191. [Google Scholar] [CrossRef]
- Smith, B.A.; Soderblom, L.A.; Beebe, R.; Boyce, J.; Briggs, G.; Carr, M.; Collins, S.A.; Cook, A.F.; Danielson, G.E.; Davies, M.E. The Galilean satellites and Jupiter: Voyager 2 imaging science results. Science 1979, 206, 927–950. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.A.; Soderblom, L.A.; Johnson, T.V.; Ingersoll, A.P.; Collins, S.A.; Shoemaker, E.M.; Hunt, G.; Masursky, H.; Carr, M.H.; Davies, M.E. The Jupiter system through the eyes of Voyager 1. Science 1979, 204, 951–972. [Google Scholar] [CrossRef] [PubMed]
- Stone, E.; Miner, E. Voyager 1 encounter with the Saturnian system. Science 1981, 212, 159–163. [Google Scholar] [CrossRef] [Green Version]
- Stone, E.; Miner, E. The Voyager 2 encounter with the Uranian system. Science 1986, 233, 39–43. [Google Scholar] [CrossRef]
- Smith, B.A.; Soderblom, L.A.; Banfield, D.; Barnet, C.; Basilevsky, A.; Beebe, R.; Bollinger, K.; Boyce, J.; Brahic, A.; Briggs, G. Voyager 2 at Neptune: Imaging science results. Science 1989, 246, 1422–1449. [Google Scholar] [CrossRef] [Green Version]
- Collins, G.C.; Head, J.W., III; Pappalardo, R.T. The role of extensional instability in creating Ganymede grooved terrain: Insights from Galileo high-resolution stereo imaging. Geophys. Res. Lett. 1998, 25, 233–236. [Google Scholar] [CrossRef] [Green Version]
- White, O.L.; Schenk, P.M.; Nimmo, F.; Hoogenboom, T. A new stereo topographic map of Io: Implications for geology from global to local scales. J. Geophys. Res. Planets 2014, 119, 1276–1301. [Google Scholar] [CrossRef]
- Schenk, P.; Wilson, D.; Morris, R.; Parker, T. The Stereo View of the Solar Sytem. In Proceedings of the 25th Lunar and Planetary Science Conference, Houston, TX, USA, 14–18 March 1994; p. 1205. [Google Scholar]
- Young, R.E. The Galileo Probe Mission to Jupiter: Science Overview; Wiley Online Library: Hoboken, NJ, USA, 1998; Volume 103, pp. 22775–22790. [Google Scholar]
- Klaasen, K.P.; Breneman, H.H.; Cunningham, W.F.; Kaufman, J.M.; Klemaszewski, J.E.; Magee, K.P.; McEwen, A.S.; Mortensen, H.B.; Pappalardo, R.T.; Senske, D.A. Calibration and performance of the Galileo solid-state imaging system in Jupiter orbit. Opt. Eng. 1999, 38, 1178–1199. [Google Scholar] [CrossRef] [Green Version]
- Keszthelyi, L.; McEwen, A.; Phillips, C.; Milazzo, M.; Geissler, P.; Turtle, E.; Radebaugh, J.; Williams, D.; Simonelli, D.; Breneman, H. Imaging of volcanic activity on Jupiter’s moon Io by Galileo during the Galileo Europa Mission and the Galileo Millennium Mission. J. Geophys. Res. Planets 2001, 106, 33025–33052. [Google Scholar] [CrossRef]
- Greeley, R.; Sullivan, R.; Klemaszewski, J.; Homan, K.; Head, J.W., III; Pappalardo, R.T.; Veverka, J.; Clark, B.E.; Johnson, T.V.; Klaasen, K.P. Europa: Initial Galileo geological observations. Icarus 1998, 135, 4–24. [Google Scholar] [CrossRef] [Green Version]
- Matson, D.L.; Spilker, L.J.; Lebreton, J.-P. The Cassini/Huygens mission to the Saturnian system. Cassini-Huygens Mission 2003, 104, 1–58. [Google Scholar]
- Lorenz, R.D.; Lopes, R.M.; Paganelli, F.; Lunine, J.I.; Kirk, R.L.; Mitchell, K.L.; Soderblom, L.A.; Stofan, E.R.; Ori, G.; Myers, M. Fluvial channels on Titan: Initial Cassini RADAR observations. Planet. Space Sci. 2008, 56, 1132–1144. [Google Scholar] [CrossRef]
- Mastrogiuseppe, M.; Hayes, A.G.; Poggiali, V.; Lunine, J.I.; Lorenz, R.; Seu, R.; Le Gall, A.; Notarnicola, C.; Mitchell, K.L.; Malaska, M. Bathymetry and composition of Titan’s Ontario Lacus derived from Monte Carlo-based waveform inversion of Cassini RADAR altimetry data. Icarus 2018, 300, 203–209. [Google Scholar] [CrossRef]
- Mastrogiuseppe, M.; Poggiali, V.; Seu, R.; Martufi, R.; Notarnicola, C. Titan dune heights retrieval by using Cassini Radar Altimeter. Icarus 2014, 230, 191–197. [Google Scholar] [CrossRef]
- Liu, Z.Y.-C.; Radebaugh, J.; Harris, R.A.; Christiansen, E.H.; Neish, C.D.; Kirk, R.L.; Lorenz, R.D.; Team, C.R. The tectonics of Titan: Global structural mapping from Cassini RADAR. Icarus 2016, 270, 14–29. [Google Scholar] [CrossRef]
- Corlies, P.; Hayes, A.; Birch, S.; Lorenz, R.; Stiles, B.; Kirk, R.; Poggiali, V.; Zebker, H.; Iess, L. Titan’s topography and shape at the end of the Cassini mission. Geophys. Res. Lett. 2017, 44, 11754–11761. [Google Scholar] [CrossRef] [Green Version]
- Kirk, R.; Howington-Kraus, E.; Redding, B.; Aharonson, O.; Bills, B.; Hayes, A.; Iess, L.; Lopes, R.; Lorenz, R.; Lucas, A. Topographic mapping of Titan: Completion of a global radargrammetric control network opens the floodgates for stereo DTM production. In Proceedings of the 44th Annual Lunar and Planetary Science Conference, Woodlands, TX, USA, 18–22 March 2013; p. 2898. [Google Scholar]
- Kirk, R.; Howington-Kraus, E.; Stiles, B.; Hensley, S.; Team, C.R. Digital Topographic Models of Titan Produced by Radargrammetry with a Rigorous Sensor Model. In Proceedings of the 39th Annual Lunar and Planetary Science Conference, League, TX, USA, 10–14 March 2018; p. 2320. [Google Scholar]
- Elachi, C.; Wall, S.; Allison, M.; Anderson, Y.; Boehmer, R.; Callahan, P.; Encrenaz, P.; Flamini, E.; Franceschetti, G.; Gim, Y. Cassini radar views the surface of Titan. Science 2005, 308, 970–974. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stiles, B.W.; Hensley, S.; Gim, Y.; Bates, D.M.; Kirk, R.L.; Hayes, A.; Radebaugh, J.; Lorenz, R.D.; Mitchell, K.L.; Callahan, P.S. Determining Titan surface topography from Cassini SAR data. Icarus 2009, 202, 584–598. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Stiles, B.W.; Aharonson, O.; Lucas, A.; Hayes, A.G.; Kirk, R.L.; Zebker, H.A.; Turtle, E.P.; Neish, C.D.; Stofan, E.R. A global topographic map of Titan. Icarus 2013, 225, 367–377. [Google Scholar] [CrossRef] [Green Version]
- Roatsch, T.; Jaumann, R.; Stephan, K.; Thomas, P. Cartographic mapping of the icy satellites using ISS and VIMS data. In Saturn from Cassini-Huygens; Springer: Berlin/Heidelberg, Germany, 2009; pp. 763–781. [Google Scholar]
- Young, L.A.; Stern, S.A.; Weaver, H.A.; Bagenal, F.; Binzel, R.P.; Buratti, B.; Cheng, A.F.; Cruikshank, D.; Gladstone, G.R.; Grundy, W.M. New Horizons: Anticipated scientific investigations at the Pluto system. Space Sci. Rev. 2008, 140, 93–127. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.M.; McKinnon, W.B.; Spencer, J.R.; Howard, A.D.; Schenk, P.M.; Beyer, R.A.; Nimmo, F.; Singer, K.N.; Umurhan, O.M.; White, O.L. The geology of Pluto and Charon through the eyes of New Horizons. Science 2016, 351, 1284–1293. [Google Scholar] [CrossRef] [Green Version]
- Nimmo, F.; Umurhan, O.; Lisse, C.M.; Bierson, C.J.; Lauer, T.R.; Buie, M.W.; Throop, H.B.; Kammer, J.A.; Roberts, J.H.; McKinnon, W.B. Mean radius and shape of Pluto and Charon from New Horizons images. Icarus 2017, 287, 12–29. [Google Scholar] [CrossRef] [Green Version]
- Weaver, H.; Buie, M.; Buratti, B.; Grundy, W.; Lauer, T.; Olkin, C.; Parker, A.; Porter, S.; Showalter, M.; Spencer, J. The small satellites of Pluto as observed by New Horizons. Science 2016, 351, aae0030. [Google Scholar] [CrossRef] [Green Version]
- Weaver, H.; Gibson, W.; Tapley, M.; Young, L.; Stern, S. Overview of the New Horizons science payload. In New Horizons; Springer: Berlin/Heidelberg, Germany, 2009; pp. 75–91. [Google Scholar]
- Schenk, P.M.; Beyer, R.A.; Moore, J.; Spencer, J.R.; McKinnon, W.B.; Howard, A.D.; White, O.L.; Umurhan, O.M.; Singer, K.N.; Stern, A. Topographic mapping of Pluto and Charon using New Horizons data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 487–489. [Google Scholar] [CrossRef] [Green Version]
- Schenk, P.M.; Beyer, R.A.; McKinnon, W.B.; Moore, J.M.; Spencer, J.R.; White, O.L.; Singer, K.; Nimmo, F.; Thomason, C.; Lauer, T.R. Basins, fractures and volcanoes: Global cartography and topography of Pluto from New Horizons. Icarus 2018, 314, 400–433. [Google Scholar] [CrossRef]
- Lohse, V.; Heipke, C.; Kirk, R.L. Derivation of planetary topography using multi-image shape-from-shading. Planet. Space Sci. 2006, 54, 661–674. [Google Scholar] [CrossRef]
- Alexandrov, O.; Beyer, R.A. Multiview Shape-From-Shading for Planetary Images. Earth Space Sci. 2018, 5, 652–666. [Google Scholar] [CrossRef] [Green Version]
- Thomas, J.; Kober, W.; Leberl, F. Multiple image SAR shape-from-shading. Photogramm. Eng. Remote Sens. 1991, 57, 51–59. [Google Scholar]
- Gugan, D.; Dowman, I. Topographic mapping from SPOT imagery. Photogramm. Eng. Remote Sens. 1988, 12, 787–796. [Google Scholar]
- Orun, A.B.; Natarajan, K. A modified bundle adjustment software for SPOT imagery and photography- Tradeoff. Photogramm. Eng. Remote Sens. 1994, 60, 1431–1438. [Google Scholar]
- Acton, C.; Bachman, N.; Semenov, B.; Turner, F.; Wright, E. SPICE Products and Services Available to the Planetary Cartography Community; NASA: Washington, DC, USA, 2001.
- Acton, C. An Overview of SPICE; Jet Propulsion Laboratory: Oak Grove, KY, USA, 1998. [Google Scholar]
- Acton, C.H., Jr. Ancillary data services of NASA’s navigation and ancillary information facility. Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Di, K.; Jia, M.; Xin, X.; Wang, J.; Liu, B.; Li, J.; Xie, J.; Liu, Z.; Peng, M.; Yue, Z. High-resolution large-area digital orthophoto map generation using LROC NAC images. Photogramm. Eng. Remote Sens. 2019, 85, 481–491. [Google Scholar] [CrossRef]
- Geng, X.; Xu, Q.; Xing, S.; Lan, C. A generic pushbroom sensor model for planetary photogrammetry. Earth Space Sci. 2020, 7, e2019EA001014. [Google Scholar] [CrossRef] [Green Version]
- Edmundson, K.L. Jigsaw: The ISIS3 bundle adjustment for extraterrestrial photogrammetry. In Proceedings of the XXII ISPRS Congress, Melbourne, VIC, Australia, 25 August–1 September 2012. [Google Scholar]
- Speyerer, E.; Wagner, R.; Robinson, M.; Licht, A.; Thomas, P.; Becker, K.; Anderson, J.; Brylow, S.; Humm, D.; Tschimmel, M. Pre-flight and on-orbit geometric calibration of the Lunar Reconnaissance Orbiter Camera. Space Sci. Rev. 2016, 200, 357–392. [Google Scholar] [CrossRef]
- Beyer, R.A.; Alexandrov, O.; McMichael, S. The Ames Stereo Pipeline: NASA’s open source software for deriving and processing terrain data. Earth Space Sci. 2018, 5, 537–548. [Google Scholar] [CrossRef]
- Sutton, S.; Boyd, A.; Kirk, R.L.; Cook, D.; Backer, J.; Fennema, A.; Heyd, R.; McEwen, A.; Mirchandani, S. Correcting spacecraft jitter in HiRISE images. In Planetary Remote Sensing and Mapping; CRC Press: Boca Raton, FL, USA, 2018; pp. 91–106. [Google Scholar]
- Spiegel, M.; Baumgartner, A.; Ebner, H. Orientation of Mars Express/HRSC imagery using laser altimeter data as control information. In Proceedings of the ISPRS Workshop High Resolution Mapping from Space, Hannover, Germany, 6–8 October 2003; pp. 6–8. [Google Scholar]
- Neumann, G.A.; Rowlands, D.D.; Lemoine, F.G.; Smith, D.E.; Zuber, M.T. Crossover analysis of Mars orbiter laser altimeter data. J. Geophys. Res. Planets 2001, 106, 23753–23768. [Google Scholar] [CrossRef] [Green Version]
- Ebner, H.; Spiegel, M.; Baumgartner, A.; Giese, B.; Neukum, G. Improving the exterior orientation of Mars Express HRSC imagery. Int. Arch. Photogramm. Remote Sens. 2004, 35, 852–857. [Google Scholar]
- Strunz, G. Bildorientierung und Objektrekonstruction Mit Punkten, Linien und Flächen; Verlag C. H. Beck: Munich, Germany, 1993. [Google Scholar]
- Ebner, H.; Ohlhof, T. Utilization of ground control points for image orientation without point identification in image space. In Proceedings of the ISPRS Commission III Symposium: Spatial Information from Digital Photogrammetry and Computer Vision, Munich, Germany, 5–9 September 1994; pp. 206–211. [Google Scholar]
- Heipke, C.; Schmidt, R.; Brand, R.; Oberst, J.; Neukum, G. Performance of automatic tie point extraction using HRSC imagery of the Mars Express mission. Int. Arch. Photogramm. Remote Sens. 2004, 35, 846–851. [Google Scholar]
- Spiegel, M. Improvement of interior and exterior orientation of the three line camera HRSC with a simultaneous adjustment. Int. Arch. Photogramm. Remote Sens. 2007, 36, 161–166. [Google Scholar]
- Scholten, F.; Oberst, J.; Matz, K.D.; Roatsch, T.; Wählisch, M.; Speyerer, E.; Robinson, M. GLD100: The near-global lunar 100 m raster DTM from LROC WAC stereo image data. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Scholten, F. DLR-Software for the Generation of Level-4 Data; DLR Photogrammetry Tutorial; DLR-Software: Córdoba, Argentina, 2003. [Google Scholar]
- Kim, J.-R.; Muller, J.-P. Multi-resolution topographic data extraction from Martian stereo imagery. Planet. Space Sci. 2009, 57, 2095–2112. [Google Scholar] [CrossRef]
- Hu, H.; Wu, B. Block adjustment and coupled epipolar rectification of LROC NAC images for precision lunar topographic mapping. Planet. Space Sci. 2018, 160, 26–38. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. IKONOS geometric accuracy. In Proceedings of the Joint Workshop of ISPRS Working Groups I/2, I/5 and IV/7 on High Resolution Mapping from Space, Hannover, Germany, 19–21 September 2001; pp. 19–21. [Google Scholar]
- Grodechi, J.; Dial, G. Block adjustment of high-resolution satellite images described by rational polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Gruen, A. Adaptive least squares correlation: A powerful image matching technique. S. Afr. J. Photogramm. Remote Sens. Cartogr. 1985, 14, 175–187. [Google Scholar]
- Derpanis, K.G. Overview of the RANSAC Algorithm. Image Rochester NY 2010, 4, 2–3. [Google Scholar]
- Preusker, F.; Scholten, F.; Matz, K.-D.; Roatsch, T.; Jaumann, R.; Raymond, C.A.; Russell, C.T. Topography of Vesta from Dawn FC stereo images. In Proceedings of the 43rd Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2012. [Google Scholar]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef]
- Dini, G.R.; Jacobsen, K.; Heipke, C. Delineation of building footprints from high resolution satellite stereo imagery using image matching and a GIS database. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2013, 40, 81–85. [Google Scholar] [CrossRef] [Green Version]
- Wurm, M.; d’Angelo, P.; Reinartz, P.; Taubenböck, H. Investigating the applicability of Cartosat-1 DEMs and topographic maps to localize large-area urban mass concentrations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4138–4152. [Google Scholar] [CrossRef] [Green Version]
- Kim, T. A study on the epipolarity of linear pushbroom images. Photogramm. Eng. Remote Sens. 2000, 66, 961–966. [Google Scholar]
- Chen, H.; Hu, X.; Gläser, P.; Xiao, H.; Ye, Z.; Zhang, H.; Tong, X.; Oberst, J. CNN-Based Large Area Pixel-Resolution Topography Retrieval From Single-View LROC NAC Images Constrained With SLDEM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9398–9416. [Google Scholar] [CrossRef]
- Tenthoff, M.; Wohlfarth, K.; Wöhler, C. High resolution digital terrain models of Mercury. Remote Sens. 2020, 12, 3989. [Google Scholar] [CrossRef]
- Bertone, S.; Mazarico, E.; Barker, M.K.; Siegler, M.A.; Martinez-Camacho, J.M.; Hamill, C.D.; Glantzberg, A.K.; Chabot, N.L. Highly Resolved Topography and Illumination at Mercury’s South Pole from MESSENGER MDIS NAC. Planet. Sci. J. 2023, 4, 21. [Google Scholar] [CrossRef]
- Mizuno, T.; Kase, T.; Shiina, T.; Mita, M.; Namiki, N.; Senshu, H.; Yamada, R.; Noda, H.; Kunimori, H.; Hirata, N. Development of the laser altimeter (LIDAR) for Hayabusa2. Space Sci. Rev. 2017, 208, 33–47. [Google Scholar] [CrossRef]
- Xiao, H.; Stark, A.; Steinbrügge, G.; Hussmann, H.; Oberst, J. Processing of laser altimeter Time-of-Flight measurements to geodetic coordinates. J. Geod. 2021, 95, 22. [Google Scholar] [CrossRef]
- Xiao, H.; Stark, A.; Chen, H.; Oberst, J. Recomputation and updating of MOLA geolocation. Remote Sens. 2022, 14, 2201. [Google Scholar] [CrossRef]
- Harding, D.J.; Bufton, J.L.; Frawley, J.J. Satellite laser altimetry of terrestrial topography: Vertical accuracy as a function of surface slope, roughness, and cloud cover. IEEE Trans. Geosci. Remote Sens. 1994, 32, 329–339. [Google Scholar] [CrossRef]
- Gardner, C.S. Ranging Performance of Satellite Laser Altimeters; NASA: Washington, DC, USA, 1992.
- Bufton, J.L. Laser altimetry measurements from aircraft and spacecraft. Proc. IEEE 1989, 77, 463–477. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Abshire, J.B.; McGarry, J.F.; Neumann, G.A.; Smith, J.C.; Cavanaugh, J.F.; Harding, D.J.; Zwally, H.J.; Smith, D.E.; Zuber, M.T. Space lidar developed at the NASA Goddard Space Flight Center—The first 20 years. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1660–1675. [Google Scholar] [CrossRef]
- Garvin, J.; Bufton, J.; Blair, J.; Harding, D.; Luthcke, S.; Frawley, J.; Rowlands, D. Observations of the Earth’s topography from the Shuttle Laser Altimeter (SLA): Laser-pulse echo-recovery measurements of terrestrial surfaces. Phys. Chem. Earth 1998, 23, 1053–1068. [Google Scholar] [CrossRef]
- Nishiyama, G.; Stark, A.; Hüttig, C.; Hussmann, H.; Gwinner, K.; Hauber, E.; Lara, L.M.; Thomas, N. Simulation of Laser Pulse Shapes Received by the BepiColombo Laser Altimeter (BELA): Implications for Future Constraints on Surficial Properties of Mercury. In Proceedings of the 16th Europlanet Science Congress 2022, Granada, Spain, 18–23 September 2022. [Google Scholar]
- Neumann, G.A.; Smith, D.; Zuber, M.; Mazarico, E.; Torrence, M.; Cavanaugh, J. Meter-scale Roughness on the Moon from Lunar Orbiter Laser Altimeter (LOLA) Pulse Spreading: Implications for Exploration. In Proceedings of the Annual Meeting of the Lunar Exploration Analysis Group, Houston, TX, USA, 17 November 2008. [Google Scholar]
- Neumann, G.A.; Abshire, J.B.; Aharonson, O.; Garvin, J.B.; Sun, X.; Zuber, M.T. Mars Orbiter Laser Altimeter pulse width measurements and footprint-scale roughness. Geophys. Res. Lett. 2003, 30, 4. [Google Scholar] [CrossRef]
- Lemelin, M.; Lucey, P.; Neumann, G.; Mazarico, E.; Barker, M.; Kakazu, A.; Trang, D.; Smith, D.; Zuber, M. Improved calibration of reflectance data from the LRO Lunar Orbiter Laser Altimeter (LOLA) and implications for space weathering. Icarus 2016, 273, 315–328. [Google Scholar] [CrossRef]
- Deutsch, A.N.; Neumann, G.A.; Head, J.W. New evidence for surface water ice in small-scale cold traps and in three large craters at the north polar region of Mercury from the Mercury Laser Altimeter. Geophys. Res. Lett. 2017, 44, 9233–9241. [Google Scholar] [CrossRef] [Green Version]
- Fisher, E.A.; Lucey, P.G.; Lemelin, M.; Greenhagen, B.T.; Siegler, M.A.; Mazarico, E.; Aharonson, O.; Williams, J.-P.; Hayne, P.O.; Neumann, G.A. Evidence for surface water ice in the lunar polar regions using reflectance measurements from the Lunar Orbiter Laser Altimeter and temperature measurements from the Diviner Lunar Radiometer Experiment. Icarus 2017, 292, 74–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wildey, R.L. Radarclinometry for the Venus Radar Mapper. Photogramm. Eng. Remote Sens. 1986, 52, 41–50. [Google Scholar]
- Kim, J.; Wan, W.; Kim, Y. Reconstruction of Titan topography using CASSINI radar images and generic stereo processor. In Proceedings of the 47th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 21–25 March 2016; p. 1411. [Google Scholar]
- Connors, C. Determining heights and slopes of fault scarps and other surfaces on Venus using Magellan stereo radar. J. Geophys. Res. Planets 1995, 100, 14361–14381. [Google Scholar] [CrossRef]
- Maurice, K.E.; Leberl, F.W.; Norikane, L.; Hensley, S. Venus Surface Roughness and Magellan Stereo Data; NASA: Washington, DC, USA, 1994.
- Cochrane, C.G.; Ghail, R.C. Topographic constraints on impact crater morphology on Venus from high-resolution stereo synthetic aperture radar digital elevation models. J. Geophys. Res. Planets 2006, 111. [Google Scholar] [CrossRef]
- Legresy, B.; Papa, F.; Remy, F.; Vinay, G.; Van den Bosch, M.; Zanife, O.-Z. ENVISAT radar altimeter measurements over continental surfaces and ice caps using the ICE-2 retracking algorithm. Remote Sens. Environ. 2005, 95, 150–163. [Google Scholar] [CrossRef]
- Poggiali, V.; Mastrogiuseppe, M.; Hayes, A.G.; Seu, R.; Mullen, J.P.; Birch, S.P.D.; Raguso, M.C. High-resolution topography of Titan adapting the delay/Doppler algorithm to the Cassini RADAR altimeter data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7262–7268. [Google Scholar] [CrossRef]
- Herrick, R.R.; Stahlke, D.L.; Sharpton, V.L. Fine-scale Venusian topography from Magellan stereo data. Eos Trans. Am. Geophys. Union 2012, 93, 125–126. [Google Scholar] [CrossRef]
- Kirk, R.; Cook, D.; Howington-Kraus, E.; Barrett, J.; Becker, T.; Neish, C.; Thomson, B.; Bussey, D. Radargrammetry with Chandrayaan-1 and LRO Mini-RF images of the Moon. In Proceedings of the Joint symposium of ISPRS Technical Commission IV & AutoCarto in Conjunction with ASPRS/CaGIS 2010 Fall Specialty Conference, Orlando, FL, USA, 15–19 November 2010. [Google Scholar]
- Lopes, R.; Stofan, E.; Peckyno, R.; Radebaugh, J.; Mitchell, K.; Mitri, G.; Wood, C.; Kirk, R.; Wall, S.; Lunine, J. Distribution and interplay of geologic processes on Titan from Cassini radar data. Icarus 2010, 205, 540–558. [Google Scholar] [CrossRef]
- Zebker, H.A.; Stiles, B.; Hensley, S.; Lorenz, R.; Kirk, R.L.; Lunine, J. Size and shape of Saturn’s moon Titan. Science 2009, 324, 921–923. [Google Scholar] [CrossRef] [Green Version]
- Davies, M.E. The control net of Mars: May 1977. J. Geophys. Res. Solid Earth 1978, 83, 2311–2312. [Google Scholar] [CrossRef]
- Wu, S.S.; Billideau, J.S.; Spare, B.A. Publication of topographic atlas and control network of Mars. In Reports of Planetary Geology and Geophysics Program, 1990; NASA: Washington, DC, USA, 1991. [Google Scholar]
- Wu, S.; Schafer, F. Mars control network. Tech. Pap. Am. Soc. Photogramm 1984, 50, 456–463. [Google Scholar]
- Zeitler, W.; Oberst, J. The Mars Pathfinder landing site and the Viking control point network. J. Geophys. Res. Planets 1999, 104, 8935–8941. [Google Scholar] [CrossRef] [Green Version]
- Heller, J.; Wählisch, M.; Zeitler, W.; Scholten, F. Improved 3D Mars Control Net from a Combined Adjustment of VIKING images and Mars Orbiter Laser Altimeter data. In Proceedings of the ISPRS Working Group IV/9: Extraterrestrial Mapping Workshop, Flagstaff, CA, USA, 29 January 2001. [Google Scholar]
- Archinal, B.; Sides, S.; Weller, L.; Cushing, G.; Titus, T.; Kirk, R.; Soderblom, L.; Duxbury, T. Model Development and Testing for THEMIS Controlled Mars Mosaics. In Proceedings of the 36th Annual Lunar and Planetary Science Conference, League, TX, USA, 14–18 March 2005; p. 2052. [Google Scholar]
- Li, R.; Archinal, B.A.; Arvidson, R.E.; Bell, J.; Christensen, P.; Crumpler, L.; Des Marais, D.J.; Di, K.; Duxbury, T.; Golombek, M. Spirit rover localization and topographic mapping at the landing site of Gusev crater, Mars. J. Geophys. Res. Planets 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Archinal, B.A.; Lee, E.M.; Kirk, R.L.; Duxbury, T.; Sucharski, R.M.; Cook, D.; Barrett, J.M. A new Mars digital image model (MDIM 2.1) control network. Int. Arch. Photogramm. Remote Sens. 2004, 35, B4. [Google Scholar]
- Davies, M.E.; Hauge, T.A.; Katayama, F.Y.; Roth, J.A. Control Networks for the Galilean Satellites, November 1979; NASA: Washington, DC, USA, 1979; Volume 2532.
- Davies, M.E.; Katayama, F.Y. The control networks of Tethys and Dione. J. Geophys. Res. Space Phys. 1983, 88, 8729–8735. [Google Scholar] [CrossRef]
- Gwinner, K.; Jaumann, R.; Hauber, E.; Hoffmann, H.; Heipke, C.; Oberst, J.; Neukum, G.; Ansan, V.; Bostelmann, J.; Dumke, A. The High Resolution Stereo Camera (HRSC) of Mars Express and its approach to science analysis and mapping for Mars and its satellites. Planet. Space Sci. 2016, 126, 93–138. [Google Scholar] [CrossRef]
- Raymond, C.; Jaumann, R.; Nathues, A.; Sierks, H.; Roatsch, T.; Preusker, F.; Scholten, F.; Gaskell, R.; Jorda, L.; Keller, H.-U. The Dawn topography investigation. In The Dawn Mission to Minor Planets 4 Vesta and 1 Ceres; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; pp. 487–510. [Google Scholar]
- Mazarico, E.; Neumann, G.; Rowlands, D.; Smith, D. Geodetic constraints from multi-beam laser altimeter crossovers. J. Geod. 2010, 84, 343–354. [Google Scholar] [CrossRef]
- Gläser, P.; Haase, I.; Oberst, J.; Neumann, G. Co-registration of laser altimeter tracks with digital terrain models and applications in planetary science. Planet. Space Sci. 2013, 89, 111–117. [Google Scholar] [CrossRef] [Green Version]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Head, J.W. Improved LOLA elevation maps for south pole landing sites: Error estimates and their impact on illumination conditions. Planet. Space Sci. 2021, 203, 105119. [Google Scholar] [CrossRef]
- Xiao, H.; Stark, A.; Steinbrügge, G.; Thor, R.; Schmidt, F.; Oberst, J. Prospects for mapping temporal height variations of the seasonal CO2 snow/ice caps at the Martian poles by co-registration of MOLA Profiles. Planet. Space Sci. 2022, 214, 105446. [Google Scholar] [CrossRef]
- Stark, A.; Oberst, J.; Hussmann, H.; Steinbrügge, G. Mercury’s Rotational State from Self-Registration of Mercury Laser Altimeter Profiles. In Proceedings of the European Planetary Science Congress 2018, Berlin, Germany, 16–21 September 2018. [Google Scholar]
- Lin, S.-Y.; Muller, J.-P.; Mills, J.P.; Miller, P.E. An assessment of surface matching for the automated co-registration of MOLA, HRSC and HiRISE DTMs. Earth Planet. Sci. Lett. 2010, 294, 520–533. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A.; Wilkinson, B.E. Elements of Photogrammetry with Applications in GIS; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Zhang, L.; Aksakal-Kocaman, S.; Akca, D.; Kornus, W.; Baltsavias, E.P. Tests and performance evaluation of DMC images and new methods for their processing. ISPRS Arch. 2006, 36. [Google Scholar] [CrossRef]
- Mills, J.P.; Buckley, S.J.; Mitchell, H.L. Synergistic fusion of GPS and photogrammetrically generated elevation models. Photogramm. Eng. Remote Sens. 2003, 69, 341–349. [Google Scholar] [CrossRef]
- Mills, J.P.; Buckley, S.J.; Mitchell, H.; Clarke, P.; Edwards, S. A geomatics data integration technique for coastal change monitoring. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2005, 30, 651–664. [Google Scholar] [CrossRef]
- Eliason, E.; Anderson, J.; Barrett, J.; Becker, K.; Becker, T.; Cook, D.; Soderblom, L.; Sucharski, T.; Thompson, K. ISIS image processing capabilities for MGS/MOC imaging data. In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 12–16 March 2001; p. 2081. [Google Scholar]
- Kirk, R.L.; Squyres, S.W.; Neukum, G. Topographic Mapping of Mars: From Hectometer to Micrometer Scales. In Proceedings of the XXth ISPRS Congress Technical Commission IV, Istanbul, Turkey, 12-23 July 2004. [Google Scholar]
- Di, K.; Hu, W.; Liu, Y.; Peng, M. Co-registration of Chang’E-1 stereo images and laser altimeter data with crossover adjustment and image sensor model refinement. Adv. Space Res. 2012, 50, 1615–1628. [Google Scholar] [CrossRef]
- Shoemaker, E.M.; Hackman, R.J. Stratigraphic basis for a lunar time scale. In The Moon; USGS: Melon Park, CA, USA; Washiongton, DC, USA, 1962; pp. 289–300. [Google Scholar]
- Shoemaker, E.; Hackman, R. Lunar photogeologic chart LPC 58. In Copernicus, Prototype Chart; USGS: Reston, VA, USA, 1961; unpublished. [Google Scholar]
- Tanaka, K.L.; Skinner, J.A., Jr.; Dohm, J.M.; Irwin, R.P., III; Kolb, E.J.; Fortezzo, C.M.; Platz, T.; Michael, G.G.; Hare, T.M. Geologic Map of Mars; USGS: Reston, VA, USA, 2014.
- Tanaka, K.L.; Moore, H.J.; Schaber, G.; Chapman, M.; Stofan, E.; Campbell, D.; Davis, P.; Guest, J.; McGill, G.; Rogers, P. The Venus Geologic Mappers’ Handbook; US Department of the Interior, US Geological Survey: Reston, VA, USA, 1994. [Google Scholar]
- Williams, D.A.; Keszthelyi, L.P.; Crown, D.A.; Yff, J.A.; Jaeger, W.L.; Schenk, P.M.; Geissler, P.E.; Becker, T.L. Geologic Map of Io; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2011. [Google Scholar]
- Tanaka, K.L. The stratigraphy of Mars. J. Geophys. Res. Solid Earth 1986, 91, E139–E158. [Google Scholar] [CrossRef]
- Baker, V.R.; Hamilton, C.W.; Burr, D.M.; Gulick, V.C.; Komatsu, G.; Luo, W.; Rice, J.W., Jr.; Rodriguez, J. Fluvial geomorphology on Earth-like planetary surfaces: A review. Geomorphology 2015, 245, 149–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carr, M.H. The fluvial history of Mars. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 2193–2215. [Google Scholar] [CrossRef] [Green Version]
- Cabrol, N.A.; Grin, E.A. The evolution of lacustrine environments on Mars: Is Mars only hydrologically dormant? Icarus 2001, 149, 291–328. [Google Scholar] [CrossRef]
- Khawja, S.; Ernst, R.; Samson, C.; Byrne, P.; Ghail, R.; MacLellan, L. Tesserae on Venus may preserve evidence of fluvial erosion. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
- Hurwitz, D.M.; Head, J.W.; Hiesinger, H. Lunar sinuous rilles: Distribution, characteristics, and implications for their origin. Planet. Space Sci. 2013, 79, 1–38. [Google Scholar] [CrossRef]
- Schenk, P.M.; Williams, D.A. A potential thermal erosion lava channel on Io. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Hurwitz, D.M.; Head, J.W.; Byrne, P.K.; Xiao, Z.; Solomon, S.C.; Zuber, M.T.; Smith, D.E.; Neumann, G.A. Investigating the origin of candidate lava channels on Mercury with MESSENGER data: Theory and observations. J. Geophys. Res. Planets 2013, 118, 471–486. [Google Scholar] [CrossRef]
- Byrne, P.K.; Klimczak, C.; Williams, D.A.; Hurwitz, D.M.; Solomon, S.C.; Head, J.W.; Preusker, F.; Oberst, J. An assemblage of lava flow features on Mercury. J. Geophys. Res. Planets 2013, 118, 1303–1322. [Google Scholar] [CrossRef] [Green Version]
- Gulick, V.; Kargel, J.; Lewis, J. Channels and Valleys on Venus: Preliminary Analysis of Magellan Data; Wiley Online Library: Hoboken, NJ, USA, 1992. [Google Scholar]
- Balme, M.R.; Gallagher, C.; Page, D.P.; Murray, J.B.; Muller, J.-P.; Kim, J.-R. 10–The Western Elysium Planitia paleolake. In Lakes on Mars; Elsevier: Amsterdam, The Netherlands, 2010; pp. 275–305. [Google Scholar]
- Hynek, B.M.; Beach, M.; Hoke, M.R. Updated global map of Martian valley networks and implications for climate and hydrologic processes. J. Geophys. Res. Planets 2010, 115. [Google Scholar] [CrossRef]
- Matsubara, Y.; Howard, A.D.; Gochenour, J.P. Hydrology of early Mars: Valley network incision. J. Geophys. Res. Planets 2013, 118, 1365–1387. [Google Scholar] [CrossRef]
- Luo, W.; Cang, X.; Howard, A.D. New Martian valley network volume estimate consistent with ancient ocean and warm and wet climate. Nat. Commun. 2017, 8, 15766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jaumann, R.; Reiss, D.; Frei, S.; Neukum, G.; Scholten, F.; Gwinner, K.; Roatsch, T.; Matz, K.D.; Mertens, V.; Hauber, E. Interior channels in Martian valleys: Constraints on fluvial erosion by measurements of the Mars Express High Resolution Stereo Camera. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Warner, N.; Gupta, S.; Muller, J.-P.; Kim, J.-R.; Lin, S.-Y. A refined chronology of catastrophic outflow events in Ares Vallis, Mars. Earth Planet. Sci. Lett. 2009, 288, 58–69. [Google Scholar] [CrossRef]
- Ansan, V.; Mangold, N. 3D morphometry of valley networks on Mars from HRSC/MEX DEMs: Implications for climatic evolution through time. J. Geophys. Res. Planets 2013, 118, 1873–1894. [Google Scholar] [CrossRef] [Green Version]
- Bamber, E.R.; Goudge, T.; Fassett, C.; Osinski, G.; Stucky de Quay, G. Paleolake inlet valley formation: Factors controlling which craters breached on early Mars. Geophys. Res. Lett. 2022, 49, e2022GL101097. [Google Scholar] [CrossRef]
- Goddard, K.; Warner, N.H.; Gupta, S.; Kim, J.R. Mechanisms and timescales of fluvial activity at Mojave and other young Martian craters. J. Geophys. Res. Planets 2014, 119, 604–634. [Google Scholar] [CrossRef]
- Morgan, A.; Howard, A.; Hobley, D.E.; Moore, J.M.; Dietrich, W.E.; Williams, R.M.; Burr, D.M.; Grant, J.A.; Wilson, S.A.; Matsubara, Y. Sedimentology and climatic environment of alluvial fans in the martian Saheki crater and a comparison with terrestrial fans in the Atacama Desert. Icarus 2014, 229, 131–156. [Google Scholar] [CrossRef] [Green Version]
- McIntyre, N.; Warner, N.H.; Gupta, S.; Kim, J.R.; Muller, J.P. Hydraulic modeling of a distributary channel of Athabasca Valles, Mars, using a high-resolution digital terrain model. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Kim, J.-R.; Schumann, G.; Neal, J.C.; Lin, S.-Y. Megaflood analysis through channel networks of the Athabasca Valles, Mars based on multi-resolution stereo DTMs and 2D hydrodynamic modeling. Planet. Space Sci. 2014, 99, 55–69. [Google Scholar] [CrossRef]
- Neukum, G.; Jaumann, R.; Hoffmann, H.; Hauber, E.; Head, J.; Basilevsky, A.; Ivanov, B.; Werner, S.; Van Gasselt, S.; Murray, J. Recent and episodic volcanic and glacial activity on Mars revealed by the High Resolution Stereo Camera. Nature 2004, 432, 971–979. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.B.; de Vries, B.v.W.; Marquez, A.; Williams, D.A.; Byrne, P.; Muller, J.-P.; Kim, J.-R. Late-stage water eruptions from Ascraeus Mons volcano, Mars: Implications for its structure and history. Earth Planet. Sci. Lett. 2010, 294, 479–491. [Google Scholar] [CrossRef]
- Musiol, S.; Holohan, E.; Cailleau, B.; Platz, T.; Dumke, A.; Walter, T.; Williams, D.; Van Gasselt, S. Lithospheric flexure and gravity spreading of Olympus Mons volcano, Mars. J. Geophys. Res. Planets 2016, 121, 255–272. [Google Scholar] [CrossRef] [Green Version]
- Sori, M.M.; Sizemore, H.G.; Byrne, S.; Bramson, A.M.; Bland, M.T.; Stein, N.T.; Russell, C.T. Cryovolcanic rates on Ceres revealed by topography. Nat. Astron. 2018, 2, 946–950. [Google Scholar] [CrossRef] [Green Version]
- Peterson, G.A.; Johnson, C.L.; Byrne, P.K.; Phillips, R.J. Fault structure and origin of compressional tectonic features within the smooth plains on Mercury. J. Geophys. Res. Planets 2020, 125, e2019JE006183. [Google Scholar] [CrossRef]
- Murri, M.; Domeneghetti, M.C.; Fioretti, A.M.; Nestola, F.; Vetere, F.; Perugini, D.; Pisello, A.; Faccenda, M.; Alvaro, M. Cooling history and emplacement of a pyroxenitic lava as proxy for understanding Martian lava flows. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Wiedeking, S.; Lentz, A.; Pasckert, J.H.; Raack, J.; Schmedemann, N.; Hiesinger, H. Rheological properties and ages of lava flows on Alba Mons, Mars. Icarus 2023, 389, 115267. [Google Scholar] [CrossRef]
- Borykov, T.; Mège, D.; Mangeney, A.; Richard, P.; Gurgurewicz, J.; Lucas, A. Empirical investigation of friction weakening of terrestrial and Martian landslides using discrete element models. Landslides 2019, 16, 1121–1140. [Google Scholar] [CrossRef] [Green Version]
- Donzé, F.-V.; Klinger, Y.; Bonilla-Sierra, V.; Duriez, J.; Jiao, L.; Scholtès, L. Assessing the brittle crust thickness from strike-slip fault segments on Earth, Mars and Icy moons. Tectonophysics 2021, 805, 228779. [Google Scholar] [CrossRef]
- Head, J.W.; Marchant, D.; Agnew, M.; Fassett, C.; Kreslavsky, M. Extensive valley glacier deposits in the northern mid-latitudes of Mars: Evidence for Late Amazonian obliquity-driven climate change. Earth Planet. Sci. Lett. 2006, 241, 663–671. [Google Scholar] [CrossRef]
- Hubbard, B.; Souness, C.; Brough, S. Glacier-like forms on Mars. Cryosphere 2014, 8, 2047–2061. [Google Scholar] [CrossRef] [Green Version]
- Balme, M.; Gallagher, C. An equatorial periglacial landscape on Mars. Earth Planet. Sci. Lett. 2009, 285, 1–15. [Google Scholar] [CrossRef]
- Warner, N.; Gupta, S.; Kim, J.-R.; Lin, S.-Y.; Muller, J.-P. Hesperian equatorial thermokarst lakes in Ares Vallis as evidence for transient warm conditions on Mars. Geology 2010, 38, 71–74. [Google Scholar] [CrossRef]
- Howard, A.D.; Moore, J.M.; Umurhan, O.M.; White, O.L.; Anderson, R.S.; McKinnon, W.B.; Spencer, J.R.; Schenk, P.M.; Beyer, R.A.; Stern, S.A. Present and past glaciation on Pluto. Icarus 2017, 287, 287–300. [Google Scholar] [CrossRef]
- Schmidt, B.E.; Hughson, K.H.; Chilton, H.T.; Scully, J.E.; Platz, T.; Nathues, A.; Sizemore, H.; Bland, M.T.; Byrne, S.; Marchi, S. Geomorphological evidence for ground ice on dwarf planet Ceres. Nat. Geosci. 2017, 10, 338–343. [Google Scholar] [CrossRef]
- Brough, S.; Hubbard, B.; Hubbard, A. Area and volume of mid-latitude glacier-like forms on Mars. Earth Planet. Sci. Lett. 2019, 507, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Souness, C.; Hubbard, B.; Milliken, R.E.; Quincey, D. An inventory and population-scale analysis of martian glacier-like forms. Icarus 2012, 217, 243–255. [Google Scholar] [CrossRef]
- Butcher, F.E.; Balme, M.R.; Conway, S.J.; Gallagher, C.; Arnold, N.S.; Storrar, R.D.; Lewis, S.R.; Hagermann, A.; Davis, J.M. Sinuous ridges in Chukhung crater, Tempe Terra, Mars: Implications for fluvial, glacial, and glaciofluvial activity. Icarus 2021, 357, 114131. [Google Scholar] [CrossRef]
- Williams, J.M.; Scuderi, L.A.; Newsom, H.E. Numerical Analysis of Putative Rock Glaciers on Mount Sharp, Gale Crater, Mars. Remote Sens. 2022, 14, 1887. [Google Scholar] [CrossRef]
- Schmidt, L.S.; Hvidberg, C.S.; Kim, J.R.; Karlsson, N.B. Non-linear flow modelling of a Martian Lobate Debris Apron. J. Glaciol. 2019, 65, 889–899. [Google Scholar] [CrossRef] [Green Version]
- Smith, I.; Schlegel, N.J.; Larour, E.; Isola, I.; Buhler, P.; Putzig, N.; Greve, R. Carbon dioxide ice glaciers at the south pole of Mars. J. Geophys. Res. Planets 2022, 127, e2022JE007193. [Google Scholar] [CrossRef]
- Sori, M.M.; Byrne, S.; Hamilton, C.W.; Landis, M.E. Viscous flow rates of icy topography on the north polar layered deposits of Mars. Geophys. Res. Lett. 2016, 43, 541–549. [Google Scholar] [CrossRef] [Green Version]
- Choudhary, P.; Holt, J.W.; Kempf, S.D. Surface clutter and echo location analysis for the interpretation of SHARAD data from Mars. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1285–1289. [Google Scholar] [CrossRef]
- Spagnuolo, M.; Grings, F.; Perna, P.; Franco, M.; Karszenbaum, H.; Ramos, V. Multilayer simulations for accurate geological interpretations of SHARAD radargrams. Planet. Space Sci. 2011, 59, 1222–1230. [Google Scholar] [CrossRef]
- Gupta, V.; Gupta, S.K.; Kim, J. Automated discontinuity detection and reconstruction in subsurface environment of mars using deep learning: A case study of SHARAD observation. Appl. Sci. 2020, 10, 2279. [Google Scholar] [CrossRef] [Green Version]
- Dundas, C.M.; Bramson, A.M.; Ojha, L.; Wray, J.J.; Mellon, M.T.; Byrne, S.; McEwen, A.S.; Putzig, N.E.; Viola, D.; Sutton, S. Exposed subsurface ice sheets in the Martian mid-latitudes. Science 2018, 359, 199–201. [Google Scholar] [CrossRef] [Green Version]
- Stuurman, C.; Osinski, G.; Holt, J.; Levy, J.; Brothers, T.; Kerrigan, M.; Campbell, B. SHARAD detection and characterization of subsurface water ice deposits in Utopia Planitia, Mars. Geophys. Res. Lett. 2016, 43, 9484–9491. [Google Scholar] [CrossRef] [Green Version]
- Chojnacki, M.; Moersch, J.E.; Burr, D.M. Climbing and falling dunes in Valles Marineris, Mars. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Silvestro, S.; Di Achille, G.; Ori, G. Dune morphology, sand transport pathways and possible source areas in east Thaumasia Region (Mars). Geomorphology 2010, 121, 84–97. [Google Scholar] [CrossRef]
- Bourke, M.; Balme, M.; Beyer, R.; Williams, K.; Zimbelman, J. A comparison of methods used to estimate the height of sand dunes on Mars. Geomorphology 2006, 81, 440–452. [Google Scholar] [CrossRef]
- Davis, J.M.; Grindrod, P.M.; Boazman, S.J.; Vermeesch, P.; Baird, T. Quantified aeolian dune changes on Mars derived from repeat Context Camera images. Earth Space Sci. 2020, 7, e2019EA000874. [Google Scholar] [CrossRef] [Green Version]
- Bridges, N.; Ayoub, F.; Avouac, J.; Leprince, S.; Lucas, A.; Mattson, S. Earth-like sand fluxes on Mars. Nature 2012, 485, 339–342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altena, B.; Kääb, A. Elevation change and improved velocity retrieval using orthorectified optical satellite data from different orbits. Remote Sens. 2017, 9, 300. [Google Scholar] [CrossRef] [Green Version]
- Kääb, A.; Leprince, S. Motion detection using near-simultaneous satellite acquisitions. Remote Sens. Environ. 2014, 154, 164–179. [Google Scholar] [CrossRef] [Green Version]
- Leprince, S.; Ayoub, F.; Klinger, Y.; Avouac, J.-P. Co-registration of optically sensed images and correlation (COSI-Corr): An operational methodology for ground deformation measurements. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1943–1946. [Google Scholar]
- Jackson, D.W.; Bourke, M.C.; Smyth, T.A. The dune effect on sand-transporting winds on Mars. Nat. Commun. 2015, 6, 8796. [Google Scholar] [CrossRef] [Green Version]
- Hood, D.; Ewing, R.; Roback, K.; Runyon, K.; Avouac, J.-P.; McEnroe, M. Inferring airflow across martian dunes from ripple patterns and dynamics. Front. Earth Sci. 2021, 9, 702828. [Google Scholar] [CrossRef]
- Tokano, T. Dune-forming winds on Titan and the influence of topography. Icarus 2008, 194, 243–262. [Google Scholar] [CrossRef]
- Sachse, M.; Kappel, D.; Tirsch, D.; Otto, K.A. Discrete Element Modeling of Aeolian-like Morphologies on Comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2022, 662, A2. [Google Scholar] [CrossRef]
- Runyon, K.; Bridges, N.; Ayoub, F.; Newman, C.; Quade, J. An integrated model for dune morphology and sand fluxes on Mars. Earth Planet. Sci. Lett. 2017, 457, 204–212. [Google Scholar] [CrossRef]
- Mandt, K.E.; de Silva, S.L.; Zimbelman, J.R.; Crown, D.A. Origin of the Medusae Fossae Formation, Mars: Insights from a synoptic approach. J. Geophys. Res. Planets 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- De Silva, S.; Bailey, J.; Mandt, K.; Viramonte, J. Yardangs in terrestrial ignimbrites: Synergistic remote and field observations on Earth with applications to Mars. Planet. Space Sci. 2010, 58, 459–471. [Google Scholar] [CrossRef]
- Liu, J.; Di, K.; Gou, S.; Yue, Z.; Liu, B.; Xiao, J.; Liu, Z. Mapping and spatial statistical analysis of Mars Yardangs. Planet. Space Sci. 2020, 192, 105035. [Google Scholar] [CrossRef]
- Poggiali, V.; Mastrogiuseppe, M.; Callegari, M.; Martufi, R.; Seu, R.; Casarano, D.; Pasolli, L.; Notarnicola, C. Synergy of Cassini SAR and altimeter acquisitions for the retrieval of dune field characteristics on Titan. In Proceedings of the SAR Image Analysis, Modeling, and Techniques XII, Edinburgh, UK, 24–27 September 2012; pp. 57–64. [Google Scholar]
- Hayward, R.K.; Fenton, L.; Titus, T.N. Mars Global Digital Dune Database (MGD3): Global dune distribution and wind pattern observations. Icarus 2014, 230, 38–46. [Google Scholar] [CrossRef]
- Chuang, F.C.; Crown, D.A.; Berman, D.C.; Joseph, E.C.S. Mapping lobate debris aprons and related ice-rich flow features in the Southern Hemisphere of Mars. In Proceedings of the 44th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2013. [Google Scholar]
- Robbins, S.J.; Hynek, B.M. A new global database of Mars impact craters≥ 1 km: 1. Database creation, properties, and parameters. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Lagain, A.; Bouley, S.; Baratoux, D.; Marmo, C.; Costard, F.; Delaa, O.; Rossi, A.P.; Minin, M.; Benedix, G.; Ciocco, M. Mars Crater Database: A Participative Project for the Classification of the Morphological Characteristics of Large Martian Craters; GeoScienceWorld: McLean, VA, USA, 2021. [Google Scholar]
- Stofan, E.R.; Sharpton, V.L.; Schubert, G.; Baer, G.; Bindschadler, D.L.; Janes, D.M.; Squyres, S.W. Global distribution and characteristics of coronae and related features on Venus: Implications for origin and relation to mantle processes. J. Geophys. Res. Planets 1992, 97, 13347–13378. [Google Scholar] [CrossRef]
- Balaram, J.; Aung, M.; Golombek, M.P. The ingenuity helicopter on the perseverance rover. Space Sci. Rev. 2021, 217, 56. [Google Scholar] [CrossRef]
- Smith, M.W.; Quincey, D.J.; Dixon, T.; Bingham, R.G.; Carrivick, J.L.; Irvine-Fynn, T.D.; Rippin, D.M. Aerodynamic roughness of glacial ice surfaces derived from high-resolution topographic data. J. Geophys. Res. Earth Surf. 2016, 121, 748–766. [Google Scholar] [CrossRef] [Green Version]
- Colin, J.; Faivre, R. Aerodynamic roughness length estimation from very high-resolution imaging LIDAR observations over the Heihe basin in China. Hydrol. Earth Syst. Sci. 2010, 14, 2661–2669. [Google Scholar] [CrossRef] [Green Version]
- Kleinhans, M.G. Flow discharge and sediment transport models for estimating a minimum timescale of hydrological activity and channel and delta formation on Mars. J. Geophys. Res. Planets 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Heavens, N.; Richardson, M.I.; Toigo, A.D. Two aerodynamic roughness maps derived from Mars Orbiter Laser Altimeter (MOLA) data and their effects on boundary layer properties in a Mars general circulation model (GCM). J. Geophys. Res. Planets 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Hébrard, E.; Listowski, C.; Coll, P.; Marticorena, B.; Bergametti, G.; Määttänen, A.; Montmessin, F.; Forget, F. An aerodynamic roughness length map derived from extended Martian rock abundance data. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, W.K.; Neukum, G. Cratering chronology and the evolution of Mars. In Proceedings of the Chronology and Evolution of Mars: Proceedings of an ISSI Workshop, Bern, Switzerland, 10–14 April 2000; pp. 165–194. [Google Scholar]
- Ivanov, B.A. Mars/Moon cratering rate ratio estimates. Space Sci. Rev. 2001, 96, 87–104. [Google Scholar] [CrossRef]
- Michael, G.; Neukum, G. Planetary surface dating from crater size–frequency distribution measurements: Partial resurfacing events and statistical age uncertainty. Earth Planet. Sci. Lett. 2010, 294, 223–229. [Google Scholar] [CrossRef]
- Hartmann, W.K. Martian cratering 8: Isochron refinement and the chronology of Mars. Icarus 2005, 174, 294–320. [Google Scholar] [CrossRef]
- Hartmann, W.K.; Neukum, G.; Werner, S. Confirmation and utilization of the “production function” size-frequency distributions of Martian impact craters. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Matsubara, Y.; Howard, A.D.; Irwin, R.P., III. Constraints on the Noachian paleoclimate of the Martian highlands from landscape evolution modeling. J. Geophys. Res. Planets 2018, 123, 2958–2979. [Google Scholar] [CrossRef]
- Liu, J.; Yue, Z.; Di, K.; Gou, S.; Niu, S. A Study about the Temporal Constraints on the Martian Yardangs’ Development in Medusae Fossae Formation. Remote Sens. 2021, 13, 1316. [Google Scholar] [CrossRef]
- Warner, N.; Gupta, S.; Lin, S.Y.; Kim, J.R.; Muller, J.P.; Morley, J. Late Noachian to Hesperian climate change on Mars: Evidence of episodic warming from transient crater lakes near Ares Vallis. J. Geophys. Res. Planets 2010, 115. [Google Scholar] [CrossRef]
- Warner, N.H.; Gupta, S.; Kim, J.-R.; Lin, S.-Y.; Muller, J.-P. Retreat of a giant cataract in a long-lived (3.7–2.6 Ga) martian outflow channel. Geology 2010, 38, 791–794. [Google Scholar] [CrossRef] [Green Version]
- Craddock, R.A.; Howard, A.D. Simulated degradation of lunar impact craters and a new method for age dating farside mare deposits. J. Geophys. Res. Planets 2000, 105, 20387–20401. [Google Scholar] [CrossRef]
- Palucis, M.C.; Jasper, J.; Garczynski, B.; Dietrich, W.E. Quantitative assessment of uncertainties in modeled crater retention ages on Mars. Icarus 2020, 341, 113623. [Google Scholar] [CrossRef] [Green Version]
- Warren, A.; Holo, S.; Kite, E.; Wilson, S. Overspilling small craters on a dry Mars: Insights from breach erosion modeling. Earth Planet. Sci. Lett. 2021, 554, 116671. [Google Scholar] [CrossRef]
- DeLatte, D.M.; Crites, S.T.; Guttenberg, N.; Yairi, T. Automated crater detection algorithms from a machine learning perspective in the convolutional neural network era. Adv. Space Res. 2019, 64, 1615–1628. [Google Scholar] [CrossRef]
- Lee, C. Automated crater detection on Mars using deep learning. Planet. Space Sci. 2019, 170, 16–28. [Google Scholar] [CrossRef] [Green Version]
- Tewari, A.; Verma, V.; Srivastava, P.; Jain, V.; Khanna, N. Automated crater detection from co-registered optical images, elevation maps and slope maps using deep learning. Planet. Space Sci. 2022, 218, 105500. [Google Scholar] [CrossRef]
- Chen, M.; Liu, D.; Qian, K.; Li, J.; Lei, M.; Zhou, Y. Lunar crater detection based on terrain analysis and mathematical morphology methods using digital elevation models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3681–3692. [Google Scholar] [CrossRef]
- Kim, J. Impact crater detection on optical images and DEMs. In Proceedings of the The 34th Lunar and Planetary Science Conference, League City, TX, USA, 17–21 March 2003. [Google Scholar]
- Kim, J.R.; Muller, J.-P.; Morley, J.G. Quantitative assessment of automated crater detection on Mars. In Proceedings of the XXth ISPRS Congress, Technical Commission IV, Istanbul, Turkey, 12–23 July 2004; pp. 816–821. [Google Scholar]
- Lagain, A.; Servis, K.; Benedix, G.; Norman, C.; Anderson, S.; Bland, P. Model age derivation of large martian impact craters, using automatic crater counting methods. Earth Space Sci. 2021, 8, e2020EA001598. [Google Scholar] [CrossRef]
- Kim, J.R.; Muller, J.-P.; van Gasselt, S.; Morley, J.G.; Neukum, G. Automated crater detection, a new tool for Mars cartography and chronology. Photogramm. Eng. Remote Sens. 2005, 71, 1205–1217. [Google Scholar] [CrossRef] [Green Version]
- Golombek, M.; Kipp, D.; Warner, N.; Daubar, I.J.; Fergason, R.; Kirk, R.L.; Beyer, R.; Huertas, A.; Piqueux, S.; Putzig, N. Selection of the InSight landing site. Space Sci. Rev. 2017, 211, 5–95. [Google Scholar] [CrossRef]
- Golombek, M.; Grant, J.; Kipp, D.; Vasavada, A.; Kirk, R.; Fergason, R.; Bellutta, P.; Calef, F.; Larsen, K.; Katayama, Y. Selection of the Mars Science Laboratory landing site. Space Sci. Rev. 2012, 170, 641–737. [Google Scholar] [CrossRef]
- Bridges, J.; Seabrook, A.; Rothery, D.; Kim, J.; Pillinger, C.; Sims, M.; Golombek, M.; Duxbury, T.; Head, J.; Haldemann, A. Selection of the landing site in Isidis Planitia of Mars probe Beagle 2. J. Geophys. Res. Planets 2003, 108, 1-1–1-17. [Google Scholar] [CrossRef]
- Arvidson, R.; Adams, D.; Bonfiglio, G.; Christensen, P.; Cull, S.; Golombek, M.; Guinn, J.; Guinness, E.; Heet, T.; Kirk, R. Mars Exploration Program 2007 Phoenix landing site selection and characteristics. J. Geophys. Res. Planets 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Kirk, R.L.; Mayer, D.P.; Fergason, R.L.; Redding, B.L.; Galuszka, D.M.; Hare, T.M.; Gwinner, K. Evaluating stereo Digital Terrain Model quality at Mars rover landing sites with HRSC, CTX, and HiRISE images. Remote Sens. 2021, 13, 3511. [Google Scholar] [CrossRef]
- Chiodini, S.; Pertile, M.; Debei, S.; Bramante, L.; Ferrentino, E.; Villa, A.G.; Musso, I.; Barrera, M. Mars rovers localization by matching local horizon to surface digital elevation models. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; pp. 374–379. [Google Scholar]
- Ono, M.; Rothrock, B.; Almeida, E.; Ansar, A.; Otero, R.; Huertas, A.; Heverly, M. Data-driven surface traversability analysis for Mars 2020 landing site selection. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; pp. 1–12. [Google Scholar]
- Brockers, R.; Delaune, J.; Proença, P.; Schoppmann, P.; Domnik, M.; Kubiak, G.; Tzanetos, T. Autonomous safe landing site detection for a future mars science helicopter. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; pp. 1–8. [Google Scholar]
- Zuber, M.T.; Smith, D.E.; Zellar, R.S.; Neumann, G.A.; Sun, X.; Katz, R.B.; Kleyner, I.; Matuszeski, A.; McGarry, J.F.; Ott, M.N. The lunar reconnaissance orbiter laser ranging investigation. Space Sci. Rev. 2010, 150, 63–80. [Google Scholar] [CrossRef]
- Crane, K. Structural interpretation of thrust fault-related landforms on Mercury using Earth analogue fault models. Geomorphology 2020, 369, 107366. [Google Scholar] [CrossRef]
- Ewing, R.; Lapotre, M.; Lewis, K.; Day, M.; Stein, N.; Rubin, D.; Sullivan, R.; Banham, S.; Lamb, M.; Bridges, N. Sedimentary processes of the Bagnold Dunes: Implications for the eolian rock record of Mars. J. Geophys. Res. Planets 2017, 122, 2544–2573. [Google Scholar] [CrossRef]
- Liu, T.; Baker, V.R. Hydraulic Modeling of Megaflooding Using Terrestrial and MARTIAN DEMs. PeerJ Prepr. 2018, 6, e27107v1. [Google Scholar] [CrossRef] [Green Version]
- Norini, G.; Zuluaga, M.C.; Ortiz, I.J.; Aquino, D.T.; Lagmay, A.M.F. Delineation of alluvial fans from Digital Elevation Models with a GIS algorithm for the geomorphological mapping of the Earth and Mars. Geomorphology 2016, 273, 134–149. [Google Scholar] [CrossRef]
- Foroutan, M.; Zimbelman, J. Mega-ripples in Iran: A new analog for transverse aeolian ridges on Mars. Icarus 2016, 274, 99–105. [Google Scholar] [CrossRef]
- Grotzinger, J.; Bell, J., III; Herkenhoff, K.; Johnson, J.; Knoll, A.; McCartney, E.; McLennan, S.; Metz, J.; Moore, J.; Squyres, S. Sedimentary textures formed by aqueous processes, Erebus crater, Meridiani Planum, Mars. Geology 2006, 34, 1085–1088. [Google Scholar] [CrossRef] [Green Version]
- Zaki, A.S.; Pain, C.F.; Edgett, K.S.; Castelltort, S. Global inventory of fluvial ridges on Earth and lessons applicable to Mars. Earth-Sci. Rev. 2021, 216, 103561. [Google Scholar] [CrossRef]
- Ehlmann, B.L.; Mustard, J.F.; Swayze, G.A.; Clark, R.N.; Bishop, J.L.; Poulet, F.; Des Marais, D.J.; Roach, L.H.; Milliken, R.E.; Wray, J.J. Identification of hydrated silicate minerals on Mars using MRO-CRISM: Geologic context near Nili Fossae and implications for aqueous alteration. J. Geophys. Res. Planets 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Wray, J.J.; Murchie, S.L.; Bishop, J.L.; Ehlmann, B.L.; Milliken, R.E.; Wilhelm, M.B.; Seelos, K.D.; Chojnacki, M. Orbital evidence for more widespread carbonate-bearing rocks on Mars. J. Geophys. Res. Planets 2016, 121, 652–677. [Google Scholar] [CrossRef] [Green Version]
- Barnhart, C.J.; Howard, A.D.; Moore, J.M. Long-term precipitation and late-stage valley network formation: Landform simulations of Parana Basin, Mars. J. Geophys. Res. Planets 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Goudge, T.A.; Milliken, R.E.; Head, J.W.; Mustard, J.F.; Fassett, C.I. Sedimentological evidence for a deltaic origin of the western fan deposit in Jezero crater, Mars and implications for future exploration. Earth Planet. Sci. Lett. 2017, 458, 357–365. [Google Scholar] [CrossRef]
- Parente, M.; Clark, J.T.; Brown, A.J.; Bishop, J.L. End-to-end simulation and analytical model of remote-sensing systems: Application to CRISM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3877–3888. [Google Scholar] [CrossRef]
- Hughes, C.G.; Ramsey, M.S. Super-resolution of THEMIS thermal infrared data: Compositional relationships of surface units below the 100 meter scale on Mars. Icarus 2010, 208, 704–720. [Google Scholar] [CrossRef]
- Tornabene, L.L.; Moersch, J.E.; McSween, H.Y., Jr.; McEwen, A.S.; Piatek, J.L.; Milam, K.A.; Christensen, P.R. Identification of large (2–10 km) rayed craters on Mars in THEMIS thermal infrared images: Implications for possible Martian meteorite source regions. J. Geophys. Res. Planets 2006, 111. [Google Scholar] [CrossRef]
- Helfenstein, P.; Shepard, M.K. Testing the Hapke photometric model: Improved inversion and the porosity correction. Icarus 2011, 215, 83–100. [Google Scholar] [CrossRef]
- Domingue, D.L.; Denevi, B.W.; Murchie, S.L.; Hash, C.D. Application of multiple photometric models to disk-resolved measurements of Mercury’s surface: Insights into Mercury’s regolith characteristics. Icarus 2016, 268, 172–203. [Google Scholar] [CrossRef] [Green Version]
- Fernando, J.; Schmidt, F.; Douté, S. Martian surface microtexture from orbital CRISM multi-angular observations: A new perspective for the characterization of the geological processes. Planet. Space Sci. 2016, 128, 30–51. [Google Scholar] [CrossRef]
- Schmidt, F.; Fernando, J. Realistic uncertainties on Hapke model parameters from photometric measurement. Icarus 2015, 260, 73–93. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B.W. A theoretical photometric function for the lunar surface. J. Geophys. Res. 1963, 68, 4571–4586. [Google Scholar] [CrossRef]
- Domingue, D.L.; Murchie, S.L.; Denevi, B.W.; Chabot, N.L.; Blewett, D.T.; Laslo, N.R.; Vaughan, R.M.; Kang, H.K.; Shepard, M.K. Photometric correction of Mercury’s global color mosaic. Planet. Space Sci. 2011, 59, 1873–1887. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Fewtrell, T.; Budimir, M.; Bates, P.; Mason, D. Evaluating a new LISFLOOD-FP formulation with data from the summer 2007 floods in Tewkesbury, UK. J. Flood Risk Manag. 2011, 4, 88–95. [Google Scholar] [CrossRef]
- Sori, M.M.; Byrne, S.; Bland, M.T.; Bramson, A.M.; Ermakov, A.I.; Hamilton, C.W.; Otto, K.A.; Ruesch, O.; Russell, C.T. The vanishing cryovolcanoes of Ceres. Geophys. Res. Lett. 2017, 44, 1243–1250. [Google Scholar] [CrossRef] [Green Version]
- Laskar, J.; Levrard, B.; Mustard, J.F. Orbital forcing of the Martian polar layered deposits. Nature 2002, 419, 375–377. [Google Scholar] [CrossRef]
- Tang, Y.; Birch, S.; Hayes, A.; Kirk, R.; Kutsop, N.; Vincent, J.-B.; Squyres, S. Generation of photoclinometric DTMs for application to transient changes on the surface of comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2019, 630, A10. [Google Scholar] [CrossRef] [Green Version]
- Plaut, J.J.; Picardi, G.; Safaeinili, A.; Ivanov, A.B.; Milkovich, S.M.; Cicchetti, A.; Kofman, W.; Mouginot, J.; Farrell, W.M.; Phillips, R.J. Subsurface radar sounding of the south polar layered deposits of Mars. Science 2007, 316, 92–95. [Google Scholar] [CrossRef] [Green Version]
- Xiao, H.; Stark, A.; Schmidt, F.; Hao, J.; Su, S.; Gregor, S.; Oberst, J. Spatio-Temporal Level Variations of the Martian Seasonal South Polar Cap From Co-Registration of MOLA Profiles. J. Geophys. Res. Planets 2022, 127, e2022JE007196. [Google Scholar] [CrossRef]
- Mazarico, E.; Barker, M.K.; Neumann, G.A.; Zuber, M.T.; Smith, D.E. Detection of the lunar body tide by the Lunar Orbiter Laser Altimeter. Geophys. Res. Lett. 2014, 41, 2282–2288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bertone, S.; Mazarico, E.; Barker, M.; Goossens, S.; Sabaka, T.; Neumann, G.; Smith, D.E. Deriving Mercury geodetic parameters with altimetric crossovers from the Mercury Laser Altimeter (MLA). J. Geophys. Res. Planets 2021, 126, e2020JE006683. [Google Scholar] [CrossRef]
- Thor, R.N.; Kallenbach, R.; Christensen, U.R.; Gläser, P.; Stark, A.; Steinbrügge, G.; Oberst, J. Determination of the lunar body tide from global laser altimetry data. J. Geod. 2021, 95, 4. [Google Scholar] [CrossRef]
- Wagner, N.; James, P.; Ermakov, A.; Sori, M. Quantifying lithospheric deflection caused by seasonal mass transport from the Polar Layered Deposits on Mars. LPI Contrib. 2022, 2678, 2352. [Google Scholar]
- Xiao, Z.; Zeng, Z.; Ding, N.; Molaro, J. Mass wasting features on the Moon–how active is the lunar surface? Earth Planet. Sci. Lett. 2013, 376, 1–11. [Google Scholar] [CrossRef]
- Fanara, L.; Gwinner, K.; Hauber, E.; Oberst, J. Present-day erosion rate of north polar scarps on Mars due to active mass wasting. Icarus 2020, 342, 113434. [Google Scholar] [CrossRef]
- Xiao, H.; Stark, A.; Schmidt, F.; Hao, J.; Steinbrügge, G.; Wagner, N.L.; Su, S.; Cheng, Y.; Oberst, J. Spatio-Temporal Level Variations of the Martian Seasonal North Polar Cap From Co-Registration of MOLA Profiles. J. Geophys. Res. Planets 2022, 127, e2021JE007158. [Google Scholar] [CrossRef]
- Bagheri, A.; Efroimsky, M.; Castillo-Rogez, J.; Goossens, S.; Plesa, A.-C.; Rambaux, N.; Rhoden, A.; Walterová, M.; Khan, A.; Giardini, D. Tidal insights into rocky and icy bodies: An introduction and overview. In Geophysical Exploration of the Solar System; Elsevier: Amsterdam, The Netherlands, 2022; Volume 63, pp. 231–320. [Google Scholar]
- Stark, A.; Xiao, H.; Hu, X.; Fienga, A.; Hussmann, H.; Oberst, J.; Rambaux, N.; Mémin, A.; Briaud, A.; Baguet, D. Measurement of tidal deformation through self-registration of laser profiles: Application to Earth’s Moon. In Proceedings of the 24th EGU General Assembly, Vienna, Austria, 23–27 May 2022. EGU22–10626. [Google Scholar]
- Thomas, N.; Spohn, T.; Barriot, J.-P.; Benz, W.; Beutler, G.; Christensen, U.; Dehant, V.; Fallnich, C.; Giardini, D.; Groussin, O. The BepiColombo Laser Altimeter (BELA): Concept and baseline design. Planet. Space Sci. 2007, 55, 1398–1413. [Google Scholar] [CrossRef]
- Hussmann, H.; Lingenauber, K.; Kallenbach, R.; Enya, K.; Thomas, N.; Lara, L.M.; Althaus, C.; Araki, H.; Behnke, T.; Castro-Marin, J.M. The Ganymede laser altimeter (GALA): Key objectives, instrument design, and performance. CEAS Space J. 2019, 11, 381–390. [Google Scholar] [CrossRef]
- Besse, S.; Vallat, C.; Barthelemy, M.; Coia, D.; Costa, M.; De Marchi, G.; Fraga, D.; Grotheer, E.; Heather, D.; Lim, T. ESA’s Planetary Science Archive: Preserve and present reliable scientific data sets. Planet. Space Sci. 2018, 150, 131–140. [Google Scholar] [CrossRef]
- Koehler, U.; Neukum, G.; Gasselt, S.v.; Jaumann, R.; Roatsch, T.; Hoffmann, H.; Zender, J.; Acton, C.; Drigani, F. Public Outreach and Archiving of Data from the High Resolution Stereo Camera Onboard Mars Express: 2004 The First Year. In Lunar and Planetary Science XXXVI, Part 11; NASA: Washington, DC, USA, 2005. [Google Scholar]
- Ayachit, U. The Paraview Guide: A Parallel Visualization Application; Kitware, Inc.: Clifton Park, NY, USA, 2015. [Google Scholar]
- Kim, J.-R.; Lin, S.-Y.; Hong, J.-W.; Kim, Y.-H.; Park, C.-K. Implementation of Martian virtual reality environment using very high-resolution stereo topographic data. Comput. Geosci. 2012, 44, 184–195. [Google Scholar] [CrossRef]
- Eliason, E.M.; LaVoie, S.K.; Soderblom, L.A. The imaging node for the Planetary Data System. Planet. Space Sci. 1996, 44, 23–32. [Google Scholar] [CrossRef]
- Hare, T.; Gaddis, L.; Bailen, M.; LaVoie, S. Astropedia Annex: A PDS Imaging Node Repository for Geospatial Planetary Research Products. In Proceedings of the 44th Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 18–22 March 2013; p. 2044. [Google Scholar]
- Walter, S.; Muller, J.P.; Sidiropoulos, P.; Tao, Y.; Gwinner, K.; Putri, A.; Kim, J.R.; Steikert, R.; van Gasselt, S.; Michael, G. The Web-Based Interactive Mars Analysis and Research System for HRSC and the iMars Project. Earth Space Sci. 2018, 5, 308–323. [Google Scholar] [CrossRef]
- Raugh, A.; Hughes, J.S. The Road to an Archival Data Format—Data Structures. Planet. Sci. J. 2021, 2, 204. [Google Scholar] [CrossRef]
- Deen, R.G.; Levoe, S.R. Java Image I/O for VICAR, PDS, and ISIS; NASA: Washington, DC, USA, 2011.
- Rossi, A.P.; Hare, T.; Baumann, P.; Misev, D.; Marmo, C.; Erard, S.; Cecconi, B.; Figuera, R.M. Planetary coordinate reference systems for OGC web services. In Proceedings of the 47th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 21–25 March 2016; p. 1422. [Google Scholar]
- Ghail, R.C.; Hall, D.; Mason, P.J.; Herrick, R.R.; Carter, L.M.; Williams, E. VenSAR on EnVision: Taking earth observation radar to Venus. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 365–376. [Google Scholar] [CrossRef]
- Smrekar, S.; Dyar, M.; Hensley, S.; Helbert, J.; Team, V.S. VERITAS (Venus Emissivity, Radio Science, InSAR, Topo-graphy and Spectroscopy): A Proposed Discovery Mission. In Proceedings of the AAS/Division for Planetary Sciences Meeting Abstracts#48; IEEE: Location, UL, 2016; p. 216.207. [Google Scholar]
- Howell, S.M.; Pappalardo, R.T. NASA’s Europa Clipper—A mission to a potentially habitable ocean world. Nat. Commun. 2020, 11, 1–4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tosi, F.; Roatsch, T.; Cremonese, G.; Fonti, S.; Palumbo, P.; Stephan, K.; Jaumann, R.; Migliorini, A.; Hoffmann, H.; Mancarella, F. The JUICE mission and the future exploration of the icy Galilean satellites: Complementarities and synergies in visible and near-infrared remote sensing. In Proceedings of the 42nd COSPAR Scientific Assembly, Pasadena, CA, USA, 14–22 July 2018; Volume 42. B5. 3-51-18. [Google Scholar]
- Hussmann, H.; Lingenauber, K.; Kallenbach, R.; Oberst, J.; Enya, K.; Kobayashi, M.; Namiki, N.; Kimura, J.; Thomas, N.; Lara, L. The Ganymede Laser Altimeter (GALA) for ESA’s Jupiter Icy Moons Explorer (JUICE) Mission. In Proceedings of the European Planetary Science Congress, Berlin, Germany, 16–21 September 2018. EPSC2018–2904. [Google Scholar]
- Lorenz, R.D.; Turtle, E.P.; Barnes, J.W.; Trainer, M.G.; Adams, D.S.; Hibbard, K.E.; Sheldon, C.Z.; Zacny, K.; Peplowski, P.N.; Lawrence, D.J. Dragonfly: A rotorcraft lander concept for scientific exploration at Titan. Johns Hopkins APL Tech. Dig. 2018, 34, 14. [Google Scholar]
- Ye, P.; Sun, Z.; Rao, W.; Meng, L. Mission overview and key technologies of the first Mars probe of China. Sci. China Technol. Sci. 2017, 60, 649–657. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, B.; Li, S. Overview of China’s 2020 Mars mission design and navigation. Astrodynamics 2018, 2, 1–11. [Google Scholar] [CrossRef]
- Haider, S.A.; Bhardwaj, A.; Shanmugam, M.; Goyal, S.; Sheel, V.; Pabari, J.; Prasad Karanam, D. Indian Mars and Venus missions: Science and exploration. In Proceedings of the 42nd COSPAR Scientific Assembly, Pasadena, CA, USA, 14–22 July 2018; Volume 42. B4. 1-10-18. [Google Scholar]
- Wörner, L.; Root, B.C.; Bouyer, P.; Braxmaier, C.; Dirkx, D.; Encarnarcao, J.; Hauber, E.; Hussmann, H.; Karatekin, O.; Koch, A. MaQuIs-Mars Quantum Gravity Mission. Authorea Prepr. 2023. [Google Scholar] [CrossRef]
- Calvin, W.M.; Putzig, N.E.; Dundas, C.M.; Bramson, A.M.; Horgan, B.H.; Seelos, K.D.; Sizemore, H.G.; Ehlmann, B.L.; Morgan, G.A.; Holt, J.W. The Mars Orbiter for Resources, Ices, and Environments (MORIE) Science Goals and Instrument Trades in Radar, Imaging, and Spectroscopy. Planet. Sci. J. 2021, 2, 76. [Google Scholar] [CrossRef]
- Oberst, J.; Wickhusen, K.; Gwinner, K.; Hauber, E.; Stark, A.; Elgner, S.; Grott, M.; Fanara, L.; Hussmann, H.; Steinbrügge, G. Planetary polar explorer–the case for a next-generation remote sensing mission to low Mars orbit. Exp. Astron. 2022, 54, 695–711. [Google Scholar] [CrossRef]
- Frazier, W.; Bearden, D.; Mitchell, K.L.; Lam, T.; Prockter, L.; Dissly, R. Trident: The Path to Triton on a Discovery Budget. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–12. [Google Scholar]
- MacKenzie, S.M.; Neveu, M.; Davila, A.F.; Lunine, J.I.; Craft, K.L.; Cable, M.L.; Phillips-Lander, C.M.; Hofgartner, J.D.; Eigenbrode, J.L.; Waite, J.H. The Enceladus Orbilander mission concept: Balancing return and resources in the search for life. Planet. Sci. J. 2021, 2, 77. [Google Scholar] [CrossRef]
- Sandwell, D.; Rosen, P.; Moore, W.; Gurrola, E. Radar interferometry for measuring tidal strains across cracks on Europa. J. Geophys. Res. Planets 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Blazej, J.; Prochazka, I.; Hamal, K.; Fedyszynova, M.; Yang, F.; Huang, P.; Michaelis, H.; Schreiber, U. Photon counting laser altimeter for planetary exploration—The technology demonstrator. J. Opt. A Pure Appl. Opt. 2007, 9, S98. [Google Scholar] [CrossRef]










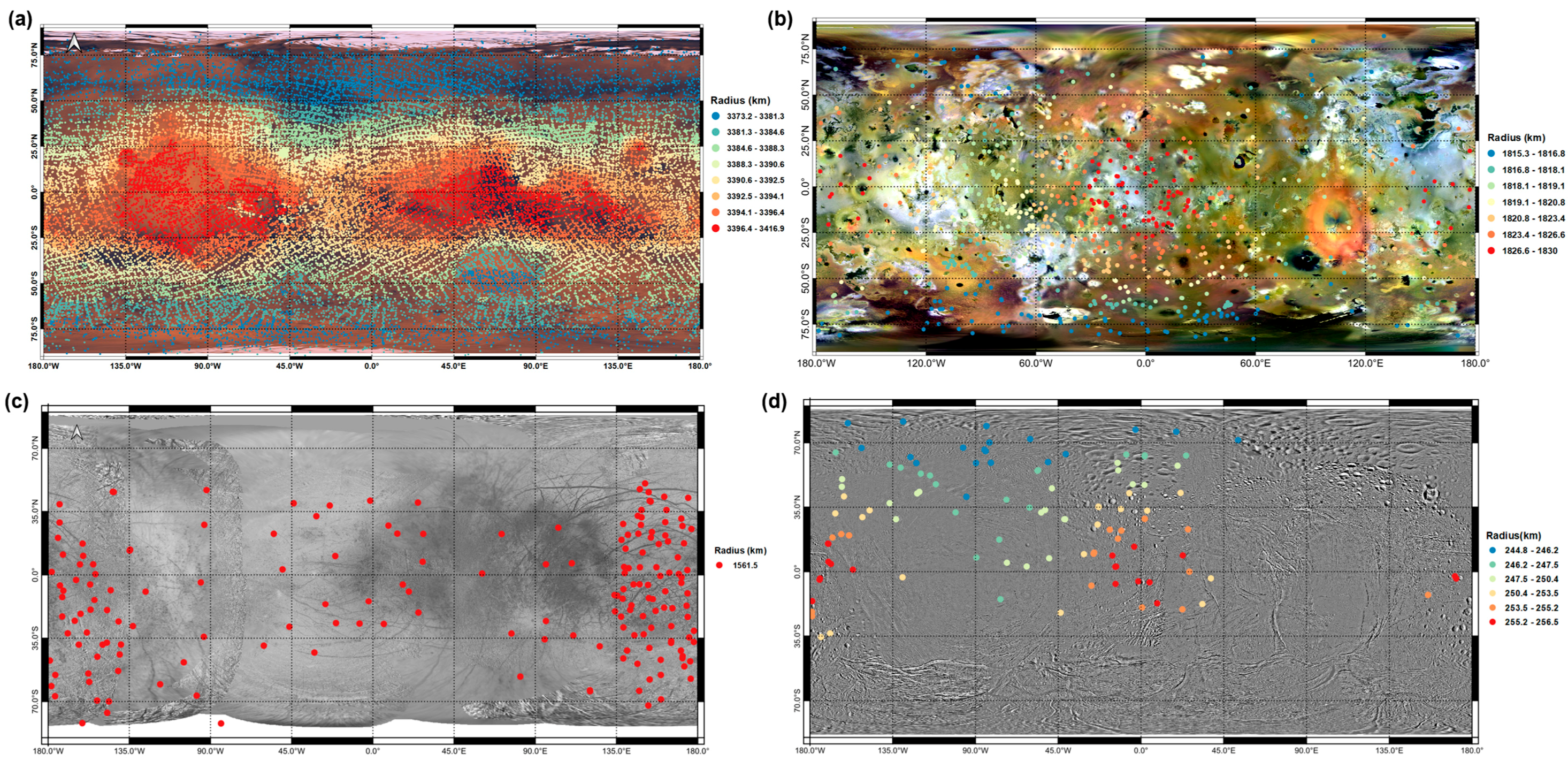






| Mission | Launch Year | Sensor | Configuration | Resolution |
|---|---|---|---|---|
| SELENE | 2007 | Terrain camera (TC) [36] | Two cameras (stereo) | 10 m (Spatial) |
| Laser altimeter (LALT) [37] | Nd:YAG laser shot with pulse interval of 1 Hz | 5 m (Elevation) | ||
| Chang’e 1 | 2007 | Terrain camera (TC) [19] | Three-line array CCD stereo camera | 120 m (Spatial) |
| Laser altimeter (LAM) [38] | Nd:YAG laser shot with 1 s interval | 60 m (Elevation) | ||
| Chandrayaan-1 | 2008 | Terrain mapping camera (TMC) [39] | Three cameras (stereo) | 10 m (Spatial) |
| Lunar laser ranging instrument (LLRI) [40] | Pulsed Nd:YAG laser with 10 measurements per second | 10 m (Elevation) | ||
| LRO | 2009 | Lunar Reconnaissance Orbiter camera (LROC) [41] | Two narrow angle cameras (NACs) | 0.5 m (Spatial) |
| One wide angle camera (WAC) | 100 m (Spatial) | |||
| Lunar orbiter laser altimeter (LOLA) [42] | Nd:YAG laser transmitter with 28 Hz | 1 m (Elevation) |
| Laser Type | Q-Switched, Diode-Pumped Nd:YAG |
| Wavelength | 1.064 micrometre |
| Laser energy | 40–30 mJ pulse−1 |
| Laser power consumption | 13.7 W |
| Pulse width | ~8.5 ns |
| Pulse repetition rate | 10 s−1 |
| Beam cross-section | 25 × 25 mm2 |
| Beam divergence | 0.25 mrad |
| ±Footprint size (at 400 km) | 120 m |
| Footprint spacing (a velocity = 3 km/s) (center-to-center, along-track) | 300 m |
| SPICE Kernel Name | Information |
|---|---|
| CK | Pointing data for an instrument |
| EK | Spacecraft and science instrument events including science plan (ESP), sequence of events (ESQ) and experimenter’s notebook (ENB) |
| IK | Instrument mounting, field of view, axis specification |
| LSK | Transformation value between Universal Time coordinates and Ephemeris |
| PcK | Altitude and body shape information (size, shape and orientation) |
| FK | Reference frame specifications |
| SLCK | Spacecraft clock coefficients |
| SPK | Spacecraft, orbiter and planet/satellite body trajectory |
| Orbit Number | Altitude (km) | σX (m) (without/with Bundle Adjustment) | σY (m) (without/with Bundle Adjustment) | σZ (m) (without/with Bundle Adjustment) |
|---|---|---|---|---|
| 18 | 275–347 | 12.1/6.6 | 10.7/6.0 | 33.4/18.1 |
| 22 | 311–941 | 13.0/8.6 | 17.2/9.1 | 41.6/21.9 |
| 68 | 269–505 | 31.2/11.0 | 29.2/10.4 | 50.6/17.9 |
| Instrument | Roll (Degree) | Pitch (Degree) | Yaw (Degree) |
|---|---|---|---|
| MOLA | −0.00290 | −0.00860 | 0.05900 |
| MOC-NA | 0.11463 | −0.07162 | 0.18000 |
| MOC-WA R | 1.04764 | −0.45229 | −0.78644 |
| MOC-WA B | 1.01022 | −0.35472 | −0.30189 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Lin, S.-Y.; Xiao, H. Remote Sensing and Data Analyses on Planetary Topography. Remote Sens. 2023, 15, 2954. https://doi.org/10.3390/rs15122954
Kim J, Lin S-Y, Xiao H. Remote Sensing and Data Analyses on Planetary Topography. Remote Sensing. 2023; 15(12):2954. https://doi.org/10.3390/rs15122954
Chicago/Turabian StyleKim, Jungrack, Shih-Yuan Lin, and Haifeng Xiao. 2023. "Remote Sensing and Data Analyses on Planetary Topography" Remote Sensing 15, no. 12: 2954. https://doi.org/10.3390/rs15122954
APA StyleKim, J., Lin, S.-Y., & Xiao, H. (2023). Remote Sensing and Data Analyses on Planetary Topography. Remote Sensing, 15(12), 2954. https://doi.org/10.3390/rs15122954







