Comprehensive Ocean Information-Enabled AUV Motion Planning Based on Reinforcement Learning
Abstract
1. Introduction
- To create a realistic ocean current environment, the AUV motion model and real ocean current data are introduced into the environment modeling based on reinforcement learning. This method effectively minimized the distance between practical applications and the simulations. Therefore, this method brings more significant practical value to AUV motion planning.
- We proposed the RLBMPA-COI AUV motion planning algorithm based on a real ocean environment. By incorporating local ocean current information into the objective function of the action-value network, this algorithm successfully minimizes the overestimation error interference and enhances the efficiency of motion planning. According to the influence of the ocean current, target distance, obstacles, and steps on the motion planning task, we also established a corresponding reward function. This ensures the efficient training of the algorithm, further improving its exploration ability and better adaptability.
- Multiple simulations, including complex obstacles and dynamic multi-objective tasks in path planning, as well as a trajectory-tracking task are designed to verify the performance of the proposed algorithms comprehensively. Compared with state-of-art algorithms, the performance of RLBMPA-COI has been evaluated and proven by numerical results, which demonstrate efficient motion planning and high flexibility for expansion into different ocean environments.
2. Background
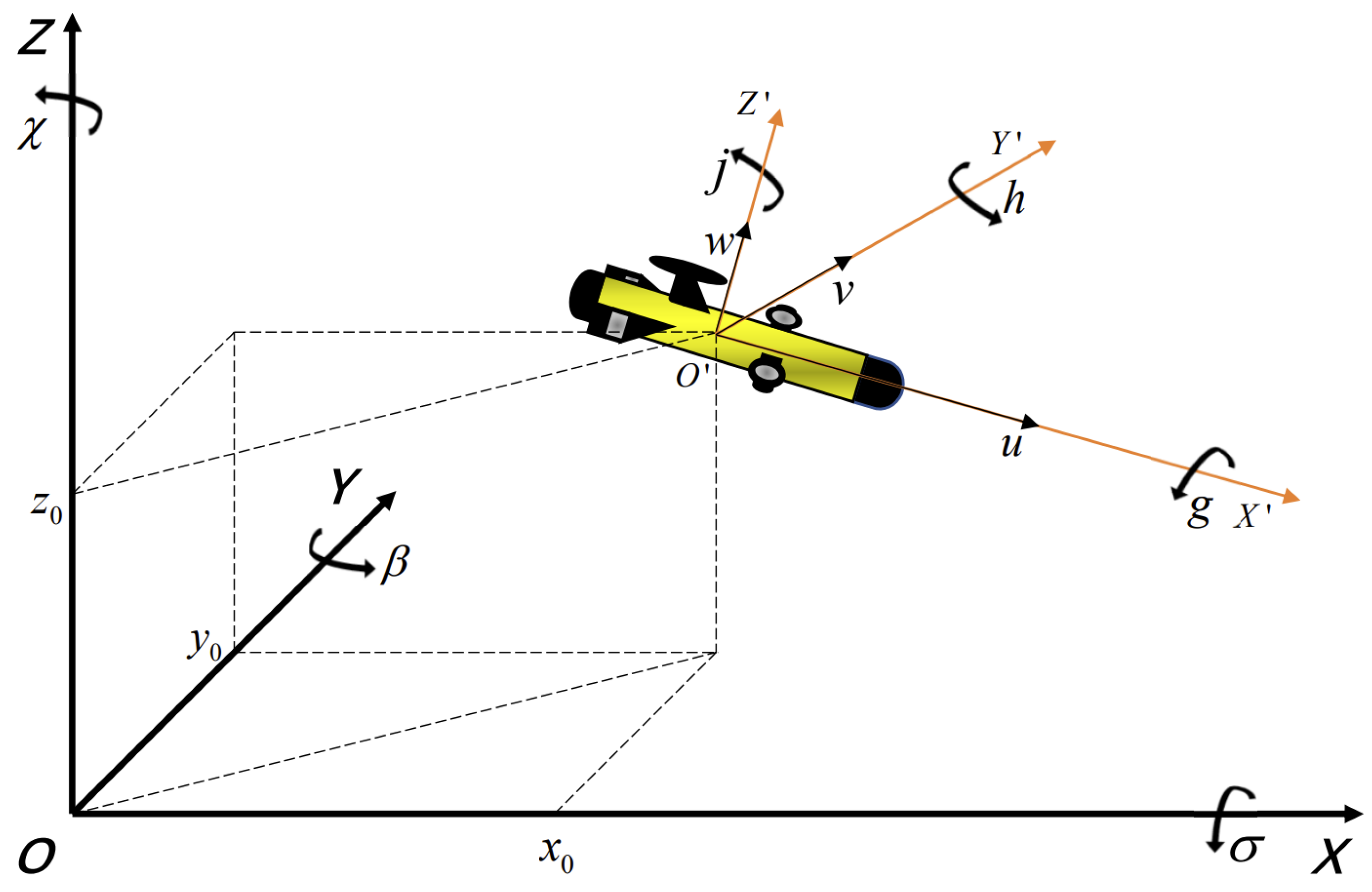
2.1. AUV Motion Model
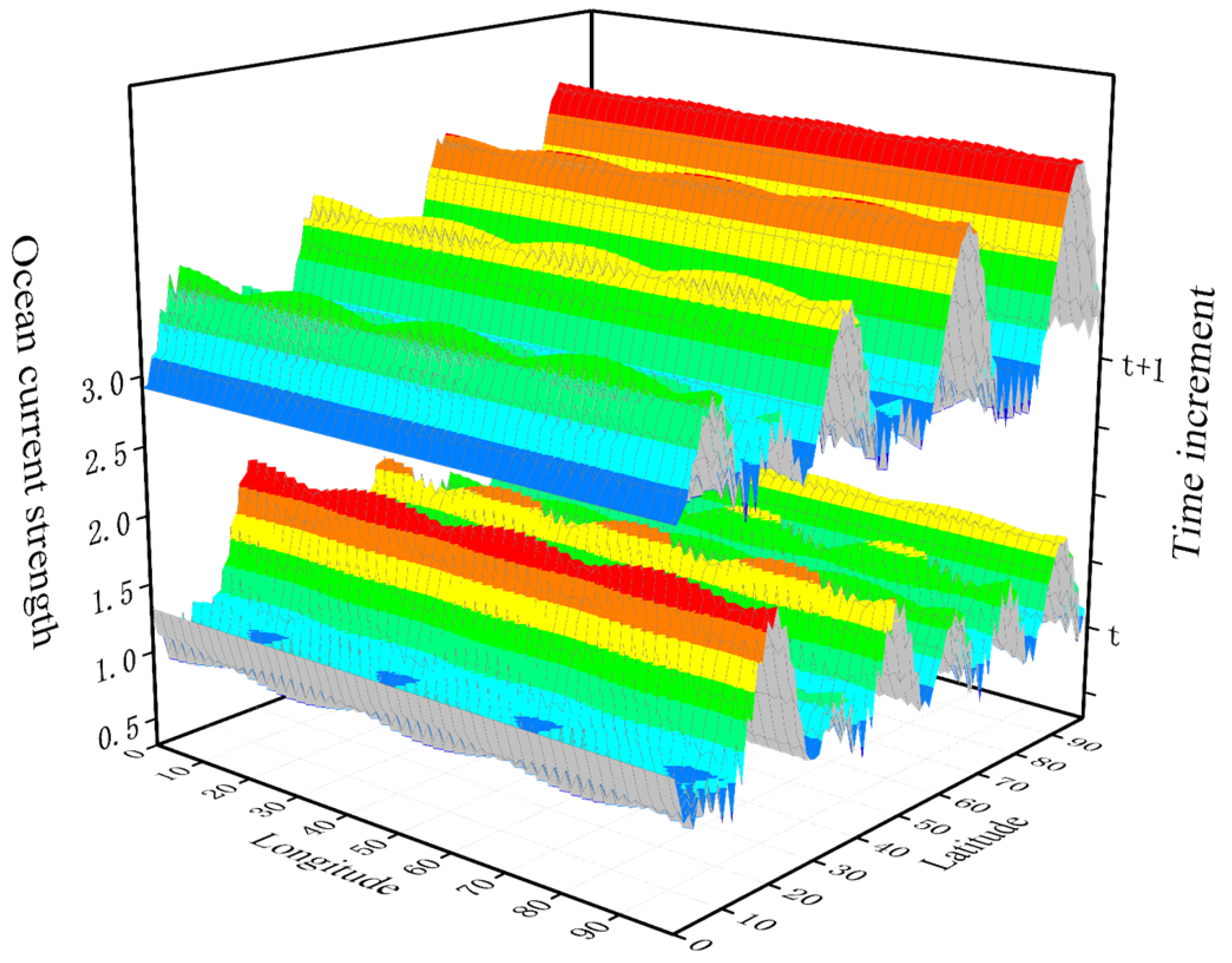
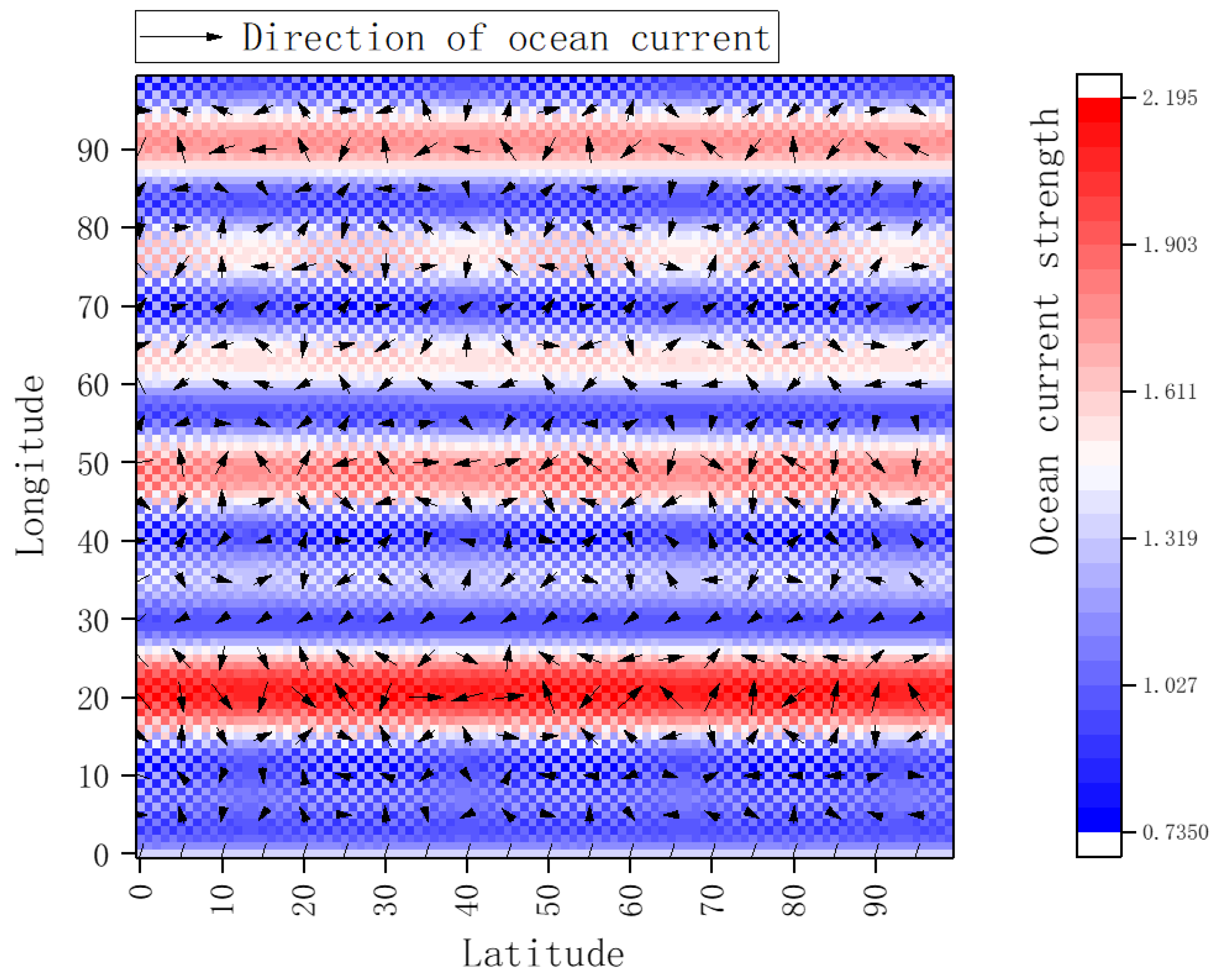
2.2. Ocean Current Modeling
2.3. Soft Actor–Critic
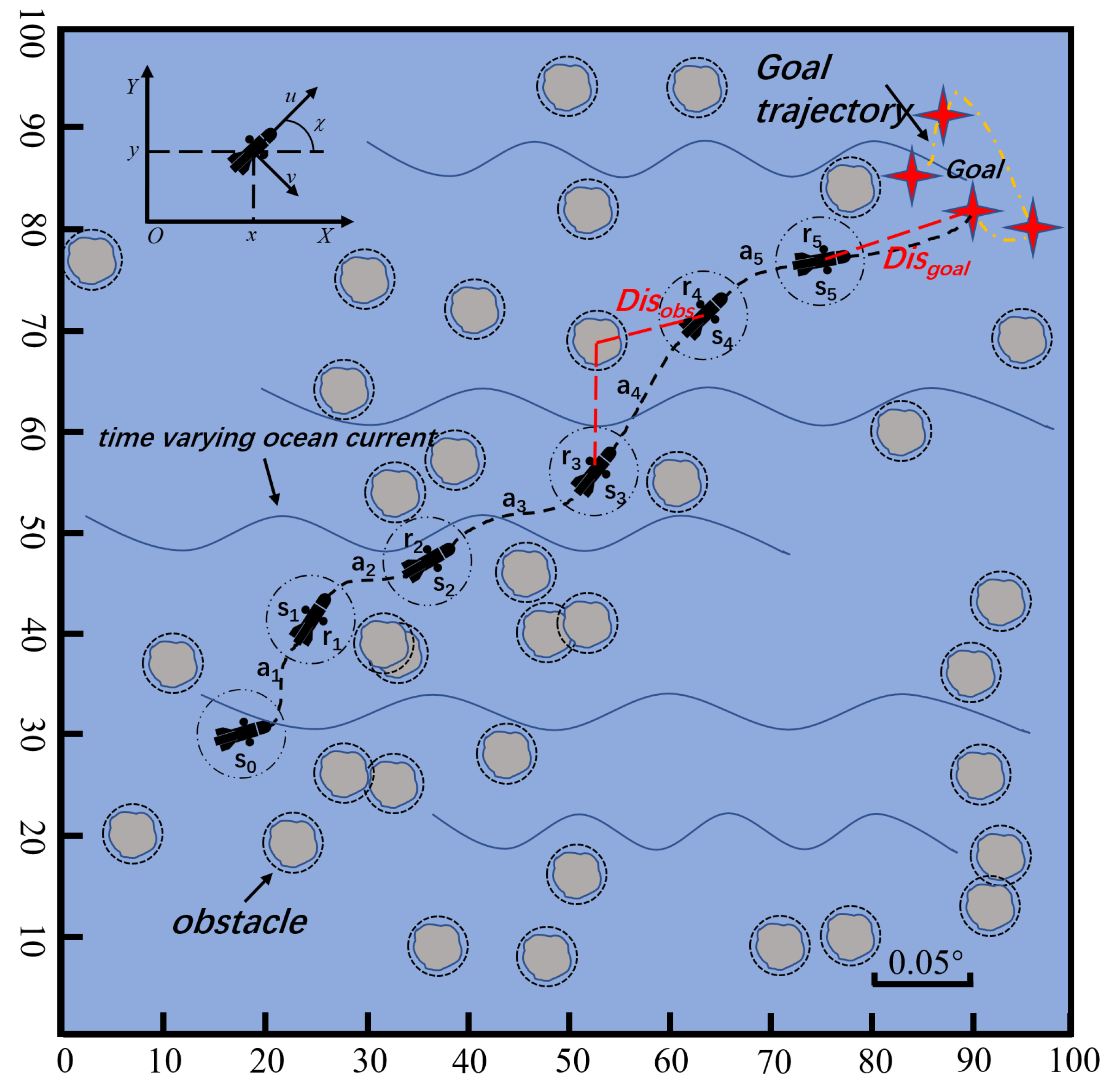
3. Methods
3.1. Marine Environmental Information Model
3.2. Reinforcement Learning Environment
3.2.1. State Transition Function
3.2.2. Reward Function
3.3. RLBMPA-COI Algorithm
| Algorithm 1: RLBMPA-COI algorithm. | |||||||||
| 1 | Initialize the environment and set the number of episodes ; | ||||||||
| 2 | Initialize a replay buffer D with a capacity of ; | ||||||||
| 3 | Randomly initialize the policy network and state-action value networks with parameter vectors , , ; | ||||||||
| 4 | Initialize the target state-action value networks with parameter vectors ; | ||||||||
| 5 | Define the total training steps T, episode training steps ; | ||||||||
| 6 | foreach n in set T do | ||||||||
| 7 | Reset the step counter for each episode ; | ||||||||
| 8 | Clear the event trigger flag , ; | ||||||||
| 9 | Clear the task completion flag ; | ||||||||
| 10 | Reset the environment, AUV start point , initial state ; | ||||||||
| 11 | while or not or not do | ||||||||
| 12 | Integrate ocean current information and AUV motion state | ||||||||
| ; | |||||||||
| 13 | Based on the AUV motion model and state , take action according to | ||||||||
| policy ; | |||||||||
| 14 | if then | ||||||||
| 15 | Trigger obstacle collision reward, end this episode | ||||||||
| 16 | else | ||||||||
| 17 | if then | ||||||||
| 18 | , trigger obstacle warning reward | ||||||||
| 19 | else | ||||||||
| 20 | pass; | ||||||||
| 21 | end | ||||||||
| 22 | end | ||||||||
| 23 | if then | ||||||||
| 24 | , trigger target tracking reward | ||||||||
| 25 | end | ||||||||
| 26 | Get an AUV state , update the rewards | ||||||||
| , and calculate the total reward r; | |||||||||
| 27 | Integrate to obtain the state and various rewards of the next moment, | ||||||||
| determining the triggering of the obstacle events and target events, and | |||||||||
| calculate the total reward r; | |||||||||
| 28 | Store the experience in D; | ||||||||
| 29 | ; | ||||||||
| 30 | end | ||||||||
| 31 | ; | ||||||||
| 32 | if then | ||||||||
| 33 | Sample a segment of experience from D; | ||||||||
| 34 | Extract the weight of the ocean current reward to the queue ; | ||||||||
| 35 | Calculate the average ocean current weight in the queue ; | ||||||||
| 36 | Update ; | ||||||||
| 37 | Update ; | ||||||||
| 38 | Update ; | ||||||||
| 39 | Update ; | ||||||||
| 40 | Update ; | ||||||||
| 41 | end | ||||||||
| 42 | end | ||||||||
4. Experiments and Discussions
4.1. Basic Settings
4.2. Path Planning Tasks
4.2.1. Path Planning Task with Complex Obstacles
4.2.2. Multi-Objective Path Planning Task
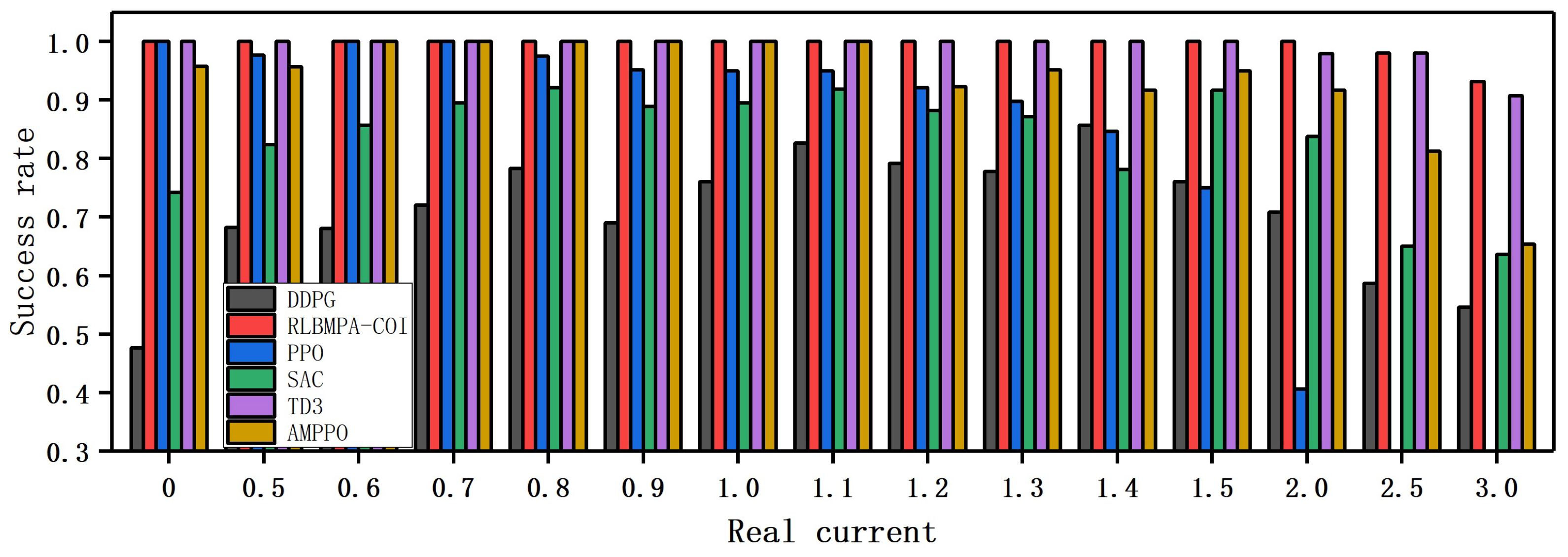
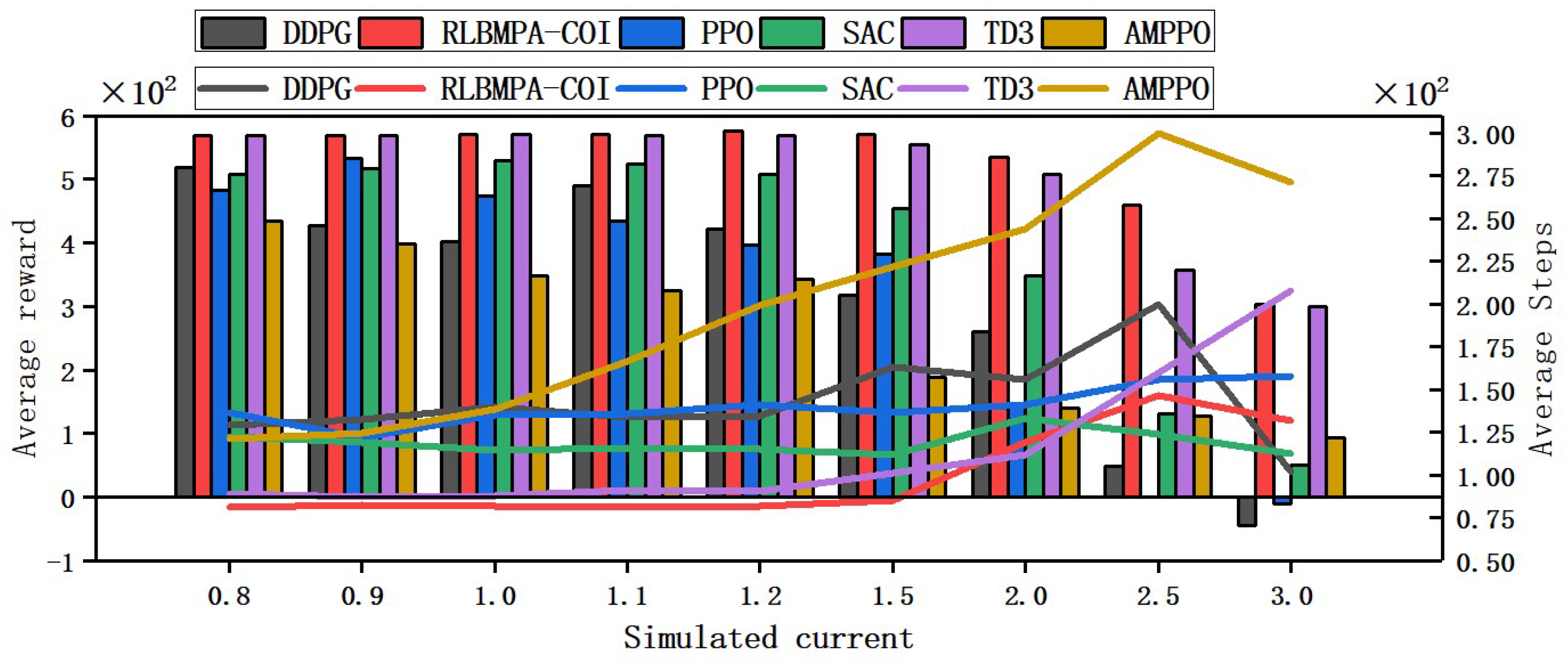
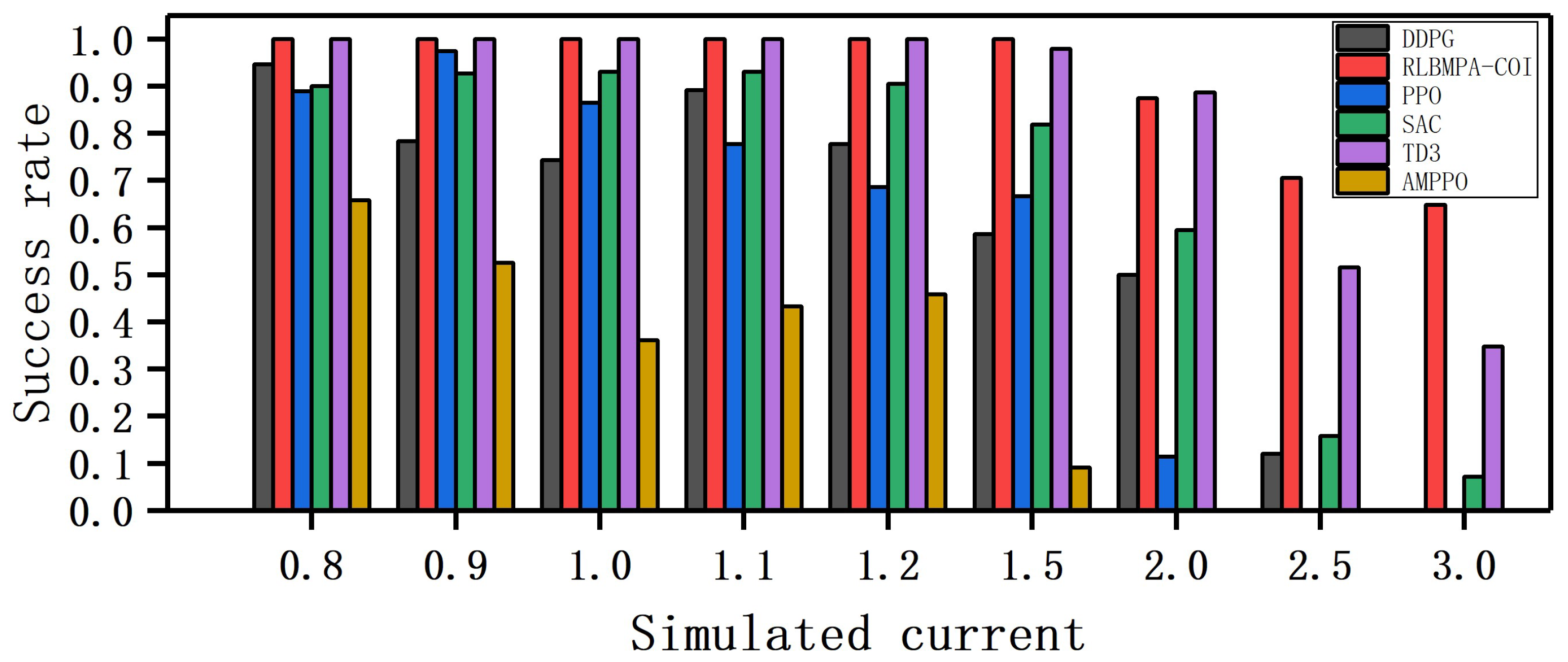
4.2.3. Ocean Current Strength Robustness Experiment
4.2.4. Ocean Current Adaptation Experiment
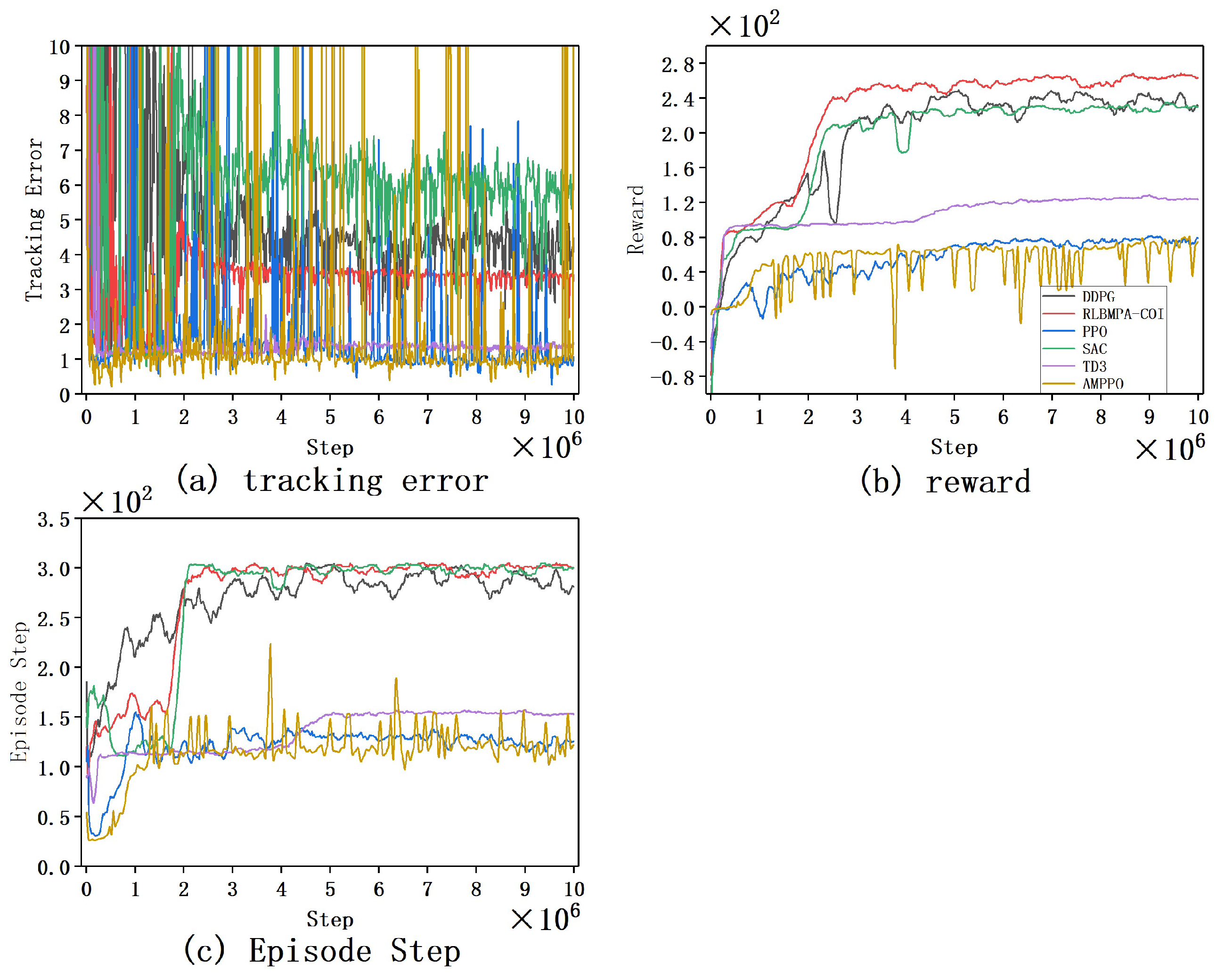
4.3. Trajectory-Tracking Task
Curve Trajectory-Tracking Task
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Name | Description |
|---|---|
| AUV state vector | |
| Surge, sway and heave in the global coordinate system | |
| Roll, pitch and yaw in the global coordinate system | |
| Velocity vector of the AUV | |
| Velocity components in the body coordinate system | |
| Angular velocity components in the body coordinate system | |
| t | Moment of AUV motion |
| Maximum change in ocean current | |
| The strength of the ocean current components in the global coordinate system | |
| The vector of the ocean current at time t | |
| Environmental influence parameters | |
| Stochastic influence parameters | |
| Distance between the AUV and the obstacle | |
| Distance between the AUV and the target | |
| Relative distance between the obstacle and the nearest target | |
| Obstacle warning range | |
| Obstacle collision range | |
| Target perceived distance | |
| The range of angles output by the movement of the AUV | |
| P | The position of the AUV |
| The position of the i-th target point | |
| The completion status of the i-th target point | |
| State value network parameters | |
| Target state value network parameters | |
| Policy network parameters | |
| Action entropy value weight | |
| Systematic error caused by ocean currents in the longitudinal and transverse directions | |
| The amplitude, frequency and phase of the longitudinal ocean current | |
| The amplitude, frequency and phase of the transverse ocean current | |
| The weights of ocean currents for algorithm updates |
| Parameter | Value |
|---|---|
| Ocean current weight coefficient | 0.4 |
| Step weight coefficient | |
| The completion status of the i-th target point | 1 or |
| Obstacle warning range | 0.2 |
| Obstacle collision range | 0.05 |
| Target perceived distance | 0.05 |
| AUV turning angle range | |
| Learning rate | |
| Replay buffer D capacity | |
| Current weight queue capacity | |
| Total training steps T | |
| Maximum training steps per episode | 300 |
| Gradient update frequency | 1 |
| Update weight of the policy network | 0.005 |
| Discount factor | 0.99 |
| Algorithm Name | DDPG | RLBMPA-COI | PPO | SAC | TD3 | AMPPO |
|---|---|---|---|---|---|---|
| Total training steps T | ||||||
| Learning rate | ||||||
| Replay buffer D capacity | None | None | ||||
| Discount factor | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| Update weight of the policy network | 0.005 | 0.005 | None | 0.005 | 0.005 | None |
| Current weight queue capacity | None | None | None | None | None | |
| Target policy noise | None | None | None | None | 0.2 | None |
| Number of processes | 1 | 1 | 1 | 1 | 1 | 2 |
| Generalized advantage estimation (GAE) | None | None | 0.95 | None | None | 0.95 |
References
- Zhao, W.; Zhao, H.; Liu, G.; Zhang, G. ANFIS-EKF-Based Single-Beacon Localization Algorithm for AUV. Remote Sens. 2022, 14, 5281. [Google Scholar] [CrossRef]
- Cai, C.; Chen, J.; Yan, Q.; Liu, F. A Multi-Robot Coverage Path Planning Method for Maritime Search and Rescue Using Multiple AUVs. Remote Sens. 2022, 15, 93. [Google Scholar] [CrossRef]
- Sun, Y.; Song, H.; Jara, A.J.; Bie, R. Internet of things and big data analytics for smart and connected communities. IEEE Access 2016, 4, 766–773. [Google Scholar] [CrossRef]
- Yu, H.; Meier, K.; Argyle, M.; Beard, R.W. Cooperative path planning for target tracking in urban environments using unmanned air and ground vehicles. IEEE/ASME Trans. Mechatronics 2014, 20, 541–552. [Google Scholar] [CrossRef]
- Takahashi, O.; Schilling, R.J. Motion planning in a plane using generalized Voronoi diagrams. IEEE Trans. Robot. Autom. 1989, 5, 143–150. [Google Scholar] [CrossRef]
- Mueller, T.G.; Pusuluri, N.B.; Mathias, K.K.; Cornelius, P.L.; Barnhisel, R.I.; Shearer, S.A. Map quality for ordinary kriging and inverse distance weighted interpolation. Soil Sci. Soc. Am. J. 2004, 68, 2042–2047. [Google Scholar] [CrossRef]
- Wang, G.; Wei, F.; Jiang, Y.; Zhao, M.; Wang, K.; Qi, H. A Multi-AUV Maritime Target Search Method for Moving and Invisible Objects Based on Multi-Agent Deep Reinforcement Learning. Sensors 2022, 22, 8562. [Google Scholar] [CrossRef]
- Yokota, Y.; Matsuda, T. Underwater Communication Using UAVs to Realize High-Speed AUV Deployment. Remote Sens. 2021, 13, 4173. [Google Scholar] [CrossRef]
- Sedighi, S.; Nguyen, D.V.; Kuhnert, K.D. Guided hybrid A-star path planning algorithm for valet parking applications. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 570–575. [Google Scholar]
- Zhu, J.; Zhao, S.; Zhao, R. Path planning for autonomous underwater vehicle based on artificial potential field and modified RRT. In Proceedings of the 2021 International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 8–10 January 2021; pp. 21–25. [Google Scholar]
- Chen, L.; Shan, Y.; Tian, W.; Li, B.; Cao, D. A fast and efficient double-tree RRT*-like sampling-based planner applying on mobile robotic systems. IEEE/ASME Trans. Mechatron. 2018, 23, 2568–2578. [Google Scholar] [CrossRef]
- Nayeem, G.M.; Fan, M.; Akhter, Y. A time-varying adaptive inertia weight based modified PSO algorithm for UAV path planning. In Proceedings of the 2021 2nd International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 5–7 January 2021; pp. 573–576. [Google Scholar]
- Yang, H.; Qi, J.; Miao, Y.; Sun, H.; Li, J. A new robot navigation algorithm based on a double-layer ant algorithm and trajectory optimization. IEEE Trans. Ind. Electron. 2018, 66, 8557–8566. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2012, 9, 132–141. [Google Scholar] [CrossRef]
- Shen, C.; Buckham, B.; Shi, Y. Modified C/GMRES algorithm for fast nonlinear model predictive tracking control of AUVs. IEEE Trans. Control. Syst. Technol. 2016, 25, 1896–1904. [Google Scholar] [CrossRef]
- Li, Z.; Deng, J.; Lu, R.; Xu, Y.; Bai, J.; Su, C.Y. Trajectory-tracking control of mobile robot systems incorporating neural-dynamic optimized model predictive approach. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 740–749. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control. Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Joseph, S.B.; Dada, E.G.; Abidemi, A.; Oyewola, D.O.; Khammas, B.M. Metaheuristic algorithms for PID controller parameters tuning: Review, approaches and open problems. Heliyon 2022, 8, e09399. [Google Scholar] [CrossRef]
- Konar, A.; Chakraborty, I.G.; Singh, S.J.; Jain, L.C.; Nagar, A.K. A deterministic improved Q-learning for path planning of a mobile robot. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1141–1153. [Google Scholar] [CrossRef]
- Du, J.; Jiang, C.; Wang, J.; Ren, Y.; Debbah, M. Machine learning for 6G wireless networks: Carrying forward enhanced bandwidth, massive access, and ultrareliable/low-latency service. IEEE Veh. Technol. Mag. 2020, 15, 122–134. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Yan, S.; Tan, M.; Yu, J. Real-time path planning and following of a gliding robotic dolphin within a hierarchical framework. IEEE Trans. Veh. Technol. 2021, 70, 3243–3255. [Google Scholar] [CrossRef]
- Han, G.; Zhou, Z.; Zhang, T.; Wang, H.; Liu, L.; Peng, Y.; Guizani, M. Ant-colony-based complete-coverage path-planning algorithm for underwater gliders in ocean areas with thermoclines. IEEE Trans. Veh. Technol. 2020, 69, 8959–8971. [Google Scholar] [CrossRef]
- Huang, B.Q.; Cao, G.Y.; Guo, M. Reinforcement learning neural network to the problem of autonomous mobile robot obstacle avoidance. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 1, pp. 85–89. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Hassabis, D. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Chu, Z.; Wang, F.; Lei, T.; Luo, C. Path planning based on deep reinforcement learning for autonomous underwater vehicles under ocean current disturbance. IEEE Trans. Intell. Veh. 2022, 8, 108–120. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, P.; Du, B.; Dong, B.; Zhang, W. AUV path tracking with real-time obstacle avoidance via reinforcement learning under adaptive constraints. Ocean Eng. 2022, 256, 111453. [Google Scholar]
- Hou, Y.; Liu, L.; Wei, Q.; Xu, X.; Chen, C. A novel DDPG method with prioritized experience replay. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 316–321. [Google Scholar]
- Du, J.; Zhou, D.; Wang, W.; Arai, S. Reference Model-Based Deterministic Policy for Pitch and Depth Control of Autonomous Underwater Vehicle. J. Mar. Sci. Eng. 2023, 11, 588. [Google Scholar]
- Hadi, B.; Khosravi, A.; Sarhadi, P. Deep reinforcement learning for adaptive path planning and control of an autonomous underwater vehicle. Appl. Ocean Res. 2023, 129, 103326. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Xu, J.; Huang, F.; Wu, D.; Cui, Y.; Yan, Z.; Du, X. A learning method for AUV collision avoidance through deep reinforcement learning. Ocean Eng. 2022, 260, 112038. [Google Scholar]
- Huang, F.; Xu, J.; Yin, L.; Wu, D.; Cui, Y.; Yan, Z.; Chen, T. A general motion control architecture for an autonomous underwater vehicle with actuator faults and unknown disturbances through deep reinforcement learning. Ocean Eng. 2022, 263, 112424. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- He, Z.; Dong, L.; Sun, C.; Wang, J. Asynchronous multithreading reinforcement-learning-based path planning and tracking for unmanned underwater vehicle. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 2757–2769. [Google Scholar]
- Wang, Y.; He, H.; Tan, X. Truly proximal policy optimization. In Proceedings of the Uncertainty in Artificial Intelligence, Tel Aviv, Israel, 22–25 July 2019; pp. 113–122. [Google Scholar]
- Jaffe, J.; Schurgers, C. Sensor networks of freely drifting autonomous underwater explorers. In Proceedings of the 1st International Workshop on Underwater Networks, Los Angeles, CA, USA, 25 September 2006; pp. 93–96. [Google Scholar]
- Xi, M.; Yang, J.; Wen, J.; Liu, H.; Li, Y.; Song, H.H. Comprehensive ocean information-enabled AUV path planning via reinforcement learning. IEEE Internet Things J. 2022, 9, 17440–17451. [Google Scholar]
- National Marine Science and Technology Center. Available online: http://mds.nmdis.org.cn/ (accessed on 1 May 2022).

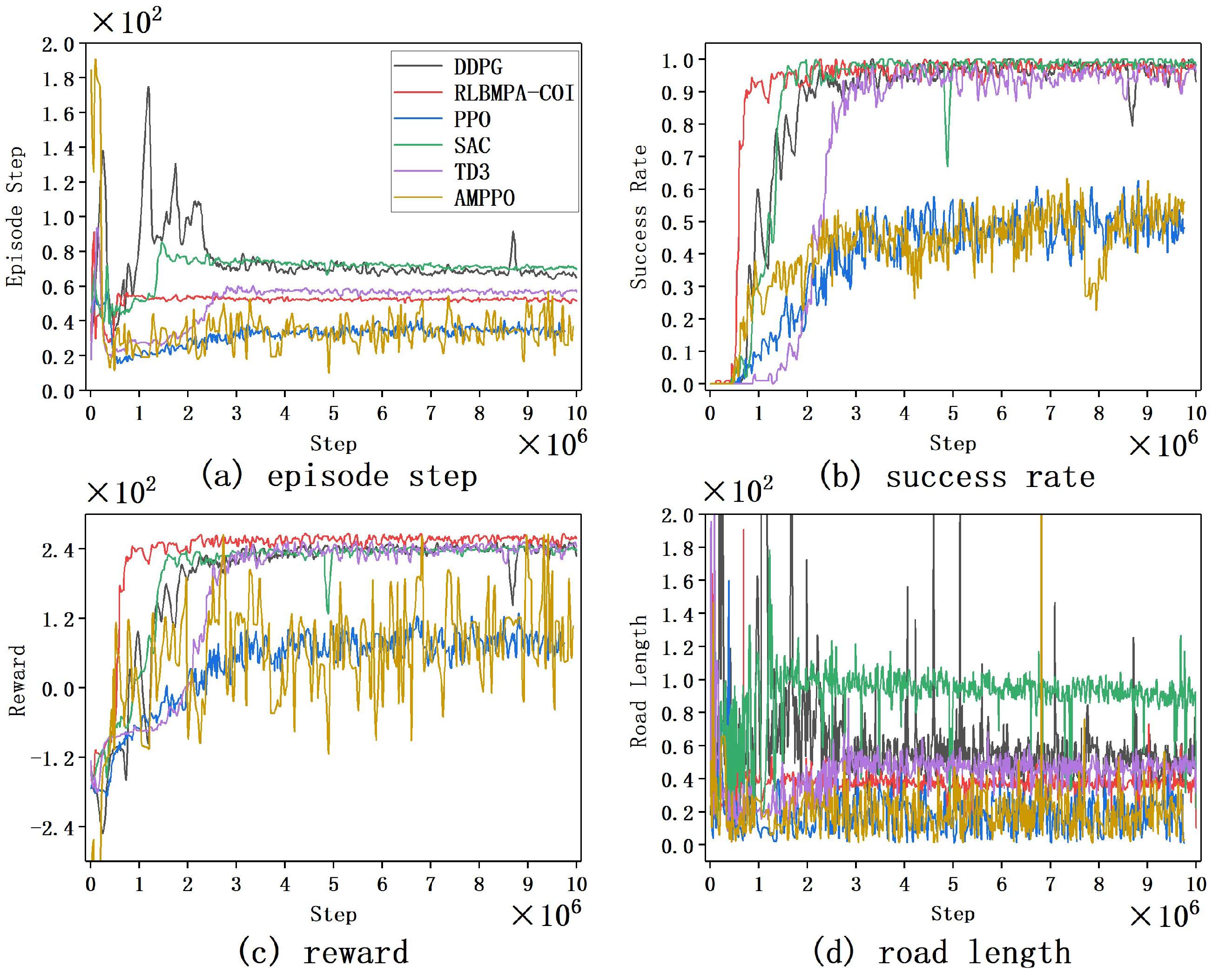

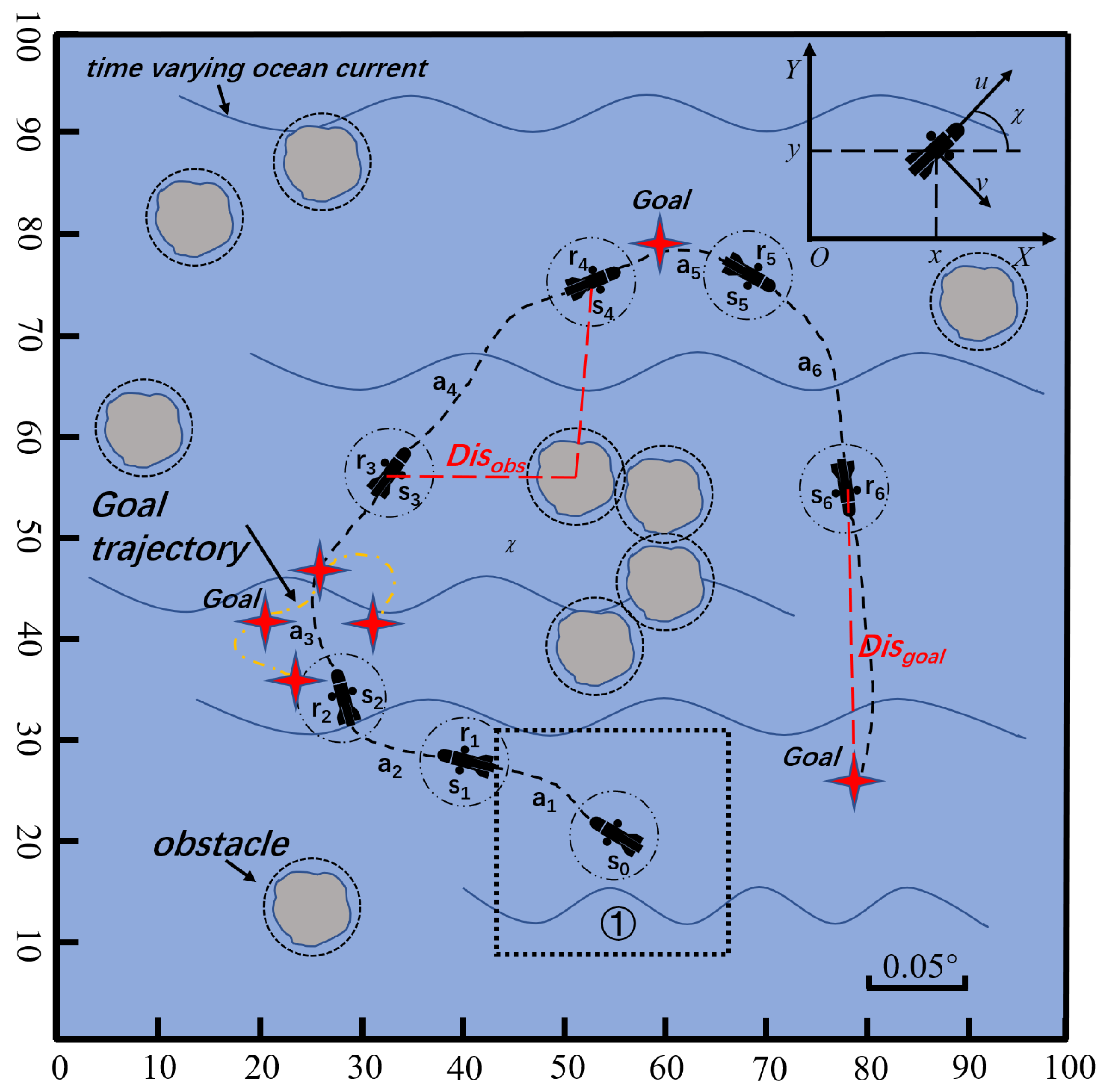

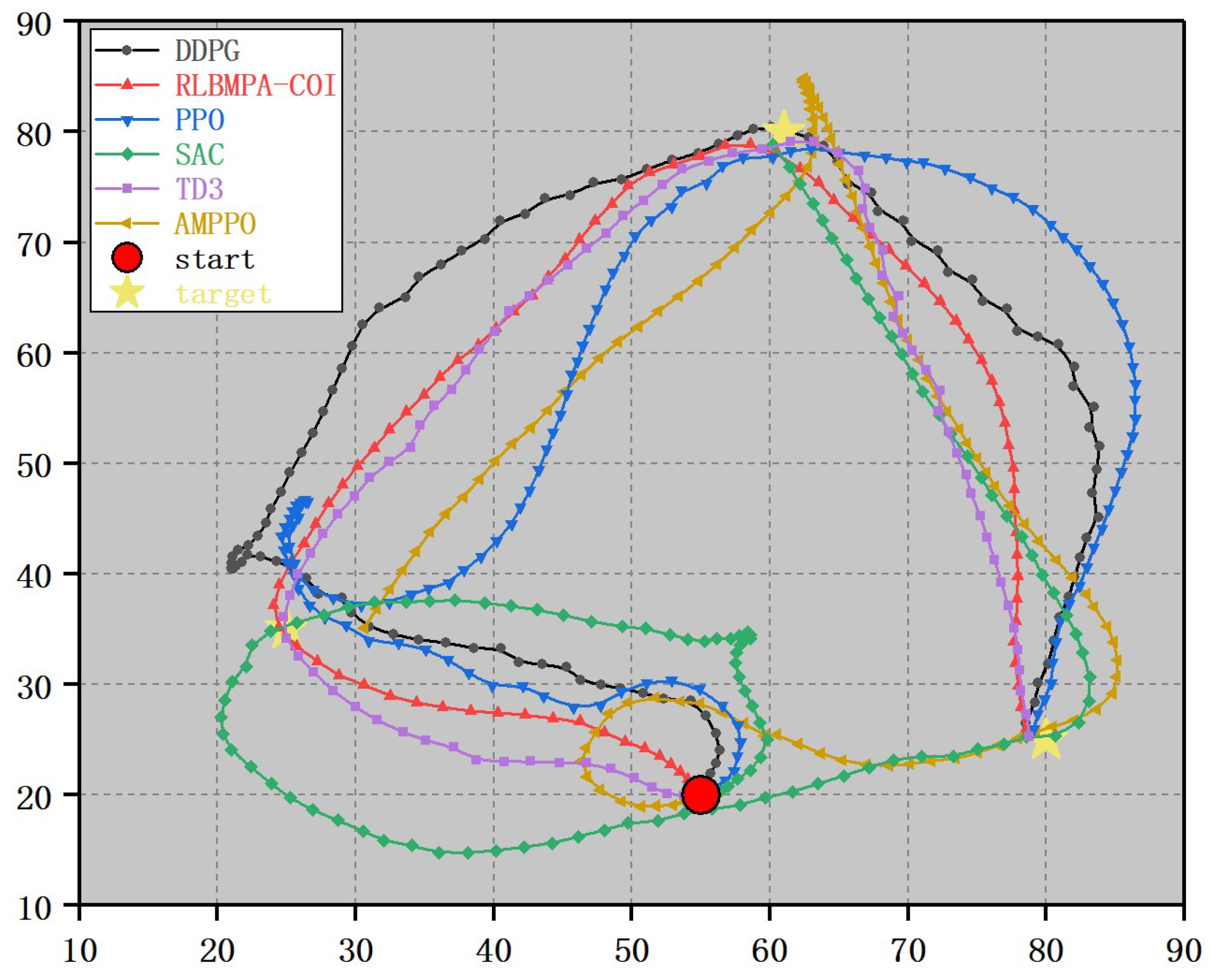
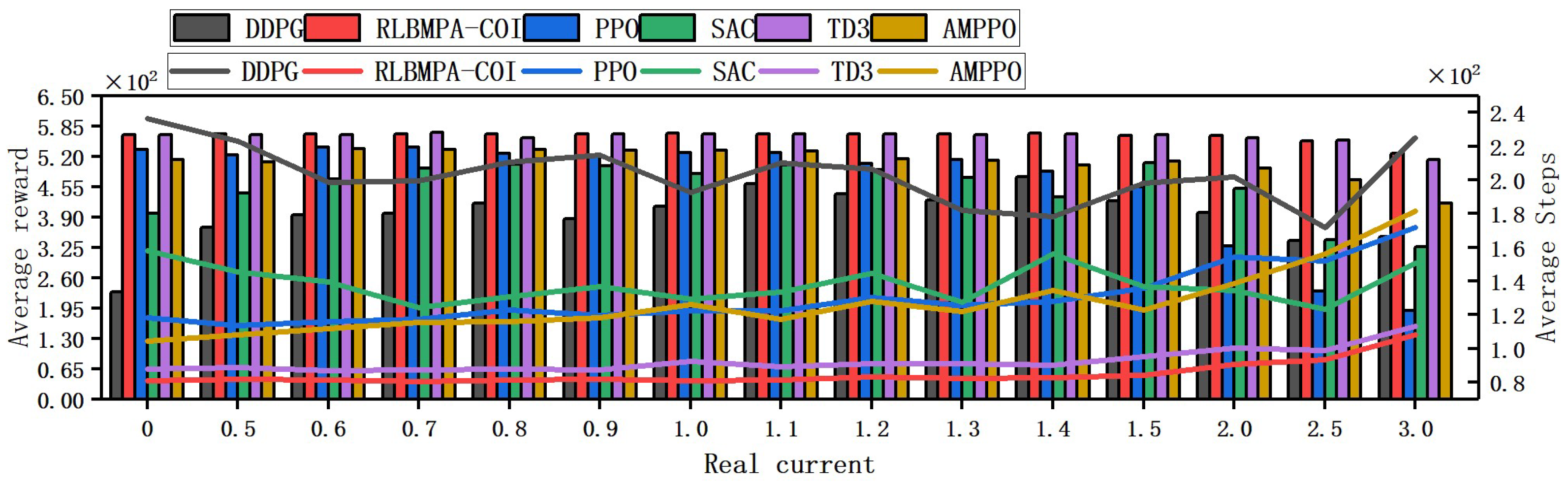


| Path | Start Point | Terminal Point | AMPPO | SAC | RLBMPA-COI | |||
|---|---|---|---|---|---|---|---|---|
| Step | Reward | Step | Reward | Step | Reward | |||
| 1 | (55,20) | (25,35), (60,80), (80,25) | 107.25 | 535.4 | 122.75 | 548.45 | 84.4 | 567.26 |
| 2 | (65,10) | (25,35), (60,80), (80,25) | 118.7 | 527.76 | 106 | 553.25 | 85 | 561.58 |
| 3 | (55,20) | (25,35), (60,65), (80,35) | 116.35 | 533.79 | 107.32 | 563.34 | 82.25 | 573.46 |
| 4 | (65,10) | (25,35), (60,65), (80,35) | 118.5 | 529.83 | 109.25 | 556.59 | 87.65 | 563.05 |
| Parameter | Value |
|---|---|
| Maximum speed of ocean currents | 1.892 |
| Environmental influence parameters of ocean currents | 3.018 |
| Environmental influence parameters of ocean currents | 3.122, 3.023, 3.034 |
| Stochastic influence parameters of ocean currents | 1.015, 0.987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; He, X.; Lu, Z.; Jing, P.; Su, Y. Comprehensive Ocean Information-Enabled AUV Motion Planning Based on Reinforcement Learning. Remote Sens. 2023, 15, 3077. https://doi.org/10.3390/rs15123077
Li Y, He X, Lu Z, Jing P, Su Y. Comprehensive Ocean Information-Enabled AUV Motion Planning Based on Reinforcement Learning. Remote Sensing. 2023; 15(12):3077. https://doi.org/10.3390/rs15123077
Chicago/Turabian StyleLi, Yun, Xinqi He, Zhenkun Lu, Peiguang Jing, and Yishan Su. 2023. "Comprehensive Ocean Information-Enabled AUV Motion Planning Based on Reinforcement Learning" Remote Sensing 15, no. 12: 3077. https://doi.org/10.3390/rs15123077
APA StyleLi, Y., He, X., Lu, Z., Jing, P., & Su, Y. (2023). Comprehensive Ocean Information-Enabled AUV Motion Planning Based on Reinforcement Learning. Remote Sensing, 15(12), 3077. https://doi.org/10.3390/rs15123077







