Abstract
The Fourier–Merlin transform method, multi-scale optical flow method, and Weibull distribution are used to integrate the GRAPES_3 km model and Radar Extrapolation Forecast (REF) both developed independently by China. Taking GRAPES_3 km, Wuhan Rapid Update Cycle (WHRUC), and the REF as examples, the prediction performance of the Blending forecast is evaluated comprehensively by the traditional point-to-point method. A new spatial test method is introduced to evaluate the applicability and difference of high-resolution model evaluation. The area, position, shape, and intensity of the precipitation area are matched through the target object test method. The potential forecast information of the spatial field is obtained and the related results are compared and analyzed. The results show that: (1) the comprehensive application of various evaluation methods can evaluate the convective storm forecast more comprehensively. The Blending forecast effect is obviously better than those of other models by using the point-to-point scoring method, especially in the heavy precipitation forecast. The shorter the prediction time is, the better the effect is. (2) The new spatial test method can evaluate the prediction effect of convective storm characteristics, and the target recognition hit rate of the Blending forecast is highest. The scores of target area, position, shape, and median intensity of precipitation are better than those of other forecasts. The variation in the east–west direction is less than that in the north–south direction, which is basically consistent with the actual observation. The variation range of the forecast grid before and after translation is the closest to the reality. (3) The Blending forecast method combines the advantages and disadvantages of the numerical model and REF, which can not only grasp the precipitation area but also improve the prediction ability of rainfall intensity. The traditional point-to-point scoring method and the new spatial test method have the same conclusion as the convective storm forecast of the high-resolution model, which has a certain reference value, and the new spatial test method can provide more detailed evaluation information.
1. Introduction
The flood and geological disasters caused by severe convective weather cause great harm to people’s life and property. It is of great significance to forecast them and provide early warnings [1,2]. The Radar Extrapolation Forecast (REF) and Meso-scale Numerical Weather Prediction (NWP) have become the key technical support for the short-term Quantitative Precipitation Forecast (QPF) at present [3,4,5]. The problem of “spin-up” always exists in the model forecast in the first few hours, which leads to poor prediction results in the first few hours and cannot be directly applied to the short-term approaching forecast. REF and NWP have their own advantages, and their combination can improve the prediction ability of 0~6 h. Therefore, the integrated precipitation forecast based on the numerical model and radar extrapolation is developing rapidly [6,7,8,9].
The spatial inspection methods of the precipitation field can be divided into the following two categories: traditional point-to-point-based inspection technology and object-oriented inspection technology [10]. Brownlee classified weather events through a two-variable forecast test contingency table [11]. He calculated a series of scoring indexes, such as hit rate and false alarm rate. Doswell found that the real skill score TSS often tended to the hit rate when calculating the forecast score of small-probability events [12]. So, he revised the HSS score. Since then, a series of scoring indicators have been developed and the deterministic prediction of binary events mainly includes: forecast deviation, probability ratio, accuracy, etc. For the deterministic prediction of classified events, the 2*K contingency table can be used to classify the probabilities of different levels to calculate the scoring criteria. In recent years, meteorologists have conducted a lot of work around the precipitation forecast test. Wang analyzed the predictability of the radar echo by the decorrelation time method and quantitatively analyzed the error of the extrapolated forecast by means of the forecasting skill score and relative absolute error [13]. In addition, the relationship between REF error and scale, and the relative importance of the echo intensity change and echo motion field change in the prediction error were also analyzed. Although the traditional lattice comparison method can reflect certain forecasting characteristics, the test results cannot give specific reasons for the deviation. It still cannot comprehensively test the prediction ability of NWP and objective methods. On the other hand, the object-oriented test technology divides the precipitation field into discrete targets and comprehensively measures the forecasting effect according to the characteristic attributes, which can provide users with more abundant information [14,15]. Xue studied the objective performance of precipitation objects and the prediction ability of the Japanese fine grid model to cases based on the MODE of object-oriented model diagnosis and analysis [16]. The methods adopted involved more advanced spatial testing [17,18], which reflect the spatial structure and scale changes of the precipitation forecast and play a leading role in the inspection industry.
Since 2016, the national self-developed GRAPES_3 km high-resolution numerical model has been widely used in severe convective weather forecast and early warning. More scientific and technical personnel have carried out a variety of inspection and evaluation work for the GRAPES_3 km model. The test results show that the GRAPES_3 km model has a good ability to predict high-threshold and small-scale convective events. Xu evaluated the precipitation forecast of the model and pointed out that the variation in the daily frequency in summer was similar to the observation [19]. The heavy-precipitation frequency and regional distribution are in good agreement with the observation and can reflect the diurnal variation characteristics of the precipitation process. Tang compared and evaluated the prediction ability of GRAPES_3 km in several typical severe convective weather processes in North China by using the fractional technique score (FSS) and discussed the good prediction performance of this model in severe convective weather [20]. The test results show that the GRAPES_3 km model has a good ability to predict high-threshold and small-scale convective events, which are difficult to forecast. However, it has not been comprehensively evaluated by a variety of test methods [21]. Therefore, this paper combines GRAPES_3 km and REF, and compares and analyzes the prediction ability of mesoscale models with different resolutions in severe convective weather by taking the Blending results as the evaluation object, to provide a reference basis for the further development of intelligent grid forecasting technology and products of severe convective weather.
2. Materials and Methods
2.1. Materials
The observation data are based on the national radar combination reflectivity data, with a spatial resolution of 0.01° and a time resolution of 6 min. The regional range is 12.2°~54.2°N and 70°~135°E. The NWP data are based on the GRAPES_3 km model prediction and Fast Update Cyclic Assimilation model (WHRUC) in Table 1. The Blending data are based on GRAPES_3 km and REF, and the bilinear interpolation method is adopted. Due to the difference in temporal and spatial resolution between GRAPES_3 km and actual observation data, which are sparse when the spatial resolution is unified, it was necessary to take the maximum value of the area around the sparse mesh so the strong echo information of convective weather could be preserved.

Table 1.
NWP model systems.
2.2. Methods
The REF aimed to calculate the moving speed and direction of precipitation based on the images observed by the radar at the previous time and the current time, and to speculate the position of the future time [22,23,24]. In view of the severe convective weather, the improved variational optical flow method was used to retrieve the wind field from the radar data and the change in the echo optical flow field was used to obtain the motion vector field. The improved variational optical flow method organically combined the local optical flow method with the global optical flow method through an energy function and added a high-order smoothing operator to solve the equation to obtain the flow field structure. Additionally, the 9-point moving average was then used to obtain the motion vector field. Finally, the semi-Lagrange method was used for extrapolation prediction.
In order to improve the ability of the short-term forecast of disastrous weather, the Institute of Heavy Rain, China Meteorological Administration established a kilometer-scale high-resolution fast updating cyclic assimilation forecast system WHRUC in 2019 [25]. The horizontal resolution of the system is 1.5 km. The update frequency of analysis is 15 min. The update frequency of prediction is 1 h and the time effectiveness of prediction is 12 h. The center of the simulation area is 113.0°E, 30.5°N. The number of horizontal grid points is 801 × 701. The vertical direction is 51 layers and the integration time step is 10 s.
GRAPES_3 km is a high-resolution numerical model developed and operated by the numerical Forecast Center of the China Meteorological Administration. In order to improve the prediction accuracy and stability of the numerical model throughout the country, the numerical Forecast Center integrates national weather radar data, formulates a quality control scheme, and assimilates SC/CD radar data. The prediction accuracy and stability of the model are improved by introducing the monotone high-order horizontal diffusion scheme, adopting the automatic modulation time step scheme, and optimizing the initial reference profile. The stability of the model is evaluated to solve the problem of instability. The physical process parameterization scheme and the prediction ability are improved under weak dynamic forcing by using in-depth analysis of the sources of prediction deviation. The spatial resolution of the model is 3 km and the current coverage is 10°~60°N. It runs four times a day. The reporting time is 02, 08, 14, and 20:00 (BT).
3. Key Technologies of Blending Forecast
The radar extrapolation prediction and intensity correction method are developed based on the RAPIDS technology of the Hong Kong Observatory, Fourier–Merlin transform, and Weibull distribution. Combined with the radar extrapolation prediction of the multi-scale optical flow variational method (multi-scale optical flow by variational analysis, MOVA), the hyperbolic tangent function is used to integrate the radar extrapolation prediction and the corrected model prediction. The Blending method is preliminarily realized and the technical flow is shown in Figure 1.
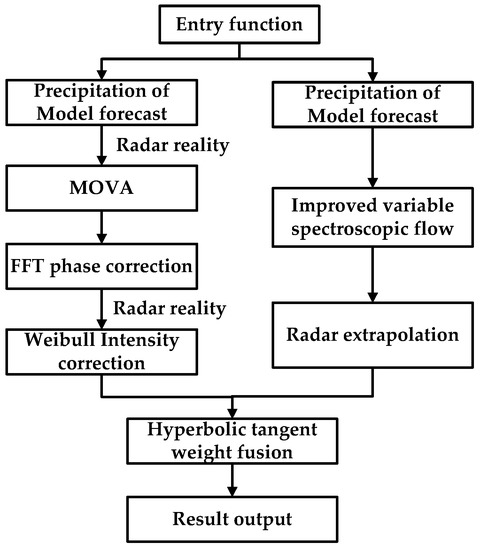
Figure 1.
The Blending technology process of numerical prediction into short-term and impending extrapolation prediction of radar echo.
3.1. Phase Correction of Precipitation Forecast by Model
The Fourier–Merlin transform is the global phase correlation between the fast Fourier transform and logarithmic polar transformation. Suppose f1(x, y) is the template image and f2(x, y) is the image to be matched. There are rotations, translations, and scaling between them, which are set to Δθ, (Δx, Δy), and λ, respectively, that is:
By the Fourier transform, the following results can be obtained:
In the formula: f1(u, v) and f2(u, v) are the Fourier transform results of f1(x, y) and f2(x, y), respectively. It can be seen from Formula (2) that the relative translation between them is only in the phase spectrum. The amplitude spectra on both sides of Formula (2) are calculated, respectively, and the following results are obtained:
In the formula: M1(u, v) and M2(u, v) are the amplitude spectra of F1(u, v) and F2(u, v), respectively. By converting the amplitude spectrum to the logarithmic–polar coordinate space, we can obtain:
In the formula: M1(lgρ, θ) and M2(lgρ, θ) are logarithmic polar transformations of M1(u, v) and M2(u, v), respectively. Because 1/λ2 only affects the value, it has no effect on the calculation results of rotation, translation, and scaling parameters. So, it can be ignored. It can be seen from Formula (4) that the rotation and scaling between f1(x, y) and f2(x, y) are converted into translation in logarithmic polar coordinates, namely (lgλ, θ). By using the phase correlation algorithm for the amplitude spectrum in logarithmic–polar coordinates, the translation can be calculated and then the rotation and scaling parameters can be obtained. The rotation and scaling parameters are applied to the template image f1(x, y) to obtain the image with only translation. Then, the translation can be obtained by using the phase correlation algorithm. Formula (4) is called the Fourier–Merlin transform. Figure 2 shows the flow chart of the algorithm.
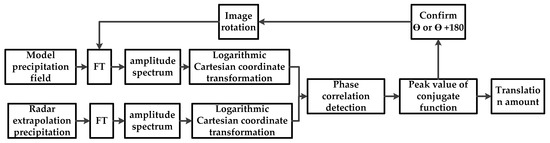
Figure 2.
Flow chart of the algorithm.
3.2. Correction of Precipitation Intensity Forecast by Model
The difference between the precipitation intensity predicted by the numerical model and the actual precipitation may be caused by the physical processes such as model resolution, convective parameterization, and cloud microphysical schemes. The intensity adjustment is adjusted by gradually moving the model forecast precipitation field toward the quantitative estimation precipitation field. Statistics show that both the model forecast precipitation and the actual precipitation satisfy the Weibull distribution, and their probability density distribution functions are the same. The model forecast precipitation intensity correction If-mod model is as follows:
In the formula: Ff(x0) and Fe(x0) are the cumulative distribution functions of model forecast precipitation and radar extrapolation forecast precipitation at the initial time, respectively.
3.3. Blending of Radar Extrapolation Prediction and Model Correction Prediction
Both kinds of forecast results are fused by combining with the optimization of the radar extrapolation forecast method after the precipitation forecast by the numerical model is corrected and adjusted according to the time series. The weight change of the model prediction is expressed by the hyperbolic tangent function and its empirical equation is as follows:
In the formula: t is time; a and b are the Blending weights of 1 h and 6 h model forecasts, respectively. The weights can be determined according to the historical statistical results of precipitation types and precipitation evolution characteristics or dynamically specified in combination with the position error and intensity error. k is the slope of W(t) in the middle part of the Blending period and its value can be determined according to the weather type. The spectral spatial correlation of radar reflectivity and the change speed of the weight curve are determined by adjusting the k value. The calculation formula of the Blending forecast is as follows:
In the formula: RGRAPES_3km(t), RRFST(t), and Rblenging(t) represent t time GRAPES_3 km, REF, and Blending forecast, respectively.
4. Test Methods
4.1. Point-to-Point Comprehensive Test
The evaluation process aims to compare the regional average value of each grid point of the precipitation forecast field (resolution is 0.01° × 0.01°, about 1 km × 1 km) and the adjacent 3 × 3 grid point with the observed precipitation of this grid point. The TS (equitable threat score) and bias forecasting skills scoring methods commonly used in the world are used to test the forecasting effect of the above four precipitation cases. The prediction accuracy cannot be directly given by the prediction skill score, so the average absolute error (mean absolute error, MAE) and hit rate (probability of detection, POD) are selected to describe the prediction accuracy.
In order to quantitatively describe the correlation between forecast precipitation and the radar quantitative estimation of precipitation, the correlation coefficient between the observed area forecast precipitation and radar quantitative precipitation estimation at the same time is calculated as follows:
where Fi is the predicted value, F is the average value of the predicted value, Oi is the observed value, and O is the average value of the observed value.
4.2. Spatial Comprehensive Test
Although the above lattice-based analysis can reflect certain forecast characteristics—it can deal with all the causes of forecast errors in the same way—it cannot distinguish the sources of forecast errors nor can it give the overall properties of the precipitation field. For this reason, the spatial diagnosis evaluation method is used to further test the results of the precipitation forecast.
4.2.1. MODE Test
MODE is a test technique based on “object”. The weight coefficients of different attributes are set on the basis of defining and calculating different attributes of the precipitation object. The characteristics of the target are calculated and compared once the “target area” is correctly identified. The fuzzy logic algorithm is used to calculate the total return function of the forecast performance to judge the overall performance of the forecast. Finally, the spatial position, strength, and shape of the prediction field and the observation field are given to provide more detailed inspection information. The target-based precipitation detection method includes three basic steps: target recognition, target pairing, and target detection. First, the Unicom targets are identified according to the input observation and forecast grid data. The multiple Unicom regions are merged according to the proximity degree and these Unicom targets are marked with serial numbers in turn. Then, the target in the forecast field is matched to the observed target. The number of forecast targets in the matching will be the same as the number of observation targets. There is a many-to-many situation between the observation field and the forecast field target. In the process of matching, the forecast targets will be further merged according to the position distribution to improve the coincidence between the observation targets and the observation targets. Finally, the axis attribute, face attribute and area, center of gravity position, and shape and strength parameters of each target object are calculated. Through the target attributes of the observation field and forecast field, the similarity matrix of observation and prediction is calculated.
(1) Area score:
where SA is the area score, Amod is the forecast target area, and Aobs is the actual target area.
(2) The score of the center of gravity:
where SGC is the center of gravity, Lmax is the maximum tolerance distance, Lmin is the best distance, the range of the east–west direction is about 940 km, and the range of the north–south direction is about 660 km. For short-term prediction, the tolerance maximum deviation Lmax is 470 km, the corresponding minimum deviation Lmin is 47 km, the corresponding minimum deviation Lmax is 330 km, and the corresponding minimum deviation Lmin is 33 km.
(3) Shape score:
where SAxial is the axial angle score and DAxA is the axial angle difference between the predicted and the real object.
where SEllip is the ellipticity difference score and DEliip is the difference between the ellipticity of the predicted object and the actual object.
(4) Intensity score of precipitation center:
The intensity score of the precipitation center is defined as follows: based on the actual precipitation level, the grade of the model is consistent with that of the real heavy precipitation center, or the absolute value of the difference between the model and the real heavy precipitation center is less than 10 mm. The score of the above two cases is 1; when the difference between the model and the actual heavy precipitation center is one grade, the score is 0.5; if the difference is more than one grade, the score is 0.
4.2.2. SAL Test
The SAL (structure, intensity, scale) method is based on the MODE algorithm, which counts the uniformity, average intensity, and centroid distribution of precipitation from the marked grid. It verifies the deviation attributes such as uniformity, average intensity, and distance between prediction and observation. During the calculation, the mesh points that are not marked as targets are first set to 0, and then the intensity error (A), distance error (L), and structure error (S) are calculated.
5. A Case of Inspection and Evaluation
5.1. Case Introductions
Since 8 August 2021, heavy rainfall occurred in the north, east, and southwest of Hubei Province, in which torrential rainfall occurred at 16 stations in Xiangyang from 20:00 on 11 August to 20:00 on 12 August 2021. The maximum daily rainfall was 519 mm in the willow forest, followed by 495 mm in Yinghe. From 8 August to 12 August 2021, there were 7 stations with an accumulated rainfall exceeding 400 mm and those with a heavier hourly rainfall had 118 mm, 105 mm, and 104 mm. From 3:00 a.m. on 12 August 2021, there was a sudden heavy rainfall at night in Liulin Town. From 11 to 12 August, the accumulated rainfall was 503 mm, the rainfall reached 373.7 mm from 4:00 to 7:00 on 12 August 2021, and the rainfall exceeded 100 mm for two consecutive hours from 5:00 to 6:00, all of which were the historical extremes since meteorological records began. The average depth of stagnant water in the rainfall center was 3.5 m and the deepest depth was 5 m.
Figure 3 shows the comparison between the extrapolation forecast, WHRUC model forecast, GRAPES_3 km forecast, and Blending forecast of 0~3 h precipitation from 04:00 (BT) on 12 August 2021. On the whole, the main areas of precipitation are basically concentrated in Jingzhou, Xianning, and Wuhan, and the location remains relatively unchanged, indicating that the predicted precipitation location is consistent with the actual situation. It is found that the Blending forecast results improve the deviation in the heavy precipitation area and precipitation intensity predicted by radar extrapolation, and the overall effect is better than that of the single numerical model forecast and radar extrapolation forecast.
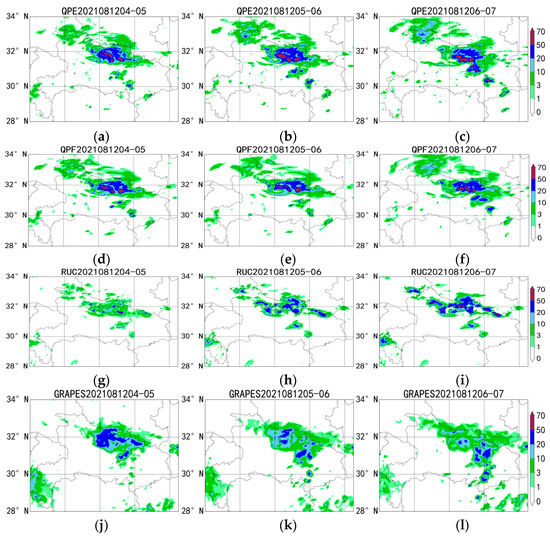
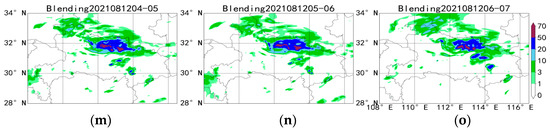
Figure 3.
Comparison of 0~3 h radar-extrapolated precipitation forecast (d–f), WHRUC model forecast (g–i), GRAPES_3 km model forecast (j–l), and Blending forecast (m–o) with real time (a–c) from 04:00 (BT) on 12 August 2021.
5.2. Forecast Effect Test
5.2.1. Point-to-Point Comprehensive Test
Zawadzki defined the “de-correlation time” L when studying the predictability of 11 precipitation cases [26], that is . It is no longer predictable when the correlation value between prediction and observation is less than 0.5. It is found that L is equal to the time constant in the index if C(t) conforms to the exponential law and corresponds to the time when the correlation coefficient decreases to 1/e = 0.37. The decorrelation time defined in the formula can be used to measure the predictability of precipitation.
The correlation coefficients calculated by the formula for each precipitation process are averaged in order to better evaluate the prediction results of 0~3 h (Figure 4). Figure 5 shows the variation in the correlation coefficients of the four methods with the prediction time. For the four methods with the forecast precipitation process, the variation in the correlation coefficient with the forecast time effect is basically decreasing exponentially. It can be seen from the straight line of stroke 1/e in Figure 5 that the decorrelation time of the QPF and Blending forecast precipitation process is much more than 3 h. The decorrelation time of the GRAPES_3 km forecast precipitation process is about 3 h and the decorrelation time of the WHRUC forecast precipitation process is less than 3 h. It can also be seen from Figure 5 that large-scale precipitation systems correspond to longer persistence, while for storms with a faster evolution and smaller scale, their persistence is shorter.
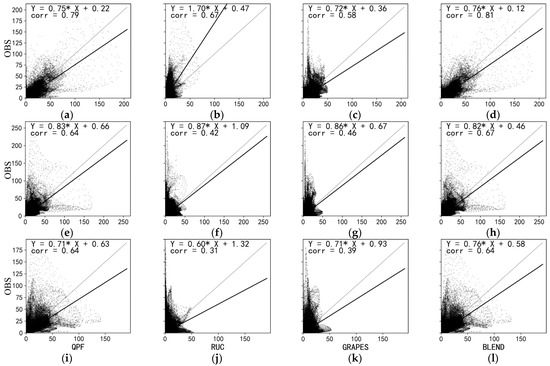
Figure 4.
Comparison of 0–3 h radar-extrapolated precipitation forecast (a,e,i), WHRUC model forecast (b,f,j), GRAPES_3 km model forecast (c,g,k), and Blending forecast (d,h,l) with real time from 04:00 (BT) on 12 August 2021.
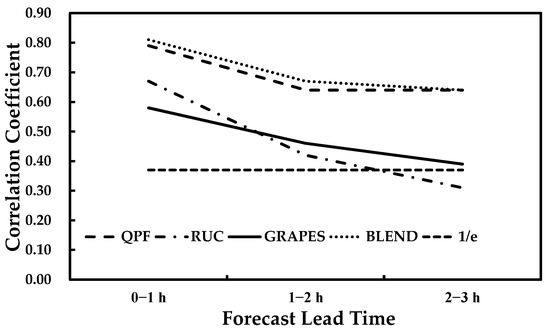
Figure 5.
The variation in the correlation coefficient of the four methods with the prediction time.
Figure 6a,c,e show the comprehensive performance of the threshold values of 1 mm, 5 mm, 10 mm, 20 mm, and 50 mm for the four prediction methods. The abscissa is the success rate and the ordinate is the hit rate. The auxiliary lines of equal bias and equal TS curves are drawn. The test results are displayed in the chart in the form of dots so that you can directly browse the test indexes such as success rate, HIT rate, BIAS, and TS. It can be seen that the accuracy of WHRUC prediction is obviously lower than those of other forecasts and the overall BIAS value is smaller. The prediction effect of QPF and Blending is the best. The BIAS value of the 1 mm precipitation threshold is too large. Additionally, the prediction accuracy is close to 0.6, which is slightly lower than that of QPF. With the increase in threshold, the prediction accuracy of the Blending forecast is obviously improved. The prediction deviation is similar to that of QPF. There is little difference between the prediction deviation of 10 mm and 20 mm and that of 5 mm. The prediction accuracy is obviously improved. As can be seen from the chart, when the threshold of WHRUC and GRAPES_3 km exceeds 50 mm, the sample of the heavy precipitation forecast is almost zero. BIAS and TS scores are the lowest. While the TS score of the QPF and Blending forecast is close to 0.3, the BIAS value is close to 1. The accuracy of each forecast shows a downward trend with the increase in time. The WHRUC forecast BIAS value gradually increases and the overall predicted value is close to the actual value. The other predicted BIAS value gradually decreases and the overall forecast value shows a trend from high to low. It can be seen from the chart that the effect of the Blending forecast with different thresholds in 1~2 h is better than those of other forecasts. The effect of the 2~3 h forecast is similar to that of QPF, which is better than those of the other forecasts especially in the heavy precipitation forecast.
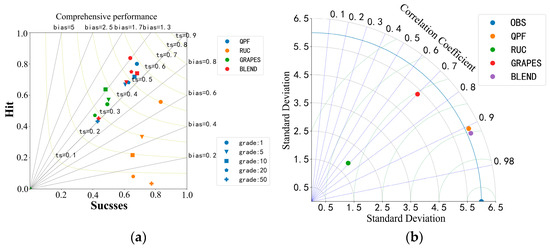
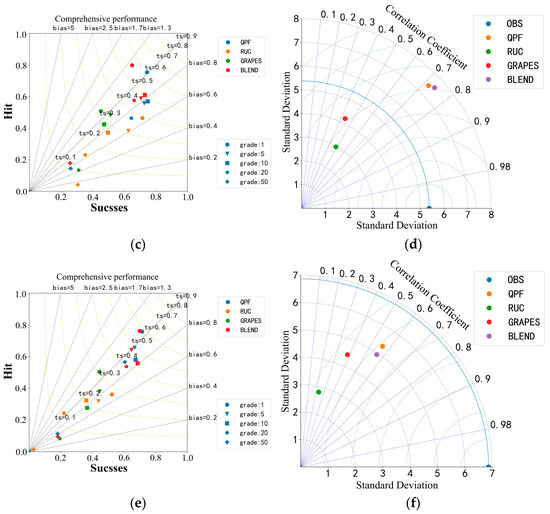
Figure 6.
Comparative Analysis of Comprehensive performance (0~1 h (a), 1~2 h (c), 2~3 h (e)) and Taylor Chart (0~1 h (b), 1~2 h (d), 2~3 h (f)) of different prescription modes.
Figure 6b,d,f show Taylor diagrams. They show the standard deviation, rmse, and correlation coefficient of both observed and predicted data, respectively. The graph is a polar coordinate system where the radius r represents the standard deviation of the observation or forecast data itself. The value of the correlation between prediction and observation can be determined according to the blue ray (dotted line) in the graph and the scale value on the outermost circle arc. The green arc (dashed line) represents the concentric circle around the observation data and its radius represents the rmse of the forecast data. The standard deviation reflects the discrete degree of the precipitation data set and rmse indicates the degree to which the predicted precipitation deviates from the observed value. It can be seen that the standard deviation of the Blending forecast is closest to the actual situation in the forecast of 0~1 h. With the increase in the forecast time, the standard deviation of the Blending forecast increases at first and then decreases. The discretization degree of the precipitation data set is closer to reality than those of other models. The correlation coefficient of the Blending forecast decreases with the increase in prediction time, which is higher than those of other models. The rmse value of the Blending forecast in 0~1 h is smallest compared to those of other models and the deviation in the predicted precipitation from the observed value is smallest. With the increase in failure, the rmse value is basically the same.
The statistical observation and forecast represent the number of samples of various categories. The frequency statistics in Figure 7a–c are drawn in the form of a histogram. The abscissa is the value category of the precipitation sample and the ordinate is the sample proportion. The observed and predicted values are sorted from small to large, respectively, and the two groups of data after sorting are drawn into a frequency matching relation in Figure 7d–f, with the abscissa as the predicted value and the ordinate as the observed value. From the frequency matching mapping diagram, it can be seen that the prediction results of WHRUC and GRAPES_3 km are smaller than the actual observations. The observed values of 0~1 h prediction results are lower than 100 mm. GRAPES_3 km is closer to the reality than WHRUC is. The QPF and Blending forecast 0–1 h are larger than the actual observation, the Blending forecast result is closer to reality, 1~2 h and 2~3 h are smaller than the actual observation, and the QPF prediction effect is closer to reality. Generally, the prediction effect of the QPF and Blending is better than that of WHRUC and GRAPES_3 km.
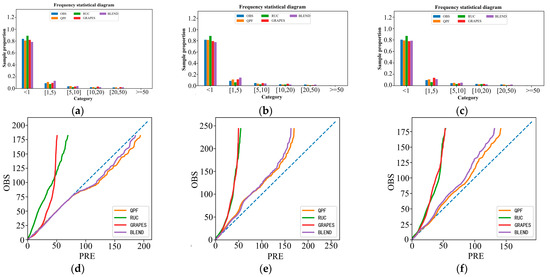
Figure 7.
Comparison of frequency statistics (a–c) and matching mapping (d–f) of different time-effect prediction methods.
5.2.2. Spatial Contrast Test
Figure 8 shows the spatial distribution of errors of the four forecasting methods. The point-to-point errors between the predicted results and the actual results of all grid points are calculated. For a grid point, the samples with different starting times and prediction times are tested together. The size of the error on the site is represented by the color of the site and the absolute value of the error is represented by the area of scattered dots. The larger the area, the greater the error. The site with large errors is highlighted by setting the site size. It can be seen that the precipitation intensity predicted by WHRUC is obviously smaller than those of other methods and the precipitation error is obviously larger.
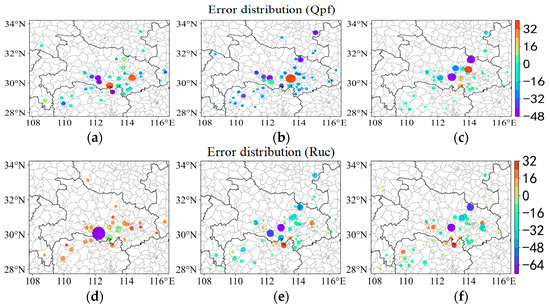
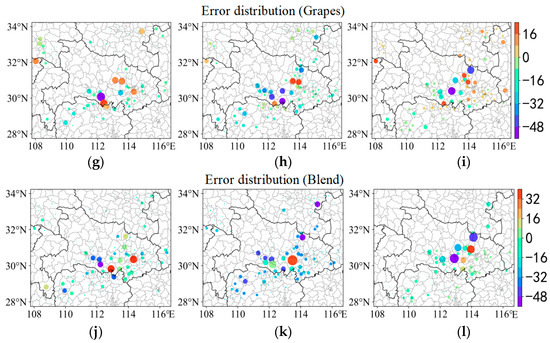
Figure 8.
From 04:00 (Beijing time) on 12 August 2021, the error spatial distribution maps of the 0–3 h radar-extrapolated precipitation forecast (a–c), WHRUC model forecast (d–f), GRAPES_3 km model forecast (g–i), and Blending forecast (j–l).
Grid data are used for target recognition and the recognition steps include the following: (1) select a disk convolution kernel with a radius of smooth = 5, and convolution-smooth the observation field and the prediction field; (2) set threshold to 5 and set the grid value of the smoothed value to less than threshold, 0; (3) identify the targets in the observation and prediction field by the connected domain extraction algorithm; (4) set minsize = 100 and delete targets whose area (number of grid points) in the forecast or observation field is less than minsize; (5) judge the closeness between two targets and take the maximum value of multiple closeness. Merge the corresponding two targets if it is greater than near_rate; (6) repeat step 5 until the closeness between all pairwise targets is less than the termination of the near_rate algorithm.
Figure 9 shows the hourly target recognition results of different prediction methods for 0~3 h. It can be seen that the ellipses identified and matched by MODE can basically reflect the scale and shape of convective storms. It can be used as a basis for model evaluation. Three target objects, which are completely consistent with the actual precipitation area, are identified by the target object method. Table 2 shows the number of targets matched (hit), missed, and empty.
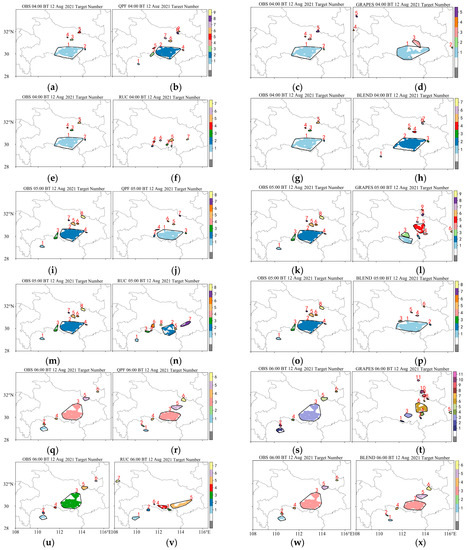
Figure 9.
From 04:00 (BT) on 12 August 2021, the live observation (a,c,e,g,i,k,m,o,q,s,u,w), the 0~3 h radar-extrapolated precipitation forecast (b,j,r), the WHRUC model forecast (f,n,v), the GRAPES_3 km model forecast (d,l,t), and the Blending forecast (h,p,x) target recognition results.

Table 2.
Statistics of target matching results.
Two classification test indexes are calculated for inspection, scoring, and evaluation (Figure 10a) based on the attribute information of the identified target, and the specific prediction of the model is obtained. Figure 10b shows the intensity error (A), distance error (L), and structure error (S) of the SAL test. It can be seen that the prediction ability of GRAPES_3 km for the intensity of the 0~1 h rain areas is better than those of location and shape. The prediction ability of rainfall intensity is larger with the passage of time. The prediction ability of the WHRUC model is worse compared to those of other models and the prediction of precipitation intensity is obviously smaller. The rain area and rainfall intensity forecast of the Blending forecast are close to the actual situation. The rain intensity error also fluctuates due to the influence of the GRAPES_3 km model. On the whole, the Blending forecast integrates the advantages and disadvantages of the model and extrapolation forecast. It can grasp the precipitation area forecast of the system and the forecast ability of rainfall intensity improves.
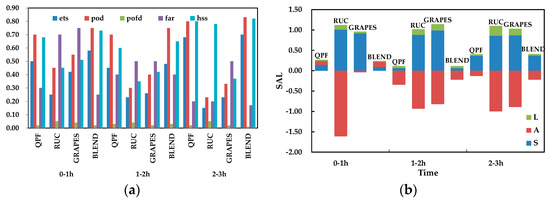
Figure 10.
Target matching evaluation (a) and SAL test of different forecasting methods (b).
According to the scoring results in Table 3, the Blending forecast has the highest score for the actual goal of 1 and the area scores of 0~3 h are 0.88, 0.79, and 0.88, respectively, which are higher than those of the GRAPES_3 km model. The Blending forecast is obviously superior in the area score of identifying targets in terms of area ratio and overlap area ratio. The position score of the two models in 0~3 h is 1 and there is basically no deviation from the predicted center of gravity of target 1. The centroid distance of the 1~2 h Blending forecast is 0.1, which is less than the centroid distance predicted by GRAPES_3 km at the same time. The hourly axial angle differences of the two prediction methods are 1.2, 7.5, and 0, respectively, while those of the Blending forecasts are 3.1, 6.9, and 1.6, respectively, which are all less than 10°. The score of ellipticity is 1, except that predicted by GRAPES_3 km for 2~3 h and the difference between the ellipticity and real object is less than 0.1. The intensity score is calculated based on the precipitation intensity of the 50% quantile and the values are both 1. The precipitation intensity predicted by the two methods is consistent with the actual precipitation grade. From the intensity difference, it can be seen that GRAPES_3 km is small and the Blending forecast is larger. However, the deviation is obviously less than that of GRAPES_3 km. Generally, the score of the Blending forecast is significantly higher than that of GRAPES_3 km for the forecast of goal 1. The target object test method not only gives the evaluation of area, location, shape, and the extreme value of the precipitation center, but also analyzes the forecast performance of heavy precipitation in terms of precipitation area and precipitation intensity, which provides the scientific calculation and test results for forecasters and can mine more valuable information from failed forecast cases.

Table 3.
Comprehensive test of target attributes.
In a plane field, the values of two points in different positions are different and the difference between them usually increases with the increase in distance. The variogram is used to detect whether the above increasing trend in the prediction field is consistent with that in the observation field. Figure 11 shows the variation chart with a grid number of 10 in east–west and south–north trends. It can be seen from the above variation diagram that the larger the number of translation grids, the lower the coincidence of grid field before and after translation. The variation predicted by QPF and BLEND is smaller than that in the south–north direction, which is basically consistent with the actual observation. This is consistent with the fact that the north–south gradient of the temperature field is greater than that of the east–west gradient. WHRUC and GRAPES_3 km predict that the variation in the east–west direction is similar to that in the north–south direction. In addition, it is impossible to directly identify the slight deviation between the forecast and the actual situation when the observation and prediction are close. It is necessary to further test the variation range of the variation with distance.
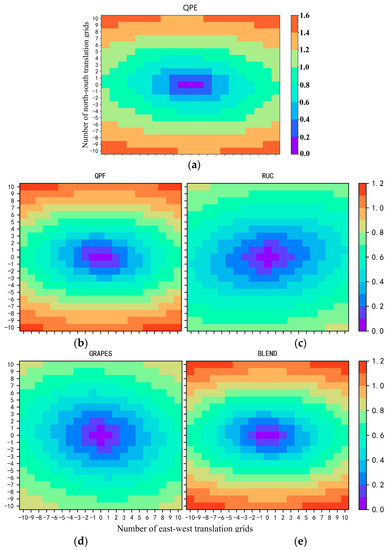
Figure 11.
Comparative analysis of precipitation variation maps predicted by live product (a), radar-extrapolated precipitation forecast (b), WHRUC model forecast (c), GRAPES_3 km model forecast (d), and Blending forecast (e).
Figure 12 shows the amplitude of change before and after the grid translation of different prediction methods. The maximum number of grid points of horizontal and vertical translation is the upper half of the graph, which is the average value (thick real line) of the variation value of elements in a certain interval. Further statistics are made of the standard deviation of the variation value in the same distance interval and the average value is added (minus) to the standard deviation in two dotted lines on the top (bottom) of the graph, which is used to represent the approximate range of the variation value. The lower part is the statistics sample number, which is used to calculate the variation. The result corresponding to a moving mode is recorded as one. In the above example, the maximum distance of the horizontal and vertical translation is set to 100. The translation step is set to 5 and the types of horizontal and vertical movement are both 41. The total movement mode is 41 × 41 = 1681. It can be seen from the figure that the change range of the BLEND forecast grid before and after translation is closer to reality.
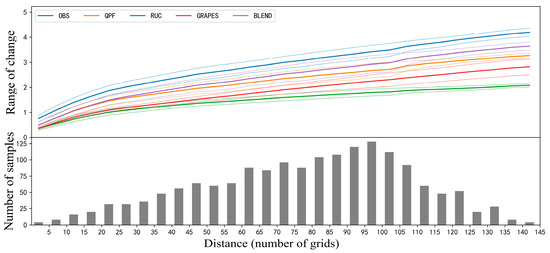
Figure 12.
Comparative analysis of the variation range of precipitation variation with distance predicted by different forecasting methods.
6. Conclusions and Prospects
In this paper, the prediction abilities of the Radar Extrapolation Forecast (REF), WHRUC, GRAPES_3 km, and Blending are compared and analyzed by using traditional point-to-point evaluation and the new spatial test method. The conclusions are as follows:
(1) The comprehensive application of various evaluation methods can evaluate the convective storm forecast more comprehensively. By using the point-to-point scoring method, for the forecasts with different time limits, the shorter the time effect is, the better the prediction effect is. The Blending forecast effect of 1~2 h is obviously better than that of other models, and that of 2~3 h is similar to that of QPF and better than those of the others, especially in the heavy precipitation forecast.
(2) The new spatial test method can evaluate the prediction effect of convective storm features. The precipitation intensity of Blending is larger than those of other models. The error is smallest and the target recognition hit rate is highest. The scores of target area, position, shape, and median intensity of precipitation are better than those of other forecasts.
(3) The variation in the Blending-identified target in the east–west direction is less than that in the north–south direction, which is basically consistent with the actual observation, and the variation range of the forecast grid before and after translation is the closest to the reality.
It can be seen that Blending is obviously better than the single forecast, especially in the heavy precipitation echo forecast, and plays a positive role in the convective forecast. Blending technically has an important operational reference value for the 0~3 h quantitative precipitation forecast. The Blending method combines the advantages and disadvantages of NWP and EP, which can not only grasp the precipitation area forecast of the system but also improve the prediction ability of rainfall intensity. The traditional point-to-point scoring method and the new spatial test method have the same conclusion to the convective storm forecast of the high-resolution model, which has a certain reference value, and the new spatial test method can provide more detailed evaluation information.
Author Contributions
J.W., Z.W. and H.M. contributed to the conception and design of the study. Z.W. and J.Y. organized the database. J.W. and J.Y. performed the statistical analysis. Z.W. and A.L. wrote the first draft of the manuscript. W.Z., H.M. and J.W. wrote sections of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Special Project of Innovation and Development of China Meteorological Administration (National and Provincial Co-ordination, CXFZ2022J018, CXFZ2022-J019), Hubei Provincial Natural Science Foundation (2022CFD129, 2018CFB706), the Open Research Fund of Hubei Key Laboratory of Intelligent Yangtze and Hydroelectric Science, China Yangtze Power Co., Ltd. (242202000907) and the Science and Basic Research Fund of WHIHR (202306, 202314).
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data is unavailable due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Zhang, X.L. Review on Severe Convective Weather Short-Term Forecasting and Nowcasting. Meteorol. Mon. 2010, 36, 33–42. [Google Scholar]
- Wang, J.; Zhang, J.G. Methods and Techniques of Multiscale Composite Rainfall Nowcasting. Meteorol. Sci. Technol. 2008, 36, 524–528. [Google Scholar]
- Han, L.; Wang, H.Q. Application of Optical Flow Method to Nowcasting Convective Weather. Acta Sci. Nat. Univ. Pekin. 2008, 44, 751–755. [Google Scholar]
- Kong, R.; Wang, J.J. Applying Scale Decomposition Method to Verification of Quantitative Precipitation Nowcasts. J. Appl. Meteor. Sci. 2010, 21, 535–544. [Google Scholar]
- Cheng, C.L.; Chen, M.X. Short-term quantitative precipitation forecast experiments based on blending of nowcasting with numerical weather prediction. Acta Meteorol. Sin. 2013, 71, 397–415. [Google Scholar]
- Wang, D.; Wang, G.L. Comparisons Analysis on Short-Term Precipitation between the Radar-Based Extrapolation and the Meso-Scale Numerical Model Weather Prediction. Plateau Meteorol. 2014, 33, 811–822. [Google Scholar]
- Cao, C.Y.; Chen, Y.Z. The optical flow method and its application to nowcasting. Acta Meteorol. Sin. 2015, 73, 471–480. [Google Scholar]
- Guo, H.Y.; Chen, M.X. High resolution nowcasting experiment of severe convections based on deep learning. Acta Meteorol. Sin. 2019, 77, 715–727. [Google Scholar]
- Pan, L.J.; Zhang, H.F. Neighborhood-Based Precipitation Forecasting Capability Analysis of High-Resolution Models. J. Trop. Meteorol. 2015, 31, 632–642. [Google Scholar]
- Brownlee, K.A. A Wiley Publication in Applied Statistics. In Statistical Theory and Methodology in Science and Engineering, 2nd ed.; John Wiley & Sons Wiley: New York, NY, USA, 1965; pp. 26–30. [Google Scholar]
- Doswell, C.A.; Jones, R.D. On summary measures of skill in rare event forecasting based on contingency tables. Weather. Forecast. 1990, 5, 576–585. [Google Scholar] [CrossRef]
- Wang, G.L.; Zhao, C.G. Error Analysis of Radar Echo Extrapolation. Plateau Meteorol. 2013, 32, 874–883. [Google Scholar]
- Long, F.C.; Wang, G.R. The Application Analysis of MODE Method to the Rainfall Forecast Test. Meteorol. Mon. 2011, 37, 1498–1503. [Google Scholar]
- Mao, M.; Dai, J.H. Object-Based Verification and Evaluation for Different Types of Severe Convection Forecasting Products. Meteorol. Mon. 2016, 42, 389–397. [Google Scholar]
- Xue, C.F.; Pan, L.J. Diagnostic Analysis of Precipitation Forecasting from Japan Thin-Grid Model based on Mode. Plateau Meteorol. 2016, 35, 406–418. [Google Scholar]
- Liu, C.H.; Niu, R.Y. Object-Based Preciptitation Verfication Method and Its Application. Meteorol. Mon. 2013, 39, 681–690. [Google Scholar]
- Qu, Q.N.; Sheng, C.Y. Comparison of the multi-model forecasts for severe precipitation based on the object verification. Meteorol. Mon. 2019, 45, 908–919. [Google Scholar]
- Xu, C.L.; Wang, J.J. Evaluation on QPF of GRAPES-Meso4.0 model at convection-permitting resolution. Acta Meteorol. Sin. 2017, 75, 851–876. [Google Scholar]
- Tang, W.Y.; Zeng, Y.G. FSS-based evaluation on convective weather forecasts in North China from high resolution models. J. Appl. Meteorol. Sci. 2018, 29, 513–523. [Google Scholar]
- Zhang, X.W.; Tang, W.Y. Comprehensive evaluations of GRAPES_3 km numerical model in forecasting convective storms using various verification methods. Meteorol. Mon. 2020, 46, 367–380. [Google Scholar]
- Horn, B.K.; Schunck, B.G. Determing optical flow. Artif. Intell. 1981, 17, 185–204. [Google Scholar] [CrossRef]
- Aubert, G.; Deriche, R. Computing optical flow via variational techniques. SIAM J. Appl. Math. 1999, 60, 156–182. [Google Scholar] [CrossRef]
- Wang, Z.B.; Xiao, Y.J. Implementation of Improved Variational Optical Flow Parallel Algorithm. Comput. Appl. Softw. 2019, 36, 105–110. [Google Scholar]
- Lai, A.W.; Ma, H.D. A Squall Line Case Study of Assimilating the Radar Data, Retrieval of Water Vapor and In-Cloud Potential Temperature from Reflectivity in a 3DVAR Framework. Meteorol. Mon. 2021, 47, 932–952. [Google Scholar]
- Zawadzki, I.; Torlaschi, E.; Sauvageau, R. The Relationship between Mesoscale Thermodynamic Variables and Convective Precipitation. J. Atmos. Sci. 1981, 38, 1535–1540. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).