Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges
Abstract
1. Introduction
- (1)
- (2)
- Insufficient relevance. Although some recent related reviews contain some relatively advanced methods [19,20,21], they do not focus directly on the field of target detection, but broadly on hyperspectral image processing, which is not relevant enough. In addition, most of these reviews only list the advanced methods, and the summary and comparison of these methods are not satisfactory.
- (3)
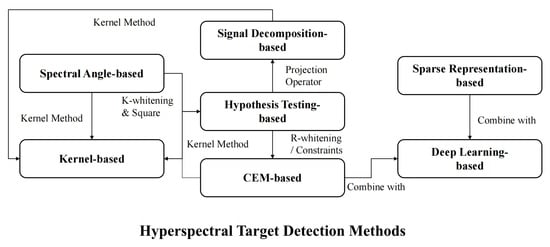
- Neglect of connections between methods. Most of the existing reviews only focus on the differences between the various methods and introduce each type of method independently, neglecting to explore the connections between different types of methods.
2. Target Detection Methods
2.1. Overview
2.2. Hypothesis Testing-Based Methods
2.3. Spectral Angle-Based Methods
2.4. Signal Decomposition-Based Methods
2.5. Constrained Energy Minimization (CEM)-Based Methods
2.6. Kernel-Based Methods
2.7. Sparse Representation-Based Methods
2.8. Deep Learning-Based Methods
2.8.1. End-to-End Detection
2.8.2. Detection by Reconstruction
3. Summary and Comparison
4. Datasets and Metrics
4.1. Datasets
4.2. Evaluation Metrics
4.2.1. Receiver Operating Characteristic (ROC) Curve and Area under ROC Curve (AUC)
4.2.2. 3D-ROC
5. Discussion
5.1. Experiments
5.1.1. Acquisition of the Target Spectrum
5.1.2. Experiment Performances
5.2. Future Challenges
5.2.1. Spectral Variability
5.2.2. Acquisition of the Ground Truth
5.2.3. Causal Real-Time Detection
5.2.4. Challenges in Deep Learning-Based Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thenkabail, P. Remote Sensing Handbook-Three Volume Set; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- DiPietro, R.S.; Truslow, E.; Manolakis, D.G.; Golowich, S.E.; Lockwood, R.B. False-alarm characterization in hyperspectral gas-detection applications. Proc. SPIE 2012, 8515, 138–148. [Google Scholar]
- Farrand, W.H.; Harsanyi, J.C. Mapping the distribution of mine tailings in the Coeur d’Alene River Valley, Idaho, through the use of a constrained energy minimization technique. Remote Sens. Environ. 1997, 59, 64–76. [Google Scholar] [CrossRef]
- Tiwari, K.; Arora, M.K.; Singh, D. An assessment of independent component analysis for detection of military targets from hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 730–740. [Google Scholar] [CrossRef]
- Winter, E.M.; Miller, M.A.; Simi, C.G.; Hill, A.B.; Williams, T.J.; Hampton, D.; Wood, M.; Zadnick, J.; Sviland, M.D. Mine detection experiments using hyperspectral sensors. In Proceedings of the Detection and Remediation Technologies for Mines and Minelike Targets IX, Orlando, FL, USA, 12–16 April 2004; Volume 5415, pp. 1035–1041. [Google Scholar]
- Makki, I.; Younes, R.; Francis, C.; Bianchi, T.; Zucchetti, M. A survey of landmine detection using hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2017, 124, 40–53. [Google Scholar] [CrossRef]
- Lin, C.; Chen, S.Y.; Chen, C.C.; Tai, C.H. Detecting newly grown tree leaves from unmanned-aerial-vehicle images using hyperspectral target detection techniques. ISPRS J. Photogramm. Remote Sens. 2018, 142, 174–189. [Google Scholar] [CrossRef]
- De Almeida, D.R.A.; Broadbent, E.N.; Ferreira, M.P.; Meli, P.; Zambrano, A.M.A.; Gorgens, E.B.; Resende, A.F.; de Almeida, C.T.; Do Amaral, C.H.; Dalla Corte, A.P.; et al. Monitoring restored tropical forest diversity and structure through UAV-borne hyperspectral and lidar fusion. Remote Sens. Environ. 2021, 264, 112582. [Google Scholar] [CrossRef]
- Rahimzadegan, M.; Sadeghi, B.; Masoumi, M.; Taghizadeh Ghalehjoghi, S. Application of target detection algorithms to identification of iron oxides using ASTER images: A case study in the North of Semnan province, Iran. Arab. J. Geosci. 2015, 8, 7321–7331. [Google Scholar] [CrossRef]
- Hoang, N.T.; Koike, K. Comparison of hyperspectral transformation accuracies of multispectral Landsat TM, ETM+, OLI and EO-1 ALI images for detecting minerals in a geothermal prospect area. ISPRS J. Photogramm. Remote Sens. 2018, 137, 15–28. [Google Scholar] [CrossRef]
- Eismann, M.T.; Stocker, A.D.; Nasrabadi, N.M. Automated hyperspectral cueing for civilian search and rescue. Proc. IEEE 2009, 97, 1031–1055. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Zhang, C.; Lee, D.; Margenot, A.J.; Ge, Y.; Peng, J.; Zhou, W.; Zhou, Q.; Huang, Y. Using soil library hyperspectral reflectance and machine learning to predict soil organic carbon: Assessing potential of airborne and spaceborne optical soil sensing. Remote Sens. Environ. 2022, 271, 112914. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process. Mag. 2013, 31, 34–44. [Google Scholar] [CrossRef]
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T.; Brueggeman, M. Detection algorithms in hyperspectral imaging systems: An overview of practical algorithms. IEEE Signal Process. Mag. 2013, 31, 24–33. [Google Scholar] [CrossRef]
- Poojary, N.; D’Souza, H.; Puttaswamy, M.; Kumar, G.H. Automatic target detection in hyperspectral image processing: A review of algorithms. In Proceedings of the 2015 IEEE 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17 August 2015; pp. 1991–1996. [Google Scholar]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral image processing for automatic target detection applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Amigo, J.M.; Babamoradi, H.; Elcoroaristizabal, S. Hyperspectral image analysis. A tutorial. Anal. Chim. Acta 2015, 896, 34–51. [Google Scholar] [CrossRef]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine learning based hyperspectral image analysis: A survey. arXiv 2018, arXiv:1802.08701. [Google Scholar]
- Sneha; Kaul, A. Hyperspectral imaging and target detection algorithms: A review. Multimed. Tools Appl. 2022, 81, 44141–44206. [Google Scholar] [CrossRef]
- Manolakis, D.; Lockwood, R.; Cooley, T.; Jacobson, J. Is there a best hyperspectral detection algorithm? In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XV; SPIE: Orlando, FL, USA, 2009; Volume 7334, pp. 13–28. [Google Scholar]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Chang, C.I. Hyperspectral Target Detection: Hypothesis Testing, Signal-to-Noise Ratio, and Spectral Angle Theories. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–23. [Google Scholar] [CrossRef]
- Kraut, S.; Scharf, L.L. The CFAR adaptive subspace detector is a scale-invariant GLRT. IEEE Trans. Signal Process. 1999, 47, 2538–2541. [Google Scholar] [CrossRef]
- Wang, T.; Du, B.; Zhang, L. An automatic robust iteratively reweighted unstructured detector for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2367–2382. [Google Scholar] [CrossRef]
- Zeng, J.; Wang, Q. Sparse Tensor Model-Based Spectral Angle Detector for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Kraut, S.; Scharf, L.L.; McWhorter, L.T. Adaptive subspace detectors. IEEE Trans. Signal Process. 2001, 49, 1–16. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Du, Q.; Chang, C.I. A signal-decomposed and interference-annihilated approach to hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2004, 42, 892–906. [Google Scholar]
- Chang, C.I.; Chen, J. Orthogonal subspace projection using data sphering and low-rank and sparse matrix decomposition for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8704–8722. [Google Scholar] [CrossRef]
- Thai, B.; Healey, G. Invariant subpixel material detection in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 599–608. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Detection and Classification of Subpixel Spectral Signatures in Hyperspectral Image Sequences; University of Maryland: Baltimore County, MD, USA, 1993. [Google Scholar]
- Chang, C.I.; Ren, H. Linearly constrained minimum variance beamforming approach to target detection and classification for hyperspectral imagery (Cat. No. 99CH36293). In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium, IGARSS’99, Hamburg, Germany, 28 June 1999; Volume 2, pp. 1241–1243. [Google Scholar]
- Zhang, J.; Zhao, R.; Shi, Z.; Zhang, N.; Zhu, X. Bayesian Constrained Energy Minimization for Hyperspectral Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8359–8372. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, S. Robust high-order matched filter for hyperspectral target detection. Electron. Lett. 2010, 46, 1065–1066. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, S.; Jiang, Z. Hyperspectral target detection using regularized high-order matched filter. Opt. Eng. 2011, 50, 057201. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, S.; Jiang, Z. Target detection using difference measured function based matched filter for hyperspectral imagery. Opt.-Int. J. Light Electron Opt. 2013, 124, 3017–3021. [Google Scholar] [CrossRef]
- Yang, S.; Shi, Z.; Tang, W. Robust hyperspectral image target detection using an inequality constraint. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3389–3404. [Google Scholar] [CrossRef]
- Zou, Z.; Shi, Z.; Wu, J.; Wang, H. Quadratic constrained energy minimization for hyperspectral target detection. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4979–4982. [Google Scholar]
- Yang, X.; Zhao, M.; Shi, S.; Chen, J. Deep constrained energy minimization for hyperspectral target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8049–8063. [Google Scholar] [CrossRef]
- Zou, Z.; Shi, Z. Hierarchical suppression method for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 330–342. [Google Scholar] [CrossRef]
- Zhao, R.; Shi, Z.; Zou, Z.; Zhang, Z. Ensemble-based cascaded constrained energy minimization for hyperspectral target detection. Remote Sens. 2019, 11, 1310. [Google Scholar] [CrossRef]
- Ren, H.; Chang, C.I. A target-constrained interference-minimized filter for subpixel target detection in hyperspectral imagery (Cat. No. 00CH37120). In Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Proceedings of the IGARSS 2000, IEEE 2000 International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 4, pp. 1545–1547. [Google Scholar]
- Gao, L.; Yang, B.; Du, Q.; Zhang, B. Adjusted spectral matched filter for target detection in hyperspectral imagery. Remote Sens. 2015, 7, 6611–6634. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, X.; Li, Y.; Wang, K.; Du, Q. Background learning based on target suppression constraint for hyperspectral target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5887–5897. [Google Scholar] [CrossRef]
- Shi, Y.; Li, J.; Zheng, Y.; Xi, B.; Li, Y. Hyperspectral target detection with RoI feature transformation and multiscale spectral attention. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5071–5084. [Google Scholar] [CrossRef]
- Kwon, H.; Nasrabadi, N.M. Kernel spectral matched filter for hyperspectral imagery. Int. J. Comput. Vis. 2007, 71, 127–141. [Google Scholar] [CrossRef]
- Kwon, H.; Nasrabadi, N.M. Kernel adaptive subspace detector for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2006, 3, 271–275. [Google Scholar] [CrossRef]
- Liu, X.; Yang, C. A kernel spectral angle mapper algorithm for remote sensing image classification. In Proceedings of the 2013 6th International Congress on Image and Signal Processing (CISP), Hangzhou, China, 16–18 December 2013; Volume 2, pp. 814–818. [Google Scholar]
- Kwon, H.; Nasrabadi, N.M. Kernel orthogonal subspace projection for hyperspectral signal classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2952–2962. [Google Scholar] [CrossRef]
- Jiao, X.; Chang, C.I. Kernel-based constrained energy minimization (K-CEM). In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XIV; SPIE: Bellingham, WA, USA, 2008; Volume 6966, pp. 523–533. [Google Scholar]
- Ma, K.Y.; Chang, C.I. Kernel-based constrained energy minimization for hyperspectral mixed pixel classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–23. [Google Scholar] [CrossRef]
- Wang, T.; Du, B.; Zhang, L. A kernel-based target-constrained interference-minimized filter for hyperspectral sub-pixel target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 626–637. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Kernel principal component analysis. In Proceedings of the International Conference on Artificial Neural Networks, Lausanne, Switzerland, 8–10 October; Springer: Berlin/Heidelberg, Germany, 1997; pp. 583–588. [Google Scholar]
- Kumar, S.; Mohri, M.; Talwalkar, A. On sampling-based approximate spectral decomposition. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 553–560. [Google Scholar]
- Williams, C.; Seeger, M. Using the Nyström method to speed up kernel machines. Adv. Neural Inf. Process. Syst. 2000, 13, 1–7. [Google Scholar]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse representation for target detection in hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Tropp, J.A.; Wright, S.J. Computational methods for sparse solution of linear inverse problems. Proc. IEEE 2010, 98, 948–958. [Google Scholar] [CrossRef]
- Zhu, D.; Du, B.; Zhang, L. Target dictionary construction-based sparse representation hyperspectral target detection methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1254–1264. [Google Scholar] [CrossRef]
- Wright, J.; Ma, Y.; Mairal, J.; Sapiro, G.; Huang, T.S.; Yan, S. Sparse representation for computer vision and pattern recognition. Proc. IEEE 2010, 98, 1031–1044. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Huang, Z.; Shi, Z.; Yang, S. Nonlocal similarity regularized sparsity model for hyperspectral target detection. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1532–1536. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, Y.; Zhang, L. Spatially adaptive sparse representation for target detection in hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1923–1927. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted l1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, Z.; Qin, Z. Convex relaxation based sparse algorithm for hyperspectral target detection. Optik 2013, 124, 6594–6598. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. A sparse representation-based binary hypothesis model for target detection in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1346–1354. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Wu, H.; Wang, J.; Sun, K.; Lin, A.; Wang, Q. A double dictionary-based nonlinear representation model for hyperspectral subpixel target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Guo, T.; Luo, F.; Fang, L.; Zhang, B. Meta-pixel-driven embeddable discriminative target and background dictionary pair learning for hyperspectral target detection. Remote Sens. 2022, 14, 481. [Google Scholar] [CrossRef]
- Yang, S.; Shi, Z. SparseCEM and SparseACE for hyperspectral image target detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2135–2139. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, B. Combined sparse and collaborative representation for hyperspectral target detection. Pattern Recognit. 2015, 48, 3904–3916. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, M.; Fan, G.; Liu, W.; Ma, Y.; Mei, X. Dictionary Learning-Cooperated Matrix Decomposition for Hyperspectral Target Detection. Remote Sens. 2022, 14, 4369. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Freitas, S.; Silva, H.; Almeida, J.M.; Silva, E. Convolutional neural network target detection in hyperspectral imaging for maritime surveillance. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419842991. [Google Scholar] [CrossRef]
- Sharma, M.; Dhanaraj, M.; Karnam, S.; Chachlakis, D.G.; Ptucha, R.; Markopoulos, P.P.; Saber, E. YOLOrs: Object detection in multimodal remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1497–1508. [Google Scholar] [CrossRef]
- Du, J.; Li, Z. A hyperspectral target detection framework with subtraction pixel pair features. IEEE Access 2018, 6, 45562–45577. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Qin, H.; Xie, W.; Li, Y.; Du, Q. HTD-VIT: Spectral-Spatial Joint Hyperspectral Target Detection with Vision Transformer. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 1967–1970. [Google Scholar]
- Li, W.; Wu, G.; Du, Q. Transferred deep learning for hyperspectral target detection. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5177–5180. [Google Scholar]
- Zhu, D.; Du, B.; Zhang, L. Two-stream convolutional networks for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6907–6921. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, S.; Li, W.; Du, Q.; Ran, Q.; Tao, R. HTD-net: A deep convolutional neural network for target detection in hyperspectral imagery. Remote Sens. 2020, 12, 1489. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, Y.; Yu, X. Hyperspectral Target Detection with an Auxiliary Generative Adversarial Network. Remote Sens. 2021, 13, 4454. [Google Scholar] [CrossRef]
- Alayrac, J.B.; Donahue, J.; Luc, P.; Miech, A.; Barr, I.; Hasson, Y.; Lenc, K.; Mensch, A.; Millican, K.; Reynolds, M.; et al. Flamingo: A visual language model for few-shot learning. Adv. Neural Inf. Process. Syst. 2022, 35, 23716–23736. [Google Scholar]
- Parnami, A.; Lee, M. Learning from few examples: A summary of approaches to few-shot learning. arXiv 2022, arXiv:2203.04291. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 6–11 July 2015; Volume 2. [Google Scholar]
- Dou, Z.; Gao, K.; Zhang, X.; Wang, J.; Wang, H. Deep learning-based hyperspectral target detection without extra labeled data. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1759–1762. [Google Scholar]
- Zhang, X.; Gao, K.; Wang, J.; Hu, Z.; Wang, H.; Wang, P. Siamese Network Ensembles for Hyperspectral Target Detection with Pseudo Data Generation. Remote Sens. 2022, 14, 1260. [Google Scholar] [CrossRef]
- Rao, W.; Gao, L.; Qu, Y.; Sun, X.; Zhang, B.; Chanussot, J. Siamese Transformer Network for Hyperspectral Image Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Wang, F.; Song, M.; Yu, C. Meta-Learning Based Hyperspectral Target Detection Using Siamese Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Xue, B.; Yu, C.; Wang, Y.; Song, M.; Li, S.; Wang, L.; Chen, H.M.; Chang, C.I. A subpixel target detection approach to hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5093–5114. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Shi, Y.; Lei, J.; Yin, Y.; Cao, K.; Li, Y.; Chang, C.I. Discriminative feature learning with distance constrained stacked sparse autoencoder for hyperspectral target detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1462–1466. [Google Scholar] [CrossRef]
- Shi, Y.; Li, J.; Yin, Y.; Xi, B.; Li, Y. Hyperspectral target detection with macro-micro feature extracted by 3-D residual autoencoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4907–4919. [Google Scholar] [CrossRef]
- Xie, W.; Yang, J.; Lei, J.; Li, Y.; Du, Q.; He, G. SRUN: Spectral regularized unsupervised networks for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1463–1474. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, J.; Lei, J.; Li, Y.; Jia, X. Self-spectral learning with GAN based spectral–spatial target detection for hyperspectral image. Neural Netw. 2021, 142, 375–387. [Google Scholar] [CrossRef]
- Xie, W.; Lei, J.; Yang, J.; Li, Y.; Du, Q.; Li, Z. Deep latent spectral representation learning-based hyperspectral band selection for target detection. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2015–2026. [Google Scholar] [CrossRef]
- Kaya, M.; Bilge, H.Ş. Deep metric learning: A survey. Symmetry 2019, 11, 1066. [Google Scholar] [CrossRef]
- Liao, S.; Shao, L. Graph sampling based deep metric learning for generalizable person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 7359–7368. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9729–9738. [Google Scholar]
- Zhang, H.; Li, F.; Liu, S.; Zhang, L.; Su, H.; Zhu, J.; Ni, L.M.; Shum, H.Y. Dino: Detr with improved denoising anchor boxes for end-to-end object detection. arXiv 2022, arXiv:2203.03605. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning, PMLR, Online, 13–15 April 2021; pp. 8748–8763. [Google Scholar]
- Zhu, D.; Du, B.; Dong, Y.; Zhang, L. Target Detection with Spatial-Spectral Adaptive Sample Generation and Deep Metric Learning for Hyperspectral Imagery. IEEE Trans. Multimed. 2022. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Zhao, E.; Song, M. Self-supervised Spectral-level Contrastive Learning for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5510515. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J.A. Hyperspectral anomaly detection with attribute and edge-preserving filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Snyder, D.; Kerekes, J.; Fairweather, I.; Crabtree, R.; Shive, J.; Hager, S. Development of a web-based application to evaluate target finding algorithms. In Proceedings of the IGARSS 2008–2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 8–11 July 2008; Volume 2, pp. 2–915. [Google Scholar]
- Chang, C.I. An effective evaluation tool for hyperspectral target detection: 3D receiver operating characteristic curve analysis. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5131–5153. [Google Scholar] [CrossRef]
- Jiao, C.; Chen, C.; McGarvey, R.G.; Bohlman, S.; Jiao, L.; Zare, A. Multiple instance hybrid estimator for hyperspectral target characterization and sub-pixel target detection. ISPRS J. Photogramm. Remote Sens. 2018, 146, 235–250. [Google Scholar] [CrossRef]
- Manolakis, D.; Siracusa, C.; Shaw, G. Hyperspectral subpixel target detection using the linear mixing model. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1392–1409. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M.; Richard, C.; Chanussot, J.; Drumetz, L.; Tourneret, J.Y.; Zare, A.; Jutten, C. Spectral variability in hyperspectral data unmixing: A comprehensive review. IEEE Geosci. Remote Sens. Mag. 2021, 9, 223–270. [Google Scholar] [CrossRef]
- Bucher, M.; Vu, T.H.; Cord, M.; Pérez, P. Zero-shot semantic segmentation. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. arXiv 2023, arXiv:2304.02643. [Google Scholar]
- Fowler, J.E. Compressive pushbroom and whiskbroom sensing for hyperspectral remote-sensing imaging. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 684–688. [Google Scholar]
- Chen, S.Y.; Wang, Y.; Wu, C.C.; Liu, C.; Chang, C.I. Real-time causal processing of anomaly detection for hyperspectral imagery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1511–1534. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, L.; Wu, T.; Zhang, H. Fast real-time target detection via target-oriented band selection. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5868–5871. [Google Scholar]
- Ding, M.; Yang, Z.; Hong, W.; Zheng, W.; Zhou, C.; Yin, D.; Lin, J.; Zou, X.; Shao, Z.; Yang, H.; et al. Cogview: Mastering text-to-image generation via transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 19822–19835. [Google Scholar]
- Yu, J.; Xu, Y.; Koh, J.Y.; Luong, T.; Baid, G.; Wang, Z.; Vasudevan, V.; Ku, A.; Yang, Y.; Ayan, B.K.; et al. Scaling autoregressive models for content-rich text-to-image generation. arXiv 2022, arXiv:2206.10789. [Google Scholar]
- Chang, H.; Zhang, H.; Barber, J.; Maschinot, A.; Lezama, J.; Jiang, L.; Yang, M.H.; Murphy, K.; Freeman, W.T.; Rubinstein, M.; et al. Muse: Text-To-Image Generation via Masked Generative Transformers. arXiv 2023, arXiv:2301.00704. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. Training language models to follow instructions with human feedback. Adv. Neural Inf. Process. Syst. 2022, 35, 27730–27744. [Google Scholar]






| Methodology | Basic Idea | Example Algorithms | Input/Required | Limitations |
|---|---|---|---|---|
| Hypothesis testing | Calculating the likeli- hood ratio under the two hypotheses | MF [22] | target , HSI | Limited performance on non-Gaussian data |
| ACE [25] | target , HSI | |||
| ASD [28] | target , HSI | |||
| Spectral angle | Calculating the cosine similarity between two spectral vectors | SAM | target , HSI | Limited robustness to spectral variations |
|
Signal decomposition | Decomposing the signal into subspaces according to certain rules | OSP [29] | target , undesired target matrix , HSI | Too much input information required |
| SDIN [30] | target , interference subspace , HSI | |||
| SBN [32] | target , background matrix , HSI | |||
| CEM-based | Designing the FIR filter that minimizes the output energy and allows only the target to pass | CEM [33] | target , HSI | Limited performance on non-Gaussian data |
| LCMV [34] | target matrix , target constraint vector , HSI | |||
| TCIMF [44] | target matrix , undesired target matrix , HSI | |||
| RHMF [36] | target , HSI , tolerance , high-order differentiable function | |||
| hCEM [42] | target , HSI , tolerance | |||
| ECEM [43] | target , HSI , window number n, detection layer number k, CEM number per layer m | |||
| Kernel-based | Mapping the data to a high-dimensional kernel space | KSAM [50] | target , HSI , kernel function | High computation and memory cost |
| KMF [48] | target , HSI , kernel function | |||
| KOSP [51] | target , undesired target matrix , HSI , kernel function | |||
| KCEM [52] | target , HSI , kernel function | |||
| Sparse representation | Utilizing a linear combination of elements in the dictionary to represent the HSI | STD [58] | dictionary , HSI | Potential instability due to different dictionaries |
| CSCR [71] | dictionary , HSI , regularization parameter ,, window size , | |||
| SASTD [64] | dictionary , HSI , sparsity level l, window sizes , , | |||
| SRBBH [67] | dictionary , HSI , sparsity level l, dual-window sizes , | |||
| Deep learning | Learning the intrinsic patterns and representation of sample data using neural networks etc. | TSCNTD [83] | target , HSI | Low data availability and limited model transferability |
| HTD-Net [84] | target samples , HSI | |||
| DCSSAED [96] | target samples , HSI , adjustable parameter , | |||
| SRUN [98] | target , HSI , parameters depth d, number of hidden nodes h, regularization parameter , threshold | |||
| BLTSC [46] | target , HSI , normalized initial detection result , parameter | |||
| 3DMMRAED [97] | target , HSI , number of iteration i |
| Dataset | Sensor | Spatial Size (Pixels) | Spectral Bands | Size of the Part Used for Target Detection (Pixels) | Number of Target Pixels |
|---|---|---|---|---|---|
| Cuprite [98] | AVIRIS | 512 × 614 | 224 | 250 × 191 | 39 |
| San Diego [99] | AVIRIS | 400 × 400 | 224 | 200 × 200 | 134 |
| Airport-Beach-Urban [108] | AVIRIS and ROSIS-03 | 100 × 100 | 224 | 100 × 100 | / |
| HYDICE Urban [96] | HYDICE | 307 × 307 | 210 | 80 × 100 | 21 |
| HYDICE Forest [84] | HYDICE | 64 × 64 | 210 | 100 × 100 | 19 |
| Cooke City [109] | HyMap | 280 × 800 | 126 | 100 × 300 | 118 |
| Methodology | Algorithm | |||||
|---|---|---|---|---|---|---|
| Hypothesis testing | MF | 0.8969 | 0.4031 | 0.2190 | 1.8405 | 1.0810 |
| ACE | 0.8955 | 0.1910 | 0.0051 | 37.2919 | 1.0814 | |
| Spectral angle | SAM | 0.7633 | 0.1969 | 0.0900 | 2.1869 | 0.8701 |
| CEM-based | CEM | 0.8937 | 0.3968 | 0.2103 | 1.8872 | 1.0803 |
| hCEM | 0.9916 | 0.5128 | 0.0155 | 33.1421 | 1.4890 | |
| ECEM | 0.9922 | 0.5243 | 0.0150 | 34.9697 | 1.5015 | |
| Sparse representation model | CSCR | 0.9842 | 0.6060 | 0.4776 | 1.2688 | 1.1126 |
| Deep learning | BLTSC | 0.8999 | 0.1428 | 0.0018 | 80.7670 | 1.0409 |
| Methodology | Algorithm | |||||
|---|---|---|---|---|---|---|
| Hypothesis testing | MF | 0.9743 | 0.5050 | 0.2585 | 1.9534 | 1.2208 |
| ACE | 0.9489 | 0.1825 | 0.0096 | 19.0289 | 1.1218 | |
| Spectral angle | SAM | 0.9119 | 0.4146 | 0.1743 | 2.3779 | 1.1522 |
| CEM-based | CEM | 0.9759 | 0.5097 | 0.2573 | 1.9808 | 1.2283 |
| hCEM | 0.9918 | 0.3984 | 0.0197 | 20.2127 | 1.3705 | |
| ECEM | 0.9792 | 0.6534 | 0.0805 | 8.1122 | 1.5520 | |
| Sparse representation model | CSCR | 0.9709 | 0.8997 | 0.7931 | 1.1344 | 1.0775 |
| Deep learning | BLTSC | 0.9620 | 0.2658 | 0.0083 | 31.8302 | 1.2194 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Liu, L.; Zou, Z.; Shi, Z. Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges. Remote Sens. 2023, 15, 3223. https://doi.org/10.3390/rs15133223
Chen B, Liu L, Zou Z, Shi Z. Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges. Remote Sensing. 2023; 15(13):3223. https://doi.org/10.3390/rs15133223
Chicago/Turabian StyleChen, Bowen, Liqin Liu, Zhengxia Zou, and Zhenwei Shi. 2023. "Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges" Remote Sensing 15, no. 13: 3223. https://doi.org/10.3390/rs15133223
APA StyleChen, B., Liu, L., Zou, Z., & Shi, Z. (2023). Target Detection in Hyperspectral Remote Sensing Image: Current Status and Challenges. Remote Sensing, 15(13), 3223. https://doi.org/10.3390/rs15133223