Disturbing Variability in Microwave Emission from a Non-Gaussian Distributed and Correlated Multiscale Rough Surface
Abstract
:1. Introduction
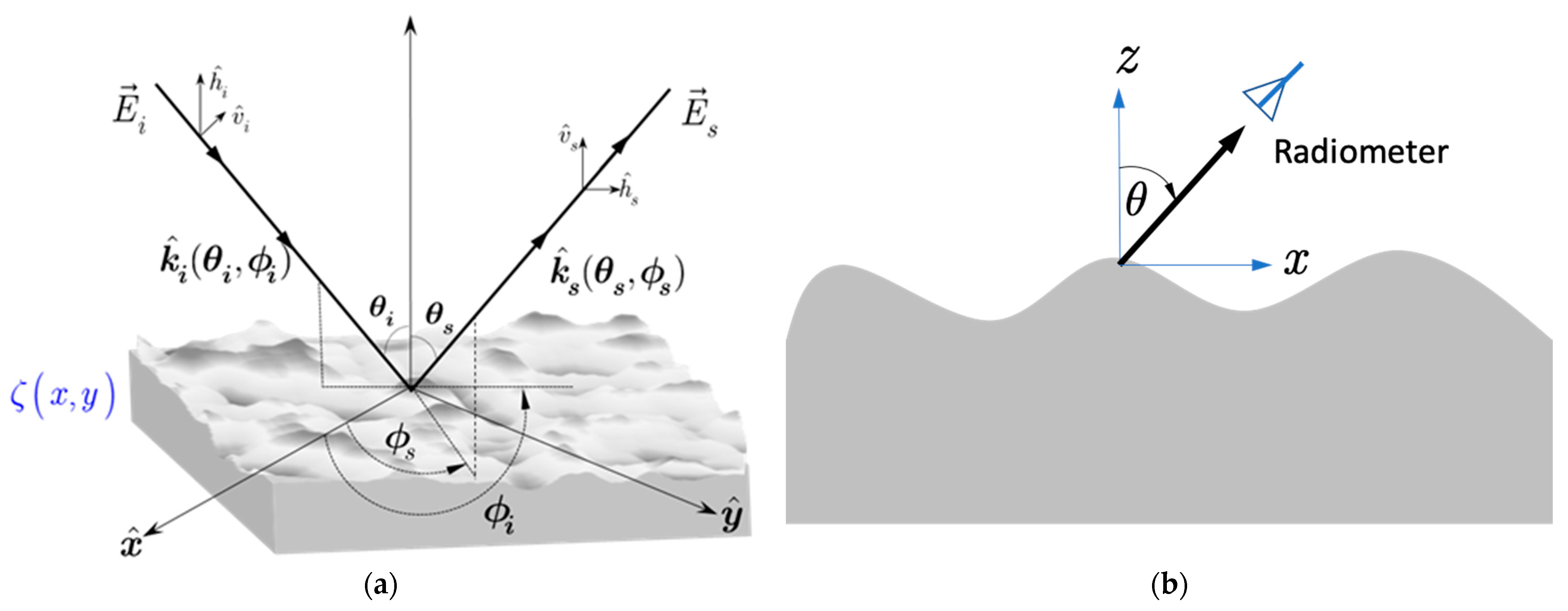
2. Scattering and Emission from Non-Gaussian Distributed Rough Surface
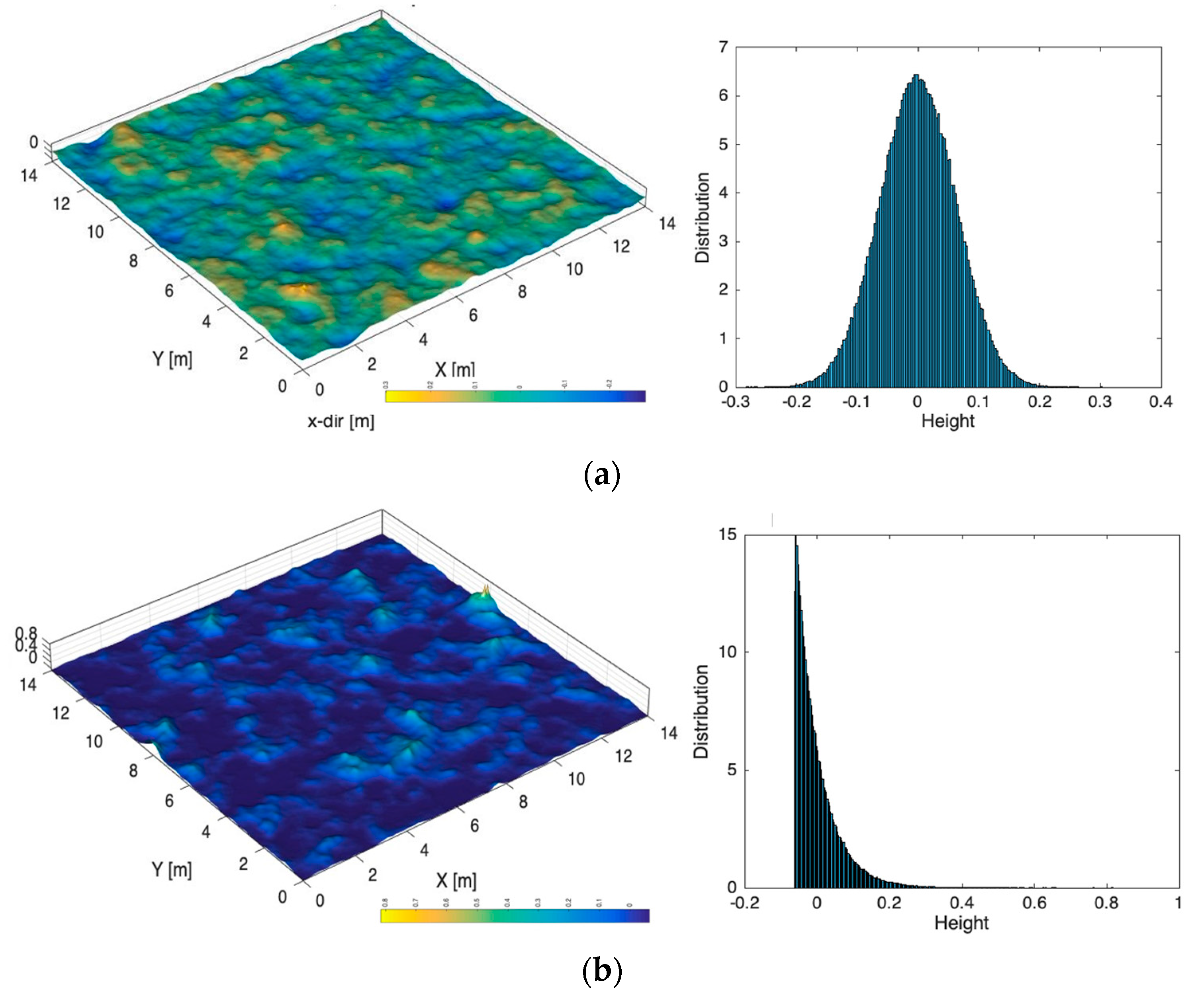
2.1. Height Probability Density (HPD)
2.2. Power Spectrum Density (PSD)
2.3. Bistatic Scattering Coefficients and Emissivity
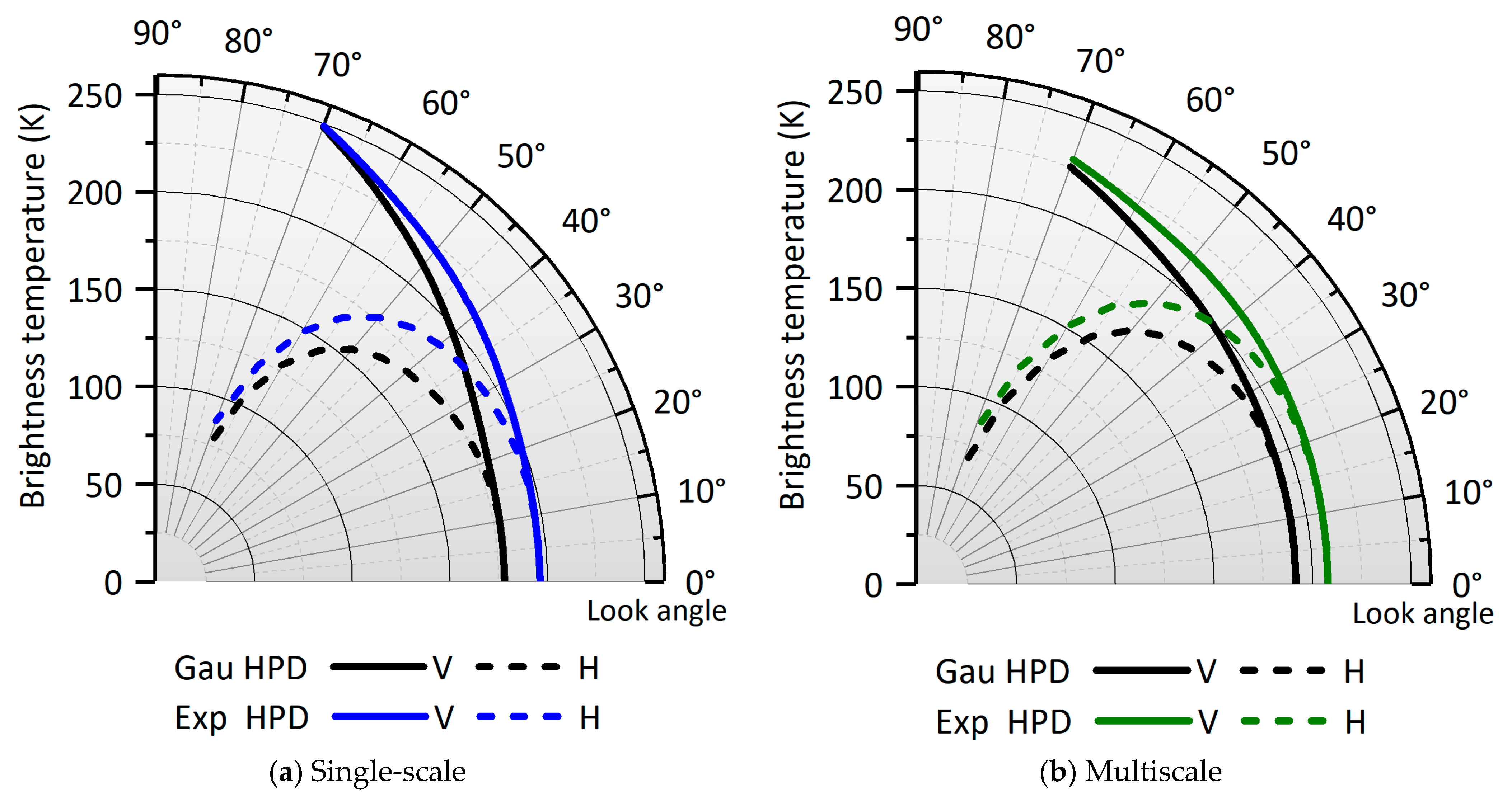
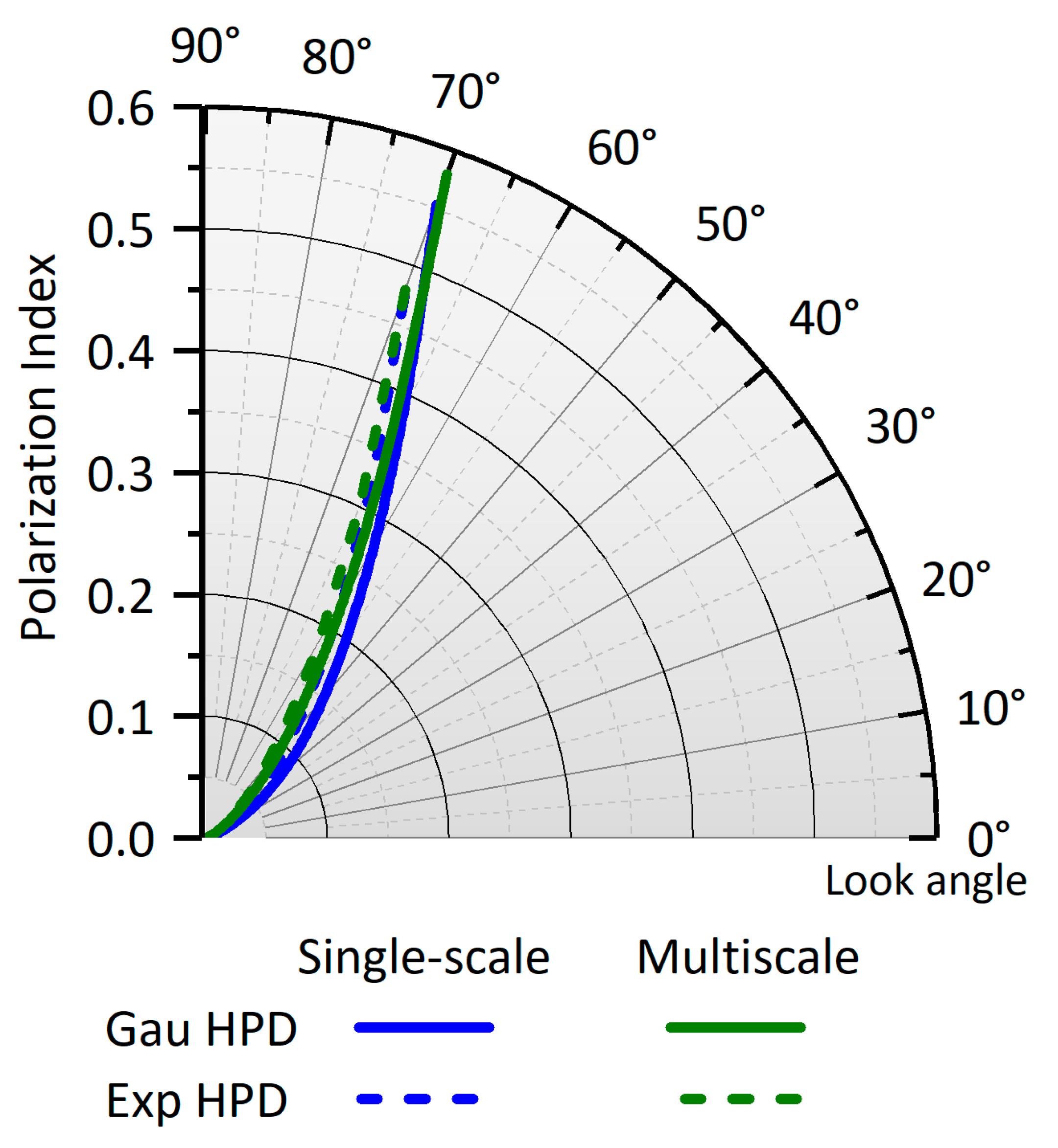
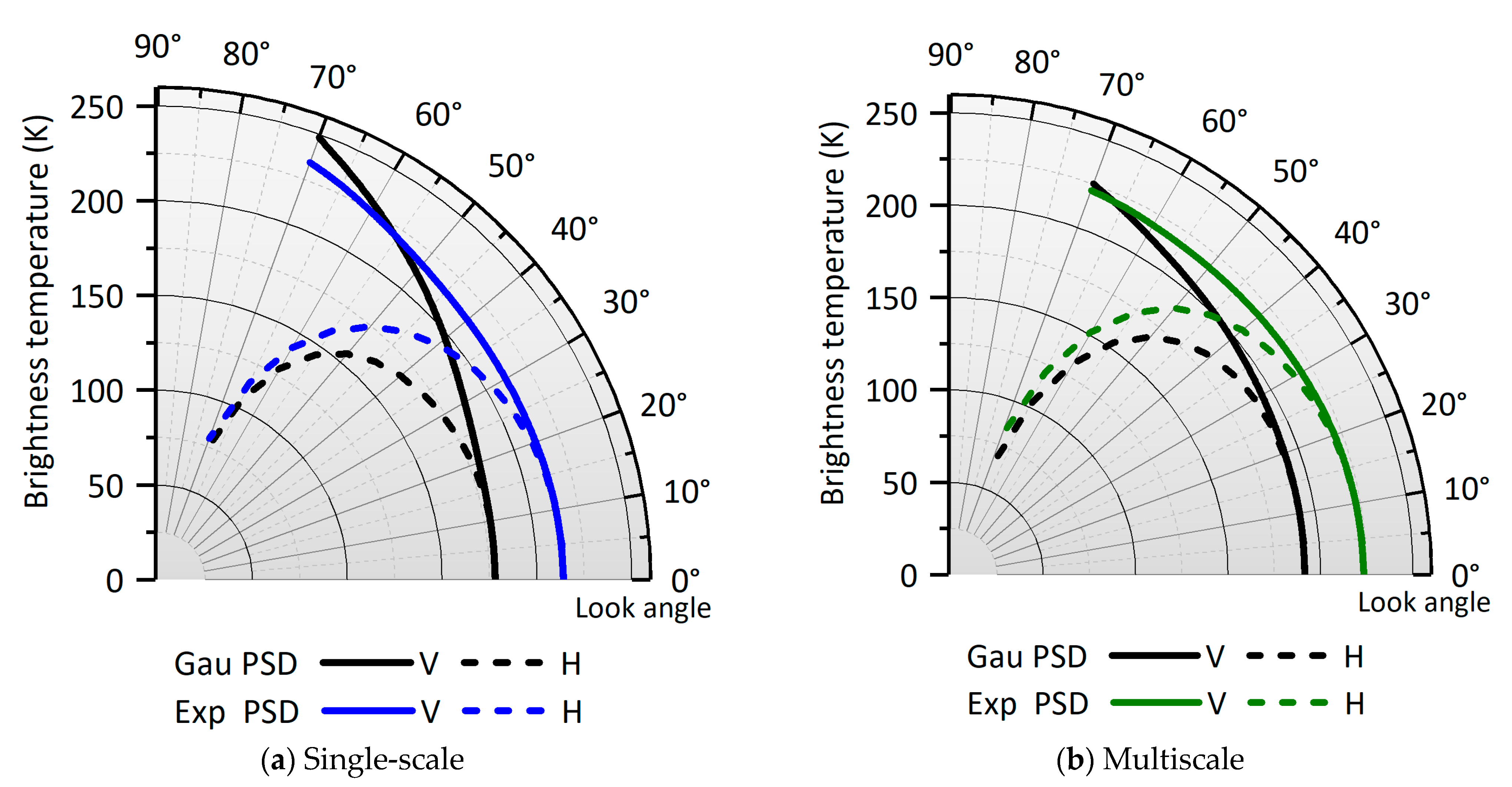
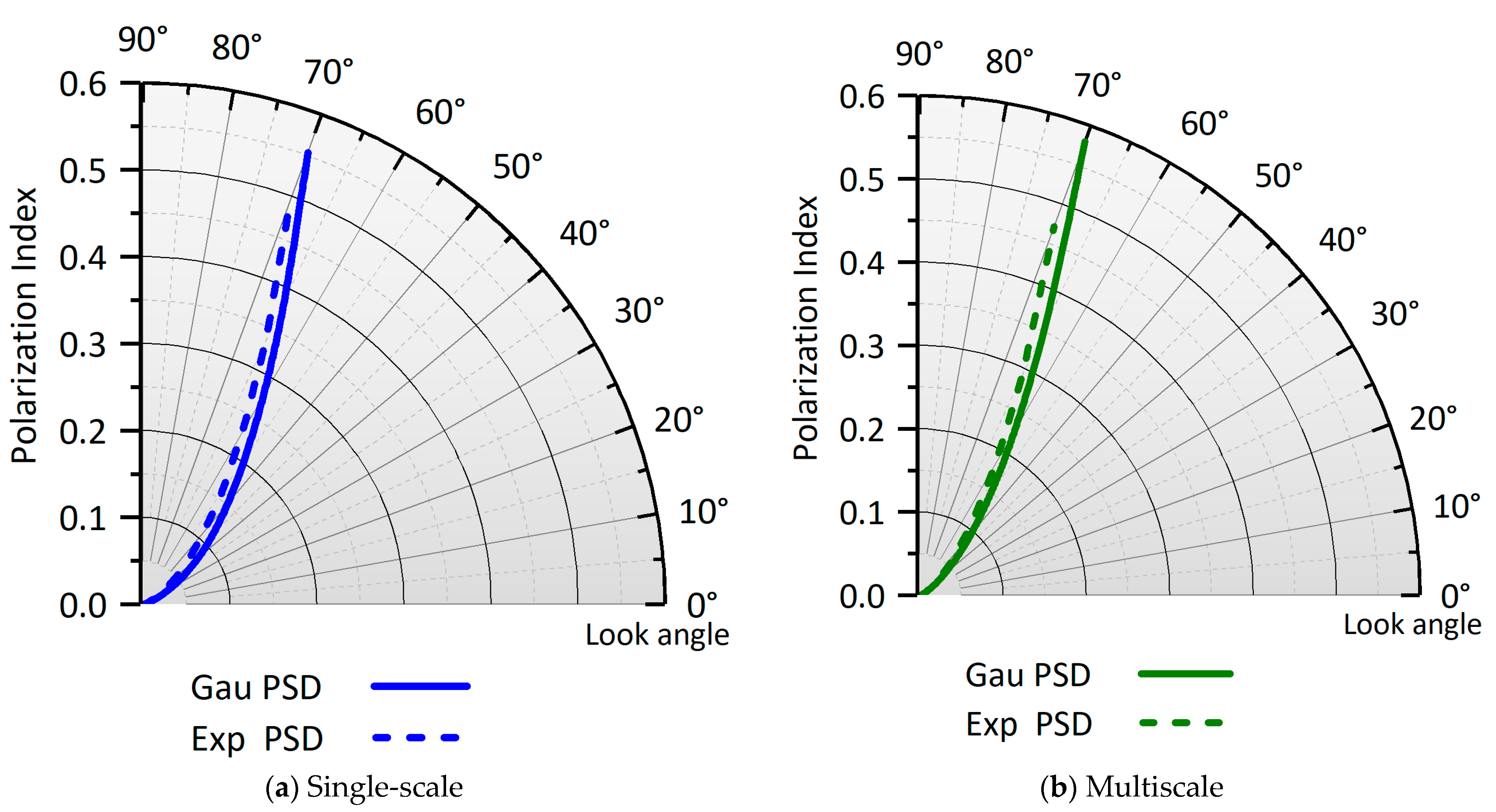
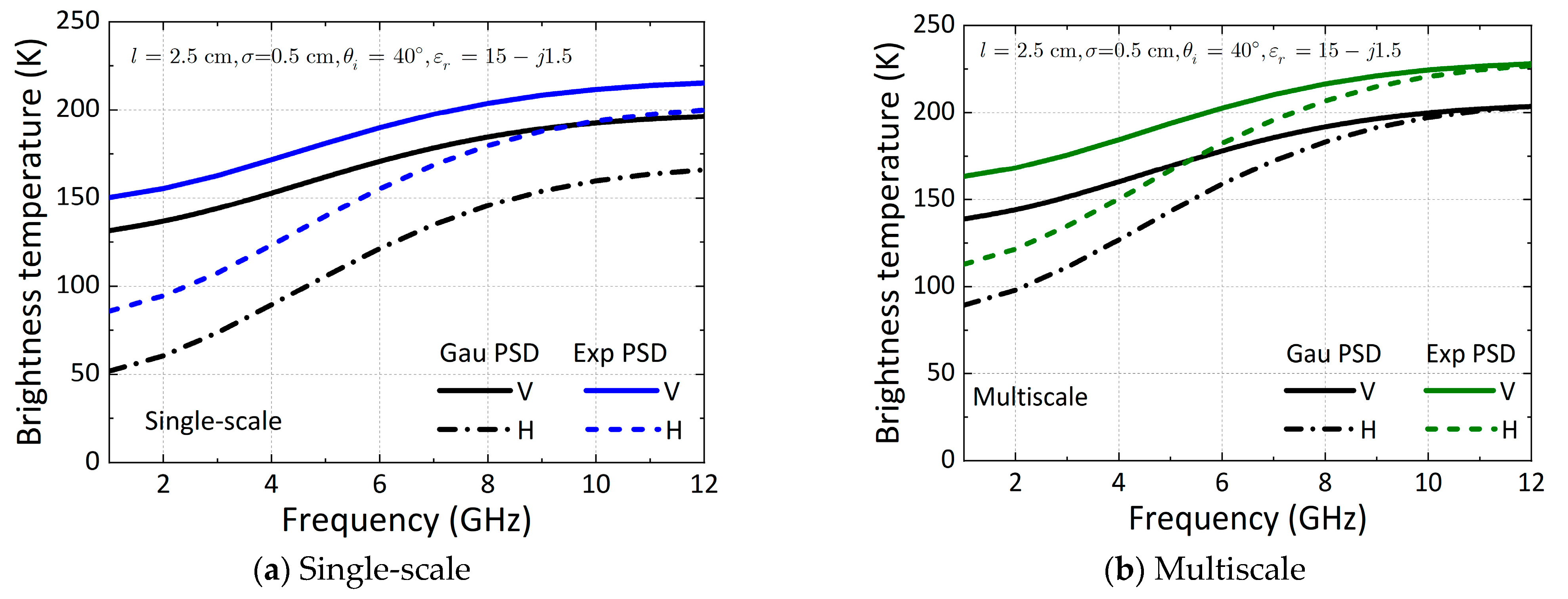
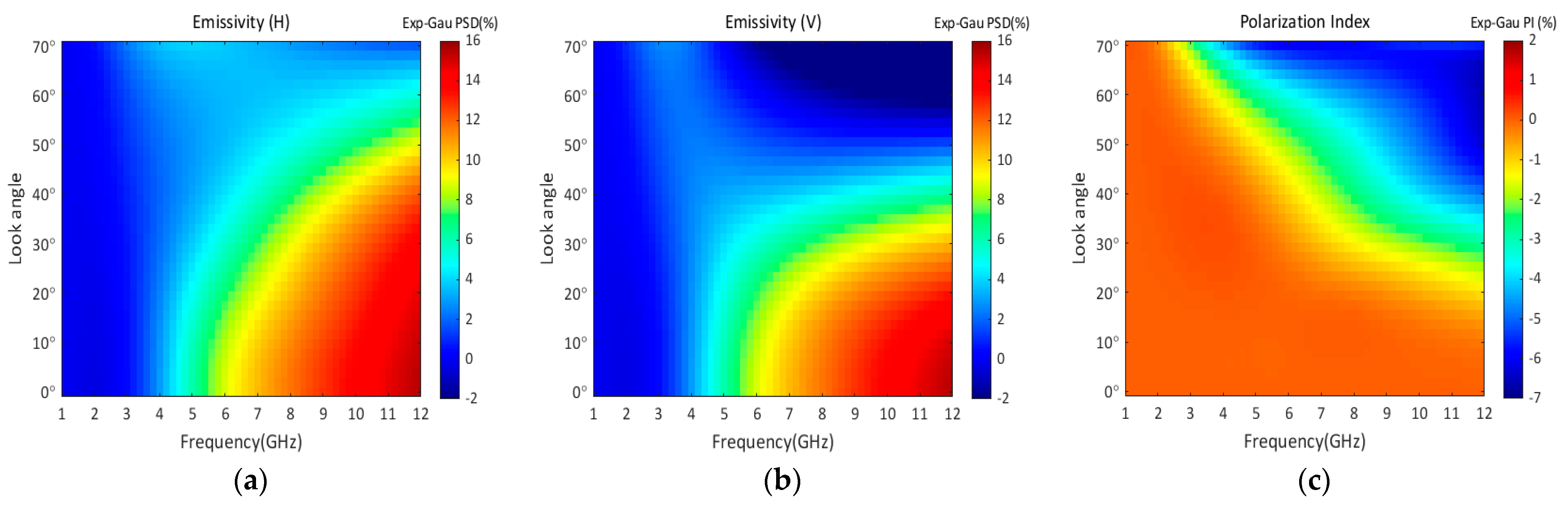
3. Polarized Emissions from Non-Gaussian Distributed Surfaces
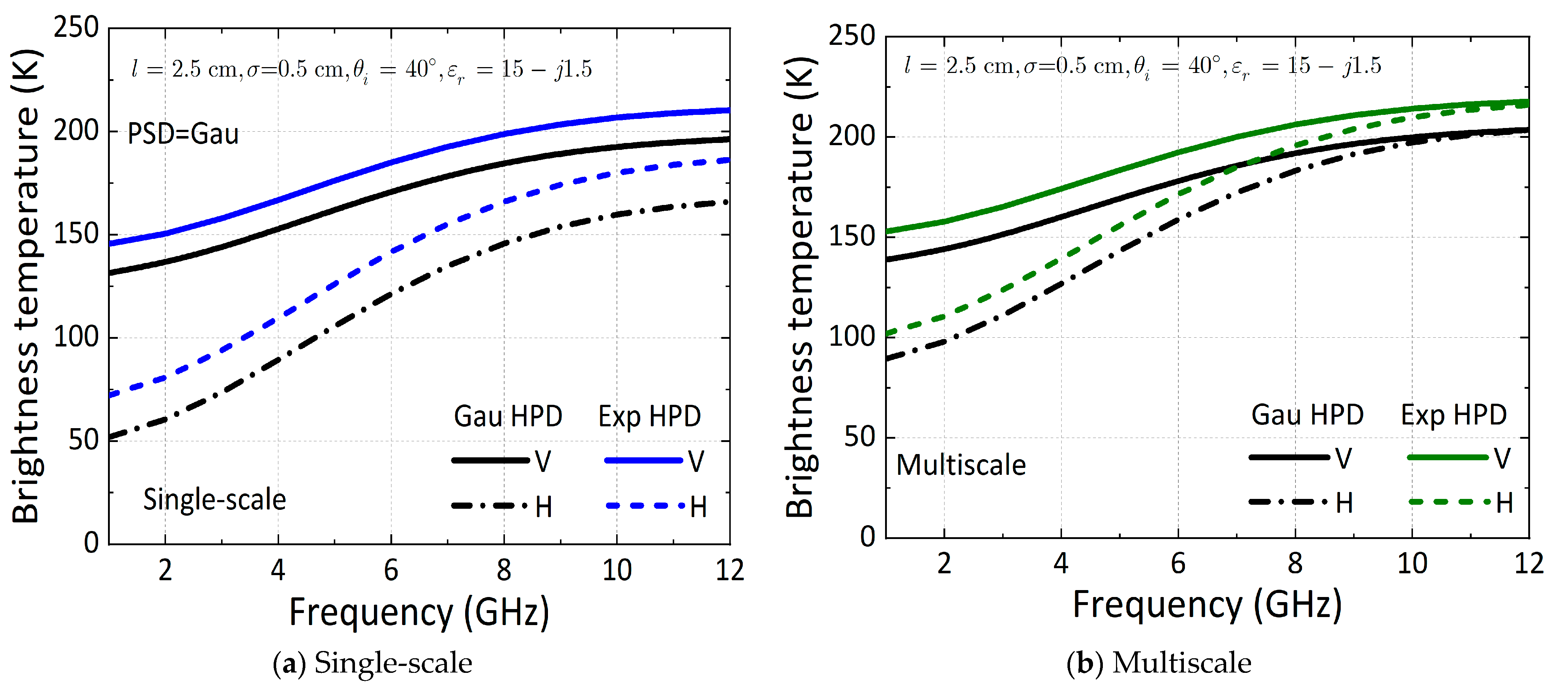
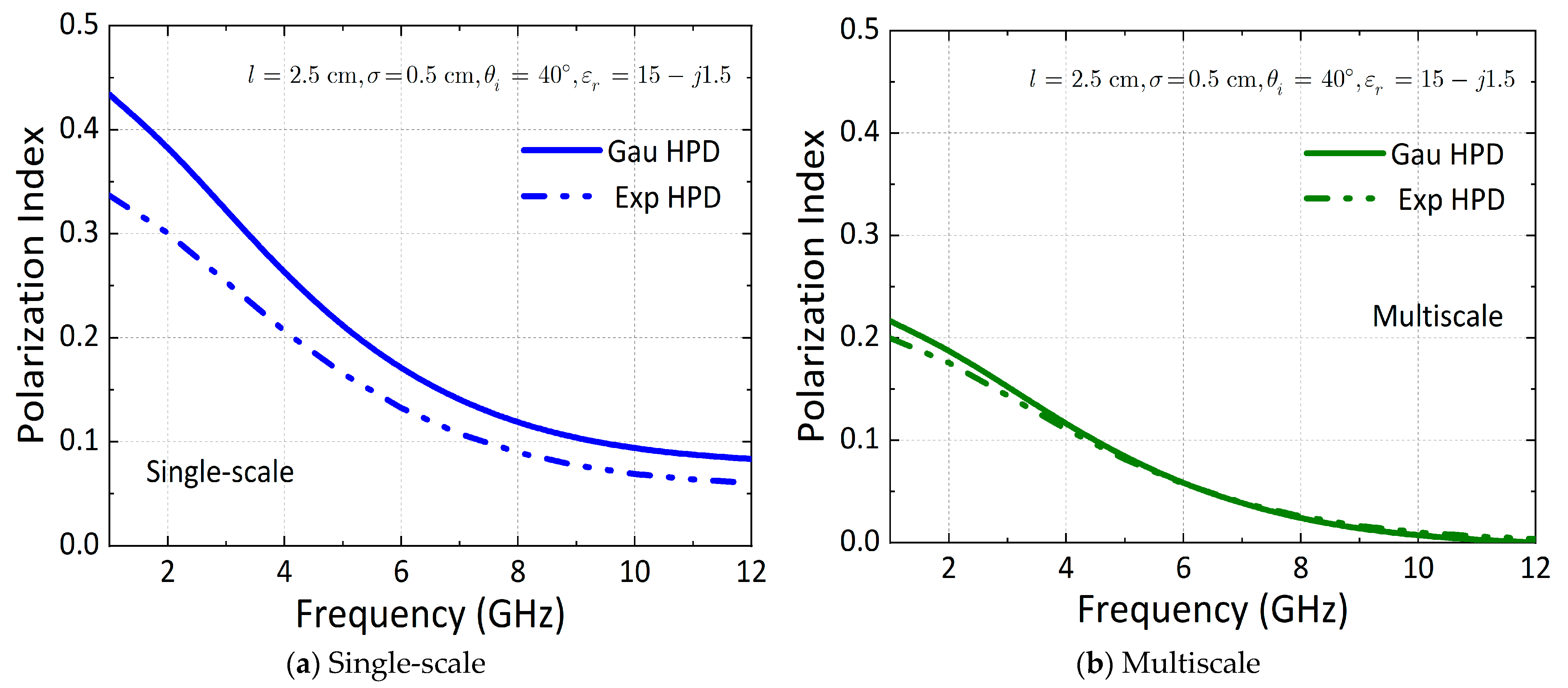
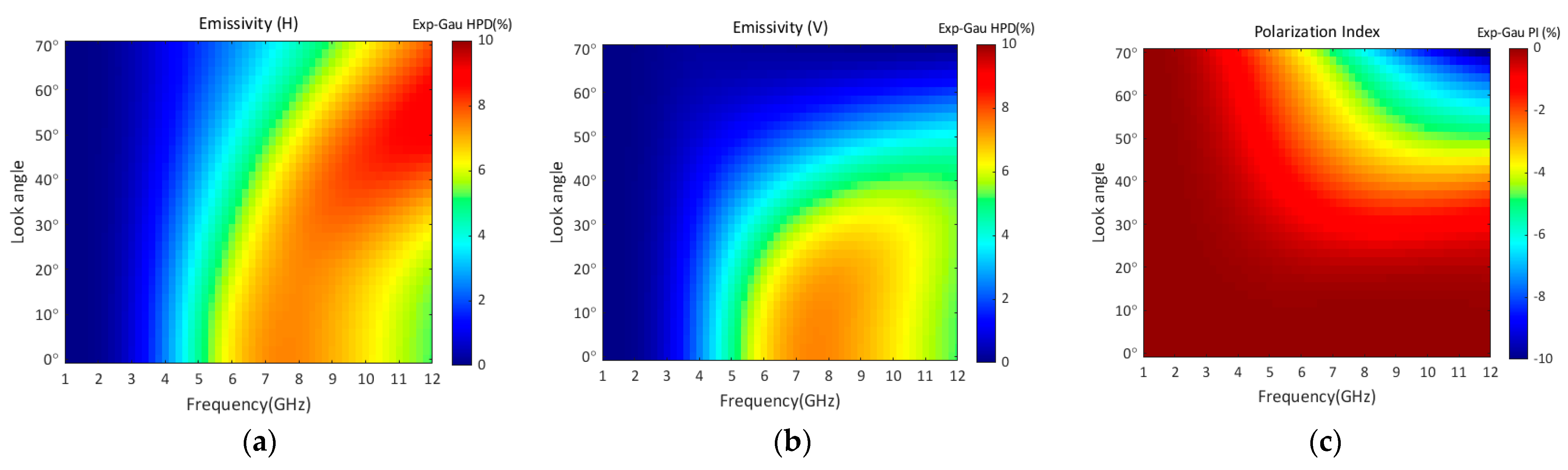
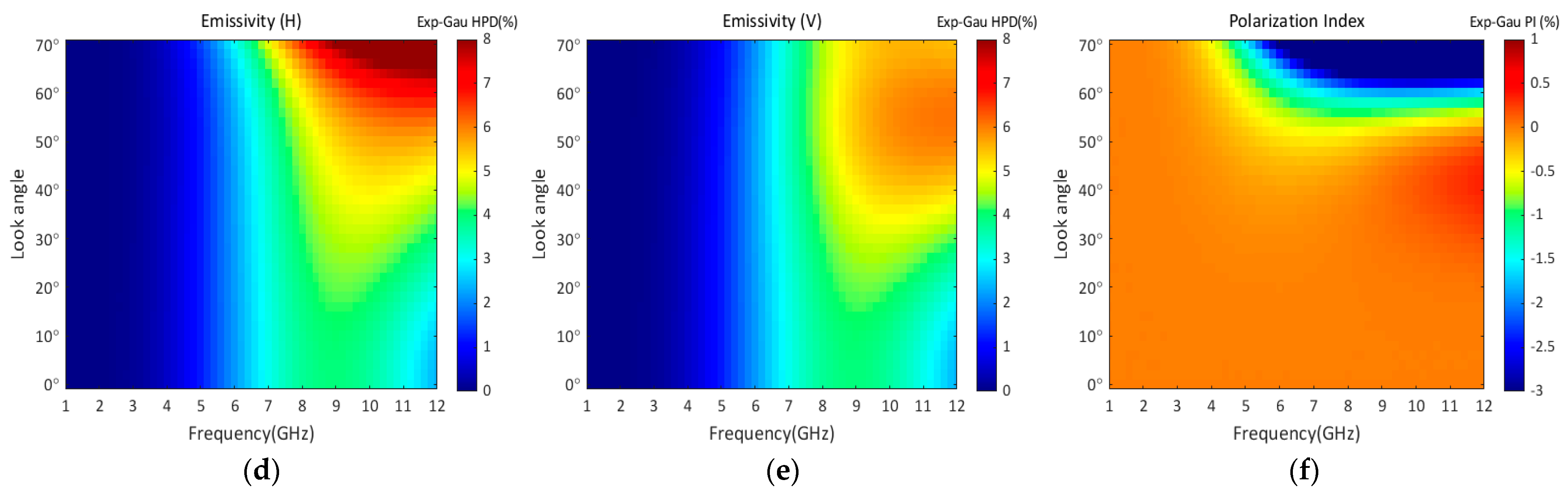
3.1. Non-Gaussian HPD Effect
3.2. Non-Gaussian PSD Effect
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- For Gaussian distribution
- (2)
- For exponential distribution
References
- Huang, N.E.; Long, S.R.; Tung, C.-C.; Yuan, Y.; Bliven, L.F. A non-Gaussian statistical model for surface elevation of nonlinear random wave fields. J. Geophys. Res. 1983, 88, 7597. [Google Scholar] [CrossRef]
- Beckers, J.F.; Renner, A.H.; Spreen, G.; Gerland, S.; Haas, C. Sea-ice surface roughness estimates from airborne laser scanner and laser altimeter observations in Fram Strait and north of Svalbard. Ann. Glaciol. 2015, 56, 235–244. [Google Scholar] [CrossRef]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; MacMillan: New York, NY, USA, 1963. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing; Volume 2: Radar Remote Sensing and Surface Scattering and Emission Theory; Artech House: Norwood, MA, USA, 1982. [Google Scholar]
- Tsang, L.; Kong, J.A.; Shin, R.T. Theory of Microwave Remote Sensing; Wiely: Hoboken, NJ, USA, 1985. [Google Scholar]
- Sanamzadeh, M.; Tsang, L.; Johnson, J. Scattering and emission of electromagnetic waves from random layered media with random rough interfaces: A partially coherent cascading approach. IEEE Trans. Antenn. Propag. 2020, 68, 3094–3102. [Google Scholar] [CrossRef]
- Beckmann, P. Scattering by non-Gaussian surfaces. IEEE Trans. Antenn. Propag. 1973, 21, 169–175. [Google Scholar] [CrossRef]
- Brown, G.S. A theory for near-normal incidence microwave scattering from first-year sea ice. Radio Sci. 1982, 17, 233–243. [Google Scholar] [CrossRef]
- Eom, H.J.; Fung, A.K. A Comparison between backscattering coefficients using Gaussian and non-Gaussian surface statistics. IEEE Trans. Antenn. Propag. 1983, 31, 635–638. [Google Scholar] [CrossRef]
- Fung, A.K.; Chen, K.S. Kirchhoff Model for a Skewed Random Surface. J. Electromagn. Waves Appl. 1991, 5, 205–216. [Google Scholar] [CrossRef]
- Chen, K.S.; Fung, A.K.; Amar, F. An empirical bispectrum model for sea surface scattering. IEEE Trans. Geosci. Remote Sens. 1993, 31, 830–835. [Google Scholar] [CrossRef]
- Wu, S.C.; Chen, M.F.; Fung, A.K. Scattering from non-Gaussian randomly rough surfaces-cylindrical case. IEEE Trans. Geosci. Remote Sens. 1988, 26, 790–798. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, K.S.; Wang, S. Bistatic radar scattering from non-Gaussian height distributed rough surfaces. Remote Sens. 2022, 18, 4457–4461. [Google Scholar] [CrossRef]
- Stephen, H.; Long, D.G. Modeling microwave emissions of erg surfaces in the Sahara Desert. IEEE Trans. Geosci. Remote Sens. 2005, 12, 2822–2830. [Google Scholar] [CrossRef]
- Yueh, S.H.; Chaubell, J. Sea surface salinity and wind retrieval using combined passive and active L-band microwave observations. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1022–1032. [Google Scholar] [CrossRef]
- Njoku, E.G.; Chan, S. Comprehensive Remote Sensing. In Water Cycle Components over Land; Liang, S., Ed.; Elsevier: Amsterdam, The Netherland, 2018. [Google Scholar]
- Yang, Y.; Chen, K.S.; Ren, C. Radar Scattering from a Modulated Rough Surface: Simulations and Applications. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9842–9850. [Google Scholar] [CrossRef]
- Chen, K.S. Radar Scattering and Imaging of Rough Surface: Modeling and Applications with MATLAB®; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Szego, G. Orthogonal Polynomials; Colloquium Publications; American Mathematical Society Press: Providence, RI, USA, 1939; Volume XXIII. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Chen, K.-S. Disturbing Variability in Microwave Emission from a Non-Gaussian Distributed and Correlated Multiscale Rough Surface. Remote Sens. 2023, 15, 3297. https://doi.org/10.3390/rs15133297
Yang Y, Chen K-S. Disturbing Variability in Microwave Emission from a Non-Gaussian Distributed and Correlated Multiscale Rough Surface. Remote Sensing. 2023; 15(13):3297. https://doi.org/10.3390/rs15133297
Chicago/Turabian StyleYang, Ying, and Kun-Shan Chen. 2023. "Disturbing Variability in Microwave Emission from a Non-Gaussian Distributed and Correlated Multiscale Rough Surface" Remote Sensing 15, no. 13: 3297. https://doi.org/10.3390/rs15133297
APA StyleYang, Y., & Chen, K.-S. (2023). Disturbing Variability in Microwave Emission from a Non-Gaussian Distributed and Correlated Multiscale Rough Surface. Remote Sensing, 15(13), 3297. https://doi.org/10.3390/rs15133297






