Analysis of PlanetScope Dove Digital Surface Model Accuracy Using Geometrically Simulated Images
Abstract
:1. Introduction
2. Methodology
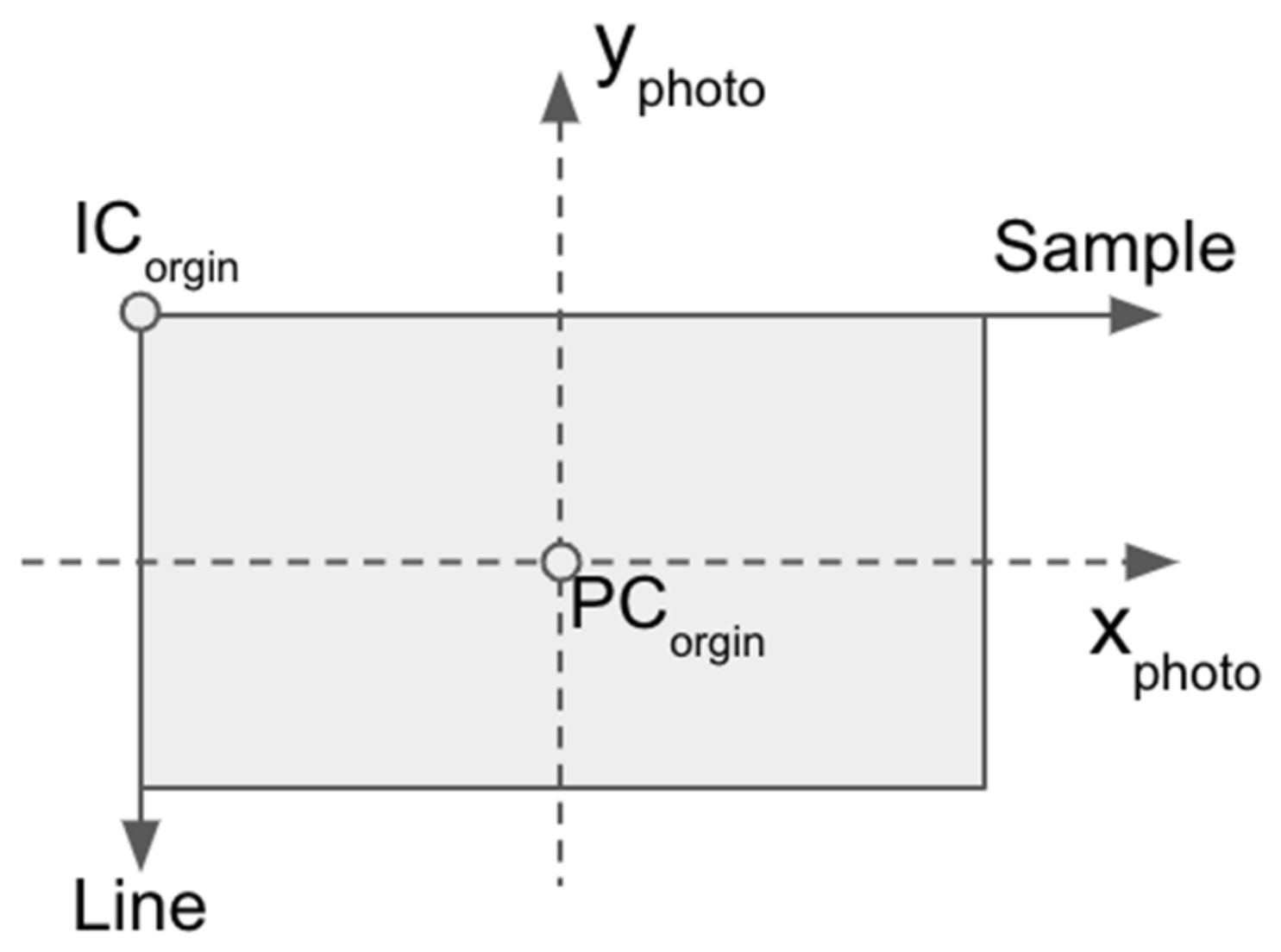
2.1. Retrieval of Orientation Parameters by Self-Calibrating Bundle Adjustment
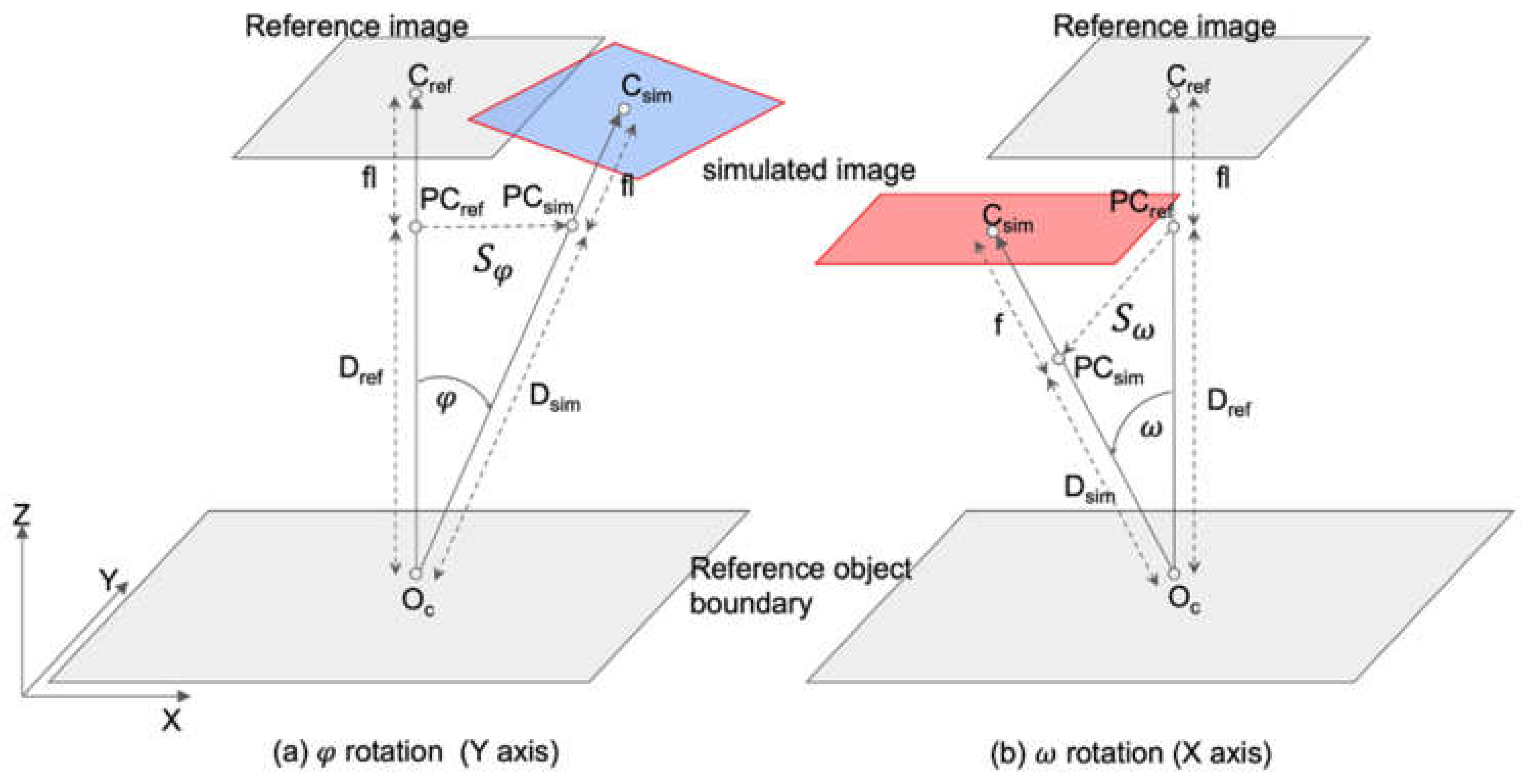
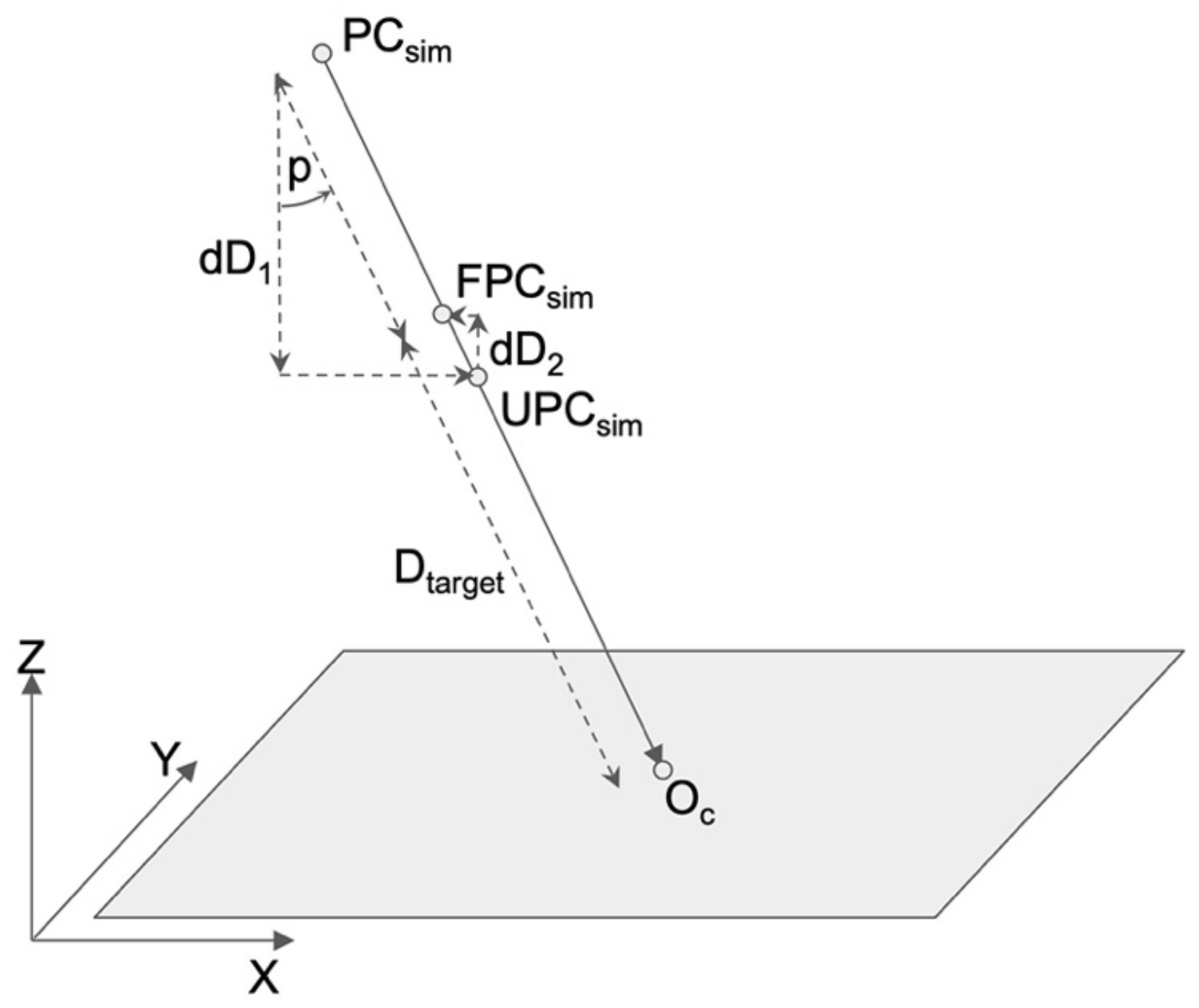
2.2. EOPs for Simulated Images
2.3. Simulated Image Generation
2.4. DSM Generation with the Simulated Images
3. Experimental Results
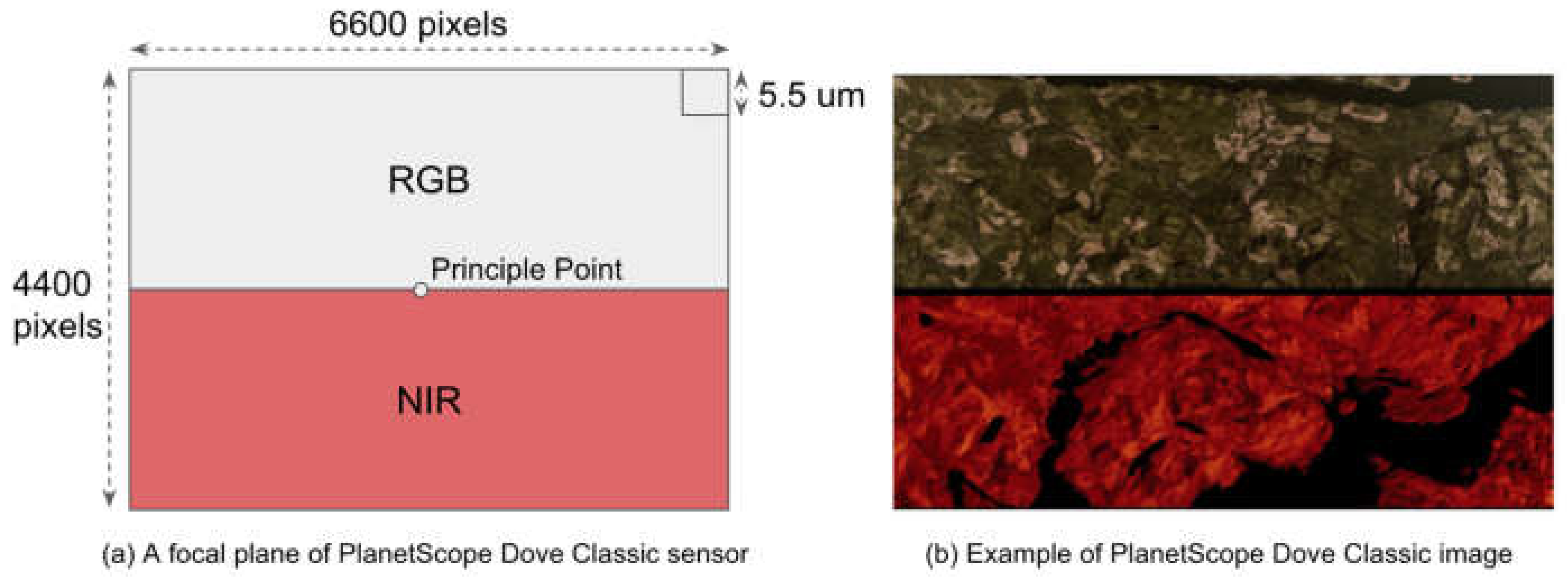
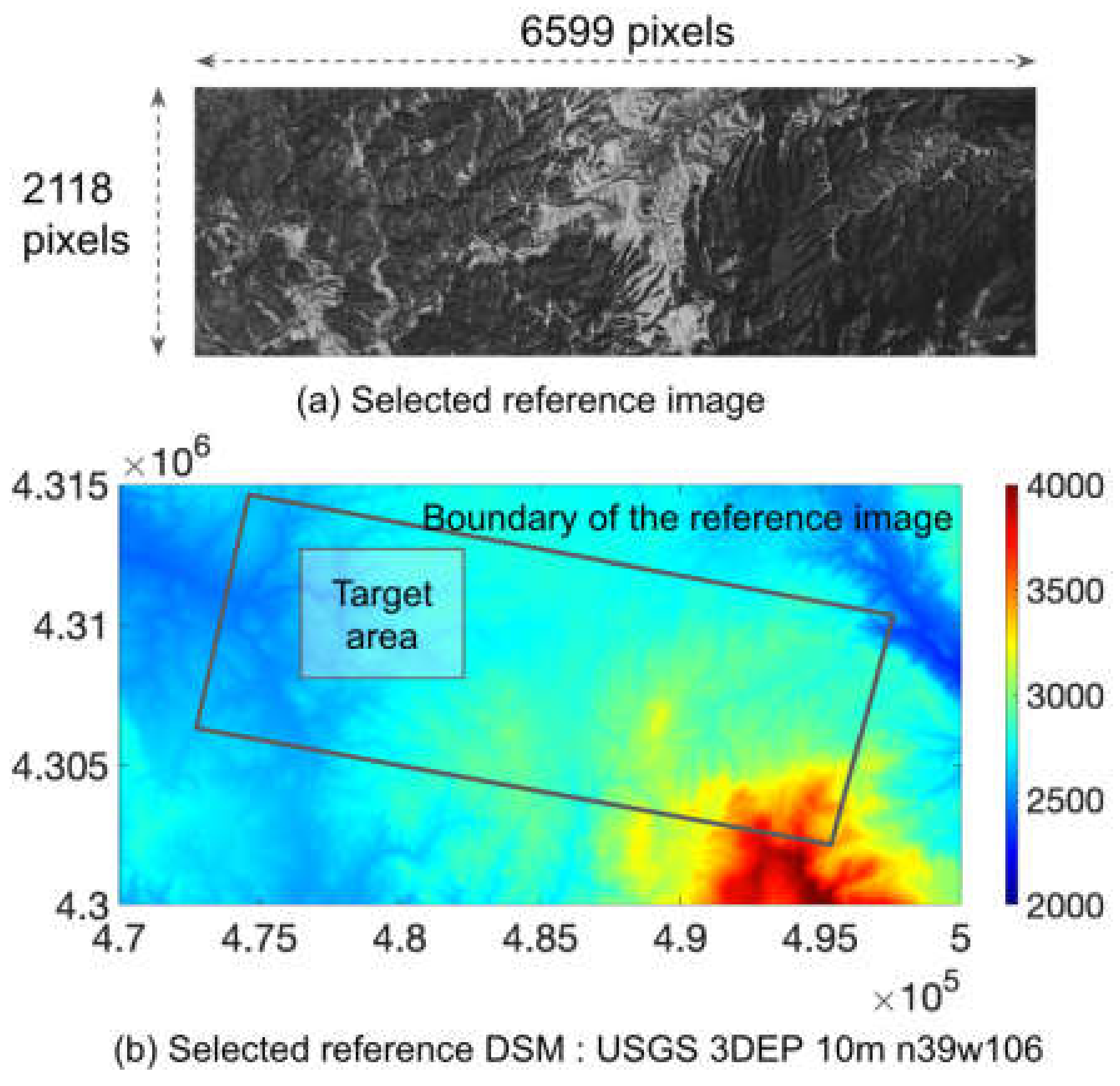
3.1. PlanetScope Dove Classic Images and the Reference DSM
3.2. Self-Calibrating Bundle Adjustment for the Reference Image
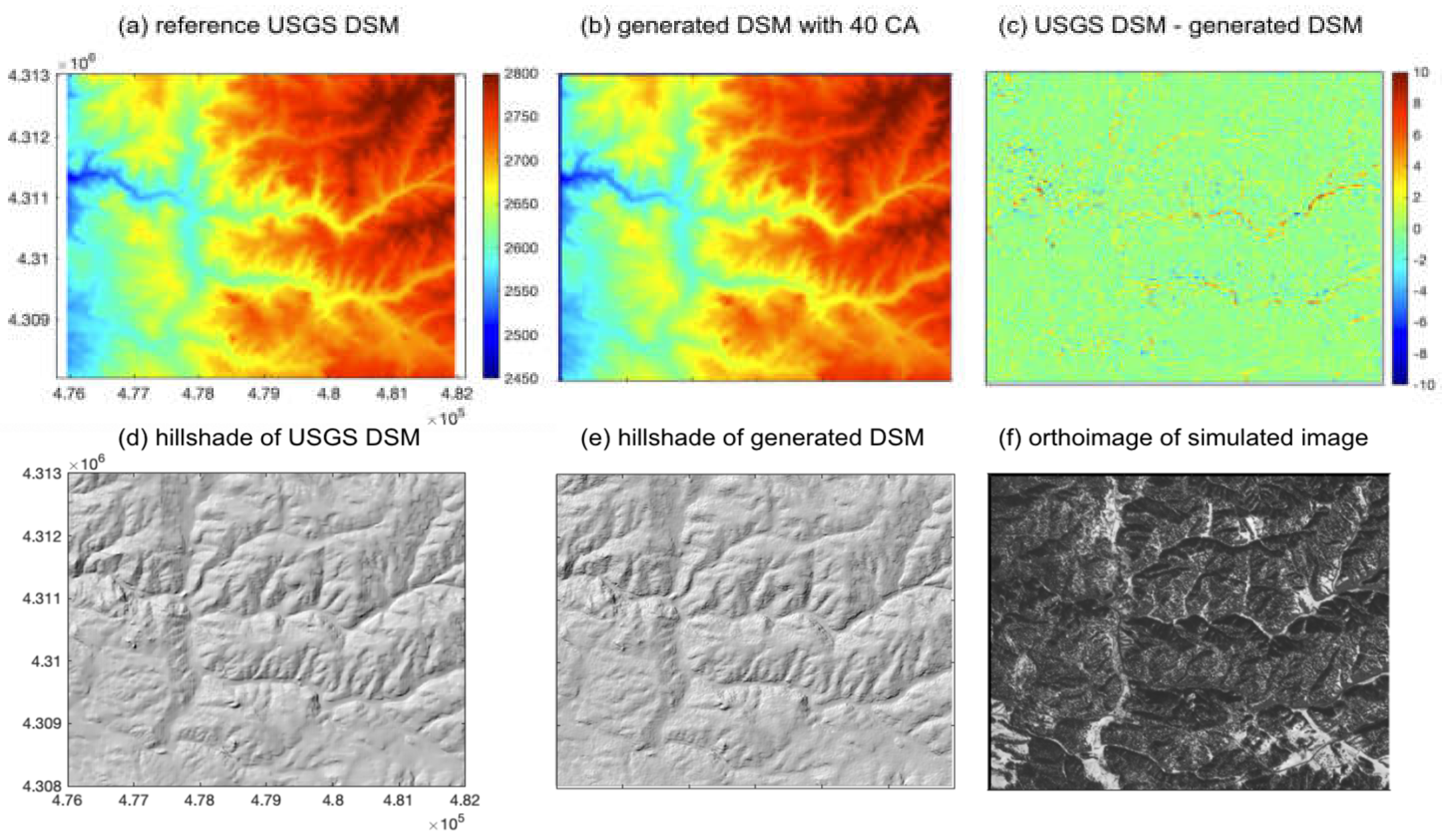
3.3. Example of Simulated Images
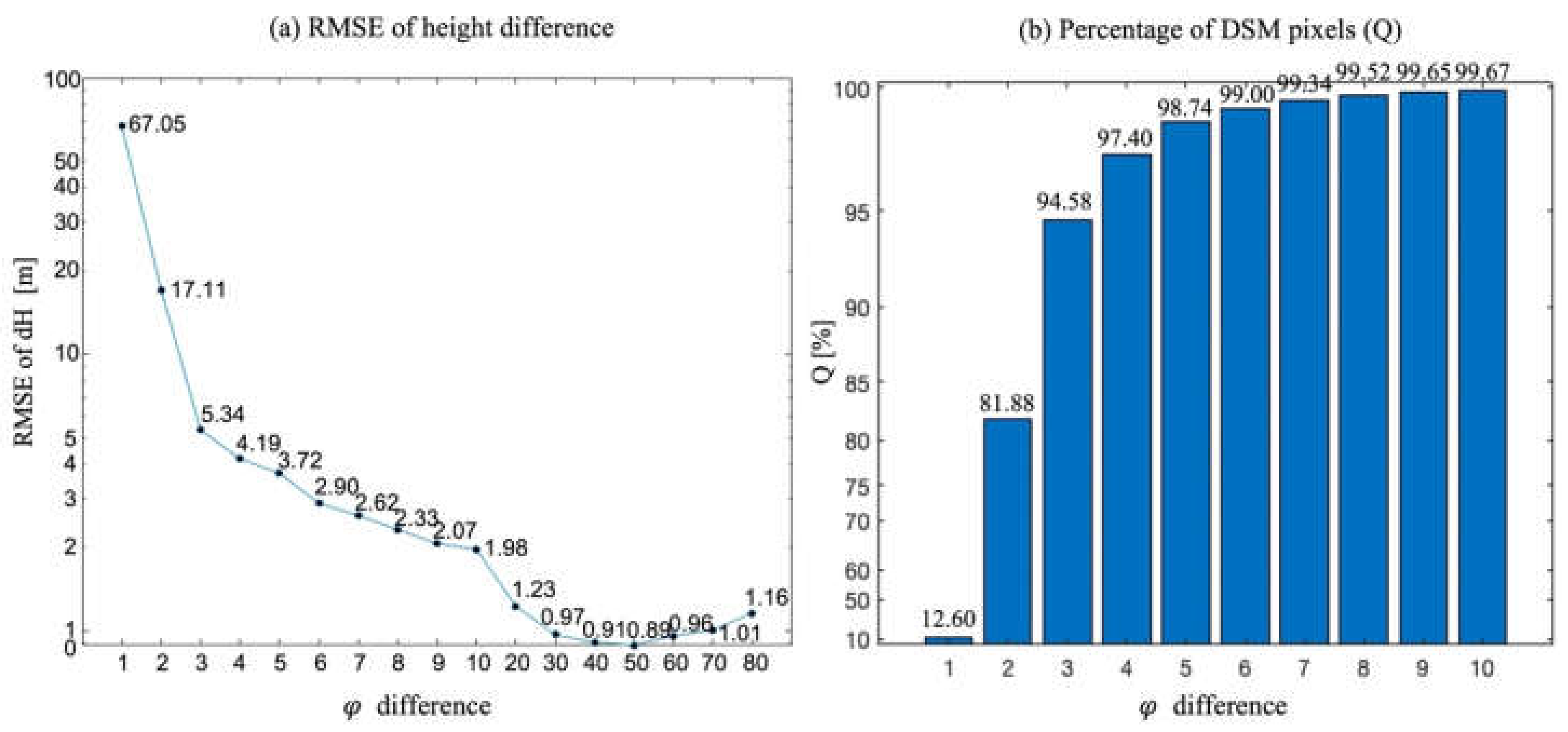
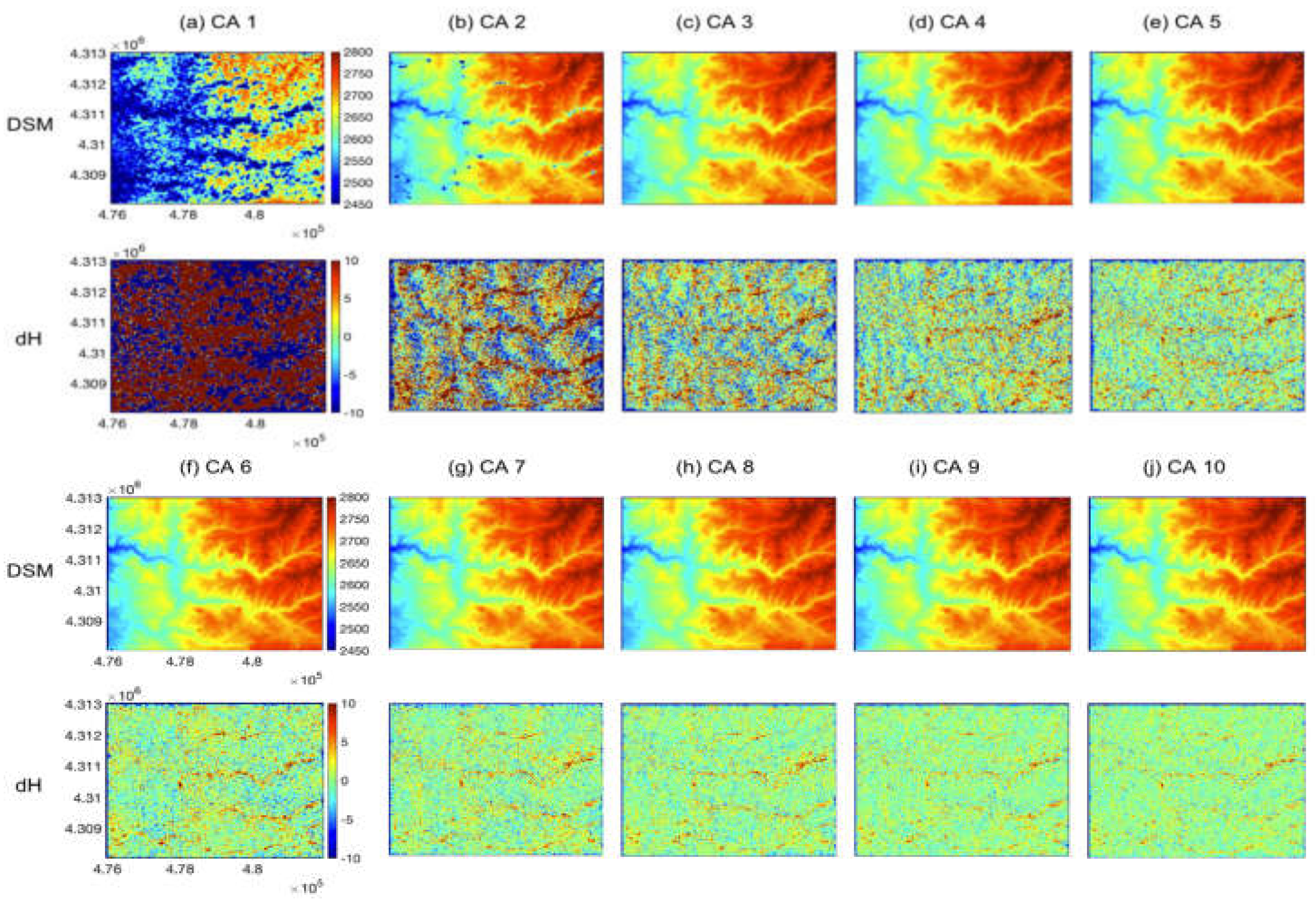
3.4. Accuracy Analysis of Simulated DSMs
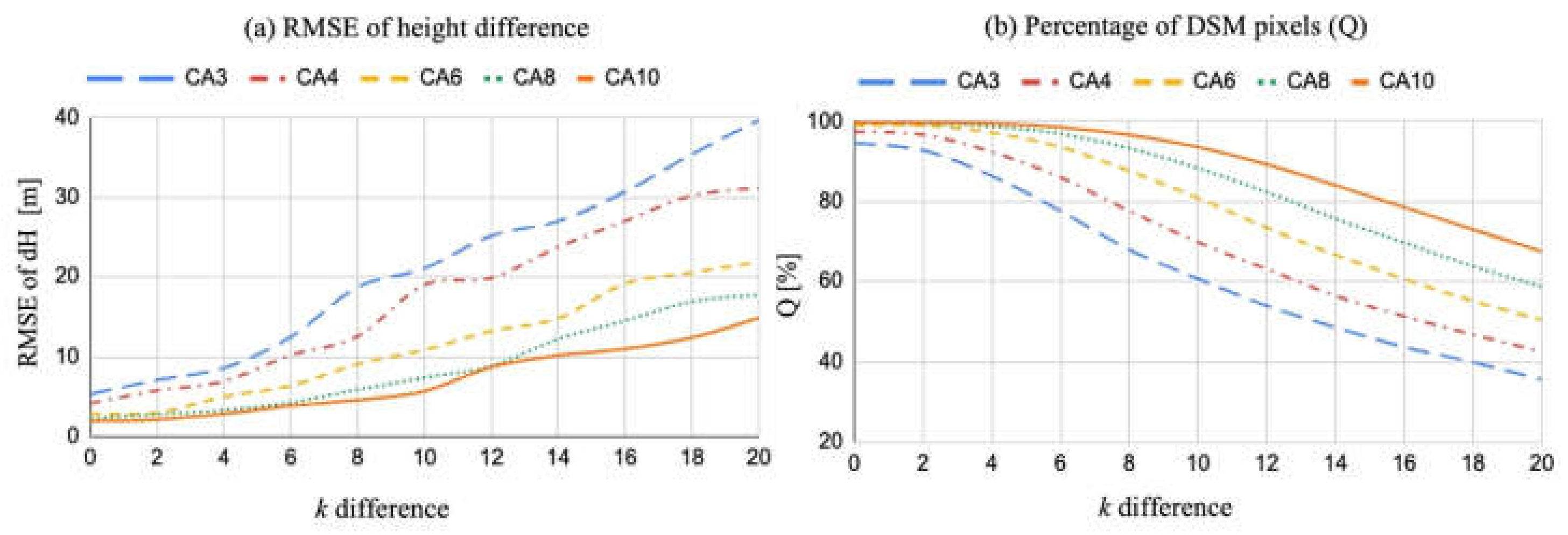
3.4.1. Convergence Angle Analysis with
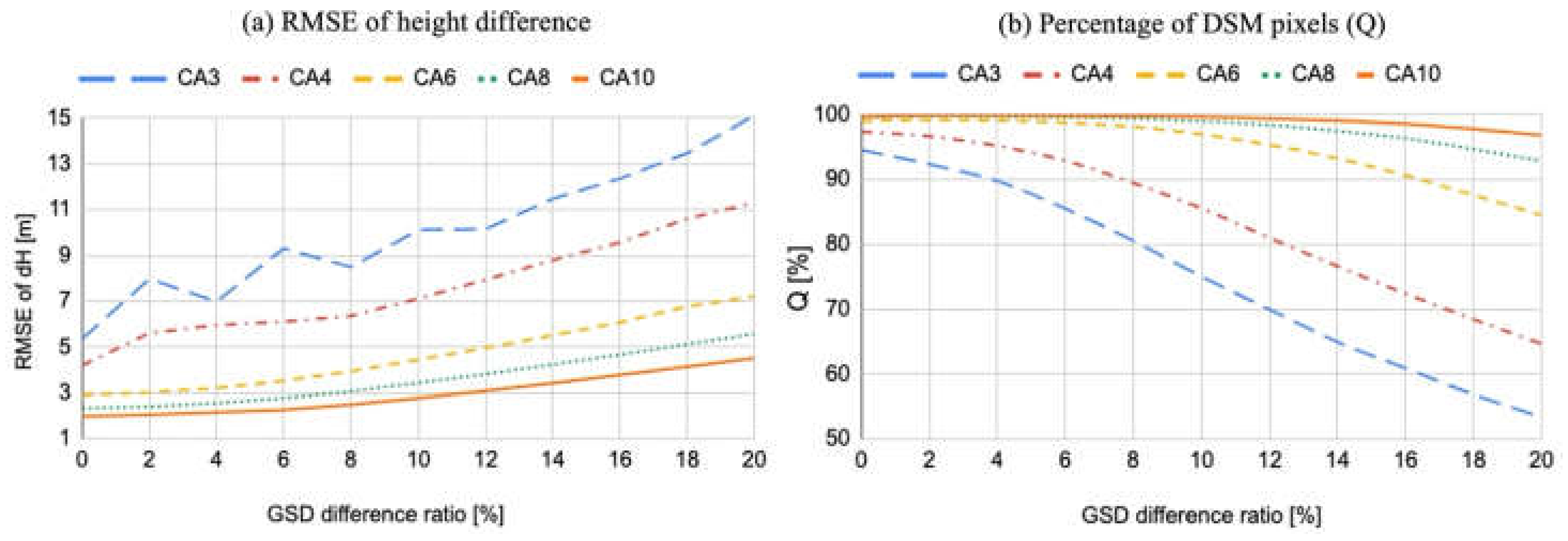
3.4.2. Analysis of Convergence Angle with Respect to the Difference in and Azimuth Angles from
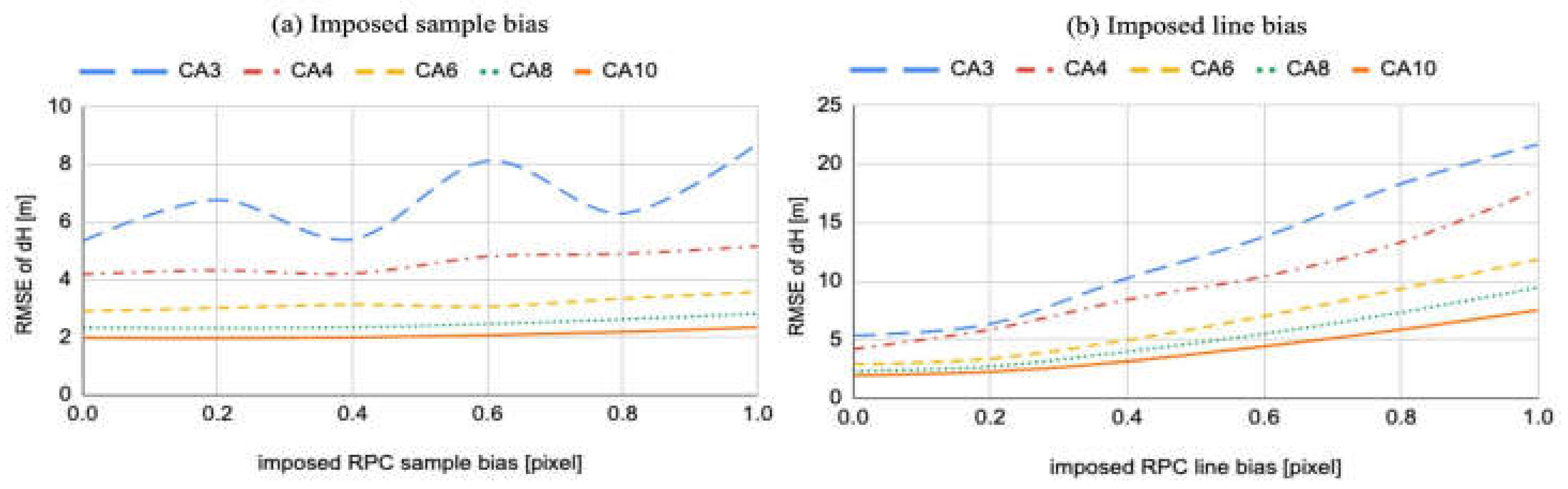
3.4.3. Scale and RPCs Bias Analysis
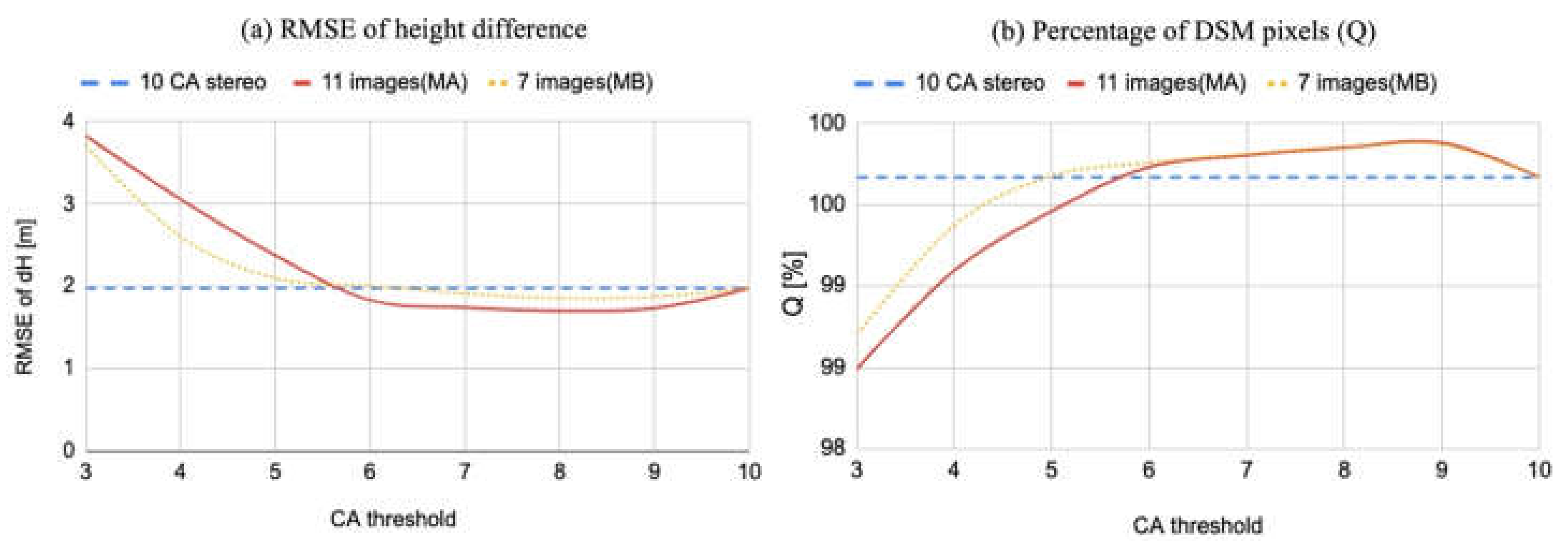
3.4.4. Multi-Pair DSM Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary of Acronyms
| ALOS | Advanced Land Observing Satellite | |
| B/H | Base-to-Height | |
| CA | Convergence Angle | |
| CCD | Charge-Coupled Device | |
| DEM | Digital Elevation Model | |
| DN | Digital Number | |
| DSM | Digital Surface Model | |
| EOP | Exterior Orientation Parameter | |
| GCP | Ground Control Point | |
| GSD | Ground Sample Distance | |
| IOP | Interior Orientation Parameters | |
| LiDAR | Light Detection And Ranging | |
| NIR | Near Infrared | |
| NTSC | National Television System Committee | |
| REMA | Reference Elevation Model of Antarctica | |
| RFM | Rational Function Model | |
| RMSE | Root Mean Square Error | |
| RPC | Rational Polynomial Coefficient | |
| PRISM | Panchromatic Remote-sensing Instrument for Stereo Mapping | |
| RSM | Rigorous Sensor Model | |
| SETSM | Surface Extraction from TIN-based Search-space Minimization | |
| SRTM | Shuttle Radar Topography Mission | |
| TIN | Triangulated Irregular Network | |
| USGS | United State Geological Survey | |
| UTM | Universal Transverse Mercator | |
| 3DEP | 3D Elevation Program | |
| Glossary of Variables | ||
| Ln, Sn | normalized line and sample image coordinates in RPCs | |
| P, L, H | normalized latitude, longitude, and height coordinates in RPCs | |
| , λ, h | actual latitude and longitude coordinates, and height. | |
| Line | image line pixel number starting from the center of the first line | |
| Sample | sample pixel number starting from the center of the left-top sample | |
| c, d, e, f | 78 RPCs (c and d are numerator and denominator of 38 RPCs for Ln, and e and f are numerator and denominator of 38 RPCs for Sn) | |
| np, nl | number of GCP spacing in latitude and longitude direction for GCP distribution by the provided RPCs | |
| hl | number of height layer for GCP distribution by the provided RPCs | |
| X, Y, Z | 3D object coordinates | |
| Xc, Yc, Zc | 3D projection center coordinates of image | |
| xphoto, yphoto | x and y image coordinates in photo coordinate system | |
| x, y | measured photo coordinates corresponding to 3D object point | |
| photo coordinates of the projection center | ||
| photo coordinates of the principal point | ||
| symmetric radial lens distortion coefficients | ||
| decentering distortion coefficients | ||
| fl | calibrated focal length | |
| omega, phi, and kappa angles corresponding to X, Y, and Z axes | ||
| m | rotation matrix in terms of three angular attitudes ) | |
| ICorigin | origin of the image coordinate system | |
| PCorigin | origin of the photo coordinate system | |
| C | image point | |
| PC | projection center point | |
| O | object point | |
| Oc | center object point of the reference object boundary | |
| shifted distance corresponding to and rotations | ||
| D | Euclidean distance | |
| SC | image’s scale | |
| Xadj, Yadj | adjusted distance estimated from the photo coordinate difference between reference and simulated projection center | |
| FPC | projection center after applying distance adjustment | |
| UPC | iteratively updated projection center by ray tracing | |
| CS | cell size of the charge-coupled device sensor | |
| dD | difference between Euclidean distance | |
| ZD | distance in Z axis | |
| n | iteration number | |
| projection ray vector | ||
| normalized vector corresponding to X, Y, and Z axes | ||
| Q | percentage of the pixels within ±10 m of height difference. | |
References
- Planet Imagery and Archive. Available online: https://www.planet.com/products/planet-imagery (accessed on 25 March 2023).
- Ghuffar, G. DEM generation from Multi Satellite PlanetScope Imagery. Remote Sens. 2018, 10, 1462. [Google Scholar] [CrossRef] [Green Version]
- Aati, S.; Avouac, J.-P. Optimization of Optical Image Geometric Modeling, Application to Topography Extraction and Topographic Change Measurements Using PlanetScope and Skysat Imagery. Remote Sens. 2020, 12, 3418. [Google Scholar] [CrossRef]
- D’angelo, P.; Reinartz, P. Digital Elevation Models from Stereo, Video and Multi-View Imagery Captured by Small Satellites. Int. Soc. Photogramm. Remote Sens. (ISPRS)-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 77–82. [Google Scholar] [CrossRef]
- Huang, D.; Tang, Y.; Qin, R. An evaluation of planetscope images for 3D reconstruction and change detection—Experimental validations with case studies. GIScience Remote Sens. 2022, 59, 744–761. [Google Scholar] [CrossRef]
- Jacobsen, K.; Topan, H. DEM generation with short base length Pleiades triplet. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences Joint ISPRS Conference, Munich, Germany, 25–27 March 2015. [Google Scholar]
- Noh, M.-J.; Howat, I.M. The Surface Extraction from TIN based Search-space Minimization (SETSM) algorithm. Int. Soc. Photogramm. Remote Sens. (ISPRS) J. Photogramm. Remote Sens. 2017, 129, 55–76. [Google Scholar] [CrossRef]
- Noh, M.-J.; Howat, I.M. Automated stereo-photogrammetric DEM generation at high latitudes: Surface Extraction with TIN-based Search-space Minimization (SETSM) validation and demonstration over glaciated regions. GIScience Remote Sens. 2015, 52, 198–217. [Google Scholar] [CrossRef]
- Howat, I.M.; Porter, C.; Smith, B.E.; Noh, M.-J.; Morin, P. The Reference Elevation Model of Antarctica. Cryosphere 2019, 13, 665–674. [Google Scholar] [CrossRef] [Green Version]
- Tao, C.V.; Hu, Y. A Comprehensive Study of the Rational Function Model for Photogrammetric Processing. Photogramm. Eng. Remote Sens. 2001, 64, 1347–1357. [Google Scholar]
- Grodecki, J.; Dial, G. Block adjustment of high-resolution satellite images described by rational polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A.; Wilkinson, B.E. Elements of Photogrammetry with Applications in GIS, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2014; pp. 490–491. [Google Scholar]
- USGS. Available online: https://www.sciencebase.gov/catalog/item/61b19badd34eb8f531255a27 (accessed on 30 May 2023).
- Understanding PlanetScope Instruments. Available online: https://developers.planet.com/docs/apis/data/sensors (accessed on 25 March 2023).
- Noh, M.-J.; Howat, I.M. Automated Coresistration of Repeat Digital Elevation Models for Surface Elevation Change Measurement Using Geometric Constraints. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2247–2260. [Google Scholar] [CrossRef]
- Noh, M.-J.; Howat, I.M. Automatic relative RPC image model bias compensation through hierarchical image matching for improving DEM quality. Int. Soc. Photogramm. Remote Sens. (ISPRS) J. Photogramm. Remote Sens. 2018, 136, 120–133. [Google Scholar] [CrossRef]






| Case | Interior Orientation Parameters | RMSE | Max Difference | ||
|---|---|---|---|---|---|
| Object (m) | Image (Pixel) | Object (m) | Image (Pixel) | ||
| 1 | fl | 9.92 | 2.60 | 26.96 | 7.06 |
| 2 | fl, xp, yp | 9.76 | 2.56 | 27.30 | 7.16 |
| 3 | fl, xp, yp, q1, q2, q3 | 0.70 | 0.20 | 1.63 | 0.45 |
| 4 | fl, xp, yp, q1, q2, q3, p1, p2 | 0.25 | 0.10 | 0.65 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, M.-J.; Howat, I.M. Analysis of PlanetScope Dove Digital Surface Model Accuracy Using Geometrically Simulated Images. Remote Sens. 2023, 15, 3496. https://doi.org/10.3390/rs15143496
Noh M-J, Howat IM. Analysis of PlanetScope Dove Digital Surface Model Accuracy Using Geometrically Simulated Images. Remote Sensing. 2023; 15(14):3496. https://doi.org/10.3390/rs15143496
Chicago/Turabian StyleNoh, Myoung-Jong, and Ian M. Howat. 2023. "Analysis of PlanetScope Dove Digital Surface Model Accuracy Using Geometrically Simulated Images" Remote Sensing 15, no. 14: 3496. https://doi.org/10.3390/rs15143496
APA StyleNoh, M.-J., & Howat, I. M. (2023). Analysis of PlanetScope Dove Digital Surface Model Accuracy Using Geometrically Simulated Images. Remote Sensing, 15(14), 3496. https://doi.org/10.3390/rs15143496





