PointCNT: A One-Stage Point Cloud Registration Approach Based on Complex Network Theory
Abstract
:1. Introduction
- (1)
- An efficient, high-precision and end-to-end one-stage point cloud registration framework is proposed.
- (2)
- A deep learning network design method based on complex network theory is proposed, and a multipath feature extraction network based on the above method for point clouds is designed.
- (3)
- A self-supervised module is introduced to improve the feature extraction ability of the network.
- (4)
- GBSelf-attention and FBCorss-attention based on nonlocal neural networks are designed.
2. Related Work
2.1. Traditional Registration Methods
2.2. Learning-Based Two-Stage Registration Methods
2.3. Learning-Based One-Stage Registration Methods
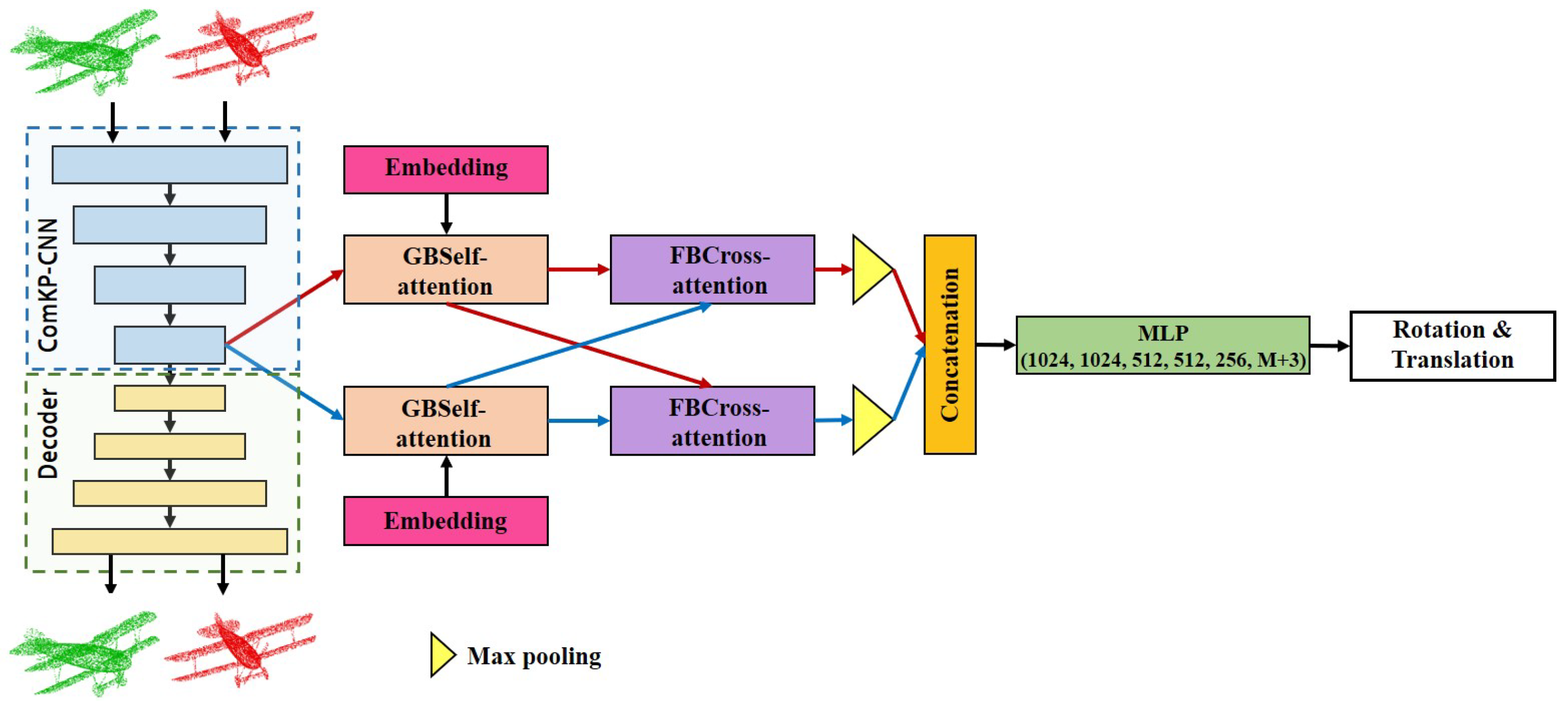
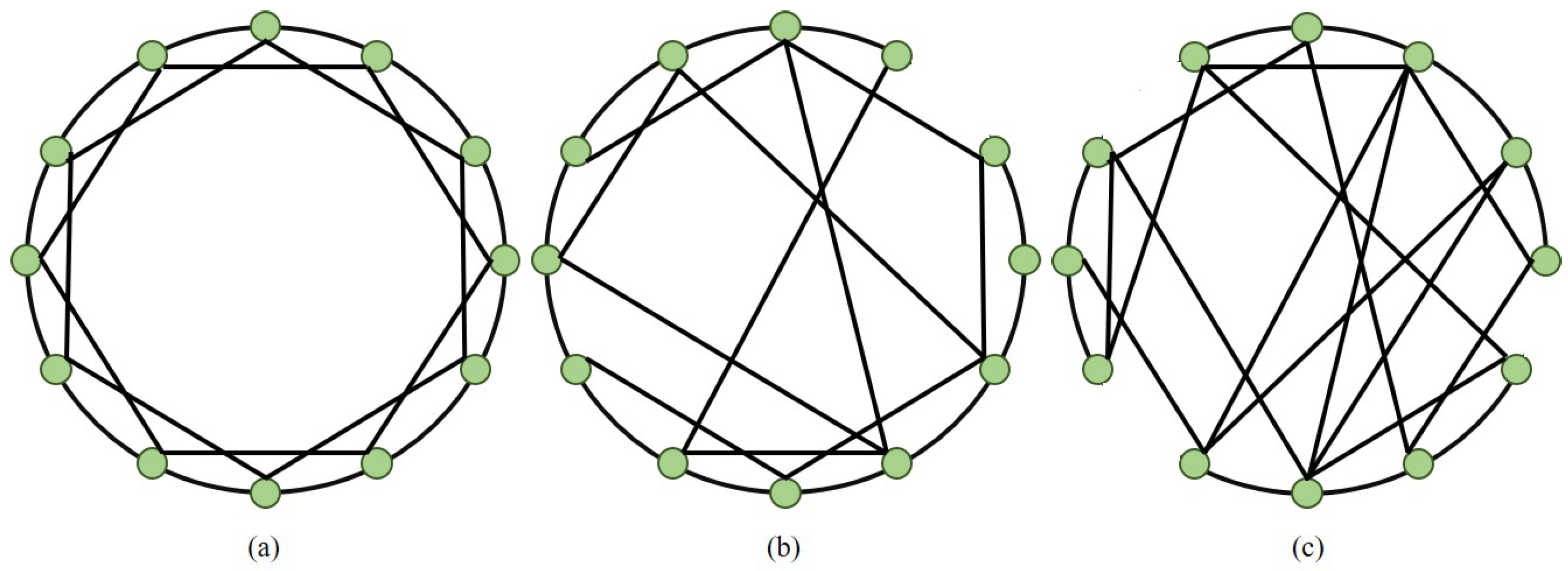
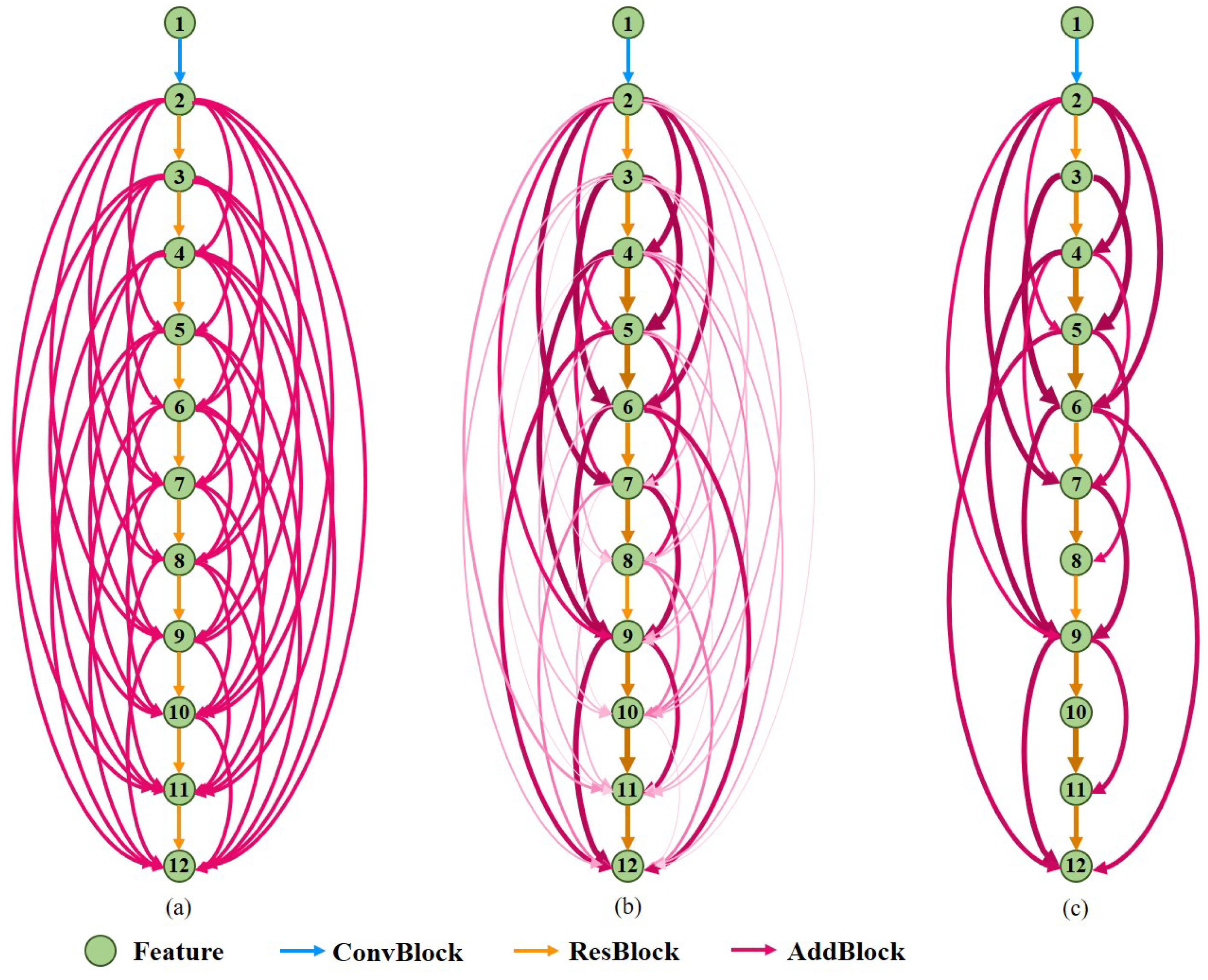
3. PointCNT
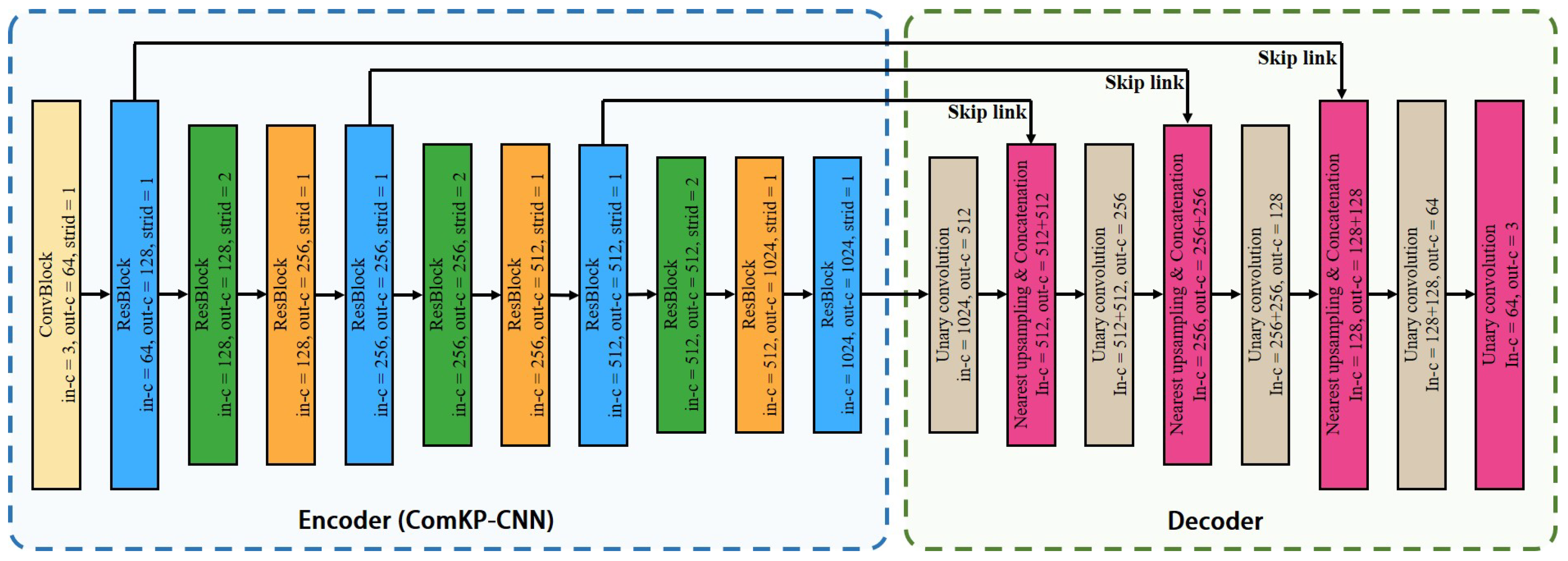
3.1. Feature Extraction Module
3.2. Feature Embedding Module
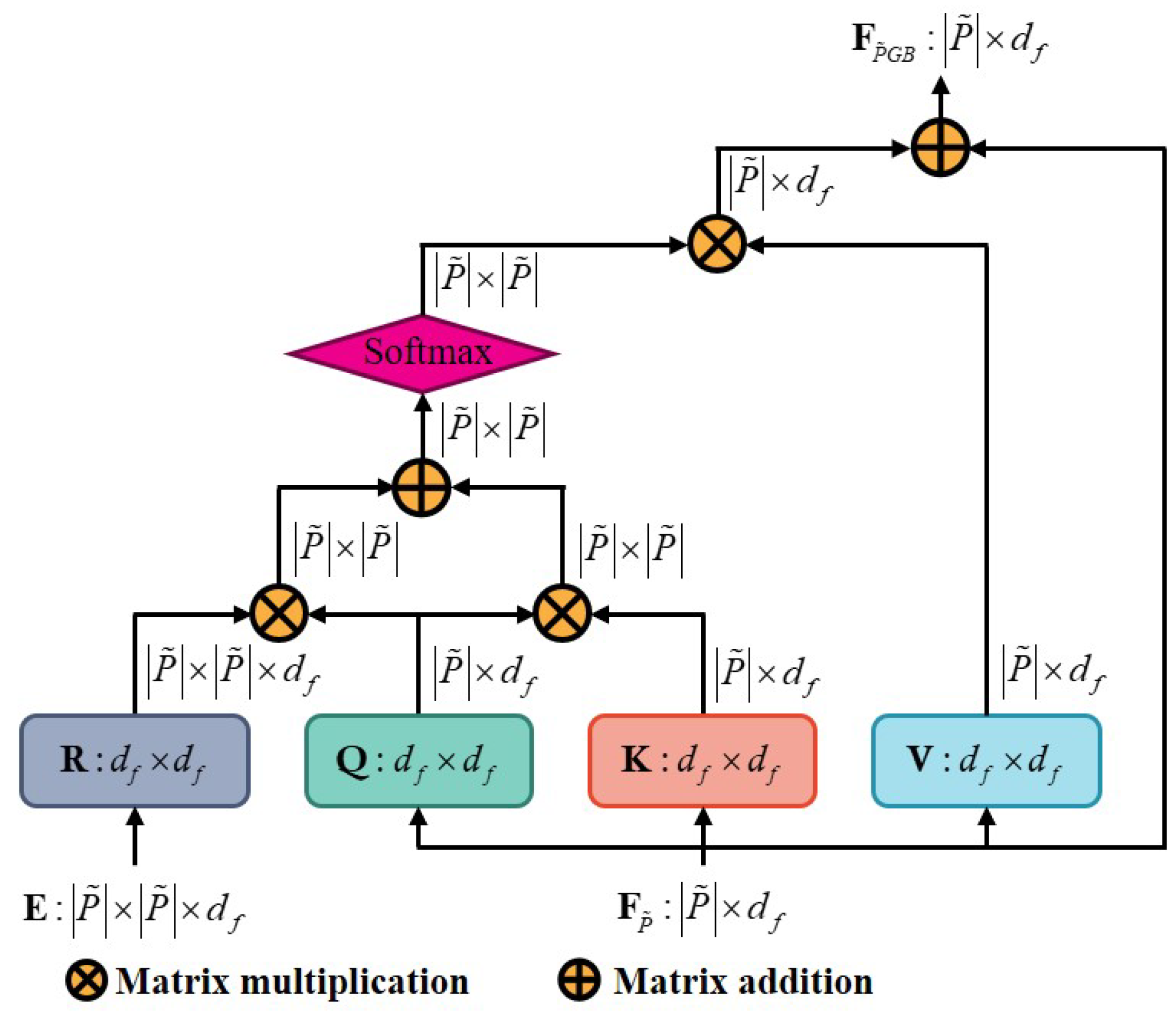
3.2.1. GBSelf-Attention
3.2.2. Coordinate Embedding
3.2.3. Distance Embedding
3.3. Feature Fusion Module
3.4. Registration Module
3.5. Loss Function
4. Experiments and Results
4.1. Implementation Details
4.1.1. Dataset Used in the Experiments
4.1.2. Evaluation Metrics
4.2. Model Evaluation Experiment
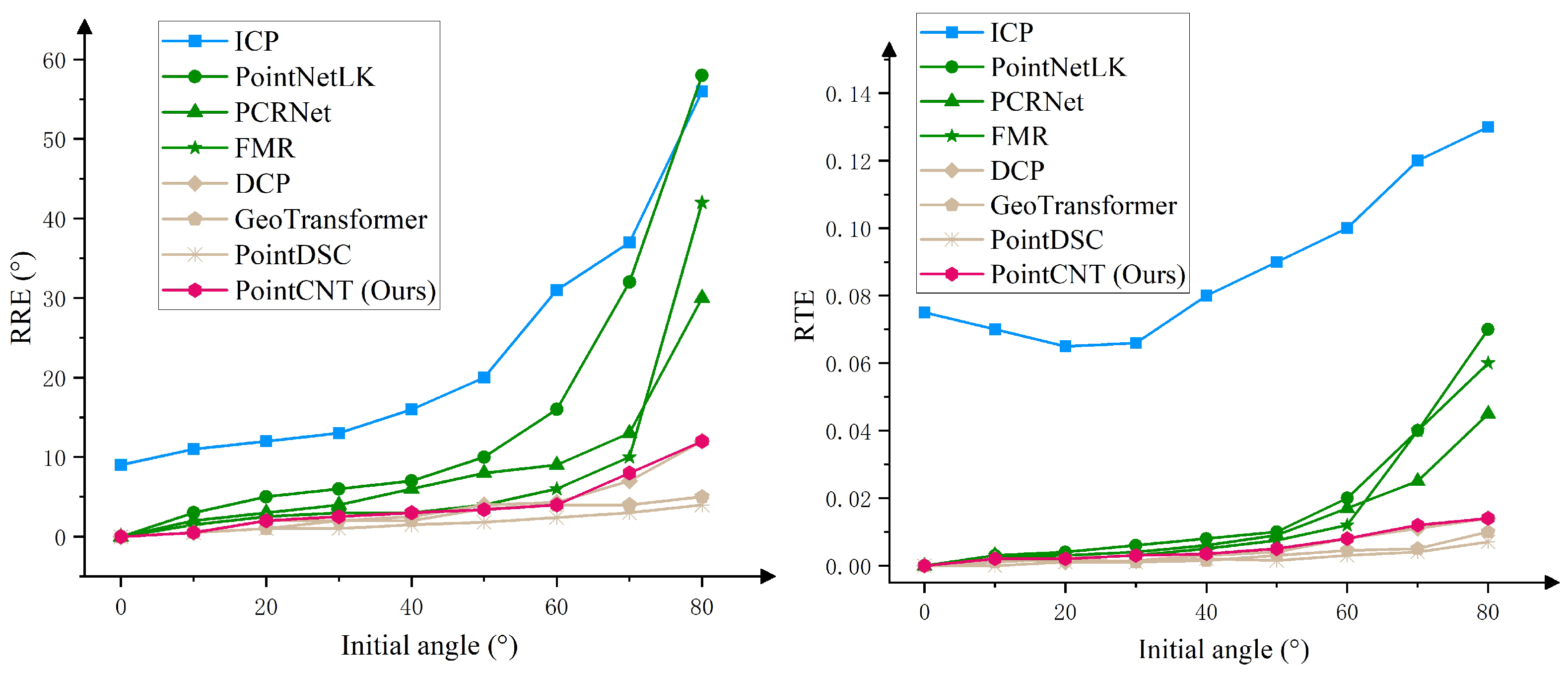
4.2.1. Train and Test on Same Object Categories
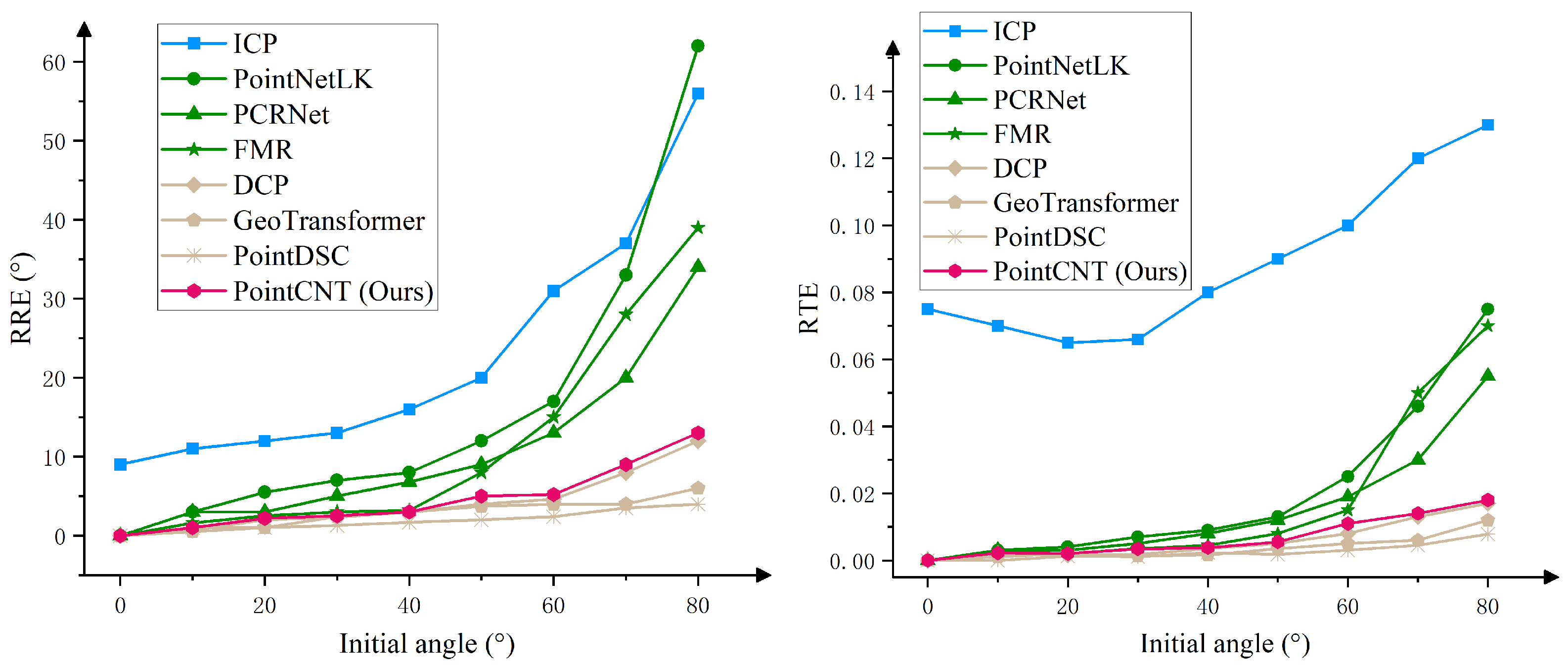
4.2.2. Train and Test on Different Object Categories
4.2.3. Gaussian Noise Experiments
4.2.4. Partial Overlap Experiments
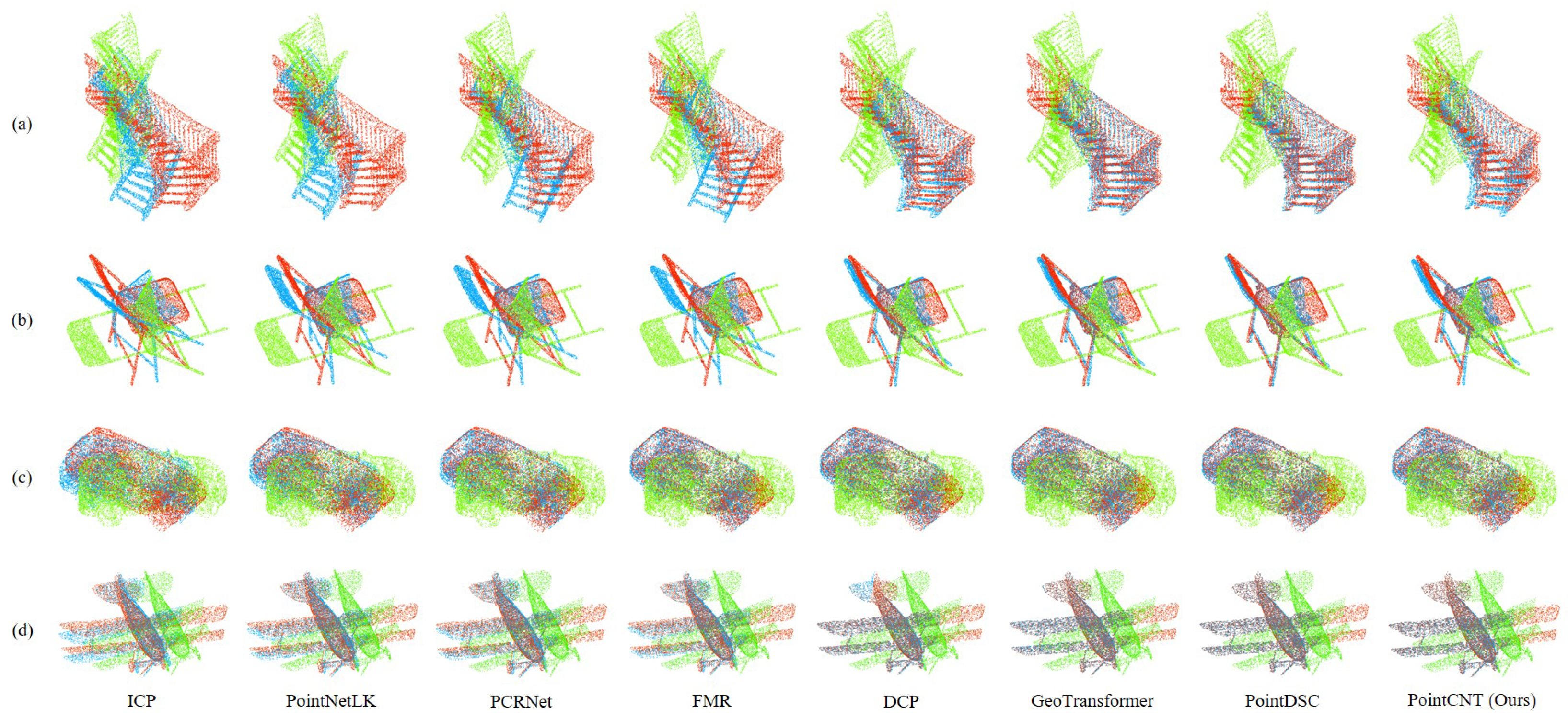
4.2.5. Effectiveness of PointCNT
4.3. Ablation Experiments
4.4. Effectiveness of ComKP-CNN
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| 3DRegNet | Deep Neural Network for 3D Point Registration |
| 3Dsc | 3D Shape Context |
| 4PCS | 4-Points Congruent Sets |
| ANNs | Artificial Neural Networks |
| CAD | Computer-Aided Design |
| ComKP-CNN | Complex Kernel Point Convolution Neural Network |
| ConvBlock | KPConv Block |
| DCP | Deep Closest Point |
| DeepVCP | Deep Virtual Corresponding Points |
| DGR | Deep Global Registration |
| FBCross-attention | Feature-based Cross-attention |
| FMR | Feature-Metric Registration |
| FPFH | Fast Point Feature Histogram |
| GBSelf-attention | Geometric-based Self-attention |
| GeoTransformer | Geometric Transformer |
| Go-ICP | A Globally Optimal Solution to 3D ICP Point-set Registration |
| GPU | Graphic Processing Unit |
| ICP | Iterative Closest Point |
| KP-CNN | Kernel Point Convolution Neural Network |
| KPConv | Kernel Point Convolution |
| LiDAR | Light Detection and Ranging |
| LK | Lucas–Kanade Algorithm |
| MLP | Multilayer Perceptron |
| NDT | Normal Distributions Transform |
| PCA | Principal Component Analysis |
| PCRNet | Point Cloud Registration Network using PointNet Encoding |
| PFH | Point Feature Histogram |
| PointCNT | A One-Stage Point Cloud Registration Approach Based on Complex |
| Network Theory | |
| PointDSC | Robust Point Cloud Registration using Deep Spatial Consistency |
| PointNetLK | Robust and Efficient Point Cloud Registration using PointNet |
| PRNet | Partial Registration Network |
| RANSAC | Random Sample Consensus |
| ResBlock | Residual Blocks |
| RGM | Robust Point Cloud Registration Framework Based on Deep Graph Matching |
| RR | Registration Recall |
| RRE | Relative Rotation Error |
| RTE | Relative Translation Error |
| SVD | Singular Value Decomposition |
References
- Huang, X.; Mei, G.; Zhang, J.; Abbas, R. A comprehensive survey on point cloud registration. arXiv 2021, arXiv:2103.02690. [Google Scholar]
- Lu, W.; Wan, G.; Zhou, Y.; Fu, X.; Yuan, P.; Song, S. DeepVCP: An End-to-End Deep Neural Network for Point Cloud Registration. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 12–21. [Google Scholar] [CrossRef]
- Wang, Y.; Solomon, J.M. Deep Closest Point: Learning Representations for Point Cloud Registration. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3522–3531. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Wei, X.; Xu, H.; He, W.; Sun, C.; Zhang, L.; Li, Y.; Fang, Y. Radar-absorbing materials damage detection through microwave images using one-stage object detectors. NDT E Int. 2022, 127, 102604. [Google Scholar] [CrossRef]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. PointNetLK: Robust & Efficient Point Cloud Registration Using PointNet. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7156–7165. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y. Inverstigation of Parallel Visual Pathways through Pulvinar Nuclei and V2 in Macaque Monkeys. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2021. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Chen, H.; Li, L.; Hu, Z.; Fu, H.; Tai, C.L. PointDSC: Robust Point Cloud Registration using Deep Spatial Consistency. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 15854–15864. [Google Scholar] [CrossRef]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local Neural Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. RepMLP: Re-parameterizing Convolutions into Fully-connected Layers for Image Recognition. arXiv 2021, arXiv:2105.01883. [Google Scholar]
- Guo, M.H.; Liu, Z.N.; Mu, T.J.; Hu, S.M. Beyond Self-Attention: External Attention Using Two Linear Layers for Visual Tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5436–5447. [Google Scholar] [CrossRef] [PubMed]
- Melas-Kyriazi, L. Do You Even Need Attention? A Stack of Feed-Forward Layers Does Surprisingly Well on ImageNet. arXiv 2021, arXiv:2105.02723. [Google Scholar]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Keysers, D.; Uszkoreit, J.; Lucic, M.; et al. MLP-Mixer: An all-MLP Architecture for Vision. In Proceedings of the Neural Information Processing Systems, Online, 6–14 December 2021; Volume 34, pp. 24261–24272. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar] [CrossRef]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing Objects in Range Data Using Regional Point Descriptors. In Computer Vision-ECCV 2004, Proceedings of the 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; Pajdla, T., Matas, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 224–237. [Google Scholar]
- Biber, P.; Strasser, W. The Normal Distributions Transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 3, pp. 2743–2748. [Google Scholar] [CrossRef]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-Points Congruent Sets for Robust Pairwise Surface Registration. ACM Trans. Graph. 2008, 27, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Abdi, H.; Williams, L.J. Principal Component Analysis. In Wiley Interdisciplinary Reviews: Computational Statistics; John Wiley & Sons, Inc.: Hoboken, HJ, USA, 2010; Volume 2, pp. 433–459. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 14–15 November 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Bouaziz, S.; Tagliasacchi, A.; Pauly, M. Sparse Iterative Closest Point. In Proceedings of the Eleventh Eurographics/ACMSIGGRAPH Symposium on Geometry Processing, Genova, Italy, 3–5 July 2013; pp. 113–123. [Google Scholar] [CrossRef] [Green Version]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric Deep Learning: Going beyond Euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Jampani, V.; Sun, D.; Maji, S.; Kalogerakis, E.; Yang, M.H.; Kautz, J. SPLATNet: Sparse Lattice Networks for Point Cloud Processing. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2530–2539. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A Globally Optimal Solution to 3D ICP Point-set Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2241–2254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial Neural Networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Choy, C.; Dong, W.; Koltun, V. Deep Global Registration. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 2511–2520. [Google Scholar] [CrossRef]
- Wang, Y.; Solomon, J.M. PRNet: Self-Supervised Learning for Partial-to-Partial Registration. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32, pp. 8812–8824. [Google Scholar]
- Qin, Z.; Yu, H.; Wang, C.; Guo, Y.; Peng, Y.; Xu, K. Geometric Transformer for Fast and Robust Point Cloud Registration. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11133–11142. [Google Scholar] [CrossRef]
- Pais, G.D.; Ramalingam, S.; Govindu, V.M.; Nascimento, J.C.; Chellappa, R.; Miraldo, P. 3DRegNet: A Deep Neural Network for 3D Point Registration. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7191–7201. [Google Scholar] [CrossRef]
- Fu, K.; Liu, S.; Luo, X.; Wang, M. Robust Point Cloud Registration Framework Based on Deep Graph Matching. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8889–8898. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the IJCAI’81: 7th International Joint Conference on Artificial Intelligence, San Francisco, CA, USA, 24–28 August 1981; Volume 2, pp. 674–679. [Google Scholar]
- Sarode, V.; Li, X.; Goforth, H.; Aoki, Y.; Srivatsan, R.A.; Lucey, S.; Choset, H. PCRNet: Point Cloud Registration Network using PointNet Encoding. arXiv 2019, arXiv:1908.07906. [Google Scholar]
- Huang, X.; Mei, G.; Zhang, J. Feature-Metric Registration: A Fast Semi-Supervised Approach for Robust Point Cloud Registration Without Correspondences. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11363–11371. [Google Scholar] [CrossRef]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv: Flexible and Deformable Convolution for Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6410–6419. [Google Scholar] [CrossRef] [Green Version]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Choy, C.; Park, J.; Koltun, V. Fully Convolutional Geometric Features. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8957–8965. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-Free Local Feature Matching with Transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8918–8927. [Google Scholar] [CrossRef]
- Yu, H.; Li, F.; Saleh, M.; Busam, B.; Ilic, S. CoFiNet: Reliable coarse-to-fine correspondences for robust pointcloud registration. Adv. Neural Inf. Process. Syst. 2021, 34, 23872–23884. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar] [CrossRef] [Green Version]
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 199–208. [Google Scholar] [CrossRef] [Green Version]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Huang, S.; Gojcic, Z.; Usvyatsov, M.; Wieser, A.; Schindler, K. PREDATOR: Registration of 3D Point Clouds with Low Overlap. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 4265–4274. [Google Scholar] [CrossRef]




| Method | Category | Proposed Year | Advantage | Disadvantage |
|---|---|---|---|---|
| ICP | Traditional Registration Method | 1992 | No need for a large amount of data for training. | Sensitive to the initial position of the point cloud and prone to falling into local optima. |
| Go-ICP | 2016 | Adopting a global solution for higher registration accuracy. | Running speed is very slow. | |
| DCP | Learning-based Two-stage Method | 2019 | Has good robustness to noise. | Not applicable for partial overlap. |
| PointDSC | 2021 | High registration accuracy, suitable for partial overlap. | Slow running speed, requires additional algorithms to find corresponding points. | |
| GeoTransformer | 2022 | High registration accuracy, suitable for partial overlap, without the need for additional algorithms to find corresponding points. | Slow running speed, registration accuracy constrained by key point matching. | |
| PointNetLK | Learning-based One-stage Method | 2019 | Applying deep learning to point cloud registration for the first time. | Low registration accuracy, robustness and poor generalization. |
| PCRNet | 2019 | Has good robustness to noise, is an end-to-end model, and runs fast. | The model has a simple structure and low registration accuracy. | |
| FMR | 2020 | The unsupervised learning method is used to extract point cloud features, and the inverse synthesis algorithm is used to calculate the transformation matrix. | Poor registration performance when applied to point clouds with only partial overlap. |
| DNN | Average Path Length | Clustering Coefficient | |
|---|---|---|---|
| DNN for images | VGG16 | 5.647 | 0 |
| ResNet50 | 6.93 | 0 | |
| DNN for point clouds | KP-CNN | 3.972 | 0 |
| ComKP-CNN | 1.597 | 0.684 |
| Initial Angle (°) | ICP | PointNetLK | PCRNet | FMR | DCP | GeoTransformer | PointDSC | PointCNT (Ours) | |
|---|---|---|---|---|---|---|---|---|---|
| RRE | 0 | 9.0583 | 0.0291 | 0.0867 | 0.0559 | 0.0484 | 0.0341 | 0.0574 | 0.0081 |
| 10 | 11.1343 | 3.1020 | 2.1663 | 1.5260 | 0.6368 | 0.6518 | 0.5333 | 0.5488 | |
| 20 | 12.0865 | 5.1491 | 3.1363 | 2.6720 | 2.1669 | 1.1784 | 1.0502 | 2.1426 | |
| 30 | 13.1300 | 6.0747 | 4.0494 | 3.1946 | 2.0129 | 2.0468 | 1.1013 | 2.5567 | |
| 40 | 16.0468 | 7.0898 | 6.0083 | 3.1537 | 2.6155 | 2.0655 | 1.5227 | 3.1776 | |
| 50 | 20.1213 | 10.0190 | 8.0598 | 4.0932 | 4.1018 | 3.6256 | 1.8021 | 3.4471 | |
| 60 | 31.1141 | 16.1352 | 9.0943 | 6.0841 | 4.3775 | 4.0737 | 2.5845 | 4.0157 | |
| 70 | 37.1181 | 32.1661 | 13.0590 | 10.0162 | 7.1807 | 4.0254 | 3.0133 | 8.1355 | |
| 80 | 56.0147 | 58.1466 | 30.1745 | 42.0883 | 12.1429 | 5.1880 | 4.0809 | 12.1752 | |
| RTE | 0 | 0.0752 | 0.0001 | 0.0001 | 0.0003 | 0.0003 | 0.0001 | 0.0002 | 0.0002 |
| 10 | 0.0702 | 0.0031 | 0.0031 | 0.0031 | 0.0020 | 0.0011 | 0.0002 | 0.0021 | |
| 20 | 0.0653 | 0.0041 | 0.0031 | 0.0021 | 0.0011 | 0.0020 | 0.0012 | 0.0021 | |
| 30 | 0.0661 | 0.0062 | 0.0041 | 0.0031 | 0.0018 | 0.0012 | 0.0010 | 0.0031 | |
| 40 | 0.0801 | 0.0080 | 0.0062 | 0.0050 | 0.0033 | 0.0018 | 0.0020 | 0.0037 | |
| 50 | 0.0903 | 0.0102 | 0.0090 | 0.0075 | 0.0043 | 0.0031 | 0.0017 | 0.0053 | |
| 60 | 0.1000 | 0.0202 | 0.0171 | 0.0121 | 0.0083 | 0.0047 | 0.0033 | 0.0083 | |
| 70 | 0.1201 | 0.0402 | 0.0251 | 0.0402 | 0.0111 | 0.0051 | 0.0042 | 0.0122 | |
| 80 | 0.1300 | 0.0701 | 0.0452 | 0.0601 | 0.0141 | 0.0102 | 0.0072 | 0.0140 |
| Initial Angle (°) | ICP | PointNetLK | PCRNet | FMR | DCP | GeoTransformer | PointDSC | PointCNT (Ours) | |
|---|---|---|---|---|---|---|---|---|---|
| RRE | 0 | 9.0959 | 0.1845 | 0.1469 | 0.0092 | 0.0133 | 0.0554 | 0.1145 | 0.0278 |
| 10 | 11.0771 | 3.1107 | 3.1902 | 1.6782 | 0.7943 | 0.5084 | 1.1477 | 1.0007 | |
| 20 | 12.0457 | 5.6493 | 3.0634 | 2.6482 | 2.1269 | 1.1253 | 1.1978 | 2.3915 | |
| 30 | 13.0583 | 7.0153 | 5.1618 | 3.0255 | 2.3756 | 2.4167 | 1.3391 | 2.6777 | |
| 40 | 16.0784 | 8.1973 | 6.9155 | 3.2291 | 3.1534 | 3.0080 | 1.7222 | 3.0906 | |
| 50 | 20.0064 | 12.1962 | 9.0828 | 8.1173 | 4.0734 | 3.8179 | 2.1880 | 5.1831 | |
| 60 | 31.1160 | 17.0211 | 13.1846 | 15.0505 | 4.6581 | 4.0699 | 2.5154 | 5.3267 | |
| 70 | 37.1035 | 33.1767 | 20.1443 | 28.1324 | 8.1459 | 4.0913 | 3.5691 | 9.0556 | |
| 80 | 56.0563 | 62.0186 | 34.0484 | 39.1745 | 12.1727 | 6.1058 | 4.1685 | 13.0916 | |
| RTE | 0 | 0.0749 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 10 | 0.0699 | 0.0030 | 0.0029 | 0.0020 | 0.0020 | 0.0010 | 0.0000 | 0.0022 | |
| 20 | 0.0650 | 0.0041 | 0.0029 | 0.0019 | 0.0014 | 0.0021 | 0.0011 | 0.0020 | |
| 30 | 0.0659 | 0.0070 | 0.0050 | 0.0036 | 0.0018 | 0.0014 | 0.0009 | 0.0033 | |
| 40 | 0.0799 | 0.0090 | 0.0080 | 0.0044 | 0.0034 | 0.0016 | 0.0024 | 0.0037 | |
| 50 | 0.0901 | 0.0130 | 0.0119 | 0.0079 | 0.0050 | 0.0036 | 0.0017 | 0.0055 | |
| 60 | 0.1185 | 0.0251 | 0.0190 | 0.0150 | 0.0079 | 0.0050 | 0.0031 | 0.0110 | |
| 70 | 0.1150 | 0.0459 | 0.0300 | 0.0501 | 0.0130 | 0.0060 | 0.0045 | 0.0140 | |
| 80 | 0.1271 | 0.0750 | 0.0549 | 0.0701 | 0.0169 | 0.0120 | 0.0079 | 0.0181 |
| Gaussian Standard Deviation | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | |
|---|---|---|---|---|---|---|---|
| RRE | 0 | 0.0029 | 0.0123 | 0.0133 | 0.0125 | 0.0071 | 0.0002 |
| 10 | 0.5095 | 0.4869 | 0.5851 | 0.7079 | 0.6462 | 0.6709 | |
| 20 | 2.0118 | 2.1917 | 2.1138 | 2.3090 | 2.2119 | 2.3873 | |
| 30 | 2.5086 | 2.5101 | 2.6973 | 2.6055 | 2.7947 | 2.6089 | |
| 40 | 3.0057 | 3.4008 | 3.1896 | 3.5051 | 3.4001 | 3.1924 | |
| 50 | 3.3896 | 3.6013 | 3.6986 | 3.4945 | 3.7084 | 3.7896 | |
| 60 | 3.9989 | 4.2122 | 4.3876 | 4.1903 | 4.4972 | 4.5954 | |
| 70 | 7.9855 | 8.3915 | 8.1942 | 8.4931 | 8.7858 | 8.6007 | |
| 80 | 11.9947 | 13.0138 | 13.0043 | 13.4954 | 13.1888 | 13.7911 | |
| RTE | 0 | 0.0000 | 0.0001 | 0.0000 | 0.0001 | 0.0000 | 0.0001 |
| 10 | 0.0020 | 0.0020 | 0.0017 | 0.0021 | 0.0021 | 0.0024 | |
| 20 | 0.0019 | 0.0022 | 0.0025 | 0.0024 | 0.0024 | 0.0026 | |
| 30 | 0.0029 | 0.0029 | 0.0035 | 0.0038 | 0.0036 | 0.0036 | |
| 40 | 0.0036 | 0.0039 | 0.0036 | 0.0037 | 0.0040 | 0.0042 | |
| 50 | 0.0051 | 0.0053 | 0.0054 | 0.0054 | 0.0055 | 0.0056 | |
| 60 | 0.0082 | 0.0084 | 0.0083 | 0.0083 | 0.0083 | 0.0084 | |
| 70 | 0.0119 | 0.0118 | 0.0130 | 0.0133 | 0.0125 | 0.0135 | |
| 80 | 0.0143 | 0.0155 | 0.0150 | 0.0152 | 0.0161 | 0.0161 |
| Model | RRE (°) | RTE | RR (%) | Time (s) |
|---|---|---|---|---|
| ICP | 17.3752 | 0.0253 | 82.3 | 0.12 |
| PointNetLK | 17.3752 | 0.0253 | 82.3 | 0.12 |
| PCRNet | 9.5863 | 0.0229 | 85.7 | 0.16 |
| FMR | 8.8724 | 0.0183 | 88.2 | 0.08 |
| DCP | 4.7283 | 0.0067 | 95.2 | 0.21 |
| GeoTransformer | 3.6878 | 0.0042 | 97.1 | 0.23 |
| PointDSC | 3.4586 | 0.0036 | 97.3 | 0.24 |
| PointCNT (Ours) | 4.5128 | 0.0064 | 96.4 | 0.15 |
| Dataset | RRE (°) | RTE (cm) | RR (%) |
|---|---|---|---|
| 3DMatch | 0.3258 | 7.3854 | 93.6 |
| KITTI | 0.2614 | 7.9368 | 97.2 |
| CK | SS | CE | DE | FB | MP | AP | RQ | RM | RRE (°) | RTE | RR (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| baseline | ✓ | ✓ | 6.7322 | 0.0135 | 85.9 | |||||||
| CK | ✓ | ✓ | ✓ | 5.3264 | 0.0083 | 89.3 | ||||||
| SS | ✓ | ✓ | ✓ | 5.7217 | 0.0087 | 87.4 | ||||||
| CE | ✓ | ✓ | ✓ | 5.6429 | 0.0086 | 87.6 | ||||||
| DE | ✓ | ✓ | ✓ | 5.8141 | 0.0088 | 86.9 | ||||||
| FB | ✓ | ✓ | ✓ | 5.5833 | 0.0085 | 88.1 | ||||||
| MP | ✓ | ✓ | 6.0135 | 0.0090 | 86.6 | |||||||
| RQ | ✓ | ✓ | 6.1078 | 0.0091 | 86.4 | |||||||
| SS+CE+DE+FB+MP+RQ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.8463 | 0.0075 | 94.1 | |||
| CK+CE+DE+FB+MP+RQ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.7234 | 0.0067 | 95.2 | |||
| CK+SS+DE+FB+MP+RQ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.7832 | 0.0070 | 94.8 | |||
| CK+SS+CE+FB+MP+RQ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.7138 | 0.0066 | 95.3 | |||
| CK+SS+CE+DE+MP+RQ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.8195 | 0.0073 | 94.4 | |||
| CK+SS+CE+DE+FB+AP+RQ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.6618 | 0.0069 | 95.6 | ||
| CK+SS+CE+DE+FB+MP+RM | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.6576 | 0.0068 | 95.8 | ||
| CK+SS+CE+DE+FB+MP+RQ (Ours) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | 4.5128 | 0.0064 | 96.4 |
| Initial Angle | 20° | 40° | 60° | 80° | ||||
|---|---|---|---|---|---|---|---|---|
| Metrics | RRE (°) | RTE | RRE (°) | RTE | RRE (°) | RTE | RRE (°) | RTE |
| Using ComKP-CNN | 2.4273 | 0.0026 | 3.2351 | 0.0041 | 4.6168 | 0.0085 | 13.8413 | 0.0162 |
| Using KP-CNN | 2.5185 | 0.0031 | 3.5017 | 0.0048 | 4.8912 | 0.0097 | 14.376 | 0.0177 |
| Using self-supervised modeule | 2.4273 | 0.0026 | 3.2351 | 0.0041 | 4.6168 | 0.0085 | 13.8413 | 0.0162 |
| No self-supervised modeule | 2.5032 | 0.0029 | 3.4926 | 0.0045 | 4.8128 | 0.0092 | 14.1734 | 0.0169 |
| Using coordinate embedding | 2.4273 | 0.0026 | 3.2351 | 0.0041 | 4.6168 | 0.0085 | 13.8413 | 0.0162 |
| No coordinate embedding | 2.4984 | 0.0028 | 3.4586 | 0.0044 | 4.8326 | 0.0091 | 14.0128 | 0.0168 |
| Using distance embedding | 2.4273 | 0.0026 | 3.2351 | 0.0041 | 4.6168 | 0.0085 | 13.8413 | 0.0162 |
| No distance embedding | 2.4815 | 0.0029 | 3.4125 | 0.0044 | 4.8402 | 0.0091 | 13.9821 | 0.0166 |
| Using FBCross-attention | 2.4273 | 0.0026 | 3.2351 | 0.0041 | 4.6168 | 0.0085 | 13.8413 | 0.0162 |
| No FBCross-attention | 2.5148 | 0.003 | 3.4824 | 0.0046 | 4.8621 | 0.0094 | 14.2675 | 0.0172 |
| Using max pooling | 2.4273 | 0.0026 | 3.2351 | 0.0041 | 4.6168 | 0.0085 | 13.8413 | 0.0162 |
| Using average pooling | 2.4637 | 0.0028 | 3.3861 | 0.0043 | 4.8236 | 0.0087 | 13.9643 | 0.0165 |
| PointNetLK | PCRNet | FMR | DCP | GeoTransformer | PointDSC | ||
|---|---|---|---|---|---|---|---|
| Without ComKP-CNN | RRE (°) | 17.3752 | 9.5863 | 8.8724 | 4.7283 | 3.6878 | 3.4586 |
| RTE | 0.0253 | 0.0229 | 0.0183 | 0.0067 | 0.0042 | 0.0036 | |
| RR (%) | 82.3 | 85.7 | 88.2 | 95.2 | 97.1 | 97.3 | |
| With ComKP-CNN | RRE (°) | 14.8463 | 7.8362 | 7.2156 | 3.6748 | 3.1163 | 3.0376 |
| RTE | 0.0221 | 0.0204 | 0.0168 | 0.0055 | 0.0037 | 0.0034 | |
| RR (%) | 86.6 | 87.8 | 90.4 | 96.3 | 97.7 | 97.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wei, X.; Xu, H.; Li, C.; Hou, Y.; Yin, Y.; He, W. PointCNT: A One-Stage Point Cloud Registration Approach Based on Complex Network Theory. Remote Sens. 2023, 15, 3545. https://doi.org/10.3390/rs15143545
Wu X, Wei X, Xu H, Li C, Hou Y, Yin Y, He W. PointCNT: A One-Stage Point Cloud Registration Approach Based on Complex Network Theory. Remote Sensing. 2023; 15(14):3545. https://doi.org/10.3390/rs15143545
Chicago/Turabian StyleWu, Xin, Xiaolong Wei, Haojun Xu, Caizhi Li, Yuanhan Hou, Yizhen Yin, and Weifeng He. 2023. "PointCNT: A One-Stage Point Cloud Registration Approach Based on Complex Network Theory" Remote Sensing 15, no. 14: 3545. https://doi.org/10.3390/rs15143545
APA StyleWu, X., Wei, X., Xu, H., Li, C., Hou, Y., Yin, Y., & He, W. (2023). PointCNT: A One-Stage Point Cloud Registration Approach Based on Complex Network Theory. Remote Sensing, 15(14), 3545. https://doi.org/10.3390/rs15143545







