Experiences with the RTM Method in Local Quasi-Geoid Modeling

Abstract

In local quasi-geoid modeling, the residual terrain modeling (RTM) method is often used to remove short-wavelength gravity field signals from the measured gravity on the ground in order to obtain a regularized and smooth gravity field that is suited for field interpolation and modeling. Accurate computation of RTM corrections plays a crucial role in computing an accurate local quasi-geoid, and it requires a set of fine-tuned parameters, including the combination of DEMs with different resolutions for suitably representing the real topography, the choice of integration radius for properly defining the extent of the computation zone, and the determination of reference topography to properly describe the RTM-reduced Earth’s surface. To our knowledge, this has not been systematically documented, despite its obvious importance. This study aims to systematically investigate the impact of these factors on RTM correction computation and, consequently, on local quasi-geoid modeling to provide practical guidelines for real-world applications. The tesseroid-based gravity forward modeling technique is employed to investigate the following issues existing in the practical use of the RTM method: ① Can the combination of a high-resolution DEM and a DEM with a lower resolution replace the single use of the high-resolution DEM for RTM correction computation while maintaining accuracy and improving efficiency? If it does, how do I properly choose the resolution of this coarse DEM as well as the integration radius r₁ for the inner zone and r₂ for the outer zone? ② How large would the differences between the RTM corrections computed by three types of reference topographies, which are obtained from the direct averaging (DA) approach, the moving averaging (MA) approach, and the spherical harmonic (SH) approach, be, and how large would their impact on quasi-geoid modeling be? To obtain objective findings, two research regions were selected for this investigation. One is the Colorado test area (USA) with rugged terrain, and the other is the Auvergne test area (France) with moderate terrain. The main numerical findings are: (1) the combination of the 3” resolution DEM (inner zone) and the 30″ resolution DEM (outer zone) is sufficient for accurate and efficient RTM correction computation; (2) if the resolution of the reference topography is 5′ or slightly lower, all three types of reference topographies are able to obtain local quasi-geoid models at a similar accuracy level, while the values of r₁ and r₂ are preferred to be at least 20 km and 111 km, respectively; (3) if the reference topography has a resolution of 30′ or lower, the MA or SH reference topography is recommended, especially for the latter one, and the values of r₁ and r₂ are suggested to be at least 20 km and 222 km, respectively. The above numerical findings can be taken as a reference for local quasi-geoid determination in areas with different topographic regimes than the two selected test areas.

1. Introduction

Local quasi-geoid modeling is one of the routine tasks in physical geodesy [1,2], since the quasi-geoid serves as the reference surface for the normal height, which is adopted in many countries [3,4,5,6,7,8,9]. In order to obtain an accurate local quasi-geoid model, the remove-compute-restore (RCR) technique is widely applied [4], and it is briefly described as follows: First, the contributions of a global geopotential model (GGM) and of the topography are removed from the gravity data. The former reduces the long-wavelength signals in the data, so that the effect of the data far away from the area of interest can possibly be ignored in computing the local quasi-geoid model. The latter ensures that the short-wavelength signals have less energy in the residual field, making it smoother than the original one and easier for field interpolation and modeling. Second, the residual gravity data are transformed into the residual height anomalies via various methods, such as the Stokes’s integral [10,11,12], the least-squares collocation [13,14,15], and the radial basis functions [6,16,17,18]. Third, the height anomaly contributions from the GGM and the topography are added to the residual height anomalies, yielding the final quasi-geoid model.

Obviously, besides the data coverage and quality, accurate determination of the local quasi-geoid model greatly depends on the selection of the most appropriate GGM, modeling method, and topography reduction scheme for the research area. In this study, we only focus on the topographic reduction, and more specifically, the so-called residual terrain modeling (RTM) reduction [19,20]. For other types of topographic reductions that may be used in local quasi-geoid modeling, we refer to the reviews in [21,22].

In the RCR procedure, the RTM reduction aims to reduce the gravity data for the gravitational signals of topographic masses that are not captured by the used GGM. To achieve this, the real Earth’s topography is replaced by a smoothed reference topography with a resolution relevant to the half-wavelength resolution of the GGM, but only in approximation. In fact, the filtering of DEM heights in the topography domain is not exactly equivalent to the filtering in the gravity domain, leading to the so-called spectral filter problem of the RTM method. For more in-depth discussions on this issue, refer to [23]. After determining the reference topography based on the real topography, the residual terrain is defined by the masses between the two topographies. The terrain above the reference topography has actual masses with a positive density, while the parts below the reference topography are filled by masses with a negative density (see Figure 1). The data are then reduced by removing the gravitational effects of these masses. For the sake of conciseness, we refer to the Earth after the RTM reduction as the RTM-reduced Earth, which is bounded by the reference topography, and call the gravitational effects caused by the residual terrain the RTM corrections or effects.

To obtain an accurate local quasi-geoid model, accurate RTM correction computation is necessary, and it is affected by several factors, such as the selection of high-resolution digital elevation models (DEMs) for suitably representing the real topography, the choice of integration radius for properly defining the extent of the computation zone, and the determination of reference topography to properly describe the RTM-reduced Earth’s surface (see Figure 1).

An ideal case for representing the real topography over the whole research area is to use an ultra-high resolution DEM, for example, the shuttle radar topography mission (SRTM) DEM [24] and the MERIT DEM [25], both with a resolution of 3” (see the left panel of Figure 2). In this case, the computational burden would be high since the number of mass elements included in one-point computation is usually large, especially for large-scale research areas. Considering the fact that the gravitational potential and its derivatives decay with the distance of the mass element to the computation point, the whole computation zone centered at each computation point is usually divided into two zones. The inner zone uses a high-resolution DEM and is defined by the integration radius r₁. The outer zone employs a DEM with a lower resolution and is defined by the integration radius r₂ (see the right panel of Figure 2). In some studies, more than two computation zones are selected [26,27,28]. In this study, we focus on the two-zone scheme, which has been implemented in the widely-used prism-based “tc.for” program in the GRAVSOFT software [29] and the recently developed tesseroid-based programs in the TCTESS software [30]. While considering the accuracy and efficiency of the RTM correction computation for practical use, it is straightforward for us to ask the question, “can the combination of a high-resolution DEM and a DEM with a lower resolution really replace the single use of the high-resolution DEM while maintaining accuracy and improving efficiency?” If it does, how do I properly choose the resolution of this coarse DEM as well as the integration radius r₁ for the inner zone and r₂ for the outer zone? This is the first research question to be addressed in this study. Recently, the performance of using different combinations of DEM resolutions on terrain correction computation was investigated in [31]. It verified that the use of the 1” resolution DEM in the inner zone and the 15” resolution DEM in the outer zone can lead to sub-mGal accuracy with less computational time in rough topography. Here we focus on the RTM correction computation and use the original 3” resolution DEM.

In local quasi-geoid modeling using the RCR technique and the RTM reduction, the reference topography should be chosen as the one closest to the topography that is captured by the GGM, so that the errors caused by spectral inconsistencies can be reduced significantly, although such errors cannot be totally eliminated. To do so, the resolution of the reference topography is usually set to be equal to the half-wavelength resolution of the GGM, albeit in approximation [23]. When the resolution is known, three commonly used approaches, namely the direct averaging (DA) approach (i.e., block-mean values), the moving averaging (MA) approach, and the spherical harmonic (SH) approach, can be applied to filter the original high-resolution DEM to generate the reference topography. The former two approaches can be implemented by the “tcgrid.for” program in the GRAVSOFT software. The SH approach first estimates the SH coefficients of the detailed topography via the surface SH analysis and then computes the heights of the reference topography via the SH synthesis. For more details about this approach, we refer to [32,33]. It should be noted that the RTM method utilizing the reference topography obtained from the SH approach has been successfully used for high-frequency GGM augmentation in many areas with different topographic regimes [26,28,33,34,35]. In addition to the above-mentioned three approaches, the reference topography can also be obtained by applying a circular sharp cutoff filter [7] or a spherical Gaussian low-pass filter [36] to a high-resolution DEM. To our understanding, both filters are similar to the MA approach and thus are not further discussed here. It is clear that the reference topographies obtained by different approaches would differ from each other, and so the resulting residual terrain would also differ. The performance of using them on RTM correction computation and quasi-geoid modeling has not been investigated yet. Therefore, the second research question is: how large would the differences between the RTM corrections computed by using different types of reference topographies be, and how large would their impact on quasi-geoid modeling be?

Although the importance of these factors (i.e., combination of DEM resolutions, choice of integration radius, and determination of reference topography type) is obvious, to the best of our knowledge, they have not been systematically investigated. Therefore, the main purpose of this study is to systematically investigate the impact of these factors on RTM correction computation and quasi-geoid modeling to provide practical guidelines for real-world applications.

The remainder of this paper is organized as follows: Section 2 explains why we compute RTM corrections to gravity anomalies and height anomalies in local quasi-geoid modeling and gives corresponding mathematical descriptions. Various numerical experiments with the aim of investigating the DEM resolution combination effect, integration radius effect, and reference topography effect on RTM correction computation are first presented in Section 3. Secondly, the impact of the integration radius for the outer zone and of the type of reference topography on local quasi-geoid modeling is investigated. Finally, some conclusions and suggestions on using the RTM method in local quasi-geoid determination are given in Section 4.

2. RTM Corrections to Gravity Anomalies and Height Anomalies

The real Earth is replaced by the RTM-reduced Earth after the RTM reduction. Since mass redistribution exists during this procedure, gravity and potential actually change. In this section, we try to mathematically describe how gravity observations on the Earth’s surface are reduced by the RTM method; more specifically, how the free-air gravity anomalies on the Earth’s surface are transformed into the so-called RTM-reduced gravity anomalies and how the height anomalies referring to the RTM-reduced Earth are converted to those referring to the real Earth.

Let P be an arbitrary point on the Earth’s surface, $g\left(P\right)$ and $W\left(P\right)$ are denoted as the measured gravity and potential at this point, respectively. The RTM-reduced gravity and potential after removing the gravitational attraction $\delta g_{\mathrm{RTM}}\left(P\right)={\left.-\frac{\partial \delta V_{\mathrm{RTM}}}{\partial r}\right|}_P$ and gravitational potential $\delta V_{\mathrm{RTM}}\left(P\right)$ caused by the residual terrain are expressed as

$$g^{\mathrm{RTM}}\left(P\right)=g\left(P\right)-\delta g_{\mathrm{RTM}}\left(P\right),$$

(1)

$$W^{\mathrm{RTM}}\left(P\right)=W\left(P\right)-\delta V_{\mathrm{RTM}}\left(P\right).$$

(2)

Equation (2) shows that the potential on the Earth’s surface also changes due to the mass redistribution occurring in the RTM reduction. According to the definition of the telluroid, on which the normal potential is equal to the potential on the Earth’s surface [1,2], it is easy to infer that a displacement of the telluroid happens after the RTM reduction. Let $H^N\left(P\right)$ be the distance from the real telluroid to the reference ellipsoid with the normal potential of $U=W_0$ along the normal to the reference ellipsoid, which can be explicitly expressed as

$$H^N\left(P\right)=\frac{W_0-W\left(P\right)}{\overline{\gamma }},$$

(3)

where $\overline{\gamma }$ is the mean value of the normal gravity between the reference ellipsoid and the real telluroid. It should be emphasized that $H^N\left(P\right)$ is actually equal to the normal height of the point P, referring to the real topography.

In a similar way, the distance of the RTM-reduced telluroid to the reference ellipsoid (i.e., the normal height of the point P referring to the RTM-reduced Earth) is given as

$${\left(H^N\right)}^{\mathrm{RTM}}\left(P\right)=\frac{W_0-W^{\mathrm{RTM}}\left(P\right)}{{\overline{\gamma }}^{\mathrm{RTM}}},$$

(4)

where ${\overline{\gamma }}^{\mathrm{RTM}}$ is the mean value of the normal gravity between the reference ellipsoid and the RTM-reduced telluroid. Since the displacement between the real and RTM-reduced telluroids is quite small, ${\overline{\gamma }}^{\mathrm{RTM}}$ can be approximated by $\overline{\gamma }$, resulting in a negligible error in ${\left(H^N\right)}^{\mathrm{RTM}}\left(P\right)$. Upon this approximation, we have the following relation:

$${\left(H^N\right)}^{\mathrm{RTM}}\left(P\right)-H^N\left(P\right)=\frac{W\left(P\right)-W^{\mathrm{RTM}}\left(P\right)}{\overline{\gamma }}=\frac{\delta V_{\mathrm{RTM}}\left(P\right)}{\overline{\gamma }}.$$

(5)

Let $\zeta$ and ${\left(\zeta \right)}^{\mathrm{RTM}}$ be the height anomaly before and after the RTM reduction, respectively, and we then obtain the following relation:

$$\zeta +H^N={\left(\zeta \right)}^{\mathrm{RTM}}+{\left(H^N\right)}^{\mathrm{RTM}}.$$

(6)

Inserting Equation (6) into Equation (5), we then have

$$\zeta \left(P\right)-{\zeta }^{\mathrm{RTM}}\left(P\right)=\underset{{\zeta }_{\mathrm{RTM}}\left(P\right)}{\underbrace{\frac{\delta V_{\mathrm{RTM}}\left(P\right)}{\overline{\gamma }}}}.$$

(7)

The above correction can be considered analogous to the primary indirect effect appearing in Helmert’s method of condensation [37,38,39]. When the height anomalies referring to the RTM-reduced Earth are computed, the right-hand side term of Equation (7) must be added back in order to generate the height anomalies referring to the real Earth. Because this term has the same form as that of the Bruns’ formula that estimates the height anomaly by means of dividing the disturbing potential by the normal gravity [1,2], we refer to it as the RTM correction to height anomalies ${\zeta }_{\mathrm{RTM}}$.

Since the gravity anomaly on the Earth’s surface is defined as the difference between the measured gravity and the normal gravity at the corresponding point on the telluroid, the RTM-reduced gravity anomaly on the Earth’s surface is defined as

$$\mathsf{\Delta }{g}^{\mathrm{RTM}}\left(P\right)=g^{\mathrm{RTM}}\left(P\right)-\gamma \left[r\left(P\right)-{\zeta }^{\mathrm{RTM}}\left(P\right)\right]=g^{\mathrm{RTM}}\left(P\right)-\gamma \left[r_0+{\left(H^N\right)}^{\mathrm{RTM}}\left(P\right)\right],$$

(8)

where $r_0$ is the geocentric radius of the reference ellipsoid and $r\left(P\right)$ is the geocentric radius of the point P.

Taking the following approximation

$$\begin{array}{l}\gamma \left[r_0+{\left(H^N\right)}^{\mathrm{RTM}}\left(P\right)\right]\doteq \gamma \left[r_0+H^N\left(P\right)\right]+\frac{\partial \gamma }{\partial n}\left[{\left(H^N\right)}^{\mathrm{RTM}}\left(P\right)-H^N\left(P\right)\right]\\ =\gamma \left[r_0+H^N\left(P\right)\right]+\frac{\partial \gamma }{\partial n}\left[\frac{\delta V_{\mathrm{RTM}}\left(P\right)}{\overline{\gamma }}\right]\\ \approx \gamma \left[r_0+H^N\left(P\right)\right]-\frac{2\delta V_{\mathrm{RTM}}\left(P\right)}{r\left(P\right)}\end{array}$$

(9)

and Equation (1) into account, Equation (8) can be rewritten as

$$\mathsf{\Delta }{g}^{\mathrm{RTM}}\left(P\right)=\underset{\mathsf{\Delta }{g}_{\mathrm{obs}}\left(P\right)}{\underbrace{g\left(P\right)-\gamma \left[r_0+H^N\left(P\right)\right]}}-\underset{\mathsf{\Delta }{g}_{\mathrm{RTM}}\left(P\right)}{\underbrace{\left[\delta g_{\mathrm{RTM}}\left(P\right)-\frac{2\delta V_{\mathrm{RTM}}\left(P\right)}{r\left(P\right)}\right]}}.$$

(10)

On the right-hand side of Equation (10), the first two terms actually denote the free-air gravity anomaly on the Earth’s surface, such as the observed terrestrial gravity anomaly. The third term is the gravitational attraction caused by the residual terrain, and the fourth term can be considered analogous to the second indirect effect appearing in Helmert’s method of condensation [37,38,39]. Note that the expression in the second square bracket of Equation (10) has the same form as the fundamental equation of physical geodesy that defines the gravity anomaly based on the disturbing potential [1,2]. Therefore, we refer to it as the RTM correction to gravity anomalies $\mathsf{\Delta }{g}_{\mathrm{RTM}}$.

In principle, the RTM correction should be harmonic. It satisfies this condition for points above the reference topography but fails for points below the reference topography. In the latter case, harmonic correction is added in order to obtain a harmonically downward continued value. Various harmonic correction approaches have been studied in the past decades [3,19,20,32,33,36,40,41,42]. In this study, we follow the classical approach of [19,20], in which the harmonic correction is computed based on the concept of mass condensation and is only applied to gravity.

3. Numerical Experiments

The experiments are divided into two parts. First, RTM corrections to gravity anomalies and height anomalies computed by different parameter settings are compared and analyzed with the goal of quantifying their impact on RTM correction computation. Second, local quasi-geoid models are computed by using various RTM corrections and then validated against GNSS/leveling data in order to illustrate how these parameter settings affect the determination of quasi-geoid.

Numerical experiments are carried out in two regions with different topographic regimes. The first region is located in the Colorado area of the USA and has quite rugged terrain. Recently, this area has been selected as the test area for “the 1 cm geoid experiment” [43]. The second region is located in the Auvergne area of France and has moderate terrain. In the past, it has been chosen as the test area to compare different methods for local quasi-geoid modeling [44,45].

The “tctessv3omp.f90” program from the TCTESS software is used for all RTM correction computations. It has almost the same structure as that of the “tc.for” program and is further parallelized by OpenMP. For more details about this program and the TCTESS software, refer to [30]. All computations are performed on a single node of a cluster equipped with two 12-core Intel(R) Xeon(R) Gold 6126 @ 2.60 GHz CPUs with one thread per core. The used FORTRAN compiler is an Intel compiler (ifort version 18.0.1) executed in GNU/Linux.

3.1. Data Sets

In the Colorado test area, there are 59,303 terrestrial gravity observations irregularly distributed in the area bounded by ${35}^{\circ }\mathrm{N}\le \phi \le {40}^{\circ }\mathrm{N}$ and ${250}^{\circ }\mathrm{E}\le \lambda \le {258}^{\circ }\mathrm{E}$. After deleting those observations with absolute values of the differences between the given heights and the corresponding heights from the DEM that were larger than 100 m, 58,913 observations are left for the numerical experiments. 222 GSVS17 (Geoid Slop Validation Survey 2017) [46] GNSS/leveling benchmarks would provide geoid undulations with an accuracy of about 1.5 cm and height anomalies with an accuracy of about 1.2 cm for validation purposes. The DEM used for precisely representing the topography of the test area is chosen as the MERIT DEM with a resolution of 3”, covering the area of ${34}^{\circ }\mathrm{N}\le \phi \le {41}^{\circ }\mathrm{N}$ and ${249}^{\circ }\mathrm{E}\le \lambda \le {259}^{\circ }\mathrm{E}$. For more details about this data set, refer to [43].

The Auvergne data set contains 243,954 terrestrial gravity observations, which are irregularly distributed in the area bounded by ${43}^{\circ }\mathrm{N}\le \phi \le {49}^{\circ }\mathrm{N}$ and $-1^{\circ }\mathrm{E}\le \lambda \le 7^{\circ }\mathrm{E}$; the SRTM DEM with a resolution of 3”, covering a larger area bounded by ${42}^{\circ }\mathrm{N}\le \phi \le {50}^{\circ }\mathrm{N}$ and $-2^{\circ }\mathrm{E}\le \lambda \le 8^{\circ }\mathrm{E}$; and 75 GNSS/leveling benchmarks located in the middle of the test area. For more details about this data set, refer to [44].

In each test area, the quasi-geoid computation area is selected to be smaller than that covered by gravity observations and DEM, in order to avoid edge effects. The computation points are regularly distributed in this area with a resolution of 1′, resulting in 65,341 points in the Colorado test area and 43,621 points in the Auvergne test area. Figure 3 shows the locations of all data points, the DEM, as well as the quasi-geoid computation area.

3.2. Parameter Settings

According to the two research questions posed in Section 1, the issues to be investigated in this study can be summarized as the DEM resolution combination effect, the integration radius effect, and the reference topography effect. For the DEM resolution combination effect, we will design several scenarios using two DEMs with different resolutions and compare the differences between RTM corrections computed by using different DEM resolution combination scenarios. The integration radius effect includes the effect of the integration radius r₁ for the inner zone and the effect of the integration radius r₂ for the outer zone. For each case, the RTM corrections computed by using various values of r₁ and r₂ will be compared and analyzed. The reference topography effect is used to investigate how large the differences between RTM corrections will be if using the reference topographies obtained by the DA approach, the MA approach, and the SH approach. In addition, these RTM corrections are also compared for gravity anomaly reduction.

Table 1. Details of the parameters used for the numerical experiments in this study. In the row of DEM resolution combinations, for example, 3″ + 30″ means the 3″ resolution DEM is used in the inner zone and the 30″ resolution DEM is employed in the outer zone. The other DEM resolution combination scenarios have a similar meaning as that of 3″ + 30″.

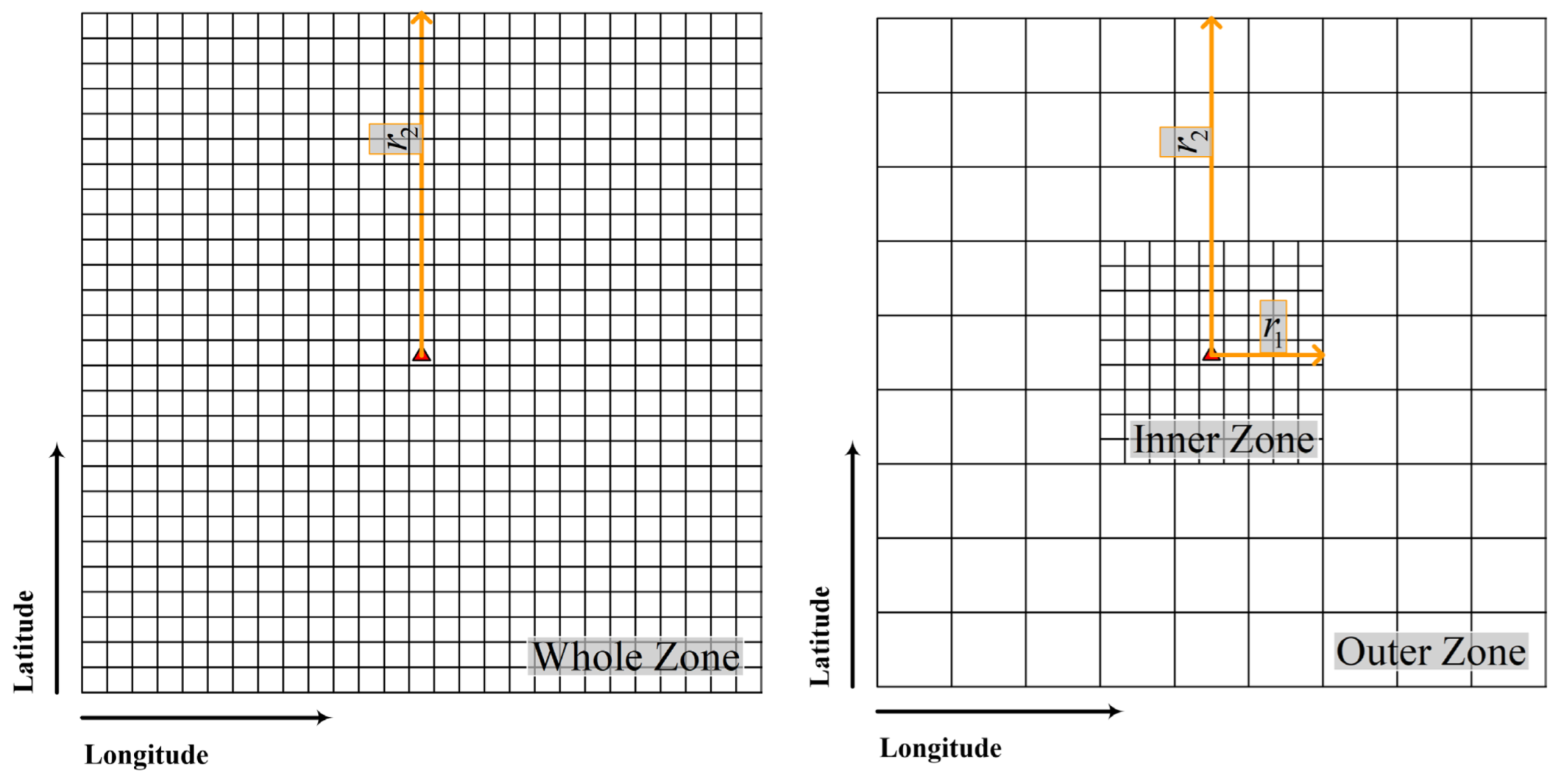
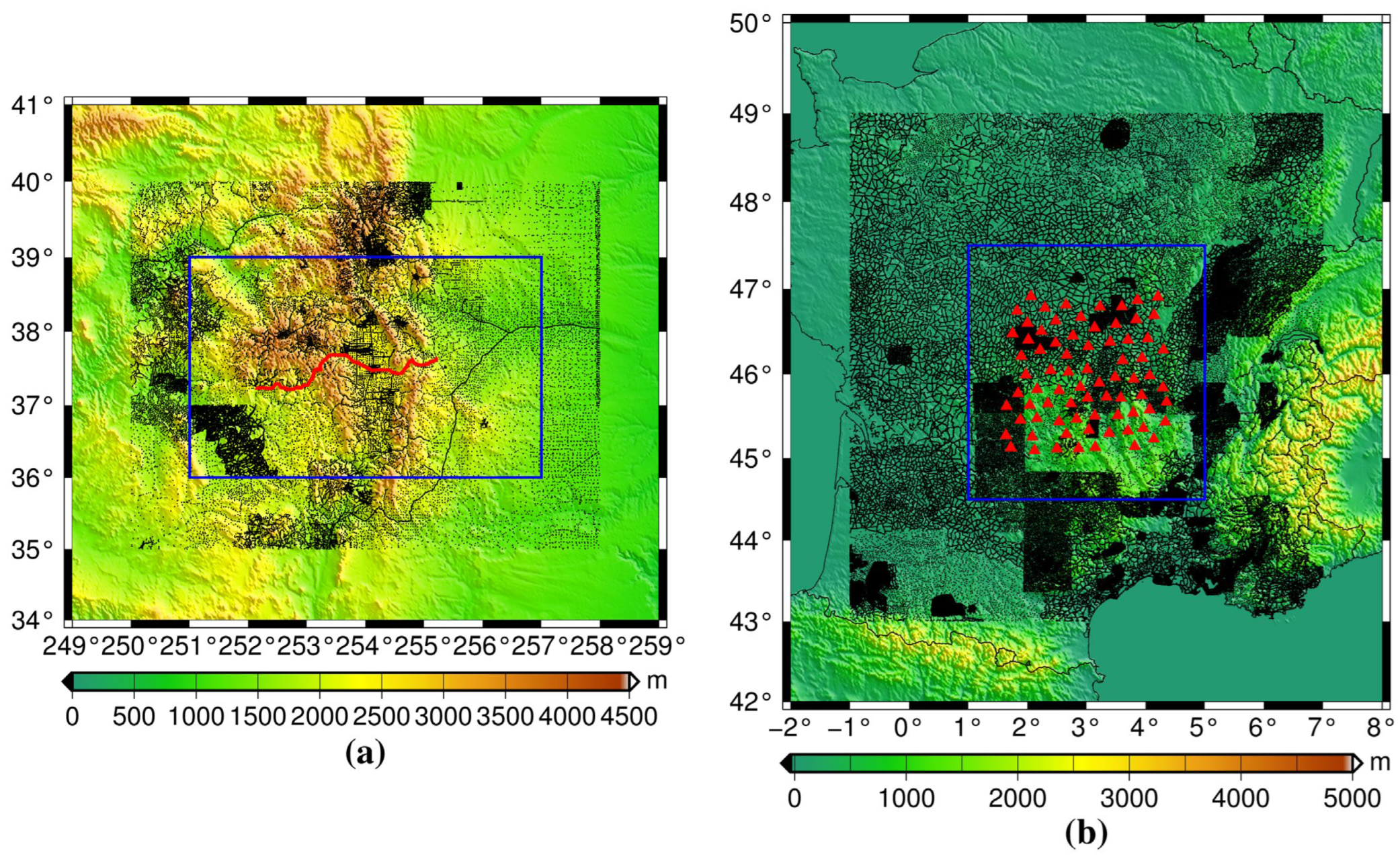
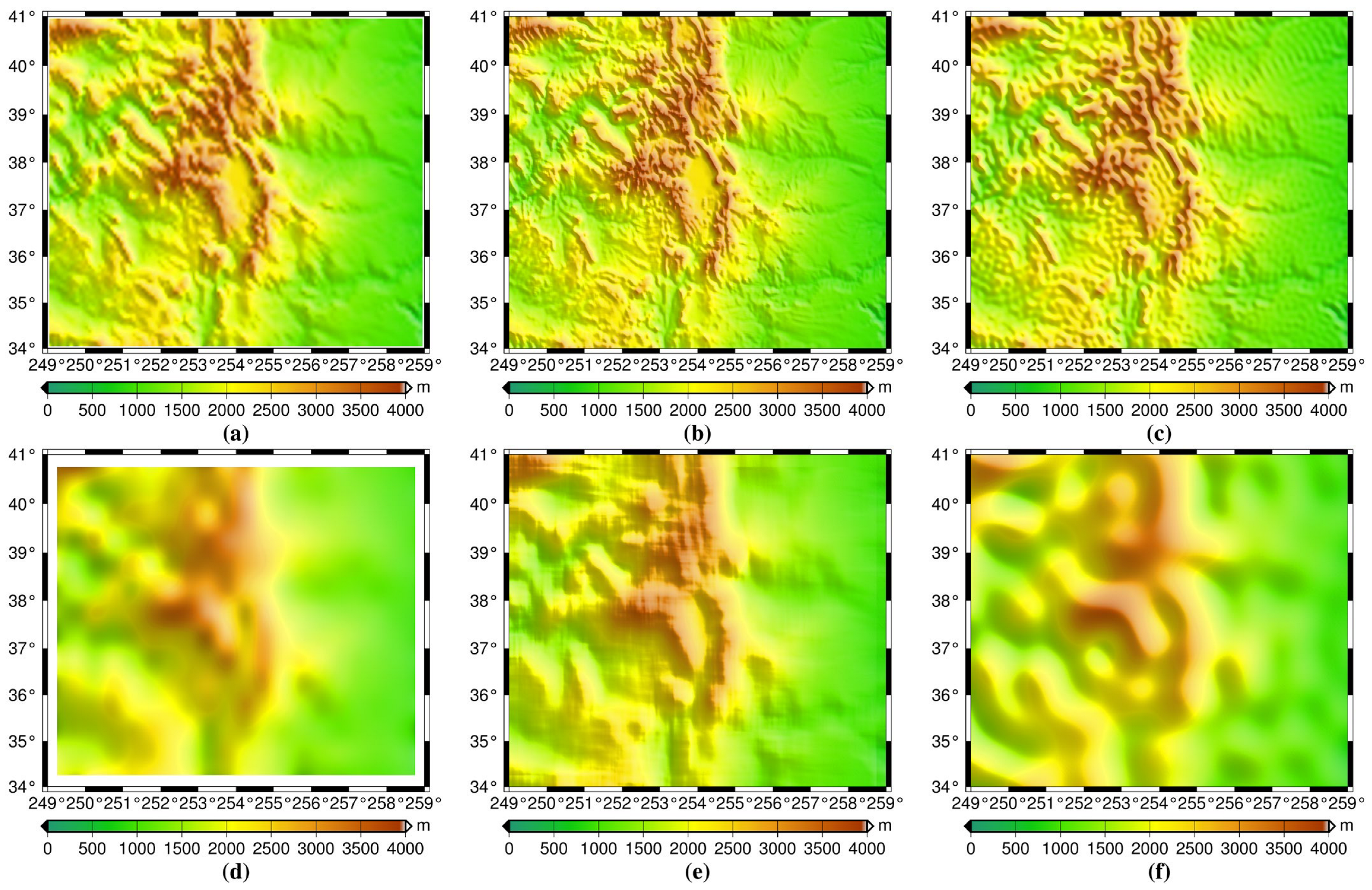
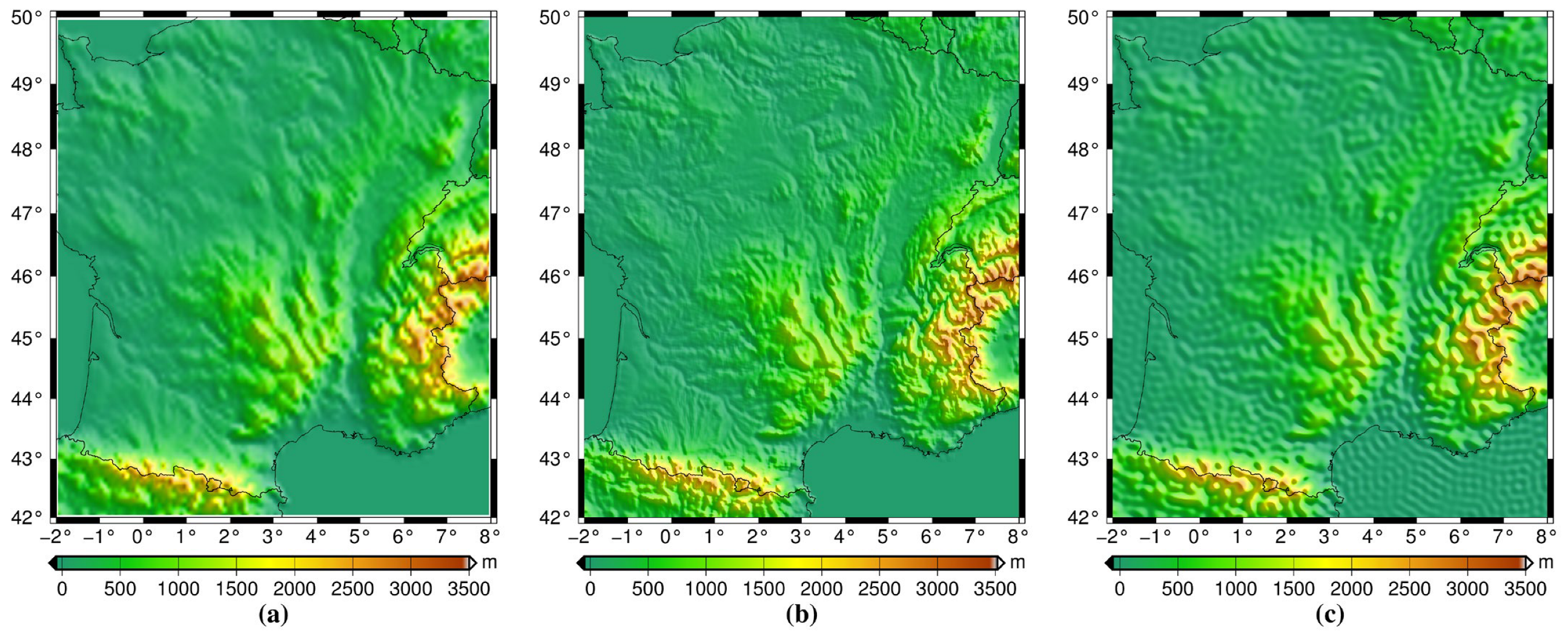
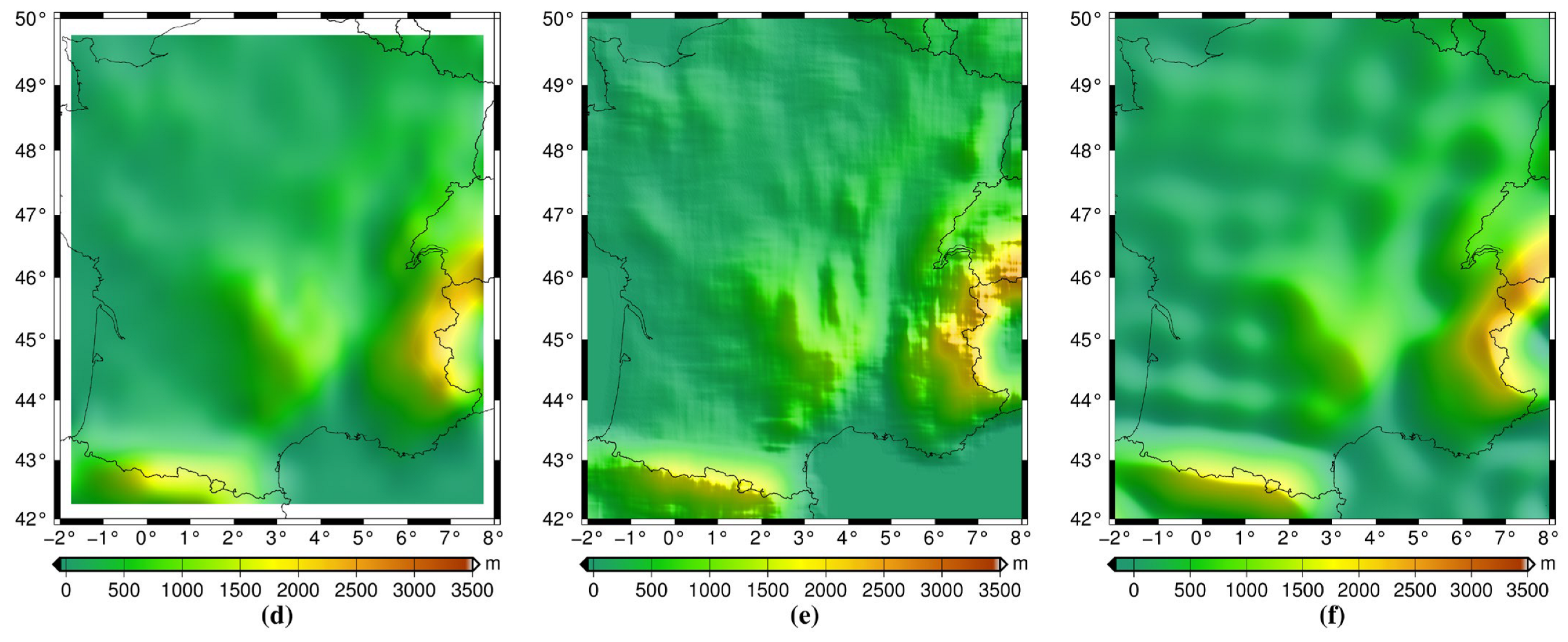
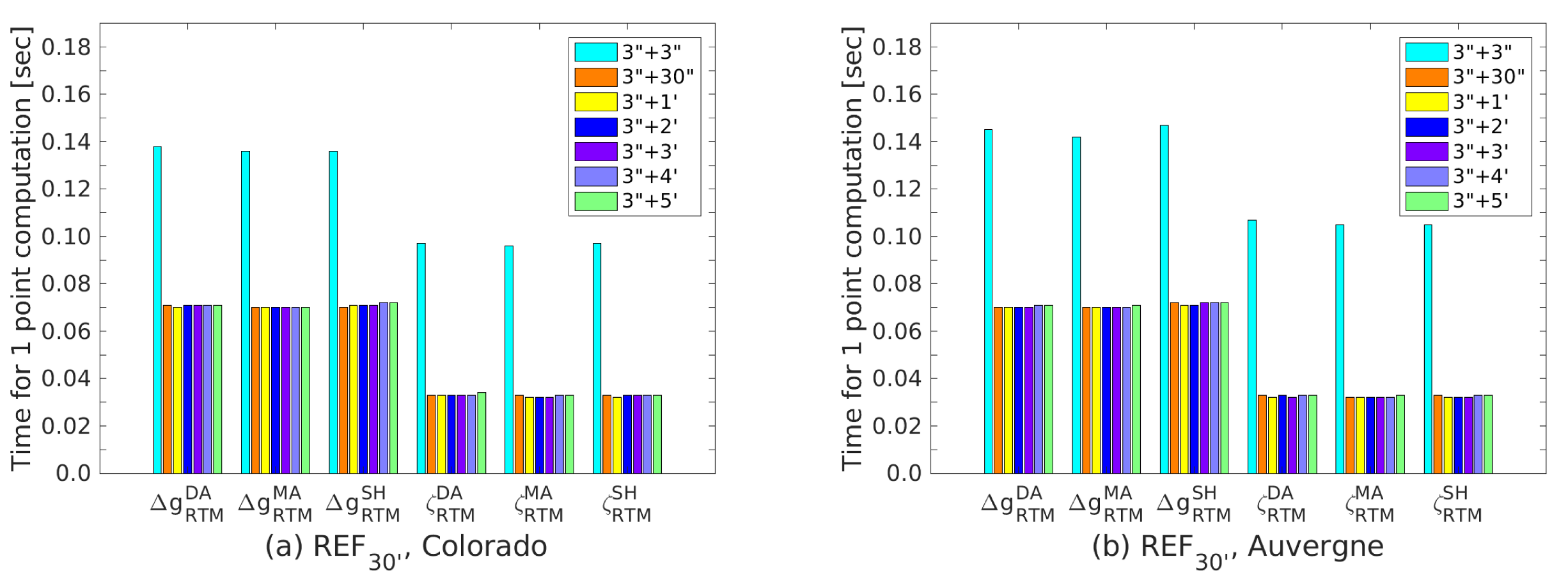
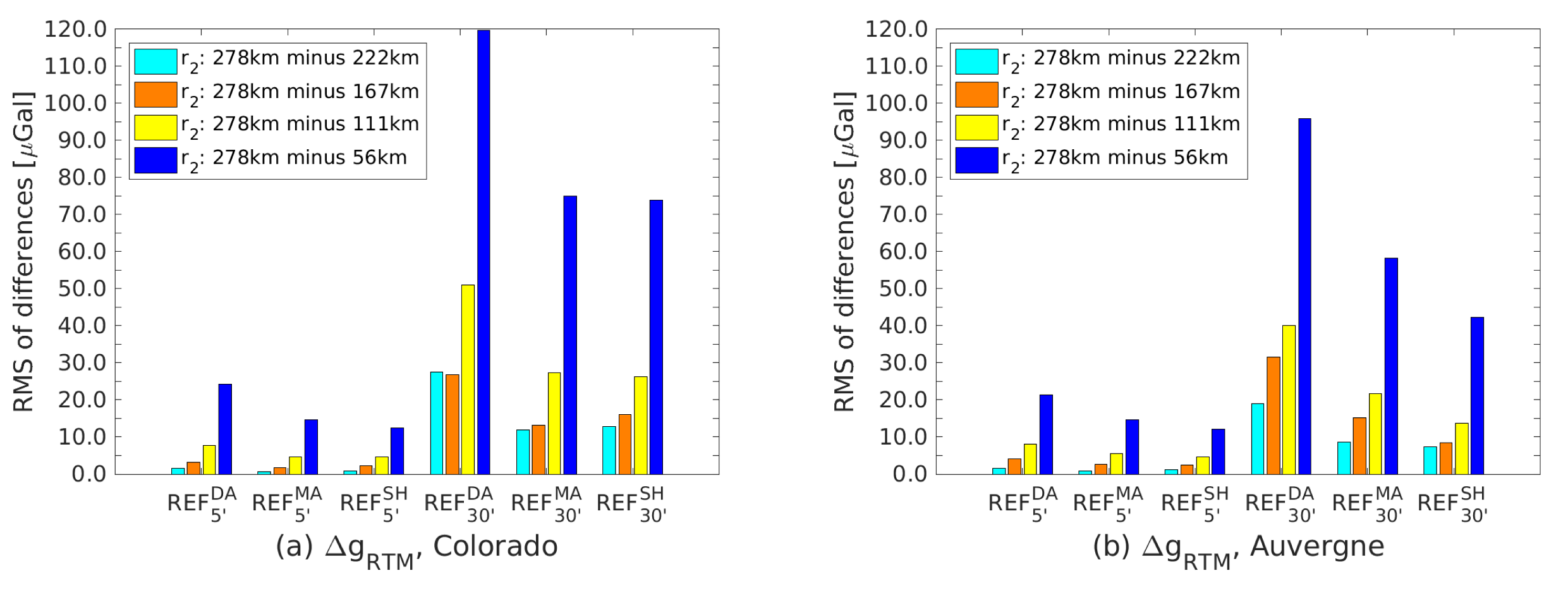
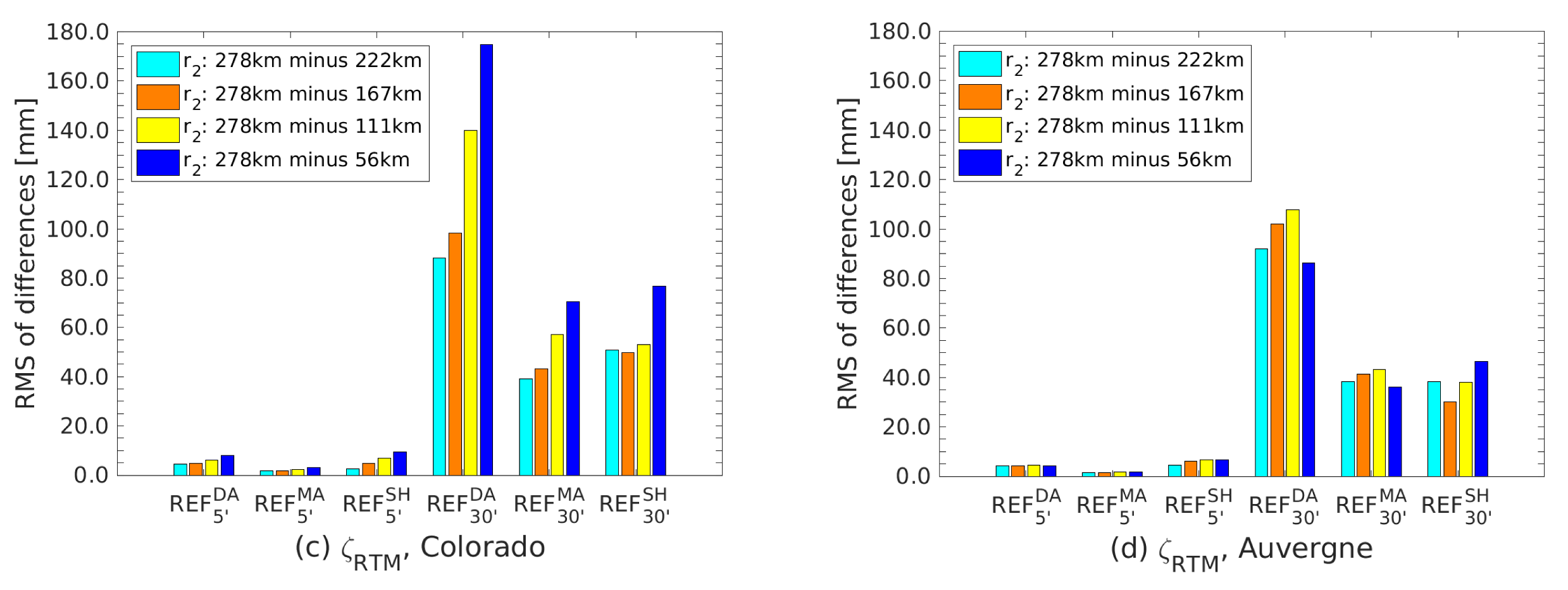
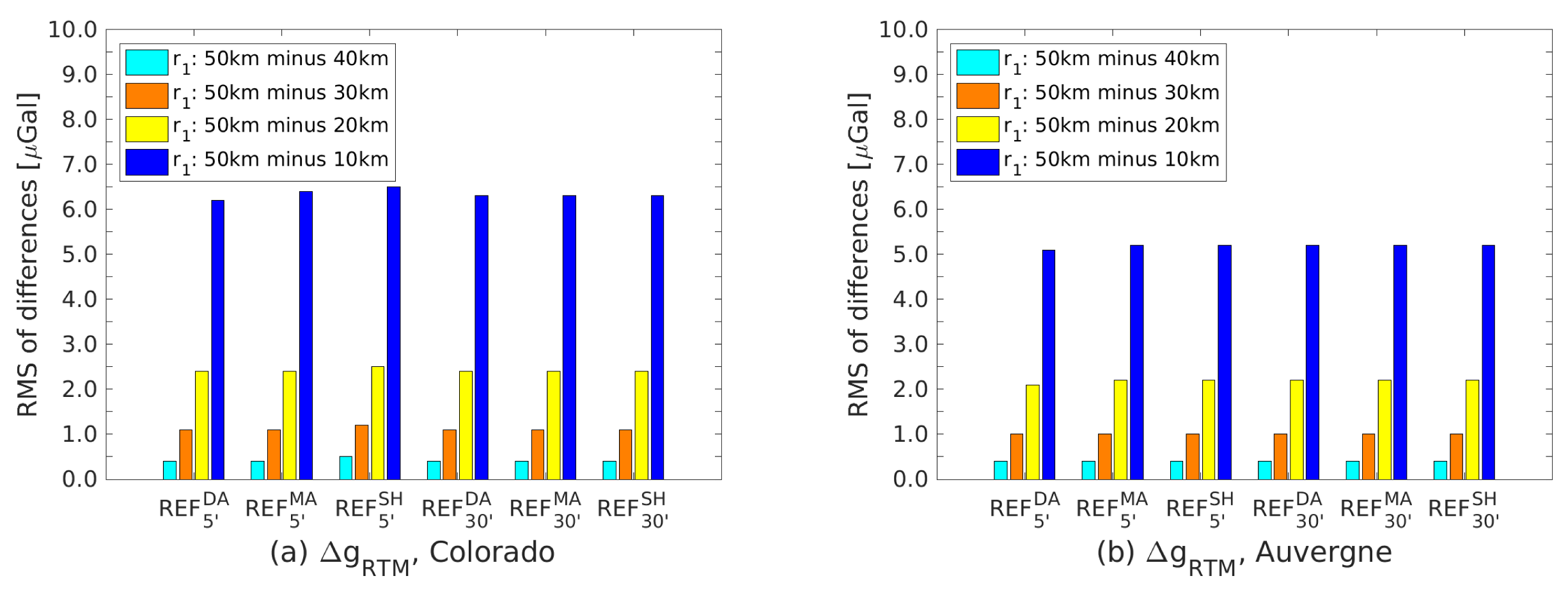
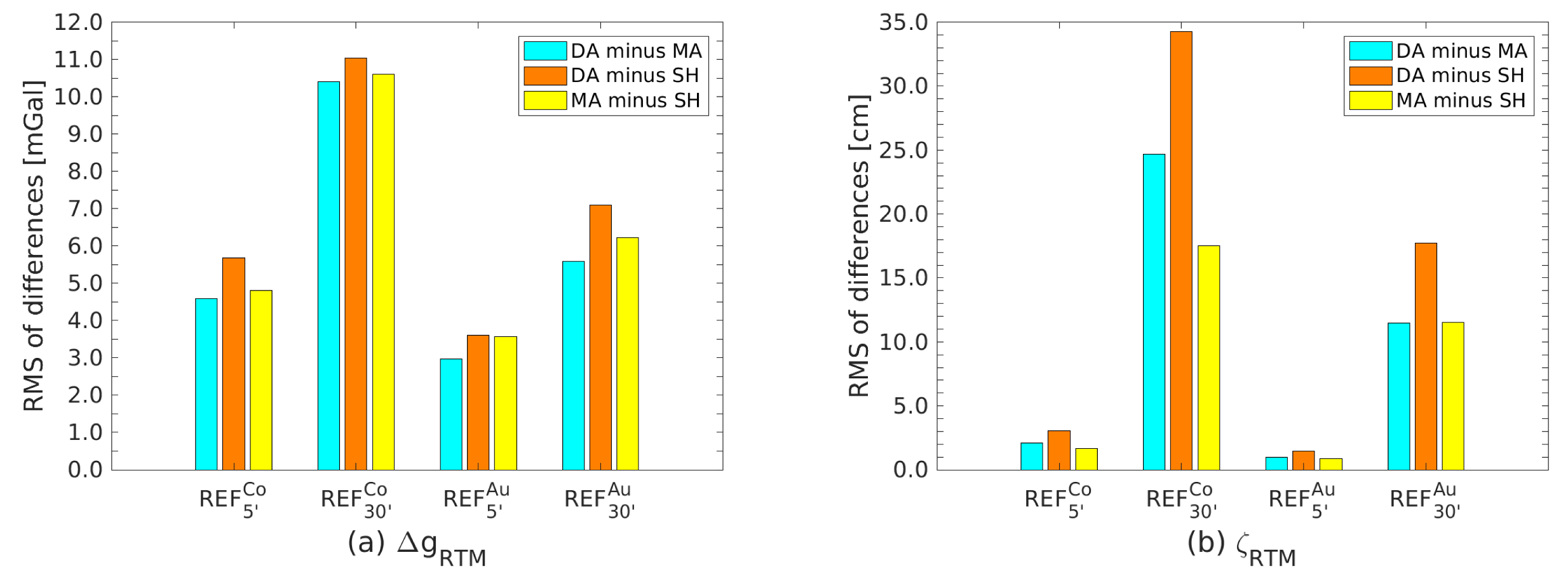
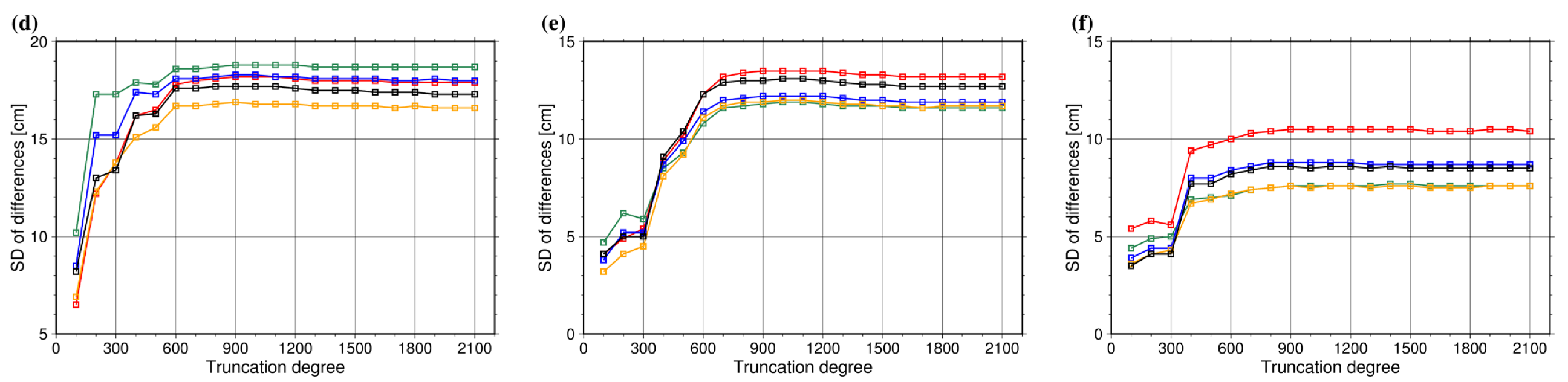
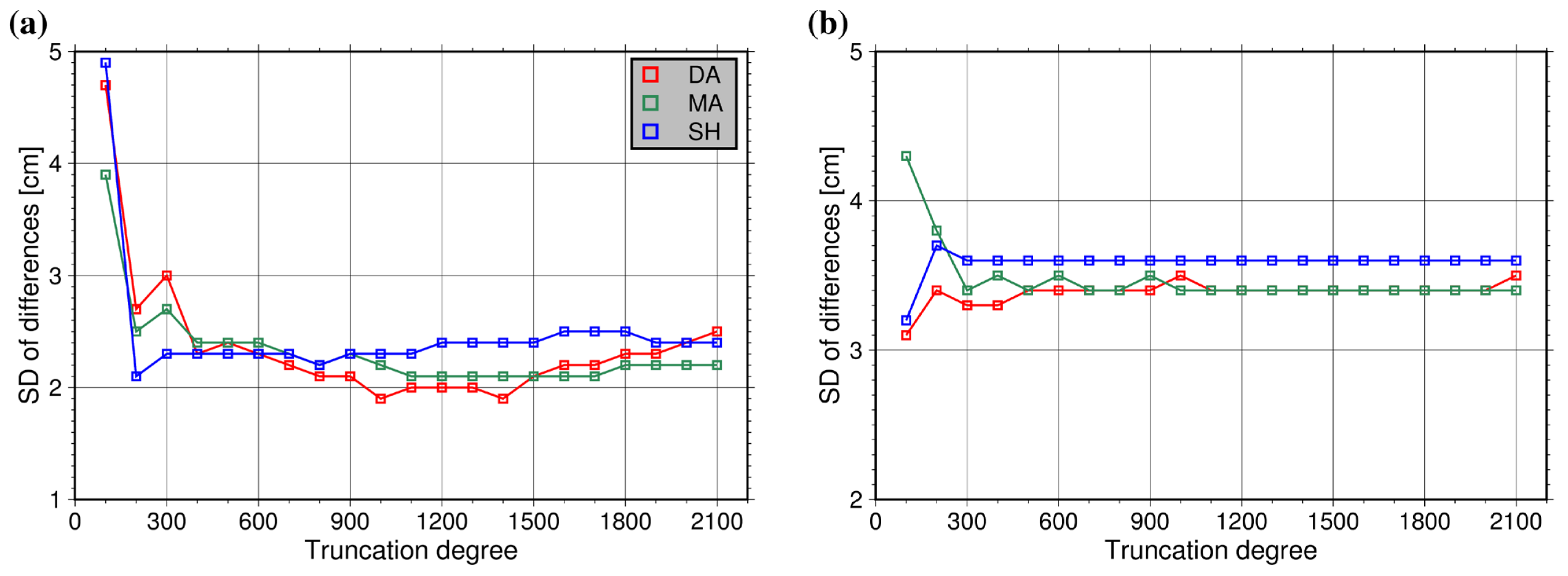
Parameters	Scenarios	Remarks
DEM resolution combination	3″ + 3″ 3″ + 30″ 3″ + 1′ 3″ + 2′ 3″ + 3′ 3″ + 4′ 3″ + 5′	In this case, the values of r1 and r2, the type of reference topography are pre-fixed
Integration radius r1	r1 = 10 km r1 = 20 km r1 = 30 km r1 = 40 km r1 = 50 km	In this case, the DEM resolution combination scenario, the value of r2, and the type of reference topography are pre-fixed
Integration radius r2	r2 = 56 km r2 = 111 km r2 = 167 km r2 = 222 km r2 = 278 km	In this case, the DEM resolution combination scenario, the value of r1, and the type of reference topography are pre-fixed
Reference topography	DA approach MA approach SH approach	In this case, the DEM resolution combination scenario, the values of r1 and r2 are pre-fixed

summarizes the details of the parameter settings that will be used in the following numerical experiments.

For each test case, two reference topographies with different smoothnesses are computed. The first one assumes that the data are reduced by the contribution of an ultra-high-resolution GGM up to d/o 2160 (e.g., EGM2008 [47], EIGEN-6C4 [48]). The second reference topography assumes that the contribution of the GGM is only complete to d/o 360. Since the resolution of the reference topography is set equal to the half-wavelength resolution of the GGM, i.e., ${180}^{\circ }/N$ with N being the maximum degree of the GGM, the resolution of the reference topography is equal to 5′, corresponding to N = 2160, and 30′, corresponding to N = 360. For the sake of simplicity, we refer to the two reference topographies as REF_5′ and REF_30′, respectively. Furthermore, if REF_5′ is obtained by the DA approach, we then denote it as ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{DA}}$. As a consequence, there are six reference topographies for each test area, which are denoted as ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{DA}}$, ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{MA}}$, ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{SH}}$, ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{DA}}$, ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$, and ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$. The details of obtaining the reference topographies ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{SH}}$ and ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$ are briefly described as follows: First, the original 3″ resolution DEM that provides point heights is spatially averaged to the 15″ resolution DEM; second, the SH coefficients of the 15″ resolution DEM are computed up to degree 43,200 via the surface SH analysis; and finally, the point heights of the reference topographies ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{SH}}$ and ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$ are calculated via the SH synthesis from the estimated SH coefficients to maximum degrees 2160 and 360, respectively. Figure 4 and Figure 5 show three types of reference topographies with two resolutions over the Colorado test area and the Auvergne test area, respectively. For the same resolution, different types of reference topographies display similar long-wavelength topographic features but have different details. The reference topographies obtained by the DA and SH approaches look smoother than those from the MA approach. As expected, REF_5′ contains much more details than REF_30′ due to its higher resolution. It should be noted that, since the DA reference topography actually presents block-mean heights, its extent is slightly smaller than the other two types of reference topographies.

3.3. RTM Correction Comparison

In this section, various RTM corrections computed using different parameter settings (see Table 1) will be compared and analyzed. RTM corrections to gravity anomalies are calculated on the observation points, while corrections to height anomalies are computed on the $1^{\prime }\times 1^{\prime }$ grid nodes of the quasi-geoid computation area (see Section 3.1 and Figure 3).

3.3.1. DEM Resolution Combination Effect on RTM Corrections

First, let us see how large the effect of a combined use of a dense DEM and a coarse DEM instead of fully using the dense DEM on RTM correction computation would be.

In this experiment, as illustrated in Table 1, the inner zone always uses the 3″ resolution DEM, while the resolution of the DEM used in the outer zone is selected as 3″, 30″, and 1′ to 5′. The integration radius r₁ and r₂ are fixed at 50 km and 167 km, respectively. The RTM corrections obtained by fully using the 3″ resolution DEM are taken as references, and the results of other scenarios are evaluated in terms of the RMS of the differences with respect to the reference (see Figure 6).

Figure 6 shows that the RMS of gravity anomaly differences ranges from about 1 to 20 μGal in both test areas. If the DEM resolution for the outer zone is equal to or smaller than 1′, the RMS difference is less than 3 μGal. The RMS of height anomaly differences ranges from about 0.1 to 8.0 mm. If the resolution of the DEM for the outer zone is equal to or smaller than 1′, the RMS difference is less than 0.5 mm. The DEM resolution combination effect looks similar regardless of the resolution of the reference topography. The lower the resolution of the DEM used in the outer zone, the larger the RMS difference is.

Figure 7 shows the computational time for 1 point computation for different DEM resolution combination scenarios when using REF_30′ in the two test areas. It can be seen that, in comparison with fully using the 3″ resolution DEM, the replacement of the 30″ resolution DEM in the outer zone can improve the numerical efficiency by about two times for gravity anomalies and three times for height anomalies in both test areas. However, the use of coarser DEMs cannot further improve efficiency but will increase the RMS difference. The possible reason is given as follows: Although the number of mass elements (i.e., tesseroids) would be reduced by using a coarser DEM, the tesseriodal approach applied to those tesseroids having the same center but different sizes might be different because the selection of the tesseroidal approach actually depends on the so-called distance-size ratio. This implies that, for those tesseroids having the same distance to the computation point, the tesseroids with a larger size might be evaluated by a more time-consuming tesseroidal approach than those with a smaller size [30]. It should be noted that similar results are obtained when using REF_5′, and thus they are not presented here.

According to the above numerical results, the combination of the 3″ resolution DEM and the 30″ resolution DEM is preferred regarding both accuracy and efficiency. And this combination scenario will be applied to the rest of the numerical experiments.

3.3.2. Integration Radius Effect on RTM Corrections

The integration radius effect consists of the effect of the integration radius r₁ for the inner zone and the effect of the integration radius r₂ for the outer zone (see Figure 2). Let us first see the r₂ effect.

In this experiment, the value of r₁ is fixed at 50 km, while the value of r₂ is selected at 56, 111, 167, 222, and 278 km, approximately corresponding to 0.5°, 1.0°, 1.5°, 2.0°, and 2.5°, respectively. The results obtained by using r₂ = 278 km are taken as references, as we assume that the larger the value of r₂, the higher the accuracy of the computed RTM corrections. The results of other scenarios are evaluated in terms of the RMS of the differences with respect to the reference (see Figure 8). An obvious feature that can be seen from Figure 8 is that the r₂ effect is much larger when using REF_30′ than when using REF_5′ in both test areas. This is due to the fact that the residual terrain contains more long-wavelength signal in the former case, and hence the contributions from distant tesseroids are still significant.

In the case of using REF_5′, the RMS values of differences are generally within 25 μGal for gravity anomalies and within 1 cm for height anomalies. The RMS difference becomes much smaller if the value of r₂ is chosen to be equal to or larger than 111 km. In the case of using REF_30′, the RMS of differences ranges from about 7 to 120 μGal for gravity anomalies and from about 3 to 17.5 cm for height anomalies. Definitely, the r₂ effect is significant in this case, especially for the height anomaly. And thus, the value of r₂ should be selected with caution when using REF_30′. We can also infer that more attention should be paid to choosing the value of r₂ when using a satellite-derived GGM whose maximum degree is smaller than 360 in the RCR procedure because the corresponding resolution of reference topography is lower than 30′.

We then consider the r₁ effect. In this experiment, the value of r₂ is chosen as 167 km for REF_5′ and 278 km for REF_30′ based on the numerical results regarding the r₂ effect, while the value of r₁ varies from 10 to 50 km with a step of 10 km (see Table 1). The results computed by using r₁ = 50 km are taken as references, and the results of other scenarios are evaluated in terms of the RMS of the differences with respect to the reference (see Figure 9). Because the computed RTM corrections to height anomalies are almost the same for the five selected values of r₁, we only present RTM corrections to gravity anomalies here. It is clear that the RMS values of differences are within 6.5 μGal in the two test areas, demonstrating that the r₁ effect is quite small in computing RTM corrections to gravity anomalies. If the value of r₁ is equal to 20 km or larger, the RMS values of differences are less than 2.5 μGal in the Colorado test area and 2.0 μGal in the Auvergne test area. From the two experiments, it is easy to see that the r₂ effect is sensitive to the resolution of the reference topography but not to the r₁ effect.

3.3.3. Reference Topography Effect on RTM Corrections

As shown in Figure 4 and Figure 5, the details of the reference topographies obtained from the DA, MA, and SH approaches are different. Here we show an inter-comparison of RTM corrections computed by three types of reference topographies. On the basis of previous numerical results, the value of r₁ is fixed to be 30 km (see Figure 9), while the value of r₂ is chosen as 167 km in the case of using REF_5′ and 278 km in the case of using REF_30′ (see Figure 8). The RMS values of differences are displayed in Figure 10. As can be seen, the RMS of differences ranges from about 3 to 11 mGal for gravity anomalies and from about 1 to 34 cm for height anomalies. This clearly indicates that the reference topography effect is quite large on the RTM correction computation, especially for height anomalies. Moreover, the RMS values of differences corresponding to REF_5′ are much smaller than those for REF_30′ in both test areas, implying that the magnitude of the reference topography effect depends on the resolution of the reference topography.

From the above experiment, the fact that the RTM corrections computed by different types of reference topographies deviate much from each other has been verified. However, this experiment does not provide any information about which reference topography is best for gravity anomalies. One commonly used way to assess this issue is to remove the contributions of both GGM and RTM from the observed gravity anomalies and then analyze the resulting residual gravity anomalies for smoothness. Here we choose the GGM as the EIGEN-6C4 model. When using REF_5′ and REF_30′, the contribution of the EIGEN-6C4 model is computed up to d/o 2160 and 360, respectively. The statistics of residual gravity anomalies are presented in

Table 2. Statistics of residual gravity anomalies (mGal) computed by using three types of reference topographies in the Colorado test area.

Residual Gravity Anomaly	Reference Topography	Mean	SD	RMS	Min	Max
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{DA}}$	${\mathrm{REF}}_{5^{\prime }}^{\mathrm{DA}}$	1.369	5.961	6.117	−39.698	43.531
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{MA}}$	${\mathrm{REF}}_{5^{\prime }}^{\mathrm{MA}}$	0.283	5.450	5.458	−33.184	38.287
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{SH}}$	${\mathrm{REF}}_{5^{\prime }}^{\mathrm{SH}}$	0.344	3.527	3.544	−27.436	29.674
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{DA}}$	${\mathrm{REF}}_{30^{\prime }}^{\mathrm{DA}}$	0.287	15.681	15.684	−57.729	54.017
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{MA}}$	${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$	−1.953	14.332	14.464	−51.354	54.711
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{SH}}$	${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$	0.201	10.007	10.009	−40.868	55.576

for the Colorado test case and

Table 3. Statistics of residual gravity anomalies (mGal) computed by using three types of reference topographies in the Auvergne test area.

Residual Gravity Anomaly	Reference Topography	Mean	SD	RMS	Min	Max
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{DA}}$	${\mathrm{REF}}_{5^{\prime }}^{\mathrm{DA}}$	0.540	4.644	4.676	−63.663	64.943
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{MA}}$	${\mathrm{REF}}_{5^{\prime }}^{\mathrm{MA}}$	0.195	4.668	4.672	−63.417	65.381
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{SH}}$	${\mathrm{REF}}_{5^{\prime }}^{\mathrm{SH}}$	0.296	2.730	2.746	−19.592	21.382
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{DA}}$	${\mathrm{REF}}_{30^{\prime }}^{\mathrm{DA}}$	1.454	9.623	9.732	−50.121	72.149
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{MA}}$	${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$	−0.406	9.082	9.091	−42.874	52.153
$\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{SH}}$	${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$	−0.215	7.564	7.567	−27.356	49.728

for the Auvergne test case. Both tables clearly show that the use of the SH reference topography is able to yield the most smooth residual gravity anomalies in terms of both SD and RMS, followed by the MA reference topography. From this perspective, the SH reference topography performs the best for gravity anomaly reduction.

Because our final goal is to determine a local quasi-geoid model, the next issue of interest is which type of reference topography is more suited for quasi-geoid modeling. In the following, another two experiments will be conducted to investigate this issue.

3.4. Local Quasi-Geoid Model Comparison

In this study, the local quasi-geoid computation uses the RCR technique, the RTM method, and the Stokes integral. Assuming that the DA reference topography is employed, the computation and validation steps are briefly described as follows:

① The reference gravity anomalies $\mathsf{\Delta }{g}_{\mathrm{GGM}}^N$ are computed at the observation points by a selected GGM up to d/o N and then subtracted from the observed gravity anomalies $\mathsf{\Delta }{g}_{\mathrm{obs}}$, yielding $\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{GGM}}^N$;

② The RTM corrections to gravity anomalies $\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{DA}}$ are computed at the observation points and then subtracted from $\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{GGM}}^N$, yielding the residual gravity anomalies $\mathsf{\Delta }{g}_{\mathrm{res}}^{\mathrm{DA}}=\mathsf{\Delta }{g}_{\mathrm{obs}}-\mathsf{\Delta }{g}_{\mathrm{GGM}}^N-\mathsf{\Delta }{g}_{\mathrm{RTM}}^{\mathrm{DA}}$;

③ The irregularly distributed residual gravity anomalies are interpolated at the grid nodes of the quasi-geoid computation area by bicubic spline interpolation, yielding the gridded residual gravity anomalies. They are then transformed into the gridded residual height anomalies ${\zeta }_{\mathrm{res}}^{\mathrm{DA}}$ by using the Stokes’s integral with modified kernels [49] (i.e., the low degree terms of the Stokes kernel are removed), assuming that the contribution from the gravity data far away from the computation point is negligible after removing the GGM contribution;

④ The RTM corrections to height anomalies ${\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}$ and the reference height anomalies ${\zeta }_{\mathrm{GGM}}^N$ derived from the GGM are calculated at the grid nodes and then added to the gridded residual height anomalies, yielding the local quasi-geoid model ${\zeta }^{\mathrm{DA}}={\zeta }_{\mathrm{GGM}}^N+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}+{\zeta }_{\mathrm{res}}^{\mathrm{DA}}$;

⑤ The computed local quasi-geoid model is finally validated by comparing the interpolated height anomalies to the observed values at the given GNSS/leveling benchmarks. The standard deviation (SD) of differences is used to measure the accuracy of the local quasi-geoid model.

In the following two experiments, the GGM is directly selected as EIGEN-6C4 without additional comparisons because the selection of an optimal GGM is out of the scope of this study. Since the GSVS17 GNSS/leveling benchmarks actually provide geoid heights, they are transformed into height anomalies via the equation $\zeta =N-\frac{\mathsf{\Delta }{g}_{\mathrm{SB}}}{\overline{\gamma }}H$, with $\mathsf{\Delta }{g}_{\mathrm{SB}}$ the simple Bouguer gravity anomaly, $\overline{\gamma }$ the mean normal gravity, and $H$ the orthometric height [1,2,50,51], before validating the local quasi-geoid model.

The first experiment uses the RTM corrections computed by REF_30′ for quasi-geoid modeling. As demonstrated by previous numerical experiments, the choice of the integration radius r₂ causes large RTM correction changes when using REF_30′. In addition to considering the effect of using different types of reference topographies, the effect of using different values of r₂ is also taken into account in this experiment. The value of r₁ is fixed to be 30 km for all computations, while the selected values of r₂ are the same as those used in Section 3.3.2 (see also Figure 8). The results of validating various local gravimetric quasi-geoid models by GNSS/leveling benchmarks are presented in Figure 11.

In the Colorado test area, while using the same type of reference topography, the local quasi-geoid model obtained by using r₂ = 222 km has a smaller SD value than those obtained from the other values of r₂. Using the SH reference topography provides local quasi-geoid models with a smaller SD value, followed by the models obtained by using the MA reference topography.

In the Auvergne test area, while using the MA and SH reference topographies (i.e., ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$ and ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$), using larger values of r₂ (e.g., 222 and 278 km) can yield local quasi-geoid models with a smaller SD value. However, this rule does not work well in the case of using the DA reference topography (i.e., ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{DA}}$). In general, the use of ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$ and ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$ can produce more accurate local quasi-geoid models than those obtained by using ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{DA}}$.

Table 4. Statistics of differences (cm) between the height anomalies derived from 222 GSVS17 GNSS/leveling benchmarks and various local quasi-geoid models in the Colorado test area. The quasi-geoid models include the ones obtained from the EIGEN-6C4 model, the ones obtained as a combination of GGM and RTM, and the ones shown in Figure 11a–c using the optimal values of r₂ and truncation degree.

Quasi-Geoid Model	Integration Radius r2	Truncation Degree	Mean	SD	RMS	Min	Max
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}$	/	/	−31.3	22.2	38.3	−73.1	29.8
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}$	222 km	/	−46.3	24.0	52.1	−95.6	−5.0
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}$	222 km	/	−28.2	16.1	32.5	−58.5	4.3
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}$	222 km	/	−22.0	12.0	25.1	−47.9	3.2
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}+{\zeta }_{\mathrm{res}}^{\mathrm{DA}}$	222 km	100	−47.8	9.5	48.7	−65.3	−24.5
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}+{\zeta }_{\mathrm{res}}^{\mathrm{MA}}$	222 km	200	−24.5	6.3	25.3	−39.5	−10.4
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}+{\zeta }_{\mathrm{res}}^{\mathrm{SH}}$	222 km	200	−16.4	4.5	17.0	−25.9	−3.5

and

Table 5. Statistics of differences (cm) between the height anomalies derived from 75 GNSS/leveling benchmarks and various local quasi-geoid models in the Auvergne test area. The quasi-geoid models include the ones obtained from the EIGEN-6C4 model, the ones obtained as a combination of GGM and RTM, and the ones shown in Figure 11d–f using the optimal values of r₂ and truncation degree.

Quasi-Geoid Model	Integration Radius r2	Truncation Degree	Mean	SD	RMS	Min	Max
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}$	/	/	−9.9	17.1	19.7	−54.6	27.9
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}$	56 km	/	−13.6	17.9	22.4	−53.3	22.4
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}$	222 km	/	−12.6	11.7	17.2	−41.4	15.1
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}$	278 km	/	−9.7	8.6	12.9	−24.4	11.7
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}+{\zeta }_{\mathrm{res}}^{\mathrm{DA}}$	56 km	100	−12.9	6.5	14.5	−29.5	−0.1
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}+{\zeta }_{\mathrm{res}}^{\mathrm{MA}}$	222 km	100	−12.7	3.2	13.1	−22.9	−6.4
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{360}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}+{\zeta }_{\mathrm{res}}^{\mathrm{SH}}$	278 km	100	−9.7	3.5	10.3	−19.1	−0.4

summarize the validation results for various local quasi-geoid models, including the ones obtained purely from the EIGEN-6C4 model (denoted as the GGM-based model), the ones obtained as a combination of the GGM and RTM (denoted as the GGM+RTM-based model), and the ones shown in Figure 11 using the optimal values of truncation degree and r₂ (denoted as the final model). It is easy to see that adding the RTM contribution to the GGM contribution can significantly improve quasi-geoid models in terms of SD, except in the case of using the reference topography ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{DA}}$. This implies that the reference topography ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{DA}}$ is not a proper choice in this case, and it would introduce additional errors into RTM corrections. For the GGM+RTM-based models, the use of the reference topography ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$ provides better quasi-geoid models than those obtained by using ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$, indicating that spectral inconsistencies between the GGM and RTM are well reduced by using ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$. Therefore, the SH reference topography is highly recommended for high-frequency GGM augmentation [52,53]. For the final quasi-geoid models presented in Figure 11, the addition of residual height anomalies, which are transformed from the Stokes’s integral, indeed improves the quasi-geoid models in comparison with the GGM+RTM-based models. In the Colorado test area, the quasi-geoid model with the smallest SD is obtained by using ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$. However, ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$ yields the best model in the Auvergne test area. Although ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$ performs the best in GGM augmentation, either ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{SH}}$ or ${\mathrm{REF}}_{30^{\prime }}^{\mathrm{MA}}$ is able to yield an accurate local quasi-geoid model. To this end, we may conclude that the MA and SH reference topographies are preferred in local quasi-geoid determination when using REF_30′, while the value of r₂ is better at 222 km or larger.

The second experiment uses the RTM corrections computed by REF_5′ for local quasi-geoid modeling. As shown in Section 3.3.2, the integration radius effect, including r₁ and r₂, is insignificant on computing RTM corrections when using REF_5′. Therefore, only the performance of using different types of reference topographies is investigated here on local quasi-geoid determination by fixing the values of r₁ and r₂ to be 30 km and 167 km, respectively. The results of validating various local quasi-geoid models by GNSS/leveling benchmarks are presented in Figure 12. It is easy to see that the quasi-geoid models computed by different reference topographies are at a similar accuracy level in each test area, demonstrating that the quality of local quasi-geoid is not significantly influenced by the type of reference topography if the resolution of the reference topography is high. This finding is quite different from the previous experiment, in which the resolution of the reference topography was much lower.

Table 6. Statistics of differences (cm) between the height anomalies derived from 222 GSVS17 GNSS/leveling benchmarks and various local quasi-geoid models in the Colorado test area. The quasi-geoid models include the ones obtained from the EIGEN-6C4 model, the ones obtained as a combination of GGM and RTM, and the ones shown in Figure 12a using the optimal truncation degree.

Quasi-Geoid Model	Truncation Degree	Mean	SD	RMS	Min	Max
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}$	/	−11.9	3.6	12.4	−21.8	−1.4
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}$	/	−9.5	2.7	9.9	−18.2	−2.6
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}$	/	−10.6	2.8	11.0	−17.9	−2.7
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}$	/	−11.9	2.4	12.1	−17.2	−4.2
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}+{\zeta }_{\mathrm{res}}^{\mathrm{DA}}$	1000	−10.2	1.9	10.4	−17.5	−5.4
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}+{\zeta }_{\mathrm{res}}^{\mathrm{MA}}$	1100	−10.9	2.1	11.1	−16.2	−3.7
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}+{\zeta }_{\mathrm{res}}^{\mathrm{SH}}$	200	−11.7	2.1	11.9	−17.9	−4.1

and

Table 7. Statistics of differences (cm) between the height anomalies derived from 75 GNSS/leveling benchmarks and various local quasi-geoid models in the Auvergne test area. The quasi-geoid models include the ones obtained from the EIGEN-6C4 model, the ones obtained as a combination of GGM and RTM, and the ones shown in Figure 12b using the optimal truncation degree.

Quasi-Geoid Model	Truncation Degree	Mean	SD	RMS	Min	Max
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}$	/	−9.8	3.8	10.5	−18.8	4.7
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}$	/	−10.0	3.6	10.6	−18.2	3.0
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}$	/	−9.9	3.6	10.5	−18.2	3.7
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}$	/	−9.7	3.6	10.3	−18.4	0.9
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{DA}}+{\zeta }_{\mathrm{res}}^{\mathrm{DA}}$	100	−10.4	3.1	10.9	−17.9	−2.4
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{MA}}+{\zeta }_{\mathrm{res}}^{\mathrm{MA}}$	300	−9.9	3.4	10.5	−19.1	−0.9
${\zeta }_{\mathrm{EIGEN}\text{-}6\mathrm{C}4}^{2160}+{\zeta }_{\mathrm{RTM}}^{\mathrm{SH}}+{\zeta }_{\mathrm{res}}^{\mathrm{SH}}$	100	−10.1	3.2	10.6	−17.9	−0.6

present validation results similar to those in Table 4 and Table 5. In this case, the GGM+RTM-based models have a smaller SD value than the GGM-based models, regardless of the type of reference topography used. This means the RTM corrections computed by all reference topographies have a positive impact on local quasi-geoid modeling. Furthermore, the use of ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{SH}}$ is able to compute a GGM+RTM-based model with a slightly smaller SD value than the cases of using ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{DA}}$ and ${\mathrm{REF}}_{5^{\prime }}^{\mathrm{MA}}$ in both test areas, demonstrating again the suitability of using the SH reference topography for high-frequency GGM augmentation. When optimal values of the truncation degree are chosen, the final quasi-geoid models shown in Figure 12 have an SD value of about 2.0 cm in the Colorado test area and 3.2 cm in the Auvergne test area. It should be noted that the best final quasi-geoid models in terms of SD are obtained by using the DA reference topography in both test areas. This is in fact beyond our expectations, and now the true reason is not clear to us. A possible reason is that the GNSS/leveling benchmarks are located in the valleys for the Colorado test case and in the flat area for the Auvergne test case, making the RTM corrections computed by different types of reference topographies to these points quite close to each other. In-depth investigations on this issue should be conducted in our future work. In comparison with the GGM+RTM-based models, the final models are slightly improved in terms of SD. However, the rate of improvement is smaller than that given in Table 4 and Table 5. This is because the GGM up to d/o 2160 is used in this experiment, containing most of the powers of the local quasi-geoid. And thus, the contribution from residual height anomalies is much smaller but still important.

4. Summary and Conclusions

In this paper, we have studied the impact of three factors, i.e., the combination of DEMs with different resolutions for suitably representing the real topography, the choice of integration radius for properly defining the extent of the computation zone, and the determination of reference topography for properly describing the RTM-reduced Earth’s surface, on accurate RTM correction computation and, furthermore, on local quasi-geoid modeling. To do so, various numerical experiments concerning the DEM resolution combination effect, the integration radius effect, and the reference topography effect were conducted in the Colorado test area with rugged terrain and the Auvergne test area with moderate terrain. The numerical findings are given as follows.

The combination of a dense DEM and a coarse DEM can replace the sole use of the dense DEM while maintaining accuracy and improving efficiency. If the resolution of the dense DEM is 3”, the resolution of the coarse DEM used in the outer zone is recommended to be 30”. The changes in RTM corrections caused by this replacement are negligible, while the numerical efficiency is improved about two times in computing the gravity anomaly and three times in computing the height anomaly. The decreasing resolution of the coarse DEM will increase the changes but cannot further improve the efficiency.

The integration radius r₂ for the outer zone has a minor impact on computing RTM corrections when the reference topography has a resolution of 5′. In this case, its value is preferred to be 111 km or larger. However, if the resolution of the reference topography decreases to 30′, its impact becomes significant. For gravity anomalies, the RMS of changes ranges from about 7 to 120 μGal. For height anomalies, the RMS of changes ranges from about 3 to 17.5 cm. Therefore, the value of r₂ should be selected with caution in this case. In general, we prefer the value of r₂ to be as large as possible if the computation burden is acceptable. In comparison with r₂, the changes in RTM corrections computed by using different values of r₁ are insignificant no matter whether the reference topography has a resolution of 5′ or 30′, especially for computing the height anomaly. Its value is preferred to be 20 km or larger.

The impact of using three types of reference topographies is significant in computing RTM corrections. When using the 5′ resolution reference topography, it causes gravity anomaly changes with an RMS value ranging from about 3 to 6 mGal and height anomaly changes with an RMS value ranging from about 1 to 3 cm. When using the 30′ resolution reference topography, it causes gravity anomaly changes with an RMS value ranging from about 6 to 11 mGal and height anomaly changes with an RMS value ranging from about 11 to 34 cm. The lower the resolution of the used reference topography, the more significant the effect of the type of reference topography on RTM correction computation is. For gravity anomaly reduction, the SH reference topography performs better than the other two types of reference topographies.

The determination and validation of the local quasi-geoid models calculated by various RTM corrections in two test areas demonstrated that the choice of the integration radius r₂ and the type of reference topography indeed affect the quality of the computed quasi-geoid models when using the 30′ resolution reference topography. In both test areas, the value of r₂ ≥ 222 km outperforms the other values if using the same type of reference topography. The SH reference topography usually yields better results than the other two, while the DA reference topography delivers the worst models. In the case of using the 5′ resolution reference topography, local quasi-geoid models obtained by using three types of reference topographies are at a similar accuracy level in both test areas. This indicates that the type of reference topography is not critical in the determination of local quasi-geoid if the resolution of the reference topography is high.

According to the above-mentioned numerical findings, we summarized some guidelines that might be helpful for using the RTM method in local quasi-geoid modeling: (1) The combination of the 3″ resolution DEM and the 30″ resolution is sufficient for accurate and efficient RTM correction computation if the highest resolution of the DEM we have is 3″; (2) if the reference topography has a resolution of 5′ or slightly lower, such as 10′, all three types of reference topographies can be used for RTM correction computation and, consequently, in local quasi-geoid modeling. The values of r₁ and r₂ are preferred to be at least 20 km and 111 km, respectively; (3) if the reference topography has a resolution of 30′ or lower, the MA or SH reference topography is suggested, especially for the latter one. The advantage of using the MA reference topography is that it is much easier to calculate than the SH reference topography. The values of r₁ and r₂ are recommended to be at least 20 km and 222 km, respectively. Finally, we would like to mention that the guidelines may also work when using those programs that have a similar structure as that of the “tctessv3omp.f90” program used in this study, such as the “tc.for” program, to accurately compute RTM corrections.