1. Introduction
The utility and prominence of image segmentation algorithms in the remote sensing [
1,
2] domain are well established. The processing and interpretation of satellite and aerial imagery have been drastically transformed, unlocking a diverse array of applications. This has allowed for more nuanced environmental monitoring, detailed urban planning, and intricate military surveillance, among other applications. As the need for high-resolution feature extraction and object identification becomes increasingly pressing, so does the importance of refining and improving these segmentation algorithms.
Fully Convolutional Networks (FCNs) [
3], U-Net [
4], and SegNet [
5] stand as noteworthy examples among the plethora of image segmentation algorithms employed. FCNs [
3,
6,
7] are prized for their ability to handle varying input sizes, an attribute that has led to admirable segmentation results across several scenarios. However, FCNs’ scope in extracting global features is limited. This drawback often becomes evident in tasks that require a broader contextual understanding. On the other hand, U-Net-based methods [
4,
8,
9] boast an efficient encoder–decoder architecture, which has been particularly successful in biomedical image segmentation. Yet, their application in remote sensing is constrained due to their limited capacity to manage large-scale, high-resolution images. SegNet [
5,
10] demonstrates proficiency in segmenting complex scenes but exhibits shortcomings in accurately delineating boundaries and effectively handling occluded objects’ essential capabilities in remote sensing image segmentation. The advent of Transformer-based models has revolutionized numerous fields, primarily due to their ability to model long-range dependencies without the constraints of local receptive fields, as is the case with CNNs [
11,
12]. Swin Transformers [
13], a variant of the Transformer family [
14,
15,
16,
17], offer an additional advantage by enabling both local representations. However, they limit global modeling capabilities in the Transformer-based methods.
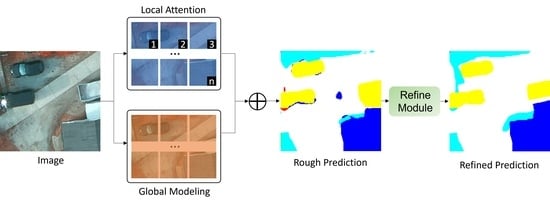
To address these limitations, we have developed the Spatial-Aware Transformer, a constituent of the Swin Transformer block, to optimize the employment of self-attention strategies, forge pixel-level correspondences, and augment the faculty of feature representation. As
Figure 1a shows, our segmentation algorithm may encounter challenges in accurately identifying certain areas within the image. For instance, in the white box, the algorithm faces difficulty in distinguishing between an impervious surface and a car within the local region. Similarly, as illustrated by the yellow box, the algorithm struggles to differentiate between regions that belong to a car and those that are part of a building. As
Figure 1b shows, the integration of spatial data within the Swin Transformer block via the Spatial-Aware component engenders a nuanced comprehension of pixel interrelationships, thereby facilitating improved segmentation accuracy. This approach equips the model with the capability to take into account not only the immediate local context but also the wider spatial context, thereby aiding in modeling obscured entities and extracting complex features. The integration of the Spatial-Aware component into our methodological approach yields several benefits. It enhances the feature representation capacity, equipping the model with the ability to capture the subtleties and complex structures present in remote sensing imagery with greater finesse. Furthermore, the module augments the model’s capacity to model global dependencies through the utilization of the self-attention mechanism. This allows the model to perceive the spatial interrelations between objects, resulting in precise segmentation.
Another critical challenge that plagues remote sensing image segmentation pertains to the accuracy of edge or boundary segmentation. The complexity of remote sensing imagery is often exacerbated due to the top-view perspective of many images in datasets. Such a perspective can obscure the clear demarcation between objects, leading to inaccurate segmentation outputs, particularly around the objects’ boundaries. It is essential to address this limitation, given the significance of precise boundary segmentation to the overall accuracy and utility of the segmentation task. We have integrated a boundary-aware module into our decoder, serving as a refinement tool that markedly improves boundary delineation. To this end, we propose the integration of a boundary-aware module into our decoder. This module brings about substantial improvements in boundary segmentation and functions as a refinement tool. The boundary-aware module exhibits a heightened sensitivity to boundary structures, which leads to more precise delineation of segmented regions. Consequently, the characterization of objects within the scene is significantly enhanced, contributing to more accurate segmentation outputs. Furthermore, our model employs a hybrid loss function, incorporating Binary Cross-Entropy (BCE) loss, Structural Similarity Index (SSIM) loss, and Intersection over Union (IoU) loss. This enables the model to learn from different aspects of the image.
Experimental evaluations of our proposed modules have exhibited impressive results and achieved state-of-the-art performance on three renowned datasets: Potsdam, Vaihingen, and Aerial. These results testify to the SAT’s capability to effectively manage occlusion, delineate intricate features, and precisely segregate object boundaries, outperforming existing models.
To sum up, this study presents a pioneering approach toward refining image segmentation in remote sensing. By strategically addressing recognized limitations in current methods and incorporating unique, targeted enhancements, we offer an innovative solution that not only meets the field’s current needs but also lays a strong foundation for future advancements.
2. Related Work
2.1. CNN-Based Remote Sensing Image Segmentation
Convolutional Neural Networks (CNNs) [
11,
12,
18,
19] have long been recognized as powerful tools for image analysis due to their ability to learn hierarchical feature representations from raw image data. They have been particularly successful in various segmentation tasks, thanks to their robustness in extracting spatial features from images.
Early works applied traditional CNN architectures, such as LeNet [
20] and AlexNet [
21], to remote sensing image segmentation tasks. These initial efforts demonstrated the potential of CNNs in this domain, revealing substantial improvements over traditional machine learning methods. However, the relatively shallow architectures of these initial CNNs were limited in their ability to capture complex patterns and structures inherent in remote sensing imagery.
The advent of deeper architectures, such as VGGNet [
22] and ResNet [
23], brought about significant improvements. These deep CNNs, armed with an increased number of layers, improved the capacity to capture more complex features and patterns within the remote sensing images. Particularly, ResNet introduced the concept of skip connections, which mitigated the vanishing gradient problem, thereby allowing for the effective training of deep networks.
Although deep CNNs offered substantial improvements over their predecessors, they were primarily constrained by their limited receptive fields, inhibiting their global modeling capabilities. In the context of remote sensing images, which often encompass intricate spatial structures and long-range dependencies, this limitation becomes particularly significant.
A range of methods have been proposed to tackle this issue. One notable approach is the integration of multi-scale features, as demonstrated in the Pyramid Scene Parsing Network (PSPNet) [
24] and the Deeplab family of models [
25,
26,
27]. These architectures employ spatial pyramid pooling and dilated convolutions, respectively, to capture contextual information at various scales.
Despite these advancements, conventional CNN-based segmentation algorithms still struggle to fully capture the complex spatial relationships and global context inherent in remote sensing imagery. This limitation underscores the need for new approaches, particularly those leveraging Transformer-based models, as explored in the next section.
2.2. Remote Sensing Image Segmentation Based on Self-Attention Mechanisms
The self-attention mechanism, also known as the Transformer, was introduced by [
28]. In the domain of natural language processing, unlike CNNs, Transformers are not restricted by local receptive fields and are capable of capturing long-range dependencies in data, making them a promising solution for the global modeling challenge in remote sensing image segmentation.
The self-attention mechanism computes the response at a position as a weighted sum of the features at all positions in the data. This global context-awareness allows the Transformer to better capture intricate spatial structures and long-range dependencies that are characteristic of remote sensing images [
19,
29,
30,
31].
Initial applications of the Transformer in remote sensing image segmentation used hybrid models, combining CNNs for local feature extraction and Transformers for global context aggregation [
32]. Examples include the Vision Transformer (ViT) [
33] and the TransUNet [
34]. These models achieved promising results, underscoring the potential of Transformers in this domain.
Despite their merits, the application of traditional Transformers to remote sensing image segmentation is not straightforward due to their high computational cost and the requirement for large-scale datasets for effective training [
35]. To address this, researchers introduced the Swin Transformer [
13], a variant that allows for both local and global representations, making it more suitable for segmentation tasks.
The Swin Transformer divides the input image into non-overlapping patches and processes them in a hierarchical manner, thus effectively capturing spatial information at multiple scales [
13]. This characteristic is particularly advantageous in handling the complex spatial structures of remote sensing images.
Our research builds upon the aforementioned works, seeking to further advance the field of remote sensing image segmentation. We extend the Swin Transformer model by incorporating spatial awareness, enhancing its capacity to handle intricate and interconnected objects in remote sensing imagery. Additionally, we introduce a boundary-aware module to improve edge segmentation, addressing a critical challenge in this domain.
In summary, the research landscape of remote sensing image segmentation reveals significant progress, with CNN-based models providing the initial groundwork and Transformer-based models introducing exciting new possibilities. Our work seeks to contribute to this ongoing progress, offering a novel and comprehensive approach to enhance global modeling abilities and improve boundary segmentation accuracy.
3. Methods
This section outlines the details of the methods adopted in this research, specifically focusing on two primary components: the Spatial-Aware Transformer module, which enhances the global modeling capabilities of our segmentation algorithm, and the Boundary-Aware Refinement module, which sharpens the boundary segmentation in our output. These modules operate in conjunction and facilitate a novel and effective approach to remote sensing image segmentation.
3.1. Network Architecture
Figure 2 presents the comprehensive structure of our algorithm, melding U-Net’s straightforward yet sophisticated traits. This is achieved by employing a skip connection layer to bridge the encoder and decoder and integrating two primary components: the SAT and the mask refinement module.
In the encoder segment, the initial step involves taking the remote sensing image slated for division as the input and dissecting it into non-overlapping segments, each of which we consider as a token. These tokens are not inherently connected in the context of the language model. However, in the Vision Transformer (ViT), not only are the segments interconnected, but the pixels within these segments also share robust linkages.
To augment the semantic correlation among pixels, we establish the segment size at and set the overlapping percentage to . Subsequently, each divided segment undergoes a Linear Embedding process, acquiring the feature of the c-dimension. This feature is then inserted into the Spatial-Aware Transformer module, effectively mitigating the constraint of window self-attention, allowing for global pixel-level information pairing, and reducing the semantic uncertainty induced by obstruction.
Next, the encoder’s output is routed into the bottleneck layer, constructed from a pair of Spatial-Aware Transformer modules, without altering the feature dimension. This process enables the maximum possible exploration within the features. The resultant output from the bottleneck layer is then fed into the decoder layer to generate a preliminary prediction mask. Then, this mask is processed through the Boundary-Aware module to produce the final refined prediction mask.
3.2. Transform Module with Spatial Awareness
The basis of our Spatial-Aware Transformer module is the Swin Transformer, a specialized variant of the generic Transformer model, which has seen significant success in a myriad of visual tasks. We first delineate the fundamental principles behind the Swin Transformer before delving into the specifics of our proposed module.
3.2.1. Swin Transformer
The distinctive feature of the Swin Transformer is its “shifted window” approach to partitioning an input image. The process commences by dividing the input image into miniature patches, each measuring 4 px by 4 px. Each of these patches has three channels, summing up to 48 feature dimensions ().
These patches, each of 48 dimensions, are subsequently linearly transformed into a dimensionality denoted as C, effectively converting these patches into vectors of dimension C. The choice of C is a design choice that impacts the size of the Transformer model and, consequently, the number of hidden parameters in the model’s fully connected layers.
The Swin Transformer revolutionizes image processing by transitioning from the Vision Transformer’s quadratic computational approach to a more streamlined linear complexity. This is achieved by focusing self-attention within local windows rather than globally, making the Swin Transformer more adept at dense recognition tasks and versatile in remote sensing applications.
Moving on, as depicted in
Figure 3, the blue box signifies the Swin Transformer’s primary operation. We designate the input as ‘I’. Prior to feeding ‘I’ into the transformer, an initial patch merging is executed, which serves the dual purpose of downsampling and setting the stage for hierarchical structure formation. This not only minimizes resolution but optimizes the channel count, conserving computational resources. In particular, each downsampling doubles, selecting elements at intervals of two both in rows and columns of the input feature ‘I’, which are then amalgamated into a single tensor. At this stage, the channel dimension increases 4-fold, which is subsequently fine-tuned to twice its original size via a fully connected layer.
Diving into specifics, the output from the fully connected layer is input into the transformer module. Here, post layer normalization, Window Self-Attention (Win-SA) is performed. The resultant attention-modulated features are then passed through another layer normalization layer followed by a Multilayer Perception (MLP) layer. The mathematical representation is as follows:
where
denotes the input feature of the transformer module, ‘LNorm’ signifies layer normalization, and ‘Win-SA’ represents Window Multi-head Self-Attention. The term
reflects the sum of the output feature from Window Self-Attention and the input feature. At this juncture, input image features are segmented into
blocks, with each block treated as a window where self-attention is performed. This strategy effectively mitigates the computational strain of the Vision Transformer, which can struggle with handling large image features. Additionally, the window size is a flexible hyper-parameter that is typically chosen based on computational efficacy and task demands. In this experiment, we chose
W as 8 for ease of feature computation and practicality.
However, partitioning image features into smaller windows comes at the expense of the self-attention mechanism’s core premise, wherein any feature point should be able to communicate with others. The fact that attention is restricted within windows results in a lack of inter-window information exchange. To counter this, a window shift operation is employed, involving passing the
feature through the layer normalization layer and feeding it into the Shifted Window Self-Attention (SWin-SA) module. Thereafter, the attention-matched feature is passed through another layer normalization layer and an MLP layer. This process can be mathematically represented as follows:
where
indicates the combined output features and input feature after the Shifted Window Self-Attention operation, and
represents the combined output of the MLP layer and
. This step helps ensure that the essential aspect of self-attention—interaction between different feature points—is retained.
3.2.2. Spatial-Aware Transformer
As we pivot to the Spatial-Aware Transformer, it is important to recognize a trade-off with the Swin Transformer block. Although it efficiently establishes relationships among patch tokens within a bounded window and reduces memory consumption, there is a downside: it marginally impedes the Transformer’s ability to model global relationships. This constraint remains despite the use of alternating standard and shifted windows.
Delving into the specifics, in remote sensing imagery, the obscuring of ground objects frequently leads to indistinct boundaries. Addressing this requires the integration of spatial information for sharpening the edges. Hence, as a solution, we introduce the Spatial-Aware Transformer (SAT) in alliance with the W-Transform and SW-Transform blocks. This integration facilitates enriched information exchange and encodes more nuanced spatial details.
Notably, SAT distinguishes itself by employing attention mechanisms across two spatial dimensions. In doing so, it focuses on the interrelationships between individual pixels, rather than solely on patch tokens. This adaptation makes the transformer particularly adept at handling image segmentation tasks. For visual clarity, the constituents of SAT are graphically represented in
Figure 3.
During stage m, the W-Transform block takes an input feature and reshapes it into . For clarity, let’s define , , and . The next step involves processing feature through a dilated convolution layer with a dilation rate of 2. This operation revitalizes the structural information of the feature map by expanding its receptive field and, at the same time, reduces the number of channels to for the sake of efficiency.
Following this, global average pooling comes into play to distill the spatial statistics in both vertical and horizontal directions from the feature map. To provide more detail on this aspect, the calculation for elements in each direction is articulated as follows:
where
i,
j, and
act as indices for the vertical and horizontal directions, and the channel, respectively, where
. We formulate the feature
as
, with
denoting a dilated convolution layer, incorporating batch normalization and the GELU activation function. The accumulated tensors in the vertical and horizontal directions, calculated as per Equation (
3), are represented as
and
, respectively.
The tensors
and
merge the pixel-level weights of the feature map spatially. The resulting product forms the position-aware attention map
, defined as
. Subsequently, the output feature map
of SAT is achieved by combining
and the output of the SWin-Transform block, denoted as
. It is vital to remember that a convolutional layer enlarges the dimensions of
to align with the dimensions of feature
. Thus, feature
emerges, as depicted below:
where “⊗” represents matrix multiplication and “⊕” is used to denote element-wise addition. Furthermore, “
” is indicative of a
convolutional layer, which employs batch normalization coupled with the GELU activation function.
In summary, the Swin Transformer block, with its local window-based self-attention operation and accompanying MLP, provides an efficient and effective method for handling image data within the Transformer model context. Its design and operations have made significant contributions to the field of remote sensing image segmentation tasks.
3.3. Boundary-Aware Refinement Module
To address the challenge of accurate boundary segmentation in Spatial-Aware Transformers, we introduce a two-step modification: integrating a bottleneck layer behind the encoder and inputting the coarse prediction mask into a boundary refinement module.
3.3.1. Bottleneck Layer Integration
The Bottleneck Layer Integration module is designed to leverage the hierarchical representation power of the Swin Transformer and enhance its segmentation performance. By incorporating two consecutive Swin Transformer modules as the bottleneck layer, we enable the model to capture more complex spatial dependencies and obtain deeper contextual information.
Let denote the input feature map to the Bottleneck Layer Integration module, where H represents the height, W represents the width, and C represents the number of channels. The feature map X is processed by the first Swin Transformer module, denoted as . This module applies self-attention mechanisms and feed-forward networks to refine the feature representation. The output of is denoted as , where represents the number of output channels.
The output feature map Y is then fed into the second Swin Transformer module, denoted as . This module further refines the feature representation by applying self-attention mechanisms and feed-forward networks. The output of is denoted as , where represents the final number of output channels.
To integrate the bottleneck layer into the overall segmentation architecture, the output feature map Z is concatenated with the input feature map X. The concatenation operation is performed along the channel dimension, resulting in a fused feature map .
To ensure the consistency of feature dimensions throughout the network, a convolutional layer is applied to to adjust the number of channels back to the original value. The output of this convolutional layer is denoted as , representing the integrated bottleneck layer.
The Bottleneck Layer Integration module enriches the segmentation model with deeper contextual information and enhances its ability to capture complex spatial dependencies. By employing two consecutive Swin Transformer modules as the bottleneck layer, our model achieves improved segmentation performance and higher-level feature representation.
3.3.2. Refinement Module
As
Figure 4 shows, the refinement module is comprised of several components: a
convolutional layer, batch normalization, a ReLU activation function, and a max-pooling operation. Each of these components is integrated into every convolutional kernel layer during the encoding phase. Transitioning to the decoding phase, the model employs bilinear interpolation as its upsampling technique. Post-upsampling, convolutional layers and long skip connections are strategically implemented. These connections bridge the respective decoders and encoders, thereby facilitating the incorporation of supplemental contextual information. This streamlined structure ensures efficiency while preserving the critical attributes of the data through various stages of processing.
3.3.3. Conjoint Loss Function
The model utilizes a conjoint loss function, incorporating BCE loss, SSIM loss, and IoU loss. This allows the model to glean insights from various facets of the image. The hybrid loss function is defined as follows:
In the given formulation, we have , , and representing the BCE loss, SSIM loss, and IoU loss, respectively. The ground truth is denoted by U, the predicted output is , and , , and are the weights assigned to each loss component.
The BCE loss function is extensively employed for binary classification tasks. It assesses the performance of a classification model that generates probability values ranging from 0 to 1. The BCE loss is defined as:
where
U represents the actual label,
represents the predicted label.
The Structural Similarity Index (SSIM) loss function is a perceptual loss function employed to quantify the similarity between two images. It compares the local patterns of normalized pixel intensities and is commonly employed as a metric for image similarity. The SSIM index is computed using image windows:
Here, U and represent the ground truth image and the predicted (reconstructed) image, respectively, and denote their respective averages, represents the covariance between U and , and X and Y are variables employed to stabilize the division with a weak denominator.
The IoU loss measures the overlap between two bounding boxes and can be employed as a loss function for object detection tasks. The IoU is computed by dividing the area of intersection between two bounding boxes by the area of their union, as follows:
where we denote the intersection area as “Ar_intersect” and the union area as “Ar_union”.
In conclusion, the proposed method produces an optimized prediction mask, demonstrating improved boundary segmentation performance. This highlights the novel application of the Spatial-Aware Transformer in addressing existing challenges in remote sensing image segmentation.