Machine Learning (ML)-Based Copper Mineralization Prospectivity Mapping (MPM) Using Mining Geochemistry Method and Remote Sensing Satellite Data
Abstract
1. Introduction
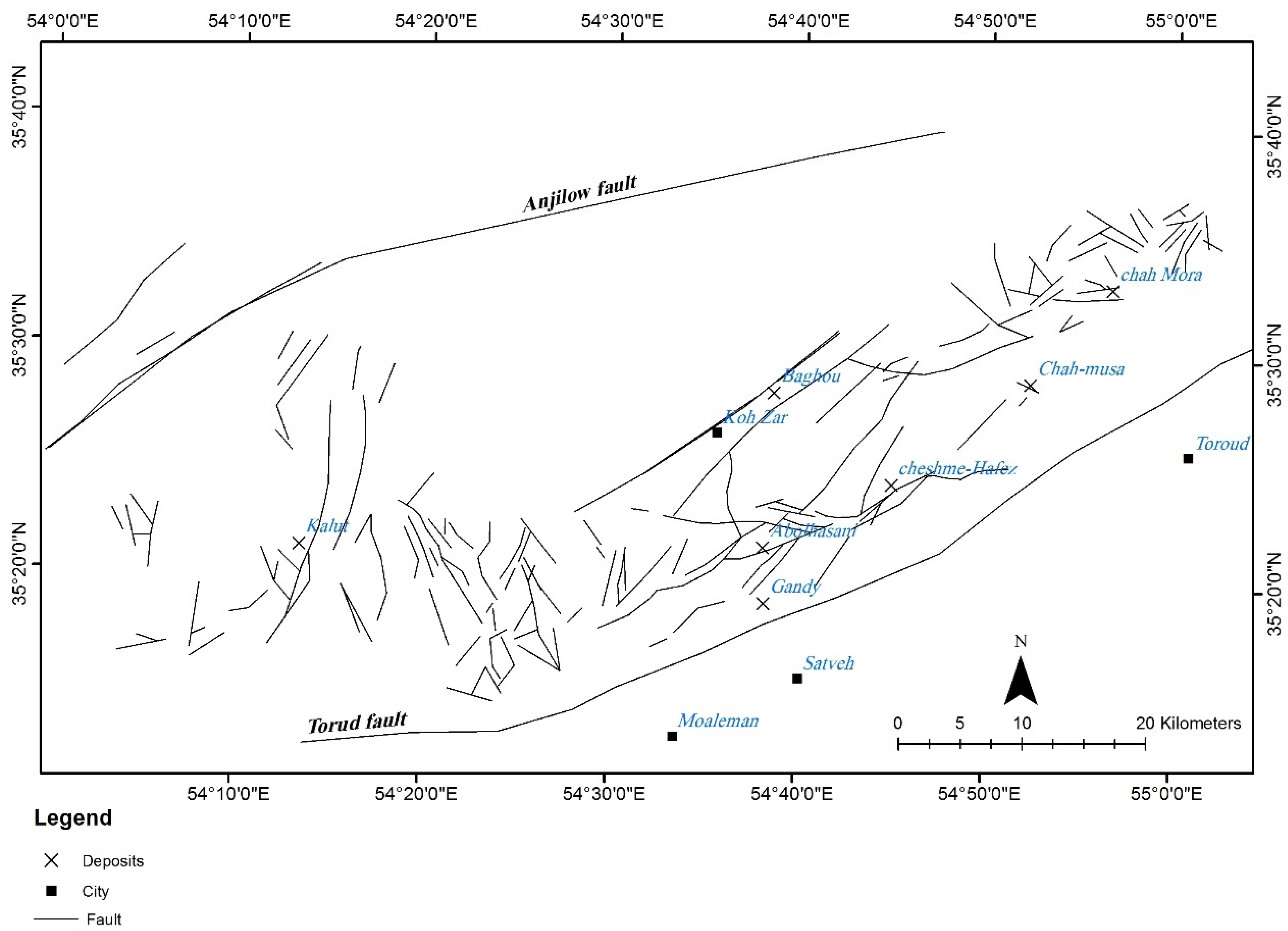
2. Geological Setting

3. Methodology
3.1. Big Data Analytics
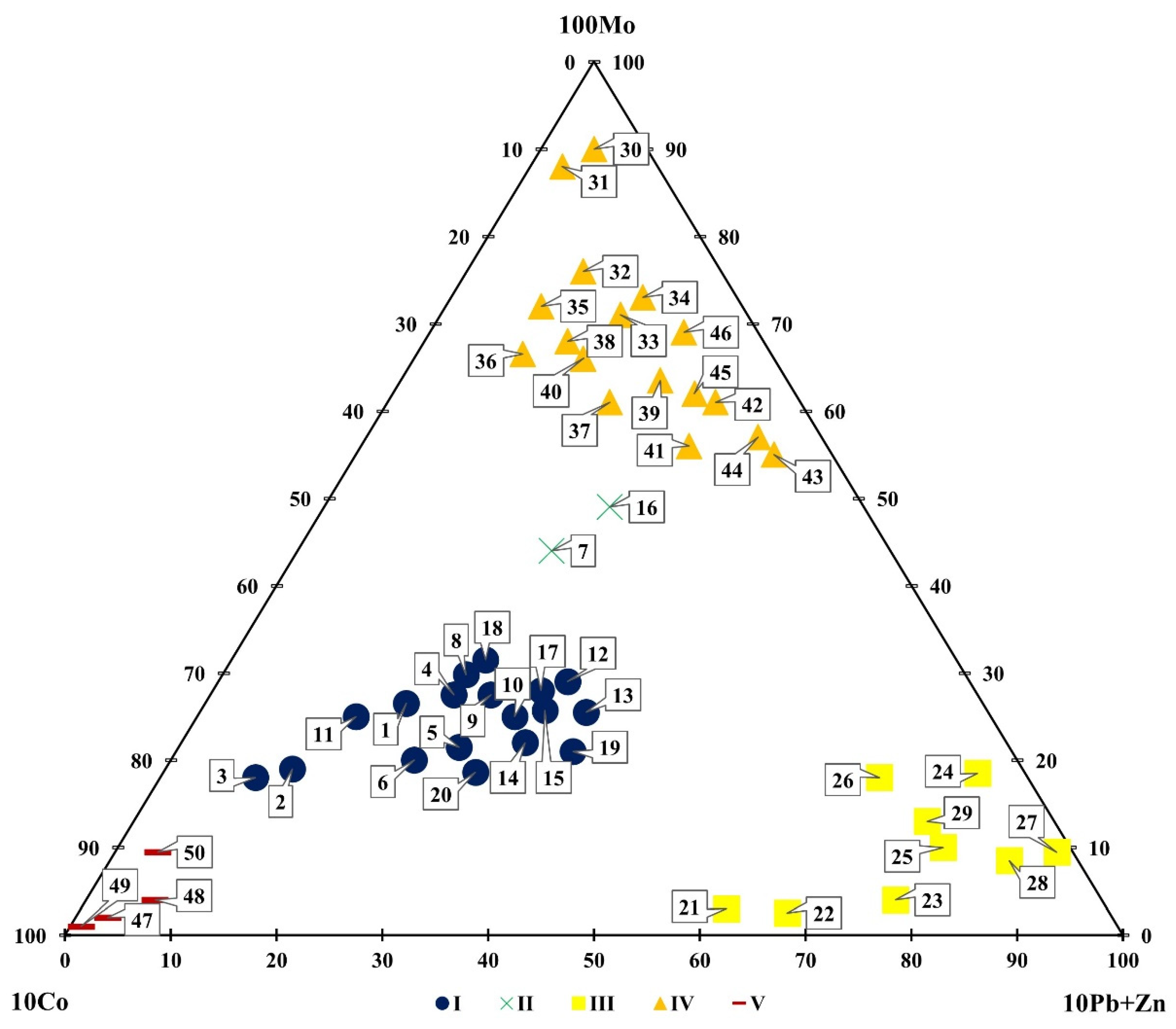
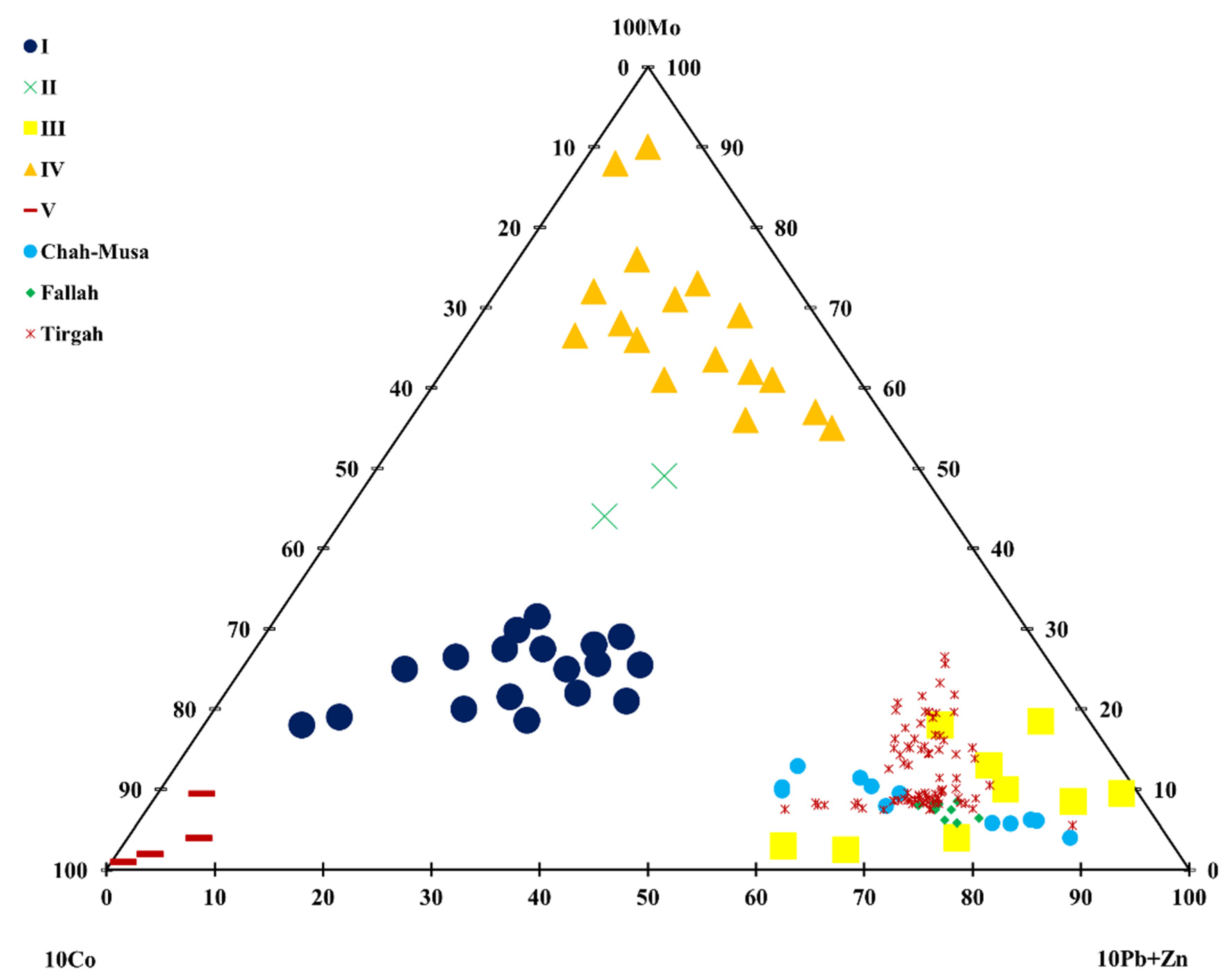
3.2. Mineralogical and Geochemical Type (MGT)
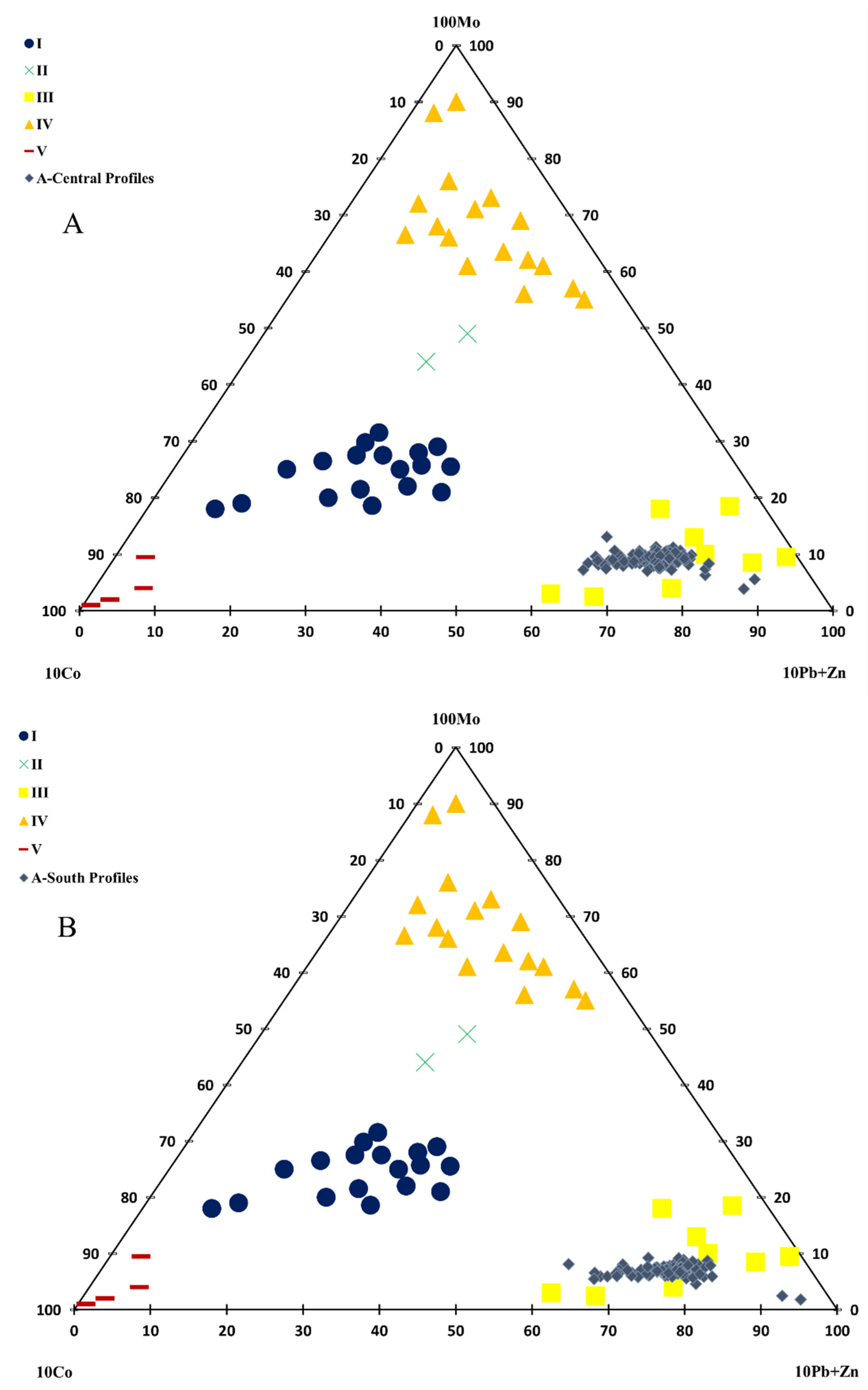
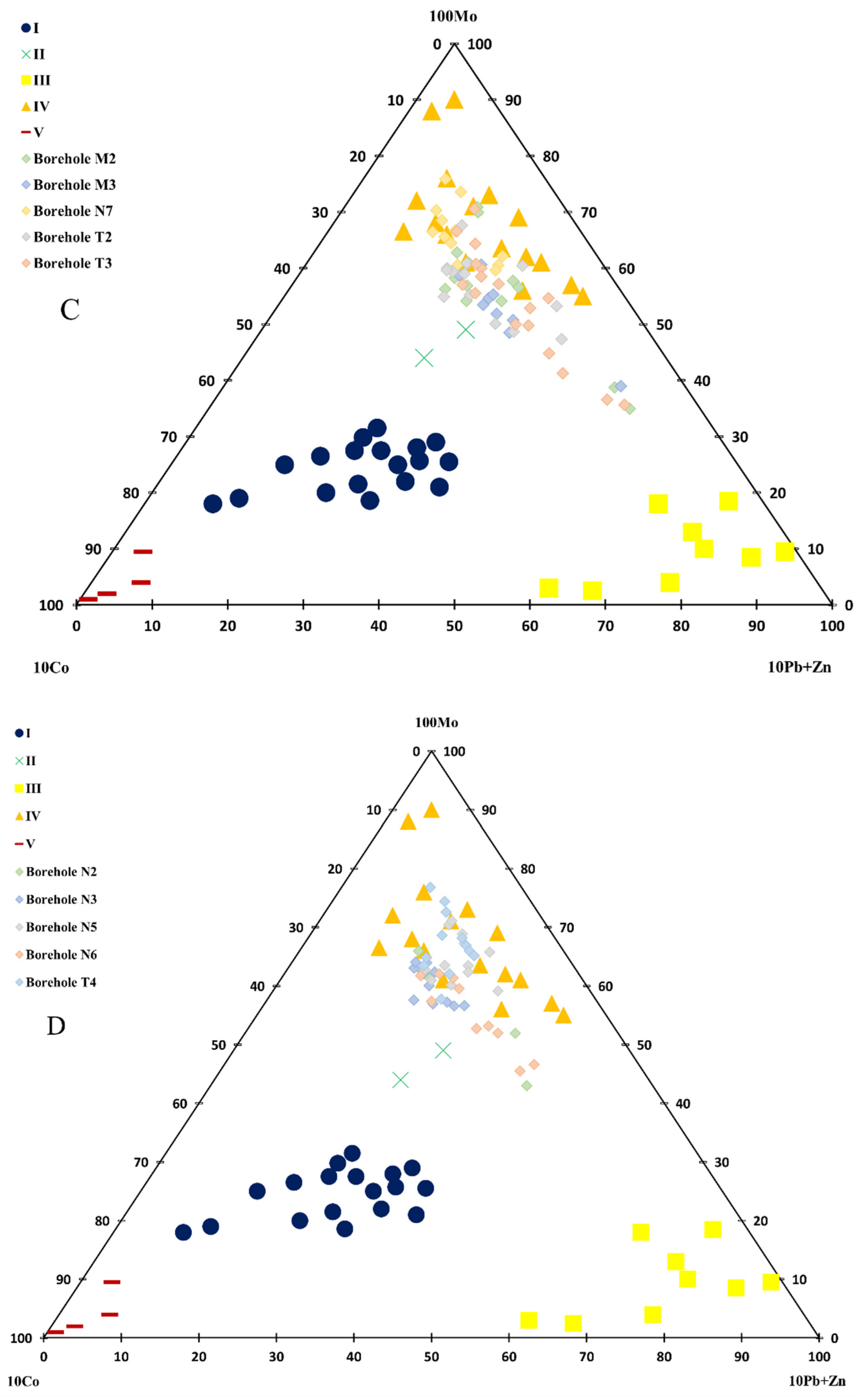
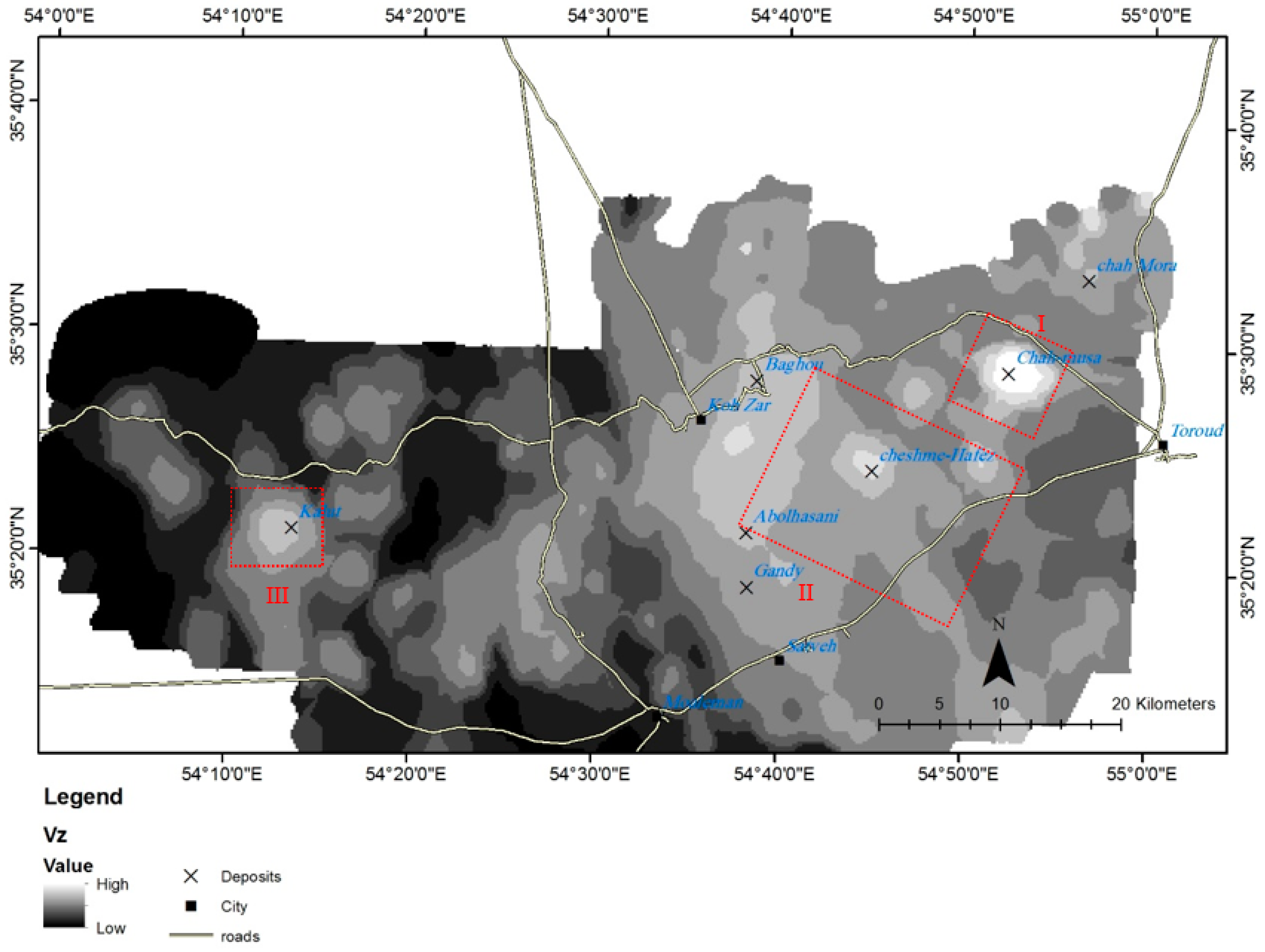
3.3. Vertical Geochemical Zonality Method
3.4. Remote Sensing Data
3.4.1. Landsat ETM+ Data Characteristics, Preprocessing and Processing Techniques
Principal Component Analysis (PCA)
3.5. Machine Learning Algorithms
Random Forest (RF)
3.6. Properties of Geochemical Data
3.7. Spatial Dataset
4. Analysis and Results
4.1. The Mineralogical and Geochemical Model
4.2. Vertical Geochemical Zonality Model
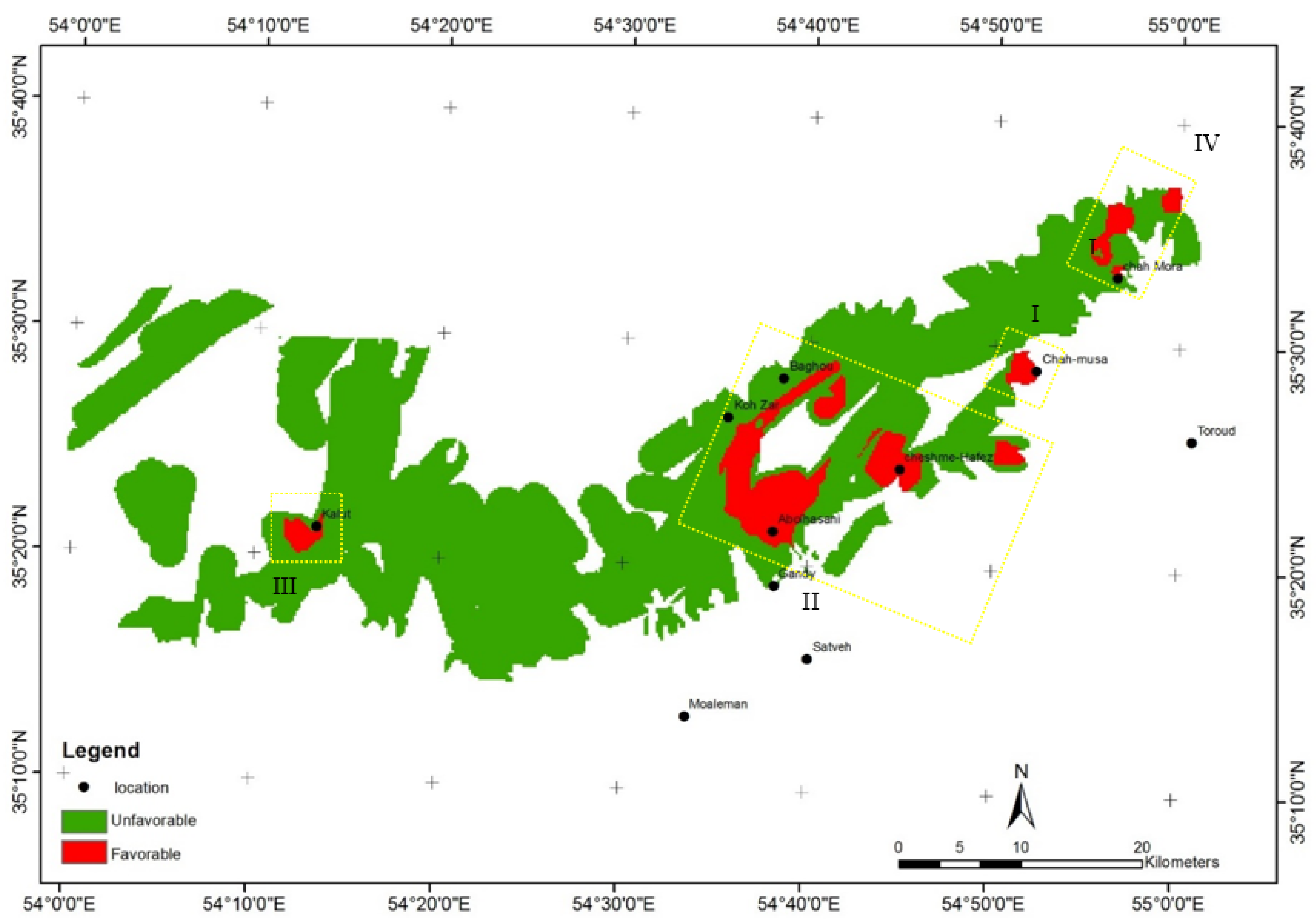
4.3. Mineral Prospectivity Mapping Model for Porphyry Copper Deposits
4.3.1. Spatial Evidence of Prospectivity for Porphyry Copper Deposit
Lithological and Structural Evidence
Alteration Evidence
Geochemical Evidence
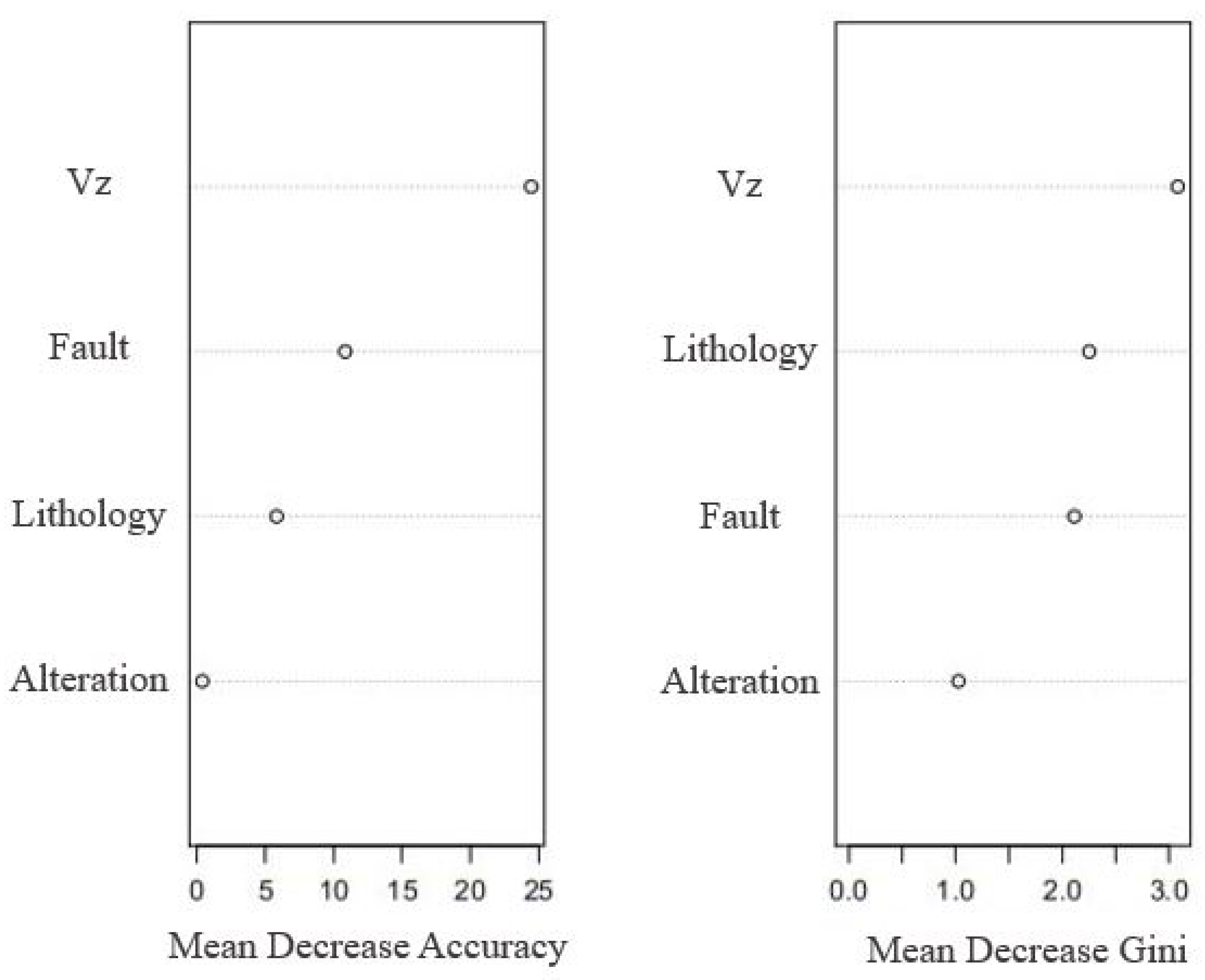
4.3.2. Integration of Evidential Layers Using RF Algorithm
4.3.3. Validation
5. Discussion
6. Conclusions
- A novel approach was accomplished in this study to optimize remote sensing-based evidential variables using mining geochemistry models for an RF-based copper mineralization prospectivity mapping (MPM).
- The MGT and Vz models were applied around the Chah-Musa deposit to identify the MGTs of the anomalies related to copper mineralization, and to evaluate anomalies (BM, ZDM, and outcropping) and the erosional surfaces. The mining geochemistry models determined that the Saghari deposit belongs to the polymetallic type (on the surface, oxide part) and porphyry copper type (at a depth, sulfide part). The possibilities for the occurrence of blind mineralization associated with the anomalies around the Chah-Musa deposit were assessed. The hydrothermal alteration zones associated with porphyry copper mineralization (argillic and phyllic alteration) were identified using PCA on ETM+ spectral bands.
- The random forest algorithm was applied to merge the evidence variables to develop a provincial-scale prospectivity map of porphyry copper deposits. Furthermore, a geochemical zonality coefficient (Pb × Zn/Cu × Mo) was used as one of several evidential maps to construct MPM based on RF for porphyry copper mineralization in the TCS belt. The result showed high applicability of the (MGT + Vz)-in-RF for mineral prospectivity mapping of porphyry copper deposits. This study explored buried copper deposits in the TCS belt through innovative approaches by integrating multi-source geoscientific datasets. The study contributes to the current efforts in searching for innovative and cost-effective methods for mineral exploration in mining sectors, and the approach can be used for MPM in metallogenic provinces around the world.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Beus, A.A.; Grigorian, S.V. Geochemical Exploration Methods for Mineral Deposits; Applied Publishing Ltd.: Wilmette, IL, USA, 1977; 287p. [Google Scholar]
- Levinson, A.A. Introduction to Exploration Geochemistry; Applied Publishing: Wilmette, IL, USA, 1980; 924p. [Google Scholar]
- Grigorian, S.V. Secondary Lithochemical Haloes in Prospecting for Hidden Mineralization; Nedra Publishing House: Moscow, Russia, 1985; p. 176. (In Russian) [Google Scholar]
- Grigorian, S.V. Mining Geochemistry; Nedra Publishing House: Moscow, Russia, 1992; p. 310. (In Russian) [Google Scholar]
- Chen, Y.; Zhao, P. Zonation in primary halos and geochemical prospecting pattern for the Guilaizhuang gold deposit, eastern China. Nonrenew. Resour. 1998, 7, 37–44. [Google Scholar]
- Ziaii, M.; Pouyan, A.A.; Ziaii, M. Geochemical anomaly recognition using fuzzy C-means cluster analysis. Wseas Trans. Syst. 2006, 5, 2424–2430. [Google Scholar]
- Cheng, Q. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, J.; Liang, Z. Geochemical characteristics and zonation of primary halos of Pulang porphyry copper deposit, Northwestern Yunnan Province, Southwestern China. J. China Univ. Geosci. 2008, 19, 371–377. [Google Scholar]
- Carranza, E.J.M.; Owusu, E.A.; Hale, M. Mapping of prospectivity and estimation of number of undiscovered prospects for lode gold, southwestern Ashanti Belt, Ghana. Miner. Depos. 2009, 44, 915–938. [Google Scholar] [CrossRef]
- Ziaii, M.; Pouyan, A.A.; Ziaei, M. Neuro-fuzzy modelling in mining geochemistry: Identification of geochemical anomalies. J. Geochem. Explor. 2009, 100, 25–36. [Google Scholar] [CrossRef]
- Zuo, R.; Cheng, Q.; Agterberg, F.; Xia, Q. Application of singularity mapping technique to identify local anomalies using stream sediment geochemical data, a case study from Gangdese, Tibet, western China. J. Geochem. Explor. 2009, 101, 225–235. [Google Scholar] [CrossRef]
- Sun, X.; Gong, Q.; Wang, Q.; Yang, L.; Wang, C.; Wang, Z. Application of local singularity model to delineate geochemical anomalies in Xiong’ershan gold and molybdenum ore district, Western Henan province, China. J. Geochem. Explor. 2010, 107, 21–29. [Google Scholar] [CrossRef]
- Hamedani, M.L.; Plimer, I.R.; Xu, C. Orebody modelling for exploration: The Western mineralization, Broken Hill, NSW. Nat. Resour. Res. 2012, 21, 325–345. [Google Scholar] [CrossRef]
- Cheng, Q. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas. J. Geochem. Explor. 2012, 122, 55–70. [Google Scholar] [CrossRef]
- Ziaii, M.; Ardejani, F.D.; Ziaei, M.; Soleymani, A.A. Neuro-fuzzy modeling based genetic algorithms for identification of geochemical anomalies in mining geochemistry. Appl. Geochem. 2012, 27, 663–676. [Google Scholar] [CrossRef]
- Zuo, R.; Xia, Q.; Zhang, D. A comparison study of the C–A and S–A models with singularity analysis to identify geochemical anomalies in covered areas. Appl. Geochem. 2013, 33, 165–172. [Google Scholar] [CrossRef]
- Safari, S.; Ziaii, M.; Ghoorchi, M. Integration of singularity and zonality methods for prospectivity map of blind mineralization. Int. J. Min. Geo-Eng. 2016, 50, 189–194. [Google Scholar]
- Safari Sinegani, S.; Ziaii, M.; Ghoorchi, M.; Sadeghi, M. Application of concentration gradient coefficients in mining geochemistry: A comparison of copper mineralization in Iran and Canada. J. Min. Environ. 2018, 9, 277–292. [Google Scholar]
- Ziaii, M.; Safari, S.; Timkin, T.; Voroshilov, V.; Yakich, T. Identification of geochemical anomalies of the porphyry–Cu deposits using concentration gradient modelling: A case study, Jebal-Barez area, Iran. J. Geochem. Explor. 2019, 199, 16–30. [Google Scholar] [CrossRef]
- Safari, S.; Ziaii, M. Singularity of zonality, the indicator for quantitative evaluation of anomalies in mining geochemistry, Case study: Kerver. J. Min. Eng. 2019, 14, 76–91. [Google Scholar]
- Macheyeki, A.S.; Li, X.; Kafumu, D.P.; Yuan, F. Applied Geochemistry: Advances in Mineral Exploration Techniques; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Timkin, T.; Abedini, M.; Ziaii, M.; Ghasemi, M.R. Geochemical and Hydrothermal Alteration Patterns of the Abrisham-Rud Porphyry Copper District, Semnan Province, Iran. Minerals 2022, 12, 103. [Google Scholar] [CrossRef]
- Sun, W.; Zheng, Y.; Wang, W.; Feng, X.; Zhu, X.; Zhang, Z.; Hou, H.; Ge, L.; Lv, H. Geochemical Characteristics of Primary Halos and Prospecting Significance of the Qulong Porphyry Copper–Molybdenum Deposit in Tibet. Minerals 2023, 13, 333. [Google Scholar] [CrossRef]
- Ziaii, M.; Carranza, E.J.M.; Ziaei, M. Application of geochemical zonality coefficients in mineral prospectivity mapping. Comput. Geosci. 2011, 37, 1935–1945. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Sadeghi, M. Predictive mapping of prospectivity and quantitative estimation of undiscovered VMS deposits in Skellefte district (Sweden). Ore Geol. Rev. 2010, 38, 219–241. [Google Scholar] [CrossRef]
- Carranza, E.J.M. From predictive mapping of mineral prospectivity to quantitative estimation of number of undiscovered prospects. Resour. Geol. 2010, 61, 30–51. [Google Scholar] [CrossRef]
- Yousefi, M.; Kamkar-Rouhani, A.; Carranza, E.J.M. Geochemical mineralization probability index (GMPI): A new approach to generate enhanced stream sediment geochemical evidential map for increasing probability of success in mineral potential mapping. J. Geochem. Explor. 2012, 115, 24–35. [Google Scholar] [CrossRef]
- Yousefi, M.; Kamkar-Rouhani, A.; Carranza, E.J.M. Application of staged factor analysis and logistic function to create a fuzzy stream sediment geochemical evidence layer for mineral prospectivity mapping. Geochem. Explor. Environ. Anal. 2014, 14, 45–58. [Google Scholar] [CrossRef]
- Chattoraj, S.L.; Prasad, G.; Sharma, R.U.; van der Meer, F.D.; Guha, A.; Pour, A.B. Integration of remote sensing, gravity and geochemical data for exploration of Cu-mineralization in Alwar basin, Rajasthan, India. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102162. [Google Scholar] [CrossRef]
- Bai, S.; Zhao, J. A New Strategy to Fuse Remote Sensing Data and Geochemical Data with Different Machine Learning Methods. Remote Sens. 2023, 15, 930. [Google Scholar] [CrossRef]
- Zuo, R.; Xiong, Y. Big data analytics of identifying geochemical anomalies supported by machine learning methods. Nat. Resour. Res. 2018, 27, 5–13. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R.; Carranza, E.J.M. Mapping mineral prospectivity through big data analytics and a deep learning algorithm. Ore Geol. Rev. 2018, 102, 811–817. [Google Scholar] [CrossRef]
- Liu, Y.; Carranza, E.J.M.; Xia, Q. Developments in Quantitative Assessment and Modeling of Mineral Resource Potential: An Overview. Nat. Resour. Res. 2022, 31, 1825–1840. [Google Scholar] [CrossRef]
- Matveev, A.A.; Solovov, A.P. Geochemical Methods of Prospecting for Ore Deposits; Moscow State University Publishing House: Moscow, Russia, 1985; 232p. (In Russian) [Google Scholar]
- Arkhipov, A.Y.; Bugrov, V.A.; Vorobyov, S.A.; Gershman, D.M.; Grigorian, S.V.; Kiyatovsky, E.M.; Matveev, A.A.; Milyaev, S.A.; Nikolaev, V.A.; Perelman, A.I.; et al. Handbook of Geochemical Prospecting for Minerals; Nedra: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Ziaii, M. Method of Rational Mineralogical and Geochemical Sampling of Gold Ore Occurrences. Ph.D. Thesis, Russian Academy of Science (IGEM RAN), Moscow, Russia, 1999. (In Russian). [Google Scholar]
- Garigorin, S.V.; Liakhovich, T.T.; Getmansky, I.I.; Ziaii, M. Trace elements in minerals as a criterion of geochemical anomaly estimations. J. Sci. Technol. 1999, 1, 22–26, (In Russian with English Abstract). [Google Scholar]
- Grigorian, S.V.; Liakhovich, T.T.; Getmansky, I.I.; Ziaii, M. Geochemical spectrum of minerals as a criterion of gold ores type identification. J. Sci. Technol. 1999, 3, 5–8, (In Russian with English Abstract). [Google Scholar]
- Ziaii, M.; Abedi, A.; Ziaei, M. Geochemical and mineralogical pattern recognition and modeling with a Bayesian approach to hydrothermal gold deposits. Appl. Geochem. 2009, 24, 1142–1146. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, Y.; Yin, B.; Sun, S.; Zuo, R. Recognizing geochemical patterns related to mineralization using a self-organizing map. Appl. Geochem. 2023, 151, 105621. [Google Scholar] [CrossRef]
- Kazemi, H. Exploring Promising Areas for Copper Deposits in the Trood Area—Using Remote Sensing and GIS. Master’s Thesis, Shahrood University of Technology, Shahrood, Iran, 2007. [Google Scholar]
- Ziaii, M.; Abedi, A.; Ziaei, M.; Kamkar Rouhani, A.; Zendahdel, A. GIS modelling for Au-Pb-Zn potential mapping in Torud-Chah Shirin area-Iran. J. Min. Environ. 2010, 1, 17–27. [Google Scholar]
- Noori, L.; Pour, A.B.; Askari, G.; Taghipour, N.; Pradhan, B.; Lee, C.W.; Honarmand, M. Comparison of different algorithms to map hydrothermal alteration zones using ASTER remote sensing data for polymetallic vein-type ore exploration: Toroud–Chahshirin Magmatic Belt (TCMB), North Iran. Remote Sens. 2019, 11, 495. [Google Scholar] [CrossRef]
- Zamyad, M.; Afzal, P.; Pourkermani, M.; Nouri, R.; Jafari, M.R. Determination of hydrothermal alteration zones using remote sensing methods in Tirka Area, Toroud, NE Iran. J. Indian Soc. Remote Sens. 2019, 47, 1817–1830. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Beiranvand Pour, A.; Muslim, A.M.; Müller, R.D.; Chandra, R. Integration of selective dimensionality reduction techniques for mineral exploration using ASTER satellite data. Remote Sens. 2020, 12, 1261. [Google Scholar] [CrossRef]
- Pour, A.B.; Zoheir, B.; Pradhan, B.; Hashim, M. Editorial for the special issue: Multispectral and hyperspectral remote sensing data for mineral exploration and environmental monitoring of mined areas. Remote Sens. 2021, 13, 519. [Google Scholar] [CrossRef]
- Mamouch, Y.; Attou, A.; Miftah, A.; Ouchchen, M.; Dadi, B.; Achkouch, L.; Et-tayea, Y.; Allaoui, A.; Boualoul, M.; Randazzo, G.; et al. Mapping of Hydrothermal Alteration Zones in the Kelâat M’Gouna Region Using Airborne Gamma-Ray Spectrometry and Remote Sensing Data: Mining Implications (Eastern Anti-Atlas, Morocco). Appl. Sci. 2022, 12, 957. [Google Scholar] [CrossRef]
- Yousufi, A.; Ahmadi, H.; Bekbotayeva, A.; Arshamov, Y.; Baisalova, A.; Omarova, G.; Pekkan, E. Integration of Remote Sensing and Field Data in Ophiolite Investigations: A Case Study of Logar Ophiolite Complex, SE Afghanistan. Minerals 2023, 13, 234. [Google Scholar] [CrossRef]
- Solovov, A.P. Geochemical Prospecting for Mineral Deposits; Englsih Edition; Mir Publication: Moscow, Russia, 1987; 287p. [Google Scholar]
- Moon, C.J. Towards a quantitative model of downstream dilution of point source geochemical anomalies. J. Geochem. Explor. 1999, 65, 111–132. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M.J.O.G.R. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Data-driven predictive mapping of gold prospectivity, Baguio district, Philippines: Application of Random Forests algorithm. Ore Geol. Rev. 2015, 71, 777–787. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Comput. Geosci. 2015, 74, 60–70. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Data-driven predictive modeling of mineral prospectivity using random forests: A case study in Catanduanes Island (Philippines). Nat. Resour. Res. 2016, 25, 35–50. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, K.; Carranza, E.J.M.; Yang, F. Maximum entropy and random forest modeling of mineral potential: Analysis of gold prospectivity in the Hezuo–Meiwu district, west Qinling Orogen, China. Nat. Resour. Res. 2019, 28, 645–664. [Google Scholar] [CrossRef]
- Wang, C.; Pan, Y.; Chen, J.; Ouyang, Y.; Rao, J.; Jiang, Q. Indicator element selection and geochemical anomaly mapping using recursive feature elimination and random forest methods in the Jingdezhen region of Jiangxi Province, South China. Appl. Geochem. 2020, 122, 104760. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Xiao, K.; Wei, H.; Yang, F.; Chen, Z.; Li, N.; Xiang, J. Mineral prospectivity mapping based on isolation forest and random forest: Implication for the existence of spatial signature of mineralization in outliers. Nat. Resour. Res. 2022, 31, 1981–1999. [Google Scholar] [CrossRef]
- Alavi, M. Tectonostratigraphic synthesis and structural style of the Alborz Mountain system in northern Iran. J. Geodyn. 1996, 21, 1–33. [Google Scholar] [CrossRef]
- Shamanian, G.H.; Hedenquist, J.W.; Hattori, K.H.; Hassanzadeh, J. The Gandy and Abolhassani epithermal prospects in the Alborz magmatic arc, Semnan province, Northern Iran. Econ. Geol. 2004, 99, 691–712. [Google Scholar] [CrossRef]
- TaleFazel, E.; Mehrabi, B.; Siani, M.G. Epithermal systems of the Torud–Chah Shirin district, northern Iran: Ore-fluid evolution and geodynamic setting. Ore Geol. Rev. 2019, 109, 253–275. [Google Scholar] [CrossRef]
- Mehrabi, B.; Ghasemi, S.M.; Tale, F.E. Structural control on epithermal mineralization in the Troud-Chah Shirin belt using point pattern and Fry analyses, north of Iran. Geotectonics 2015, 49, 320–331. [Google Scholar] [CrossRef]
- Imamjomeh, A.; Rastad, E.; Bouzari, F.; Omran, N.R. An introduction to individual disseminated-veinlet and vein mineralization system of Cu (Pb-Zn) in the Chahmoosa-Gholekaftaran mining district, eastern part of Toroud-Chahshirin magmatic arc. Sci. Q. J. Geosci. 2008, 70, 112–125. [Google Scholar]
- Seifivand, A.; Sheibi, M. Ballooning emplacement and alteration of the Chah-Musa subvolcanic intrusion (NE Iran) inferred from magnetic susceptibility and fabric. Geol. Mag. 2020, 157, 621–639. [Google Scholar] [CrossRef]
- Khalaj, M.; Hassan-Nezhad, A.; Alizadeh, H.; Babaei, A.H.; Ghorbani, G. Investigation of mineralization fluid evolution of hydrothermal vein copper deposits: Based on studies of fluid inclusions at Chah Mousa area (north of central Iran). Adv. Appl. Geol. 2021, 11, 116–135. [Google Scholar]
- Bugrov, V. Geochemical sampling techniques in the Eastern Desert of Egypt. J. Geochem. Explor. 1974, 3, 67–75. [Google Scholar] [CrossRef]
- Perelman, A.I. Landscape Geochemistry; Higher School: Moscow, Russia, 1975; 341p. (In Russian) [Google Scholar]
- Li, Q.; Xi, X.; Ren, T.; Zhao, Y.; Che, G. Geochemical exploration in the semiarid steppe terrain of eastern Inner Mongolia—A case history. J. Geochem. Explor. 1989, 33, 27–46. [Google Scholar]
- Houshmandzadeh, A.R.; Alavi, M.N.; Haghipour, A.A. Evolution of Geological Phenomenon in Toroud Area (Precambrian to Recent); Report H5; Geological Survey & Mineral Exploration of Iran: Tehran, Iran, 1978. [Google Scholar]
- Geological Survey of Iran (GSI). Geological Map of Toroud; 1:250,000 Series; Geological Survey of Iran (GSI): Tehran, Iran, 1978. [Google Scholar]
- Kitaev, N.A. Multidimensional analysis of geochemical fields. Math. Geol. 1991, 23, 15–32. [Google Scholar] [CrossRef]
- Baranov, E.V. Endogenetic Haloes Associated with Massive Sulphide Deposits; Nedra Publishing House: Moscow, Russia, 1987; p. 294. (In Russian) [Google Scholar]
- Safonov, Y.G. Hydrothermal gold deposits: Distribution, geological-genetic types, and productivity of ore-forming systems. Geol. Ore Depos. 1997, 30, 20–32. [Google Scholar]
- Mars, J.C.; Rowan, L.C. Regional mapping of phyllic- and argillic-altered rocks in the Zagros magmatic arc, Iran, using Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) data and logical operator algorithms. Geosphere 2006, 2, 161–186. [Google Scholar] [CrossRef]
- Di Tommaso, I.; Rubinstein, N. Hydrothermal alteration mapping using ASTER data in the Infiernillo porphyry deposit, Argentina. Ore Geol. Rev. 2007, 32, 275–290. [Google Scholar] [CrossRef]
- Pour, B.A.; Hashim, M. The application of ASTER remote sensing data to porphyry copper and epithermal gold deposits. Ore Geol. Rev. 2012, 44, 1–9. [Google Scholar] [CrossRef]
- Lowell, J.D.; Guilbert, J.M. Lateral and vertical alteration-mineralization zoning in porphyry ore deposits. Econ. Geol. Bull. Soc. Econ. Geol. 1970, 65, 373–408. [Google Scholar] [CrossRef]
- Hunt, G.R.; Ashley, P. Spectra of altered rocks in the visible and near infrared. Econ. Geol. 1979, 74, 1613–1629. [Google Scholar] [CrossRef]
- Crowley, J.K.; Vergo, N. Near-infrared reflectance spectra of mixtures of kaolin group minerals: Use in clay mineral studies. Clays Clay Miner. 1988, 36, 310–316. [Google Scholar] [CrossRef]
- Pour, B.A.; Hashim, M. Identification of hydrothermal alteration minerals for exploring of porphyry copper deposit using ASTER data, SE Iran. J. Asian Earth Sci. 2011, 42, 1309–1323. [Google Scholar] [CrossRef]
- Pour, B.A.; Hashim, M. Identifying areas of high economic-potential copper mineralization using ASTER data in Urumieh-Dokhtar Volcanic Belt, Iran. Adv. Space Res. 2012, 49, 753–769. [Google Scholar] [CrossRef]
- Hu, B.; Xu, Y.; Wan, B.; Wu, X.; Yi, G. Hydrothermally altered mineral mapping using synthetic application of Sentinel-2A MSI, ASTER and Hyperion data in the Duolong area, Tibetan Plateau, China. Ore Geol. Rev. 2018, 101, 384–397. [Google Scholar] [CrossRef]
- Pour, A.B.; Hashim, M.; Hong, J.K.; Park, Y. Lithological and alteration mineral mapping in poorly exposed lithologies using Landsat-8 and ASTER satellite data: North-eastern Graham Land, Antarctic Peninsula. Ore Geol. Rev. 2019, 108, 112–133. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Yang, J.; Cheng, Q. A comparative study of independent component analysis with principal component analysis in geological objects identification, Part I: Simulations. J. Geochem. Explor. 2015, 149, 127–135. [Google Scholar] [CrossRef]
- Prado, I.M.; Crosta, A.P. Evaluating Geoscan AMSS Mk-II for gold exploration in the Fazenda Maria Preta District, Rio Itapicuru Greenstone Belt, Bahia State, Brazil. Boletim IG-USP. Série Científica 1997, 28, 63–83. [Google Scholar] [CrossRef]
- Pour, A.B.; Park, T.S.; Park, Y.; Hong, J.K.; Zoheir, B.; Pradhan, B.; Ayoobi, I.; Hashim, M. Application of Multi-Sensor Satellite Data for Exploration of Zn-Pb Sulfide Mineralization in the Franklinian Basin, North Greenland. Remote Sens. 2018, 10, 1186. [Google Scholar] [CrossRef]
- Pour, A.B.; Park, T.-Y.S.; Park, Y.; Hong, J.K.; Muslim, A.M.; Läufer, A.; Crispini, L.; Pradhan, B.; Zoheir, B.; Rahmani, O.; et al. Landsat-8, advanced spaceborne thermal emission and reflection radiometer, and WorldView-3 multispectral satellite imagery for prospecting copper-gold mineralization in the northeastern Inglefield Mobile Belt (IMB), northwest Greenland. Remote Sens. 2019, 11, 2430. [Google Scholar] [CrossRef]
- Pour, A.B.; Park, Y.; Crispini, L.; Läufer, A.; Kuk Hong, J.; Park, T.-Y.S.; Zoheir, B.; Pradhan, B.; Muslim, A.M.; Hossain, M.S.; et al. Mapping Listvenite Occurrences in the Damage Zones of Northern Victoria Land, Antarctica Using ASTER Satellite Remote Sensing Data. Remote Sens. 2019, 11, 1408. [Google Scholar] [CrossRef]
- Crosta, A.P.; De Souza Filho, C.R.; Azevedo, F.; Brodie, C. Targeting key alteration minerals in epithermal deposits in Patagonia, Argentina, using ASTER imagery and principal component analysis. Int. J. Remote Sens. 2003, 24, 4233–4240. [Google Scholar] [CrossRef]
- Loughlin, W.P. Principal component analysis for alteration mapping. Photogramm. Eng. Remote Sens. 1991, 57, 1163–1169. [Google Scholar]
- Honarmand, M.; Ranjbar, H.; Shahabpour, J. Application of principal component analysis and spectral angle mapper in the mapping of hydrothermal alteration in the Jebal–Barez Area, Southeastern Iran. Resour. Geol. 2012, 62, 119–139. [Google Scholar] [CrossRef]
- Khaleghi, M.; Ranjbar, H.; Shahabpour, J.; Honarmand, M. Spectral angle mapping, spectral information divergence, and principal component analysis of the ASTER SWIR data for exploration of porphyry copper mineralization in the Sarduiyeh area, Kerman province, Iran. Appl. Geomat. 2014, 6, 49–58. [Google Scholar] [CrossRef]
- Zuo, R. Machine learning of mineralization-related geochemical anomalies: A review of potential methods. Nat. Resour. Res. 2017, 26, 457–464. [Google Scholar] [CrossRef]
- Zuo, R.; Xiong, Y.; Wang, J.; Carranza, E.J.M. Deep learning and its application in geochemical mapping. Earth-Sci. Rev. 2019, 192, 1–14. [Google Scholar] [CrossRef]
- Zuo, R.; Wang, J.; Xiong, Y.; Wang, Z. The processing methods of geochemical exploration data: Past, present, and future. Appl. Geochem. 2021, 132, 105072. [Google Scholar] [CrossRef]
- Zuo, R.; Wang, Z. Effects of random negative training samples on mineral prospectivity mapping. Nat. Resour. Res. 2020, 29, 3443–3455. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
- Ziaii, M. Lithogeochemical Exploration Methods for Porphyry Copper Deposit in Sungun, NW Iran. Unpublished Master’s Thesis, Moscow State University (MSU), Moscow, Russia, 1996; p. 98. (In Russian). [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- R Development Core Team. The R Project for Statistical Computing. 2008. Available online: http://www.R-project.org (accessed on 28 October 2018).
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Barton, M.D. Granitic magmatism and metallogeny of southwestern North America. Earth Environ. Sci. Trans. R. Soc. Edinb. 1996, 87, 261–280. [Google Scholar]
- Groves, D.I.; Vielreicher, R.M.; Goldfarb, R.J.; Condie, K.C. Controls on the heterogeneous distribution of mineral deposits through time. Geol. Soc. Lond. Spec. Publ. 2005, 248, 71–101. [Google Scholar] [CrossRef]
- Kesler, S.E.; Wilkinson, B.H. The role of exhumation in the temporal distribution of ore deposits. Econ. Geol. 2006, 101, 919–922. [Google Scholar] [CrossRef]
- Zürcher, L.; Hammarstrom, J.M.; Mars, J.C.; Ludington, S.D.; Zientek, M.L. Relationship between Porphyry Systems, Crustal Preservation Levels, and Amount of Exploration in Magmatic Belts of the Central Tethys Region; Society of Economic Geologists: Littleton, CO, USA, 2016. [Google Scholar]




| Soil Samples | Vz Index | Assessment | Rock Samples | Vz Index | Assessment |
|---|---|---|---|---|---|
| A-Central Profiles | 12.32 | Blind mineralization | A-Central Boreholes | 7.54 | BM |
| 35T-51T | 13.60 | Blind mineralization | A2 | 7.64 | BM |
| 52T-67T | 8.84 | Blind mineralization | A3 | 30.23 | BM |
| 68T-82T | 10.86 | Blind mineralization | B7 | 4.50 | BM |
| Three Profiles | 10.73 | Blind mineralization | B2 | 3.17 | BM |
| C3 | 10.03 | BM | |||
| A-South Profiles | 2.11 | Outcropping mineralization | A-South Boreholes | 0.42 | Outcropping |
| 33L-41L | 2.13 | Outcropping mineralization | B2 | 1.80 | Outcropping |
| 34M-41M | 1.34 | Outcropping mineralization | B3 | 0.79 | Outcropping |
| 34N-44N | 2.08 | Outcropping mineralization | B4 | 0.04 | Outcropping |
| 35O-46O | 2.51 | Outcropping mineralization | B5 | 0.11 | Outcropping |
| 34P-47P | 1.85 | Outcropping mineralization | B6 | 0.76 | Outcropping |
| Five Profiles | 1.90 | Outcropping mineralization | C1 | 1.85 | Outcropping |
| C4 | 0.17 | Outcropping |
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | |
|---|---|---|---|---|---|---|
| Band 1 | 0.31 | 0.46 | 0.52 | 0.40 | 0.25 | 0.44 |
| Band 2 | 0.35 | 0.37 | 0.21 | 0.02 | −0.09 | −0.83 |
| Band 3 | 0.49 | 0.31 | −0.19 | −0.59 | −0.41 | 0.32 |
| Band 4 | 0.38 | 0.11 | −0.77 | 0.39 | 0.32 | −0.01 |
| Band 5 | 0.47 | −0.58 | 0.15 | 0.40 | −0.50 | 0.03 |
| Band 7 | 0.42 | −0.45 | 0.20 | −0.42 | 0.64 | −0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abedini, M.; Ziaii, M.; Timkin, T.; Pour, A.B. Machine Learning (ML)-Based Copper Mineralization Prospectivity Mapping (MPM) Using Mining Geochemistry Method and Remote Sensing Satellite Data. Remote Sens. 2023, 15, 3708. https://doi.org/10.3390/rs15153708
Abedini M, Ziaii M, Timkin T, Pour AB. Machine Learning (ML)-Based Copper Mineralization Prospectivity Mapping (MPM) Using Mining Geochemistry Method and Remote Sensing Satellite Data. Remote Sensing. 2023; 15(15):3708. https://doi.org/10.3390/rs15153708
Chicago/Turabian StyleAbedini, Mahnaz, Mansour Ziaii, Timofey Timkin, and Amin Beiranvand Pour. 2023. "Machine Learning (ML)-Based Copper Mineralization Prospectivity Mapping (MPM) Using Mining Geochemistry Method and Remote Sensing Satellite Data" Remote Sensing 15, no. 15: 3708. https://doi.org/10.3390/rs15153708
APA StyleAbedini, M., Ziaii, M., Timkin, T., & Pour, A. B. (2023). Machine Learning (ML)-Based Copper Mineralization Prospectivity Mapping (MPM) Using Mining Geochemistry Method and Remote Sensing Satellite Data. Remote Sensing, 15(15), 3708. https://doi.org/10.3390/rs15153708







