Point Cloud Registration Based on Fast Point Feature Histogram Descriptors for 3D Reconstruction of Trees
Abstract
1. Introduction
- (1)
- An association description and assessment method, based on an FPFH and the Bhattacharyya distance, is proposed. This method is rotationally invariant to point clouds and is more accurate for point clouds with noise and low overlap.
- (2)
- A matching pair pruning strategy with RANSAC is developed. By evaluating the correlation between matching pairs, the erroneous matches are removed more effectively, leading to an increased proportion of correct matching pairs.
- (3)
- A series of registration experiments on real-world tree point clouds and synthesized point clouds with Gaussian noise demonstrate the effectiveness of the proposed method.
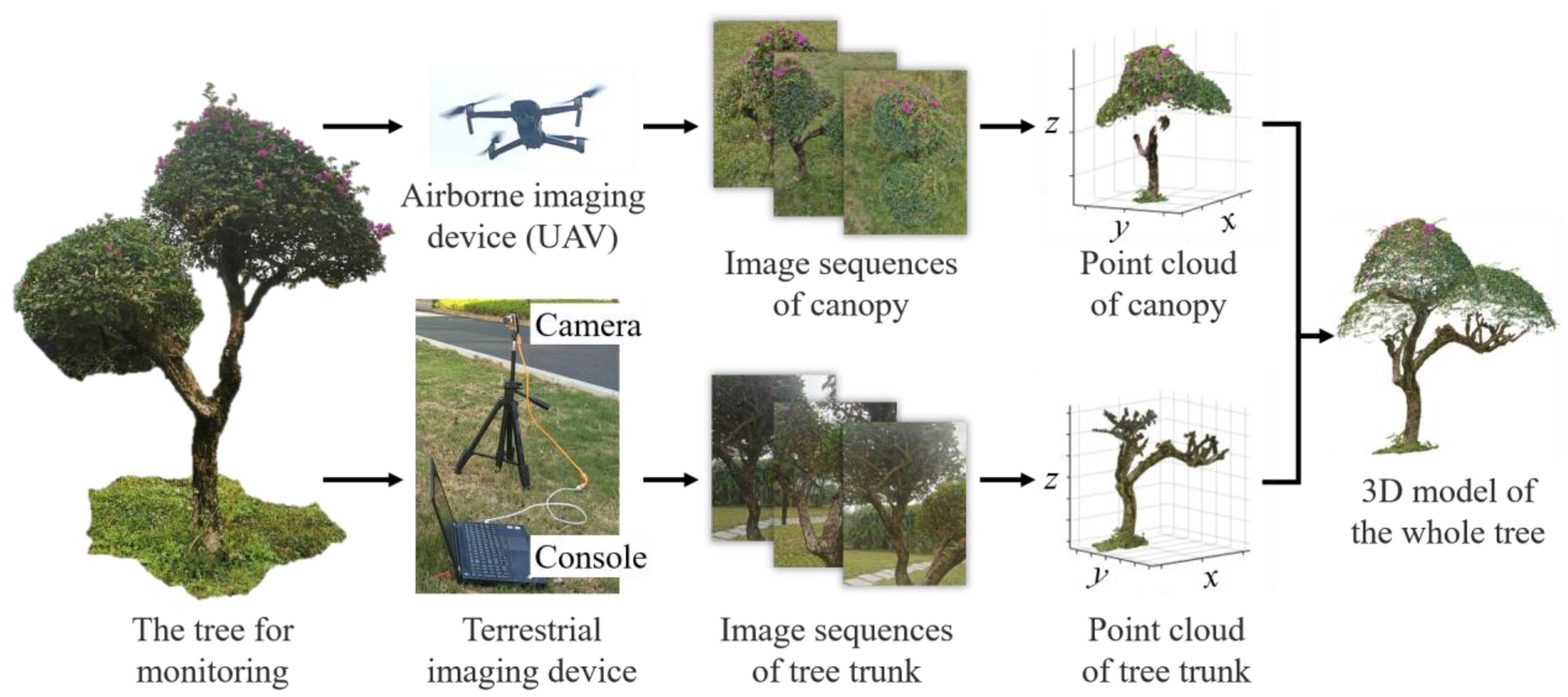
2. Phenotypic Structure Monitoring System for Tall Plants
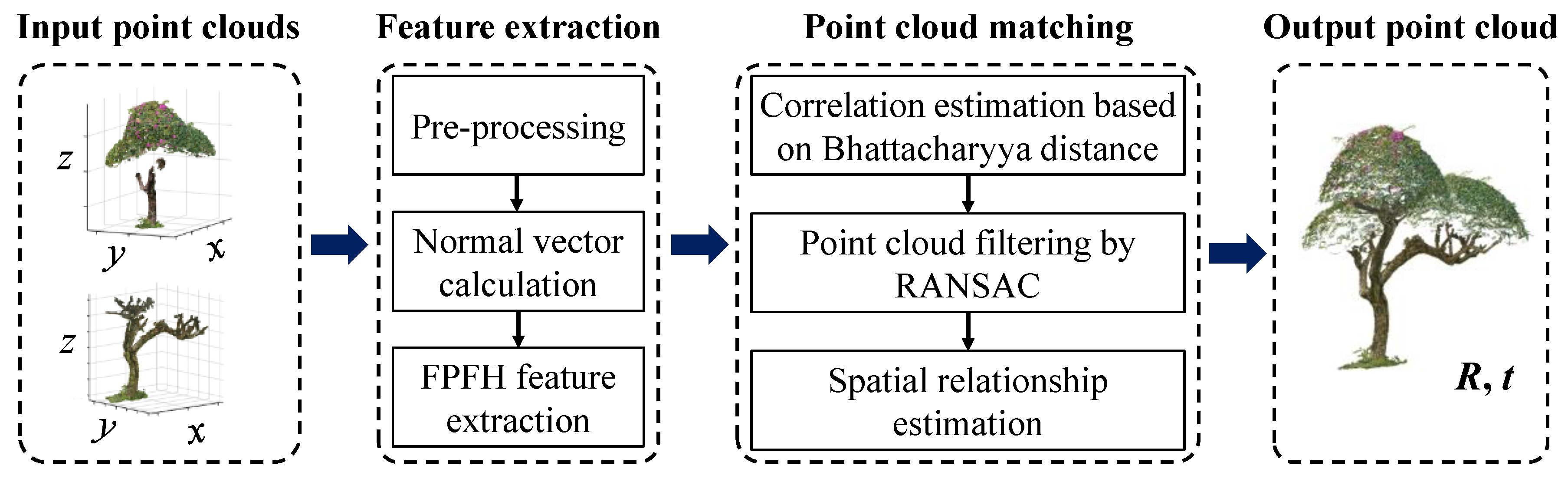
3. Improved Point Cloud Registration Method Based on FPFH
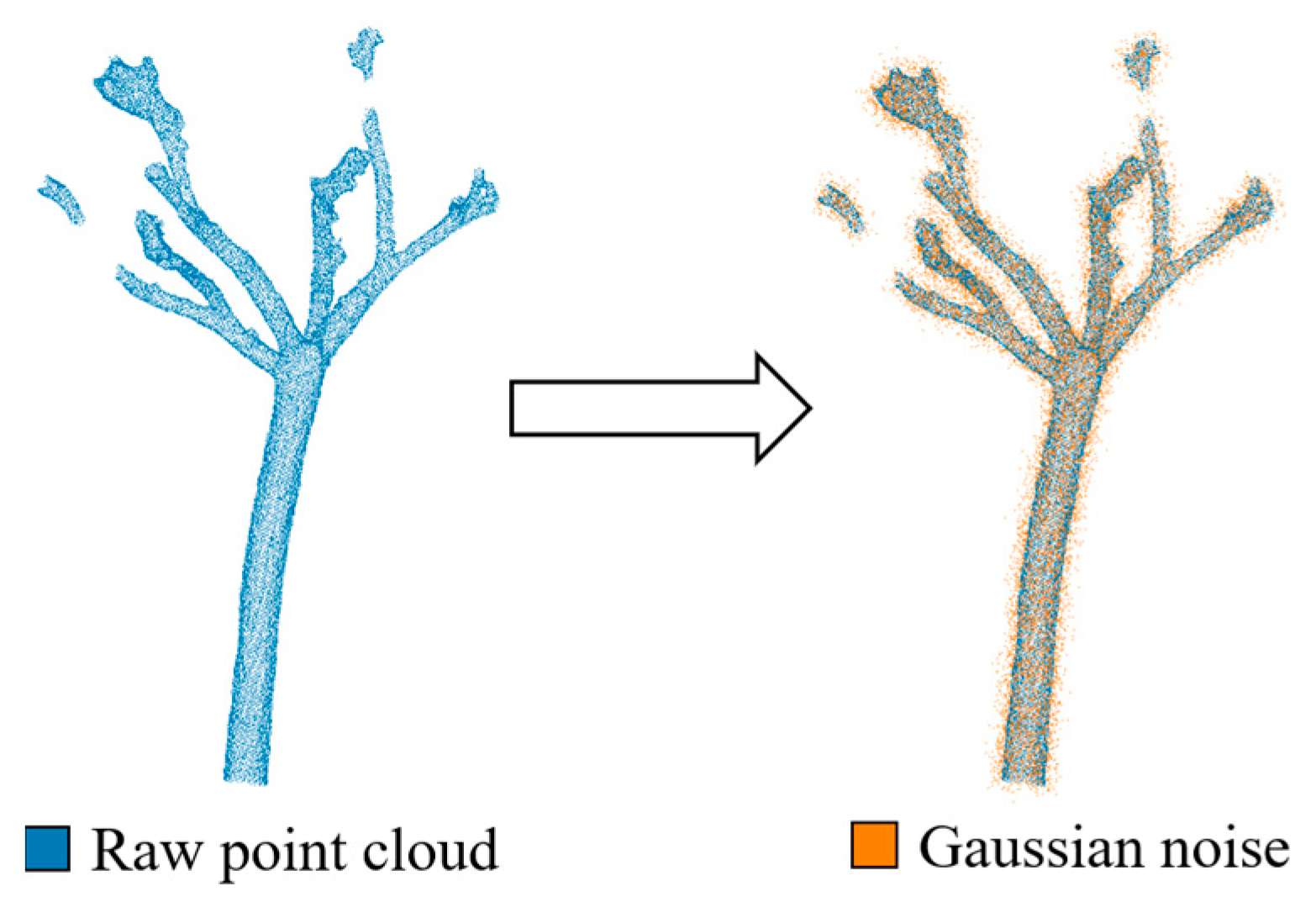
3.1. Point Cloud Data Preprocessing
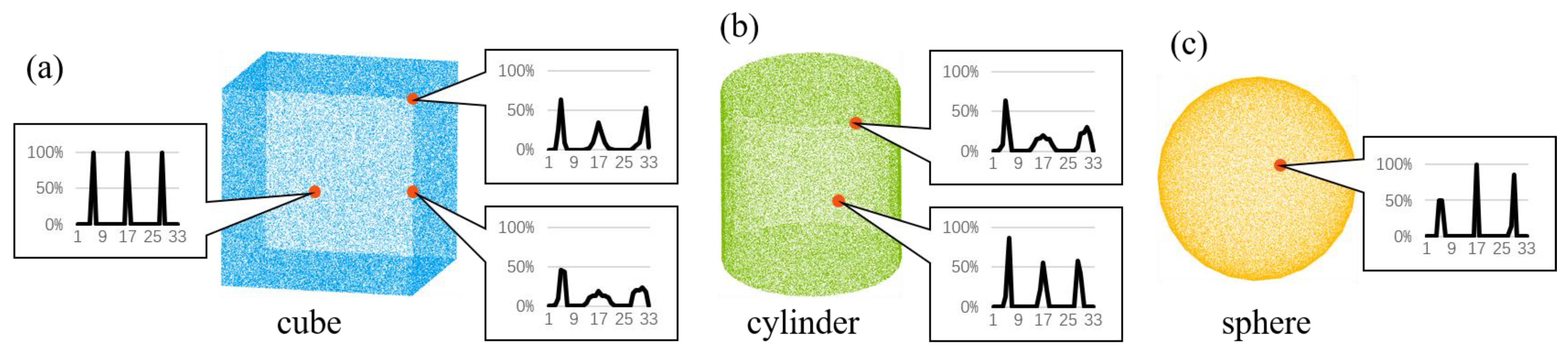
3.2. 3D Point Cloud Feature Descriptor Extraction
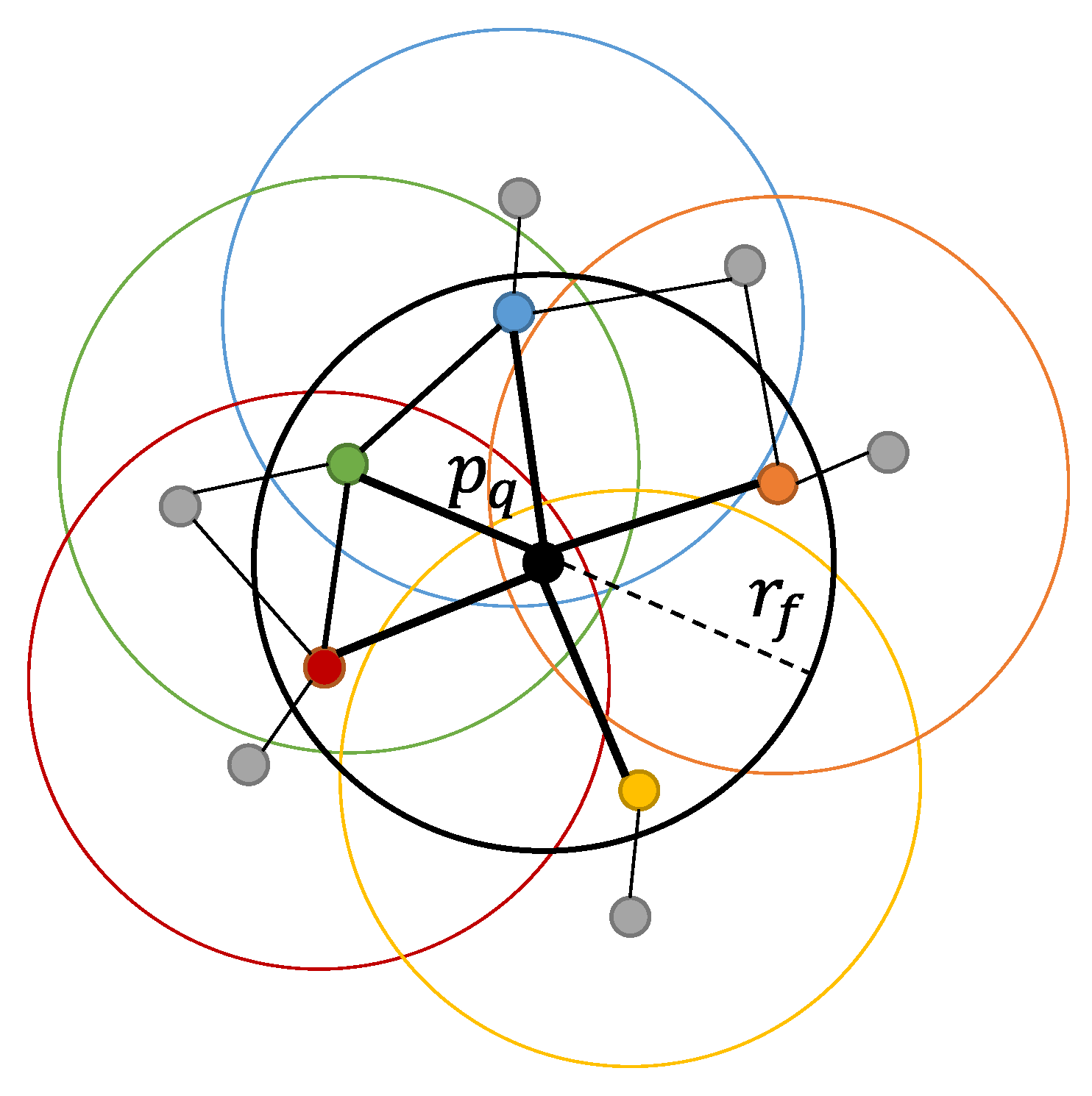
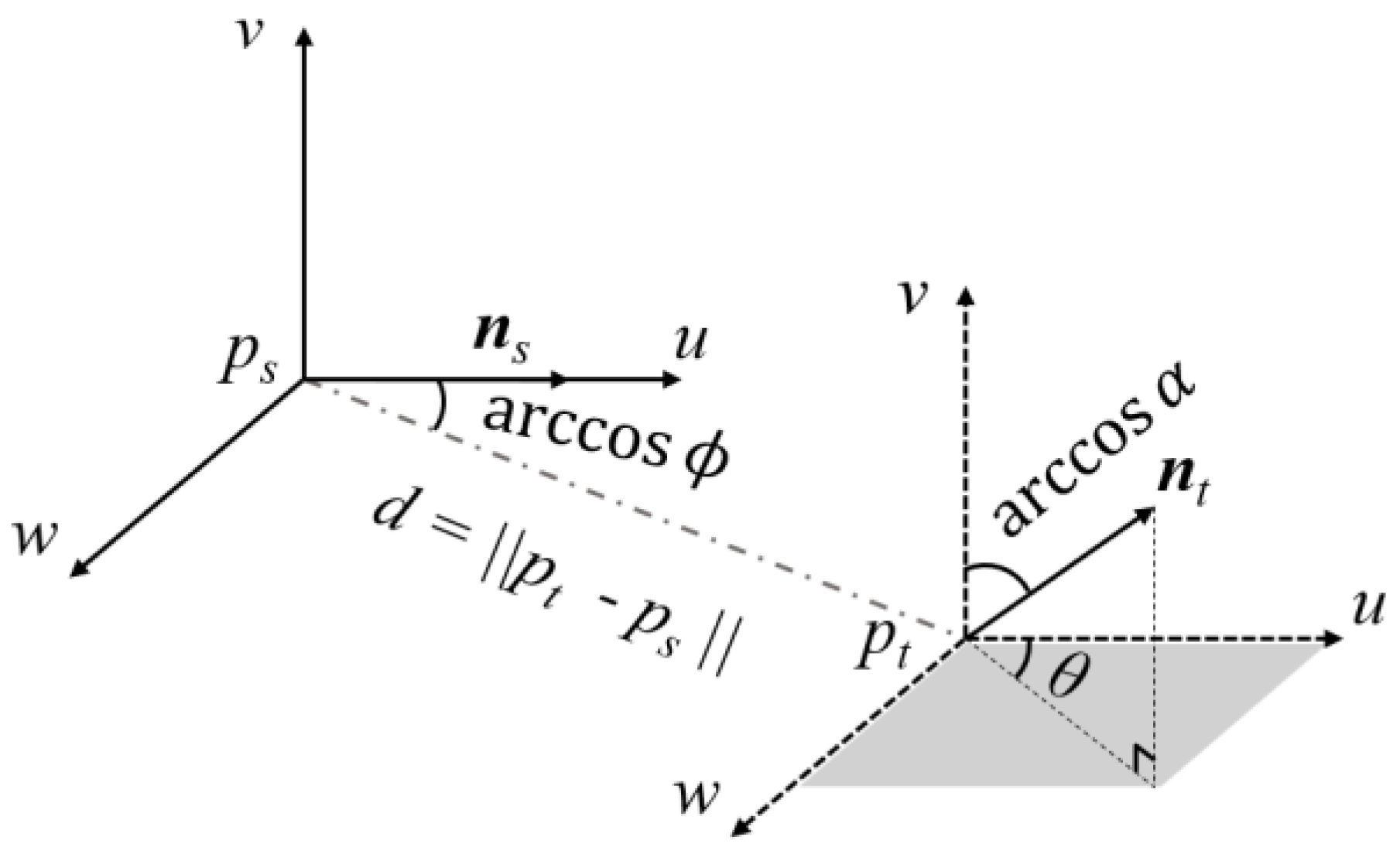
3.3. Correspondence Estimation of Point Clouds
| Algorithm 1: Iterative selection of correct matching pairs |
| Input: : the initial matching pair set; : the number of matching pairs to be selected; : the Euclidean distance threshold; Output: : the accurate matching pair set; |
| 1: Initialization: ; ; 2: for = 1 : size() do 3: if the point in the target point cloud is selected multiple times, 4: then point reversely selects its most similar point as the 5: matching pair; delete other duplicate matching pair(s) of point 6: ; 7: end if 8: end for 9: Sort the matching pairs in ; 10: Put the first matching pair into ; 11: Put the source point of the first matching pair to ; 12: for = 1 : size() do 13: if then 14: ; 15: ; 16: end if 17: if then 18: break; 19: end if 20: end for 21: Apply RANSAC to , get the inlier set . |
3.4. Estimation of Spatial Transformations
4. Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, S.; Su, Y.; Zhang, Y.; Song, S.; Li, Q.; Liu, Z.; Ma, Q.; Ge, Y.; Liu, L.; Ding, Y. Exploring seasonal and circadian rhythms in structural traits of field maize from LiDAR time series. Plant Phenomics 2021, 2021, 9895241. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, W.; Yang, G.; Lei, L.; Han, S.; Xu, W.; Chen, R.; Zhang, C.; Yang, H. Maize Ear Height and Ear–Plant Height Ratio Estimation with LiDAR Data and Vertical Leaf Area Profile. Remote Sens. 2023, 15, 964. [Google Scholar] [CrossRef]
- Yuan, H.; Bennett, R.S.; Wang, N.; Chamberlin, K.D. Development of a peanut canopy measurement system using a ground-based lidar sensor. Front. Plant Sci. 2019, 10, 203. [Google Scholar] [CrossRef] [PubMed]
- Ninomiya, S. High-throughput field crop phenotyping: Current status and challenges. Breed. Sci. 2022, 72, 3–18. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, W.; Mou, Y.; Li, Y.; Yin, L. Microscopic 3D reconstruction based on point cloud data generated using defocused images. Meas. Control UK 2021, 54, 1309–1318. [Google Scholar] [CrossRef]
- Mirzaei, K.; Arashpour, M.; Asadi, E.; Masoumi, H.; Bai, Y.; Behnood, A. 3D point cloud data processing with machine learning for construction and infrastructure applications: A comprehensive review. Adv. Eng. Inform. 2022, 51, 101501. [Google Scholar] [CrossRef]
- Yang, T.; Ye, J.; Zhou, S.; Xu, A.; Yin, J. 3D reconstruction method for tree seedlings based on point cloud self-registration. Comput. Electron. Agric. 2022, 200, 107210. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, D.; Xu, H.; Zhu, Y.; He, Y.; Cen, H. Optimization of 3D point clouds of oilseed rape plants based on time-of-flight cameras. Sensors 2021, 21, 664. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Z.; Yang, L.; Mannan, A.; Khan, T.U.; Zhao, Z.; Cheng, Z. Extraction of sample plot parameters from 3D point cloud reconstruction based on combined RTK and CCD continuous photography. Remote Sens. 2018, 10, 1299. [Google Scholar] [CrossRef]
- Feng, H.; Tao, H.; Li, Z.; Yang, G.; Zhao, C. Comparison of UAV RGB Imagery and Hyperspectral Remote-Sensing Data for Monitoring Winter Wheat Growth. Remote Sens. 2022, 14, 3811. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Han, J.; Zhang, L.; Bian, C.; Jin, L.; Liu, J. The estimation of crop emergence in potatoes by UAV RGB imagery. Plant Methods 2019, 15, 15. [Google Scholar] [CrossRef]
- Zhang, Y.; Ta, N.; Guo, S.; Chen, Q.; Zhao, L.; Li, F.; Chang, Q. Combining Spectral and Textural Information from UAV RGB Images for Leaf Area Index Monitoring in Kiwifruit Orchard. Remote Sens. 2022, 14, 1063. [Google Scholar] [CrossRef]
- Velumani, K.; Lopez-Lozano, R.; Madec, S.; Guo, W.; Gillet, J.; Comar, A.; Baret, F. Estimates of maize plant density from UAV RGB images using Faster-RCNN detection model: Impact of the spatial resolution. Plant Phenomics 2021, 2021, 9824843. [Google Scholar] [CrossRef]
- Song, R.; Zhang, W.; Zhao, Y.; Liu, Y. Unsupervised multi-view CNN for salient view selection and 3D interest point detection. Int. J. Comput. Vis. 2022, 130, 1210–1227. [Google Scholar] [CrossRef]
- Bletterer, A.; Payan, F.; Antonini, M. A local graph-based structure for processing gigantic aggregated 3D point clouds. IEEE Trans. Vis. Comput. Graph. 2020, 28, 2822–2833. [Google Scholar] [CrossRef]
- Wu, S.; Wen, W.; Wang, Y.; Fan, J.; Wang, C.; Gou, W.; Guo, X. MVS-Pheno: A portable and low-cost phenotyping platform for maize shoots using multiview stereo 3D reconstruction. Plant Phenomics 2020, 2020, 1848437. [Google Scholar] [CrossRef]
- Li, D.; Xu, L.; Tang, X.-s.; Sun, S.; Cai, X.; Zhang, P. 3D imaging of greenhouse plants with an inexpensive binocular stereo vision system. Remote Sens. 2017, 9, 508. [Google Scholar] [CrossRef]
- Pound, M.P.; French, A.P.; Murchie, E.H.; Pridmore, T.P. Automated recovery of three-dimensional models of plant shoots from multiple color images. Plant Physiol. 2014, 166, 1688–1698. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, Y.; Zhao, G.; Sun, C.; Zhang, F.; He, S. Sugarcane biomass prediction with multi-mode remote sensing data using deep archetypal analysis and integrated learning. Remote Sens. 2022, 14, 4944. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar]
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3dmatch: Learning local geometric descriptors from rgb-d reconstructions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1802–1811. [Google Scholar]
- El Banani, M.; Gao, L.; Johnson, J. Unsupervisedr&r: Unsupervised point cloud registration via differentiable rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7129–7139. [Google Scholar]
- Zheng, L.; Yu, M.; Song, M.; Stefanidis, A.; Ji, Z.; Yang, C. Registration of long-strip terrestrial laser scanning point clouds using ransac and closed constraint adjustment. Remote Sens. 2016, 8, 278. [Google Scholar] [CrossRef]
- Peng, Y.; Tang, Z.; Zhao, G.; Cao, G.; Wu, C. Motion blur removal for UAV-based wind turbine blade images using synthetic datasets. Remote Sens. 2022, 14, 87. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhao, D.; Cheng, D.; Zhang, J.; Tian, D. A Fast and Precise Plane Segmentation Framework for Indoor Point Clouds. Remote Sens. 2022, 14, 3519. [Google Scholar] [CrossRef]
- Lin, S.; Peng, Y.; Cao, G. Low Overlapping Plant Point Cloud Registration and Splicing Method Based on FPFH. In Proceedings of the Image and Graphics Technologies and Applications: 17th Chinese Conference, Bejing, China, 23–24 April 2022; pp. 103–117. [Google Scholar]
- Liu, W.; Li, Z.; Zhang, G.; Zhang, Z. Applications. Adaptive 3D shape context representation for motion trajectory classification. Multimed. Tools Appl. 2017, 76, 15413–15434. [Google Scholar] [CrossRef]
- Zhou, W.; Ma, C.; Yao, T.; Chang, P.; Zhang, Q.; Kuijper, A. Histograms of Gaussian normal distribution for 3D feature matching in cluttered scenes. Vis. Comput. 2019, 35, 489–505. [Google Scholar] [CrossRef]
- Salti, S.; Tombari, F.; Di Stefano, L.; Understanding, I. SHOT: Unique signatures of histograms for surface and texture description. Comput. Vis. Image Und. 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A comprehensive performance evaluation of 3D local feature descriptors. Int. J. Comput. Vis. 2016, 116, 66–89. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D object recognition in cluttered scenes with local surface features: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2270–2287. [Google Scholar] [CrossRef]
- Aggarwal, A.; Kampmann, P.; Lemburg, J.; Kirchner, F. Haptic Object Recognition in Underwater and Deep-sea Environments. J. Field Robot. 2015, 32, 167–185. [Google Scholar] [CrossRef]
- Lalonde, J.F.; Vandapel, N.; Huber, D.F.; Hebert, M. Natural terrain classification using three-dimensional ladar data for ground robot mobility. J. Field Robot. 2006, 23, 839–861. [Google Scholar] [CrossRef]
- Hetzel, G.; Leibe, B.; Levi, P.; Schiele, B. 3D object recognition from range images using local feature histograms. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001; Volume 2, pp. 394–399. [Google Scholar]
- Schonberger, J.L.; Frahm, J. Structure-from-motion revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]



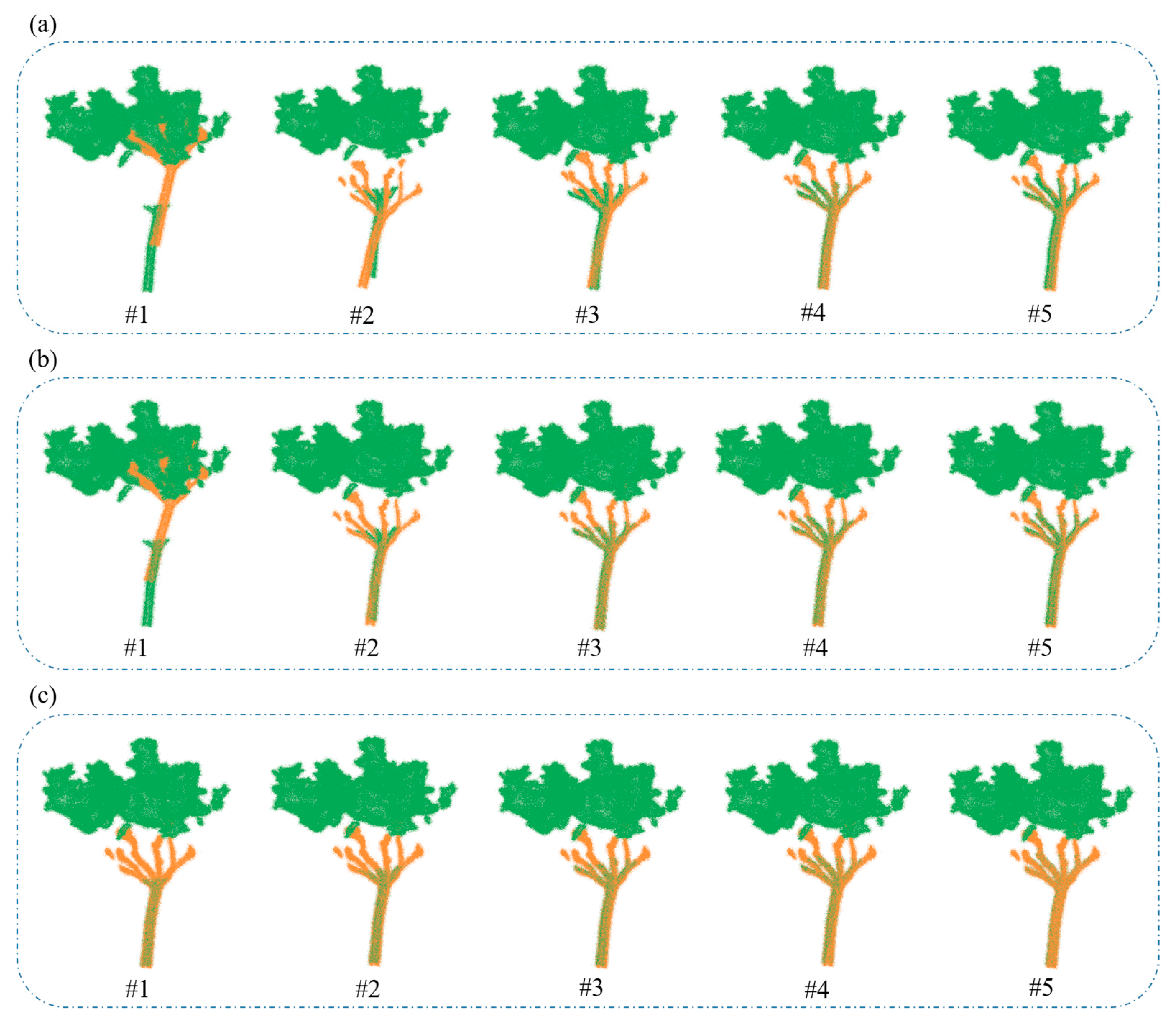
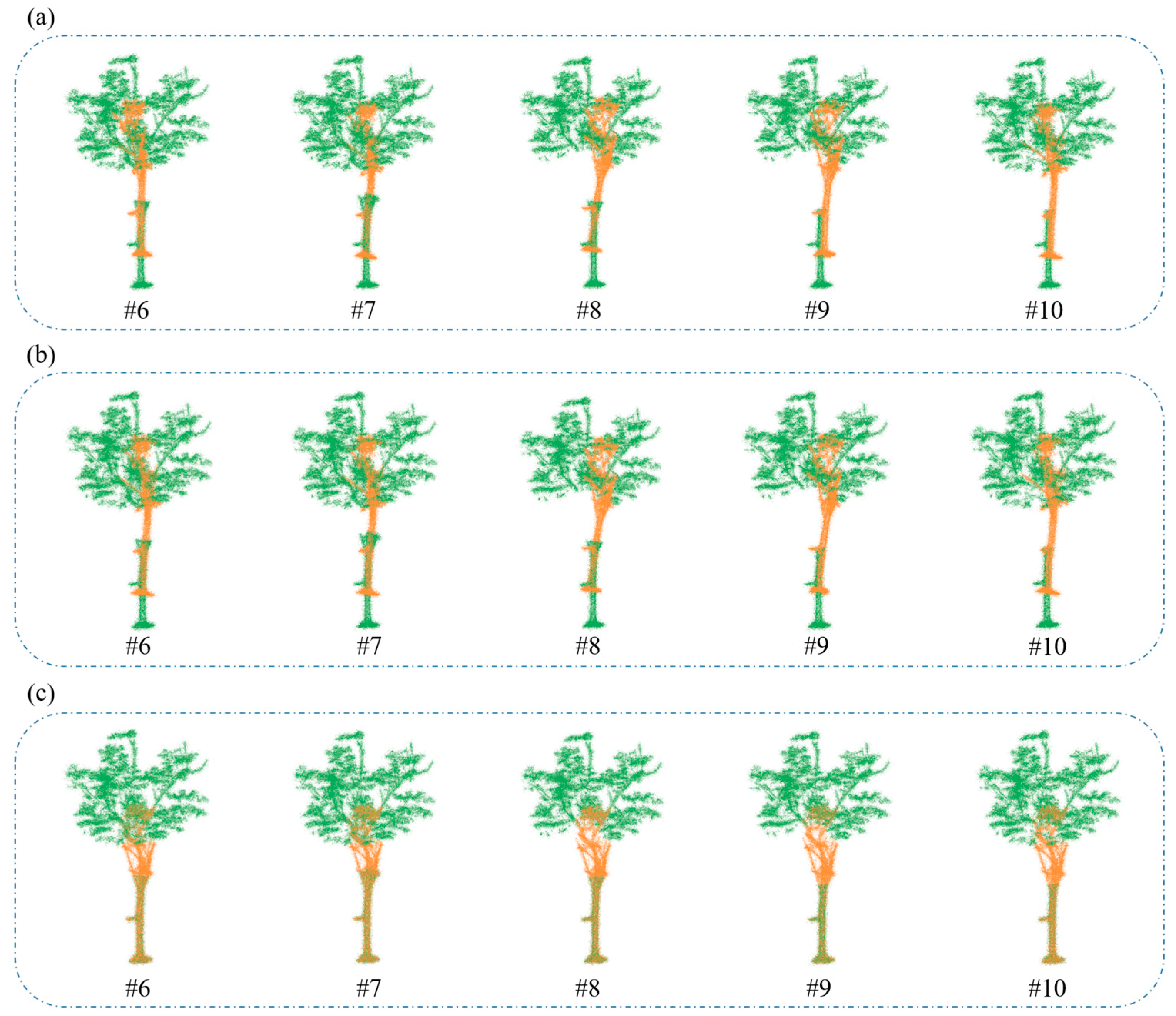
| Point Cloud Umber | SAC-IA (cm) | SAC-IA + ICP (cm) | Proposed (cm) |
|---|---|---|---|
| #1 | 210.9800 | 197.4900 | 0.0037 |
| #2 | 92.6800 | 93.3900 | 0.0064 |
| #3 | 0.8700 | 0.0036 | 0.0000 |
| #4 | 0.2500 | 0.0080 | 0.0002 |
| #5 | 0.3100 | 0.0370 | 0.0069 |
| #6 | 65.2200 | 64.3700 | 0.0022 |
| #7 | 0.0870 | 0.0007 | 0.0007 |
| #8 | 53.5400 | 57.6000 | 0.0052 |
| #9 | 56.0100 | 61.3400 | 0.0009 |
| #10 | 48.1900 | 50.8000 | 0.0007 |
| Mean# | 0.3793 | 0.0123 | 0.0027 |
| Point Cloud Umber | SAC-IA (cm) | SAC-IA + ICP (cm) | Proposed (cm) |
|---|---|---|---|
| #1 | 126.5200 | 118.6100 | 0.0084 |
| #2 | 3.6700 | 0.8800 | 0.0037 |
| #3 | 0.1500 | 0.0720 | 0.0033 |
| #4 | 0.2500 | 0.1500 | 0.0067 |
| #5 | 0.4000 | 0.2200 | 0.0014 |
| #6 | 43.8200 | 47.7500 | 0.0009 |
| #7 | 41.1500 | 50.2100 | 0.0020 |
| #8 | 60.1600 | 61.0900 | 0.0022 |
| #9 | 47.4700 | 56.1400 | 0.0008 |
| #10 | 45.5200 | 54.8500 | 0.0097 |
| Mean# | 1.1175 | 0.3305 | 0.0039 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Lin, S.; Wu, H.; Cao, G. Point Cloud Registration Based on Fast Point Feature Histogram Descriptors for 3D Reconstruction of Trees. Remote Sens. 2023, 15, 3775. https://doi.org/10.3390/rs15153775
Peng Y, Lin S, Wu H, Cao G. Point Cloud Registration Based on Fast Point Feature Histogram Descriptors for 3D Reconstruction of Trees. Remote Sensing. 2023; 15(15):3775. https://doi.org/10.3390/rs15153775
Chicago/Turabian StylePeng, Yeping, Shengdong Lin, Hongkun Wu, and Guangzhong Cao. 2023. "Point Cloud Registration Based on Fast Point Feature Histogram Descriptors for 3D Reconstruction of Trees" Remote Sensing 15, no. 15: 3775. https://doi.org/10.3390/rs15153775
APA StylePeng, Y., Lin, S., Wu, H., & Cao, G. (2023). Point Cloud Registration Based on Fast Point Feature Histogram Descriptors for 3D Reconstruction of Trees. Remote Sensing, 15(15), 3775. https://doi.org/10.3390/rs15153775









