Information Leakage in Deep Learning-Based Hyperspectral Image Classification: A Survey
Abstract
1. Introduction
- HSI data is high-dimensional, and labeling cost is high. Therefore, fewer training samples are commonly used in training, which will bring difficulties to feature extraction, affect model performance, and cause the Hughes phenomenon [30];
- When HSI data is used to train the network by using random sampling strategy and the input is patch format, some information of the test set will be leaked. This affects the generalization ability of the model [31], making the model only learn the distribution of one domain.
- 1.
- Some of the existing problems in the field of deep learning-based HSI classification are summarized. The information leakage problem caused by the introduction of spatial information is introduced in detail;
- 2.
- Depending on the cause of information leakage, this paper discusses some mitigation methods in the field of deep learning-based HSI classification. Based on this, we explore the performance of some existing related models and algorithms on the information leakage problem. All the mentioned methods are summarized in terms of sample related phase and feature extraction phase;
- 3.
- This paper experimentally compares the effectiveness of some models and algorithms for mitigating information leakage.
2. Methods
2.1. Problems and Challenges
2.1.1. Limited Training Samples
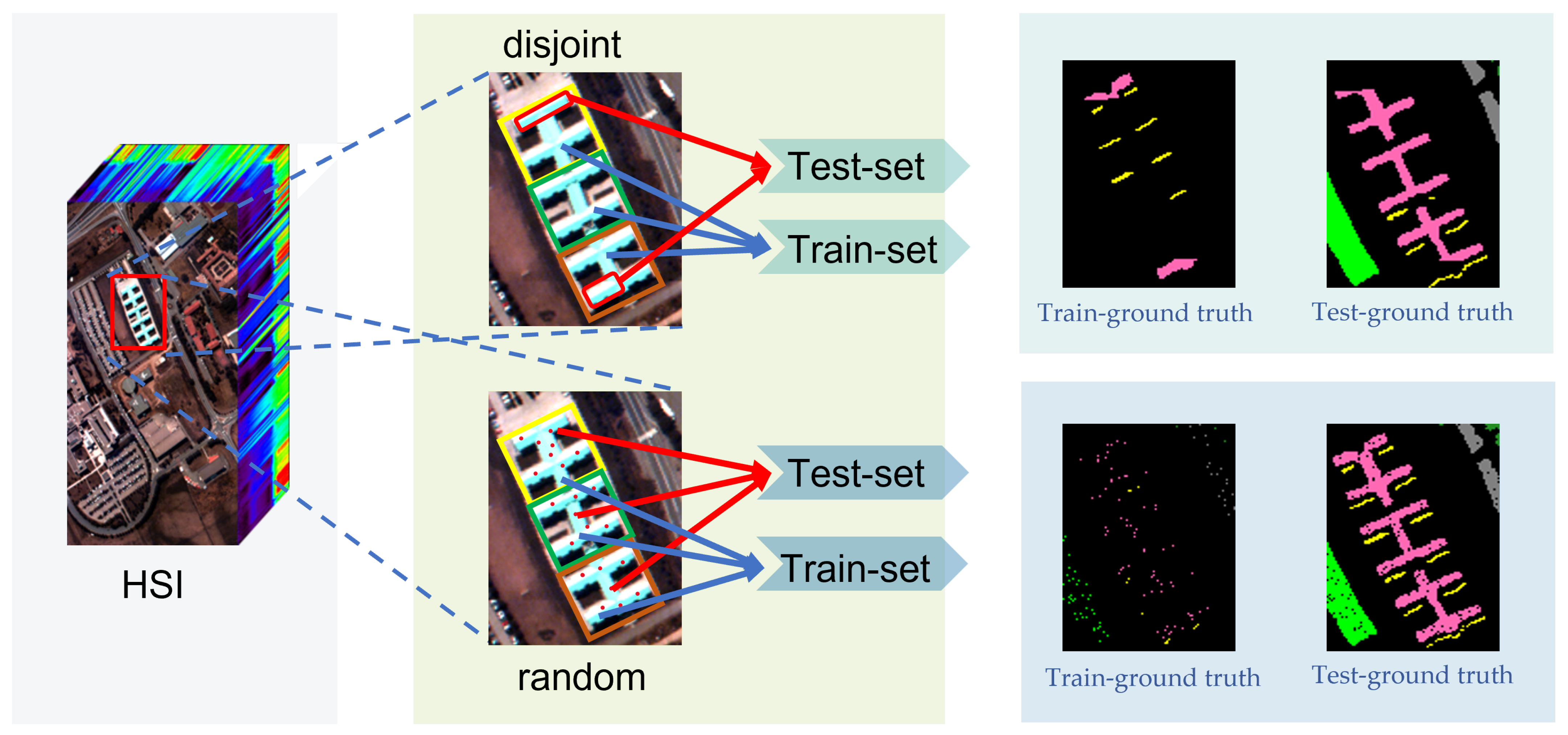
2.1.2. Information Leakage
2.2. Overfitting between Datasets Caused by Information Leakage
- 1.
- It is an approximate process, not exactly equivalent to constructing a homogeneous dataset, because spatially disjoint sampling is not completely immune to information leakage. In the spatially disjoint sampling strategy, the samples at the edges of the training set still contain some test pixels. These patches lose some spatial information to some extent;
- 2.
- It was experimentally found that the difference of classification accuracy between spatially disjoint sampling strategies and random sampling strategies was related to the chosen datasets;
- 3.
- Some semi-supervised methods can make the model learn the test data in a spatially disjoint sampling way by constructing pseudo-labels for unlabeled samples [53]. As a result, the networks can achieve great classification accuracy under both sampling methods. However, the learning paradigm still suffers from information leakage and needs to be retrained when classifying other homogeneous datasets.
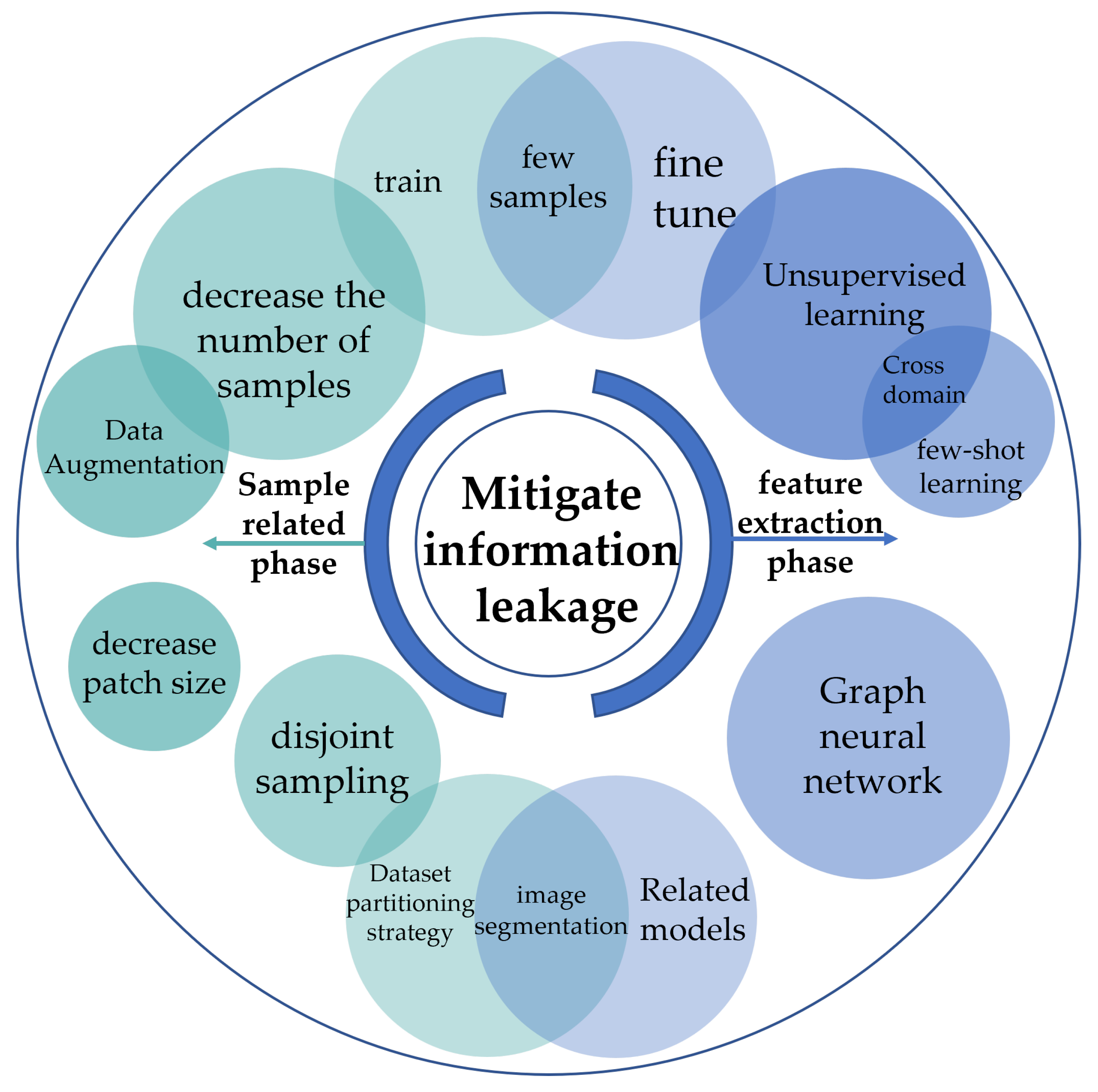
2.3. Methods to Mitigate the Impact of Information Leakage
2.4. Sample-Related Phase
2.4.1. Data Augmentation Strategies
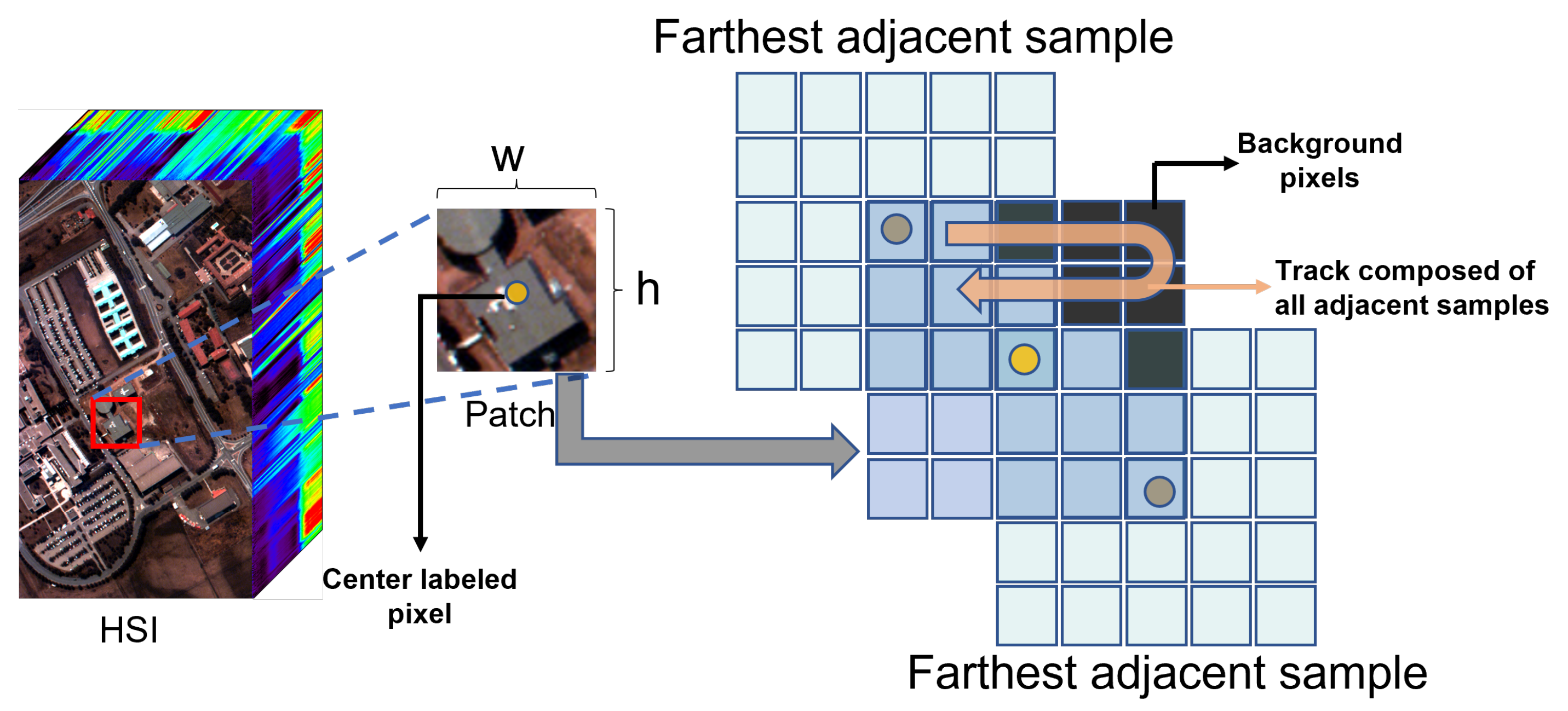
2.4.2. Spatially Disjoint Sampling Strategies
- Controlled Random Sampling Strategy: Liang et al. [45], inspired by the region-growing algorithm, performed controlled random sampling through the following three steps. First, disconnected partitions are selected for each class. Second, training samples are generated in each partition by expanding the region with seed pixels. Finally, after all classes have been processed, the samples in the labeled growing region are used as the training set and the remaining samples are used as the test set. At the same time, a paradox of sampling methods is presented in this work. Not only should the overlap between the test set and the training set be avoided as much as possible, but also the training samples should contain sufficiently different classes of spectral data variants. The former tends to select training samples centrally, while the latter requires training samples to be distributed in more different regions;
- Continuous Sampling Strategy: In order to reduce the influence of random sampling on classification accuracy, Zhou et al. [34] adopted the sampling method of sampling continuously from local regions for each class. This method selects different local regions, which do not completely avoid data leakage. However, the training samples contain more spectral variations;
- Cluster Sampling Strategy: Hansch et al. [65] proposed a cluster sampling method to minimize the correlation between the training set and the test set. For each class, it is clustered into two clusters according to its spatial coordinates. The training samples are randomly selected from a cluster, and the remaining classes are used as the test set;
- Density-Based Clustering Algorithm Sampling Strategy: Lange et al. [66] detect subgroups in a set by recursively evaluating the density threshold of neighbor points around the sample with parameter as the search radius. Therefore, independent regions can be determined by clustering the coordinates of pixels of a particular class.
2.5. Feature Extraction Phase
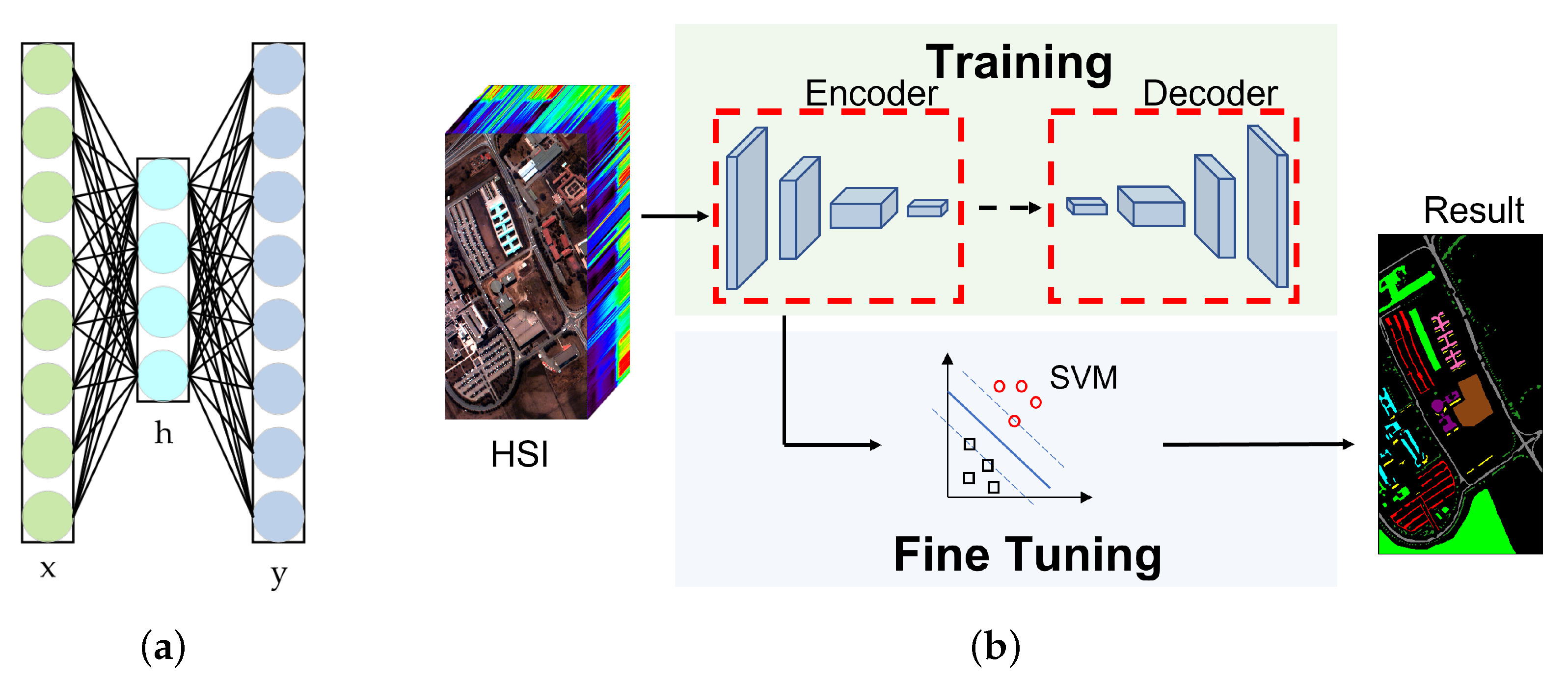
2.5.1. Unsupervised Learning and Semi-Supervised Learning
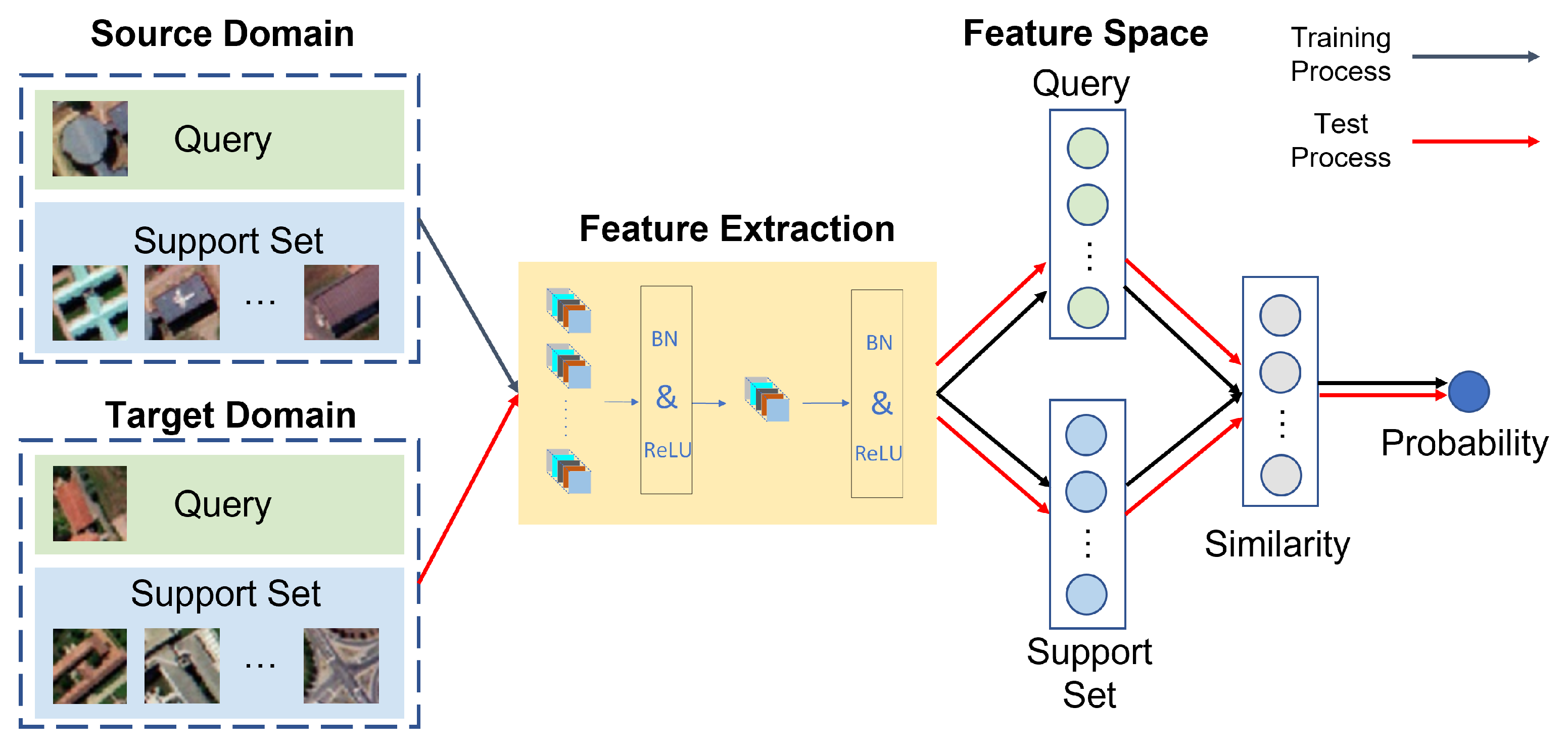
2.5.2. Few-Shot Learning
3. Results
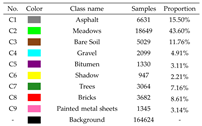
3.1. Datasets
3.2. Experimental Setups
3.2.1. Experiment 1: Convolutions in Different Dimensions
3.2.2. Experiment 2: Data Augmentation with Disjoint Sampling
3.2.3. Experiment 3: Cross-Domain Learning with Disjoint Sampling
3.3. Experimental Results and Discussion
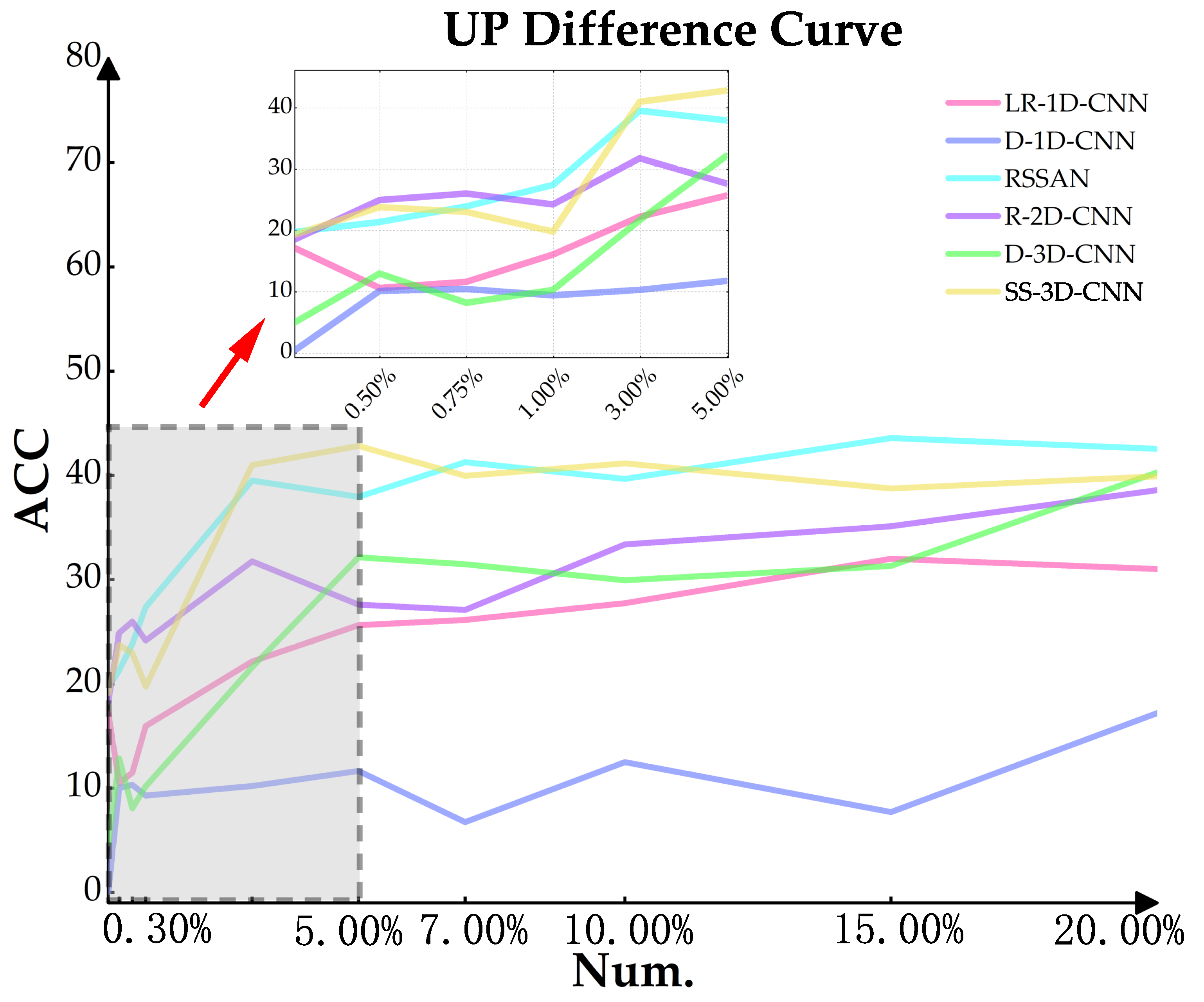
3.3.1. Analysis of Convolutions in Different Dimensions
3.3.2. The Effect of Different Data Augmentation Methods
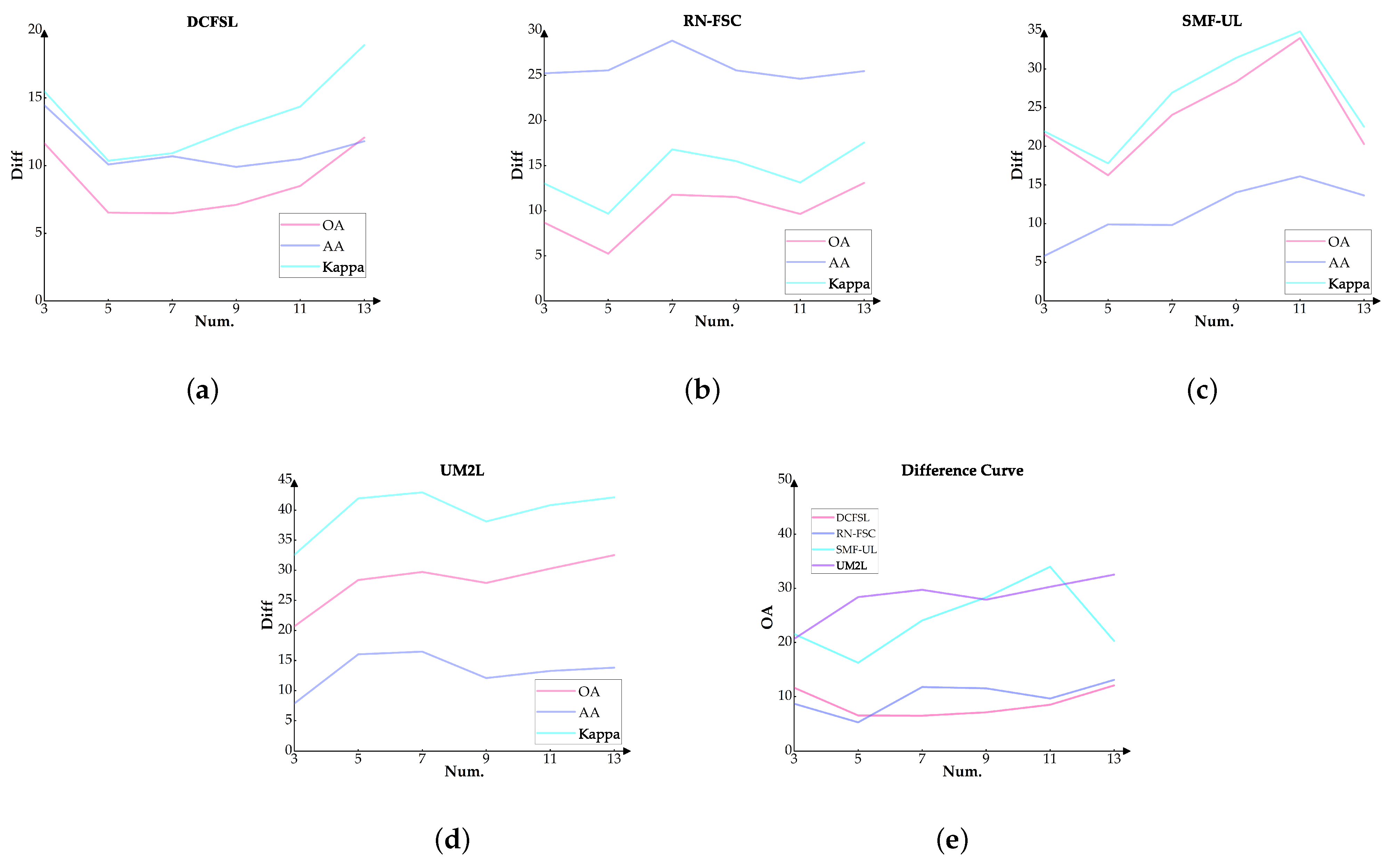
3.3.3. The Ability of Cross-Domain Learning to Mitigate Information Leakage
4. Future Lines
- As most current data augmentation methods obtain additional samples by processing labeled samples, the newly generated samples inevitably contain features of the original samples. For HSI data, spectra of the same ground-based object in different regions may have large variability. When a random sampling strategy is used, multiple spectral variants of the same class can be augmented to obtain an improvement in classification accuracy. However, the classification accuracy may be negatively affected under spatially disjoint sampling strategies. Samples of the same type selected in these strategies may have only a limited or even a single spectral variant type, which will cause the model to overfit the variants in these training samples. Therefore, it is possible to consider fusing some unlabeled samples with labeled samples. Methods such as hyperspectral unmixing and image edge segmentation are used to find objects of same classes at long spatial distances. These pixels can be fused with each other or added noise to obtain additional samples, allowing the model to learn different spectral variations;
- Recently, transformer networks have shown great potential in image processing. Several scholars have introduced vision transformer models into the field of hyperspectral classification and achieved advanced classification performance [92]. In HSI classification tasks, objects of the same class tend to be more concentrated in spatial locations. The self-attention mechanism used in transformers allows the network to focus more on the impact of each neighborhood pixel on the classification performance. Moreover, vision transformer models have better global feature extraction capabilities than CNN models. This ability to consider both neighbor and global information requires transformer models to introduce positional information at the input stage. From the information leakage perspective, most transformer models in classification tasks are identical to models, which do not remove test pixel information during training. Positional embedding may further exacerbate model overfitting to a single dataset. The combination of transformer models and graph structures can be considered as a future research direction. Specifically, some graph sample construction methods can strictly avoid the test information involved in training. The adjacency matrix in GCNs can be used to extract positional information;
- In practical applications, especially real-time remote sensing HSI classification, HSIs acquired by the same hyperspectral imaging platform usually share some features of homogeneous datasets. Examples are identical spatial resolution, spectral resolution or certain environmental conditions. The spectral response of objects in each pixel region will be more accurate with HSI spatial super-resolution or hyperspectral unmixing techniques, which mitigates the effect of object mixing on the spectrum. When the spectral variation is reduced, the samples obtained by the spatial disjoint sampling strategy have better generalization characteristics. To some extent, the problem of overfitting between datasets caused by information leakage is mitigated. Based on this, hyperspectral super-resolution technology and the construction of more accurate standard spectral libraries can be considered as future research directions;
- The current data augmentation methods struggle to achieve better performance of the model under spatial disjoint sampling strategies. Therefore they cannot steadily improve accuracy while reducing information leakage. The reason is that these data augmentation methods struggle to simulate the real spectral variation process. The task of super-resolution reconstruction based on deep learning is to simulate the degradation process of remote sensing images, and then use the original image as a supervision signal to construct a super-resolution model [93]. Inspired by this reconstruction technique, the variability process of spectra in HSI data can also be viewed as a degradation process. First, some bands in the original HSI that are likely to produce variation are identified based on prior knowledge, and then the degree of variation in that band is amplified as input to the model. The supervised signal is also the original HSI. The processed HSI is made closer to the original HSI data to construct the corresponding degradation model of the spectral variation process. Different from the HSI super-resolution, the process of amplifying spectral variation in this degradation model is more difficult to simulate real processes. The required prior knowledge may be affected by imaging platforms and environmental conditions in different regions;
- Most current deep learning-based HSI classification models need to be retrained when predicting different datasets. Based on this, several cross-domain learning methods have emerged. However, few models have been trained to directly classify various specifications of HSI without fine-tuning. The classification accuracy of these models also has room for improvement. This is a practical future research direction;
- In addition, the issue of information leakage in this field still requires the design of spatial autocorrelation evaluation indicators for hyperspectral occurrences. For example, mutual information can be used to obtain the degree of correlation between different samples. The reconstruction error of sparse representation can also be used to analyze the strength of correlations between samples. These methods can measure the independence of the test and training sets. In addition to spatially disjoint sampling strategies in HSI classification tasks, constructing perturbed samples can be an alternative approach to approximate homogeneous datasets. Based on this, it may be possible to add adversarial attacks to analyze the effectiveness of the model to mitigate information leakage.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| LR-1D-CNN | D-1D-CNN | RSSAN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 0.30% | 59.045 | 59.594 | −0.549 | 20.822 | 21.470 | −0.648 | 60.837 | 42.276 | 18.561 |
| 0.50% | 60.202 | 59.999 | 0.203 | 20.823 | 20.841 | −0.018 | 69.590 | 45.765 | 23.825 |
| 0.75% | 63.131 | 64.457 | −1.326 | 20.823 | 20.838 | −0.015 | 74.593 | 49.205 | 25.388 |
| 1% | 64.885 | 65.827 | −0.942 | 20.822 | 20.860 | −0.038 | 76.990 | 49.475 | 27.515 |
| 3% | 78.754 | 73.525 | 5.229 | 29.864 | 29.869 | −0.005 | 72.759 | 64.716 | 8.043 |
| 5% | 79.448 | 74.366 | 5.082 | 50.213 | 48.883 | 1.330 | 81.496 | 59.244 | 22.252 |
| 7% | 82.872 | 75.944 | 6.928 | 59.895 | 58.688 | 1.207 | 85.848 | 75.773 | 10.075 |
| 10% | 82.525 | 71.369 | 11.156 | 63.810 | 64.739 | −0.929 | 89.772 | 77.211 | 12.561 |
| 15% | 83.273 | 76.599 | 6.674 | 71.429 | 68.269 | 3.160 | 90.383 | 80.578 | 9.805 |
| 20% | 85.915 | 76.794 | 9.121 | 76.399 | 70.411 | 5.988 | 91.262 | 80.698 | 10.564 |
| R-2D-CNN | D-3D-CNN | SS-3D-CNN | |||||||
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 0.30% | 60.746 | 46.042 | 14.704 | 40.217 | 38.741 | 1.476 | 78.021 | 55.864 | 22.157 |
| 0.50% | 66.633 | 48.268 | 18.365 | 49.674 | 40.294 | 9.380 | 76.395 | 49.038 | 27.357 |
| 0.75% | 74.186 | 48.875 | 25.311 | 58.243 | 40.701 | 17.542 | 82.355 | 60.223 | 22.132 |
| 1% | 77.285 | 48.921 | 28.364 | 64.949 | 47.949 | 17.000 | 85.665 | 61.888 | 23.777 |
| 3% | 79.293 | 59.427 | 19.866 | 79.970 | 68.980 | 10.990 | 90.993 | 77.263 | 13.730 |
| 5% | 87.177 | 66.082 | 21.095 | 81.491 | 76.974 | 4.517 | 91.552 | 76.096 | 15.456 |
| 7% | 89.453 | 73.717 | 15.736 | 85.997 | 77.350 | 8.647 | 90.748 | 77.055 | 13.693 |
| 10% | 93.360 | 75.662 | 17.698 | 87.962 | 77.091 | 10.871 | 92.885 | 77.770 | 15.115 |
| 15% | 92.441 | 81.527 | 10.914 | 89.799 | 71.377 | 18.422 | 92.200 | 79.256 | 12.944 |
| 20% | 94.352 | 81.709 | 12.643 | 90.076 | 78.968 | 11.108 | 92.787 | 80.230 | 12.557 |
| LR-1D-CNN | D-1D-CNN | RSSAN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 0.30% | 40.459 | 33.102 | 7.357 | 27.348 | 20.657 | 6.691 | 29.312 | 27.007 | 2.305 |
| 0.50% | 44.724 | 39.331 | 5.393 | 29.114 | 21.896 | 7.218 | 38.723 | 28.878 | 9.845 |
| 0.75% | 46.225 | 39.902 | 6.323 | 33.228 | 23.519 | 9.709 | 39.342 | 31.394 | 7.948 |
| 1% | 48.187 | 45.303 | 2.884 | 38.849 | 27.902 | 10.947 | 49.735 | 40.347 | 9.388 |
| 3% | 60.900 | 50.107 | 10.793 | 43.781 | 33.281 | 10.500 | 59.281 | 53.129 | 6.152 |
| 5% | 66.673 | 54.397 | 12.276 | 48.127 | 39.039 | 9.088 | 69.209 | 57.634 | 11.575 |
| 7% | 67.634 | 55.718 | 11.916 | 50.720 | 45.236 | 5.484 | 73.864 | 58.574 | 15.290 |
| 10% | 71.862 | 58.914 | 12.948 | 58.873 | 50.078 | 8.795 | 77.405 | 61.921 | 15.484 |
| 15% | 74.650 | 58.953 | 15.697 | 61.717 | 52.339 | 9.378 | 76.626 | 60.939 | 15.687 |
| 20% | 76.129 | 64.280 | 11.849 | 63.929 | 54.809 | 9.120 | 85.659 | 64.296 | 21.363 |
| R-2D-CNN | D-3D-CNN | SS-3D-CNN | |||||||
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 0.30% | 37.967 | 29.766 | 8.201 | 32.468 | 27.007 | 5.461 | 49.058 | 44.558 | 4.500 |
| 0.50% | 52.331 | 37.783 | 14.548 | 32.981 | 28.878 | 4.103 | 54.984 | 54.308 | 0.676 |
| 0.75% | 55.131 | 42.301 | 12.830 | 37.691 | 31.394 | 6.297 | 68.236 | 55.025 | 13.211 |
| 1% | 58.000 | 41.473 | 16.527 | 40.386 | 40.347 | 0.039 | 64.008 | 55.262 | 8.746 |
| 3% | 69.392 | 54.760 | 14.632 | 59.855 | 53.129 | 6.726 | 83.150 | 55.998 | 27.152 |
| 5% | 75.312 | 59.424 | 15.888 | 66.309 | 57.634 | 8.675 | 83.723 | 58.439 | 25.284 |
| 7% | 77.856 | 60.401 | 17.455 | 74.935 | 58.574 | 16.361 | 86.964 | 62.352 | 24.612 |
| 10% | 84.594 | 62.552 | 22.042 | 79.005 | 61.921 | 17.084 | 90.212 | 64.124 | 26.088 |
| 15% | 86.650 | 65.301 | 21.349 | 80.949 | 60.939 | 20.010 | 91.205 | 63.927 | 27.278 |
| 20% | 90.755 | 70.545 | 20.210 | 85.446 | 64.296 | 21.150 | 93.069 | 66.728 | 26.341 |
| LR-1D-CNN | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Without Data Augmentation | Radiation Noise | Mixture Noise | |||||||
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 3 | 35.079 | 34.387 | 0.692 | 32.585 | 34.198 | −1.613 | 36.105 | 33.936 | 2.169 |
| 5 | 39.809 | 39.172 | 0.637 | 36.450 | 36.501 | −0.051 | 35.807 | 35.693 | 0.114 |
| 7 | 41.772 | 40.834 | 0.938 | 40.098 | 36.827 | 3.271 | 37.653 | 36.458 | 1.195 |
| 9 | 48.060 | 42.070 | 5.990 | 49.809 | 41.151 | 8.658 | 44.639 | 41.999 | 2.640 |
| 11 | 51.812 | 45.231 | 6.581 | 51.071 | 48.178 | 2.893 | 49.970 | 42.079 | 7.891 |
| 13 | 53.597 | 49.658 | 3.939 | 53.377 | 50.101 | 3.276 | 52.074 | 48.265 | 3.809 |
| R-2D-CNN | |||||||||
| Without data augmentation | Flip | Radiation noise | |||||||
| Numb. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 3 | 41.164 | 30.125 | 11.039 | 42.268 | 34.347 | 7.921 | 38.975 | 33.163 | 5.812 |
| 5 | 50.619 | 38.754 | 11.865 | 55.953 | 40.528 | 15.425 | 49.153 | 40.786 | 8.367 |
| 7 | 51.819 | 40.748 | 11.071 | 57.364 | 42.435 | 14.929 | 53.596 | 40.608 | 12.988 |
| 9 | 52.464 | 41.654 | 10.810 | 53.610 | 44.216 | 9.394 | 53.240 | 41.850 | 11.390 |
| 11 | 53.687 | 43.711 | 9.976 | 56.262 | 44.945 | 11.317 | 53.798 | 42.539 | 11.259 |
| 13 | 58.543 | 44.665 | 13.878 | 61.774 | 45.229 | 16.545 | 61.568 | 43.843 | 17.725 |
| SS-3D-CNN | |||||||||
| Without data augmentation | Flip | Radiation noise | |||||||
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 3 | 53.615 | 41.719 | 11.896 | 54.684 | 45.162 | 9.522 | 50.219 | 43.413 | 6.806 |
| 5 | 60.772 | 50.761 | 10.011 | 65.326 | 57.330 | 7.996 | 64.201 | 54.068 | 10.133 |
| 7 | 65.456 | 53.659 | 11.797 | 67.781 | 54.637 | 13.144 | 68.098 | 55.190 | 12.908 |
| 9 | 63.079 | 55.178 | 7.901 | 64.388 | 55.358 | 9.030 | 65.013 | 51.732 | 13.281 |
| 11 | 68.087 | 55.824 | 12.263 | 69.054 | 58.029 | 11.025 | 71.250 | 52.045 | 19.205 |
| 13 | 71.939 | 57.570 | 14.369 | 75.224 | 60.140 | 15.084 | 74.513 | 57.200 | 17.313 |
Appendix B
| DCFSL | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Random | Disjoint | diff | |||||||
| Numb. | OA | AA | Kappa | OA | AA | Kappa | OA | AA | Kappa |
| 3 | 72.018 | 78.238 | 64.275 | 60.373 | 63.782 | 48.795 | 11.645 | 14.456 | 15.480 |
| 5 | 72.610 | 76.996 | 66.118 | 66.086 | 66.910 | 55.759 | 6.524 | 10.086 | 10.360 |
| 7 | 73.324 | 75.347 | 67.760 | 66.844 | 64.656 | 56.845 | 6.480 | 10.691 | 10.915 |
| 9 | 74.352 | 74.258 | 69.968 | 67.251 | 64.353 | 57.201 | 7.101 | 9.905 | 12.767 |
| 11 | 76.298 | 76.193 | 72.459 | 67.798 | 65.710 | 58.094 | 8.500 | 10.483 | 14.365 |
| 13 | 77.264 | 74.054 | 74.054 | 65.196 | 61.374 | 55.154 | 12.068 | 11.800 | 18.900 |
| RN-FSC | |||||||||
| Random | Disjoint | diff | |||||||
| Numb. | OA | AA | Kappa | OA | AA | Kappa | OA | AA | Kappa |
| 3 | 68.393 | 73.739 | 60.268 | 59.711 | 48.507 | 47.242 | 8.682 | 25.232 | 13.026 |
| 5 | 66.369 | 76.341 | 58.956 | 61.125 | 50.786 | 49.278 | 5.244 | 25.554 | 9.678 |
| 7 | 73.593 | 80.638 | 67.230 | 61.820 | 51.794 | 50.428 | 11.773 | 28.843 | 16.802 |
| 9 | 73.777 | 78.026 | 66.634 | 62.248 | 52.471 | 51.133 | 11.530 | 25.556 | 15.501 |
| 11 | 73.212 | 78.913 | 66.050 | 63.568 | 54.293 | 52.922 | 9.643 | 24.620 | 13.128 |
| 13 | 77.789 | 82.824 | 71.781 | 64.707 | 57.353 | 54.228 | 13.082 | 25.471 | 17.553 |
| SMF-UL | |||||||||
| Random | Disjoint | diff | |||||||
| Num. | OA | AA | Kappa | OA | AA | Kappa | OA | AA | Kappa |
| 3 | 65.520 | 65.307 | 56.905 | 43.957 | 59.494 | 34.955 | 21.563 | 5.813 | 21.950 |
| 5 | 70.847 | 70.155 | 63.909 | 54.598 | 60.261 | 46.116 | 16.249 | 9.894 | 17.793 |
| 7 | 74.135 | 72.126 | 67.645 | 50.075 | 62.307 | 40.720 | 24.060 | 9.819 | 26.924 |
| 9 | 75.417 | 74.154 | 69.040 | 47.092 | 60.123 | 37.612 | 28.325 | 14.031 | 31.428 |
| 11 | 78.097 | 76.302 | 72.131 | 44.107 | 60.189 | 37.291 | 33.990 | 16.113 | 34.840 |
| 13 | 78.055 | 75.984 | 72.097 | 57.764 | 62.336 | 49.562 | 20.291 | 13.648 | 22.535 |
| UM2L | |||||||||
| Random | Disjoint | diff | |||||||
| Num. | OA | AA | Kappa | OA | AA | Kappa | OA | AA | Kappa |
| 3 | 63.919 | 65.257 | 54.565 | 43.244 | 57.403 | 32.690 | 21.874 | 7.854 | 21.874 |
| 5 | 73.554 | 76.502 | 67.698 | 45.173 | 60.474 | 34.560 | 33.138 | 16.028 | 33.138 |
| 7 | 74.535 | 77.131 | 69.656 | 44.810 | 60.660 | 34.184 | 35.472 | 16.471 | 35.472 |
| 9 | 74.363 | 74.208 | 70.509 | 46.458 | 62.127 | 36.102 | 34.407 | 12.081 | 34.407 |
| 11 | 75.049 | 75.634 | 71.023 | 44.770 | 62.365 | 34.806 | 36.217 | 13.270 | 36.217 |
| 13 | 76.006 | 75.603 | 72.338 | 43.485 | 61.792 | 33.484 | 38.854 | 13.811 | 38.854 |
References
- Wang, C.; Liu, B.; Liu, L.; Zhu, Y.; Hou, J.; Liu, P.; Li, X. A review of deep learning used in the hyperspectral image analysis for agriculture. Artif. Intell. Rev. 2021, 54, 5205–5253. [Google Scholar] [CrossRef]
- Awad, M.M. An innovative intelligent system based on remote sensing and mathematical models for improving crop yield estimation. Inf. Process. Agric. 2019, 6, 316–325. [Google Scholar] [CrossRef]
- Caballero, D.; Calvini, R.; Amigo, J.M. Hyperspectral imaging in crop fields: Precision agriculture. In Data Handling in Science and Technology; Elsevier: Amsterdam, The Netherlands, 2019; Volume 32, pp. 453–473. [Google Scholar]
- Liu, B.; Liu, Z.; Men, S.; Li, Y.; Ding, Z.; He, J.; Zhao, Z. Underwater hyperspectral imaging technology and its applications for detecting and mapping the seafloor: A review. Sensors 2020, 20, 4962. [Google Scholar] [CrossRef] [PubMed]
- Jay, S.; Guillaume, M. A novel maximum likelihood based method for mapping depth and water quality from hyperspectral remote-sensing data. Remote Sens. Environ. 2014, 147, 121–132. [Google Scholar] [CrossRef]
- Gross, W.; Queck, F.; Vögtli, M.; Schreiner, S.; Kuester, J.; Böhler, J.; Mispelhorn, J.; Kneubühler, M.; Middelmann, W. A multi-temporal hyperspectral target detection experiment: Evaluation of military setups. In Proceedings of the Target and Background Signatures VII. SPIE, Online, 13–17 September 2021; Volume 11865, pp. 38–48. [Google Scholar]
- Contreras Acosta, I.C.; Khodadadzadeh, M.; Gloaguen, R. Resolution enhancement for drill-core hyperspectral mineral mapping. Remote Sens. 2021, 13, 2296. [Google Scholar] [CrossRef]
- Khan, U.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V.K. Trends in deep learning for medical hyperspectral image analysis. IEEE Access 2021, 9, 79534–79548. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Li, F.; Lu, H.; Zhang, P. An innovative multi-kernel learning algorithm for hyperspectral classification. Comput. Electr. Eng. 2019, 79, 106456. [Google Scholar] [CrossRef]
- Liu, G.; Wang, L.; Liu, D.; Fei, L.; Yang, J. Hyperspectral Image Classification Based on Non-Parallel Support Vector Machine. Remote Sens. 2022, 14, 2447. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Liu, W.; Fowler, J.E.; Zhao, C. Spatial logistic regression for support-vector classification of hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 439–443. [Google Scholar] [CrossRef]
- Wang, X. Kronecker factorization-based multinomial logistic regression for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. A subspace-based multinomial logistic regression for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2105–2109. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Li, J.; Li, S.S.; Zhang, B.; Benediktsson, J.A. Spectral-spatial hyperspectral image classification using subspace-based support vector machines and adaptive Markov random fields. Remote Sens. 2016, 8, 355. [Google Scholar] [CrossRef]
- Samat, A.; Gamba, P.; Abuduwaili, J.; Liu, S.; Miao, Z. Geodesic flow kernel support vector machine for hyperspectral image classification by unsupervised subspace feature transfer. Remote Sens. 2016, 8, 234. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Zhang, N.; Li, Z.; Zhao, Z.; Gao, Y.; Xu, D.; Ben, G. Orientation-First Strategy With Angle Attention Module for Rotated Object Detection in Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8492–8505. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Zhang, N.; Zhang, Y.; Zhao, Z.; Xu, D.; Ben, G.; Gao, Y. Deep Learning-Based Object Detection Techniques for Remote Sensing Images: A Survey. Remote Sens. 2022, 14, 2385. [Google Scholar] [CrossRef]
- Huang, B.; He, B.; Wu, L.; Guo, Z. Deep residual dual-attention network for super-resolution reconstruction of remote sensing images. Remote Sens. 2021, 13, 2784. [Google Scholar] [CrossRef]
- Wen, D.; Huang, X.; Bovolo, F.; Li, J.; Ke, X.; Zhang, A.; Benediktsson, J.A. Change detection from very-high-spatial-resolution optical remote sensing images: Methods, applications, and future directions. IEEE Geosci. Remote Sens. Mag. 2021, 9, 68–101. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, L.; Ghamisi, P.; Jia, X.; Li, G.; Tang, L. Hyperspectral images classification with Gabor filtering and convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2355–2359. [Google Scholar] [CrossRef]
- Zhu, J.; Fang, L.; Ghamisi, P. Deformable convolutional neural networks for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1254–1258. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Roy, S.K.; Manna, S.; Song, T.; Bruzzone, L. Attention-based adaptive spectral–spatial kernel ResNet for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 7831–7843. [Google Scholar] [CrossRef]
- Pal, D.; Bundele, V.; Banerjee, B.; Jeppu, Y. SPN: Stable prototypical network for few-shot learning-based hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Bai, J.; Huang, S.; Xiao, Z.; Li, X.; Zhu, Y.; Regan, A.C.; Jiao, L. Few-shot hyperspectral image classification based on adaptive subspaces and feature transformation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A survey: Deep learning for hyperspectral image classification with few labeled samples. Neurocomputing 2021, 448, 179–204. [Google Scholar]
- Molinier, M.; Kilpi, J. Avoiding overfitting when applying spectral-spatial deep learning methods on hyperspectral images with limited labels. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5049–5052. [Google Scholar]
- Nalepa, J.; Myller, M.; Kawulok, M. Validating hyperspectral image segmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1264–1268. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, J.; Qian, Y.; Wen, L.; Bai, X.; Gao, Y. On the sampling strategy for evaluation of spectral-spatial methods in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 862–880. [Google Scholar] [CrossRef]
- Zhou, J.; Liang, J.; Qian, Y.; Gao, Y.; Tong, L. On the sampling strategies for evaluation of joint spectral-spatial information based classifiers. In Proceedings of the 2015 7th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Tokyo, Japan, 2–5 June 2015; pp. 1–4. [Google Scholar]
- Qu, L.; Zhu, X.; Zheng, J.; Zou, L. Triple-attention-based parallel network for hyperspectral image classification. Remote Sens. 2021, 13, 324. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Deep learning for classification of hyperspectral data: A comparative review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Mei, S.; Ji, J.; Geng, Y.; Zhang, Z.; Li, X.; Du, Q. Unsupervised spatial–spectral feature learning by 3D convolutional autoencoder for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6808–6820. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Unsupervised spectral–spatial feature learning via deep residual Conv–Deconv network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 391–406. [Google Scholar] [CrossRef]
- Li, G.; Ma, S.; Li, K.; Zhou, M.; Lin, L. Band selection for heterogeneity classification of hyperspectral transmission images based on multi-criteria ranking. Infrared Phys. Technol. 2022, 125, 104317. [Google Scholar] [CrossRef]
- Moharram, M.A.; Sundaram, D.M. Dimensionality reduction strategies for land use land cover classification based on airborne hyperspectral imagery: A survey. Environ. Sci. Pollut. Res. 2023, 30, 5580–5602. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Wang, J.; Zhang, E.; Yu, K.; Zhang, Y.; Peng, J. RMCNet: Random Multiscale Convolutional Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1826–1830. [Google Scholar] [CrossRef]
- Zhang, T.; Shi, C.; Liao, D.; Wang, L. Deep spectral spatial inverted residual network for hyperspectral image classification. Remote Sens. 2021, 13, 4472. [Google Scholar] [CrossRef]
- Thoreau, R.; Achard, V.; Risser, L.; Berthelot, B.; Briottet, X. Active learning for hyperspectral image classification: A comparative review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 256–278. [Google Scholar] [CrossRef]
- Friedl, M.; Woodcock, C.; Gopal, S.; Muchoney, D.; Strahler, A.; Barker-Schaaf, C. A note on procedures used for accuracy assessment in land cover maps derived from AVHRR data. Int. J. Remote Sens. 2000, 21, 1073–1077. [Google Scholar] [CrossRef]
- Belward, A.; Lambin, E. Limitations to the identification of spatial structures from AVHRR data. Int. J. Remote Sens. 1990, 11, 921–927. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Stehman, S.V.; Zhang, L. Impact of training and validation sample selection on classification accuracy and accuracy assessment when using reference polygons in object-based classification. Int. J. Remote Sens. 2013, 34, 6914–6930. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. Deep learning classifiers for hyperspectral imaging: A review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Zou, L.; Zhu, X.; Wu, C.; Liu, Y.; Qu, L. Spectral–Spatial exploration for hyperspectral image classification via the fusion of fully convolutional networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 659–674. [Google Scholar] [CrossRef]
- Xue, Z.; Zhou, Y.; Du, P. S3Net: Spectral–spatial Siamese network for few-shot hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent advances on spectral–spatial hyperspectral image classification: An overview and new guidelines. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1579–1597. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, B.; Yu, X.; Yu, A.; Gao, K.; Ding, L. Perceiving Spectral Variation: Unsupervised Spectrum Motion Feature Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Cao, X.; Liu, Z.; Li, X.; Xiao, Q.; Feng, J.; Jiao, L. Nonoverlapped Sampling for Hyperspectral Imagery: Performance Evaluation and a Cotraining-Based Classification Strategy. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Du, Q. Diverse region-based CNN for hyperspectral image classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Zhang, M.; Li, H.; Du, Q. Data augmentation for hyperspectral image classification with deep CNN. IEEE Geosci. Remote Sens. Lett. 2018, 16, 593–597. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, J.; Cao, X.; Chen, Z.; Zhang, Y.; Li, C. Dynamic data augmentation method for hyperspectral image classification based on Siamese structure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8063–8076. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Zhang, N.; Xu, D.; Luo, H.; Chen, B.; Ben, G. Spectral–spatial fractal residual convolutional neural network with data balance augmentation for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10473–10487. [Google Scholar] [CrossRef]
- Shang, X.; Han, S.; Song, M. Iterative spatial-spectral training sample augmentation for effective hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Neagoe, V.E.; Diaconescu, P. CNN hyperspectral image classification using training sample augmentation with generative adversarial networks. In Proceedings of the 2020 13th International Conference on Communications (COMM), Bucharest, Romania, 18–20 June 2020; pp. 515–519. [Google Scholar]
- Dam, T.; Anavatti, S.G.; Abbass, H.A. Mixture of spectral generative adversarial networks for imbalanced hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Liang, H.; Bao, W.; Shen, X.; Zhang, X. Spectral–spatial attention feature extraction for hyperspectral image classification based on generative adversarial network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10017–10032. [Google Scholar] [CrossRef]
- Wang, G.; Ren, P. Delving into classifying hyperspectral images via graphical adversarial learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2019–2031. [Google Scholar] [CrossRef]
- Hänsch, R.; Ley, A.; Hellwich, O. Correct and still wrong: The relationship between sampling strategies and the estimation of the generalization error. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Worth, TX, USA, 23–28 July 2017; pp. 3672–3675. [Google Scholar]
- Lange, J.; Cavallaro, G.; Götz, M.; Erlingsson, E.; Riedel, M. The influence of sampling methods on pixel-wise hyperspectral image classification with 3D convolutional neural networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spai, 22–27 July 2018; pp. 2087–2090. [Google Scholar]
- Li, J.; Wang, H.; Zhang, A.; Liu, Y. Semantic Segmentation of Hyperspectral Remote Sensing Images Based on PSE-UNet Model. Sensors 2022, 22, 9678. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Hu, X.; Li, T.; Zhou, T.; Liu, Y.; Peng, Y. Contrastive learning based on transformer for hyperspectral image classification. Appl. Sci. 2021, 11, 8670. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Cao, Z.; Zhao, L. ROBYOL: Random-Occlusion-Based BYOL for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, L.; Du, Q. Class-wise distribution adaptation for unsupervised classification of hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 508–521. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Yu, A. Unsupervised meta learning with multiview constraints for hyperspectral image small sample set classification. IEEE Trans. Image Process. 2022, 31, 3449–3462. [Google Scholar] [CrossRef]
- Fang, L.; Zhao, W.; He, N.; Zhu, J. Multiscale CNNs ensemble based self-learning for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1593–1597. [Google Scholar] [CrossRef]
- Zhao, J.; Ba, Z.; Cao, X.; Feng, J.; Jiao, L. Deep Mutual-Teaching for Hyperspectral Imagery Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5966–5978. [Google Scholar] [CrossRef]
- Sha, A.; Wang, B.; Wu, X.; Zhang, L. Semisupervised classification for hyperspectral images using graph attention networks. IEEE Geosci. Remote Sens. Lett. 2020, 18, 157–161. [Google Scholar] [CrossRef]
- He, Z.; Xia, K.; Li, T.; Zu, B.; Yin, Z.; Zhang, J. A constrained graph-based semi-supervised algorithm combined with particle cooperation and competition for hyperspectral image classification. Remote Sens. 2021, 13, 193. [Google Scholar] [CrossRef]
- Xi, B.; Li, J.; Li, Y.; Du, Q. Semi-supervised graph prototypical networks for hyperspectral image classification. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2851–2854. [Google Scholar]
- Cai, Y.; Zhang, Z.; Cai, Z.; Liu, X.; Jiang, X. Hypergraph-structured autoencoder for unsupervised and semisupervised classification of hyperspectral image. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Tang, H.; Huang, Z.; Li, Y.; Zhang, L.; Xie, W. A Multiscale Spatial–Spectral Prototypical Network for Hyperspectral Image Few-Shot Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Sun, J.; Shen, X.; Sun, Q. Hyperspectral Image Few-Shot Classification Network Based on the Earth Mover’s Distance. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Li, Z.; Liu, M.; Chen, Y.; Xu, Y.; Li, W.; Du, Q. Deep Cross-Domain Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Qin, J.; Zhang, P.; Tan, X. Deep relation network for hyperspectral image few-shot classification. Remote Sens. 2020, 12, 923. [Google Scholar] [CrossRef]
- 2013 IEEE GRSS Image Analysis and Data Fusion Contest. Available online: http://www.grss-ieee.org/community/technical-committees/data-fusion/ (accessed on 13 July 2022).
- Debes, C.; Merentitis, A.; Heremans, R.; Hahn, J.; Frangiadakis, N.; van Kasteren, T.; Liao, T.; Bellens, R.; Pižurica, A.; Gautama, S.; et al. Hyperspectral and LiDAR Data Fusion: Outcome of the 2013 GRSS Data Fusion Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2405–2418. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Zhu, M.; Jiao, L.; Liu, F.; Yang, S.; Wang, J. Residual spectral–Spatial attention network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 449–462. [Google Scholar] [CrossRef]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.; Zhang, X.; Huang, X. Hyperspectral image classification with deep learning models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- He, W.; Huang, W.; Liao, S.; Xu, Z.; Yan, J. CSiT: A Multiscale Vision Transformer for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 60, 9266–9277. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Y.; Zhang, X.; Xu, D.; Wang, X.; Ben, G.; Zhao, Z.; Li, Z. A multi-degradation aided method for unsupervised remote sensing image super resolution with convolution neural networks. IEEE Trans. Geosci. Remote Sens. 2020, 60, 1–14. [Google Scholar] [CrossRef]







| Source | Problem | Mitigation Methods |
|---|---|---|
| Excessively similar samples | Overly optimistic classification performance | Spatially disjoint sampling strategies |
| Overlap between samples | Reduced generalization ability | Fewer training samples |
| Training samples contain test information | Practical applications are limited | Extraction of general features |
| Indian Pines | Salinas Valley | Houston |
|---|---|---|
 |  |  |
 |  |  |
| University of Pavia | ||
 |  | |
| Experiments | Models | Datasets | The Number of Samples | |
|---|---|---|---|---|
| Convolutions in different dimensions | LR-1D-CNN RSSAN SS-3D-CNN | D-1D-CNN R-2D-CNN D-3D-CNN | UP SA HS | 0.3%, 0.5%, 0.75%, 1%, 3% 5%, 7%, 10%, 15%, 20% |
| Data augmentation with disjoint sampling | LR-1D-CNN SS-3D-CNN | R-2D-CNN | UP HS | 3, 5, 7, 9, 11, 13 (per class) |
| Cross-domain learning with disjoint sampling | DCFSL SMF-UL | RN-FSC UM2L | IP UP | 3, 5, 7, 9, 11, 13 (per class) |
| Models | Learning Rate | Epoch | Patch Size | Batch Size | Optimizer |
|---|---|---|---|---|---|
| LR-1D-CNN | 0.01 | 300 | 1 | 100 | SGD |
| D-1D-CNN | 0.01 | 100 | 1 | 100 | SGD |
| RSSAN | 0.001 | 100 | 9 | 128 | SGD |
| R-2D-CNN | 0.001 | 100 | 9 | 128 | SGD |
| SS-3D-CNN | 0.001 | 100 | 5 | 100 | SGD |
| D-3D-CNN | 0.001 | 100 | 5 | 100 | SGD |
| SMF-UL | 0.0001 | 1000 | - | 4 | Adam |
| Models | Learning rate | Episode | Patch size | Way | Optimizer |
| DCFSL | 0.001 | 20,000 | 9 | 9 | Adam |
| RN-FSC | 0.001 | 10,000 | 9 | 9 | Adam |
| UM2L | 0.001 | 40,000 | 9 | 9 | Adam |
| LR-1D-CNN | D-1D-CNN | RSSAN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 0.30% | 72.018 | 54.831 | 17.187 | 53.672 | 53.608 | 0.064 | 66.950 | 47.302 | 19.648 |
| 0.50% | 72.610 | 62.114 | 10.496 | 64.269 | 54.242 | 10.027 | 71.589 | 50.286 | 21.303 |
| 0.75% | 73.324 | 61.825 | 11.499 | 66.435 | 56.101 | 10.334 | 72.011 | 48.159 | 23.852 |
| 1% | 74.352 | 58.380 | 15.972 | 67.381 | 58.088 | 9.293 | 75.802 | 48.434 | 27.368 |
| 3% | 76.298 | 54.142 | 22.156 | 71.557 | 61.360 | 10.197 | 82.451 | 42.944 | 39.507 |
| 5% | 77.264 | 51.633 | 25.631 | 72.993 | 61.330 | 11.663 | 83.544 | 45.613 | 37.931 |
| 7% | 82.012 | 55.878 | 26.134 | 74.409 | 67.668 | 6.741 | 89.169 | 47.909 | 41.260 |
| 10% | 82.886 | 55.138 | 27.748 | 75.955 | 63.458 | 12.497 | 89.946 | 50.287 | 39.659 |
| 15% | 87.850 | 55.837 | 32.013 | 72.770 | 65.050 | 7.720 | 91.976 | 48.388 | 43.588 |
| 20% | 87.110 | 56.090 | 31.020 | 75.824 | 58.627 | 17.197 | 93.691 | 51.139 | 42.552 |
| R-2D-CNN | D-3D-CNN | SS-3D-CNN | |||||||
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 0.30% | 71.774 | 53.473 | 18.301 | 58.490 | 53.810 | 4.680 | 74.434 | 55.303 | 19.131 |
| 0.50% | 75.693 | 50.800 | 24.893 | 66.759 | 53.901 | 12.858 | 80.119 | 56.382 | 23.737 |
| 0.75% | 76.997 | 51.031 | 25.966 | 70.197 | 62.126 | 8.071 | 84.368 | 61.407 | 22.961 |
| 1% | 77.710 | 53.535 | 24.175 | 73.937 | 63.759 | 10.178 | 85.460 | 65.725 | 19.735 |
| 3% | 81.160 | 49.416 | 31.744 | 77.996 | 56.386 | 21.610 | 91.599 | 50.610 | 40.989 |
| 5% | 84.227 | 56.621 | 27.606 | 86.267 | 54.129 | 32.138 | 94.692 | 51.865 | 42.827 |
| 7% | 87.673 | 60.574 | 27.099 | 89.138 | 57.670 | 31.468 | 95.297 | 55.338 | 39.959 |
| 10% | 92.244 | 58.857 | 33.387 | 88.253 | 58.314 | 29.939 | 96.016 | 54.868 | 41.148 |
| 15% | 93.097 | 57.964 | 35.133 | 89.989 | 58.661 | 31.328 | 96.267 | 57.514 | 38.753 |
| 20% | 93.715 | 55.133 | 38.582 | 95.417 | 55.148 | 40.269 | 96.690 | 56.781 | 39.909 |
| LR-1D-CNN | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Without Data Augmentation | Radiation Noise | Mixture Noise | |||||||
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 3 | 48.180 | 46.148 | 2.032 | 42.626 | 43.430 | −0.804 | 45.559 | 47.548 | −1.989 |
| 5 | 52.528 | 50.864 | 1.664 | 46.101 | 50.680 | −4.579 | 46.148 | 47.469 | −1.321 |
| 7 | 52.645 | 50.258 | 2.387 | 50.246 | 47.984 | 2.262 | 46.148 | 47.127 | −0.979 |
| 9 | 56.697 | 53.209 | 3.488 | 52.173 | 49.348 | 2.825 | 47.270 | 45.528 | 1.742 |
| 11 | 56.560 | 51.751 | 4.809 | 49.888 | 50.230 | −0.342 | 46.654 | 47.064 | −0.410 |
| 13 | 56.697 | 50.546 | 6.151 | 52.810 | 48.561 | 4.249 | 43.942 | 43.094 | 0.848 |
| R-2D-CNN | |||||||||
| Without data augmentation | Flip | Radiation noise | |||||||
| Numb. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 3 | 48.236 | 43.935 | 4.301 | 48.671 | 36.884 | 11.787 | 59.261 | 49.820 | 9.441 |
| 5 | 56.292 | 45.705 | 10.587 | 60.382 | 42.076 | 18.306 | 54.005 | 44.908 | 9.097 |
| 7 | 58.139 | 40.869 | 17.270 | 60.972 | 38.757 | 22.215 | 57.610 | 38.373 | 19.237 |
| 9 | 54.428 | 38.128 | 16.300 | 55.644 | 35.417 | 20.227 | 54.994 | 36.178 | 18.816 |
| 11 | 58.423 | 44.233 | 14.190 | 59.100 | 34.090 | 25.010 | 56.507 | 40.724 | 15.783 |
| 13 | 60.195 | 40.527 | 19.668 | 61.083 | 37.829 | 23.254 | 62.309 | 37.676 | 24.633 |
| SS-3D-CNN | |||||||||
| Without data augmentation | Flip | Radiation noise | |||||||
| Num. | Random | Disjointed | Diff | Random | Disjointed | Diff | Random | Disjointed | Diff |
| 3 | 44.512 | 34.739 | 9.773 | 48.219 | 35.093 | 13.126 | 50.860 | 51.910 | −1.050 |
| 5 | 62.390 | 60.511 | 1.879 | 63.667 | 56.491 | 7.176 | 59.890 | 59.830 | 0.050 |
| 7 | 66.714 | 60.239 | 6.475 | 66.778 | 56.587 | 10.191 | 61.020 | 58.010 | 3.010 |
| 9 | 66.715 | 61.533 | 5.182 | 67.637 | 59.172 | 8.465 | 67.400 | 61.140 | 6.260 |
| 11 | 68.285 | 63.176 | 5.109 | 71.109 | 57.858 | 13.251 | 64.160 | 64.390 | −0.230 |
| 13 | 67.475 | 64.060 | 3.415 | 67.579 | 54.887 | 12.692 | 71.660 | 64.600 | 7.060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, H.; Wang, Y.; Li, Z.; Zhang, N.; Zhang, Y.; Gao, Y. Information Leakage in Deep Learning-Based Hyperspectral Image Classification: A Survey. Remote Sens. 2023, 15, 3793. https://doi.org/10.3390/rs15153793
Feng H, Wang Y, Li Z, Zhang N, Zhang Y, Gao Y. Information Leakage in Deep Learning-Based Hyperspectral Image Classification: A Survey. Remote Sensing. 2023; 15(15):3793. https://doi.org/10.3390/rs15153793
Chicago/Turabian StyleFeng, Hao, Yongcheng Wang, Zheng Li, Ning Zhang, Yuxi Zhang, and Yunxiao Gao. 2023. "Information Leakage in Deep Learning-Based Hyperspectral Image Classification: A Survey" Remote Sensing 15, no. 15: 3793. https://doi.org/10.3390/rs15153793
APA StyleFeng, H., Wang, Y., Li, Z., Zhang, N., Zhang, Y., & Gao, Y. (2023). Information Leakage in Deep Learning-Based Hyperspectral Image Classification: A Survey. Remote Sensing, 15(15), 3793. https://doi.org/10.3390/rs15153793







